Applied Mathematics
Vol. 3 No. 7 (2012) , Article ID: 19871 , 5 pages DOI:10.4236/am.2012.37106
Some of Semi Analytical Methods for Blasius Problem
Department of Civil Engineering, Faculty of Engineering, Dokuz Eylul University, Izmir, Turkey
Email: seval.catal@deu.edu.tr
Received July 20, 2011; revised June 1, 2012; accepted June 8, 2012
Keywords: Blasius Problem; Non-Linear Differential Equation; Adomian Decomposition Method; Differential Transform Method; Taylor Series Method
ABSTRACT
In this paper, the Adomian methods, differential transform methods, and Taylor series methods are applied to non-linear differential equations which is called Blasius problem in fluid mechanics. The solutions of the Blasius problem for two cases are obtained by using these methods and their results are shown in table.
1. Introduction
On the fluid mechanics of non-parallel flows are called Blasius flows which is an important problem is interested in recently by authors [1-10]. In addition, this non-linear third order ordinary differential equation on a half-infinite interval is solved by using perturbation method [11], transformation of independent variable and finite difference method [12], homotopy analysis method [13-16], Adomian’s method [16-18], differential transform method [19,20].
In generally, it is considered the two-dimensional flow over a semi-infinite flat plain, is governed by
 (1.1)
(1.1)
with the boundary conditions
 (1.2)
(1.2)
where the prime denotes the derivatives with respect to a non-dimensional variable h, 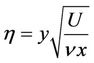 and
and 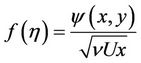 is a non-dimensional function related to the stream function
is a non-dimensional function related to the stream function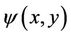 , where U is the velocity at infinity; n is the kinematic viscosity coefficient; x and y are the two independent coordinates.
, where U is the velocity at infinity; n is the kinematic viscosity coefficient; x and y are the two independent coordinates.
In this work, when 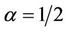 and
and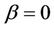 , in Equation (1.1), we obtain the following equation which is called Blasius (1908) equation [1]:
, in Equation (1.1), we obtain the following equation which is called Blasius (1908) equation [1]:
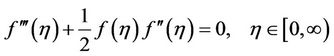 (1.3)
(1.3)
with the boundary conditions as
 (1.4)
(1.4)
The physical character of boundary layer apparently needs close and far away solution to match as was done by Blasius. So, to obtain the solution of this problem, we consider the boundary conditions as:
For inner case 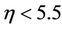
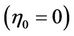 ; boundary conditions are;
; boundary conditions are;
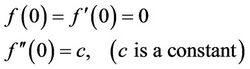 (1.5)
(1.5)
For inner-outer case 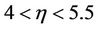
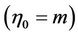 ; boundary conditions are;
; boundary conditions are;
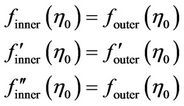 (1.6)
(1.6)
For outer case 
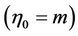 ; boundary conditions are;
; boundary conditions are;
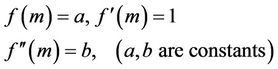 (1.7)
(1.7)
The paper is organized as follows: Blasius problem is solved by using ADM in &2; by using DTM in &3 and also, by using Taylor Series Method in &4, then it is given some concluding remarks in &5.
2. Solution of Blasius Problem by Adomian’s Decomposition Method (ADM)
For solving the following equation of the form
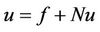 (2.1)
(2.1)
where  is non-linear mapping, X is Banach space, f is known function, by using Adomian’s decomposition method is taken that the solution u can be following convergent series form:
is non-linear mapping, X is Banach space, f is known function, by using Adomian’s decomposition method is taken that the solution u can be following convergent series form:
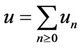 (2.2)
(2.2)
with un Î X for all n. An is a polynomial depending on u0, u1, ∙∙∙, un, An Î X for all n, are obtained from the equality;
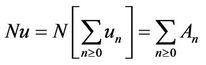 (2.3)
(2.3)
In putting the Equations (2.2) and (2.3) into the Equation (2.1), it gives
 (2.4)
(2.4)
where
 (2.5)
(2.5)
to determine the so-called Adomian’s polynomials An from un, where h is a scalar parameter
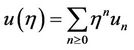 (2.6)
(2.6)
and
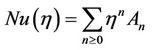 (2.7)
(2.7)
then
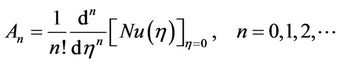 (2.8)
(2.8)
Thus,
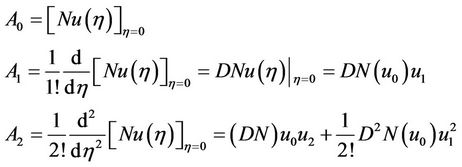 (2.9)
(2.9)
where  shows the kth Fréchet derivative of N at
shows the kth Fréchet derivative of N at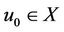 .
.
To demonstrate Adomian’s solution of the Blasius problem, the differential operator 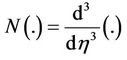 and the inverse operator
and the inverse operator 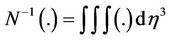 are treated. Operating with N−1 on Equation (1.3), then it gives:
are treated. Operating with N−1 on Equation (1.3), then it gives:
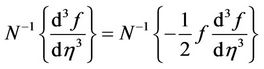 (2.10)
(2.10)
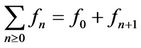
where
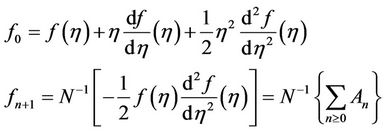 (2.11)
(2.11)
For inner case: f0 determined from the boundary conditions (1.5) and than the other components determined from Equation (2.11) as follows [16-18]:
 (2.12)
(2.12)
For outer case: Similarly, f0 determined from Equations (1.7) and than f1 determined from Equation (2.11), so on:
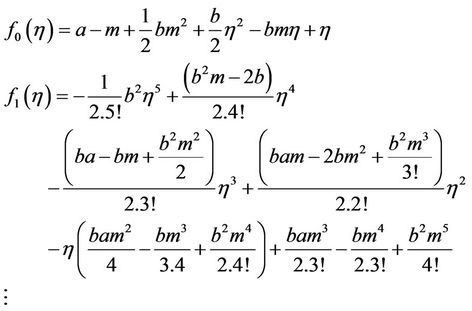 (2.13)
(2.13)
3. Solution of Blasius Problem by Differential Transform Method (DTM)
In this study, similarly [19], it is applied DTM for the Equation (1.3):
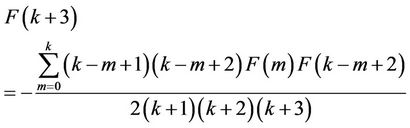 (3.1)
(3.1)
where 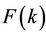 shows the differential transform of
shows the differential transform of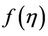 .
.
For inner case: (1.5) boundary conditions (BCs) are transformed
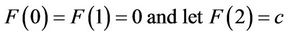 (3.2)
(3.2)
where c is an arbitrary constant. Then, we get the following equation:
 (3.3)
(3.3)
For outer case: (1.7) boundary conditions (BCs) are transformed
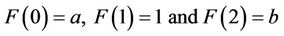 (3.4)
(3.4)
where a and b are any arbitrary constants. Then, we obtain the following equation:
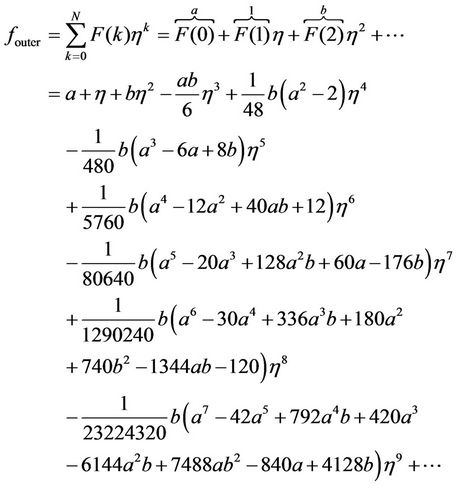 (3.5)
(3.5)
For inner-outer case: From (1.6) boundary conditions, 4 < h0 < 5 taking the interval of h0 is found a, b, and c constants, is obtained similar result as in [19].
4. Solution of Blasius Problem by Taylor Series (TS)
Taylor’s series method is used for solving Blasius problem. This method assumes that the solution 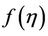 and derivative of
and derivative of 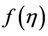 can be taken power series as
can be taken power series as
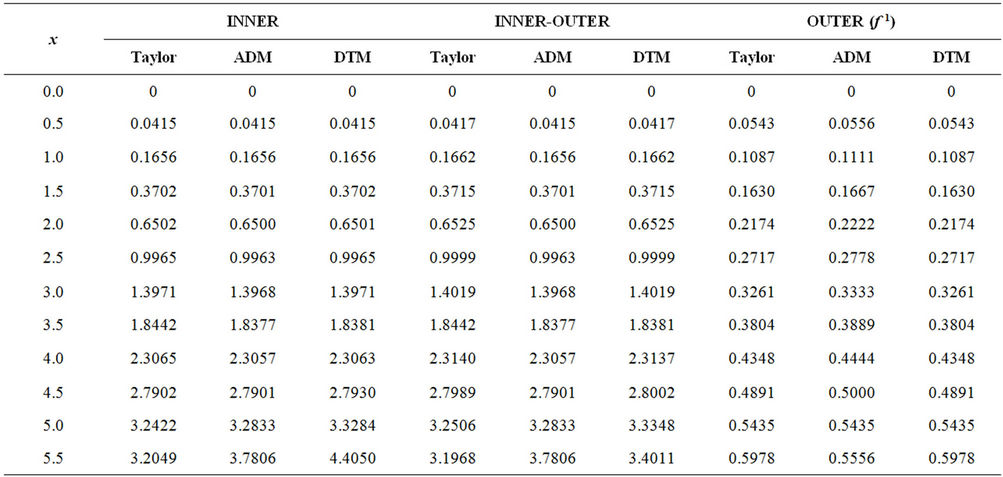
Table 1. Solutions of Blasius problem.
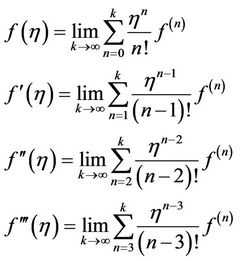 (4.1)
(4.1)
Then Equation (4.1) is substituting into Equation (1.3);
For inner case: With the boundary conditions (1.5), it gives
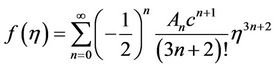 (4.2)
(4.2)
where
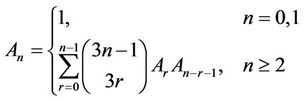 (4.3)
(4.3)
with the definition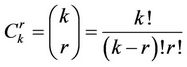 .
.
c = 0.332 [1]c = 0.332057 [21]c = 0.333338 (this paper).
For outer case: Under the boundary conditions (1.7), it gives
 (4.4)
(4.4)
5. Conclusion
In this study, some of the semi analytical methods were applied by author in the non-linear Blasius problem which names are Adomian decomposition method, differential transform method, and Taylor series method. It was obtained their results for two cases by using these methods. Their results were presented in the Table 1. The results are shown that all of these methods are powerful and efficient technique for finding semi analytical solutions for Blasius problem in the fluid mechanics.
REFERENCES
- H. Blasius, “Grenzschichtenin Flüssigkeiten mit Kleiner Reibung,” Zeitschrift für Angewandte Mathematik und Physik, Vol. 56, 1908, pp. 1-37.
- W. V. R. Malkus, “Borders of Disorder,” Studies in Applied Mathematics, Vol. 107, No. 4, 2001, pp. 325-336. doi:10.1111/1467-9590.1074189
- W. P. Kotorynski, “A Sturm-Liouvillle Problem Associated with the Falkner-Skan Equation,” SIAM Journal on Applied Mathematics, Vol. 17, No. 5, 1969, pp. 992-995. doi:10.1137/0117087
- A. Pantokratoras, “The Falkner-Skan Flow with Constant Wall Temperature and Variable Viscosity,” International Journal of Thermal Sciences, Vol. 45, No. 4, 2006, pp. 378-389. doi:10.1016/j.ijthermalsci.2005.06.004
- W. Van Oudheusden, “A Complete Crocco Integral for Two-Dimensional Laminar Boundary Layer Flow over an Adiabatic Wall for Prandtl Numbers near Unity,” Journal of Fluid Mechanics, Vol. 353, 1997, pp. 313-330. doi:10.1017/S0022112097007507
- Z. Belhachmi, B. Brighi and K. Taous, “On the Family of Differential Equations for Boundary Layer Approximations in Porous Media,” European Journal of Applied Mathematics, Vol. 12, No. 4, 2001, pp. 513-528. doi:10.1017/S0956792501004582
- V. L. Streeter and E. B. Wylie, “Fluid Mechanics,” McGraw-Hill International Editions, Civil and Mechanical Engineering Series, 1983.
- R. W. Fox, A. T. McDonald and P. J. Pritehard, “Introduction to Fluid Mechanics,” 6th Edition, John Wiley & Sons, New York, 2003.
- B. Gahan, J. J. H. Miller and G. I. Shishkin, “Accurate Numerical Method for Blasius’ Problem for Flow past a Flat Plate with Mass Transfer,” Proceedings of Fds 2000 Conference, 2000. http://www.maths.tcd.ie/report_series/tcdmath/tcdm0005.pdf
- E. Assareh, M. A. Behrang, M. Ghalambaz, A. R. Noghrehabadi and A. Ghanbarzadeh, “A New Approach to Solve Blasius Equation Using Parameter Identification of Nonlinear Functions Based on the Bees Algorithm (BA),” World Academy of Science, Engineering and Technology, Vol. 73, 2011, pp. 1119-1121.
- I. G. Shukhman, “On Stationary Solutions for Free QuasiParallel Mixing Layers with a Longitudinal Magnetic Field,” Journal of Fluid Mechanics, Vol. 452, 2002, pp. 337-359. doi:10.1017/S0022112001006760
- A. I. Zadorin, “Numerical Method for Blasius Equation on an Infinite Interval”. http://num.math.uni-goettingen.de/bail/documents/proceedings/zadorin.pdf
- S.-J. Liao, “A Uniformly Valid Analytic Solution of TwoDimensional Viscous Flow over a Semi-Infinite Flat Plate,” Journal of Fluid Mechanics, Vol. 385, 1999, pp. 101-128. doi:10.1017/S0022112099004292
- S. Abbasbandy, “A Numerical Solution of Blasius Equation by Adomian’s Decomposition Method and Comparison with Homotopy Perturbation Method,” Chaos, Solutions and Fractals, Vol. 31, No. 1, 2007, pp. 257-260. doi:10.1016/j.chaos.2005.10.071
- M. O. Miansari, M. E. Miansari, A. Barari and G. Domairry, “Analysis of Blaisus Equation for Flat-Plate Flow with Infinite Boundary Value,” International Journal for computational Methods in Engineering Science and Mechanics, Vol. 11, 2010, pp. 79-84.
- H. Bulut and O. Kelesoglu, “Comparing Numerical Methods for Response of Beams with Moving Mass,” Advances in Engineering Software, Vol. 41, No. 7-8, 2010, pp. 976-980. doi:10.1016/j.advengsoft.2010.05.006
- L. Wang, “A New Algorithm for Solving Classical Blasius Equation,” Applied Mathematics and Computation, Vol. 157, No. 1, 2004, pp. 1-9. doi:10.1016/j.amc.2003.06.011
- T. Wickramasinghe, “Studies in Numerical and Decomposition Solution Profiles of Blasius Equation,” Advanced Studies in Theoretical Physics, Vol. 4, No. 8, 2010, pp. 363-367.
- A. Arıkoğlu and İ. Özkol, “Inner-Outer Matching Solution of Blasius Equation by DTM,” Aircraft Engineering and Aerospace Technology: An International Journal, Vol. 77, No. 4, 2005, pp. 298-301. doi:10.1108/00022660510606367
- H. A. Peker, O. Karaoğlu and G. Oturanç, “The Differential Transformation Method and Pade Approximant for a Form of Blasius Equation,” Mathematical and Computational Applications, Vol. 16, No. 2, 2011, pp. 507-513.
- L. Howarth, “On the Solution of the Laminar Boundary Layer Equations,” Proceedings of the Royal Society A, Vol. 164, No. 919, 1938, pp. 547-579. doi:10.1098/rspa.1938.0037

