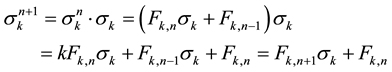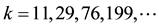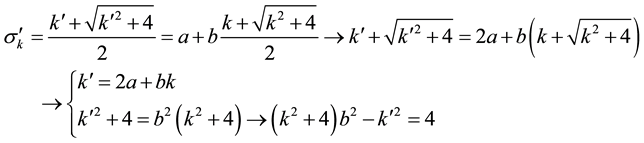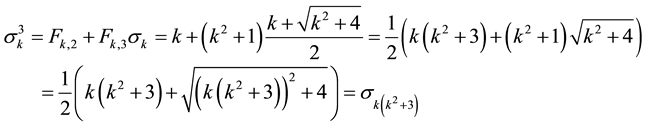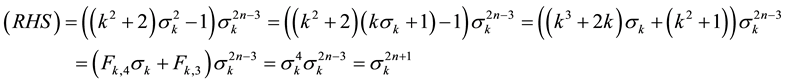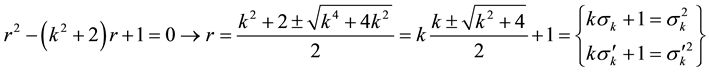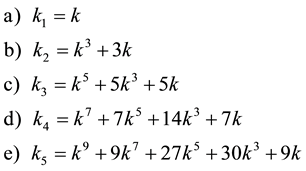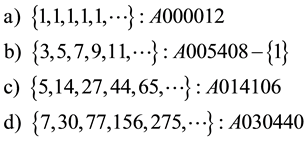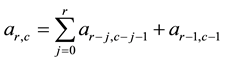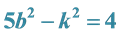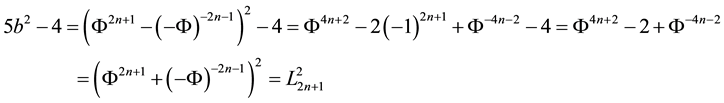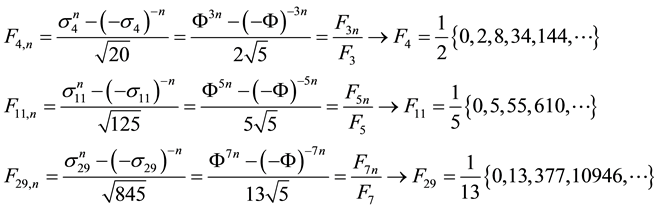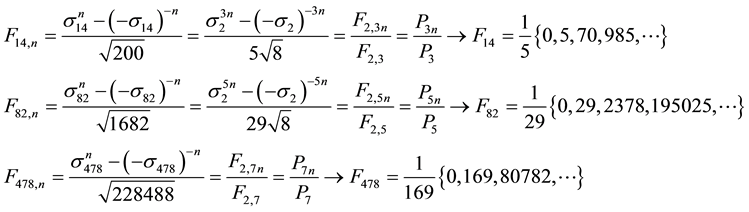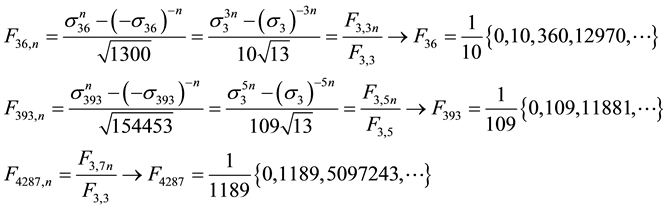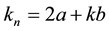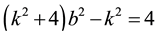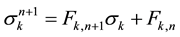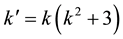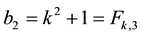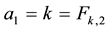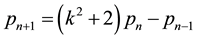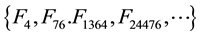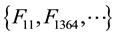Applied Mathematics
Vol.05 No.15(2014), Article ID:48593,9 pages
10.4236/am.2014.515216
Relationships between Some
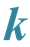 -Fibonacci Sequences
-Fibonacci Sequences
Sergio Falcon
Department of Mathematics, University of Las Palmas de Gran Canaria, Las Palmas de Gran Canaria, Spain
Email: sfalcon@dma.ulpgc.es
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 15 May 2014; revised 23 June 2014; accepted 13 July 2014

ABSTRACT
In this paper, we will see that some
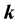 -Fibonacci sequences are related to the classical Fibonacci sequence of such way that we can express the terms of a
-Fibonacci sequences are related to the classical Fibonacci sequence of such way that we can express the terms of a
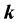 -Fibonacci sequence in function of some terms of the classical Fibonacci sequence. And the formulas will apply to any sequence of a certain set of
-Fibonacci sequence in function of some terms of the classical Fibonacci sequence. And the formulas will apply to any sequence of a certain set of
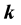 -Fibonacci sequences. Thus we find
-Fibonacci sequences. Thus we find
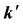 -Fibonacci sequences relating to other
-Fibonacci sequences relating to other
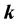 -Fibonacci sequences when
-Fibonacci sequences when
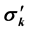 is linearly dependent of
is linearly dependent of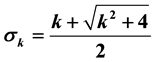 .
.
Keywords:
Fibonacci and Lucas Numbers,
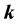 -Fibonacci Numbers, Pascal Triangle
-Fibonacci Numbers, Pascal Triangle

1. Introduction
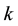 -Fibonacci sequence
-Fibonacci sequence
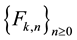 was found by studying the recursive application of two geometrical trans-
was found by studying the recursive application of two geometrical trans-
formations used in the well-known four-triangle longest-edge (4TLE) partition. This sequence generalizes the classical Fibonacci sequence [1] [2] .
1.1. Definition
For any positive real number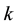 , the
, the
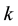 -Fibonacci sequence, say
-Fibonacci sequence, say
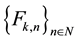 is defined recurrently by
is defined recurrently by
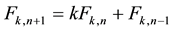 for
for
 with initial conditions
with initial conditions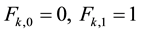
From this definition, the polynomial expression of the first
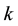
If
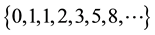
Table 1. Polynomial expression of the first k-Fibonacci numbers.
quence is the classical Pell sequence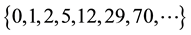
1.2. Metallic Ratios
The characteristic equation of the recurrence equation of the definition of the
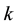
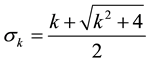
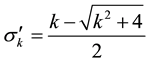
As particulars cases [3] :
1) If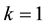
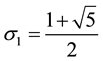
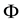
2) If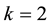
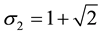
3) If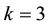
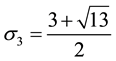
From now on, we will represent the classical Fibonacci numbers as
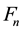
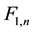
Binet identity takes the form [1]
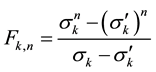
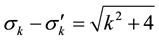
1.3. Theorem 1
Power
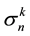
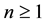
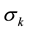
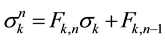
Proof. By induction. For
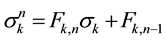
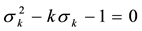
Obviously, the formulas found in [1] [2] can be applied to any
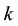
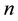
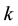
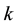
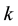
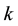
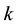
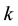
2.
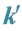
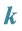
In this section, we try to find the relationships that can exist between the values of
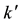
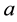
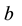
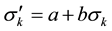
We can write this last equation as
because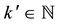
Main problem is to solve the quadratic Diophantine equation
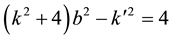
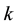
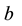
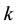
2.1. Theorem 2
The positive characteristic root
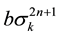
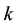
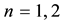
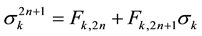
For
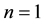
Then,
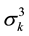
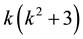
In the same way, we can prove that
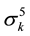
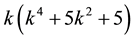
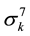
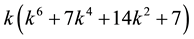
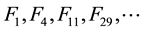
2.2. Theorem 3
For
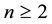
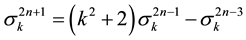
Proof. Taking into account both Table 1 and Formula (1), Right Hand Side (RHS) of Equation (2) is
It is worthy of note that Equation (2) is similar to the relationship between the elements of the
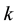
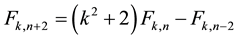
And
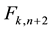
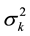
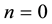
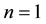
2.3. k-Fibonacci Sequences Related to an Initial f-Fibonacci Sequence
From two previous theorems, the
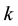
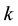
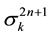
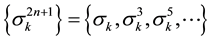
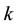
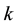
The values of the parameter of these sequences are
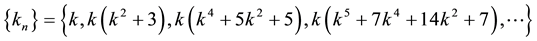

Next we present the first few values of the parameter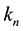
But these polynomials verify the relationship
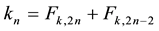
where
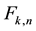
The coefficients of these polynomials generate the triangle in Table 2:
Last column is the sum by row of the coefficients, and it is a bisection of the classical Lucas sequence
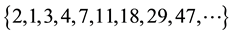
If
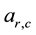
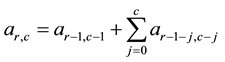
diagonal plus 27 of the row 5 is the 77 of the row 6.
All the first diagonal sequences are listed in [4] , from now on OEIS, but the unique antidiagonal sequences listed in OEIS are:
From this study, it is easy to find the values of “
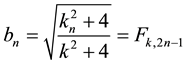
Sequence
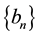
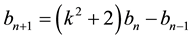
In this case, the triangle of coefficients is in Table 3 and the formto generate these numbers is the same as in table of
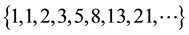
First diagonal sequences and the antidiagonal sequences are listed in OEIS.
Finally, for the values of
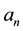
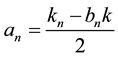
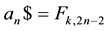
Table 2. Triangle of the coefficients of kn.
In this case, the triangle of the coefficients of the expressions of
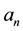
Last column is the other bisection of the classical Fibonacci sequence.
The diagonal sequence
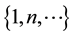
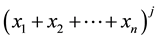
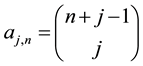
In this table, it is verified:
a)
b)
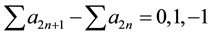
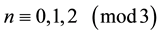
c) The diagonal sequences are listed in OEIS.
d) The elements of
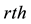
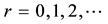
Then we will apply the results to the
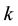
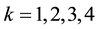
3.
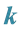
In this section we try to find the relations that could exist between the values of “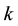
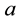
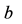
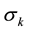
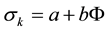
In this case, Equation (2) takes the form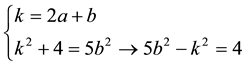
3.1. Integer Solutions of Equation
The integer solutions of Equation
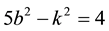
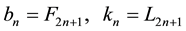
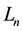
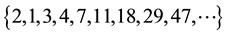
Proof. Applying Binnet Identity, and taking into account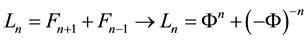
Table 3. Triangle of the coefficients of bn.
Table 4. Triangle of the coefficients of an.
Consequently, the values of the parameter “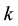
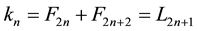
Integer solutions of this equation are expressed in Table 5, where
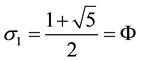
3.2. On the Sequences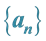
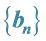
We will show some properties of the sequences of Table 5.
The sequence of values of “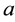
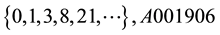
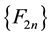
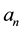
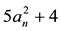
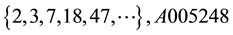
The sequence of values of “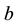
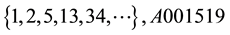
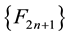
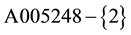
The sequence of values of “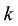
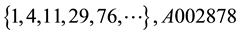
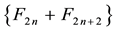
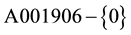
All these sequences verify the recurrence law given in Equation (2),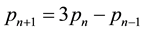
As a consequence of this situation, if we represent as
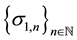
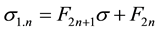
3.3. Relationships between the
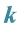
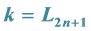
Applying Subsection 2.3 when
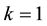
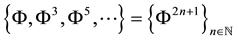
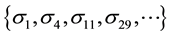
Consequently:
4.
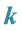
Repeating the previous process, we can solve the Diophantine equation
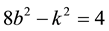
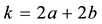
Table 5. Integer solutions of the Diophantine equation 5b2 − k2 = 4.
The values obtained are showed in Table 6:
4.1. On These Quences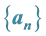
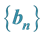
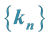
We will show some properties of the sequences of Table 4.
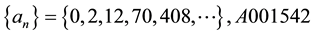
that
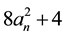
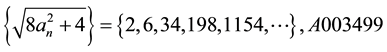
two consecutive terms of this sequence is the sequence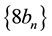
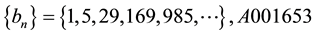
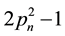
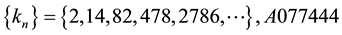
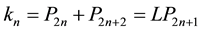
Much more interesting is the sequence obtained by dividing by 2: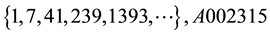
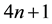
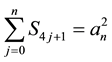
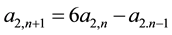
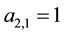
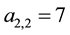
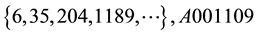
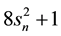
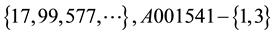
All these sequences verify the recurrence law (2),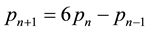
As in the preceding section, if we represent the sequence of values of “
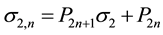
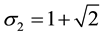
4.2. Relationships between the
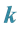
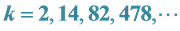
Taking into account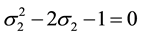
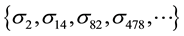
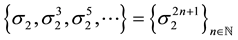
Consequently:
5.
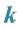
Repeating the previous process, we can solve the Diophantine equation
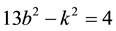
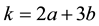
The values obtained are showed in Table 7.
Table 6. Integer solutions of the Diophantine equation 8b2 − k2 = 4.
5.1. On These Quences
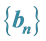
We will show some properties of the sequences of Table 7.
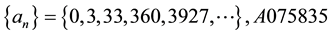
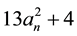
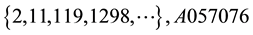
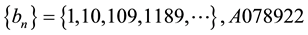
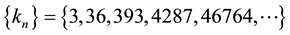
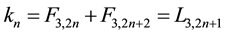
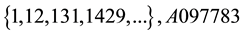
All these sequences verify the recurrence law (Equation (2)),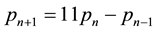
The sequence
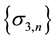
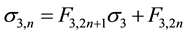
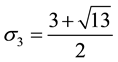
5.2. Relationships between the k−Fibonacci Sequences for
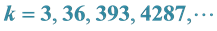
Taking into account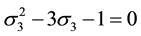
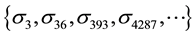
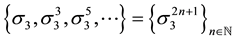
Consequently:
6. Conclusions
There are infinite
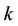
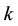
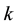
1) The relationship
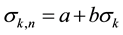
Relationship between “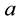
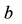
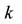
Diophantine equation:
2) Relationship between the positive characteristic root
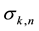
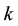
3) Second sequence related to the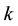
4) Two first values of “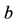
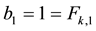
5) Two first values of “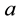
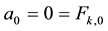
6) Recurrence law for the sequences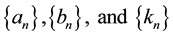
Table 7. Integer solutions of the Diophantine equation 13 b2 − k2 = 4.
It is worthy of remarking the fact the last sequence
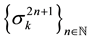
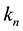
the initial
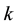
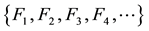
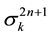
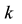
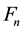
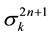
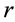
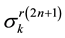
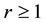
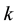
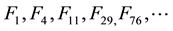
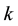
4-Fibonacci sequence:
11-Fibonacci sequence:
29-Fibonacci sequence: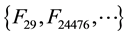
Cite this paper
SergioFalcon, (2014) Relationships between Some k -Fibonacci Sequences. Applied Mathematics,05,2226-2234. doi: 10.4236/am.2014.515216
References
- 1. Falcon, S. and Plaza, A. (2007) On the Fibonacci k-Numbers. Chaos, Solitons Fractals, 32, 1615-1624.
- 2. Falcon, S. and Plaza, A. (2007) Thek-Fibonacci Sequence and the Pascal 2-Triangle. Chaos, Solitons Fractals, 33, 38-49.
- 3. Spinadel, V.W. (1999) The family of Metallic Means. Vis Math, 1.
http://members.tripod.com/vismath/ - 4. Sloane, N.J.A. The Online Encyclopedia of Integer Sequences. http://oeis.org
- 5. Falcon, S. and Diaz-Barreiro, J.L. (2006) Some Properties of Sums Involving Pell Numbers. Missouri Journal of Mathematical of Sciences, 18, 33-40.