Received 12 September 2013; revised 12 October 2013; accepted 19 October 2013

ABSTRACT

A target is assumed to move randomly on one of two disjoint lines 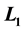and according to a stochastic process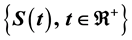. We have two searchers start looking for the lost target from some points on the two lines separately. Each of the searchers moves continuously along his line in both directions of his starting point. When the target is valuable as a person lost on one of disjoint roads, or is serious as a car filled with explosives which moves randomly in one of disjoint roads, in these cases the search effort must be unrestricted and then we can use more than one searcher. In this paper we show the existence of a search plan such that the expected value of the first meeting time between the target and one of the two searchers is minimum.

Keywords:

Stochastic Process; Expected Value; Linear Search; Optimal Search Plan

1. Introduction

The search for lost targets that are either stationary or randomly moving has recently applications, such as: searching for lost persons on roads, the search for a petroleum or gas underground, and so on (see, Abd-Elmo- neim [1] , Ohsumi [2] , El-Rayes and Abd-Elmoneim [3] , and Washburn [4] ).

When the target to be found is stationary or moves randomly on the real line, this problem is of interest because it may arise in many real world situations (see El-Rayes et al. [5] and Balkhi [6] ). Search problems with stationary target on line are well studied (see El-Rayes and Abd-Elmoneim [7] , El-Rayes et al. [8] , Balkhi [6] [9] , Rousseeuw [10] , Abd-Elmoneim and Abu-Gabl [11] , and Stone [12] ). In the case of randomly moving target on the line and the searcher starts search from the origin, a deal of work has been done for deriving conditions for optimal search path which minimizes the effort of finding the target (see El-Rayes et al. [5] , Fristedt and Heath [13] ). If the lost target is a valuable target as a person lost on one of disjoint roads, or is serious as a car filled with explosives which moves randomly in one of disjoint roads, then the effort of the search (the cost of search) must be unrestricted, in these cases using more than one searcher (see Abd El-Moneim et al. [14] ). The search problem for a randomly moving target on one of two disjoint lines will be considered, in previous studies (see Abd El-Moneim and Abu-Gabl [15] ), using a searcher for each line where each searcher starts looking for the lost target from the origin of his line, but Abd El-Moneim et al. [14] used searchers starting searching for the target from the origin that is the intersection point of these lines. Each of the searchers moves continuously along his line in both directions of the starting point, in both cases the target motion is a Brownian motion. In this article, a target is assumed to move randomly on one of two disjoint lines and 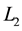according to a stochastic process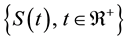, where is the set of real numbers. This stochastic process satisfies the following conditions:

(i) Let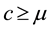, where 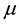is the drift of the process and 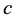is a constant. Then for any 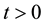and for some

, ,

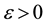(ii) Let 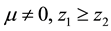and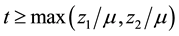, then 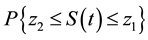is non-increasing with t,

(iii) Let T be a stopping time for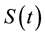, then

,

where E stands for the expectation value and is the variance and

(iv) Let

,

where is a sequence of independent identically distributed random variables (i. i. d. r. v.) and

,

then satisfies the renewal theorem.

Two searcher start looking for the target from some point f₀ for the first line L₁ and for the second line. We assume that the speeds of the searchers are n₁ and n₂. Assume that T is the set of real numbers and T⁺ is the non-negative part of T. Foe any, let be a random variable with, and assume that Z_o is the initial position of the target to be a random variable and independent of, t > 0. A search plan with speed n₁, n₂ is defined such that f : T⁺®T and: T⁺®T, respectively, such that

the first meeting time is a random variable valued in I⁺ which is defined

where Z_o = X₀ if the target moves on the first line and Z_o = Y₀ if the target moves on the second line. Let the search plan of two searchers be represented by where is the set of all search plans. The problem is to find search plan such that in this case we call is a finite search plan and if , where E terms to expectation value, then we call is optimal.

2. The Search Plans

Let z₁, z₂ be positive integers and n₁and n₂ are rational numbers such that:

1) and

2) z₁, z₂ > 1, such that

Now we shall define sequences for the searcher on the first line L₁, for the searcher on the second line L₂ and search plans with speed 1 as follows.

Let O be a finite set of numbers, such that

we have

for the first searcher, and

for the second searcher

for any t Î R⁺, if then

and if, , then,

if, then

and if, i ³ j + 1, then,and

if, then

and, , then

We use the following notations where k₁(t), , k₂(t) and are positive functions, ,

on the first line and, on the second line.

Lemma 2.1. if 0 < a, b < 1 then ab < a + b

Theorem 2.1. If is a search plan, and let g₁, g₂ are measurable induced by the initial position of the target on the first and second line respectively, then is finite if:

And

are finite

Proof: The continuity of S(t), and imply that if then X₀ + S(t) is greater than on the first line until the first meeting, also if then X₀ + S(t) is smaller than on the first line until the first meeting the same for the second line by replacing X₀ by Y₀ and by. Hence for any i ³ 0.

we get

Also

and

Hence

from Lemma 2.1 then we get:

If, then

Then

,

where

and

the other cases can be proved by similar way

Lemma 2.2. Let a_n ³ 0 for n ³ 0, and a_n+1 £ a_n, {d_n} n ³ 0 be a strictly increasing sequence of integers with d₀ = 0 then for any k £ 0,

(see EL-Rayes et al. [5] )

Theorem 2.2. The chosen search plan satisfies

where are linear functions.

Proof. We shall prove the theorem for and, since the other cases can be proved by a similar way.

,

(i) if x ³ f₀

and

(ii) if 0 £ x £ f₀

and

(iii) if x £ 0

and y £ 0

we have and in (ii)

but,

from [1]

we define the following

1)

2), where is sequence of (i. i. d. r. v.)

where is sequence of (i. i. d. r. v.)

3)

4) n₁ is an integer such that; n₂ is an integer such that

5)

6)

If and then a_(n), are non-increasing, see [15] , and we can apply Lemma 2.2 in suitable steps.

and

Since, satisfies the conditions of renwal theorem (see [15] ) hence, is bounded for all j by a constant, so

Theorem 2.3. If there exist a finite search plan then E|Z₀| is finite.

Proof. If, then

then, that is with probability 1, so

Hence, but then and

Remark A direct consequence of theorems 1, 2 and 3 in Section 2 is the existence of a finite search plan if and only if, and then the set of search plans, which defined in Section 2, satisfies the conditions of Theorem 1 if the expectation value of initial position of the lost target is finite.

3. Existence of an Optimal Path

Definition. Let be a sequence of search plans, we say that converges to as n tends to ¥ if for any , converges to on every compact subset.

Theorem 3.1. Let for any, be a process with continuous sample paths. The mapping

is lower semi-continuous on.

Proof. Let be a sample point on corresponding to the sample path of and be a sample point on corresponding to the sample path of. Let be a sequence of search paths which converges to and converges to. Given, we define for any

,

,

and

Let, and since converges uniformly on to, then there exists an integer such that for all and for any

and,

then.

Hence for all and so

by the same way we can get

since the sample paths are continuous then

, , and

we get and, we obtain

then

,

where

hence. By Fatou lemma, we get

.

Since is sequentially compact (see [2] ), then by the same way is sequentially compact. It is known that a lower semi-continuous function over a sequentially compact space attains its minimum.

4. Conclusion

We consider, here, the search for a lost target on one of two disjoint lines, where the target moves randomly according to continuous stochastic process which satisfies some conditions. Theorems conclude that there exists a finite search plan if and only if the expectation value of the initial position of the target is finite. Existence of optimal search plan is proved.

Acknowledgements

The author would like to thank the reviewers and Editorial Board of AM Journal for their helpful suggestions which would improve the article.

References