Advances in Bioscience and Biotechnology
Vol.4 No.4(2013), Article ID:29963,5 pages DOI:10.4236/abb.2013.44071
Quantum process in living cells
![]()
Department of Physics, St. John’s University, New York, USA
Email: finkelr@stjohns.edu
Copyright © 2013 Robert W. Finkel. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received 18 January 2013; revised 2 March 2013; accepted 4 April 2013
Keywords: Cooperative Process; Kleiber Law; Smallest Cell Size; Ultrafast Energy Transfer; Water Dimer
ABSTRACT
Coherent quantum effects have been confirmed for several biological processes. These processes exist in the environment of a warm wet cell where decoherence can be a serious concern. Here we propose a mechanism whereby quantum coherence may extend through the water matrix of a cell. The model is based on coherent waves of established ultrafast energy transfers in water. Computations based on the model are found to agree with several experimental results and numerical and descriptive predictions are presented. We compute wave speed, ~156 km/s, and wavelength, ~9.3 nm, and determine that these waves retain local coherence. Close agreements are found for the dipole moment of water dimers, results of microwave radiation on yeast, and the Kleiber law of metabolic rates. The theory requires that a spherical cell must have a minimum diameter of ~20 nm to accommodate a standing energy wave. The quantum properties of the model suggest that cellular chemistry favors reactions that support perpetuation of the energy waves.
1. INTRODUCTION
Quantum physics determines the cooperatively of various many-body systems like solids and superconductors suggesting that quantum physics may also play a cooperative role in biology. The appeal of this idea is that quantum coherence emulates an attribute of living cells whereby many degrees of freedom are reduced to a collective mode enabling long range coordination and order—a property clearly analogous to the coordination of individual processes in living cells. Fröhlich initiated this concept and advocated that all living cells maintain coherent vibrations generated by metabolism [1] . The present note extends this view and proposes that a cooperative process exists in water in the cell. As water is the majority substance of the cell, quantum cooperative behavior in water could have a pervasive influence.
Schrödinger posited that quantum effects might distinguish living from non-living matter revealing “new” physical behavior [2]. Until recently, this seemed unlikely because quantum effects readily decohere in warm wet environments like the cell. Investigators have since confirmed that quantum effects exist in photosynthesis [3] and other biological phenomena [4]. The model cooperative process proposed here originates from waves of energy propagating through water in cells. For our present purposes it is not necessary to identify a metabolic origin for this energy. Water has long been known to transfer energy at an ultrafast rate following Woutersen and Bakker [5]. The agents of these energy transmissions are water dimer oscillations that spread by successive excitations of dipole-dipole interactions (a Förster transfer mechanism) [5,6]. According to the matter-wave duality of quantum physics, the resulting energy waves have corresponding particle quanta here termed chaions. We address the decoherence problem and find the waves are sufficiently short and fast to evade decoherence. The model is then shown to reproduce several empirical results and make testable predictions of wave speed and wavelength.
Background
Quanta of the ultrafast energy transfers do not convey mass so chaion particles are analysed using a statistical treatment similar to that for a massless photon gas. This treatment is detailed in [7] and here we summarize results needed for our applications.
Integrating the occupation number over phase space gives the average number of energy-carrying particles, ánñ,
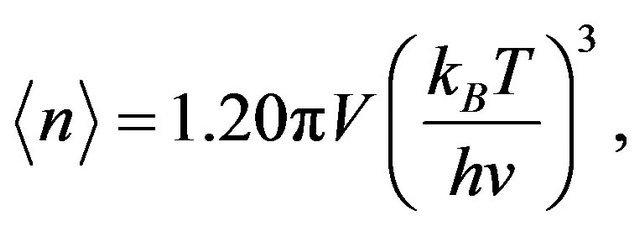 (1)
(1)
where v is the particle velocity, h is Planck’s constant, kB is Boltzmann’s constant, T is temperature, and V is the volume of water. Similarly, integrating chaion energies occupied over all of phase space gives the average energy vested in the quanta with the result that the average energy per chaion particle is 2.701 kBT. Hereafter we abbreviate the average energy per particle as 2.7 kBT while using the more precise value in computations. Frequency f is given as usual by f = 2.7 kBT/h and the energy density ρ is uniform throughout the volume.
2. WAVE PROPERTIES
We now determine chaion velocity and wavelength directly from the model. Although relativity requires that massless particles in vacuo must propagate at the speed of light, c, water transmits energy at a nonrelativistic speed, v. This is easily reconciled if excited water dimers transmit energy successively with probability p such that the effective speed is a fraction of light speed p = v/c (we neglect the transit time between dimers).
Consider an assembly of N water molecules containing one excited dimer able to emit its energy of 2.7 kBT with probability v/c. Let Vw represent the volume of a spherical water molecule with effective diameter 0.32 nm [8] . Eq.1 becomes
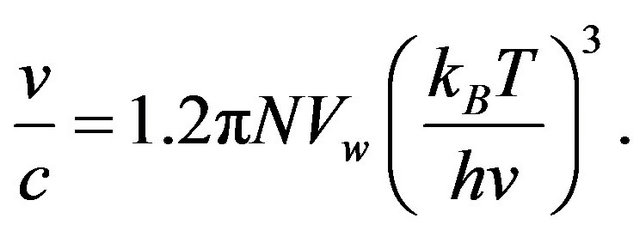
Alternatively, the probability of a single emission is also expressed by the canonical distribution for the dimer energy attributed to one molecule.
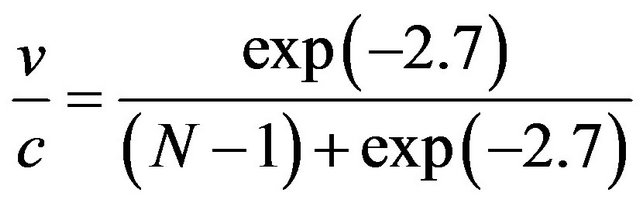 .
.
The latter two equations are solved for N and v at standard temperature giving N = 129 and v = 156 km/s. (This speed coincides with that of an electron excited with chaion energy 2.7 kBT.) The wave relation λf = v now determines the characteristic wavelength is λ = 9.3 nm.
Evade Decoherence
Although a warm wet cell seems an unlikely place for coherent quantum processes, the waves considered here are sufficiently fast and short enough to avoid decoherence. The characteristic times considered in the chaion theory are about 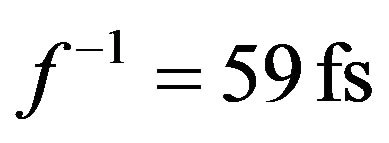 while biochemical reaction times are larger by orders of magnitude. The measured equilibration time for pure water is 0.55 ps [9] exceeding chaion transit time almost tenfold. Energy waves therefore “see” their environment as being relatively timeindependent.
while biochemical reaction times are larger by orders of magnitude. The measured equilibration time for pure water is 0.55 ps [9] exceeding chaion transit time almost tenfold. Energy waves therefore “see” their environment as being relatively timeindependent.
The chaion model presupposes that quantum coherence extends over wavelength λ in the warm wet cell. Coherent quantum behavior requires that the time for decoherence t exceeds the characteristic chaion transfer time. An approximation for massless particles with relatively long wavelengths and high temperature is given by Schlosshauer [10] ,
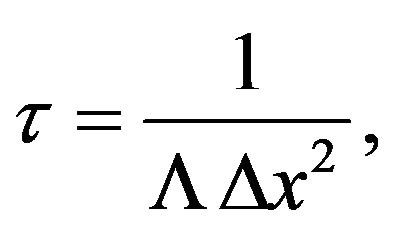 (2)
(2)
where t is the characteristic time to decohere in a distance 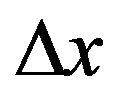 by a factor of e and L is a scattering constant,
by a factor of e and L is a scattering constant,
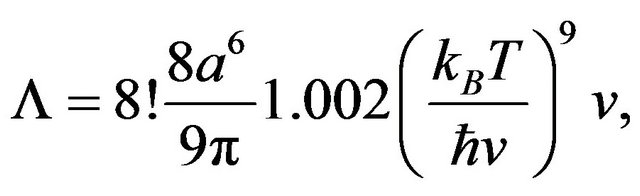
parameterized by wave speed, temperature, and water molecule size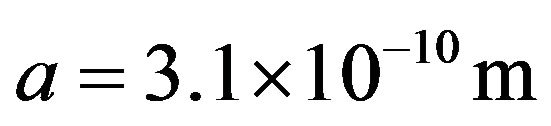 . Substituting the chaion quantities v and T = 310 K with
. Substituting the chaion quantities v and T = 310 K with 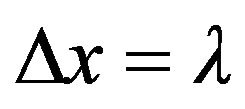 in Eq.2 gives
in Eq.2 gives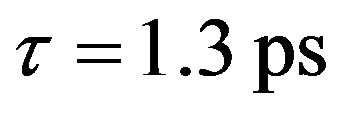 , two orders of magnitude longer than the chaion transfer time.
, two orders of magnitude longer than the chaion transfer time.
The plausibility of quantum coherent states existing in biological systems has been addressed elsewhere [11] from fundamental considerations. In contrast, our approach here was to accept the existence of coherence at the outset and then explore the consequences of the assumption. We then see after the fact that the proposed mechanism does avoid decoherence.
3. APPLICATIONS
The model is now tested against experimental data. We find accurate numerical agreements for the dipole moment of water dimers, microwave radiation on yeast, and the Kleiber law of metabolic rates. The computations use only the model quantities and standard physical values with a minimum of mathematics.
3.1. Dipole Moments
Energy transmission in water is passed along water dimers. Consider an isolated dimer that can emit only radiant energy. The average power expended by this excited dimer is the product of energy 2.7 kBT and the emission probability p divided by the time for emission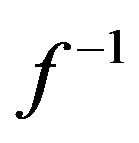 . Set this equal to the Lamor expression for the total average power emitted by a single excited dimer to obtain,
. Set this equal to the Lamor expression for the total average power emitted by a single excited dimer to obtain,
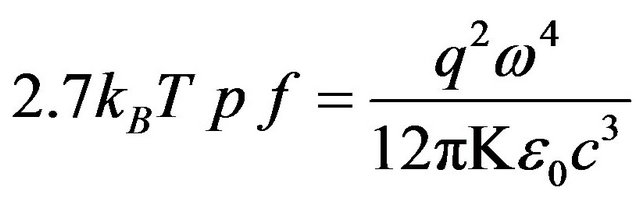
where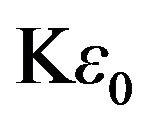 is the dielectric constant for water at 25˚C (K = 78.54), ω is the angular frequency, and q is the dipole moment. All the quantities except for q are known from the chaion model and water properties. Solving gives q = 2.66 D in excellent agreement with the experimental value 2.64 D [12].
is the dielectric constant for water at 25˚C (K = 78.54), ω is the angular frequency, and q is the dipole moment. All the quantities except for q are known from the chaion model and water properties. Solving gives q = 2.66 D in excellent agreement with the experimental value 2.64 D [12].
3.2. Microwave Experiments
In a series of experiments, Grundler and co-workers [13- 15] subjected yeast cells (Saccharomyces cerevisiae) to frequencies in the gigahertz region. They found that cell growth exhibited resonant changes of 10 to 20 percent at frequencies neighboring 41.7 GHz and determined that the effect is not thermal.
We expect that the radiation excites mechanical energy waves that can interfere with chaion energy waves. Constructive interference is then expressed as
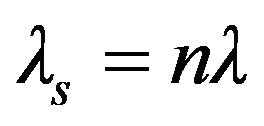
where λs represents the wavelength of the sound wave, n is a small integer, and λ is chaion wavelength. The incident microwaves of frequency fγ excite sound waves with matching frequency. In terms of fγ and the speed of sound, vs, applying the wave relation 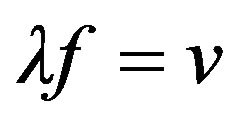 to the latter expression gives a relation for the critical frequency,
to the latter expression gives a relation for the critical frequency,
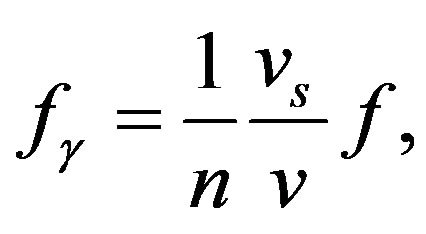
where the un-subscripted quantities apply to chaion properties evaluated at the experimental temperature 31˚C and the standard speed of sound in soft tissue is 1540 m/s [16] . The integer must be chosen to give a match within a broad absorption peak of water between 40 GHz and 100 GHz [17] necessitating n = 4. This yields a frequency of 41.6 GHz in agreement with the experimental mean value of 41.7 GHz.
The microwave experiments also showed satellite periodicities in growth recurring in approximately 10 MHz intervals in the critical region from 41.5 to 41.9 GHz. These periodicities can be estimated using the current model. Compton scattering from electrons in the cell perturb part of the incident wave and the greatest displacement from critical frequency occurs when a microwave photon is backscattered. The backscattered frequency of the sound wave is reduced by 5.5 MHz from peak to trough or 11 MHz per cycle in reasonable accord with experiment.
In principle, the calculation can be repeated for successive updated values of frequency fγ producing a series of satellite resonances with diminishing energy. Again, this is consistent with the experimental results.
3.3. Kleiber Law
The Kleiber law [18,19] is an empirical rule expressing that an organism’s metabolic rate is proportional to the 3/4 power of its mass. Here the expression is derived, including the coefficient, from general thermal considerations and the chaion model. Consider a cell to be comprised of thin nested shells. The outer surface is bounded by a thin shell of volume 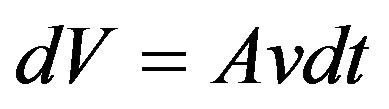 where A is the cell surface area and dt is an increment of time. This mathematical construct treats the cell as a uniform cytosol with no particular recognition of cell membranes or organelles. We focus on the outer shell where energy is lost to the outside.
where A is the cell surface area and dt is an increment of time. This mathematical construct treats the cell as a uniform cytosol with no particular recognition of cell membranes or organelles. We focus on the outer shell where energy is lost to the outside.
Energy entering the outer shell in time dt is the product of energy density ρ and dV with a geometric factor of 1/4 giving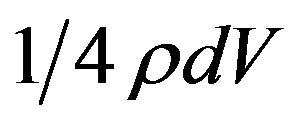 . The one quarter factor is familiar in derivations of Stefan-Boltzmann radiation from thermal energy density. This detail is elaborated in [7] , while elementary arguments cite a factor of 1/2 arising from half the particles being directed toward the surface and another 1/2 from the average component of particle velocity normal to the surface being v/2.
. The one quarter factor is familiar in derivations of Stefan-Boltzmann radiation from thermal energy density. This detail is elaborated in [7] , while elementary arguments cite a factor of 1/2 arising from half the particles being directed toward the surface and another 1/2 from the average component of particle velocity normal to the surface being v/2.
Let W represent the power expenditure generated by the whole enclosed volume so that the fraction of power generated in the outer shell is dW/W and the energy generated within the shell is ρVdW/W. The total energy in the shell, ρdV is the sum of energy generated within the shell and entering the shell
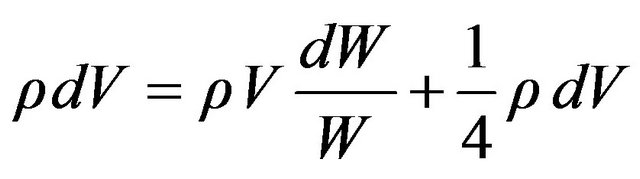
A solution to this differential equation is  where a is a constant of integration. Converting volume to equivalent mass M introduces a new coefficient b and gives the standard Kleiber form
where a is a constant of integration. Converting volume to equivalent mass M introduces a new coefficient b and gives the standard Kleiber form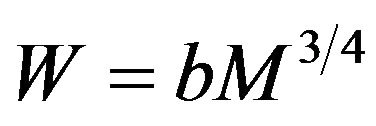 .
.
Although a single measurement can determine coefficient b, it is supportive to calculate it from first principles based on the chaion theory. Choose the special case of a single chaion occupied by volume V. The volume V containing an average of one chaion is readily found from Eq.1 and M is determined by choosing specific cell density to be 1.1 and evaluating all quantities at 37˚C. The outwardly directed linear energy transfer, μ, (energy per length) is 2.7 kBT per wavelength so the power emitted is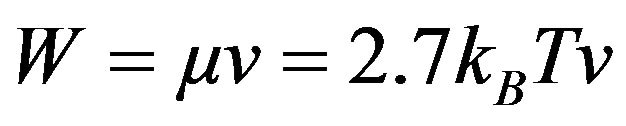 . Substitute this in
. Substitute this in 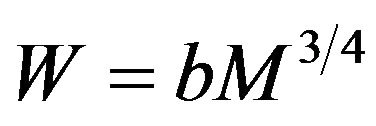 to find b = 3.4 in precise agreement with the empirical value for the Kleiber law expressed in Watts,
to find b = 3.4 in precise agreement with the empirical value for the Kleiber law expressed in Watts, 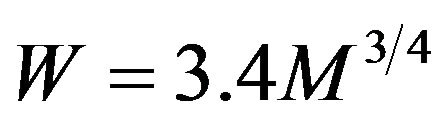 .
.
The derivation is readily extended to multicellular organisms when the idealizations of uniform temperature, density, and homogeneity hold to some approximation. Clearly, anomalies will occur when tissues or organs vary significantly in water content or energy and mass densities.
Interest in the Kleiber law was renewed by derivations based on nutrient distribution systems [20,21] that established the 3/4 factor. Our treatment complements these and offers an idealized thermal view with the benefit of producing the observed coefficient. The Kleiber law has long been controversial especially when it was alleged to be universally applicable—which it is not. Naïve scaling suggests a 2/3 power law and the actual exponent often diverges from the expected 3/4. Nevertheless, the 3/4 exponent is a consensus average [22] . Our model produces 3/4 although it is starkly idealized even for a single cell. We see that many further idealizations are needed to apply it to approximate a multicellular organism.
4. DISCUSSION AND CONCLUSION
This note posits that ultrafast energy transfers in water are a basis for cooperative properties in living cells. Direct applications of the model accurately determined disparate findings for microwaves on yeast, the Kleiber law, and the dipole moment of water dimers. It is noteworthy that no free parameters were introduced in these successful applications.
The model also predicts wave speed and wavelength as well as the energy of the associated particles. These are subject to experiment and await confirmations.
The theory implies that chaion waves tend to be selfperpetuating. Harmonic perturbations induce transitions in the neighborhood of a resonant frequency. As a familiar example, photons matching the resonant frequency of target molecules cause cascades of coherent light by stimulated emission. Similarly, chaions match the resonant frequency of excited water dimers and induce further chaion emissions. Such emissions are more probable than competing reactions and the quantum system favors this state over a multitude of possibilities. The system can then select the best choices for its perpetuation perhaps including enzyme-substrate matches or metabolic reactions that can support chaion production.
In this view the living cell favors chemistry that sustains chaion production. Proto-life forms can be imagined to select primitive enzymes and even coding systems without having to assemble the separate parts serially. Patel [23] argues that the universal coding system of 4 nucleotide bases and 20 amino acids results from an optimum quantum database search according to the Grover algorithm [24] . This may be plausible in a quantum environment on the order of ~9 nm. A sphere enclosing a single chaion is readily found from Eq.1 to have a diameter ~20 nm. If the quantum effect is required for a living state, this is a lower bound for cellular dimensions in this theory. Nanobes this small are observed [25], but are not universally accepted to be living.
Although these projected consequences are intriguing, the model must be supported first by quantitative results. We’ve seen several results that are consistent with the premise that cellular life is characterized by waves of rapid energy transfers in water. This process may assist in the chemical organization and coherence of the cell and we conclude that further study of the model is warranted.
REFERENCES
- Fröhlich, H. (1968) Long-range coherence and energy storage in biological systems. International Journal of Quantum Chemistry, 2, 641-649. doi:10.1002/qua.560020505
- Schrödinger, E. (1944) What is life? Cambridge University Press, Cambridge.
- Ball, P. (2011) Physics of life: The dawn of quantum biology. Nature, 474, 272-274. doi:10.1038/474272a
- Preoteasa, E.A. and Apostol, M.V. (2006) Puzzles of the living cell on the nanometer scale and coherent collective excitations in some biomembrane structures. Digital Journal of Nanomater Bios, 1, 81-92.
- Woutersen, S. and Bakker, H.J. (1999) Resonant intermolecular transfer of vibrational energy in liquid water. Nature, 402, 507-509. doi:10.1038/990058
- Jahnke, T., Sann, H., Havermeier, T., Kreidi, K., Stuck, C., Meckel, M., Schöffler, M., Neumann, N., Wallauer, R., Voss, S., Czasch, A., Jagutzki, O., Malakzadeh, A., Afaneh, F., Weber, F., Schmidt-Böcking, H. and Dörner, R. (2010) Ultrafast energy transfer between water molecules. Nature Physics, 6, 139-142. doi:10.1038/nphys1498
- Finkel, R.W. (2006) Model for Energy Oscillations in Cells, Journal of Theoretical Biology, 238, 286-289. doi:10.1016/j.jtbi.2005.05.002
- Chaplin, M. (2012) Water Structure and Science. http://www.lsbu.ac.uk/water/molecule.html
- Lock, A.J., Woutersen, S. and Bakker, H.J. (2001) Ultrafast energy equilibration in hydrogen-bonded liquids. Journal of Physical Chemistry A, 105, 1238. doi:10.1021/jp003158e
- Schlosshauer, M.A. (2007) Decoherence and the quantum-to-classical transition. Springer, New York.
- Salari, V., Tuszynski, J., Rahnama, M. and Bernroider, G. (2011) Plausibility of quantum coherent states in biological systems. Journal of Physics: Conference Series, 306, 012075. doi:10.1088/1742-6596/306/1/012075
- Gregory, J.K., Clary, D.C., Liu, K., Brown, M.G. and Say- kally, R.J. (1997) The water dipole moment in water clusters. Science, 275, 814-817. doi:10.1126/science.275.5301.814
- Grundler, W. and Keilmann, F. (1983) Sharp resonances in yeast growth prove non-thermal sensitivity to microwaves. Physical Review Letters, 51, 1214-1216. doi:10.1103/PhysRevLett.51.1214
- Grundler, W., Keilmann, F., Putterlik, V., Strube, D. and Zimmermann, I. (1983) Nonthermal resonant effects of 42 GHz microwaves on the growth of yeast cultures. In: Frölich, H. and Kremer, F., Eds., Coherent Excitations in Biological Systems, Springer, Berlin, 21-37.
- Grundler, W. and Kaiser, F. (1992) Experimental evidence for coherent excitations correlated with cell growth. Nanobiology, 1, 163-176.
- Shin, H.C., Prager, R., Gomersall, H., Kingsbury, N., Treece, G. and Gee, A. (2010) Estimation of average speed of sound using de-convolution of medical ultrasound data. Ultrasound Medical Biology, 36, 623-636.
- Chaplin, M. (2012) Absorption coefficients for water. http://www.lsbu.ac.uk/water/vibrat.html
- Kleiber, M. (1932) Body size and metabolism. Hilgardia, 6, 315-351.
- Kleiber, M. (1961) The fire of life. Wiley, New York.
- West, G.B., Brown, J.H. and Enquist, B.J. (1977) A general model for the origin of allometric scaling laws in biology. Science, 276, 122-126. doi:10.1126/science.276.5309.122
- Banavar, J.R., Damuth, J., Maritan, A. and Rinaldo, A. (2002) Supply-demand balance and metabolic scaling. Proceedings of National Academy Science of the USA, 99, 10506-10509. doi:10.1073/pnas.162216899
- Agutter, P.S. and Wheatley, D.N. (2004) Metabolic scaling: Consensus or controversy? Theoretical Biology and Medical Modelling, 1, 13. doi:10.1186/1742-4682-1-13
- Patel, A.D. (2000) Quantum algorithms and the genetic code. http://arXiv.org/abs/quant-ph/0002037
- Grover, L.K. (1996) A fast quantum mechanical algorithm for database search. Proceedings of the 28th Annual ACM Symposium on the Theory of Computing, New York, 212-219.
- Nanjundiah, V. (2000) The smallest form of life yet? Journal of Biosciences, 25, 9-10. doi:10.1007/BF02985175

