Combining Internal Data with Scenario Analysis

doi:10.4236/me.2015.65055

Modern Economy
Vol.06 No.05(2015), Article ID:56558,14 pages
10.4236/me.2015.65055

Elias Karam, Frédéric Planchet

●How to Cite this Article

Laboratoire SAF EA2429, ISFA, Université Claude Bernard Lyon 1, Université Lyon, Lyon, France

Email: ek.eliaskaram@gmail.com, frederic.planchet@univ-lyon1.fr

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

Received 8 April 2015; accepted 18 May 2015; published 22 May 2015

ABSTRACT

A Bayesian inference approach offers a methodical concept that combines internal data with experts’ opinions. Joining these two elements with precision is certainly one of the challenges in operational risk. In this paper, we are interested in applying a Bayesian inference technique in a robust manner to be able to estimate a capital requirement that best approaches the reality. In addition, we illustrate the importance of a consistent scenario analysis in showing that the expert opinion coherence leads to a robust estimation of risk.

Keywords:

Bayesian Inference, Operational Risk, MCMC

1. Introduction

Under the new regulations of Basel II and Solvency II, to be able to estimate their aggregate operational risk capital charge, many financial institutions have adopted a Loss Distribution Approach (LDA), consisting of a frequency and a severity distribution, based on its own internal losses. Yet, basing our models on historical losses only might not be the perfect robust approach since no future attention is being taken into consideration which can generate a biased capital charge, defined as the 0.01% quantile of the loss distribution, facing reality. On the other hand, adding scenario analysis given by the experts provide to some extent a future vision.

The main idea in this article is the following: A Bayesian inference approach offers a methodical concept that combines internal data with scenario analysis. We are searching first to integrate the information generated by the experts with our internal database; by working with conjugate family distributions, we determine a prior estimate. This estimate is then modified by integrating internal observations and experts’ opinion leading to a posterior estimate; risk measures are then calculated from this posterior knowledge. See [1] for more on the subject.

On the second half, we use Jeffreys non-informative prior and apply Monte Carlo Markov Chain with Metro- polis Hastings algorithm, thus removing the conjugate family restrictions and developing, as the article shows, a generalized application to set up a capital evaluation. For a good introduction to non-informative prior distribu- tions and MCMC see [2] .

Combining these different information sources for model estimation is certainly one of the main challenges in operational risk.

Modelling frequency and severity losses for estimating annual loss distribution, is known actuarial technique used to model, as well, solvency requirements in the insurance industry, see for e.g. [3] [4] . More literature on Operational Risk and Bayesian Inference techniques could be found in [5] - [8] .

2. Combining Two Data Sources: The Conjugate Prior

In our study, our data related to retail banking business line and external fraud event type is of size 279, collect- ed in $over 4 years. The data fits the Poission(5.8) as a frequency distribution, and 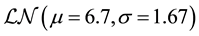as the severity distribution.

Applying Monte Carlo simulation [9] , with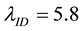, , 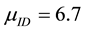and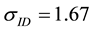, we obtained a Value-at- Risk of 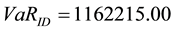at 99.9%, using internal losses only.

On the other hand, working with the scenario analysis, our experts gave us their assumptions for the frequency parameter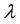. As for the severity, our experts represent a histogram reflecting the probability that a loss is in an interval of losses (see Table 1 below).

If we consider our severity distribution being Lognormal with paramters 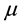and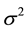, the objective is to find the parameters 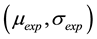that adjust our histogram in a way to approach as much as possible the theoretical lognormal distribution. For this we can use chi-squared statistic that allows us to find 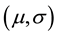that minimize the chi-squared distance:

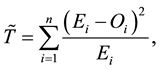
where 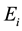and 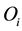are respectively the empirical and theoretical probability.

Our experts provided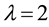, and by applying chi-squared, we obtained our lognormal parameters: 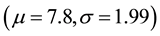with the.

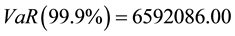The high spread between the two VaR values, can cause a problem in allocating a non-biased capital require- ment. In the next sections, we will apply the Bayesian inference techniques, thus joining our internal observa- tions with the experts opinion.

2.1. Modelling Frequency Distribution

We are going to work with the Poisson and Lognormal distributions since they are the most used distributions in Operational Risk [10] .

Consider the annual number of events N for a risk in a bank modelled as a random variable from the Poisson distribution, where is considered as a random variable with the prior distribution. So

Table 1. Scenario analysis.

we have:, and has a prior density:

As for the likelihood function, given the assumption that are independent, for:

where n is the number of historical losses and is the number of losses in month i.

Thus, the posterior density would be:, but since plays the role of a nor- malizing constant, could be rewritten as:

Which is, i.e. the same as the prior distribution with and

So we have:

To apply this, and since the only unknown parameter is that is estimated by our experts with,.

The experts may estimate the expected number of events, but cannot be certain of the estimate. Our experts specify and an uncertainty that the “true” for next month is within the interval with a probability that, then we obtain the below equations:

(1)

(2)

where is the cumulative distribution function.

Solving the above equations would give us the prior distribution parameters, and by using the formulas stated, we obtain: and as our posterior parameters distri- bution. At the end, we calculate a using Monte Carlo simulation:

• Using the estimated Posterior distribution, generate a value for;

• Generate n number of monthly loss regarding the frequency of loss distribution

• Generate n losses regarding the loss severity distribution;

• Repeat steps b and c for. Summing all the generated to obtain S which is the annual loss;

• Repeat steps a to d many times (in our case 10⁵) to obtain the annual aggregate loss distribution.

• The VaR is calculated taking the 99.9th percentile of the aggregate loss distribution.

We notice that the Value-at-Risk is close to the VaR generated by the internal losses alone, since the only thing took as unknown was, both parameters and are equal to.

2.2. Modelling Severity Distribution: with Unknown

Assume that the loss severity for a risk is modelled as a random variable from a lognormal distribution and we consider as a prior distribution.

So we have,

Taking, we calculate the posterior distribution as previously by:

since we are using a conjugate prior distribution, we know that the posterior distribution will follow a Normal distribution with parameters where:

By identification we obtain:

So, , , with and

Assuming that the loss severity for a risk is modelled as a random variable from a lognormal distribution and we consider as a prior distribution.

Since the only thing unknown is, we already have and, and the experts gave us:

(3)

(4)

where is the cumulative distribution function of the standard normal distribution.

Solving these two equations, we find that the prior distribution of is:

Hence using the formulas stated above where, , , and, with is the total number of historical losses.

We find out that the posterior distribution:.

At the end, using the posterior distribution and Monte Carlo method, we calculate the 99.9% Value-at- Risk:.

The same analysis goes here as well, since the only unknown parameter is, , the VaR calculated will be closer to our Internal Data Value-at-Risk.

2.3. Modelling Frequency and Severity Distributions

In the two previous subsections, we illustrated the case of modelling frequency and severity distributions with unknown that follows a distribution and that follows a respectively.

Joining these two distributions is relatively simple since we have the hypothesis of independence between frequency and severity, which allows us to estimate independently the two posterior distributions and estimate the parameters.

As so, we have already demonstrated the fact that our posterior density follows the distribution, with and and, , with, with.

Since we have the hypothesis of independence between frequency and severity, which allows us to estimate independently the two posterior distributions, which have been already calculated for the parameter we took the gamma distribution and for the parameter, the posterior distribution was normal with:

By simulating those two laws using Monte Carlo simulation (cf. Section 2.1), we obtain a Value-at Risk of 1199000.00 using the estimated posterior Gamma and Normal distributions.

The result is interesting, since with two unknown parameters and, the VaR is still closer to. This states that the parameter is the key parameter in this application, as we are going to see throughout this article.

The general case where all parameters are unknown will not be treated in this section since it is more complex to tackle it with the use of conjugate prior distributions.

2.4. Sensitivity Analysis

Working with this method, is generally simple since conjugate prior is involved, yet one of the main questions is how to ensure that experts opinion are consistent, relevant, and capture well the situation, which might in a way, cause a model error. In this work we did not take into consideration this aspect and the experts opinion were treated as correct. To improve our results, we can do a sensitivity test regarding our prior parameters. On the other hand, we only have the mean of the number of losses, given by our expert. So it appears difficult to obtain the distribution of with this only information. So in a way, we are immensely relying on our prior para- meters which in reality don’t give us a banking sense and are not easily comprehensive.

We are going to test out prior parameters given by the experts and highlight the direct consequence on our Capital Required. To start with the first case, where we are working with unknown; our experts gave us a value of and as seen in section 2.1, so taking into consideration a step of 0.035 for an interval and 0.1 for [6] [10] , respectively, we obtain the following VaR results (check Figure 1).

As for the cases of unknown and unknown, we took an interval for and with a step of 0.1 (see Figure 2).

The following figures show the stability of our Value-at-Risk calculations regardless of all changes in our prior parameters. Relying on the choice of our intervals, we notice that the boundaries of our VaR are in an acceptable range.

3. MCMC-Metropolis Hastings Algorithm

In this section, we will use a noninformative prior and more particularly the Jeffreys prior [11] , that attempts to represent a near-total absence of prior knowledge that is proportional to the square root of the determinant of the Fisher information:

Figure 1. Sensitivity for a₀ and b₀ respectively.

Figure 2. Sensitivity for μ₀ and σ₀ respectively.

where

Then we are going to apply an MCMC model to obtain a distribution for the parameters and generate our capital required at 99.9%. This will allow us to compare both methods’ results and develop a generalized application to set up our capital allocation, since no restrictions is made regarding the distributions. As for the parameter, it will no longer be fixed as in the previous sections. For more details on the Jeffreys prior and MCMC-Metropolis Hastings algorithm check [12] .

3.1. MCMC with Poisson(l) Distribution

Assuming that the parameter is the only thing unknown, the Jeffreys prior distribution is: (see Appendix 5.1), thus finding the posterior distribution with the use of experts Scenario Analysis and Internal Data would be:

So by applying Metropolis Hastings algorithm, (check Appendix 5.2.1 for full support on detailed algorithm), with the objective density:

and with a uniform proposal density: , we obtain the parameter distribution see Figure 3.

We have removed the first 3000 iterations so that the chain is stationary (burn-in iterations effect), [13] . We

Figure 3. MCMC for the parameter λ.

obtain a 99.9% Value-at-Risk of 1000527.00

The result is close to the VaR considered with the use of conjugate family.

3.2. MCMC with Distribution with Unknown

Assuming that the parameters and are the only things unknown, we will treat them independently and since the Poisson(l) case has already been treated, the Jeffreys prior distribution for is:

(see Appendix 5.1), thus finding the posterior distribution with the use of experts Scenario Analysis and Internal Data would be:

So by applying Metropolis Hastings algorithm, (check Appendix 5.2 for full support on detailed algorithm), with the objective density:

and with a uniform proposal density:, we obtain the parameter distribution see Figure 4.

We obtain a Value-at-Risk of 1167060.00.

Comparing this to the same case generated with conjugate prior, we can check the closeness of both values.

In the next subsection, we will tackle the general case, where all parameters are unknown, this case was not treated with conjugate prior distributions since it would be more complicated.

3.3. MCMC: The General Case

We are going to assume the general case, where all the parameters are unknown, and, we will treat them independently and since the Poisson(l) case has already been employed, the Jeffreys prior distribution for

is: (cf. Appendix 5.1), thus finding the posterior distribution with the use of experts Scenario Analysis and Internal Data would be:

Figure 4. MCMC for the parameter μ.

So by applying Metropolis Hastings algorithm, (check Appendix 5.2.3 for full support on detailed algorithm), with the objective density:

and with a uniform proposal density: and for and respectively, we obtain the parameters and distributions, illustrated in Figure 5.

We have removed as well, the first 3000 iterations so that the chain is stationary (burn-in iteration effect). We obtain a Value-at-Risk of 3061151.00.

The general case clearly generates a good combination between internal data and experts’ opinion with a capital requirement of 3,061,151$.

3.4. Confidence Interval Calculation

To recapitulate on all the calculations, Table 2 summarizes all Value-at-Risk generated. As for the calculation of the confidence interval, since we are working with order statistics, the interval would cover our quantile with a 95% probability that depends on the lower bound l, upper bound u, number of steps n and confidence level p.

In our calculations, we took, and our integers, were constructed using the normal approximation to the binomial distribution, (since n is large). Then a simple linear interpolation has been made to obtain the values of, (see [14] , pp. 183-186), for more details and demonstrations.

Table 2 clearly shows the helpful use of the Bayesian inference techniques. The results of both methods are close and comparable; though conjugate prior is simple but the distributions are restricted to the conjugate family, yet with the Jeffreys non-informative prior and MCMC-Metropolis Hastings algorithm, we will have a wider options and generate a good combination between internal data and experts’ opinion.

In addition, we are going to use the Monte Carlo confidence intervals approach [15] in order to compare it with the previous approach and ensure the similarities.

Consider a parameter X with its consistent estimator Y, with cumulative distribution function generated by some process which can be simulated. Number of simulations n and y values are independently generated and then ordered from largest to smallest. An approximate confidence level for X is

given by where j and k represent respectfully the lower and upper bound of the interval and they are set as: and. Usually j and k will not be integer; therefore we can simply round

it to the nearest integer values or even use linear interpolation.

Figure 5. MCMC for the parameters μ and σ.

Table 2. Value at risk and confidence intervals for all cases treated.

We seek to calculate, this may be found, using a conventional confidence level, by solving: and.

The actual confidence level has a beta distribution with parameters and, this is concluded when percentiles of the distribution are estimated by simulation.

Respecting that B has a beta distribution, and

In our case, by using the confidence level of 99.9% and by applying the previous calculations we have obtain- ed an approximation 95% interval for actual confidence level with, , , ,

, , and by moving 1.96 standard errors in either direction from the estimate we obtain our confidence interval:, which is very

close to the previous interval calculation in Table 2.

Furthermore, Figure 6 and Figure 7 illustrate the calculation of our Value-at-Risk for different confidence level. It clearly shows the presence of the general case, between both Internal and Scenario Analysis curves. On the other hand, the conjugate prior Figure 7, regarding all 3 unknown variables, point out the closeness of the curves which add to our previous analysis that is our key parameter.

We have to note as well, that the concept of Scenario Analysis with the expert opinion should deserve more clarification. Roughly speaking, when we refer to experts judgments, we express the idea that banks’ experts and experienced managers have some reliable intuitions on the riskiness of their business and that these intuitions are not entirely reflected in the bank’s historical, internal data. In our case, experts’ intuitions were directly plugged into severity and frequency estimations through building a loss histogram.

(a)(b)

Figure 6. Different VaR calculation for all MCMC cases, internal data and scenario analysis.

Figure 7. Different VaR calculation for all conjugate prior cases.

3.5. Bayesian Approach Reviewed

In this part, we are going to replace the experts opinions, by assuming that the experts’ parameters are set using the Basel II standardized approach calculation. Hence, the experts opinion is questionable in the meaning of when it’s used, we shift into the Markovian process which can cause problems.

3.6. Standardized Approach Reviewed

In the Standardized Approach (SA), banks’ activities are divided into 8 business lines [16] [17] : corporate finance, trading & sales, retail banking, commercial banking, payment & settlements, agency services, asset management, and retail brokerage. Within each business line, there is a specified general indicator that reflects the size of the banks’ activities in that area. The capital charge for each business line is calculated by multiply- ing gross income by a factor assigned to a particular business line (Table 3).

The total capital charge is calculated as a three year average over all positive gross income (GI) as follows:

Hence, the application of the Standardized Approach generates a capital requirement of

Numerical Results for Expert Opinion Treated as SA

Setting the parameters to give us the same Standardized approach capital requirement and treating them as the expert parameters gave us:, and.

We note that the Standardized approach from Basel II is the one to rely on when it comes to calculate the VaR with it’s confidence interval. It is interesting to compare both results in Table 2 and Table 4 where we notice

Table 3. Business lines and the beta factors.

Table 4. Value at risk and confidence intervals for all cases treated.

that the VaR results in the cases of bayesian unknown, unknown and unknown, are very close to the result in the Aggregate case. As for the MCMC approach where experts opinion are respected, in the case of unknown, and the results are close to the Scenario Analysis VaR. We conclude that, the expert opinion used parameters can be uncertain and cause an issue because it can lead to a disruption in the Markovian process. Combining these different data sources, highlights the importance of experts opinion coherence which generate an estimation risk that affects our capital required calculation.

4. Conclusions

Using the information given by the experts, we were able to determine all the parameters of our prior distri- bution, leading to the posterior distributions with the use of internal data, which allowed us to compute our own capital requirement. This approach offers a major simplicity in its application through the employment of the conjugate distributions. Therefore, allowing us to obtain explicit formulas to calculate our posterior parameters. Yet, the appliance of this approach could not be perfected since it's restricted to the conjugate family.

On the other hand, Jeffreys prior with MCMC-Metropolis Hastings algorithm provided us with wider options and generated a satisfactory result regarding all three unknown variables, and, with the only dif- ference of using complex methods. Taking unknown as well, was very essential in reflecting the credibility of estimating our capital requirement.

Yet, treating the experts outputs, the same as Basel’s operational risk Standardized approach, illustrated the necessity of calling attention to the judgments given. In our application, judgments were needed to make sensi- ble choices but these choices will influence the results. Understanding this influence, should be an important aspect of capital calculations, since it created an estimation risk that has highly influenced our capital require- ment [18] , for the judgment under uncertainty. Moreover, we did not take into consideration external data, which might be interesting to elaborate and apply in practice, more on this subject could be found in [19] .

References

Shevchenko, P.V. (2011) Modelling Operational Risk Using Bayesian Inference. Springer, Berlin. http://dx.doi.org/10.1007/978-3-642-15923-7
Robert, C.P. (2007) The Bayesian Choice: From Decision-Theoretic Foundations to Computational Implementation second edition. Springer, Berlin.
Solvency II (2010) Quantitative Impact Study 5 (Final Technical Specifications). http://www.eiopa.europa.eu
Gamonet, J. (2006) Modélisation du risque opérationnel dans l’assurance. Mémoire d’actuaire, CEA.
Berger, J.O. (1985) Statistical Decision Theory and Bayesian Analysis. 2nd Edition, Springer, New York (NY). http://dx.doi.org/10.1007/978-1-4757-4286-2
Moosa, I.A. (2007) Operational Risk Management. Palgrave Macmillan, Basingstoke. http://dx.doi.org/10.1057/9780230591486
Moosa, I.A. (2008) Quantification of Operational Risk under Basel II: The Good, Bad and Ugly. Palgrave Macmillan, Basingstoke. http://dx.doi.org/10.1057/9780230595149
Santos, C.H., Krats, M. and Munoz, F.V. (2012) Modelling Macroeconomics Effects and Expert Judgements in Operational Risk: A Bayesian Approach. Research Center ESSEC Working Paper 1206.
Frachot, A., Georges, P. and Roncalli, T. (2001) Loss Distribution Approach for Operational Risk. Groupe de Recherche Opérationelle, Crédit Lyonnais, France.
Shevchenko, P.V. and Wüthrich, M.V. (2006) The Structural Modelling of Operational Risk via Bayesian Inference: Combining Loss Data with Expert Opinions. The Journal of Operational Risk, 1, 3-26.
Jeffreys, H. (1946) An Invariant form for the Prior Probability in Estimation Problems. Proceedings of the Royal Society of London, Series A, Mathematical and Physical Sciences, 186, 453-461. http://dx.doi.org/10.1098/rspa.1946.0056
Hastings, W.K. (1970) Monte Carlo Sampling Methods Using Markov Chains and Their Applications. Biometrika, 57, 97-109. http://dx.doi.org/10.1093/biomet/57.1.97
Gilks, W.R., Richardson, S. and Spiegelhalter, D. (1996) Markov Chain Monte Carlo in Practice. Chapman & Hall, London.
David, H.A. and Nagaraja, H.N. (2003) Order Statistics. 3th Edition. John Wiley & Sons Inc., New York. http://dx.doi.org/10.1002/0471722162
Buckland, S.T. (1985) Monte Carlo Confidence Intervals. Journal of Royal statistical society, Series C (Applied statistics), 34, 296-301.
Basel Committee on Banking Supervision (2006) International Convergence of Capital Measurement and Capital Standards. BCBS, 144-146. http://www.bis.org
Basel Committee on Banking Supervision (2002) Quantitative Impact Study 3 Technical Guidance. http://www.bis.org/bcbs/qis/qis3tech.pdf
Tversky, A. and Kahneman, D. (1974) Judgment under Uncertainty: Heuristics and Biases. New Series, 185, 1124- 1131. http://dx.doi.org/10.1126/science.185.4157.1124
Lambrigger, D.D., Shevchenko, P.V. and Wüthrich, M.V. (2008) Data Combination under Basel II and Solvency 2: Operational Risk Goes Bayesian. Bulletin Françaisd’ Actuariat, 8, 4-13.

5. Appendix

5.1. Jeffreys Prior Distribution

Jeffreys prior attempts to represent a near-total absence of prior knowledge that is proportional to the square root of the determinant of the Fisher information: