Received 11 December 2014; accepted 25 December 2014; published 14 January 2015

ABSTRACT

The underlying study focuses on estimating and forecasting the volatility of exchange rate in Egypt based on ARCH type models and the State Space (SS) models, namely; the Stochastic Volatility (SV) and the Time-Varying Parameter (TVP) models. Moreover, the paper tests the predictive power of the conducted models to come up with a powerful technique that gives the best forward-looking stance of the exchange rate. Empirically, the paper utilizes daily exchange rate data spanning from January 2003 till June 2013. Evidently, it is found that the exchange rate returns in Egypt suffer from the volatility clustering phenomenon and that there exists a time-varying variance in the exchange rate series that has to be appropriately dealt with, while modelling nominal exchange rates. Additionally, with regard to the link between the volatility occurring in the stock market in Egypt and the volatility of the exchange rate market, it is found that there is a risk mismatch between the two markets. Therefore, further research is recommended in the future to suggest other exogenous variables that can help in explaining the volatility in the exchange rate returns in Egypt.

Keywords:

Exchange Rate Volatility, GARCH Models, State Space Model, Stochastic Volatility Models, Time-Varying Parameter, Egypt

1. Introduction

It is important to monitor the exchange rate dynamics in both developed and developing countries, likewise because it is a vital monetary transmission mechanism channel [1] - [4] . Recently, this has become critical, especially in a world where capital and financial markets are highly integrated and the associated risks are increasing. Moreover, in developing countries, the exchange rate plays an essential role in affecting the macroeconomic stability [5] [6] . This occurs because lending and asset price channels are underdeveloped in those economies.

Economies around the globe are prone to various shocks that lead to higher levels of volatility and uncertainty. This can render the traditional models inefficient in gauging the volatility, because the relationships among economic variables are expected to alter with changes in economic conditions [7] . Accordingly, most of the central banks are now operating in the light of a great uncertainty and a changing economic environment. This has called for new techniques that would help the policymakers to get better insights about the financial and economic variables of interest. Empirically, to model volatility, an enormous amount of literature suggests two sets of models: the Autoregressive Conditional Heteroscedasticity (ARCH) type models and the State Space (SS) models. ARCH type models capture the volatility, as a deterministic observed process as shown in [8] - [10] . Whereas, SS models estimate the variance as an unobserved random process; examples are presented by [11] - [14] . Evidently, it is indicated that the SS models outperform ARCH type models, because they fit more naturally into the theoretical framework of modern financial theory [15] .

Remarkably, in Egypt’s case, the following were the motivating reasons of the study. First, based on the fact that floated exchange rate regime, which was introduced in January 2003, affected the pattern of exchange rate movements over time and rendered the exchange rate an active monetary transmission mechanism channel¹. Second, casual observations showed differentiated patterns in the exchange rate returns over the study period that deserve the quantification of the volatility component, in addition to seeing if this could have power in forecasting the exchange rate movements in Egypt. Finally, the preliminary insights possess some suspicion on the association between the exchange rate volatility and the stock market volatility due to the role of the capital flows (in and out) especially during the recent years. However, during crises, it has been observed that the capital flight of the portfolio investments were accompanied by retarded stock market performance. Consequently, the exchange rate depreciated.Against this background, the objective of the paper is threefold; first, it focuses on estimating and forecasting the volatility in exchange rate in Egypt based on ARCH type models and the stochastic volatility (SV) models. Second, it examines the relationship between the exchange rate and the stock market index based on the Time-Varying Parameter (TVP) technique. Finally, the paper tests the predictive power of the conducted models to come up with a powerful technique that gives the best forward-looking stance of the exchange rate.

The paper gains its own significance and contribution from the fact that it applies the SV and TVP models for the first time on the Egyptian case. These models, although fashionable, have become a standard and popular modeling framework for economic and financial analysis of time series. They provide a powerful alternative to the traditional models constructed for volatility analysis of exchange rates by describing the hidden process of the latter, being one important financial variable, in general and a critical policy tool, in particular. Moreover, the paper adds to the literature by constructing statistical testing on whether the state space models do significantly better than the traditional ARCH family models especially for Egypt. In doing so, the paper serves as a useful vehicle for both policy makers and market participants to better model and forecast exchange rate movements, in the sense that SS models are a good tool for measuring market expectations and reactions to news, whether those related to the market itself or the conduct of new policies and/or interventions.

2. Literature Review

[17] tested the ability of ARCH models to adequately capture the volatility of 21 daily Australian bilateral exchange rates between January 1, 1986 and October 31, 1995. The forecasting ability of these ARCH models was then compared to that of an AR and a Mean model using a number of evaluation measures. The results indicated that the forecasting performance of ARCH models is superior in the case of the Australian foreign exchange rate.

[7] criticized the univariate forecasts of exchange rate returns. In a panel of seventeen countries using quarterly data between 1973 and 1995, they examined the ability of monetary fundamentals to forecast future exchange rate returns. In particular, they addressed whether the deviations of the exchange rate from its monetary fundamentals could prove to be indicative for future returns. They concluded that the fundamentals forecasts were significantly more accurate at the 10 percent level than the random walk predictions for 5 exchange rates under the null of co-integration and for 4 exchange rates under the null of no co-integration.

Using quarterly data from 1973: 1 to 2007: 4 for three currencies; the Euro, the British Pound and the Japanese Yen against the US dollar, [3] compared the forecasting performance of five types of models. The models employed were: the Purchasing Power Parity model, the Uncovered Interest Rate Parity model, the Sticky Price Monetary model, the model based on the Bayesian Averaging technique method, and a combined forecast of the above models. The results indicated that while no single model outperforms the other, the combined model seemed to be superior in terms of obtaining smaller root mean squared forecast error (RMSE) ratios.

Using daily data for India’s exchange rate between 4 January 1999 and 31 August 2009, [13] explored the ability of the stock index to predict the INR/USD returns. It employed three models; the simple VAR, the linear ARIMA and the time-varying parameter (TVP) VAR. The results showed higher level of accuracy for the TVP- VAR model.

[9] empirically examined the dynamics of the daily Serbian Dinar-Euro exchange rate between September 2006 and June 2010using conditional heteroscedasticity models. They identified some factors as main drivers for the changes in the exchange rate. In the period before the global financial crisis in 2008, information about past returns, changes in household savings and banks’ net purchases of foreign currency had statistically significant explanatory power. Meanwhile, after the crisis, other drivers such as changes in the country’s risk gained importance that was measured by changes in the Emerging Market Bond Index (EMBI).

[1] studied the usefulness of economic fundamentals in predicting the Euro-Dollar exchange rate using two frequencies of data; weekly and monthly between January 8, 1999 and August 6, 2010. Based on SS representation, they obtained good in-sample results with an in-sample goodness of fit of about 80 percent. In addition, in the case of out-of-sample forecasts, their results outperformed the random walk model in terms of the Mean Absolute Error (MAE) and the Mean Squared Prediction Error (MSPE) measures.

[18] employed the Artificial Neural Networks (ANN), ARCH and GARCH models to forecast the Euro/US dollar daily exchange rate. The empirical analysis conducted on the period from December 31, 2008 until December 31, 2009 showed that the ARCH and GARCH models, (particularly in static formulations) were better than the ANN for the purpose of analyzing and forecasting the dynamics of the exchange rates.

[19] have empirically gauged the volatility of the exchange rate in Egypt and its link to the exports relying on an optimal GARCH model that was chosen based on a scale-by-scale basis or wave lets. Their analysis showed that the interaction between exchange rate uncertainty and exports is mainly dependent on time scales variation and slightly on the leverage effect. According to their study, the correlation between the variables is greater at low frequency than at high frequency.

3. The Development of the Exchange Rate Policy in Egypt

The conduct of monetary policy witnessed a shift in Egypt since launching the Economic Reform and Structural Adjustment Program (ERSAP) in the early 1990s. Major changes included abolishing interest rate ceilings and other policies, which hindered an efficient allocation of resources, financial restructuring for the banking sector, and minimized the role of the Central Bank of Egypt (CBE) in financing the treasury deficits [20] .

A number of changes in monetary policy instruments encompassed lowering the reserve requirement on Egyptian Pound deposits and giving freedom to banks to set their own lending and deposits rates in a way guided by the Treasury bill rate. Moreover, a dual exchange rate system was introduced that was gradually unified into one rate. The dual system consisted of a primary market and a free market [21] .

It is worth mentioning that from 2002 onwards, the economy experienced high inflation rates (reflected in the trends of both the Wholesale Price Index (WPI) and the Consumer Price Index (CPI) following the successive devaluations of the exchange rate during 2000 and 2001. In 2003, the objective of price stability was formally declared to be the main objective of the monetary policy [20] . In addition, it was the prominent feature of the monetary policy up to 2003 to officially peg or manage the Egyptian Pound against the US Dollar. At the end of January 2003, the official exchange rate shifted to a free float [22] [23] .

Furthermore, the CBE announced its intention to adopt the policy of Inflation Targeting (IT) in 2005. This introduced a new framework for the monetary policy in Egypt. However, these developments were not sufficient to achieve the price stability objective under the lack of an official nominal anchor since 2003. In particular, the role of the exchange rate channel under the new framework was not specified clearly. The de jure floatation of the pound allowed the CBE to intervene in the foreign exchange market just in cases of major imbalances and adverse effects on the exchange rate [24] .

In 2004 and the first half of 2005, an adoption of a tight monetary policy proved to be successful in fighting the two digits inflation. This was reflected in both the WPI and the CPI. This effect was strengthened especially after the effects of the 2003 exchange rate depreciation started to fade away and the confidence in the CBE was restored. On June 2, 2005, the CBE developed a new framework for the monetary policy, which replaced the overnight interest rate on interbank transactions as an operational target instead of the excess reserve balances of banks [20] [25] .

The final, intermediate and the operational targets of the monetary policy were developed as well. As for the ultimate target, it was reshaped in the form of both achieving and maintaining price stability. Intermediate targets, mainly included the money supply and credit indicators [25] - [27] .

During 2006 and 2007, the Egyptian economy experienced positive external factors such as favorable terms of trade, high external demand and an increase in foreign capital inflows. This had an appreciating effect on the real exchange rate during the same period. This was reflected in the growth of exchange rate return, which reached around −1.3 percent in December 2006 and −2.6 percent in December 2007 “Figure 1”. On the contrary, the Egyptian Pound exchange rate depreciated by roughly 4.7 percent against the US dollar during the FY 2008/ 2009 as a result of the global downturn caused by the global financial crisis and a parallel current account deficit [28] - [30] .

Following the local political turbulence that Egypt has been experiencing since January 2011, the exchange rate has also been under several pressures. It depreciated from a rate of 5.79 L.E/$US in January 2011 to around 5.95 L.E/$US in September of the same year. Besides the political factors, there are factors related to the worsening economic situation caused by the direction towards dollarization (during February and March of the same year) and the weaknesses in the sources of international reserves. This was mainly attributed to the appetite of foreign investors to hold foreign currency, which was thought of as a more secured source of investment than the domestic currency “Figure 1”. However, with the improvement on the political spectrum in 2012, confidence in the currency lifted up, which led to a light deceleration in the dollarization process² and hence, affected the pattern of exchange rate evolution slightly [32] - [34] .

4. Modeling Exchange Rate Volatility in Egypt

The study at hand utilizes daily data for the nominal exchange rate (LE/$US) and the stock market index (EGX 30), covering the period from January, 1, 2003 till June, 30, 2013. The study applies two types of models to compare the predictive power to get accurate forecasts of the future movements in the nominal exchange rate. The first set of models deals with the univariate ARCH-type models, while the second set of models focuses on the SS models and the Kalman Filter’s (KF) recursion algorithm. Furthermore, the current section is divided into two sub-sections: the first section includes the methodological representation of the above-mentioned models, while the second sub-section, a detailed presentation for the estimated results is given.

4.1. Methodology

The volatility estimation starts by ARCH model proposed by [35] and the Generalized Autoregressive Conditional Heteroscedasticity (GARCH) models to estimate the sources of volatility embedded in the exchange rate series [36] . Both models are considered outstanding tools in capturing the time-varying variance especially for the financial indicators. Moreover, the GARCH models are capable to deal with the fat tails and volatility-clus- tering problems [10] .

The ARCH model considers the variance of the current error term (innovation) as a function of the lagged squared error terms 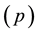[35] and [37] . The model is formulated by the following: let 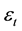denote the error term of exchange rate return residuals with respect to mean process and assume that 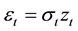where 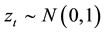and the series 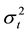are modeled by:

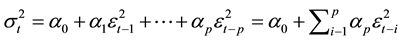(1)

The GARCH 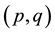model considers the variance of the current error term (innovation) as a function of lagged squared error terms 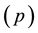and lagged volatility GARCH terms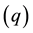. The model is formulated as follows:

(2)

In the framework of our empirical analysis, we use a combination of Seasonal Autoregressive Moving Average (SARMA) and GARCH models to examine the characteristics of the exchange rate return series. The time- series analysis starts with fitting an ARMA 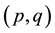model to the exchange rate return series then examining the behavior of the error term. The general form is given by the following ARMA model:

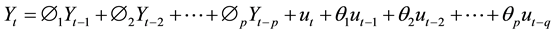(3)

where is our series of interest and is a Gaussian (white noise) error term, it is common to find financial time series lacking the characteristic of being stationary. The need to work on a stationary time series necessitates checks through the unit root tests.

The order of an ARMA model depends on the frequency of the exchange rate return series. This can be decided by analyzing the autocorrelation function (ACF) and the Partial ACF [38] . In the case of exchange rate return series studied here, it is more appropriate to depend on a Seasonal ARMA (SARMA) model to capture the seasonality of the series. The SARMA model is used when the autocorrelations appear to have a seasonal pattern. Consequently, a SAR term can be included in the equation specification for a seasonal autoregressive term with lag and a SMA term can be included to specify a seasonal moving average term with lag [39] . After checking for stationarity and conducting the SARMA model, it becomes necessary to examine the volatility of the exchange rate return series using an ARCH-GARCH framework.

As for the second set of models, the paper will apply the SS models and the KF recursion algorithm. In this context, the paper applies SV and TVP models estimation techniques to capture the latent component embedded in the exchange rate series. The SS representation of the linear dynamic system based on [40] is given by the following first-order autoregression model:

(4)

As such, the future values of for the above process depend on its lagged values only through the current value. This facilitates the dynamics analysis of the system and the forecasting process. Moreover, “Equation (4)” can be easily solved by recursive substitution:

(5)

From which the optimal m-period-ahead forecast is seen to be

(6)

The process is said to be stable if. The intuition behind the state space models is to capture the dynamics of the observed component or the signal (nominal exchange rate) in terms of a possibly unobserved state vector. The dynamics of the state vector are taken to be a vector generalization of “Equation (4)”:

(7)

The observed variables are assumed to be related to the state vector through the observation/signal equation of the system. The state “Equation (7)” and signal “Equation (8)” constitute the generic linear SS representation of with the deterministic variable and the state vector, which summarizes everything in the past that is relevant for determining the future values of. Finally, this framework could be generalized to allow for time-varying coefficient matrices.

(8)

4.2. Estimation Results

In this section, the paper presents the outcomes of the two sets of models proposed to adequately capture the volatility embedded in the exchange rate return series. First, ARCH type models are displayed showing the estimates of the observed volatility. Second, the SV models and TVP models are presented to show the quantification of the unobserved (latent) volatility.

The descriptive statistics of the exchange rate return series is presented in “Table 1” while its development is shown in “Figure 2”. The figure shows total of 3834 observations for exchange rate returns starting from January 1, 2003 and ending at June 30, 2013. The mean of the returns series is close to zero while the standard deviation is roughly 0.91 reflecting the high fluctuations in the series. As for the skewness, it indicates that the variable is skewed to the right and that it is far from being symmetric.

In addition, the Kurtosis statistic reflects the leptokurtic feature of the series (high peak or fat-tailed). The Jarque-Bera test indicates that the series is not normally distributed. Therefore, the exchange rate data indicate volatility clustering with fat tails. As such to gain efficiency in estimation, the existing ARCH/GARCH effect in data should be properly examined and modeled via formal tests.

4.2.1. SARMA and ARCH-GARCH Estimations

The time-series analysis starts with the preliminary checks for the stationarity of the exchange rate series. Thus, the Augmented Dickey-Fuller (ADF) test is utilized to decide on the degree of integration of the series. The ADF-statistics (1.668) shows the failure to reject that null hypothesis of unit root in the exchange rate series; implying that the series is non-stationary at level. Conducting the same test on the return series turns it to be sta-

tionary at all confidence levels (ADF-statistics = −46.068), refer to “Table 2” and “Table 3” for critical values checking.

Looking into the autocorrelation function and partial autocorrelation function of the return series, the weekly seasonality is explicit, which suggests using a SARMA model. Per se, SARMA specification is suggested to represent the best-fitted model for the series at hand. The autocorrelation function and partial autocorrelation function of the residuals and the residuals squared are examined. The latter indicates that the estimated errors are heteroscedastic and thus, there is a need to apply GARCH model. This conclusion is assured by carrying out the formal Lagrange Multiplier ARCH test, which suggests the rejection of the null hypothesis of homoscedastic errors as displayed in “Table 4”.

Against this background, it is concluded that ARCH model cannot completely model the volatility embedded in exchange rate thus conditional heteroscedasticity is modeled in the framework of GARCH estimation. The model includes two components; the mean equation and the variance equation [41] . A parsimonious model is implemented showing that the most appropriate specification for the mean equation is the one that contains the autoregressive terms from one to seven except the sixth term, the second moving average term and seventh seasonal moving average term. Whereas, the variance equation takes the (1, 1) specification. The estimated coefficients of the GARCH model are shown in “Table 5”.

As per the consistency checks, the estimates are in line with the econometric literature, since the mean-re- verting variance process of the estimated equation is achieved, in the sense that the coefficients of the variance equation sum up to slightly less than one (around 0.998). This conclusion implies that there exists persistency in the volatility of the exchange rate return series, i.e. the shocks in the exchange rate returns die rather slowly.

Informally, the autocorrelation function and partial autocorrelation function of the residuals squared show that the GARCH (1, 1) model was able to capture the volatility of the series and the results of the ARCH LM test indi- cates that the estimated errors are no longer heteroscedastic at 1% significance level as illustrated in “Table 6”.

To examine the robustness and forecasting performance of the different specifications, the data set is divided into two main periods; the estimation period and the forecasting period. The comparison is based on five validation sets. The first employs an in-sample period from 2003 till 30 August 2008 and an out-of-sample period from 1 September 2008 till 2013. The second encompasses an in-sample period from 2003 till 1 January 2011 and an out-of-sample period from 2 January 2011 till 30 June 2013. The third is divided into an in-sample period from 2003 till 1 January 2012 and out-of-sample period from 2 January 2012 till 30 June 2013. The fourth set has an in-sample period from 2003 till 1 January 2013 and an out-of-sample period from 2 January 2013 till30 June 2013. Finally, the fifth contains an in-sample period from 2003 till 1 April 2013 and an out-of-sample

^*MacKinnon critical values for rejection of hypothesis of a unit root.

^*MacKinnon critical values for rejection of hypothesis of a unit root.

^*if the estimated ARMA process is (covariance) stationary, then all inverse AR roots should lie inside the unit circle. If the estimated ARMA process is invertible, then inverse all MA roots should lie inside the unit circle. The terms “i” indicate that the inverted roots of the characteristic polynomial are complex and have modulus inside the complex unit circle so that the fitted model is stationary and ergodic.

period from 2 April 2013 till 30 June 2013 (see Figure A1 and Figure A2 in the statistical annex).

The comparison among different periods is based on three evaluating measures, in addition to some graphical representations (see Figure A1 and Figure A2 in the statistical Annex). In judging the predictive power of the five validation sets, the Root Mean Squared Error (RMSE), the Mean Absolute Error (MAE) and the Theil Inequality Index (TII), were used. Table 7 gives “the forecast accuracy statistics” of the different validation sets employed for the in-sample forecasting. Based on the RMSE statistic, it is clear that the last in-sample period performs the best since it possesses the minimum value for this statistic. The same conclusion could be reached when the MAE statistic is used. This reflects the best fitting performance of the same period, which contains the whole time series for the exchange rate returns.

Table 8 indicates that the best forecasting performance could be obtained via the first out-of-sample period since it has the minimum value of the RMSE and MAE statistics among the other forecasting periods. This means that the GARCH model provides better forecasts at long horizons in the case of the Egyptian exchange rate.

One interpretation to be highlighted for this finding is that the first out-of-sample period excludes the external shock caused by the global financial crisis in 2008 and the internal shock of the 25th of January revolution, which occurred in 2011 in Egypt, together with its ongoing spillovers. This constitutes an important factor in keeping the exchange rate return pattern unaffected by those two events and hence, obtaining the best out-of- sample forecast results. Moreover, considering the fitting dimension of the results, it is observed from “Table 7” and “Table 8” that model one out-performed the other models with minimum values of the TII measure.

4.2.2. State Space Models and Kalman Filter

Contrary to the traditional ARCH and GARCH models that depend chiefly on past returns to model volatility, the SS models fit more naturally to data since they utilize market news or information flows into the estimation process. As such, our concern now is not to determine the appropriate time horizon at which the model best describes and forecasts the futuristic movements in exchange rate. However, our task is to point out the appropriate estimation algorithms used to quantify the unobserved (latent) time-varying variance (state component) from the observed observations (signal component). In doing so, the paper applies an approximate Kalman filter using Quasi Maximum Likelihood (QML) estimation technique. The following state-space form may be adopted for implementing the log volatility SV model:

Ÿ Signal (Observation) equation:

where has a standard normal distribution, and the log has a log-chi-square distributions with mean approximately equals −1.2704 and variance π2/2.

Ÿ State equation:

where is.

Thus we denote as the vector of T consecutive observations, is the vector of the corresponding log-volatilities and is the vector of hyper-parameters.

Against this background, in the framework of the SV models, the problem of state estimation could be tackled as an evaluation of the conditional density, which is a predictive density when, filtering density when and smoothing density when.

Applying the above model structure on the log-squared returns of exchange rate , it is observed that the vector of the hyper-parameters includes statistically significant estimates for the three pa-

rameters. First, the estimated model has a stationary state component or mean reversion given that, thus it lies in the range. Moreover, it measures the autocorrelation embedded in the signals, wherein it reflects a moderate persistence in the volatility and a moderate volatility clustering. Second, the mode volatility is relatively low, implying the absence of major daily news, which has a limited effect on volatility in the exchange rate market in Egypt. Finally, the estimate of the variance being relatively small indicates good fit of volatility based on the applied framework of the QML estimation and Kalman Filter Algorithm (Figure 3).

The estimated results indicate that the predicted state (one-step ahead) is concentrated within the first and third quartile of the data. Moreover, there is a coincidence between the median and the mean and it witnesses limited number of outliers in contrary to the case of both the smoothed and the filtered states.

Visually, the estimated states based on both the one-step ahead and the filtered algorithms appear to capture most of the unobserved volatility embedded in the signal. Evidently, it is detected that the estimated state based on the smoothing technique represents the average of the other two algorithms. In addition, all the estimated states fit largely to the normal distribution based on the Quantile-Quantile (QQ) plot; with the exception of the smoothed state, which possesses a larger number of observations that deviate from the 45˚ line (Figure 4).

Worth noting, the filtering algorithm consists of updating the state h_t given contemporaneously available data. Thus, the updating process is motivated by the emergence of new information or updated news in the exchange rate market. As such, the predictive density is connected somehow to the filtering density. In this context, the pair-wise correlation coefficient is calculated to show a relationship between the two estimated states of about 0.65. This coefficient is relatively modest, which comes in line with the prior conclusion, which states that the volatility mode is relatively small implying the limited role of the daily news in predicting the volatility in the exchange rate market in Egypt.

Finally, the paper resorts to some diagnostic tests on the standardized prediction errors from the one-step ahead estimation of the signal. The tests include Augmented Dickey Fuller (ADF) test, QQ Plot and some descriptive indicators, among which the mean, standard deviation, skewness and kurtosis. The ADF test (statistics = −8.07) rejects the null hypothesis of unit root in residuals. The prediction errors have zero mean and a 0.95 standard deviation (Figure 5).

In addition, they are slightly skewed to the left and have negative excess kurtosis. This is why the normality hypothesis is rejected under the Jarque-Bera test. These conclusions are also supported by the QQ plot, which shows that the prediction errors broadly fit the normal distribution except for some outliers that appear in the negative side of the distribution. As such, the graphical diagnostics (histogram and QQ plot) indicate that the SV model performs quite properly in modeling and forecasting the time-varying volatility in the exchange rate returns despite they show some outliers (Figure 6).

Afterwards, the paper attempts to apply a Time Varying Parameters model to capture the structural changes that the exchange rate series in Egypt have witnessed during the study period. The model incorporates the returns on the stock market portfolio, proxied by the EGX30, being the exogenous variable to explain the exchange rate returns. However, the results show that the coefficient of the EGX30 is statistically insignificant, implying that the volatility in the stock market cannot predict the volatility in the exchange rate returns. Therefore, further research is recommended in the future to suggest other exogenous variables that can help in explaining the volatility in the exchange rate in returns in Egypt.

5. Conclusions and Policy Implications

The models estimated in the paper at hand are of high value to participants in the currency market and policymakers in the design of macroeconomic policy in Egypt. In addition, the SS models are a good tool for measuring market expectations and reactions to news, whether those related to the market itself or the conduct of new policies and/or interventions.

The paper main hypothesis is that the traditional time series models fail to gauge the movements in most of the financial indicators; due to their incorporation of what is recently known as volatility. Importantly, these vo-

latilities violate the normality assumption imposed by the traditional models, and the data suffer from some sort of skewness and kurtosis. The literature calls this phenomenon volatility clustering or fat-tailed data. Empirically, the paper utilizes daily exchange rate data spanning from January 2003 till June 2013. Evidentially, it is found that the exchange rate returns in Egypt suffer from such phenomenon. In addition after estimating the traditional ARMA model, LM ARCH test shows that errors are heteroscedastic. This suggests the existence of time-varying variance in the exchange rate series that has to be appropriately dealt with. As such, the paper in modeling the volatility in the exchange rate series, applies two types of models. The first set of models are related to the ARCH-type models, which model the conditional heteroscedasticity in errors volatility as a deterministic observed process. Meanwhile, the other set of models basically estimate the time-varying variance as an unobserved (latent) process that deal with the news and updated information that emerge in the market on daily basis.

The paper’s main findings are summarized in the following:

1) The GARCH (1, 1) specification has a good fit of data; it captures all the observed volatility in the exchange rate returns series. Although the results show that the model satisfies strictly the mean-reverting condition, yet the volatility is highly persistent, implying that volatility shocks die rather slowly. Additionally, the paper settles that the best in-sample forecasting model is the one covering the whole dataset. This can be attributed to the fact that including all the dataset will give better understanding of the data at hand. On the contrary, the best out-of-sample forecasting power is achieved in the first model, which covers the period 1, January 2003 till 30, August 2008. This can be interpreted as being the period which excludes all the breaks that have taken place, whether external (Global Financial Crisis occurred in September 2008), or internal (political transitions took place in January 2011). As such, this time span succeeds in isolating such sources of disturbance that could have affected the pattern of exchange rate movements. Importantly, excluding such shocks helps in getting better forecasts while maintaining goodness of fit of the model.

2) The estimated stochastic volatility model based on the QML and Kalman Filer recursion algorithm shows statistically significant estimates for the three hyper-parameters. First, the estimated model has a stationary state component In other words, it satisfies the mean reversion condition given that, thus it lies in the range. This also reflects a moderate persistence in the volatility and a moderate volatility clustering. As for the estimate of the variance; being relatively small indicates good fit of volatility.

3) Insightfully, the filtering algorithm consists of updating the state given contemporaneously available data. The updating process is motivated by the emerging of new information or updated news in the exchange rate market. As such, the predictive density is connected somehow to the filtering density. In this context, the pair-wise correlation coefficient between the two estimated states is about 0.65. This coefficient is relatively modest which comes in line with the prior conclusion, which states that, the mode volatility is relatively small. This implies the absence of major daily news, which has a limited effect on volatility in the exchange rate market in Egypt.

4) The diagnostic tests applied on the standardized prediction error obtained from the on-step ahead estimation of the signal show that the prediction errors broadly fit the normal distribution except for some outliers that appear in the negative side of the distribution. As such, the graphical diagnostics (histogram and QQ plot) indicate that the SV model performs quite properly in modeling and forecasting the time-varying volatility in the exchange rate returns despite they show some outliers.

5) In an attempt to apply the TVP model, to link the volatility occurring in the stock market in Egypt to the volatility in the exchange rate market. It is found that the coefficient of the EGX30 is statistically insignificant, implying that the volatility in the stock market cannot explain or predict the volatility in the exchange rate returns. A conclusion can be attributed to the fact that the stock market is extremely sensitive to market news, which affects the underlying market risks. On the contrary, based on our findings, the exchange rate market risk (volatility) is not so much sensitive to the daily news. As such, there exists risk mismatch between the two markets in Egypt. Therefore, further research is recommended in the future to suggest other exogenous variables that can help in explaining the volatility in the exchange rate in returns in Egypt.

To sum up, the paper offers examples of risk measurement that could be the input to a variety of economic decisions in Egypt. Per se, better understanding for the volatility of the exchange rate should be of crucial importance to market participants on one hand, and to the Central Bank of Egypt, on the other hand. As for the former, it can be used to hedge against currency risk resulting from exchange rate swings. As for the latter, it gives room for a better formulation of the monetary policy and effective containment of exchange rate shocks for the sake of achieving economic stability.

6. Limitations and Further Research

Despite contributing to the empirical literature, the work presented in the paper has got one limitation repre- sented in applying the estimations on the official spot rate of the nominal exchange rate. In this context, it is worth mentioning that the parallel market for exchange rate used to emerge during crisis times in Egypt, as experienced in 2008 and afterwards in 2011, which were accompanied by the Central Bank interventions to support the value of the Egyptian Pound. The tools presented in the paper could have offered better insights if the rates available in the black market would have been used instead of the official rates. However, the information was unfortunately unavailable in daily frequency. As such, it is recommended that whenever the information becomes available, further research should be carried out to have better understanding of the nominal exchange rate dynamics in Egypt, which will serve, researchers, policy makers and the market participants, likewise.

On another note, the TVP estimation results show that the coefficient of the EGX30 is statistically insignificant, implying that the volatility in the stock market cannot predict the volatility in the exchange rate returns. Therefore, further research is recommended in the future to suggest other exogenous variables that can help in explaining the volatility in the exchange rate returns in Egypt.

References

Annex

NOTES

¹As expressed in [16] , most of the emerging countries characterized by a floating exchange rate regime face more volatility than those which adopt fixed exchange rates.

²The dollarization ratio declined from roughly 21 percent in June 2011 to around 20.6 percent in June 2012. This was attributed to a decline in the proportion of foreign currency deposits in total deposits between the two time points. While local deposits comprised L.E.664.6 billion of a total of L.E.841.5 billion in June 2011, they went up to L.E.714.3 billion of 900.4 billion in June 2012 [33] .