Modern Economy
Vol.05 No.05(2014), Article ID:46197,12 pages
10.4236/me.2014.55049
Evidence of Increasing Regional Income Variation in the United States: 1969-2006
Orley M. Amos Jr.
Department of Economics and Legal Studies, Oklahoma State University, Stillwater, USA
Email: orley.amos@okstate.edu
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 29 March 2014; revised 28 April 2014; accepted 10 May 2014
ABSTRACT
This paper investigates the inter-county variation of per capita personal income within US states from 1969 to 2006. It is a test of the growth pole cycles theory of spatial-temporal economic de- velopment that combines the theory of growth poles with the theory of long wave cycles. Standard OLS regression analysis is performed using data from the Bureau of Economic. Results indicate that regional income variation increased for the majority of states with no indication of a decrease or convergence of regional incomes.
Keywords:
Regional Income Inequality, Kuznet’s Inverted-U, Income Convergence

1. Introduction
Income inequality is a dynamic that has long been used as an indicator of economic development and overall societal well-being. A working presumption in most analyses and policy considerations is that a more equal dis- tribution of income is beneficial; a goal worth pursuing. Economic literature is replete with studies into the causes and consequences of rising and falling income inequality; that is, income divergence and convergence.
Of particular interest to the study of regional economics and economic development is spatial inequality of income, or the variation of regional incomes. Perhaps the seminal study in this area, laying the foundation for decades of research that followed, is Williamson [1] . This study identifies a convergence of regional incomes in the United States, particularly at the state level, supporting the noted Kuznets inverted-U hypothesis of econom- ic development (Kuznets, [2] ).
A subsequent investigation into regional income inequality to the early 1980s using Williamson’s methodol- ogy, is undertaken by Amos [3] , which finds that regional income inequality, rather that continuing decades of convergence, demonstrates the initial signs of renewed divergence. The underlying explanation offered for these results is long-term periodic surges of economic development induced by major technological innovations af- fecting transportation and related infrastructure.
Others investigating the question of regional income inequality and regional convergence have come up with mixed results and differing explanations. Bishop, Formby and Thistle [4] using 1980 Census data provide evi- dence of greater inequality for states with higher per capita incomes. Janikas and Rey [5] analyzing the rela- tionship between spatial clustering, inequality, and convergence, also find support for the increase inequality within US states. Nissan and Carter [6] , in contrast, find support for continued convergence. Eff [7] also finds convergence, but concludes that income convergence is due to government programs.
Amos [8] [9] offers a theoretical structure of the regional income variation phenomenon as part of larger, comprehensive process of spatial-temporal social-economic development, termed the growth pole cycles theory. This theory offers insight not only into regional income inequality, but a wide range of social, cultural, and po- litical behavior, as well.
The objective of this current research is to extend the limited time period of analysis of regional income in- equality in Amos [3] from the initial 15-year period (1969 to 1983) to a substantially longer 37-year period (1969 to 2006). In so doing, a more accurate documentation of the regional income inequality trend as well as greater insight into the underlying process is possible.
2. A Theory of Spatial-Temporal Economic Development
The theory of spatial-temporal social-economic development guiding this research is presented in Amos [8] - [12] . This theory implies that patterns of regional income inequality are but one dimension of a broader economic development process. The presumptions of this theory are: 1) major technological innovations, primarily mani- fested in transportation systems and infrastructure, cause economy-wide surges in growth and development; 2) society is more receptive to innovative changes in technology and assorted cultural, social, political, and eco- nomic institutions during some periods than others; and 3) technological and institutional changes are unba- lanced, first promoting the geographic and individual concentration of income and wealth, then leading to the dispersion of income and wealth.
This theory of growth pole cycles synthesizes two extensive bodies of research, one on growth poles empha- sizing the spatial dimension of economic growth (Perroux [13] , Hansen [14] , Friedmann [15] , Martin [16] , Lau- sen [17] ), the other on long waves emphasizing the temporal dimension of economic growth (Kuznets [2] , Schumpeter [18] , van Duijn [19] , Kondratieff [20] [21] , Garvy [22] , Booth [23] , Eklund [24] ). As a generalized framework, the growth pole cycles theory offers insight into temporal trends of economic growth and why growth is not spatially homogeneous; that is, why some areas lead and others lag behind. In addition, the growth pole cycles theory implies that economic growth is not a smooth, continuous process, but is marked by 1) tem- poral surges and pauses and 2) spatial advances and retreats as the economy ratchets upward and outward. A primary manifestation of this implication of unbalanced growth is the variation of regional income.
The conventional view of income inequality (both regional and individual) that emerged in the middle of the 20th century was that the progress of economic development traversed the noted Kuznets [2] inverted-U. A na- tion in the early transition from an agrarian society to an industrialized economy might initially experience in- creasing inequality or divergence, but as the economy develops, income inequality decreases and convergence occurs. The primary indication is that the process is one-time only and that once incomes converge, they remain converged. This process is largely attributed to the neoclassical market equilibrium adjustment mechanism (Smith [25] , Borts [26] ).
By way of contrast, the theory of growth pole cycles implies that Kuznets invert-U is recurring. Rather than one-time inverted-U pattern, the theory suggests that income divergence is followed by convergence, which is then followed by divergence, then convergence, in a continuing process.
Moreover, the theory indicates that sequential repetition of divergence and convergence fundamentally re- structures the economy and society. Fueled by technological innovations that improve transportation efficiency, the realm of influence and the spatial degree of economic integration, expands with each inverted-U traversed. While one particular growth pole centered in the economic “capitol” of a nation might achieve dominance (such as New York in the 20th century, London in the 19th century, and Paris in the 18th century), the global economy invariably contains a multitude of growth poles with differing degrees of spatial influence, each traversing its own series of recurring inverted-U patterns of divergence and convergence. At any given time, the global economy is likely to see a dominant pole; two or more older, secondary growth poles that had previously domi- nated the global scene; and one or more newer growth poles, but still of secondary influence, that are candidates for eventually coming to dominate the global economy.
These assorted growth pole influences are coordinated to the extent that the dominant growth pole exerts in- fluence over, and is integrated with, other lesser growth poles. However, the influences are disjointed and con- flicting to the extent that spatial interaction with outlying, peripheral areas is temporally lagged. That is, the par- ticular position of a given locale in the inverted-U might be predominately influenced by the dominated growth pole, but also influenced by one or more secondary growth poles. The degree of divergence or convergence induced by the dominant growth pole might be partially countered by secondary growth poles.
3. Data and Methodology
This study employs standard OLS regression techniques to analyze the variation of regional income estimated using data obtained from the Bureau of Economic Analysis (BEA) [27] . The data include BEA estimates of county population and per capita income, as well as state totals and averages, from 1969 to 2006 for each of the 50 states.
3.1. Data
The BEA regularly tabulates and reports total personal income for each of the 3068 counties in the United States. Population estimates are also obtained using decennial Bureau of Census data that are then extrapolated for each year within corresponding decades. Total personal income and population data are then used to estimate per ca- pita income for each county. State data are generated using a similar methodology. These data are obtained for his study through download from the BEA website [27] .
3.2. Methodology
The measure of regional income variation is that initially specified in Williamson [1] and later estimated in Amos [3] . It is calculated as:
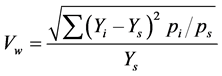
where Vw = the weighted variation of regional income, Yi = per capita personal income in region (county) i of state s, Ys = per capita personal income in state s, pi = population in region (county) i of state s, ps = total popula- tion in state s.
Standard regression analysis is then performed using Vw as the dependent variable and assorted independent variables, most notably state per capital income. Time series regression equations are estimated separately for each of the 50 states as well as comprehensive equations for pooled cross-section, time series for all 50 states combined.
Three alternative regression models are estimated:
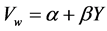 (1)
(1)
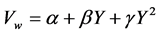 (2)
(2)
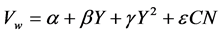 (3)
(3)
where: Vw is the variation of per capita personal income among the counties in each state weighted by popula- tion of the county, Y = state per capital personal income or year, and CN = the number of counties in the state. Equation (3) is estimated only for pool cross-section time-series data.
Convergence is indicated if b in Equation (1) is negative and significant and/or g in Equations (2) or (3) is negative and significant. Divergence is then indicated if b in Equation (1) is positive and significant and/or g in Equations (2) or (3) is positive and significant. The conventional Kuznets inverted-U is indicated if b is positive and g is negative in Equations (2) and (3). The onset of a “new” inverted-U, with the transition from conver- gence to divergence, is then indicated if b is negative and g is positive in Equations (2) and (3).
Figure 1 illustrates a hypothesized pattern of regional income inequality suggested by the growth pole cycles theory, extending the basic Kuznets inverted-U hypothesis. The first segment of the curve, up to point a, pre- sents the Kuznets inverted-U pattern of divergence then convergence. From points b to c, the curve reaches a minimum value then begins increasing, reflecting regional income divergence once again. Presumably the curve then reaches a peak between points d and e, and once again decreases, reflecting further regional income con- vergence.
Four segments of this curve are highlighted. Segment I, from a to b, is a regional income convergence (b < 0, or b = 0 and g < 0). Segment II, from b to c, captures the minimum and exhibits neither convergence nor diver- gence (b = 0 and g = 0, or b < 0 and g > 0). Segment III, from points c to d, is a regional income divergence (b > 0, or b = 0 and g > 0). And segment IV, from points d to e, captures the peak and also exhibits neither diver- gence nor convergence (b = 0 and g = 0, or b > 0 and g < 0).
This study hypothesizes that the United States, during the time period of analysis, completed the convergence phase exhibited by segment I, crossed over most of segment II, and largely occupied segment III. It is expected that most states operated in segment III, but given that states likely develop at different rates and influenced by alternative growth poles, some states might be, at least partially, in segments I, II, or IV during the study period, as well.
4. The Results: Pooled Data
The first analysis is performed on pooled cross-section, time series data using all three regression models. Re- sults of OLS regression estimates of Equations (1), (2), and (3) using state per capital personal income as the primary independent variable are presented in Table 1. The adjusted R2s for Equations (1) and (2) are relatively low, but statistically significant, falling in the range of 0.13 to 0.14. Including the county number variable, CN, in Equation (3) increases the adjusted R2 to 0.30. The b coefficient for Equation (1) and the g coefficient for Equations (2) and (3) provide support for the hypothesis that regional income variation is positively correlated with income. In that per capital personal income is increasing during the study period of 1969 to 2006, these results indicate that regional income inequality is increasing and diverging, moving up the first leg (or more likely third leg) of a Kuznets inverted-U, presumably in segment III of Figure 1.
The b coefficient for Equation (1) is highly significant. Including the squared value of per capital personal income in Equation (2) reduces the level of significance of the b coefficient well below acceptable criteria, with the primary explanatory power assumed by the g coefficient. These results are echoed with the inclusion of the CN variable in Equation (3). While the b coefficient remains well below accepted significance level, the t-sta- tistic and significance of level of the g coefficient for the squared value of per capital personal income increases notably as does the adjusted R2.
Figure 1. Augmented inverted-U.
Similar results are obtained using year as the key independent variable, intended to capture a continuing tem- poral trend of development. Table 2 presents these results. Once again the adjusted R2s for Equations (1) and (2) are relatively low, in the range of 0.10 to 0.11, but statistically significant, and the adjusted R2 increases in Equ- ation (3) with the inclusion of the CN to 0.25.
The signs and significance levels also provide similar results to Table 1, with one notable exception. The b coefficient in Equation (1) and the g coefficients in Equations (2) and (3) are all positive and significant. In this case the results indicate a clear time trend of divergence and increasing regional income inequality during the study period. The noted exception in Table 2 over Table 1 is the significance of the b coefficient in Equations (2) and (3). In both equations, the b coefficient is negative and significant, indicating a U-shaped pattern rather than an inverted-U. The minimum value reached by these quadratic equations is consistently achieved in the years 1958-1959. While this value is outside the data range, it does reinforce the conclusion that income inequality diverged during the study period. There is no comparable estimate of the minimum value for the results in Table 1, indicating only divergence during the study period.
The Results: State by State
Pooled data are then separated into states, with individual time analyses performed on each to ascertain the pat- tern exhibited for each. Equations (1) and (2) are estimated for each of the 50 states. Results of these estimates provide further support for the conclusion of income divergence and increased regional income inequality. To ascertain the existence of a general positive trend between regional income variation and per capital personal income, Table 3 summarizes OLS regression results for Equation (1) by state. A distinctive pattern of increased regional inequality is indicated in Table 3. In 43 of the 50 states, b > 0 and statistically significant at a 0.01 level, indicating regional income inequality is positively correlated with per capita personal income. Three additional states, Alaska, Louisiana, and Oklahoma, also show a positive value for b, but fall short of even a 0.01 signific- ance level. In the remaining 4 states (Mississippi, Montana, North Dakota, and West Virginia) b < 0, with Mon- tana the only state of the four coming anywhere close to a level of statistical significance.
The adjusted R2s of the 43 states demonstrating statistically significant values of b > 0 range from a low or 0.15 for Virginia to a high of 0.97 for Michigan. Over half of these states, 23, reveal adjusted R2s of over 0.70.
Table 3 not only supports the hypothesis of increasing regional inequality it also suggests that the degree of correlation between per capital personal income and regional income variation might be dependent on the level of state development. If regional income inequality is viewed as a process in which decreased inequality (or in- come convergence) gives way to increased inequality (or divergence), as depicted in Figure 1, then more de- veloped states might have traversed this pattern more so than lesser developed states during the time period of analysis. That is, some states might contain both convergence and divergence during the study period, while other states contain almost exclusively divergence.
Table 1. Pooled cross-section time series results per capita personal income (1969-2006).
*Significant at the 0.01 level. Source: Bureau of Economic Analysis, http://www.bea.gov/regional/reis/default.cfm?catable=CA1-3§ion=2 [27] .
Table 2. Pooled cross-section time series results, year (1969-2006).
*Significant at the 0.01 level. Source: Bureau of Economic Analysis, http://www.bea.gov/regional/reis/default.cfm?catable=CA1-3§ion=2 [27] .
Table 3. State results for Equation (1), per capita personal income (1969-2006).
*Significant at the 0.01 level. Data source: Bureau of Economic Analysis, http://www.bea.gov/regional/reis/default.cfm?catable=CA1-3§ion=2 [27] .
Those states with a combination of convergence and divergence are expected to demonstrate little or no cor- relation between per capita personal income and regional income variation (b = 0) or even a negative correlation (b < 0), but with relatively low adjusted R2s. Alternatively, those states with almost exclusive divergence not only demonstrate a positive correlation between per capita personal income and regional income variation (b > 0), but relatively large R2 values. The implied hypothesis can be tested with a meta OLS analysis of the statistic- al results obtained from the 50 individual state equations. This analysis demonstrates a direct correlation with state per capita personal income. Three equations are estimated, each regressing one of three statistical values from the 50 individual state equations (adjusted R2, b coefficient, and t-statistic for b) on a simple average of per capita personal income for each state over the 36-year time period. The results are expected to be consistent across all three equations. Table 4 presents results of these three equations.
In all three meta equations a positive and statistically significant correlation between average state per capita personal income and the dependent variable (adjusted R2, b coefficient, and t-statistic for b) is observed. Ad- justed R2s range from 0.12 and 0.23. All three the meta coefficients are statistically significant at the 0.01 level.
These results confirm the hypothesis that while the level of development in each state might vary, overall the states are moving through a similar pattern of convergence then divergence, albeit at different times. A small number of the states appear to contain a significant degree of convergence at the beginning of the analysis pe- riod, but most have traversed well into divergence. A number of the states reveal virtually no indication of di- vergence in the study period.
Further evidence of the pattern of convergence/divergence is obtained with OLS regression of Equation (2) for each of the 50 states. These results are presented in Table 5. A convergence/divergence pattern with b < 0 and g > 0 is exhibited in 12 of the 50 states. However in only 6 of the 12 states are both coefficients statistically significant. In 4 of the 12 states only the positive g coefficient is statistically significant. And in the remaining 2 states neither coefficient is statistically significant. This indicates definite evidence of increasing regional in- come inequality, with only modest evidence of any convergence.
The alternative set of signs with b > 0 and g < 0 for divergence turning to convergence is exhibited in 24 of the 50 states. Of these 24 states, 11 exhibit statistically significant values for both b and c, indicating a pattern of divergence that is lessening and may eventually make the transition back to convergence. Another 11 states ex- hibit statistical significance only for the positive b coefficient, indicating minimal if any convergence at work.
Table 4. Meta analysis of Equation (1) coefficients.
*Significant at the 0.01 level. Data source: Bureau of Economic Analysis, http://www.bea.gov/regional/reis/default.cfm?catable=CA1-3§ion=2 [27] .
And while the remaining 2 states exhibit b > 0 and g < 0, neither coefficient is statistically significant.
Positive values for both coefficients, b > 0 and g > 0, is exhibited in 14 of the 50 states suggesting not only divergence, but divergence at an increasing rate. However, in only one state, Connecticut, are both coefficients statistically significant. In 5 of the 14 states only the positive b coefficient is statistically significant. In 4 states only the positive g coefficient is statistically significant. And in the remaining 4 states, neither coefficient is sta- tistically significant.
Of some importance, none of the 50 states exhibit a set signs with b < 0 and g < 0, negative values for both coefficients, a result that might be expected with any degree of regional income convergence.
Results of the OLS regression estimate of Equation (2) for the 50 states overwhelmingly supports the hypo- thesis that regional income inequality increases within states over the time period of analysis. While a few of the states might be completing the transition from convergence to divergence in the period of study, most of the states exhibit strong evidence of divergence.
Further insight into the patter of convergence or divergence can be achieved by estimating turning points for each state in which Equation (2) has a sign reversal. This indicates which segment of the curve in Figure 1 a state is located during the study period. Results of these estimates are presented in Table 6.
Of the 12 states exhibiting a U-shaped set of coefficients (b < 0 and g > 0), 9 have an estimated minimum within the period of study, but only 5 of those have statistical significance for both signs. These 5 states (Ala- bama, Louisiana, Mississippi, Oklahoma, and Virginia) appear to be in segment II of Figure 1. In 2 states (Ar- kansas and Tennessee) with b < 0 and g > 0, neither b nor g are significant, suggesting the bottoming out of the transition from convergence to divergence, placing them in segment II of Figure 1. In 2 states (Arkansas and Tennessee) with b < 0 and g > 0, g is significant but b is not, suggesting a definite pattern of divergence, placing them in segment III of Figure 1. In 2 of those states (Colorado and Georgia) the estimated minimum is prior to 1969 and the b coefficient is not statistically significant, also placing them in segment III of Figure 1. The re- maining state with b < 0 and g > 0 (Montana) has an estimated minimum beyond 2006, placing it in segment I of Figure 1.
Table 6 indicates that 14 states have positive values for both coefficients in Equation (2), (b > 0 and g > 0). Only one of the 14 states (Connecticut) has statistical significance for both coefficients. In 5 of the states (Cali- fornia, Idaho, Maryland, Michigan, and New York) b is statistically significant, but g is not. And in 4 states (Rhode Island, Utah, Wisconsin, and Wyoming) g is statistically significant, but b is not. These 9 states clearly fall in segment III of Figure 1. In 4 states (Missouri, Nebraska, Nevada, and Oregon) with positive values for both coefficients (b > 0 and g > 0), neither coefficient is statistically significant. These states could be in either segment II or segment IV of Figure 1.
Table 6 indicates that 24 states have an inverted-U set of coefficients (b > 0 and g < 0). Of this group, 11 states (Alaska, Arizona, Florida, Hawaii, Illinois, Kansas, New Hampshire, New Jersey, New Mexico, South Dakota, and Vermont) have statistically significant values for both coefficients. Five of these states (Florida, Hawaii, Illinois, Kansas, and New Jersey) have estimated maximum values beyond 2006. The remaining 6 states (Alaska, Arizona, New Hampshire, New Mexico, South Dakota, and Vermont) have estimated maximums with- in the data period. In 11 of the 21 states exhibiting an inverted-U (Indiana, Iowa, Maine, Massachusetts, Minne- sota, North Carolina, Ohio, Pennsylvania, South Carolina, Texas, and Washington), only the b coefficient is sta- tistically significant. In 10 of these states, the estimated maximum is beyond 2006. Massachusetts is the excep- tion. Clearly these 10 states fall in segment III of Figure 1. The remaining 2 states (Delaware and North Dakota) exhibit no statistical significant for either variable. While this might place these states in either segment II or segment IV, segment IV is more likely for Delaware and segment II is more likely for North Dakota.
Table 5. State results for Equation (2) per capita personal income (1969-2006).
**Significant at the 0.05 level. *Significant at the 0.01 level. Data Source: Bureau of Economic Analysis, http://www.bea.gov/regional/reis/default.cfm?catable=CA1-3§ion=2 [27] .
5. Implications
Contrary to conventional wisdom and expectations of neoclassical economic theory, the equilibrium conver- gence of regional incomes is not a foregone conclusion. The convergence of regional income is only part of a more complex process of unbalanced regional or spatial growth, a process that provides the engine for national and global economic growth and development.
The pattern of increasing regional income equality identified here is consistent with other evidence of in- creasing income inequality. The inequality of personal income has been increasing in recent decades. The ratio of income received by the wealthiest 1% compared to the bottom 25% is increasing. The ratio of CEO salaries relative to workers wages is increasing.
Kuznets postulated the inverted-U hypothesis of divergence, then convergence as a pattern traversed over the course of economic development. Evidence from this analysis indicates that this pattern is largely incomplete. The development process appears to be one of divergence, convergence, then divergence once again. While what might transpire beyond the current pattern of divergence is clearly speculative, there is reason to think that divergence will once again give way to convergence, traversing a second Kuznets inverted-U. Several of the states appear to be on the verge of convergence once again. And in the same why that short-run economic insta- bility is characterized by business cycle expansion, contraction, expansion, and contraction, in repetitive fashion, long-run growth and development may very well be characterized by a repetitive pattern of divergence and con- vergence. The difficulty, of course, is that documenting such a pattern requires not merely years of date, but centuries of data, data that are unlikely to exist for some time to come.
However, to the degree that the pattern of regional income variation supports the underlying process of unba- lanced growth as outlined by the growth pole cycles theory, then other implications are worth noting. One is the relative importance of alternative political ideologies, with conservative views tending to dominate during pe- riods of increasing regional income inequality. A second is the structural transition of socio-economic institu- tions associated with an economic and financial depression that transpires as society and the economy reorients from divergence and increasing inequality to convergence and decreasing inequality. The theoretical timing would place this near the end of the third decade of 21st century.
Table 6. Minimum/maximum estimates for Equation (2).
6. Conclusions
A positive correlation between per capita personal income and regional income variation is clearly indicated by the results. Similar results are obtained using time as a dependent variable. Evidence strongly supports the hy- pothesis of increasing regional income inequality or the divergence leg of Kuznets inverted-U.
Comparable results are obtained with OLS regression estimates for each of the 50 states. With both linear and quadratic equations estimated using per capita personal income as the dependent variable, the vast majority of states (36) exhibit clear divergence of regional incomes, falling in segment III of Figure 1. And 4 states appear to have reached segment IV of Figure 1. The remaining 10 states are in segment II of Figure 1. A critical con- clusion is that none of the 50 states show an indication of definitive regional income convergence, segment I of Figure 1.
A meta analysis of the state coefficients generated with the simple linear model regressed against average per capital personal income provides greater insight into the underlying process. The meta analysis indicates that the statistically significant degree of divergence is itself dependent on the average per capita personal income in a state. That is, more prosperous, higher income states also exhibit a more distinct connection and correlation be- tween per capita personal income and regional income inequality. The implication is that some states lag behind other states in the transition from convergence to divergence and onto full blow divergence.
Clearly convergence, divergence, and transition from one to the other are not a ubiquitous process expe- rienced equally and simultaneously by all states or all regions within the United States. In the same way that the shockwaves of an earthquake diffuse outward from the epicenter affecting different points at different times, so too the process underlying the convergence and divergence of incomes affects some regions and states sooner than others.
Most pointedly, the spatial dimension of economic development and unbalanced growth is still not fully un- derstood. It remains murky in most theoretical analysis and marginally incorporated in most empirical studies. However, as suggested by the results of this analysis, the spatial dimension is critical to the process.
References
- Williamson, J.G. (1965) Regional Inequality and the Process of National Development: A Description of Patterns. Economic Development and Cultural Change, 13, 3-47. http://dx.doi.org/10.1086/450136
- Kuznets, S. (1955) Economic Growth and Income Inequality. American Economic Review, 45, 1-28.
- Amos, O.M. (1989) An Inquiry into the Causes of Increasing Regional Income Inequality in the United States. Review of Regional Studies, 19, 1-12.
- Bishop, J.A., Formby, J.P. and Thistle, P.D. (1992) Explaining Interstate Variation in Income Inequality. The Review of Economics and Statistics, 74, 553-557. http://dx.doi.org/10.2307/2109501
- Janikas, M.V. and Rey, S.J. (2004) Spatial Clustering, Inequality and Income Convergence. 51st Annual North American Meetings of the Regional Science Association International, Seattle, 16 November.
- Nissan, E. and Carter, G. (2001) Economic Growth and Convergence of Regions and States: 1983 to 2005. American Business Review, 19, 51-57.
- Eff, E.A. (1999) Myrdal contra Ohlin: Accounting for the Sources of U.S. County per Capita Income Convergence Using a Flexible Decomposition Approach. Review of Regional Studies, 29, 13-36.
- Amos, O.M. (1990) Growth Pole Cycles: A Synthesis of Growth Pole and Long Wave Theories. Review of Regional Studies, 20, 37-48.
- Amos, O.M. (1995) Secular Seasons: Long Run Trends in Socio-Economic Behavior. Papers in Regional Science: The Journal of the RSAI, 74, 187-204.
- Amos, O.M. (1988) Unbalanced Regional Growth and Regional Income Inequality in the Latter Stages of Development. Regional Science and Urban Economics, 18, 549-566. http://dx.doi.org/10.1016/0166-0462(88)90026-9
- Amos, O.M. (1989) A Re-Evaluation of Long Cycle Theories: Development as the Satisfaction of Hierarchial Needs. Social Science Quarterly, 70, 341-355.
- Amos, O.M. (1991) Divergence of Per Capita Real Gross State Product by Sector—1963 to 1986. Review of Regional Studies, 21, 221-234.
- Perroux, F. (1970) Note on the Concept of Growth Poles. In: McKee, D., Dean, R. and Leahy, W., Eds., Regional Economics: Theory and Practice, The Free Press, New York, 93-104.
- Hansen, N.M. (1967) Development Pole Theory in a Regional Context. Kyklos, 20, 709-725. http://dx.doi.org/10.1111/j.1467-6435.1967.tb00871.x
- Friedmann, J. (1972) A General Theory of Polarized Development. In: Hansen, N.M., Ed., Growth Centers in Regional Economic Development, The Free Press, New York, 82-107.
- Martin, R.C. (1978) An Empirical Inquiry into the Effectiveness of the Growth Center Approach. The Review of Regional Studies, 8, 1-19.
- Lasuen, J.R. (1969) On Growth Poles. Urban Studies, 6, 137-161. http://dx.doi.org/10.1080/00420986920080231
- Schumpeter, J.A. (1939) Business Cycles: A Theoretical, Historical, and Statistical Analysis of the Capitalistic Process, 2 Volumes. McGraw-Hill, New York.
- van Duijn, J.J. (1983) The Long Wave in Economic Life. Allen & Unwin, London.
- Kondratieff, H. (1984) The Long Wave Cycle. Richardson and Snyder, New York.
- Kondratieff, N. (1935) Long Swings in Economic Life. Review of Economics and Statistics, 17, 105-115. http://dx.doi.org/10.2307/1928486
- Garvy, G. (1943) Kondratieff’s Theory of Long Cycles. Review of Economics and Statistics, 25, 203-220. http://dx.doi.org/10.2307/1927337
- Booth, D.E. (1986) Long Waves and Uneven Regional Growth. Southern Economic Journal, 53, 448-460. http://dx.doi.org/10.2307/1059426
- Eklund, K. (1980) Long Waves in the Development of Capitalism. Kyklos, 33, 383-419. http://dx.doi.org/10.1111/j.1467-6435.1980.tb02641.x
- Smith, D.M. (1975) Neoclassical Growth Models and Regional Growth in the U.S. Journal of Regional Science, 14, 107-120.
- Borts, G.H. (1960) The Equalization of Returns and Regional Economic Growth. American Economic Review, 50, 319-347.
- Bureau of Economic Analysis, Department of Commerce. Local Area Personal Income: Population and Per Capita Personal Income, 1969-2006. http://www.bea.gov/regional/reis/default.cfm?catable=CA1-3§ion=2



