Received 24 February 2015; accepted 11 March 2015; published 16 March 2015

ABSTRACT

The main objective of this paper is to verify the necessary conditions for a possible existence of a steady state balance in an economy. This steady state balance contemplates in its long-term period, the dynamics of the inflation, the interest rate and the exchange rate. Besides, it is considered the public debt of the economy, which is indexed to these three variables in an environment where monetary politics incorporates the use of inflation target. In the stability analysis, it is possible to verify a rest position in the system framework. The conditions at this point present an economy with a mechanism of “dedollarization” of the public debt. By this first condition, the stability analysis calls attention with respect to the measure of the process of “dedollarization”. Depending on its intensity, the economy will show a positive wealth effect that could stimulate the expansion of the investments.

Keywords:

Debt, Macroeconomics, Dynamics

1. Introduction

In macroeconomics analysis, three main variables play very important role in economic policies’ inter-relations: inflation, interest and exchange rate. The analytical complexity involved in an inflation targeting economy is the change in the monetary instruments to its own new objectives by this framework. Therefore, it can see the little applicability or the inconvenient of the rigidity put forth by the adoption of a framework to explicit target based on exchange rate, monetary aggregates or interest rate. By this verification and the freedom gain concerning the basic monetary aggregates―which its relations to inflation and other macroeconomic variables as public debt almost always change and in direction not predictable―in the inflation targeting is incorporated domestic adaptations for the local changes and economic shocks as well as in the market scenery.

By the methodological point of view, the analyses of macroeconomic dynamic models systems are constituted by a group of elements, which characterizes a group of variables in a form of mathematical relationships, which is denominated movement equations. The study of such systems determines the time variation of those variables, establishing and solving, successively, the movement equations.

The main objective of this paper is to verify the necessary conditions for a possible existence of a steady state balance in an economy. This steady state balance contemplates, in its long-term period, the dynamics of the inflation, the interest rate and the exchange rate. Besides, it is considered the public debt of the economy, which is indexed to these three variables in an environment where monetary politics incorporates the use of inflation target.

Given the aims of this work, in the following section a model that incorporates the dynamics of long-term period of the inflation, of the interest and exchange rate is developed. Section 3 analyzes the implications of the conditions of stability of the model. Finally, Section 4 detaches the final considerations.

2. The Analytical Model

With the objective of gathering the dynamics effects of inflation, exchange and the interest rate, in a model that incorporates the indexation of the public debt, the economy here modeled assumes that the public expenses, g, is financed by tax income, t, as well as for emission of public titles, b.

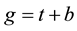(1)

The balance in the market of goods and services is equal to the equality among the generation of income in the economical activity and the aggregate demand. It is supposed in the equation (2), that y is the real aggregate income, i represents the nominal tax of interests, 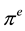the expected inflation, g the amount of expenses considered government exogenous, x corresponds to the balance of the trade balance and the autonomous component.

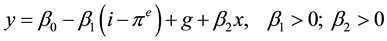(2)

The balance of monetary market is supposed between the local real offer of payment means and its domestic demand.

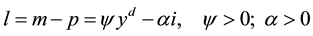(3)

In agreement with the Equation (3), l represents the real amount of means of balance payment in the monetary market; m is the nominal amount of money; p the level of prices and y^d it is the available income, discounted of the taxes.

The public debt composition is determined in Equation (4) for public titles indexed by the inflation, to the exchange and the interest, respectively:

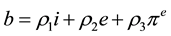(4)

In a first moment is assumed that the public debt exhibits a positive relationship in relation to the three indexed titles:

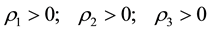
¹Based in the equation that determines the real exchange rate, given for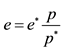, it will be supposed that the level of international prices is the same as the internal prices, so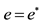. That supposition is used with the objective of guaranteeing the equalization of the real interest rate among the countries because of the capitals flows. For more details: see Frankel [1] .

The nominal exchange rate here is exogenous, in agreement with the market of a flexible exchange¹.

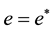(5)

The short term nominal exchange rate is determined exogenously at the level.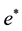

The trade balance equilibrium, x, is a positive function of the exchange rate.

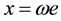, (6)

The nominal interests rate, i, is controlled by the Central Bank in the short-term as instrument of monetary politics with the objective of pursuing the inflation target.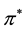

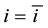(7)

In the short run the inflation is determined by the Phillips’ curve:

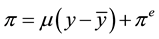(8)

Until Equation (8) the relationships of short period are already determined. Now is presented the long run dynamics. In the long run dynamics it will be described the path of the inflation, of the exchange and of the interest in relation to the time.

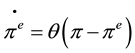(9)

(10)

(11)

The dynamics of the expected inflation is specified in the Equation (9), where this is treated as direct function among the difference between the average inflation and the expected inflation.

The Equation (10) exhibits that the exchange rate dynamics along the time is associated to variations of the public debt in relation to its optimum value. Changes in the public debt in relation to its optimum value will generate variations in the perception of the risk-country, and for this turn, It will cause negative/positive variations in the liquid entrances of capitals, what contributes to appreciate or to depreciate the nominal exchange rate.

In the Equation (11), the dynamics of the nominal interest rate is determined from the regime of monetary policy specified, in other words, the Central Bank will vary the interest rate given the existence of divergences between the observed inflation and the inflation targeted defined by the monetary authority.

Box 1. Equation system.

2.1. Short Run Equilibrium

According to Equation (7), the nominal interest rate is fixed:. The short-term exchange rate is determined exogenously, in agreement with the market of flexible exchange, so Equation (4)―the equation that determines the public debt of short period―can be expressed in the following way:

(4a)

The government expenses are equal to the total of the tax income plus the amount of emitted public titles. So, taking the Equation (1) into IS curve, the following identity is:

(2a)

where represents disposable income.

The next step is to take (5) in (6):

(6a)

Now it can be found the equation that determines in the short term. So, inserting (6a), (4a) e (7) in (2a):

(2a’)

Replacing (7) and (2a’) in the equation that determines the monetary market equilibrium (equation M):

(3a)

The balance of short run period of the effective inflation is given by the substitution of (2a’) in the Phillips’ curve

(8a)

The impacts of the variantion in, e about the short term equilibrium are:

Box 2. Short term comparative static.

2.2. Log Run Dynamic

The Equations (9), (10) and (11) determine together the long run dynamic of e. So, the Steady-State:

(9a)

(10a)

(11a)

Still of (9)-(11):

(9a’)

(10a’)

(11a’)

Puting the system in a linear form to its long term equilibrium:

(16)

(17)

(18)

Rewriting the system in a matrix form:

(19)

The characteristic equation associated to the system is given by:

(20)

As the Jacobian matrix order (Equation (19)) is 3 × 3, it is needed to use the Routh-Hurwitz criterion for third degree polynomials in the intention of verifying the stability of the system:

(21)

By Routh-Hurwitz criteria², to the system (16)-(18) be stable of the form saddle path, it must be verified the following condiditons:

(22)

So, in according to Equation (20):

(23)

In (23), to, it is assumed the following condition:

(24)

where, given that it is assumed thar.

So, according to Equation (24), if the value of is larger than the linear combination composed by the elasticity of the public debt concerning its indexed titles.

Now, it will be investigated the possibilities of e being larger than zero, in mathematical form:

(25)

(26)

If it is relaxed the hyphotesis that, or in other words, assuming now that, it can

be stablished that.

For last, but not least important condition, it is verified if the fourth and the last condidition,:

(27)

It’s known that; Then, it can be rewritten (27) in the following way:

(28)

After some algebraic manipulation in (28), it is found the following relation:

(29)

Given that and the right side of the equation is smaller than zero, it can be seen the inequality in (29).

So, the necessary condition to stability which can contemplate a rest position in the equation system (1)-(11)

need that and.

In the next section it will be done a brief discussion about the implications of these stability conditions.

3. Analysis of the Conditions of Stability

One of the necessary conditions for the stability of the system developed previously, which incorporates the indexation of the public debt in the dynamics of the interest, inflation and exchange rate, is the relaxation of the hypothesis that an exchange depreciation has the effect of increasing the public debt. So, the model exhibit a

dedollarization mechanism of its public debt, as long as is assumed that.

From the mechanism of dedollarization of the public debt, some results can be detached with the second con

dition of stability analysis:.

By Equation (2)―in mathematical ways:―it can be stated that the aggregated demand component, investment plus consume, influenced by the nominal interest rate can be decomposed in the following way:

(30)

In agreement with Tobin q, the investment volume can be determined in the relationship between the value of market of the installed capital and the value of replacement of the installed capital³:

(31)

The investment can still be put in the following equation:

32)

Taking (32) in (30):

(33)

Isolating in (33)

(34)

Inserting (34) in the Equation (24) and after some algebraic manipulations:

(35)

In (35) it is supposed that the inequality happens in function of the component, whereas it is sup-

posed that that component assumes a very close value to zero. So equation (35) can be rewritten in the following way:

(36)

From the Equation (36) it can analyzed the Tobin q value, in other words, in which situations its value is smaller or larger than 1. So:

(37)

where, given that it is assumed so far that. Besides, and. If the latter

holds, we have reached the sufficient and necesseray condition to.

(38)

As in the last condition, , given that it is assumed so far that. Besides, and

as well as. If the latter holds, we have reached the sufficient and necesseray condition to.

That’s an important result, because in agreement with Bernanke & Gertler [5] , the need to study alternative roads of transmission of the monetary policies appeared due to the empiric difficulty of identifying the effect of the interest rate on the cost of the capital (Tobin’s q). The results in (37) and (38) identified a possible channel of transmission though exchange rate to the investments, So that depending on the intensity of the dedollarization of the public debt, the value of Tobin’s q can be larger or smaller than one. Then, in the case of dedollarization

intensity, , overcome the inflation effect and interest rate overcome the public debt, , the presented value of the Tobin’s q will be smaller than one; otherwise, if, it will have a value for the Tobin’s q bigger than one.

The previous result seems not too intuitive. Nevertheless, the result is of great importance in the discussions concerning the relationships between public titles and monetary politics.

Let’s consider, for instance, the case where “q” is larger than one. This is a situation where the expansion of the capital is profitable for the companies, in other words, the market of actions considers that the installed capital is worth more than its replacement cost. That relationship is plausible, as long as in a first moment exchange rate depreciation reduces the public titles’ market value. Consequently, the private sector wealth decreases.

A decrease of the wealth of the private sector provokes a reduction in the consumption, contracting the aggregated demand, which for its turn can leave the companies inhibited in expanding their investments if the expected profits are reduced because of a smaller aggregated demand. However, that negative effect in the private sector wealth can be supplanted if together with the public debt effect of the exchange rate depreciation, causes the Central Bank reaction, as long as, these variation provoke an increase in the inflation rate, which in this turn, given the inflation target framework, provides an increase in the interest rate.

In this context, the increase of the inflation and the rise of the interest rate will generate an increase of the public debt. Given the portion of public titles indexed to the inflation and the interest rate, the final effect will allow an increase in the private sector wealth and afterwards an increase in the consumption, expanding the aggregated demand.

So, as already mentioned, if the intensity of the dedollarization, , is smaller than the united effection of the inflation and interest rate over the public debt, , there will be incentives for the companies to expand its capital, given a positive wealth effect.

4. Final Considerations

The objective of this work was to verify the necessary conditions for a possible existence of a stable balance in an economy, which contemplates, in the long term, the inflation dynamics of the interest and exchange rate, considering the public debt indexed to three variables, in a context monetary regime incorporates the use of inflation targeting.

In the development of the dynamics of long term period, it was possible to detach a rest position as long as two conditions of stability are assisted: the first demands that the economy exhibits a mechanism of dedollarization in its public debt, in other words, exchange rate depreciation should be accompanied by reductions of the size of the public debt; in function of that first condition, the second condition of stability appears for a discussion concerning the intensity of that dedollarization process, whereas depending on that intensity, the economy will exhibit an effect wealth positive that for its turn stimulates the expansion of the volume of investments.

References

Appendix 1: Demonstration of the Equation (24)

Where:

where, given that we are assuming.

Appendix 2: Demonstration of the Equation (29)

Where:

Making some algebraic manipulations:

NOTES

²For a better understanding about the analysis of the conditions of stability in dynamic systems, see Takayama [2] .

³In the Equation (32), extracted of Sargent [3] , it is assumed that if q > 1 the expansion of the capital is lucrative for the companies; if q = 0 there is no incentive for expansion of the production capacity; if q < 1, there is a reduction in the investment level, given that if it is not profitable for the companies to substitute the capital as long as its depreciates. For a more advanced reading on the q theory, see Hayashi [4] .