Modern Economy
Vol. 3 No. 8 (2012) , Article ID: 26265 , 4 pages DOI:10.4236/me.2012.38118
Legacy of the Asian Currency Crisis: The Case of Korea
Department of International Economics and Law, Hankuk University of Foreign Studies, Seoul, Korea
Email: kjryoul@hufs.ac.kr, gylim@hufs.ac.kr
Received October 24, 2012; revised November 27, 2012; accepted December 5, 2012
Keywords: Permanent and Transitory Components; Markov Regime Switching
ABSTRACT
This paper reexamines the long run effects of the 1997 Asian crisis on the Korean economy. Using unobserved components models subject to Markov regime-switching, we address two questions: 1) whether the output losses of Korea during 1997-1998 were permanent or transitory; 2) when the trend growth rate decreased. Estimation results suggest that the trend growth rate of the Korean economy has already declined around 1992-1993 prior to the 1997 crisis, and given the transition of the Korean economy into the low-growth regime in the early 90s, the effects of the crisis are mainly transitory.
1. Introduction
One long-standing issue in business cycle analysis is whether the effects of recessions are permanent or transitory. One possibility is that recessions permanently lower the trend of output level. That being the case, the long run level of output cannot regain the ground lost during the downturn, even if its long-run growth rate is intact. Most parametric models of this type benefit from Hamilton [1], in which the trend of output goes through stochastic regime switching between positive and negative growth states. In models of this strand, an occurrence of negative states results in an output loss that is permanent, since the regime switch occurs in the growth rate of the permanent component of output.
The other possibility is that recessions are caused by large negative yet transitory shocks, following which output “bounces back” or “peak reverts” to its long-run trend. Models of this strand are rooted in the work of Friedman [2,3], where recessions can be characterized by a temporary “pluck” of output. Since the large negative transitory shock dissipates over time, this type of recessions yields temporary deviations from the trend followed by a full recovery to the original growth path. The nature of the effects of recessions on output is also important in explaining the experience of the Korea economy.
The 1997 Asian currency crisis, which began in Thailand in the summer and moved eastward, may be labeled as one of the most devastating events in the region. In 1998, the Korean economy experienced a 6.9% decline in its real GDP and a 6.1% increase in unemployment rate compared with the previous year. In the following years out of the abyss, the Korean economy showed a dramatic turnaround: in 1999 and 2000, the real GDP grew at 9.5% and 8.5%, respectively. A subsequent secular slowdown in growth has appeared since then, however, registering an average growth of 4.7% over 2001-2007, before the onset of the Subprime financial crisis.
These experiences of Korea around the 1997 crisis engendered a voluminous literature on its causes and reasons for fast recovery1. In contrast, the literature on its long-run effects is relatively sparse. To cite a few, Cerra and Saxena [4] investigated the output losses associmated with the Asian crisis for 6 countries in the region, and concluded that the Korean economy suffered permanent losses in the level of output2. Examining the potential growth rate of Korea, Huh and Park [5] also found evidences supporting that the trend growth rate of Korea shifted down in the post-1997 period.
With data available for more than one decade after the 1997 crisis, the aim of the present paper is to reexamine the validity of the “mainstream view” above. More specifically, we address the following questions around the Asian currency crisis.
• Were the output losses of Korea during the crisis permanent or transitory?
• Did the trend growth rate of Korea decrease during the period?
Addressing the two questions, we construct and estimate a regime-switching unobserved components model for the Korean GDP, which is capable of: 1) distinguishing between permanent (or trend) and transitory (or cyclical) movements in output; 2) capturing inherently different dynamics in output across the expansion and recession phases. Our estimation results support that: 1) the trend growth rate declined around 1992: Q2 prior to the 1997 crisis; 2) the effects of the crisis on output level were mainly transitory, once the prior slowdown in trend growth is taken into account.
The rest of the paper is organized as follows. Section 2 presents the basic econometric models, which are essentially variants of Kim and Nelson (1999) [6]. In section 3, we present empirical results. Section 4 draws conclusions.
2. The Model
We set off with the decomposition of the log of real 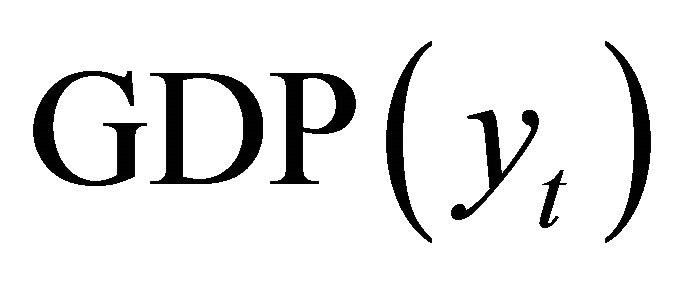 into two unobserved components
into two unobserved components
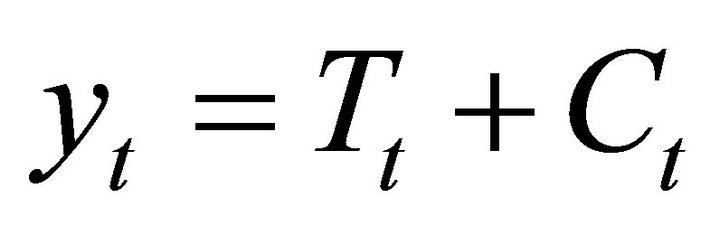 (1)
(1)
where  is the trend component and
is the trend component and 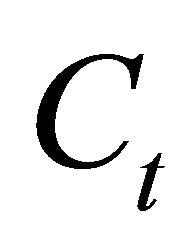 is the cyclical component of.
is the cyclical component of.
Following Friedman [4,5] and Kim and Nelson (1999) [6], we assume that the cyclical component 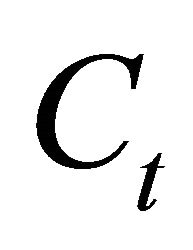 follows an AR(2) process, subject to a symmetric disturbance
follows an AR(2) process, subject to a symmetric disturbance 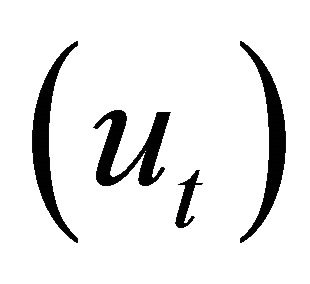 and a regime-dependent asymmetric mean
and a regime-dependent asymmetric mean 
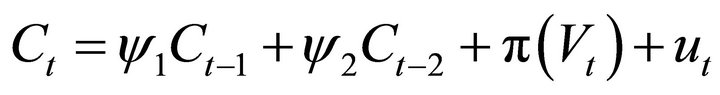 (2a)
(2a)
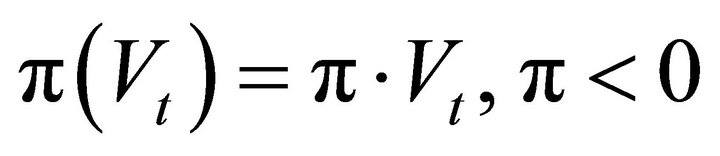 (2b)
(2b)
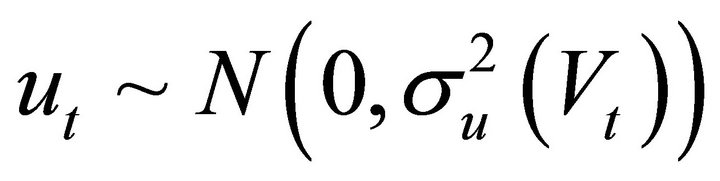 (2c)
(2c)
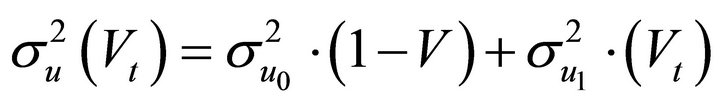 (2d)
(2d)
where  is intended to capture the temporary ‘plucking’ of the output off the trend.
is intended to capture the temporary ‘plucking’ of the output off the trend.  is an indicator variable that determine the state of the economy, taking the value of 0 in normal periods and 1 in pluck-down periods. The variance of the shock
is an indicator variable that determine the state of the economy, taking the value of 0 in normal periods and 1 in pluck-down periods. The variance of the shock 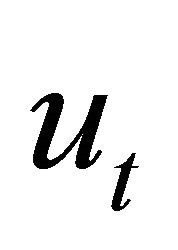 is heteroskedastic across the two states.
is heteroskedastic across the two states.
We approximate the growth rate  of the trend GDP by an AR(1) process, subject to possible shifts in the drift:
of the trend GDP by an AR(1) process, subject to possible shifts in the drift:
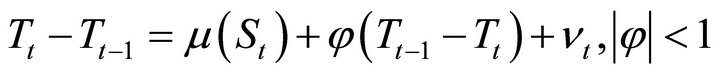 (3a)
(3a)
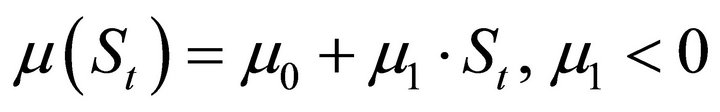 (3b)
(3b)
 (3c)
(3c)
 (3d)
(3d)
where the trend growth rate is regime-dependent in the spirit of Hamilton (1989), with the term 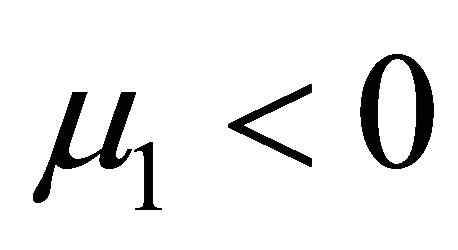 intended for abrupt slowdowns in the trend growth during contraction (i.e.,
intended for abrupt slowdowns in the trend growth during contraction (i.e.,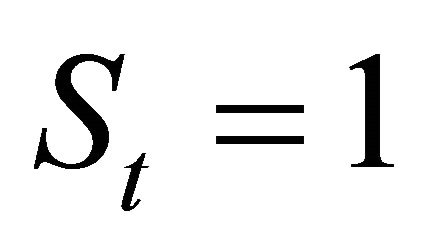 ) relative to expansion (i.e.,
) relative to expansion (i.e.,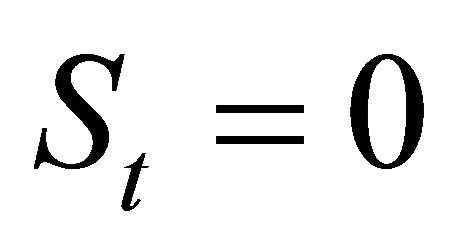 ) periods. The variance of the shock
) periods. The variance of the shock 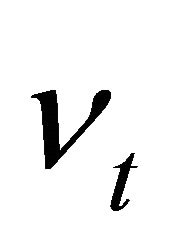 to the trend growth is also allowed to be state-dependent.
to the trend growth is also allowed to be state-dependent.
The two state variables 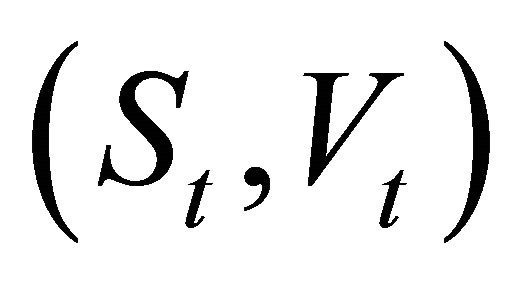 follow mutually independent first order Markov switching processes, whose transition probabilities are given by:
follow mutually independent first order Markov switching processes, whose transition probabilities are given by:
 (4a)
(4a)
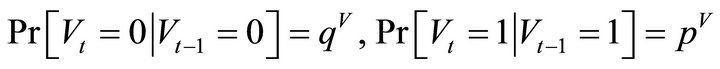 (5b)
(5b)
Most unobserved components models assume that the two disturbance terms 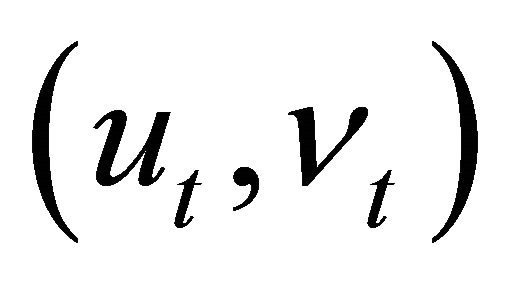 are uncorrelated. However, Morley et al. [7] find that such an assumption is not innocuous, yielding trend-cycle decompositions qualitatively different from those by Beveridge-Nelson method3. We therefore estimate two versions of the model: Model [8] with the zero correlation restriction between
are uncorrelated. However, Morley et al. [7] find that such an assumption is not innocuous, yielding trend-cycle decompositions qualitatively different from those by Beveridge-Nelson method3. We therefore estimate two versions of the model: Model [8] with the zero correlation restriction between 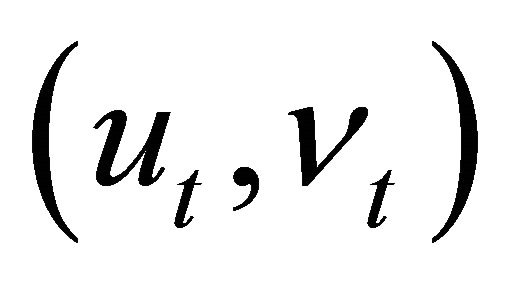 and Model [9] allowing contemporaneous correlation.
and Model [9] allowing contemporaneous correlation.
To estimate the parameters of the two models, we first cast them into a state space forms and apply Kim’s [10] approximate MLE algorithm.
3. Empirical Results
We use the seasonally adjusted real GDP of Korea spanning 1983:Q1 to 2010:Q44. The GDP series is transformed into log-differences (times 100) to ensure stationarity of the series and to allow for the use of the unconditional mean and variances of the state variable in initializing the Kalman filter5. The selection of the sample period is intentional, in that the consequences of the two economic crises and the recovery that followed are analyzed in this paper. Figure 1 plots the real GDP and growth rate series over the sample period. Evidently, the GDP series show two sharp downturns around the periods of the Asian currency crisis and the sub-prime financial crisis.
Table 1 reports the estimation results for the two models. Since the two models yield very similar estimates, we concentrate on the discussion of the results from models [8].
The cyclical component exhibits the Friedman-type asymmetry: the “plucking” parameter  for the cyclical component is sharply estimated to be −1.647, and the estimated transition probabilities indicate that the normal periods last
for the cyclical component is sharply estimated to be −1.647, and the estimated transition probabilities indicate that the normal periods last
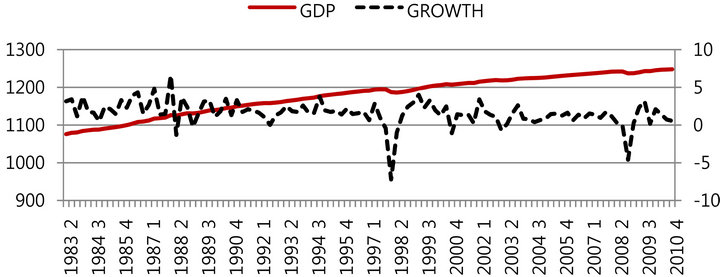
Figure 1. Real GDP and Growth, 1983:Q2-2010:Q4.

Table 1. Parameter Estimates.
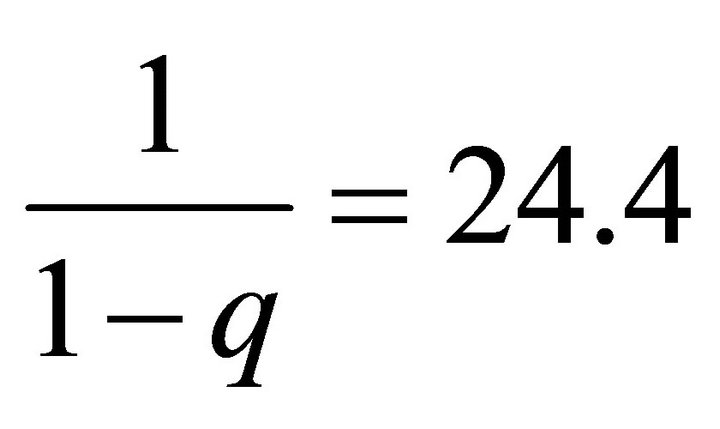
quarters, much longer than the pluck-down periods which last
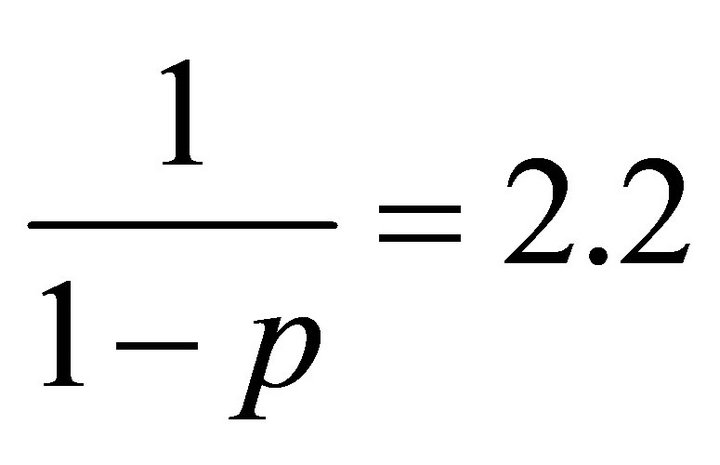
quarters. The long run AR coefficient 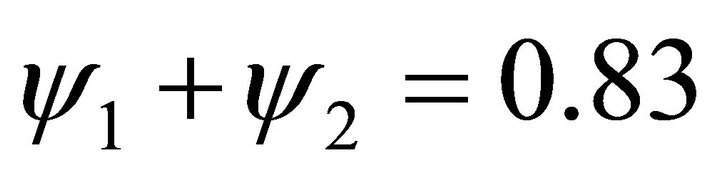 show considerable degree of inertia of a shock to the transitory component.
show considerable degree of inertia of a shock to the transitory component.
The results for the trend component also support the presence of asymmetry. The estimate of 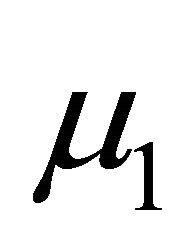 is −0.036, indicating a significant drop in the drift term in the contractionary periods: combined with the estimate
is −0.036, indicating a significant drop in the drift term in the contractionary periods: combined with the estimate  for the AR coefficient, the resulting decrease in the trend growth relative to the expansionary regime amounts to
for the AR coefficient, the resulting decrease in the trend growth relative to the expansionary regime amounts to
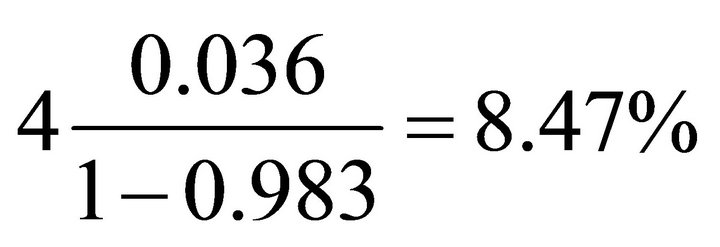
per annum. The estimates of the transition probabilities show that both the high trend growth and low trend growth phases are very persistent, which in turn implies that the shifts in the trend growth rate occur rarely. Finally, the innovations to the trend component exhibit higher degree of volatility in the contraction phase than in the expansion phase.
We now address the main questions of the paper by investigating how the trend and cyclical components of GDP have evolved during the sample period. To do so, we construct the filtered estimates of the two components and their probabilities of being in the pluck-down or contraction phase. The results are summarized in Figure 2.
Our answer to the first question lies in panels (a) and (b), which plot the estimated trend and cyclical components of GDP, respectively, along with the probabilities of cyclical pluck-down. In panel (a), the actual GDP has moved very closely around the trend, except for the periods of the Asian currency crisis and the recent Subprime financial crisis. One important finding here is that
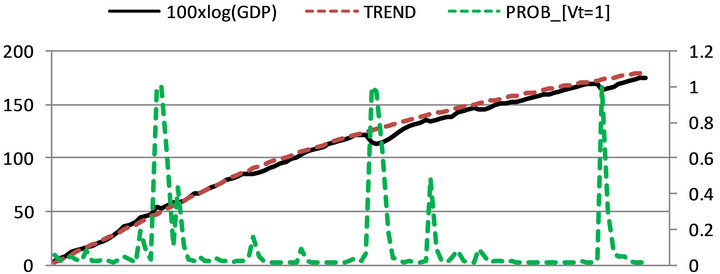
Note: PROB_[Vt = 1] and Trend denote the filtered estimates of the probability of temporary pluck-down and the trend component of GDP, respectively.
(a)

Note: C_t|t denotes the filtered estimate of the cyclical component.
(b)
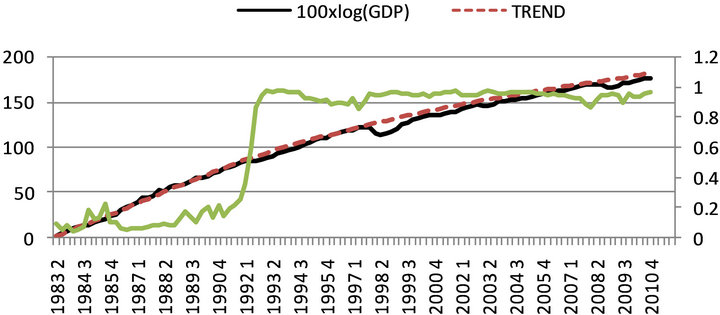
(c)
Figure 2. Estimates of unobserved components and probabilities (filtered): (a) GDP (Actual & Trend) and pluckdown probabilities; (b) transitory component and plucking probabilities; (c) GDP (Actual & Trend) and permanent plucking probabilities.
the decreases in actual output below trend during the two crises are mainly temporary: the actual GDP quickly bounced back to the trend within five years or so past the trough of the crisis-driven recession. Another piece of corroborating evidence is found in panel (b), which plots the output gap (i.e., the cyclical component) against the temporary pluck-down probabilities6. The probability of temporary plucking skyrockets to one around the onset of the Asian crisis, and then decreases toward zero past the troughs of the cyclical components. In summary, the plots in panels (a) and (b) strongly suggest that the effects of the two crises, and the Asian currency crisis in particular, were mainly temporary.
We then turn to the second question: if the effects of the Asian crisis on GDP were temporary, when the slowdown of trend growth happened? In panel (c), the probability of permanent contraction sharply increased above 60% in 1992:Q2 and stayed around 90% since then. Also, the annualized average growth rates of the trend GDP before and after 1992:Q2 are 9.58% and 4.98% respectively. These results imply that, contrary to the mainstream view, the Korean economy has entered the low growth regime years before the Asian crisis7.
In summary, once the regime switch in the permanent component around 1992 is taken into account, the trend growth rate of the Korean economy declines before the two financial crises. Being temporary in its nature, the 1997 crisis (and probably the 2008 crisis as well) caused sharp declines in transitory component of output, but left the (already lowered) trend growth rate intact.
4. Conclusion
In this paper, we reexamine the long run effects of the 1997 Asian crisis on the Korean economy. We estimate unobserved components models subject to Markov regime-switching, in order to address two questions: 1) whether the output losses of Korea during 1997-1998 were permanent or transitory; 2) when the trend growth rate decreased. Estimation results suggest that the trend growth rate of the Korean economy has already declined around 1992-1993 prior to the 1997 crisis. Given the transition of the Korean economy into the low-growth regime in the early 90s, the effects of the crisis are transitory: by the mid-2008, the GDP of Korea has regained most of the ground lost during the 1997 crisis.
5. Acknowledgements
This work was supported by Hankuk University of Foreign Studies Research Fund of 2012. This is gratefully acknowledged by the authors.
REFERENCES
- J. D. Hamilton, “A New Approach to the Economic Analysis Nonstationary Time Series and the Business Cycle,” Econometrica, Vol. 57, No. 2, 1989, pp. 357-384. doi:10.2307/1912559
- M. Friedman, “Monetary Studies of the National Bureau,” National Bureau of Economic Research, New York, 1964.
- M. Friedman, “The Plucking Model of Business Fluctuations Revisited,” Economic Inquiry, Vol. 31, No. 2, 1993, pp. 171-177. doi:10.1111/j.1465-7295.1993.tb00874.x
- V. Cerra and S. C. Saxena, “Did Output Recover from the Asian Crisis,” IMF Staff Paper, Vol. 52, No. 1, 2005, pp. 1-23.
- C. U. Huh and K. Nam, “A Preview of Tale of Korea’s Two Crises: Distinct Aftermaths of 1997 and 2008 Crises,” The Journal of the Korean Economy, Vol. 11, No. 1, 2010, pp. 1-29.
- C.-J. Kim and C. Neslon, “Friedman’s Plucking Model of Business Fluctuations: Tests and Estimates of Permanent and Transitory Components,” Journal of Money, Credit and Banking, Vol. 31, No. 3. 1999, pp. 317-334. doi:10.2307/2601114
- J. C. Morley, C. R. Nelson and E. Zivot “Why Are the Beveridge-Nelson and Unobserved-Components Decompositions of GDP So Different?” Review of Economics and Statistics, Vol. 85, No. 2, 2003, pp. 235-243. doi:10.1162/003465303765299765
- R. J. Barro, “Economic Growth in East Asia before and after the Financial Crisis,” In: D. T. Coe and S.-J. Kim, eds., Korean Crisis and Recovery, IMF, Washington DC, 2002, pp. 333-352.
- R. J. Barro and J.-W. Lee, “Growth and Investment in East Asia before and after the Financial Crisis,” Seoul Journal of Economics, Vol. 16, No. 2, 2003, pp. 84-118.
- C.-J. Kim, “Dynamic Linear Models with Markovswitching,” Journal of Econometrics, Vol. 60, No. 1-2, 1994, pp. 1-22. doi:10.1016/0304-4076(94)90036-1
NOTES
1The recessions and subsequent recoveries in the aftermath of the 1997 crisis are studied in Barro (2002) and Barro and Lee (2003), among others.
2More specifically, they argue that the cumulative output loss during 1997-1999 was 10.3% for Korea.
3Morley et al. (2003) also show that, once the usual unobserved components models are modified to allow correlations among the two disturbances, the resulting decompositions are identical to those by Beverage-Nelson.
4The choice of the initial data period is intentional, with a view to balancing the size of preand post-Asian currency crisis samples, while including the period of sustained growth since the mid 80s.
5Using the ADF test, we fail to reject the null of unit root in GDP at the 10% significance level.
6We should admit that a false alarm of recession is called during 1988:Q1-1988:Q3 by the pluck-down probabilities, in spite of the positive output gap.
7There are several explanations for the slowdown in the trend growth in early 90s: 1) rapid appreciation of the Korean currency won since 1987, 2) increases in labor cost due to political democratization and economic liberalization; 3) changes in the policy stance by the new cabinet toward moderate growth, income redistribution, and stabilization.

