Wireless Engineering and Technology
Vol.3 No.3(2012), Article ID:21469,4 pages DOI:10.4236/wet.2012.33021
Energy-Efficient and Coverage-Aware Clustering in Wireless Sensor Networks
![]()
1Department of Network Engineering and Security, Jordan University of Science and Technology, Irbid, Jordan; 2Department of Computer Engineering, Jordan University of Science and Technology, Irbid, Jordan.
Email: {fhawad, eyadtaq}@just.edu.jo, eng.aseyam@live.com
Received March 20th, 2012; revised April 17th, 2012; accepted April 25th, 2012
Keywords: WSN; Clustering; LEACH; Virtual Field Force; Lifetime; Sensing Coverage
ABSTRACT
Energy efficiency and sensing coverage are essential metrics for enhancing the lifetime and the utilization of wireless sensor networks. Many protocols have been developed to address these issues, among which, clustering is considered a key technique in minimizing the consumed energy. However, few clustering protocols address the sensing coverage metric. This paper proposes a general framework that addresses both metrics for clustering algorithms in wireless sensor networks. The proposed framework is based on applying the principles of Virtual Field Force on each cluster within the network in order to move the sensor nodes towards proper locations that maximize the sensing coverage and minimize the transmitted energy. Two types of virtual forces are used: an attractive force that moves the nodes towards the cluster head in order to reduce the energy used for communication and a repulsive force that moves the overlapping nodes away from each other such that their sensing coverage is maximized. The performance of the proposed mechanism was evaluated by applying it to the well-known LEACH clustering algorithm. The simulation results demonstrate that the proposed mechanism improves the performance of the LEACH protocol considerably in terms of the achieved sensing coverage, and the network lifetime.
1. Introduction
Wireless Sensor Networks (WSNs) are considered among the most interesting technologies in the field of communication and networking. The popularity of WSNs arises from the usage of low-power and low-cost sensor nodes that can be deployed in large numbers. These nodes are used to sense and monitor environmental and physical conditions such as temperature, pressure, humidity, and sound [1] . A WSN may contain one or more base stations (BS) and hundreds of sensor nodes that are deployed either randomly or manually over a specific region of interest. Once deployed, the sensor nodes have the ability to organize themselves into a wireless network [2] and collaborate with each other to sense and get the information from the environment, perform some data processing, aggregate the data, and send them to the BS [3] . The BS is a node with high capabilities and unlimited power that acts as a gateway to other networks. It collects the data from the sensor nodes, performs data processing, and sends the processed data to their final destination via other communication networks such as the Internet [4].
Routing algorithms are developed in accordance with the characteristics of WSNs, the underlined applications, and the requirements of the architecture. Based on the network structure, routing protocols for WSNs are classified into three types: flat routing, location-based routing, and hierarchical routing [2] . In flat routing, all sensor nodes within the sensing region have the same role in accomplishing the sensing task such as in the Sensor Protocols for Information via Negotiation (SPIN) and the Directed Diffusion Protocol [2] . In location-based routing, the sensor nodes are identified by their locations, which are used to form the routing paths towards the BS. Geography Adaptive Routing and Greedy Perimeter Stateless Routing (GPSR) are examples of the locationbased routing protocols [2] . In hierarchical routing, sensor nodes organize themselves into clusters. Each cluster consists of a number of sensor nodes and a cluster head (CH) that acts as a router to the BS [5] . A CH is a node with higher energy than other nodes since it has more advanced tasks such as collecting the data from the nodes in its cluster, processing and/or aggregating the data, and finally sending them to the BS [1] . Examples of hierarchical network routing protocols include Power-Efficient Gathering in Sensor Information Systems (PEGASIS)threshold-sensitive Energy Efficient Protocol (TEEN and APTEEN), and Low Energy Adaptive Clustering Hierarchy (LEACH) [2] .
The general assumption of most clustering protocols for WSNs is that sensor nodes are stationary and hence the network topology is simple and static. Static clustering protocols minimize the signaling overhead of the network because there is no need to maintain and manage the location information of the sensor nodes. Consequently, the sensor nodes can save more energy and extend their lifetime. On the other hand, there are many applications that demand mobility in WSNs components like habitat monitoring, animal tracking, and search and rescue [6] . The Potential Field Force (PFF) is one of the approaches that support mobility of the wireless sensor nodes by means of the applied virtual forces.
PFF is usually used in mobile robotic technologies to facilitate obstacle avoidance and local navigation [7] . PFF refers to an array of vectors each representing a force that can be either repulsive or attractive. Each force consists of two components: a magnitude (m) and a direction (d) [8] . For example, a mobile robot navigating an unknown environment is subject to repulsive forces caused by the obstacles and an attractive force caused by the target. The resultant net force directs the robot towards the target while avoiding the obstacles. When applied to a WSN cluster, every sensor node is subjected to repulsive forces caused by nearby sensor nodes in order to spread out and increase the overall sensing coverage and an attractive force by the CH in order to reduce the needed communication energy [9].
The energy constraint in WSNs is a major challenge to the development of many potential applications. Several research projects investigated such constraint [3] . Hierarchal routing protocols are considered among the most important routing protocols that are designed to reduce the energy consumption in WSNs. However, most of such protocols focused on reducing the energy consumption with no regard to the sensing coverage achieved by the network. The sensing coverage, which is an important metric in several applications such as military surveillance, represents a good measure of how efficient the deployment of the sensor nodes was and how much the network resources were utilized.
This paper proposes an efficient general framework for clustering algorithms that improves the nodes’ locations within the network in order to enhance the overall sensing coverage and reduce the overall energy consumption. This framework can be applied to any clustering algorithm such as LEACH, TEEN, APTEEN, and PEGASIS algorithms. In order to prove its concept and to evaluate its performance, the proposed framework is applied to the LEACH clustering protocol [10] to form a new clustering protocol called LEACH-VF (LEACH with Virtual Force).
The rest of this paper is organized as follows: Section 2 overviews the related state-of-the-art protocols. Section 3 presents the analytical model of the proposed algorithm. The simulation parameters and results are presented in Section 4; along with the analysis of corresponding results. Section 5 concludes the paper.
2. Related Work
The limited power of the sensor nodes is considered the most important problem that faces the design of WSNs since recharging or replacing nodes’ batteries is usually infeasible. Due to its severe impact on the operational lifetime of the network, the energy consumption problem in WSNs was addressed by several research articles. Most of the effective mechanisms proposed employ the hierarchical architecture due to its scalability and the efficient communication [11] . Also, the energy consumption in the sensor nodes has a great impact on the overall sensing coverage of the network. That is, when a sensor node consumes all its energy, it dies, creating a sensing coverage hole. Hence, extending the lifetime of the network and balancing the remaining energy of the sensor nodes enhances the sensing coverage area of whole network.
LEACH is one of the most popular clustering algorithms designed for WSNs due to its effectiveness in reducing the energy consumption in the network and extending its lifetime by balancing the remaining energy of the sensor nodes. The idea of the LEACH protocol is to organize the sensor nodes into local clusters, where each cluster has one CH that acts as a router to the BS [10] . This organization conserves energy because the transmission to the BS is done only by the CHs rather than all sensor nodes. CHs have the functionality of creating and manipulating a Time Division Multiple Access (TDMA) schedule, receiving data from non-cluster sensor nodes, aggregating, and sending the received data to the BS. The optimal number of CHs used is 5% of the total number of sensor nodes. The CHs are changed periodically in a random fashion in order to balance the remaining energy of the nodes.
Simulation results demonstrated that LEACH consumed less energy compared with direct communication, minimum-transmission-energy routing (MTE), and a conventional static clustering protocol. However, the LEACH protocol suffers from some problems, one of them is related to the random selection of CHs. This process does not consider the locations of the sensor nodes in the network, and hence the sensor nodes may be very far from their CH, causing them to consume more energy to communicate with the CH.
In [12,13], the CH selection techniques based on the nodes’ remaining energy were proposed. However, the process of selecting CHs without taking into consideration the nodes’ locations may have a negative impact on the overall performance [14] . Other research work considered clustering algorithms based on the location information of the sensor nodes as in [14-18]. However, these algorithms improved only the network lifetime and did not consider the sensing coverage.
On the other hand, in [19,20], LEACH-based algorithms that dealt with the sensing coverage were introduced. These algorithms assume simple and stationary network topologies and do not support mobility. In fact, several WSN applications that depend on tracking and searching require the mobility of the sensor nodes. Therefore, LEACH-based algorithms with mobility support were proposed in [6,21,22], but mainly focused on the data delivery and the CHs selection problems in mobile sensor networks. The mobility of the sensor nodes can be assumed for different purposes. One of these purposes is to improve the sensing coverage by allowing the sensor nodes to move to better locations. The PFF method was applied in the sensor field to satisfy various requirements such as network coverage [23], K-neighbor coverage [24], and node deployment and target localization [25].
3. The Proposed LEACH-VF Algorithm
This paper proposes a general framework to address two major issues in clustering protocols for WSNs: the network lifetime and the sensing coverage. This framework uses the principles of Virtual Field Force (VFF) [25] to determine the locations of the nodes within each cluster, in order to maximize the sensing coverage and minimize the energy consumption of these nodes, which in turn maximizes the lifetime of the network and extends its usability. The proposed framework is applied to the LEACH clustering protocol [10]. The new clustering protocol is called LEACH-VF (LEACH with Virtual Force).
To explain the idea of the LEACH-VF protocol and present its potential advantages, consider the simple LEACHbased cluster with six sensor nodes shown in Figure 1(a). The outer large circle represents the cluster area and the small circles indicate the sensing coverage of each sensor node. The circle in the middle of the cluster represents the sensing coverage of the CH. There are four problems with this cluster caused by the random distribution of nodes and the random selection of CHs:
1) There are areas with overlapped sensing coverage (i.e., areas covered by more than one sensor node). For example, sensor nodes 4 and 6 have a relatively large sensing coverage overlap.
2) There are areas with sensing holes (i.e., areas with no sensing coverage).
3) Some sensor nodes have coverage outside the cluster area. For example, sensor node 5.
4) Some sensor nodes are located relatively far from their CHs, while they can be relocated in closer places and still be useful to the cluster at a lower energy cost.
When the proposed LEACH-VF algorithm is applied to this cluster, the result is shown in Figure 1(b).
It is worth noting that the above-mentioned problems were resolved. Thus, the LEACH-VF algorithm takes a regular LEACH-based cluster as input and produces a corresponding sub-optimal LEACH-VF cluster to be used for data transmission.
3.1. Network Model and Assumptions
In this paper, we consider a WSN with one base station and N sensor nodes that are randomly distributed within a specific region.
The following assumptions related to the network are used throughout this paper:
1) The base station is stationary and is located outside the region.
 (a)
(a)  (b)
(b)
Figure 1. (a) Problems with the LEACH-based clustering and (b) Output of LEACH-VF.
2) The sensor nodes are homogeneous in terms of hardware and software capabilities.
3) The sensor nodes are energy constrained and have the same initial energy reservoir.
4) Each sensor node is able to detect its own location using some location identification algorithm.
5) The sensor nodes are mobile. However, the mobility is limited to the cluster setup duration and is dictated by the CH to which the sensor node is associated. Otherwise, the sensor nodes are considered stationary.
6) The sensor nodes have the same sensing range denoted by Rs.
7) The CH has a communication range denoted by Rc.
8) The first order radio model defined in [10] is used.
3.2. The LEACH-VF Algorithm
The LEACH-VF algorithm consists of three phases:
1) The cluster forming and set-up. This phase is very similar to that of the LEACH protocol, where the network is divided into clusters via the CH election; except that the sensor nodes report their current locations to the CH they are associated via the cluster-join message.
2) The virtual force computation and sensor nodes re-location. In this phase, each CH applies the VFF principles to the sensor nodes associated with it. After that, the CH informs the sensor nodes of the new locations, to which they should move.
3) The steady-state or data transmission. This phase is the same as in LEACH, where each sensor node, after it moves to its new location determined by the CH, senses and transmits the sensed data during the time slots assigned to it by the CH during the setup phase.
3.2.1. The Analytical Model
The main objective of the proposed algorithm is to determine the locations of the sensor nodes within each cluster such that the sensing coverage of these nodes is maximized and the energy cost of communication is minimized. That is, the sensor nodes need to be moved towards the CH in order to minimize the transmit power and away from each other in order to maximize the sensing coverage. Therefore, it is assumed that the sensor nodes are attracted towards the CH via a virtual attractive force and are repelled away from each other via a virtual repulsive force. The resultant of these forces defines the new location to which the sensor node should move.
Each force, expressed in polar coordinates, is defined by a tuple [F, θ] of two components: the magnitude, F, which represents the amount of exerted force, and the angle, θ, which represents the direction of the force. The amount of exerted force is converted into a displacement that represents the distance that the sensor node should travel, in that direction.
The types of forces used in LEACH-VF are defined and discussed as follows:
1) The Forces Exerted by the Cluster Head. The amount of attractive force exerted by the CH on a sensor node Si is directly proportional to the distance between the sensor node and the CH, dic. This only applies if dic > 2Rs, where Rs is the sensing range of the sensor node. However, if dic < 2Rs, then the sensing coverage areas of Si and the CH are overlapping. In this case, the CH exerts a repulsive force on Si, which is reversely proportional to dic, in order to maximize the sensing coverage of both nodes. The force, Fic, exerted on Si by the CH can be mathematically expressed as follows:
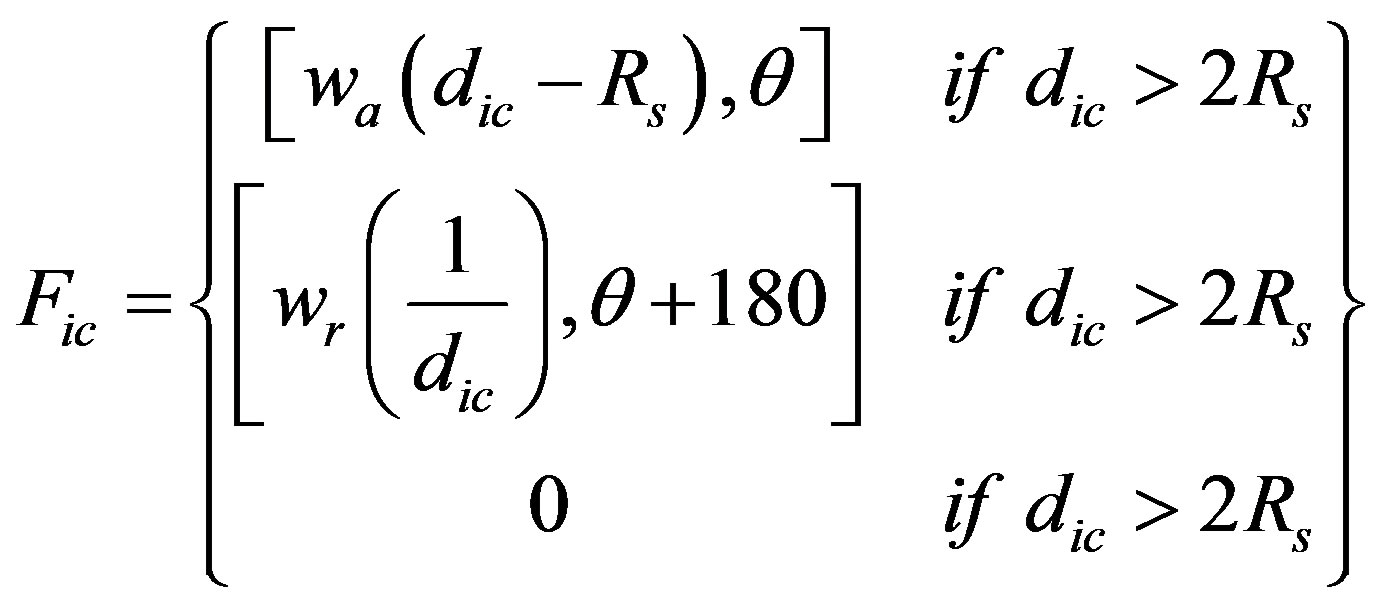 (1)
(1)
where wa and wr are the attractive and repulsive force weights; respectively, and θ is the angle of a line segment from the node to the CH. It is worth noting that wa and wr directly impact the resultant force such that high values of these parameters result in large movements of sensor nodes. According to [25] , the computed forces will be effective only if wr >> wa.
2) The Repulsive Force Exerted between the Sensor Nodes. When two sensor nodes Si and Sj are at very close proximity such that the sensing coverage areas are overlapping, each sensor node exerts a repulsive force on the other node in order to maximize the overall sensing coverage area. This force is inversely proportional to the distance between the two sensor nodes, dij, such that the overlapped area is omitted. The repulsive force between the sensor nodes is mathematically defined as follows:
 (2)
(2)
where Fij is the repulsive force that is exerted on sensor node i by sensor node j, dij is the distance between sensor nodes i and j, and θ is the angle of a line segment between the two sensor nodes.
3) Finally, the resultant force exerted on the sensor node Si is the sum of all the forces exerted by the CH and all other sensor nodes. Hence,
 (3)
(3)
3.2.2. The Virtual Force Computation Phase
The Virtual Forces Computation (VFC) is the second phase of the LEACH-VF protocol. In this phase, the forces that are exerted on each sensor node by the other nodes and the CH are computed. Each node sends its location information to the CH, which is responsible for executing the algorithm and finding the best new locations that satisfy the coverage and energy requirements. The algorithm is iterative and depends on the concept of the virtual forces as in [25] . In each iteration, the CH computes the virtual forces that are exerted on each sensor node within its cluster, moves the sensor nodes virtually to the new locations (by virtually, it is meant that no actual movements occur during the execution of the algorithm), and tests the effect of these locations on the energy and coverage requirements (the energy and coverage requirements are considered as exit conditions for the algorithm). At the end of the execution, the sensor nodes are informed of the new locations to which they should finally move. The key steps of the VFC phase are:
1) Compute the forces that are exerted on each sensor node inside the cluster.
2) Move the sensor nodes virtually to the new locations after finishing each iteration.
3) Test the exit conditions.
a) If the virtual locations satisfy the exit conditions, the sensor nodes move to the new locations, and the algorithm terminates.
b) If not, a new iteration is executed until satisfying the exit conditions or finishing the maximum number of iterations.
The pseudo-code shown in Table 1 summarizes the general process of the VFC phase.
4. Simulation Results
Since the aim of the LEACH-VF protocol is to address the coverage and energy metrics, four versions of the algorithm are presented based on the following cases:
1) Coverage Only (CO): the algorithm runs with the goal of maximizing the coverage metric only.
2) Energy Only (EO): the algorithm runs with the goal of minimizing the energy metric only.

Table 1. Pseudo code for virtual force computation.
3) Energy & Coverage (CE): the algorithm works until both the coverage and energy requirements are maximized; concurrently.
4) Energy First (EF): the algorithm runs in two steps. First, it minimizes the energy metric. Then, it runs until the coverage metric exit condition is met.
The simulation is divided into two parts. In the first part, the four cases are evaluated for different scenarios in order to choose the best case and apply it to the LEACH protocol. In the second part, the LEACH and LEACH-VF algorithms are compared in terms of the network lifetime and sensing coverage; using the best case chosen in the first part.
4.1. Evaluation of the Four Cases
In this part, the four cases presented earlier are examined in order to choose the most appropriate case to be used to evaluate the performance of the LEACH-VF protocol. For each simulation scenario, a number of sensor nodes are deployed randomly within a circular region representing the cluster. Table 2 summarizes the simulation parameters used in this part.
The four cases are evaluated and compared based on four performance metrics: the achieved sensing coverage, the average moved distance, the average distance to the CH, and the number of iterations used.
The attractive and repulsive weights, wa and wr, were fixed at constant values throughout the simulations. These values were obtained via experimentation.
Figure 2 shows the achieved sensing coverage, as a percentage of the maximum possible coverage, for the four cases. Note that the coverage area of a single sensor node is equal to 1% of the cluster area and hence the maximum possible coverage for N nodes is equal to N%. It is obvious that, regardless of the case used, the sensing coverage increases with the number of sensor nodes for two reasons:
1) In general, each added sensor node contributes to the overall coverage achieved.
2) In all cases, the repulsive forces among the sensor nodes with overlapped coverage keep moving these sen-
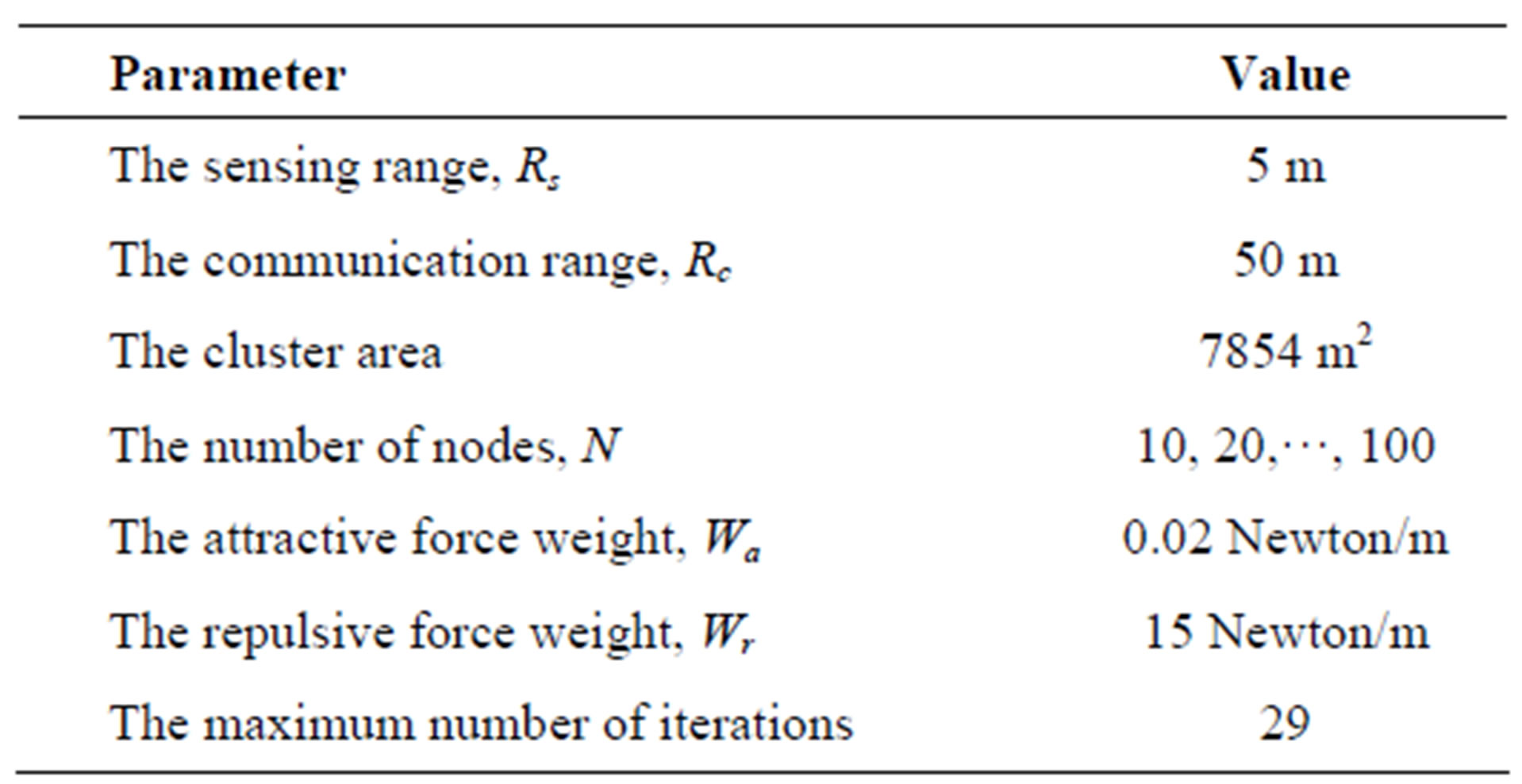
Table 2. Simulation parameters for the evaluation of the four cases.
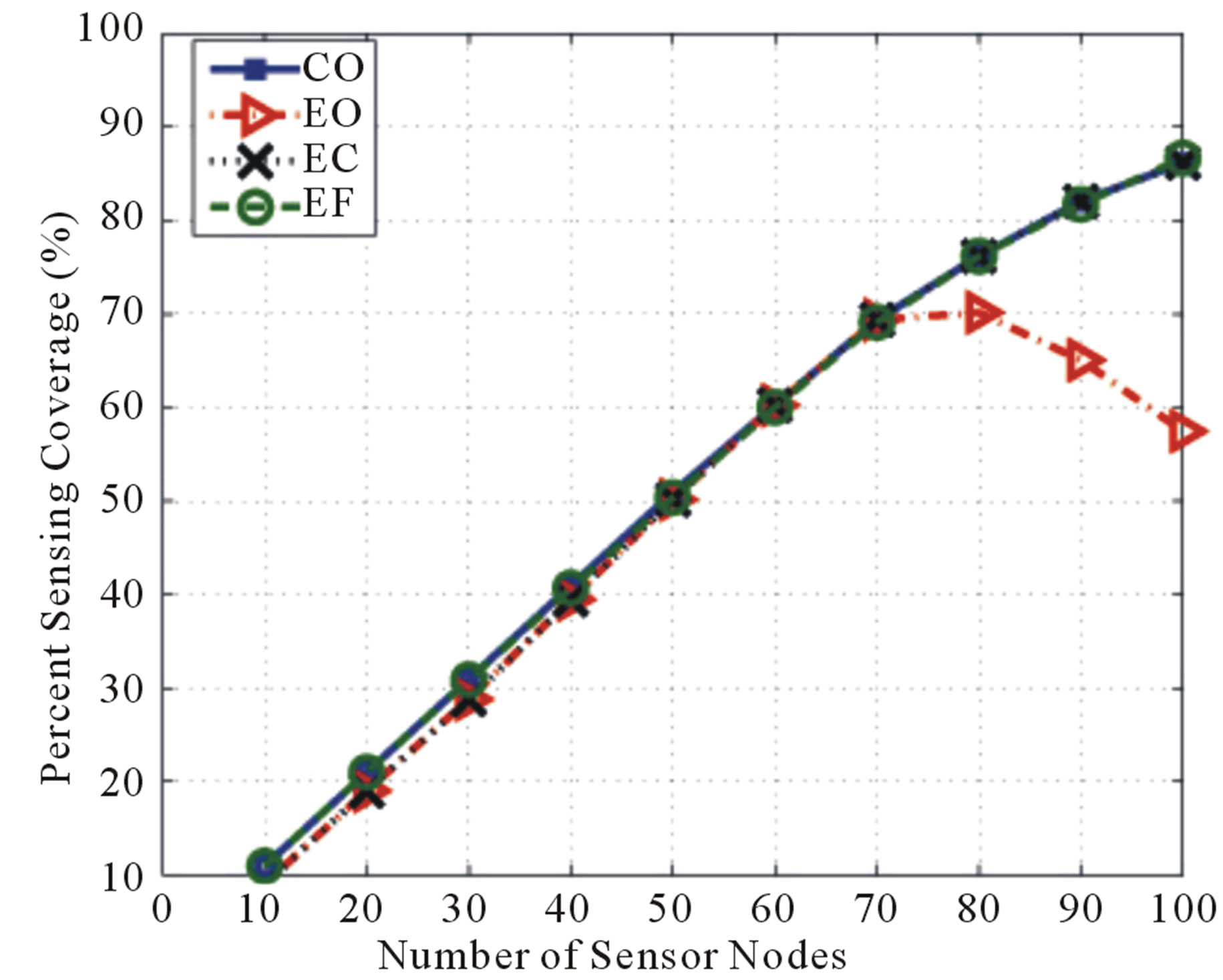
Figure 2. A comparison of the achieved sensing coverage.
sor nodes away from each other, which, in turn, increase the overall coverage.
However, as the network density changes from low (e.g. N < 40), to medium (e.g.; 40 ≤ N ≤ 70), to high (e.g. N > 70), the following observations are worth mentioning:
1) For low and medium node densities, all cases almost achieve the maximum possible coverage. This is caused by the fact that the cluster area is relatively much larger than the collective coverage of all sensor nodes. Hence, with relatively slight movements of the sensor nodes away from each other, the coverage overlap is removed and, as a result, the maximum sensing coverage is easily achieved. However, the EO and EC cases achieve slightly less sensing coverage than the maximum because the EO attempts to minimize the energy consumption regardless of the achieved coverage and the EC attempts to find the best tradeoff between both, which is harder to achieve and hence requires more iterations to perform.
2) For high node densities (e.g. N > 70), the achieved sensing coverage starts to slightly depart from the maximum possible coverage for CO, EC, and EF cases, whereas for the EO case, it starts to decline rapidly. This is generally caused by two factors:
a) As the nodes become dense, the sensor nodes become closer to each other and, as a result, the coverage overlap increases. In addition, the repulsive forces among the sensor nodes become more balanced, which limits the movements and keeps some of the overlapping areas.
b) Since the cluster area and the sensing range of the nodes are represented by circles, the coverage holes and overlapping areas are inevitable.
For the EO case, since the goal is to minimize the energy consumption in a node-dense area, the balance in the forces is reached relatively fast and the algorithm exits with a few number of iterations and hence with minimal node movements.
Figure 3 shows a comparison of the average moved distance per sensor node for the cases. It is obvious that each case behaves almost in a unique way. For high node densities, the average moved distance for all cases decreases as the node density increases. This is because, both the coverage and the energy requirements are satisfied almost up front and hence the sensor nodes need not be moved much. However, in the EO case, the drop rate in the moved distance is faster than the other cases. This only means that the energy requirements are met much faster than those of the sensing coverage as explained earlier. For low and medium node densities, the behaviors of the cases are very much different. For the CO case, the average moved distance is directly proportional to the number of nodes. The reason is that as the node density increases, so does the coverage overlapping, which causes the sensor nodes to move farther away from each other in order to spread out and achieve the coverage requirements. Whereas, for the EO and the EC cases, when the number of nodes is small, they need to move relatively long distances in an attempt to be as close to the CH as possible. On the other hand, since the EF case is a balanced combination of the CO and the EO cases, its behavior is in between the two.
Figure 4 shows the number of iterations used by the four cases. It is observed that the behavior is very similar to that of the average moved distance and for similar reasons, except that the number of iterations has a ceiling of 29. Thus, the total number of iterations for the CO case is directly proportional to the number of sensor nodes. This is due to the fact that as the number of nodes increases, the coverage overlap increases, and hence more iterations are needed to gradually remove it. However, for the EO case, a relatively large number of iterations are used for low node density and very small number of iterations at high node densities. This is related to
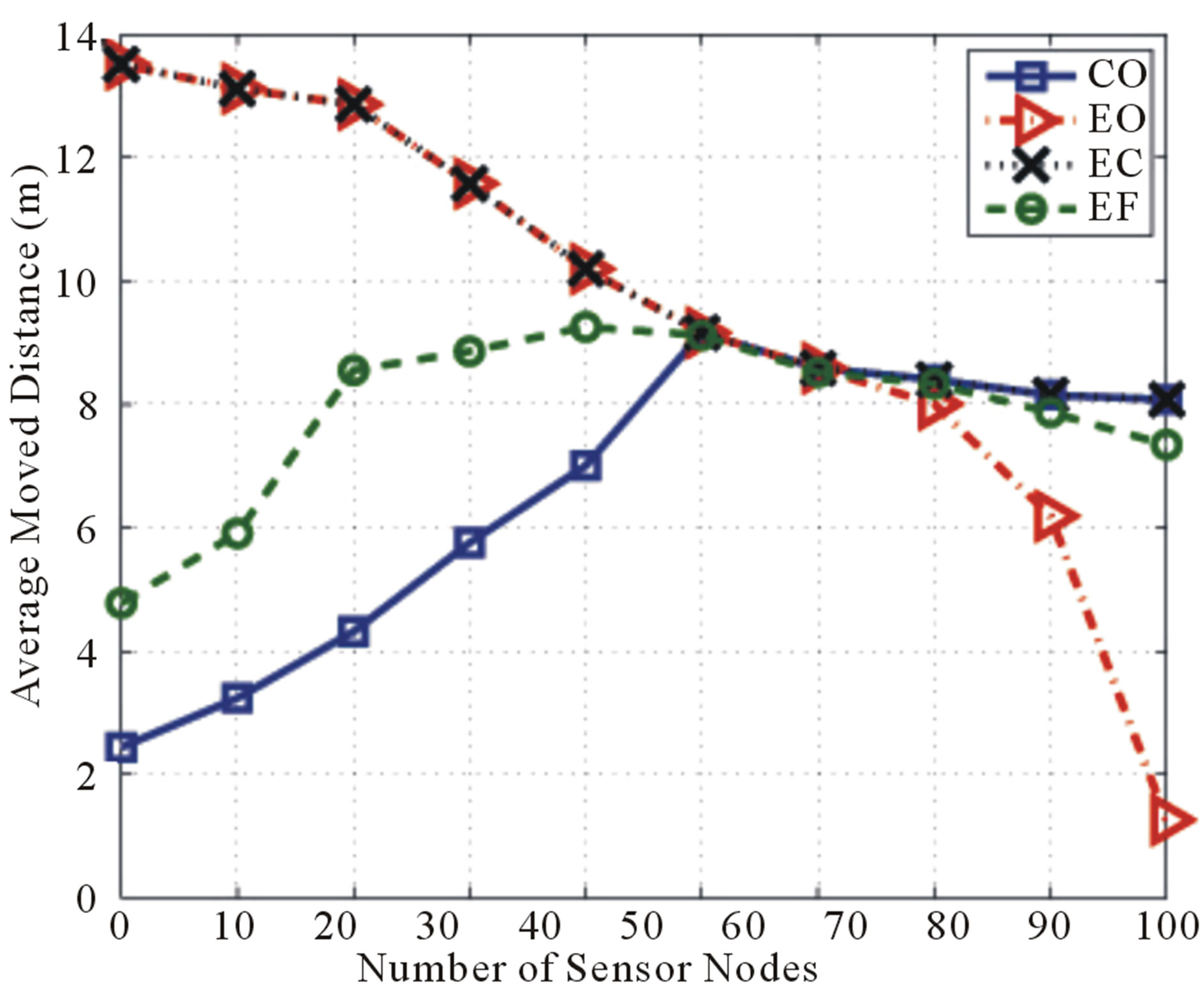
Figure 3. A comparison of the average moved distance.
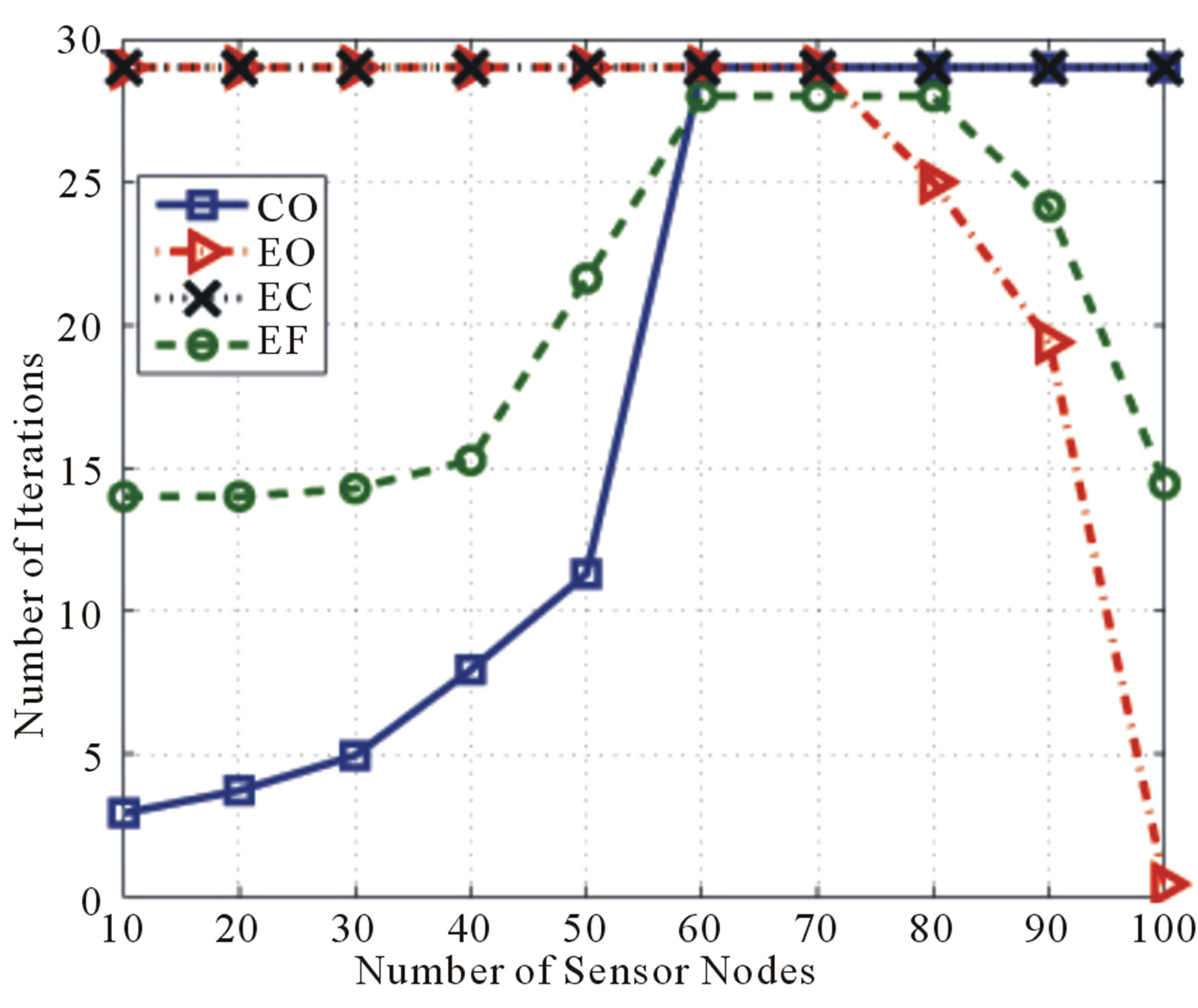
Figure 4. A comparison of the total number of iterations.
the energy requirements and the associated distance to move towards the CH, as discussed earlier. On the other hand, the EC case always takes more iterations than the EF case even though the two cases achieve their coverage and energy requirements at the end. The difference is in the way they operate in order to achieve such requirements. For the EC case, the goal is to achieve both requirements simultaneously, which is harder to do and hence it requires a larger number of iterations. Whereas, in the EF case, the goal is to satisfy the energy requirement first, with no more than half of the maximum number of iterations, then satisfy the coverage requirements. This reduces the total number of iterations used.
Figure 1 shows the average distance from the nodes to the CH for the four cases. For high node densities, all cases produce the same result, where the average distance is directly proportional to the node density. However, for low and medium node densities, the CO case produces the worst average distance among all cases because it attempts to maximize the sensing coverage only and is not concerned with moving the nodes towards the CH. Whereas the EO and the EC cases achieve the best average distance, which is expected since both attempt to minimize the energy consumption. On the other hand, for the EO case, the average distance is almost half-way between the extreme cases.
Although the goal of the proposed algorithm is to achieve the highest possible coverage and energy gains with the least number of iterations and average moved distance per sensor node, none of the cases can achieve all the requirements simultaneously. However, the best compromise among all is found to be by the EF case since it achieves the highest possible sensing coverage for low and medium node densities and 60% - 70% at high node densities, and the best balance in the other three metrics compared to the other cases. Therefore, the

Figure 5. A comparison of the average distance to CH.
EF case is selected for the LEACH-VF protocol to be compared to LEACH.
4.2. Performance Comparison of LEACH and LEACH-VF Protocols
A performance comparison between the LEACH and LEACH-VF algorithms for different node densities is presented here using the following performance metrics:
1) The sensing coverage: the percentage of the network area covered by the sensor nodes.
2) The network lifetime: the round, at which the first sensor node dies.
3) The total remaining energy: the network total remaining energy.
4) The remaining energy per node: the average remaining energy per live sensor node.
5) The average moved distance (for LEACH-VF only): the average distance moved by the sensor nodes from the initial location to the new location.
It is worth noting here that, in this part, Rc is not fixed anymore, but it is rather dependent on the distance between the CH and the farthest sensor node associated with it; based on the LEACH protocol. Table 3 summarizes the simulation parameters used.
4.2.1. Medium Sensor Node Density: N = 60
Figure 6 shows the percentage of the achieved sensing coverage during each round for both LEACH and LEACH-VF. It demonstrates that LEACH-VF outperforms LEACH by about 25% for the first 450 rounds. Beyond that, the improvement starts to rapidly increase between rounds 450 to 600, and then it starts to decrease after that. This behavior can be explained as follows:
1) For the first 450 rounds, during which both protocols are in steady-state with all nodes still alive, the percent coverage of LEACH-VF is slightly higher than that

Table 3. Simulation parameters for performance comparison.
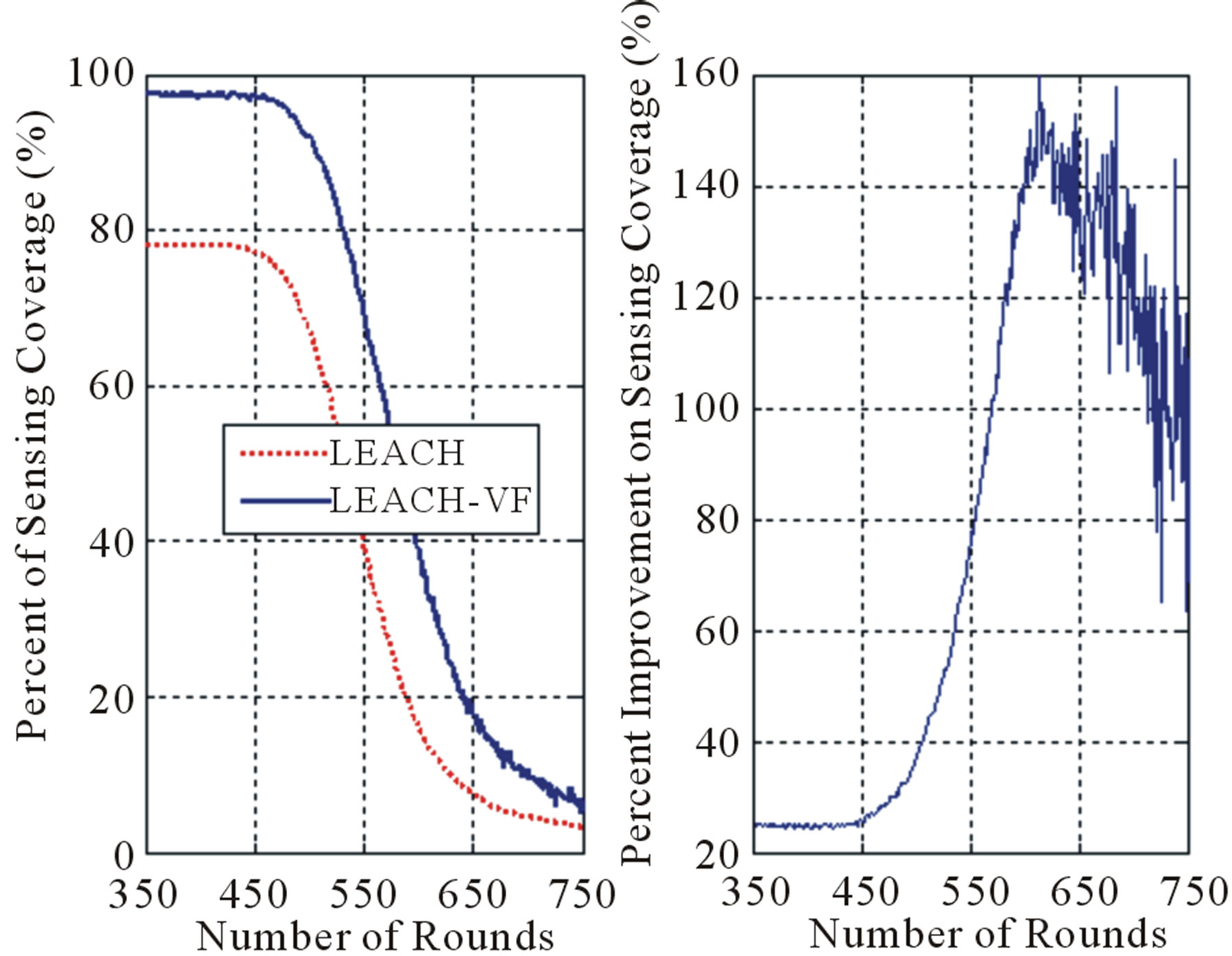
Figure 6. Percent sensing coverage for N = 60.
of LEACH, and since the node density is medium, the coverage overlap is initially medium. Therefore, LEACHVF moves the sensor nodes towards the CH to conserve in communication energy and slightly away from each other to remove the coverage overlap.
2) For rounds 450 to 600, the improvement in the sensing coverage rapidly increases to reach a maximum of about 150%. This is attributed to the fact that nodes running LEACH die very fast, as seen in Figure 7, while LEACH-VF nodes are still mostly alive. Obviously, the movement of the sensor nodes towards the CH conserves a considerable amount of the sensor nodes’ communication energy, as illustrated in Figure 8. Hence, as more LEACH nodes die, more sensing coverage is lost within the cluster.
3) For rounds 600 and above, the LEACH-VF nodes start to die at a rate slightly faster than that of LEACH, as seen in Figure 7. Therefore, the difference in the sensing coverage between the two protocols starts to diminish.
Figure 7 shows that LEACH-VF extends the percentage of live nodes by to 140%.
Figure 8 illustrates the distribution of the nodes after 570 rounds in LEACH and LEACH-VF. It is observed that the number of dead nodes in LEACH is higher than that in LEACH-VF. Is it also noticed that the live LEACH-VF sensor nodes are well-distributed over a large portion of the area around the middle.
Figure 9 shows the total remaining energy in the LEACH and LEACH-VF nodes for each round and the average amount of energy conserved per live node. It is
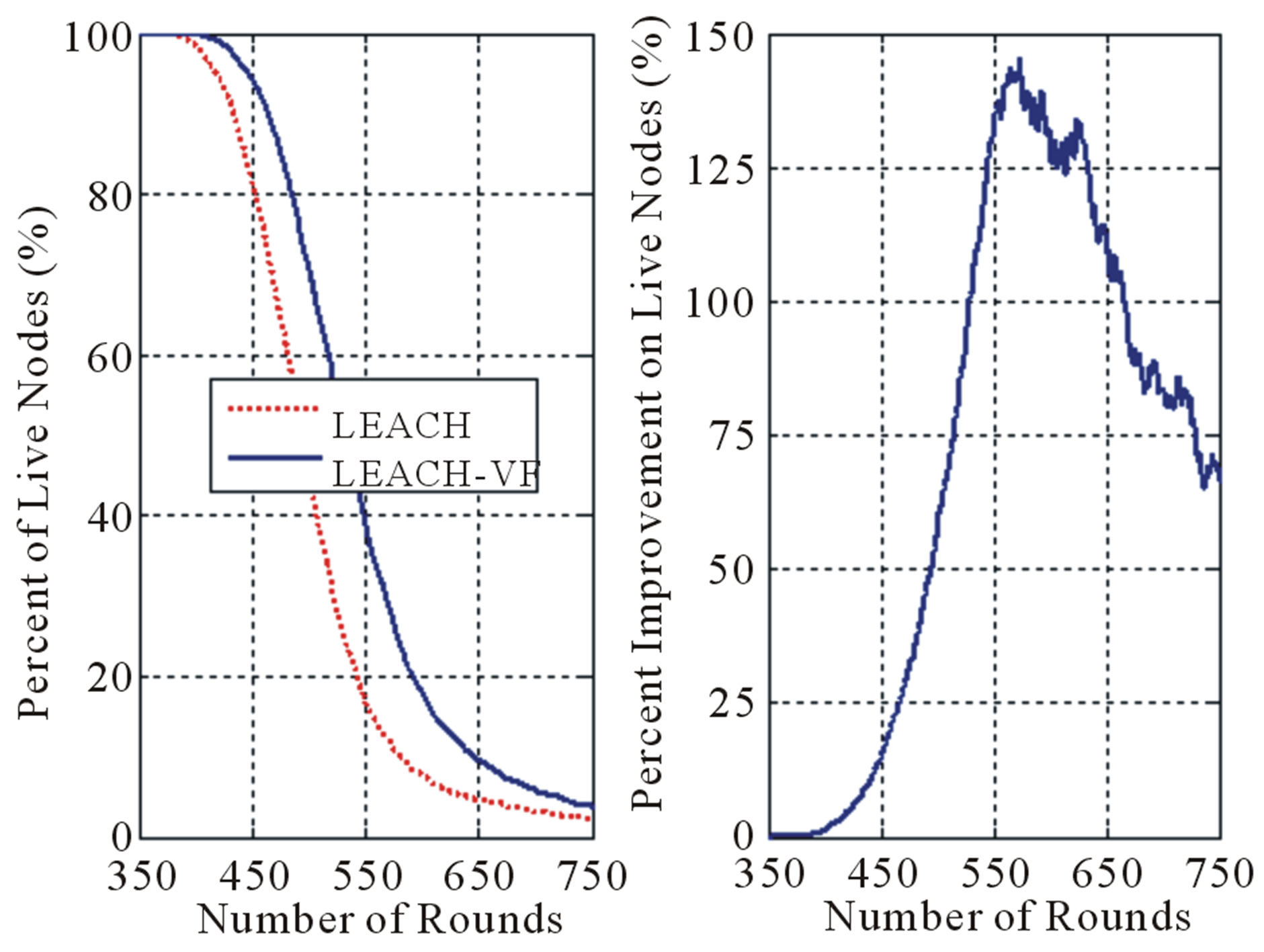
Figure 7. Live sensor nodes for N = 60.

Figure 8. Live sensor nodes (circles) vs dead sensor nodes (dots) after 570 rounds for N = 60.
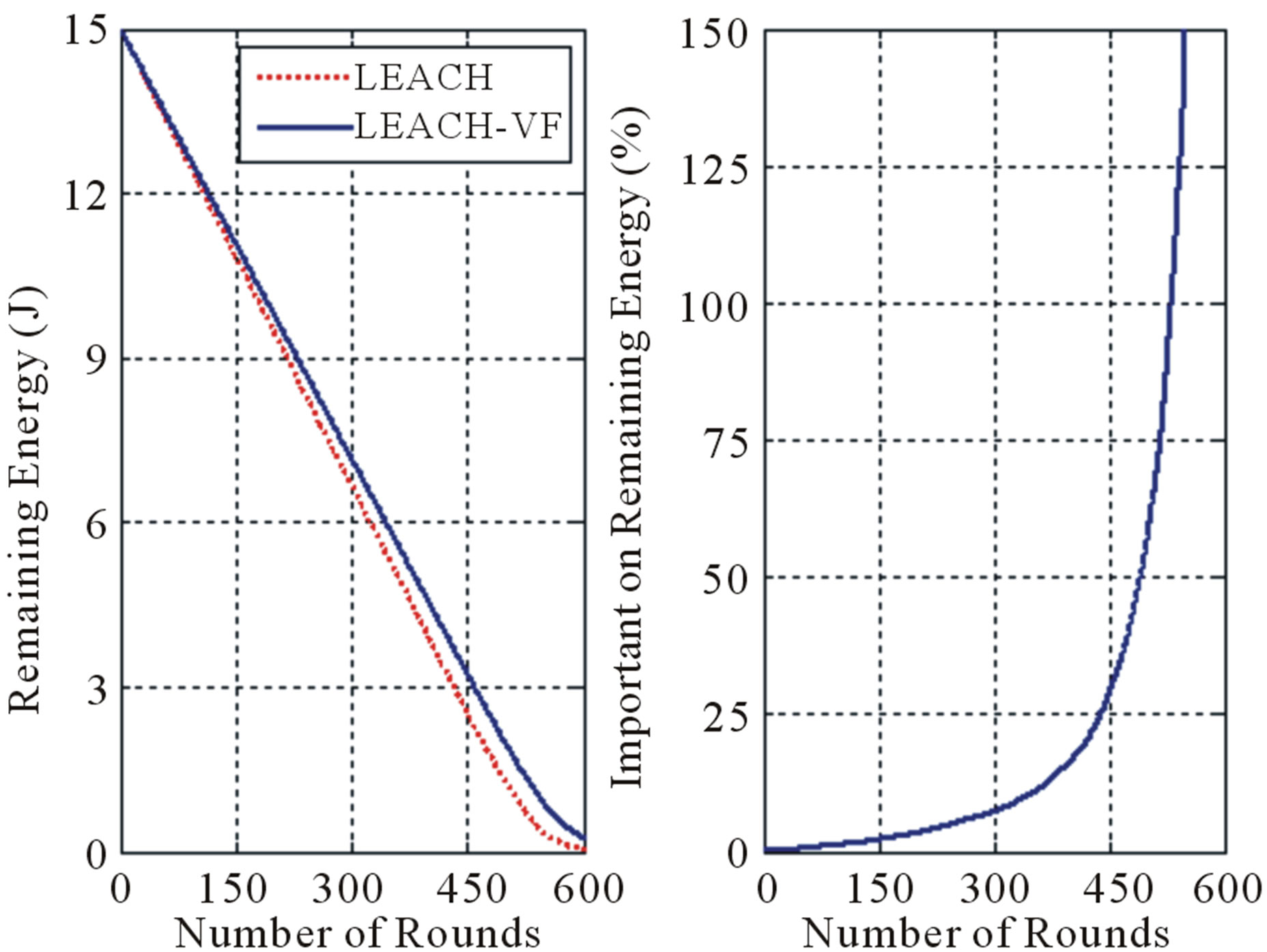
Figure 9. Total remaining energy for N = 60.
obvious that the energy depletes much faster with LEACH than with LEACH-VF.
4.2.2. Analysis of the Results
This section presents a closer look at the obtained results, where the performance of the LEACH-VF is summarized and compared for each of the performance metrics used. The results show that the LEACH-VF protocol outperforms the LEACH protocol in all cases.
Figure 10 shows the impact of the node density on the achieved sensing coverage of the network. It is evident that the improvement in the sensing coverage is mostly apparent in networks of medium density.
Figure 11 summarizes the LEACH-VF improvement regarding the number of sensor nodes that are still alive in the network. The improvement is maximum for medium density networks. Although the improvement is less for low and high density networks, there is still a relatively good improvement on the number of live sensor nodes.
5. Conclusions and Future Work
The proposed algorithm addresses both the energy con-

Figure 10. LEACH-VF sensing coverage improvement.

Figure 11. LEACH-VF improvement on live sensor nodes.
sumption and the sensing coverage issues in WSN clustering protocols, which can be applied to and integrated with about any existing WSN clustering algorithm. This framework uses the concept of the virtual field force within each cluster in order to determine the nodes’ locations such that the sensing coverage is maximized and the energy consumption used for data transfer is minimized, which in turn extends the network lifetime.
In order to demonstrate its effectiveness in addressing the energy consumption and sensing coverage problems, the proposed algorithm was applied to the LEACH protocol and the new protocol is called LEACH-VF.
The simulation results demonstrated that LEACH-VF outperforms LEACH in terms of the achieved sensing coverage and the number of live sensor nodes by 150% and 140%; respectively. Moreover, after 600 rounds, the energy in the LEACH nodes is mostly depleted whereas the LEACH-VF nodes still maintain enough energy to survive for more rounds.
As a conclusion, even though it can jointly enhance both the sensing coverage and the network lifetime, the proposed framework also provides a performance enhancement tradeoff between the two metrics. That is, depending of the application requirements of the WSN used, the framework may be tuned to maximize the coverage only, the energy only, both equally, or both with a priority, which adds a needed flexibility to the practical side of it.
One last thing to mention here is related to the energy cost of moving the nodes to the final location during each round. Even though the energy cost of node mobility was never considered in all the previously proposed protocols in the literature [21,22] (neither does the protocol presented in this research), it is believed that it is crucial issue to mention. Most probably, the reason that this important cost factor was never considered is that it is highly dependent on the mobility mechanism and the associated hardware used. To the best of our knowledge, there is no existing reference model that can be used. Therefore, it is believed that if the energy cost of the mobility is less than the energy saved by the reduced communication cost, then the proposed framework can offer a decent enhancement on both the lifetime and sensing coverage. But, if the two costs are approximately equal, then, at least, the sensing coverage can be enhanced.
REFERENCES
- J. Zheng and A. Jamalipour, “Wireless Sensor Networks: A Networking Perspective,” Wiley-IEEE Press, New York, 2009. doi:10.1002/9780470443521
- J. Al-Karaki and A. Kamal, “Routing Techniques in Wireless Sensor Networks: A Survey,” IEEE Wireless Communications, Vol. 11, No. 6, 2004, pp. 6-28. doi:10.1109/MWC.2004.1368893
- S. Singh, M. Singh and D. Singh, “Routing Protocols in Wireless Sensor Networks: A Survey,” International Journal of Computer Science and Engineering Surveys, Vol. 1, No. 2, 2010, pp. 63-83. doi:10.5121/ijcses.2010.1206
- K. Akkaya and M. Younis, “A Survey on Routing Protocols for Wireless Sensor Networks,” Ad Hoc Networks, Vol. 3, No.3, 2005, pp. 325-349. doi:10.1016/j.adhoc.2003.09.010
- L. Almazaydeh, E. Abdelfattah, M. Al-Bzoor and A. AlRahayfeh, “Performance Evaluation of Routing Protocol in Wireless Sensor Networks,” International Journal of Computer Science and Information Technology, Vol. 2, No. 2, 2010, pp. 64-73. doi:10.5121/ijcsit.2010.2206
- L. Nguyen, X. Defago, R. Beuran and Y. Shinoda, “An Energy Efficient Routing Scheme for Mobile Wireless Sensor Networks,” Proceedings of the IEEE International Symposium on Wireless Communication Systems, Reykjavik, 21-24 October 2008, pp. 568-572. doi:10.1109/ISWCS.2008.4726120
- M. Goodrich, “Potential Fields Tutorial,” 2002.
- R. Siegwart and I. Nourbakhsh, “Potential Fields Tutorial,” 2008.
- A. Ghosh and S. Das, “Coverage and Connectivity Issues in Wireless Sensor Networks: A Survey,” Pervasive Mobile Computing, Vol. 4, No. 3, 2008, pp. 303-334. doi:10.1016/j.pmcj.2008.02.001
- W. Heinzelman, A. Chandrakasan and H. Balakrishnan, “Energy-Efficient Communication Protocol for Wireless Microsensor Networks,” Proceedings of the Hawaii International Conference on System Science, Maui, 4-7 January 2000, pp. 10-19.
- X. Ma, Y. Fang and X. Bai, “A Balanced Energy Consumption Clustering Algorithm for Heterogeneous Energy Wireless Sensor Networks,” Proceedings of the IEEE International Conference on Wireless Communications, Networking and Information Security, Beijing, 25-27 June2010, pp. 382-386.
- H. Gou and Y. Yoo, “An Energy Balancing LEACH Algorithm for Wireless Sensor Networks,” Proceedings of the 7th International Conference on Information Technology: New Generations, Las Vegas, 12-14 April 2010, pp. 822-827.
- M. Thein and T. Thein, “An Energy Efficient Cluster-Head Selection for Wireless Sensor Networks,” Proceedings of the IEEE International Conference on Intelligent Systems, Modeling and Simulation, Liverpool, 27- 29 January 2010, pp.287-291.
- S. Lin, W. Liqin and Z. Zhengwei, “A Clustering Algorithm Based Geographic Location Information for Wireless Sensor Networks,” Proceeding of the 2010 International Conference on Electrical and Control Engineering, Wuhan, 25-27 June 2010, pp. 2588-2592.
- O. Buyanjargal and Y. Kwon, “An Energy Efficient Clustering Algorithm for Event-Driven Wireless Sensor Networks (EECED),” Proceedings of the 5th IEEE International Joint Conference on INC, IMS and IDC, Seoul, 25-27 August 2009, pp. 1758-1763.
- H. Choi, B. Cha and K. Kim, “Energy Efficient Location-Based Clustering for Skewed-Topology Wireless Sensor Networks,” Proceedings of the 3rd International Conference on Grid and Pervasive Computing Workshops, Kunming, 25-28 May 2008, pp. 376-381.
- T. Wang and Z. Yang, “A Location-Aware-Based Data Clustering Algorithm in Wireless Sensor Networks,” Proceedings of the 11th IEEE Singapore International Conference on Communication Systems, Guangzhou, 19- 21 November 2008, pp. 1-5. doi:10.1109/ICCS.2008.4737132
- S. Lee, H. Choe, B. Park, Y. Song and C. Kim, “LUCA: An Energy-Efficient Unequal Clustering Algorithm Using Location Information for Wireless Sensor Networks,” Wireless Personal Communications, Vol. 56, No. 4, 2011, pp. 715-731. doi:10.1007/s11277-009-9842-9
- Y. Tsai, “Coverage-Preserving Routing Protocols for Randomly Distributed Wireless Sensor Networks,” IEEE Transactions on Wireless Communications, Vol. 6, No. 4, 2007, pp. 1240-1245. doi:10.1109/TWC.2007.348320
- M. Lehsaini, H. Guyennet and M. Feham, “α-Coverage Scheme for Wireless Sensor Networks,” Proceedings in the 4th International Conference on Wireless and Mobile Communications, Athens, 27 July-1 August 2008, pp. 91-96.
- D. Kim and Y. Chung, “Self-Organization Routing Protocol Supporting Mobile Nodes for Wireless Sensor Network,” Proceedings of the 1st International MultiSymposiums on Computer and Computational Sciences, Hangzhou, 20-24 June 2006, pp. 622-626.
- S. Kumar, V. Paul and P. Jacob, “Mobility Metric Based LEACH-Mobile Protocol,” Proceedings of the 16th International Conference on Advanced Computing and Communications, Chennai, 14-17 December 2008, pp. 248- 253. doi:10.1109/ADCOM.2008.4760456
- A. Howard, M. Mataric and G. Sukhatme, “Mobile Sensor Network Deployment Using Potential Fields: A Distributed, Scalable Solution to the Area Coverage Problem,” Proceedings of the 6th International Symposium on Distributed Autonomous Robotics Systems, Fukuoka, 25- 27 June 2002.
- S. Poduri and G. Sukhatme, “Constrained Coverage for Mobile Sensor Networks,” Proceedings of the IEEE International Conference on Robotics and Automation, New Orleans, 26 April-1 May 2004, pp. 165-171.
- Y. Zou and K. Chakrabarty, “Sensor Deployment and Target Localization in Distributed Sensor Networks,” ACM Transactions on Embedded Computer Systems, Vol. 3, No. 1, 2004, pp. 61-91. doi:10.1145/972627.972631

