Journal of Environmental Protection
Vol. 3 No. 9A (2012) , Article ID: 22955 , 14 pages DOI:10.4236/jep.2012.329133
Analysis of Key Features of Non-Linear Behavior Using Recurrence Plots. Case Study: Urban Pollution at Mexico City
![]()
Campus Juriquilla, Universidad Autonoma de Queretaro, Santiago de Querétaro, México.
Email: marco.aceves@gmail.com
Received June 10th, 2012; revised July 13th, 2012; accepted August 9th, 2012
Keywords: Recurrence Plot; Air Quality; Air Pollution Modelling; Atmospheric Pollution; Recurrence Quantification Analysis
ABSTRACT
The use of Recurrence plots have been extensively used in various fields. In this work, Recurrence Plots (RPs) investigates the changes in the non-linear behaviour of urban air pollution using large datasets of raw data (hourly). This analysis has not been used before to extract information from large datasets for this type non-linear problem. Two different approaches have been used to tackle this problem. The first approach is to show results according to monitoring network. The second approach is to show the results by particle type. This analysis shows the feasibility of using Recurrence Analysis for pollution monitoring and control.
1. Introduction
The states in nature typically change in time. The importance in the investigation of these changes in complex systems helps to understand and describe such changes. A relatively new method based on non-linear data analysis has become popular to describe the changes of these systems. This method is called recurrence plot [1, 2].
In this contribution, the non-linear behaviour of urban air pollution is quantified and analysed at various sites at Mexico City, using large datasets over a number of years. This is carried out to show the feasibility of analysing key features embedded in the raw datasets.
2. Background
2.1. Urban Airborne Pollution
In recent times, urban air pollution has been a growing problem especially for urban communities. Size, shape and chemical properties govern the lifetime of particles in the atmosphere and the site of deposition within the respiratory tract. Also, air pollution has been held responsible for various health disorders, especially respiratory complications resulting in an increase in the number of asthmatic cases and hospital admissions in some parts of the world and has been widely documented [3-5].
Most major pollutants can alter pulmonary function in addition to other health effects when the exposure concentrations are high. This is especially severe in vulnerable sectors of the population such as children asthmatic and the elderly and has been vastly documented [6-9].
In this work, five particles were chosen due to the site’s availability and toxicity: Ozone (O3), Carbon Monoxide (CO), Nitrogen Dioxide (NO2), Sulphur Dioxide (SO2) and Particulate Matter of less than 10 micrometers (PM10). The datasets are separated according to month of the year and type of particle. There is one data for each hour, for each particle for all five sites, making it difficult to extract information from datasets using common methods.
2.1.1. Ozone
Ozone is a natural atmosphere component that is found on low concentrations and is crucial for life. Air pollution caused by high concentration of ozone is a common problem in large cities throughout the world [10]. Mexico City is among the ones suffering from this problem. It is a well-known fact that individuals exposed for a long period of time to high concentration of ozone may experience serious health problems [11,12]. Epidemiology studies have found associations between daily ozone levels and the hospital admission [13]. This pollutant is associated with respiratory symptoms specially coughing. This is aggravated in patients with asthma [14].
In Mexico City, there is a decreasing of ozone especially from 2009. However, there is still a risk situation for overexposure mainly in the southwest region [15], according to the official Mexican air quality standards [16].
2.1.2. Carbon Monoxide
Carbon monoxide (CO) is a tasteless, odorless gaseous pollutant ubiquitous in the outdoor atmosphere that is generated by combustion [17]. CO is produced by incomplete combustion of hydrocarbons. Its main source is vehicle exhaust emissions; secondary important sources are industry, heating, and fires. The concentrations of CO as well as their fluctuations are related to a large extent to the circulation of cars [18].
Adverse health effects of CO exposure include death from asphyxiation at high exposure levels and, at lower levels, impaired neuropsychological performance and risk for myocardial ischemia and rhythm disturbances in persons with cardiovascular disease. The most definitive evidence on CO comes largely from controlled exposure studies, involving CO inhalation at concentrations to mimic exposures previously typical of urban environments [19, 20].
Also, Carbon monoxide has been held responsible for many hospital admissions due to carbon monoxide poisoning. Only in the US, around 40,000 people are admitted in hospitals for this cause in one year [21].
In Mexico, the Official Norm NOM-021-SSA1-1993 sets the maximum level for carbon monoxide on 11.0 parts per million (ppm) for an average of 8 hours, which cannot be exceeded more than once a year. Comparatively, in the United States the federal standard is 9 ppm for 8 hours and 35 ppm for 1 hour average.
2.1.3. Nitrogen Dioxide
Nitrogen Dioxide (NO2) is a particularly important compound, not only for its health effects, but also because absorbs visible light and contributes to the visibility decrease. It also plays a critical role in production of ozone due to the photolysis of NO2 is the initial step in the photochemical reaction of the ozone [10].
In nature, there is a nitrogen dioxide concentration of 10 to 50 parts per billion (ppb). However, the high levels of nitrogen dioxide are due to industrial processes and fossil sources. Furthermore, motor vehicles substantially contribute to urban levels of nitrogen oxides through their engine combustion processes [22]. According to several authors the monitoring of NO2 is critically important, in order to assess the potential effect of NO2 on human health and ecosystems, as well as developing strategies for the effective control of NO2 pollution [23-25].
In Mexico, the official norm: NOM-023-SSA1-1993 [16] establishes a maximum allowed concentration of 0.21 ppm hourly mean, which cannot be exceeded more than once a year. Comparatively, in the United States of America, the federal standard establishes a value of 0.053 ppm annual mean. The WHO recommends a value of 40 µg/m3 (0.021 ppm) for annual mean and 200 µg/m3 (0.106 ppm) for hourly mean.
2.1.4. Sulphur Dioxide
Sulphur Dioxide gases contribute to the deterioration of air quality. Several epidemiological studies have demonstrated a direct association between atmospheric inhalable Sulphur dioxide and respiratory diseases, pulmonary damage and mortality among population [8]. In urban environments, Sulphur dioxide is generated by many sources. One of them is the burning of solid compounds or petroleum-derived products.
In the past three decades in Europe, and more recently in the United States, there have been substantial reducetions in SO2 emissions [26,27].
The World Health Organization recommends a concentration of between 100 to 150 µg/m3 24 hours mean and 40 to 60 µg/m3 the annual mean. The official Mexican Norm: NOM-022-SSA1-1993 establishes a limit of 341 µg/m3 24-hour mean once a year and 79 µg/m3 annual mean to protect vulnerable population.
2.1.5. PM10
The airborne particulate matter (PM) is a mixture of small particles and liquid droplets suspended in the atmosphere, which contributes significantly to the urban air quality such as acid rain and visibility degradation [28].
In airborne pollution particle could be any olid or liquid materials with a diameter between 0.002 and 500 micrometers (µm). Airborne particulates of 10 μm diameter and less are of concern from the perspective of air pollution. A variety of national and worldwide standards, directives and guidelines exist to define acceptable particulate levels in the air.
These types of particles are classified according to their effect on human health and their Physical characteristics.
2.2. Mexico’s Sites
Mexico City is geographically located in the Valley of Mexico. This valley, also known as the Valley of the Damned is a large valley in the high plateaus at the center of Mexico. It has an altitude of 2240 meters (7349 feet). The Federal District of Mexico City is situated in central-south Mexico and it is surrounded by the state of Mexico on the west, north and east, and by the state of Morelos on the south. The city covers an area of around 1485 km2 (571 sq mi) with the elevation of 2240 m (7349 ft).
The sites used in this work are as follows: Northeast (San Agustín-SAG), Northwest (Acatlán-FAC), Downtown (Merced-MER), Southeast (Iztapalapa-UIZ) and Southwest (Pedregal-PED). The map of the monitoring sites is shown on Figure 1.
3. Recurrence Plots
The recurrence plot (RP) exhibits characteristic patterns for typical dynamical behavior. A collection of single recurrence points, homogeneously and irregularly distributed over the whole plot, reveals a mainly stochastic process [29].
Recurrence Plot is a graphical tool introduced by Eckmann (1987) in order to extract qualitative characteristics of a time series. The recurrence of a state i at a different time j is pictured within a two-dimensional squared matrix with black and white dots, where the black dots represent a recurrence and both axes represent time [30,31].
Such RP can be mathematically expressed as:
 (1)
(1)
where, N is the number of considered states xi;  is a threshold distance,
is a threshold distance, 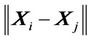 norm and
norm and  the
the
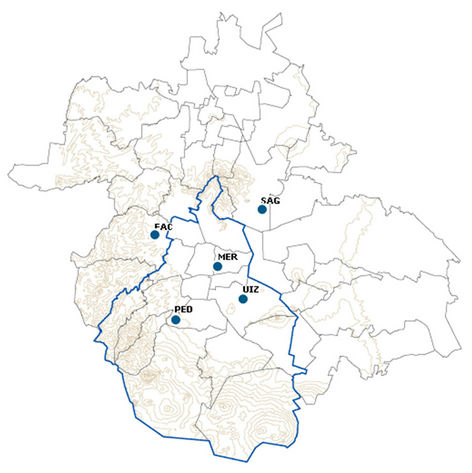
Figure 1. Map for the monitoring sites at Mexico City.
Heaviside function [32].
Since 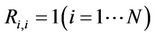 by definition, the RP has a black main diagonal line called line of identity (LOI). In this context, the Heaviside function
by definition, the RP has a black main diagonal line called line of identity (LOI). In this context, the Heaviside function 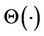 is a recurrence of a state
is a recurrence of a state 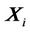 that is sufficiently close to
that is sufficiently close to 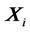 (states
(states 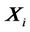 that fall into an m-dimensional neighborhood) [33].
that fall into an m-dimensional neighborhood) [33].
Using the time series of a single observable variable (particles, in this case), it is possible to reconstruct a phase space trajectory. Starting from the scalar time series 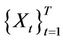 a sequence of embedded vectors
a sequence of embedded vectors 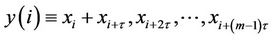 is generated [34]. The set of all embedded vectors
is generated [34]. The set of all embedded vectors 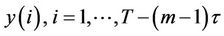 , constitutes a trajectory in
, constitutes a trajectory in  where m is the embedding dimension and τ is the time delay. Each unknown point of the phase space at time I is reconstructed by the delayed vector
where m is the embedding dimension and τ is the time delay. Each unknown point of the phase space at time I is reconstructed by the delayed vector  in an m-dimensional space called the reconstructed phase space.
in an m-dimensional space called the reconstructed phase space.
Determining the embedding parameters must be the first step for analysing nonlinear systems [29,34-37]. For this reason, a search for the best dimension and time delay must be made first. In this contribution, the best dimension value is calculated using the algorithm of false nearest neighbors (FNN) as shown on [32,38].
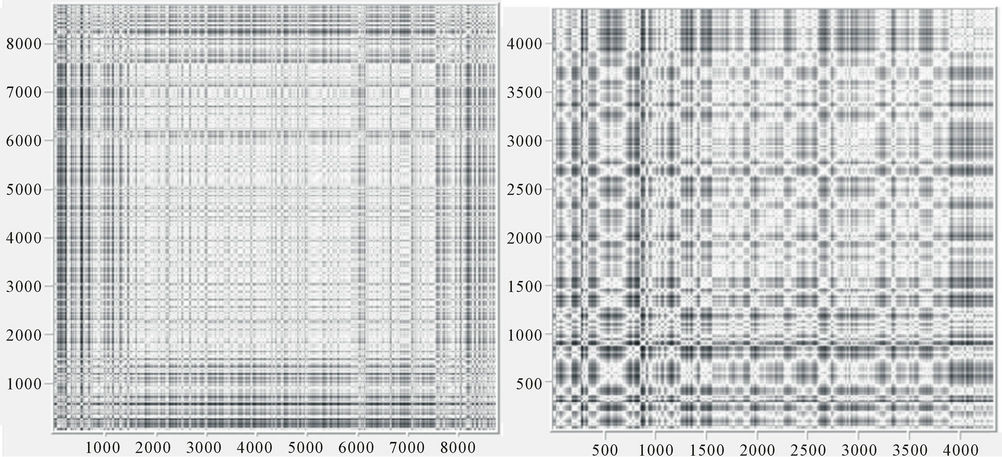
Also, when calculating an RP a norm must be chosen [39]. The most widely used norms are the L1, L2 (Euclidean norm) and L∞ [30]. In this work, the Euclidean norm was used. Figure 2 shows the recurrence plots of a random signal, a sine wave and two RPs chosen randomly for airborne particle concentration.
Although it is possible to identify each plot from figures 2(c) and (d), some experience is needed to interpret the RPs [40]. For this reason, recurrence quantification analysis (RQA) offers a window to characterize such RP structures.
The main idea of this project is to reconstruct the (unknown) system dynamics in the phase space by using time-delay embedding, and then computing the distances between all pairs of embedded vectors, generating a symmetric two-dimensional square matrix for each dataset as shown on figures 1(c) and (d), applying RQA to each dataset.
3.1. Recurrence Quantification Analysis (RQA) for RPs
Zbilut [40] have developed some of the methods used today for Quantitative Analysis of the recurrence plots. It has been shown that these measures are able to capture dynamical transitions in complex systems [38], defining measures of complexity using certain characteristics of the recurrence plots [41,42].
In general, the characteristics measured in a RP are:

(a)(b) (c)(d)
Figure 2. Recurrence plots using (a) A random signal; (b) A sine wave; (c) Particle concentration of carbon monoxide at Mexico Downtown for 2009 and (d) Particle concentration of PM10 over 2010 at Mexico North East (daily mean) showing the line of identity (diagonal line).
recurrence rate, determinism, ratio, entropy and trend. In this contribution, an extension of these characteristics was also considered such as Laminarity and Trapping time.
3.2. Recurrence Rate
The recurrence rate is a measure of recurrences, or density of recurrence points in the RP. This rate gives the mean probability of recurrences in the system [41,43]. The recurrence rate is given by:
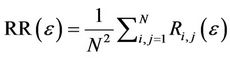 (2)
(2)
in the case of time series, and;
 (3)
(3)
in the case of spatial data [44].
The recurrence rate represents the fraction of recurrent points with respect to the total number of possible recurrences. It is a density measure of the RP.
3.3. Determinism
Determinism is a measure for predictability of the system [37]. The determinism could also be explained as the percentage of recurrent points forming line segments which parallel the Line of Identity (LOI). The determinism characteristic is given by Gao [36]:
 (4)
(4)
where P(l) denotes the probability of finding a diagonal line of length l in the RP. This measure quantifies the predictability of a system [38]. The measure of determinism (DET) ranges from 0 to 1. Numbers near zero indicate randomness while those approaching one indicate the presence of a strong signal component [32,35].
The average diagonal line length Lmean is defined as:
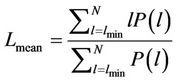 (5)
(5)
This characterizes the average time that two segments of a trajectory stay in the vicinity of each other, and is related to the mean predictability time [38].
The choice of l min can also be used in order to exclude short temporal scales that are not important [39].
3.4. Ratio
The Ratio variable is defined as the quotient of determinism (DET) divided by the recurrence (REC). It is useful to detect transitions between states: this ratio increases during transitions but settles down when a new quasi-steady state is achieved [39].
3.5. Entropy
The measure characteristic entropy refers to the Shannon entropy of the frequency distribution of the diagonal line lengths [45]. According to several authors, the basic idea is that information (Shannon) entropy of the random processes is abundantly supplied with the qualitative and quantitative data on the object under research [39,42, 43,45]. The entropy of a system is given by:
 (6)
(6)
3.6. Trend
The trend is a linear regression coefficient over the recurrence point density of the diagonals parallel to the Line of Identity (LOI). The trend measurement is given by:
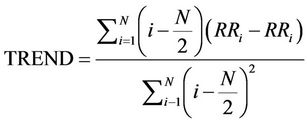 (7)
(7)
3.6. Laminarity
Laminarity may be defined as the amount of recurrence points which form vertical lines [34]. Thus, laminarity (LAM) can be quantified as expressed on equation (8)
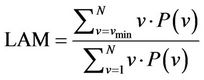 (8)
(8)
where P(v) is the frequency distribution of the lengths v of the vertical lines, which have at least a length of v min. It is noteworthy that Laminarity is evidence of chaotic transitions and is related with the amount of laminar phases in the system (intermittency) [34].
3.7. Trapping Time
Trapping Time shows the average length of the vertical lines and is given by equation (9):
 (9)
(9)
where v is the length of the vertical lines, v min is the shortest length that is considered a line segment and P(v) is the distribution of the corresponding lengths. TT shows the time that the systems have been trapped in the same state [39].
4. Experimental Results
Recurrence Quantification Analysis have been carried out for years 2005-2010 for all sites mentioned in section 2.2 for particles PM10, CO, SO2, NO2 and O3 using the raw data (hourly) obtained from the monitoring stations. The analysis has been carried out for recurrence rate (REC), determinism (DET), Ratio, Trapping Time (TT), Laminarity (LAM) and Trend.
The results were analysed separately and presented in form of boxplots according to two different approaches: by site and by type of particle. This analysis is complex due to the large quantity of the datasets. However, much useful information have been extracted from the recurrence plots using RQA.
4.1. Results by Monitoring Networks (Sites)
This approach explores the feasibility of using RQA to extract information from the Recurrence Plots by sites. As explained in section 2.2, the monitoring networks were separated as: Northwest, Northeast, Downtown, Southwest and Southeast. This approach does not take into account the type of particle, but rather the location of the monitoring network. Figure 3 shows the recurrence rate for all particles.
In figure 3 is shown the recurrence Rate for all Monitoring networks. In this figure, it is worth notice that the median recurrence rate lies from 10 to 13, with the lowest recurrence rate being for Mexico Northwest. The other sites seem to have a fairly constant spread of the percentiles.
Figure 4 shows the determinism for years 2005-2010 by monitoring network shows a fairly constant mean for all sites. However, there are outliers for all sites showing an increase of over 80 in many cases. This exceptionally higher determinism may be explained in greater detail in the analysis by particle, which could give an insight of the reason this happened.
The ratio for particle concentration (Figure 5) seems fairly stable for all sites ranging from 0 to 2 as a mean and the percentiles increasing up to 4 for some cases. The only exception for this drift is the monitoring station of the Northwest with ratios up to 10 and an outlier of about 38.
Furthermore, for entropy the frequency distribution of the data is also stable. Their median oscillates between 2 and 3 for all monitoring networks showing the percentiles reaching up to 5. This could also be due to the type of particle rather than the site. This is shown on figure 6.
Figure 7 shows the trapping time for particle concentration separated by monitoring network. In this case the average time that this non-linear system stays in the same state seems fairly constant with a low median between 10 and 13. It is also worth noting that for most sites there are outliers which cannot be explained in detailed using this approach.
Figure 8 shows the laminarity for particle concentration by monitoring network. Since the laminarity is the measurement of chaotic transitions, it can be inferred that regardless of the site the changes in laminar phases in the system seem high.
The last measure for this approach was the trend. Since the trend represents the measure of the positioning of recurrent points away from the central diagonal, that is the paling of the RP towards its edges [34]. A ‘‘flat” diagram indicates stationarity, whereas drift in the signal will result in the overall increase or reduction of distances as the signal is moved away from the main diagonal. In this respect, it could be noticed that most of the sites have a median between 11 and 14. This is shown on figure 9.
4.2. Results by Particle Type
For this approach, the recurrence quantification analysis
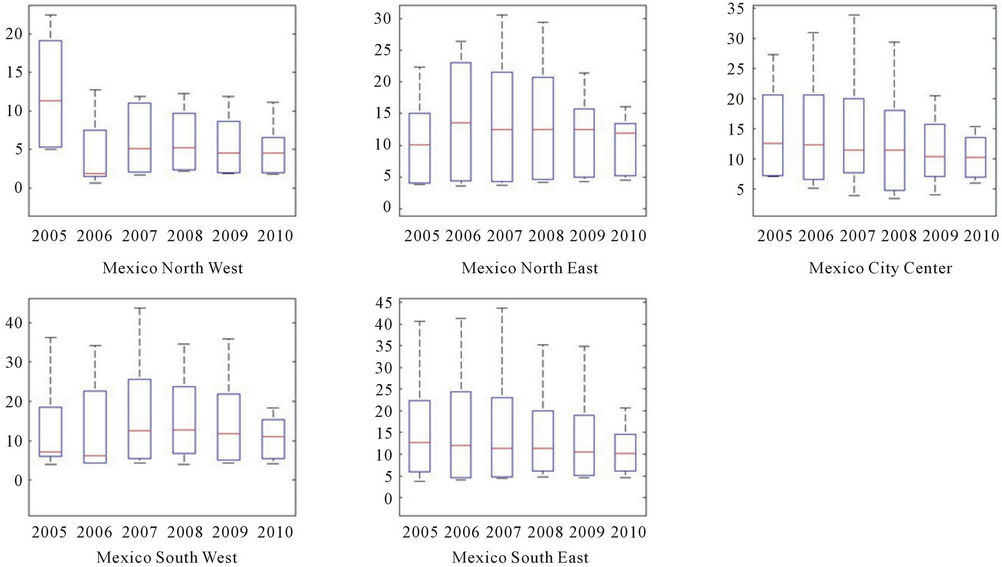
Figure 3. Recurrence rate, years 2005-2010 by monitoring network.
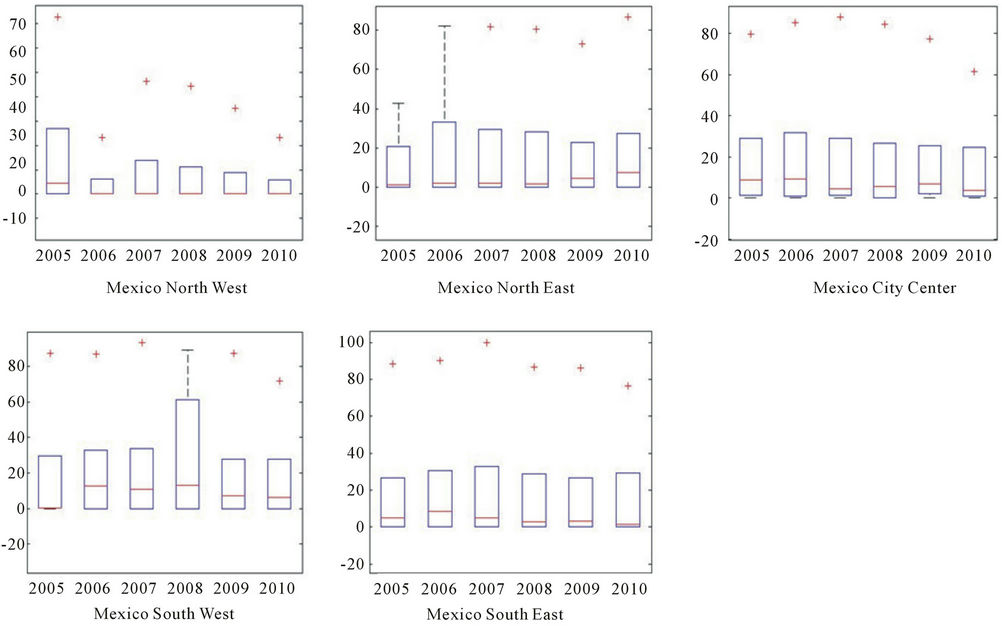
Figure 4. Determinism, years 2005-2010 by monitoring network.
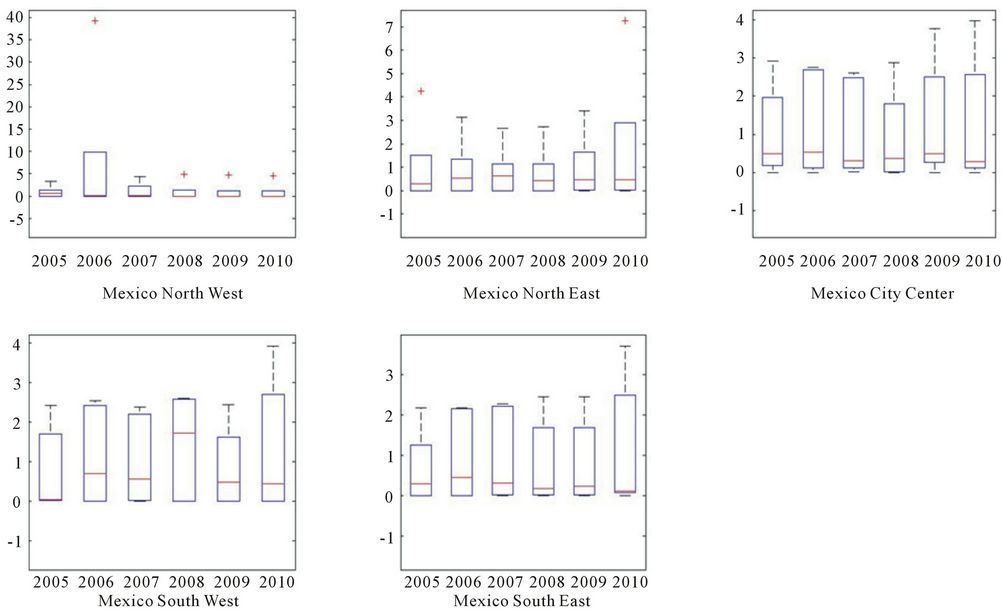
Figure 5. Ratio for particle concentration, years 2005-2010 by monitoring network.
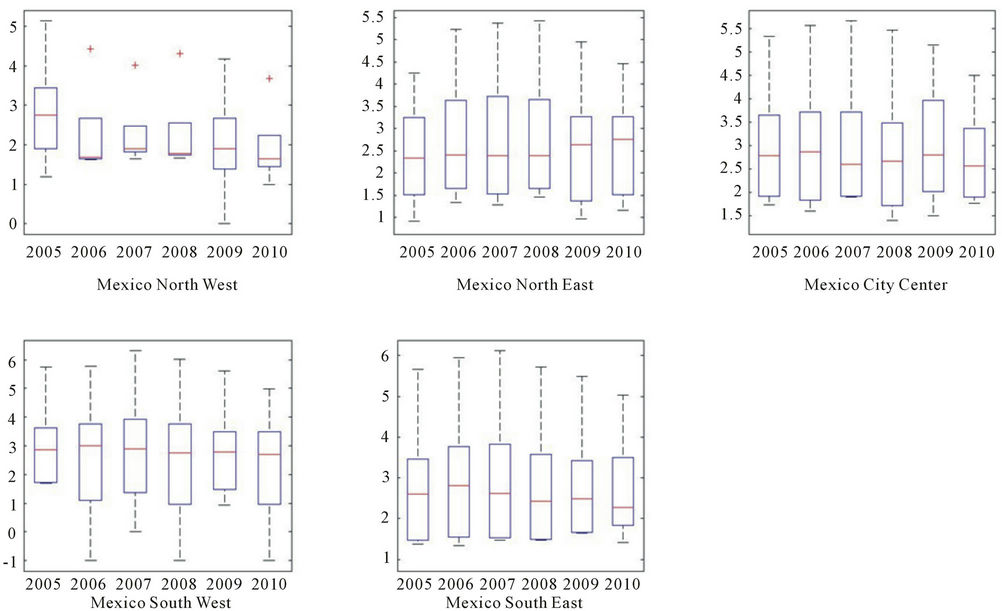
Figure 6. Entropy for particle concentration, years 2005-2010 by monitoring network.
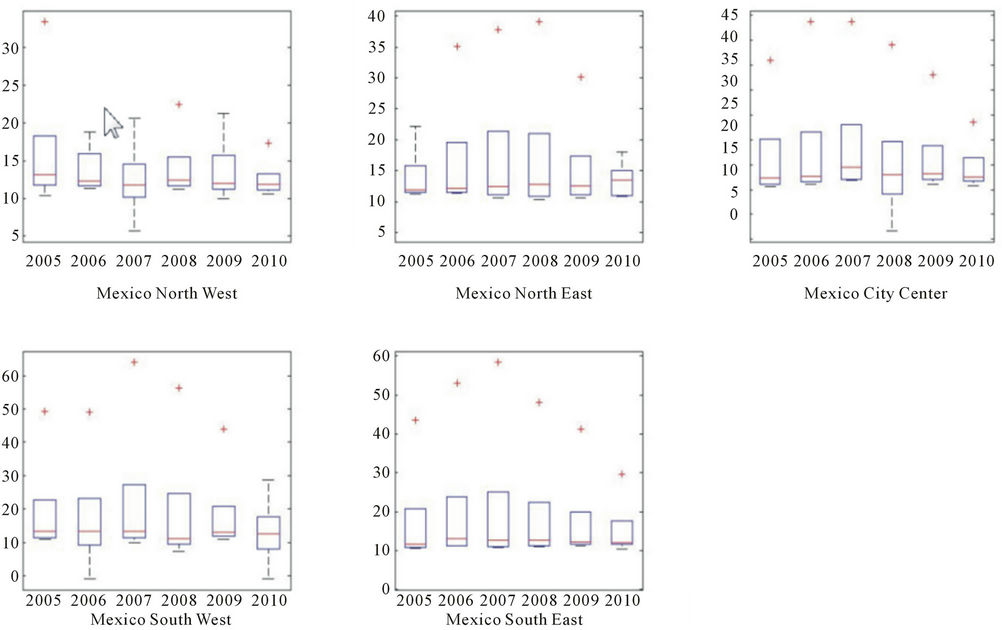
Figure 7. Trapping time for particle concentration, years 2005-2010 by monitoring network.
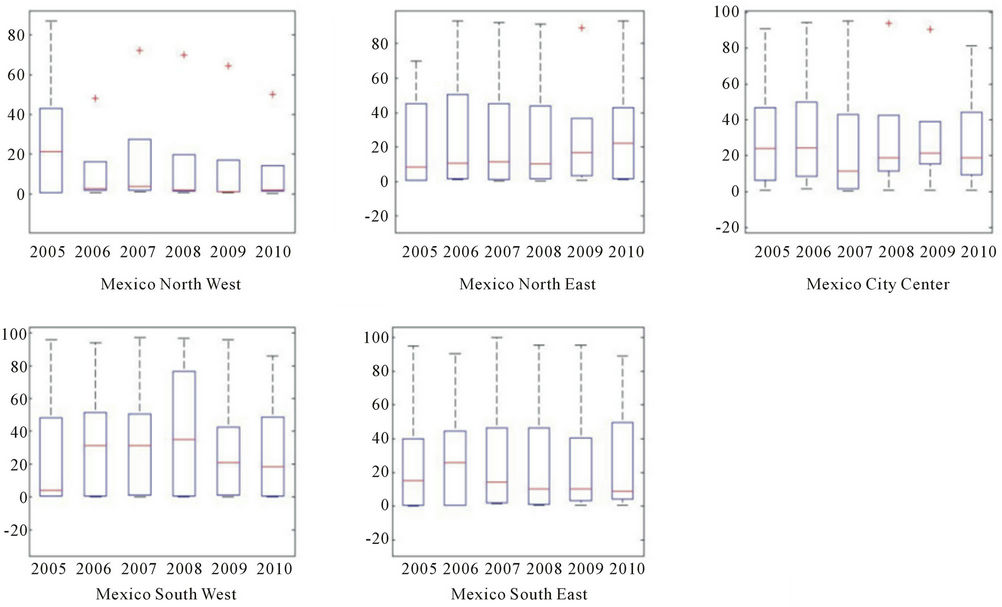
Figure 8. Laminarity for particle concentration, years 2005-2010 by monitoring network.
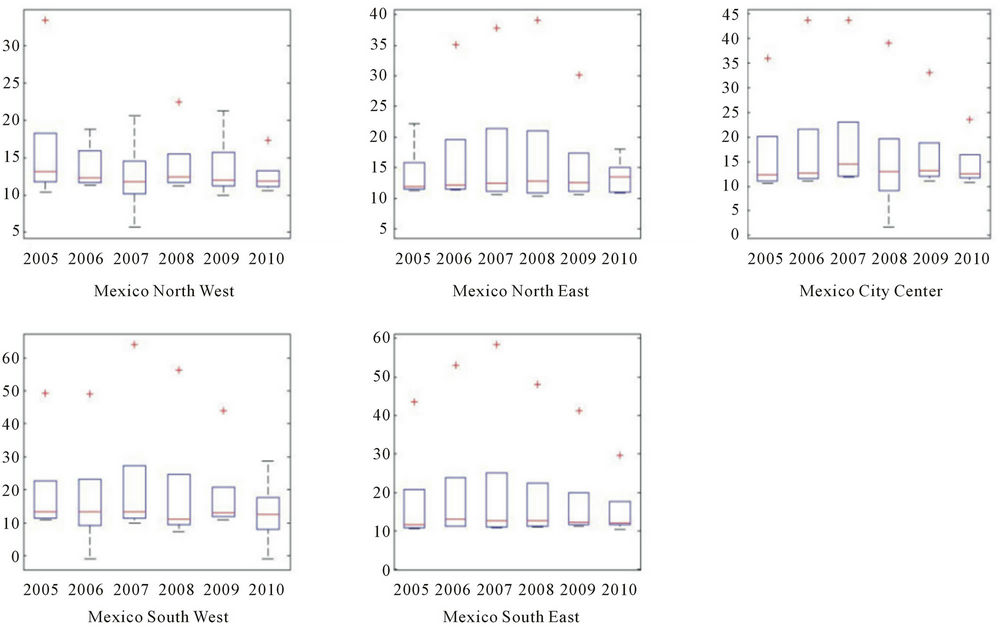
Figure 9. Trend for particle concentration, years 2005-2010 by monitoring network.
is carried out by particle type. In figure 10 the recurrence rate by particle type is shown. In this figure is shown the recurrence Rate for all five particles (CO, O3, NO2, SO2 and PM10). It is worth notice that the median recurrence rate for all particles varies. For CO, the median lies between 13 and 18. Both Ozone and particulate matter shows a low recurrence rate below 6 for all years, regardless of the monitoring sites. Nitrogen dioxide shows a slightly higher recurrence with a median between 10 and 12.
However, Sulphur dioxide shows a median above 30 for some years. This explains figure 3, where the whiskers of the boxplots show a much higher recurrence in some cases, these cases being for sulphur dioxide. This higher recurrence rate may be due to the low variances in values of the datasets for all years, making it easier for RQA to determine recurrence.
Furthermore, the determinism for SO2 is also much higher than for other particles, having a median between 70 and 90 as shown on figure 11. Although it seems lower due to the scaling of the boxplots, the median shows otherwise, the spread in the 25th to 75th percenttiles and the length of the whiskers may be due to high variances in the datasets for that type of particle.
Furthermore, it is worth notice for entropy (figure 12) that the frequency distribution of the data is slightly higher for sulphur dioxide as well. The other particles seem to have steady entropy whose median oscillates between 1 and 3.
Figure 13 shows the trapping time separated by particle type. For this figure it can be seen that Sulphur Dioxide shows also a much higher trapping time showing a median of 40 for some years (e.g. 2008 and 2009) in comparison with the other particles between 10 and 13. This explains the outliers seen on figure 7, that could not be explained using the monitoring networks’ approach.
Figure 14 shows the laminarity for particle concentration by particle type. In this figure, is shown that for Carbon Monoxide and PM10 the chaotic transitions are high, specially for sulphur dioxide. This gives another insight of the chaotic transitions, since figure 8 shows that the laminarity is high for all sites, in figure 14 can be explained that only some particles gives this high changes in laminar phases.
5. Conclusions and Future Work
Numerous experiments have been carried out with different particles and through different years. Using Recurrence Quantification Analysis it could be shown that information could be extracted from large datasets of dissimilar airborne particles during a considering time lap (six years, in this case) for 5 monitoring networks.
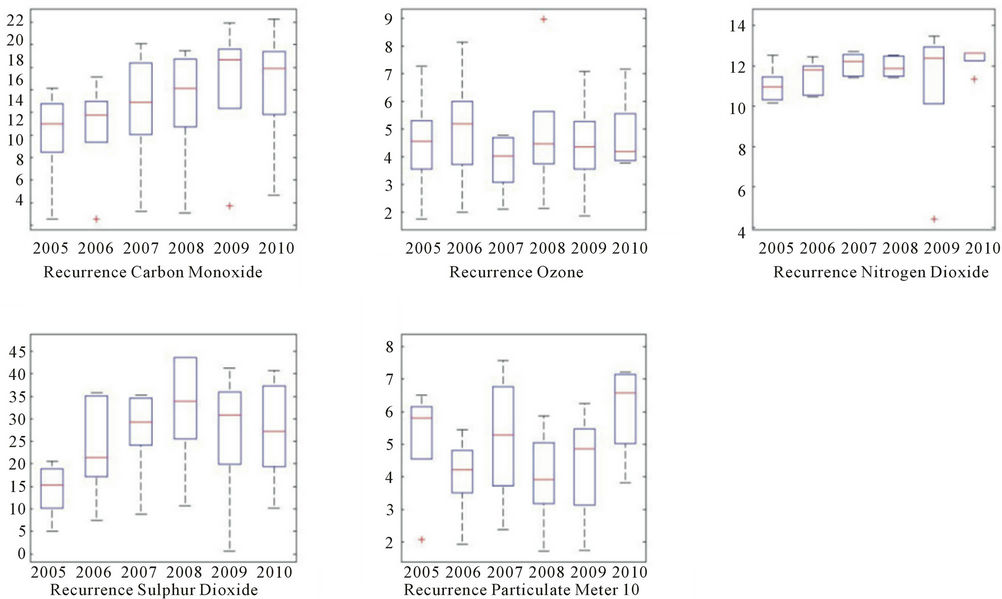
Figure 10. Recurrence rate for particle concentration, years 2005-2010 by particle type.
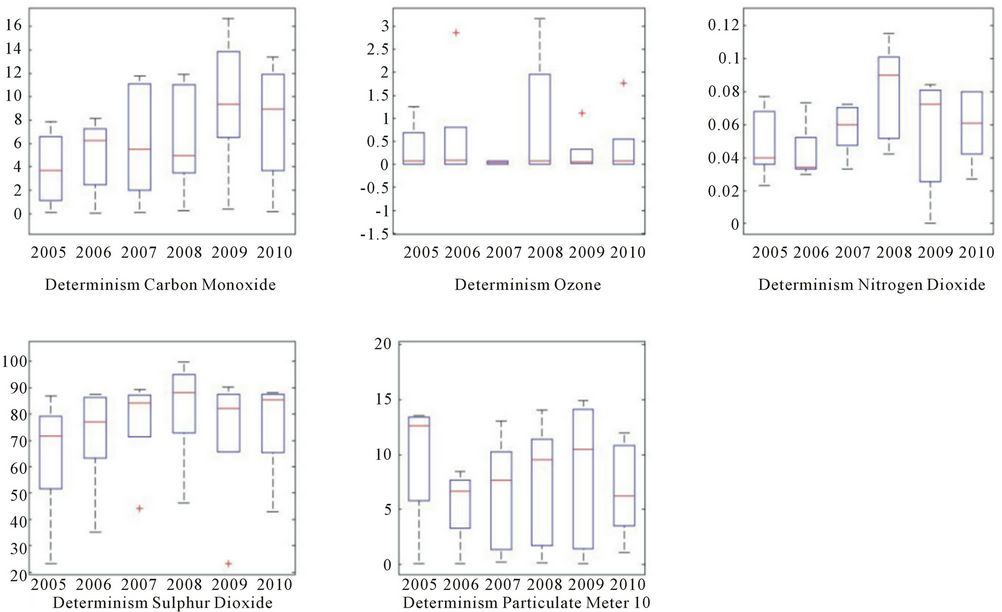
Figure 11. Determinism for particle concentration, years 2005-2010 by particle type.

Figure 12. Entropy for particle concentration, years 2005-2010 by particle type.

Figure 13. Trapping time for particle concentration, years 2005-2010 by particle type.
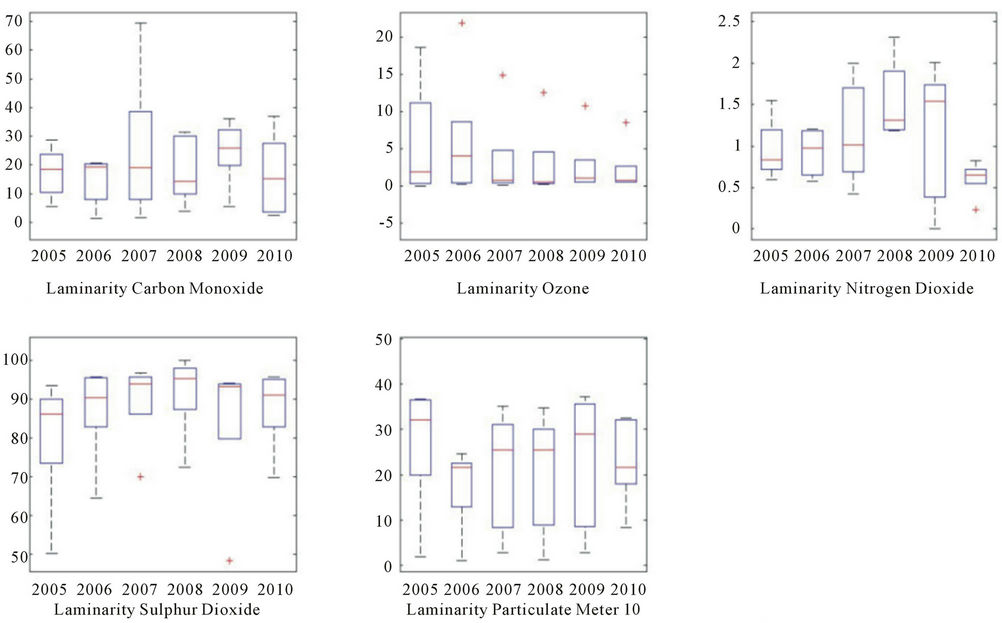
Figure 14. Laminarity for particle concentration, years 2005-2010 by particle type.
Trends could be identified using these tools and preliminary conclusions suggest that important information such as density distribution, drifts, among others could be drawn. Also, using more than one approach, some hidden features could be identified showing the feasibility of this approach.
For future work, it could be useful to use a combination o RQA with prediction algorithms such as Support Vector Machines to carry out prognosis of the airborne particle data. Another useful approach that could be carried out is the use of cross recurrence plot (CRP), making a comparison between two recurrence plots to determine trends.
6. Acknowledgements
Also, the authors would like to acknowledge the financial support of the Mexican government via PROMEP funding.
REFERENCES
- J. P. Eckmann, et al., “Recurrence Plots of Dynamical Systems,” Europhysics Letters, Vol. 4, No. 9, 1987, pp. 324-327. doi:10.1209/0295-5075/4/9/004
- T. Masaaki, et al., “Recurrence Plot Statistics and the Effect of Embedding,” Physics Letters A, Vol. 373, 2009, pp. 2031-2040.
- Y.-J. Liu, et al., “Properties of Coarse Particles in the Atmosphere of the United Kingdom,” Atmospheric Environmen, Vol. 45, No. 19, 2011, pp. 3267-3276. doi:10.1016/j.atmosenv.2011.03.039
- G. Weinmayr, et al., “Short-Term Effects of PM10 and NO2 on Respiratory Health among Children with Asthma or Asthma-Like Symptoms: A Systematic Review and Meta-Analysis,” Circulation, Vol. 121, 2010, pp. 2331- 2378.
- M. A. Arbex, et al., “Impact of Outdoor Biomass Air Pollution on Hypertension Hospital Admissions,” Journal of Epidemiology & Community Health, Vol. 64, No. 7, 2010, pp. 573-579. doi:10.1136/jech.2009.094342
- J. H. Kilabuko, et al., “Air Quality and Acute Respiratory Illness in Biomass Fuel Using Homes in Bagamoyo, Tanzania,” International Journal of Environmental Research and Public Health, Vol. 4, No. 1, 2007, pp. 39-44. doi:10.3390/ijerph2007010007
- Y. L. Lee, et al., “Effects of Ambient Air Pollution on Pulmonary Function among Schoolchildren,” International Journal of Hygiene and Environmental Health, Vol. 214, 2011, pp. 369-375.
- R. Devika, et al., “Impact of Environmental Controls on Childhood Asthma,” Current Allergy and Asthma Reports, Vol. 11, No. 5, 2011, pp. 414-420. doi:10.1007/s11882-011-0206-7
- H. Suh Helen, et al., “Chemical Properties of Air Pollutants and Cause-Specific Hospital Admissions among the Elderly in Atlanta, Georgia,” Environmental Health Perspectives, Vol. 119, No. 10, 2011, pp. 1421-1428.
- R. W. Boubel, et al., “Fundamentals of Air Pollution,” 3rd Edition, Academic Press, Waltham, 1994.
- J. A. Achcar, et al., “Comparing the Number of Ozone Exceedances in Different Seasons of the Year in Mexico City,” Environ Model Assess, Vol. 16, No. 3, 2011, pp. 251-264. doi:10.1007/s10666-010-9245-z
- United States Environmental Protection Agency (USEPA), “Air Quality Criteria for Ozone and Related Photochemical Oxidants. Volume I,” National Center for Environmental Assessment-RTP Office of Research and Development, Research Triangle Park, 2006.
- J. Pey, et al., “Monitoring of Sources and Atmospheric Processes Controlling Air Quality in an Urban Mediterranean Environment,” Atmospheric Environment, Vol. 44, No. 38, 2010, pp. 4879-4890. doi:10.1016/j.atmosenv.2010.08.034
- M. R. O’Neill, et al., “Ozone, Area Social Conditions and Mortality in Mexico City,” Environmental Research, Vol. 964, No. 3, 2004, pp. 234-242. doi:10.1016/j.envres.2003.07.002
- SIMAT, “Sistema de Monitoreo Atmosférico (Atmospheric Monitoring System),” Annual Technical Report, Mexico City, 2010, pp. 1-166.
- NOM, “Modificación a la Norma Oficial Mexicana NOM-020-SSA1-1993,” Diario Oficial de la Federación, 2002.
- J. Varon, et al., “Carbon Monoxide Poisoning: A Review for Clinicians,” The Journal of Emergency Medicine, Vol. 17, No. 1, 1999, pp. 87-93. doi:10.1016/S0736-4679(98)00128-0
- E. Samoli, et al., “Short-Term Effects of Carbon Monoxide on Mortality: An Analysis within the APHEA Project,” Environmental Health Perspectives, Vol. 115, 2007, pp. 1578-1583. doi:10.1289/ehp.10375
- C. A. Chambers, et al., “Cognitive and Affective Outcomes of More Severe Compared to Less Severe Carbon Monoxide Poisoning,” Brain Injury, Vol. 22, 2008, pp. 387-395. doi:10.1080/02699050802008075
- M. L. Bell, et al., “Emergency Hospital Admissions for Cardiovascular Diseases and Ambient Levels of Carbon Monoxide: Results for 126 United States Urban Counties, 1999-2005,” Circulation, Vol. 120, 2009, pp. 949-955. doi:10.1161/CIRCULATIONAHA.109.851113
- United States Environmental Protection Agency (USEPA), “Air Quality Criteria for Carbon Monoxide,” National Center for Environmental Assessment, Office of Research and Development, Research Triangle Park, 2000.
- L. Emberson, et al., “Air Pollution Impacts on Crops and Forests: A Global Assessment,” Air Pollution Reviews, Vol. 220, No. 1-4, 2011, pp. 141-150. doi:10.1007/s11270-011-0741-9
- S. S. Ahmad, et al., “Monitoring Nitrogen Dioxide Levels in Urban Areas in Rawalpindi, Pakistan,” Water Air Soil Pollution, Vol. 220, 2011, pp. 141-150.
- H. Takizawa, “Impact of Air Pollution on Allergic Diseases,” The Korean Journal of Internal Medicine, Vol. 26, 2011, pp. 262-273.
- M. Chiusolo, et al., “Short-Term Effects of Nitrogen Dioxide on Mortality and Susceptibility Factors in 10 Italian Cities: The EpiAir Study,” Environmental Health Perspectives, Vol. 119, No. 9, 2011.
- V. Vestreng, et al., “Twenty-Five Years of Continuous Sulphur Dioxide Emission Reduction in Europe,” Atmospheric Chemistry and Physics, Vol. 7, No. 13, 2007, pp. 3663-3681. doi:10.5194/acp-7-3663-2007
- M. Jones Alan, et al., “Temporal Trends in Sulphate Concentrations at European Sites and Relationships to Sulphur Dioxide,” Atmospheric Environment, Vol. 45, No. 4, 2011, pp. 873-882. doi:10.1016/j.atmosenv.2010.11.020
- G. l. Peng, et al., “Characteristics of Particulate Matter Pollution in the Pearl River Delta Region, China: An Observational-Based Analysis of Two Monitoring Sites,” Journal of Environmental Monitoring, Vol. 13, No. 7, 2011, pp. 1927-1934. doi:10.1039/c0em00776e
- N. Marwan, et al., “Cross Recurrence Plot Based Synchronization of TIME Series,” Nonlinear Processes in Geophysics, Vol. 9, 2002, pp. 325-331. doi:10.5194/npg-9-325-2002
- J. P. Zbilut, et al., “Recurrence Quantification Analysis: Introduction and Historical Context,” International Journal of Bifurcation and Chaos, Vol. 17, No. 10, 2007, pp. 3477-3481. doi:10.1142/S0218127407019238
- M. Aboofazeli, et al., “Comparison of Recurrence Plot Features of Swallowing and Breath Sounds,” Chaos, Solitons and Fractals, Vol. 37, No. 2, 2008, pp. 454-464. doi:10.1016/j.chaos.2006.09.026
- D. Furman Michael, et al., “Using Recurrence Quantification Analysis Determinism for Noise Removal in Cardiac Optical Mapping,” IEEE Transactions on Biomedical Engineering, Vol. 53, No. 4, 2006.
- E. Bradley, et al., “Recurrence Plots and Unstable Periodic Orbits,” Chaos, Vol. 12, No. 3, 2002, pp. 596-600.
- F. Palmieri, et al., “A Nonlinear, Recurrence-Based Approach to Traffic Classification,” Computer Networks, Vol. 53, No. 6, 2009, pp. 761-773. doi:10.1016/j.comnet.2008.12.015
- C. Ahlstrom, et al., “Distinguishing Innocent Murmurs from Murmurs Caused by Aortic Stenosis by Recurrence Quantification Analysis,” World Academy of Science, Engineering and Technology, Vol. 18, No. , 2006, pp. 40- 45.
- J. Gao, et al., “On the Structures and Quantification of Recurrence Plots,” Physics Letters A, Vol. 270, No. 1-2, 2000, pp. 75-87. doi:10.1016/S0375-9601(00)00304-2
- T. Aparicio, et al., “Detecting Determinism Using Recurrence Quantification Analysis: Three Test Procedures,” Journal of Economic Behavior & Organization, Vol. 65, No. 3-4, 2008, pp. 768-787. doi:10.1016/j.jebo.2006.03.005
- Y. Zou, et al., “Identifying Complex Periodic Windows in Continuous-Time Dynamical Systems Using Recurrence-Based Methods,” Chaos, Vol. 20, No. 4, 2010, Article ID: 043130. doi:10.1063/1.3523304
- T. E. Karakasidis, et al., “Recurrence Quantification Analysis of Temperature Fluctuations in a Horizontal Round Heated Turbulent Jet,” International Journal of Bifurcation and Chaos, Vol. 19, No. 8, 2009, pp. 2487- 2498.
- P. Zbilut, et al., “Recurrence Quantification Based Liapunov Exponents for Monitoring Divergence in Experimental Data,” Physics Letters A, Vol. 297, 2007, pp. 173-181.
- T. K. March, et al., “Recurrence Plot Statistics and the Effect of Embedding,” Physica D, Vol. 200, No. 2, 2005, pp. 171-184. doi:10.1016/j.physd.2004.11.002
- N. Marwan, et al., “Recurrence Plots for the Analysis of Complex Systems,” Physics Reports, Vol. 438, 2007, pp. 237-329.
- F. Strozzi, et al., “Recurrence Quantification Analysis and State Space Divergence Reconstruction for Financial Time Series Analysis,” Physica A, Vol. 376, 2007, pp. 487-499. doi:10.1016/j.physa.2006.10.020
- C. Mocenni, et al., “Comparison of Recurrence Quantification Methods for the Analysis of Temporal and Spatial chaos,” Mathematical and Computer Modelling, Vol. 53, No. 7-8, 2011, pp. 1535-1545. doi:10.1016/j.mcm.2010.04.008
- R. M. Yulmetyev, et al., “Dynamics of the Information Entropy in Random Processes,” Physica A, Vol. 273, No. 3-4, 1999, pp. 416-438. doi:10.1016/S0378-4371(99)00257-5

