Smart Grid and Renewable Energy
Vol.2 No.3(2011), Article ID:6648,15 pages DOI:10.4236/sgre.2011.23026
Reactive Power and FACTS Cost Models’ Impact on Nodal Pricing in Hybrid Electricity Markets
![]()
Department of Electrical Engineering, National Institute of Technology, Kurukshetra, India.
Email: ashwa_ks@yahoo.co.in
Received December 31, 2010; revised May 23, 2011; accepted May 30, 2011.
Keywords: Real and Reactive Power, Nodal Price, Reactive Power Cost Model, FACTS Cost Model, Bilateral Transactions, Hybrid Market Model
ABSTRACT
In a competitive environment reactive power management is an essential service provided by independent system operator taking into account the voltage security and transmission losses. The system operator adopts a transparent and non-discriminatory procedure to procure the reactive power supply for optimal deployment in the system. Since generators’ are the main source of reactive power generation and the cost of the reactive power should be considered for their noticeable impact on both real and reactive power marginal prices. In this paper, a method based on marginal cost theory is presented for locational marginal prices calculation for real and reactive power considering different reactive power cost models of generators’ reactive support. With the presence of FACTS controllers in the system for more flexible operation, their impact on nodal prices can not be ignored for wheeling cost determination and has also to be considered taking their cost function into account. The results have been obtained for hybrid electricity market model and results have also been computed for pool model for comparison. Mixed Integer Non-linear programming (MINLP) approach has been formulated for solving the complex problem with MATLAB and GAMS interfacing. The proposed approach has been tested on IEEE 24-bus Reliability Test System (RTS).
1. Introduction
In a competitive environment, the transmission system operator is responsible for proper coordination of generation and transmission facilities. The reactive power service is essentially required for transmission of active power, control of voltage, and normal and secure operation of a power system. Due to this reason, the reactive power support service has been identified as one of the key ancillary services in the competitive electricity market structures. Therefore, real time reactive power pricing addresses the important issue of providing information to both utility and consumers about the actual burden on the system and its better and economic operation of system. Real time reactive power price has shown to perform better than the power factor penalty scheme in terms of providing incentives to all customers to optimally manage their reactive power consumption irrespective of their power factor [1,2]. Therefore, with the growing interest in determining the costs of ancillary services needed to maintain the quality of supply, the spot price for reactive power has also gained considerable attention in competitive electricity markets.
From the economic point of view, spot pricing based on short run marginal cost (SRMC) has the potential to provide the economic signals for the system operation. Various models and approaches for determining spot pricing have been proposed in [3,4]. The concept of spot pricing was introduced in the late 1970’s. Schweppe et al. [3] utilized the concepts of classical economic dispatch and DC load flow to obtain the essential parts of spot price and provided the foundation and starting point for later research. However, the authors have not considered the pricing of reactive power. The spot price model already established in [2], was further developed by demonstrating the physical meanings and numerical properties of the generation and transmission components [5]. Ray and Alvarado used the first trial of OPF as a spot price calculation tool and utilized modified OPF model with price responsiveness of real power demand to analyze the spot pricing policies [6]. Baughman and Siddiqi developed this model introducing reactive power pricing and revealed that the Lagrangian multipliers corresponding to node power balance equations in OPF represent the marginal costs of the node power injections [1]. The account of the reactive power production cost by introducing MVAR cost curves, which are a part of MW incremental cost curve was given in [2]. The successive LP method was applied to solve this non-linear reactive power optimization problem. Reference [7] developed reactive power pricing scheme through employing P-Q decoupled OPF to obtain SRMC of active and reactive power respectively and emphasized that the production cost of reactive power should be accounted for when pricing wheeling transactions. The authors directly introduced real power loss component into reactive power spot pricing derived from the Q-sub-problem with the objective of minimizing the real power loss and the influence of reactive power on the voltage level appears in the pricing formulae. Authors determined the wheeling marginal cost of reactive power in [8].
Due to the growing interest in the determination of costs of supplying of ancillary services, spinning reserve, congestion alleviation cost, and security, the spot price must be decomposed to obtain the different pricing components [9-14]. Considering the most ancillary services and incorporating the constraints on power quality and environment, an advance pricing structure was recently introduced [11], which combined dynamic equations for load frequency control with static equations of constrained OPF, however, the method is quite complex to solve. A simple approach was presented to reactive power planning and combines the issue with reactive power pricing so as to recover the cost of installed capacitors using OPF approach [13]. Authors presented theory and simulation results of real time pricing of real and reactive power using a social benefit function [14]. In [15] a detailed discussion on reactive power service is made and it is shown that the capital costs should be included in the reactive power price. Lamont and Fu [16] introduced opportunity cost as a reactive power production cost of generator, however the computation of the cost is difficult. A summary of the modifications of OPF algorithms in reactive power pricing was presented along with their features in [17]. A methodology for reactive power prices calculation with decoupled optimization was presented in [18]. Authors determined spot prices of reactive power and proposed two practical proposals for the procurement and charging of reactive and voltage control services [19]. Authors proposed a formulation of active and reactive power has been presented considering production costs of reactive power and active losses minimization in the objective function [20]. Recently, a new formulation has been considered for calculating the cost of reactive power production by the use of nonlinear model that represents the loss of opportunity in active power including the detailed model of the heating limits of the armature and field, and under excitation limit. Active and reactive power marginal prices are calculated with a modified OPF that uses sequential linear programming technique with a modified interior point method [21].
In the present pace of power system restructuring, transmission systems are being required to provide increased power transfer capability and to accommodate a much wider range of possible generation patterns over a large geographic area. The demand of better utilization of existing power system and to increase power transfer capability by installing FACTS (Flexible AC Transmission Systems) controllers have become imperative. Installation of these controllers with their optimal location can change power flow patterns, stability, security, reliability, and economic efficiency of the system by changing wheeling cost of power due to the impact on nodal prices of both real and reactive power. Therefore, these devices cost functions should also be incorporated in an objective function for noticeable changes in nodal prices of both the real and reactive power [22,23]. Olivera, et al. presented allocation of FACTS devices and their role in the change of production cost and transmission pricing [24]. Srivastava and Verma determined the spot prices of real and reactive power maximizing social welfare function and impact of SVC and TCSC on the spot prices were also studied [25]. Recently, Shrestha and Feng presented simulation studies on the effects of TCSC on the spot price of real and reactive power using heuristic method to determine the location of TCSC [26]. Authors presented effects of optimally located SVC and TCPAR on the real and reactive power price including the costs of FACTS controllers [27]. However, the cost of FACTS controllers has not been considered in the model for their impact on nodal prices. In a deregulated environment, the number of bilateral transactions has grown rapidly [28-31]. It is therefore essential to help the system operator to evaluate their impacts on the system operation and evaluating their impact on nodal prices.
In this paper, impact on nodal prices have been determined considering three different reactive cost model for generators’ reactive power cost calculations for hybrid electricity markets where pool and bilateral transactions are occurring simultaneously. The impact of FACTS controllers have been incorporated taking their cost functions into account for evaluating their impact on nodal prices of real and reactive power. The complex problem has been solved using GAMS and MATLAB interfacing with DICOPT model in GAMS [32,33]. The comparison has been given for different reactive cost models for IEEE 24-bus reliability test system [34].
2. A Bilateral Transaction Matrix-T
The conceptual model of bilateral dispatch is that sellers and buyers enter in to transactions where the quantities traded and the trade prices are at the discretion of these parties and not a matter of ISO. These transactions are then brought to the ISO with a request that transmission facilities for the relevant amount of power be provided. If there is no violation of static and dynamic security, the ISO simply dispatches all requested transactions and charges for the service.
The bilateral concept can be generalized to the multinode case where the seller, for example a generation company called Gencos, may inject power at several nodes and the buyer bus called Discos also draw load at several nodes. Unlike pool dispatch, there will be a transaction power balance in that the aggregate injection equals the aggregate draw off for each transaction.The bilateral contract model used in this paper is basically a subset of the full transaction matrix proposed in [28]. In its general form, the transaction matrix T as shown in (1) is a collection of all possible transactions between Generation (G), Demand (D), and any other trading Entities (E) such as the marketers and the brokers.
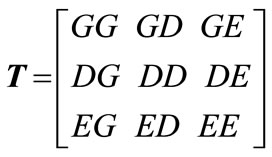 (1)
(1)
In this work, all transactions have been considered between the suppliers (G) and consumers (D). It is also noted that the diagonal block matrices (GG and DD) are zero because it is assumed that there are no contracts made between two suppliers or two consumers. Neglecting transmission losses, the transaction matrix can be simplified as:
 (2)
(2)
Each element of transaction matrix GD, namely GDij, represents a bilateral contract between a supplier (Pgi) of row i with a consumer (Pdj) of column j. Furthermore, the sum of row i represents the total power produced by generator i and the sum of column j represents the total power consumed at load j.
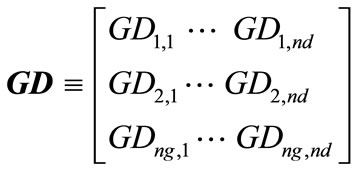 (3)
(3)
where:
ng = number of generators, and nd = number of loads.
In general, the conventional load flow variables, generation (Pg) and load (Pd) vectors, are now expanded into two dimensional transaction matrix GD as given in (4).
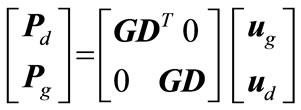 (4)
(4)
Vector ug and ud are column vectors of ones with the dimensions of ng and nd respectively. There are some intrinsic properties associated with this transaction matrix GD [25]. These are column rule, row rule, range rule, and flow rule. These properties have been explained in [25]. Each contract has to range from zero to a maximum allowable value, GDijmax. This maximum value is bounded by the value of corresponding PGimax or PDj whichever is smaller. The range rule satisfies:
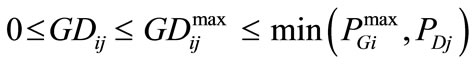 (5)
(5)
It is also possible for some contracts to be firm so that 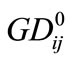 is equal to
is equal to  [30]. According to flow rule the line flows of the network using AC model can be expressed as follows:
[30]. According to flow rule the line flows of the network using AC model can be expressed as follows:
 (6)
(6)
The matrix ACDF is the distribution factors matrix [35]. If the representations of the Pg and Pd are substituted by using the definition of GD as given in (4), the line flows can be expressed in an alternative as follows:
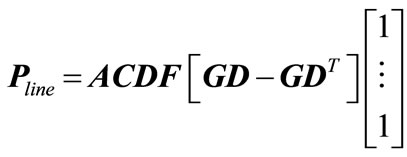 (7)
(7)
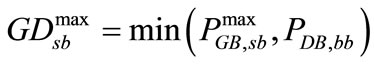 (8)
(8)
Bilateral transactions for IEEE-24 bus system have been considered and are given in Table 1. These transactions are taken as additional transactions over and above the already committed pool transactions taken in a system.
3. Reactive Power Cost Model for Generators’ Reactive Power
The cost of reactive power produced by a generator is essentially composed of two components: fixed costs or investment costs and variable costs. Variable cost in turn consists of operating costs (including fuel and maintenance cost) and the opportunity cost which depend on the reduction in its active power generation. Three methods have been considered to evaluate the cost of reactive power of generators.
3.1. Method-1: Triangular Approach [22]
This method of reactive power cost calculation is essentially based on the formulation for active power cost, in which the active power is replaced by reactive power using the triangular relationship.
 ($/hr)(9)
($/hr)(9)
where, 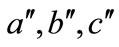 are constants depending on power fac
are constants depending on power fac

Table 1. Values of transactions between generators’ and loads.
tor (cos θ) and are calculated as follows from power triangle are:
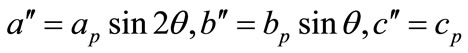 (10)
(10)
3.2. Method-2: Maximum Real Power (Pmax) Based Approach
If a generator produces (Pmax) as its maximum active power, then its cost for generating active power equals to cost (Pmax). In such a situation, no reactive power is produced and therefore, S equals Pmax. Reactive power production by a generator will reduce its capability to produce active power. Hence, provision of reactive power produced by generator will result in reduction of its active power production. To generate reactive power Qi by generator i which has been operating at its nominal power (Pmax), it is required to reduce its active power to Pi such that:
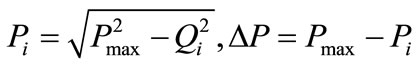 (11)
(11)
ΔP represents the amount of active power that will be reduced as a result of generating reactive power. To accurately calculate the cost of reactive power Qi, we should include all the costs imposed on generator as below:
Cost (Pmax): cost of producing active power equal to Pmax in one hour.
Cost (Pmax − ΔP): cost of generator when producing both active and reactive power with the amounts Pi and Qi , respectively.
Cost (Pmax) − Cost (Pmax − ΔP): Reduction in the cost of active power due to compulsory reduction in active power generation (ΔP) which happens due to generating reactive power with the amount of Qi . This represents the cost of reactive power production while the operating point of generator is moved from point 1 to point 2 (Figure 1) as below:
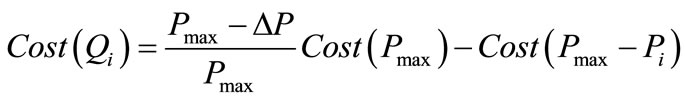 $/hr (12)
$/hr (12)
3.3. Method-3: Maximum Apparent Power Based Approach (SGmax)
Synchronous generators are rated in terms of the maximum MVA output at a specified voltage and power factor (usually 0.85 or 0.9 lagging) which they can carry continuously without overheating. The active power output is limited by the prime mover capability to a value within the MVA rating. The continuous reactive power output capability is limited by three considerations: armature current limit, field current limit, and end region heating limit. The reactive power production cost of generator is called opportunity cost. According to the loading capability diagram of a generator (Figure 2), reactive power output may reduce active power output capacity of generators which can at least serve as spinning reserve, therefore causes implicit financial loss to generators. Actually, opportunity cost depends on the real-time balance between demand and supply in the market, so it is difficult to determine the real value. For simplicity, an opportunity cost can be represented as:
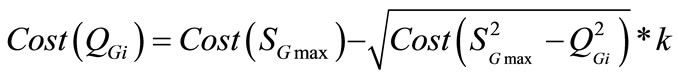 ($/h) (13)
($/h) (13)
where Sgi,max is the nominal apparent power of the generator at bus i; QGi is the reactive power output of the generator at bus i;
k is the profit rate of active power generation, taken usually between 5% and 10%. k has been considered as 10% in this work.
4. Cost Model of Facts Devices
There are three basic types of FACTS devices. One type can be characterized as injection of current in shunt, the second type as injection of voltage in series with the line, and the third type is a combination of current injection in shunt and voltage injection in series. With the introduction of these controllers in the system for flexible operation of system, their services need to be identified and remunerated. Since, these devices changes the flow patters in the network, they will have considerable impact on nodal prices and thus required to be included in the model with their cost functions. Static model of FACTS devices viz. SVC, TCSC, and UPFC has been well explained in [36]. The cost model of these devices has been given in [23].
4.1. Cost Model of FACTS Devices
According to [23], the cost functions for SVC, TCSC,
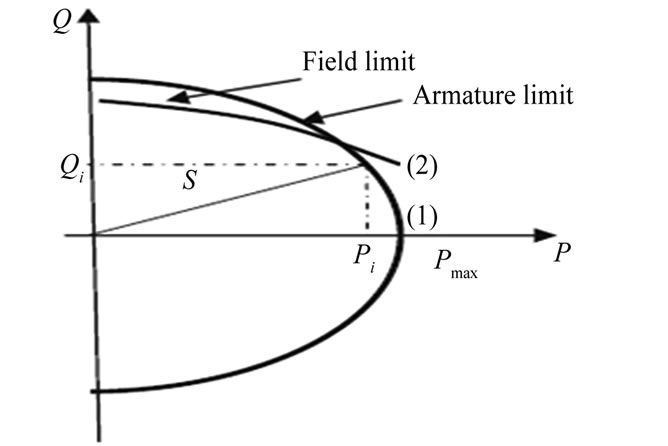
Figure 1. Capability curve of generator.
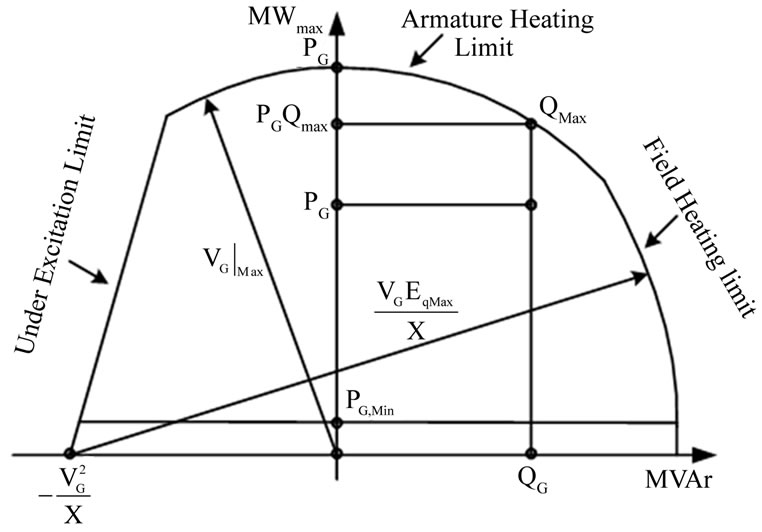
Figure 2. Loading capability curve of generator.
and UPFC are taken as follows:
Cost function of SVC:
 $/KVAr (14)
$/KVAr (14)
Cost function of TCSC:
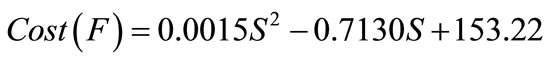 $/KVAr (15)
$/KVAr (15)
Cost function of UPFC:
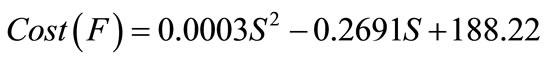 $/KVAr (16)
$/KVAr (16)
S is the operating range of the FACTS devices in MVar. The unit for generation cost is US$/h and for the investment costs of FACTS devices are US$. They must be unified into US$/h. Normally, the FACTS devices will be in-service for many years. However, only a part of its lifetime is employed to regulate the power flow. In this paper, five years has been considered to evaluate the cost function. Therefore, the average value of the investment costs is calculated using the following Equation:
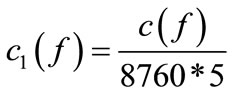 ($/hr) (17)
($/hr) (17)
where c(f) is the total investment costs of FACTS devices.
4.2. Power Flow Equation Model of FACTS Devices [36]
4.2.1. Static Model Representation of SVC
SVC is a shunt reactive current injection device whose primary function is dynamic voltage control. During steady state SVC placed at bus i can be considered as a constant reactive power injection QSVCi at bus i. It can be included in the model by modifying reactive power injection Qi as:
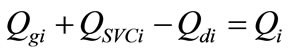 (18)
(18)
4.2.2. Static Model Representation of TCSC
Based on the principle of TCSC, the effect of TCSC on power system can be simulated as a controllable reactance xc inserted in the transmission line [36]. TCSC is generally installed in the substation for its convenient operation and maintenance. The shunt impedance (B/2) has been taken to the left side of TCSC as this approximation will have little effect on the computation accuracy. The power flow equations for the transmission lines in the presence of TCSC can be written as:
 (19)
(19)
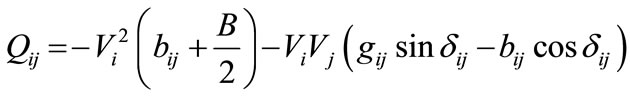 (20)
(20)
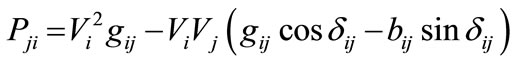 (21)
(21)
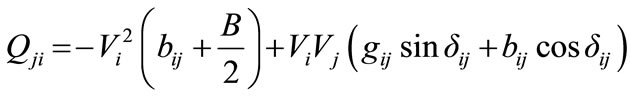 (22)
(22)
where, 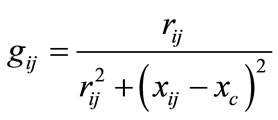 ,
, 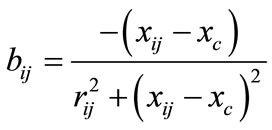 are conductance and succeptance of the line in the presence of TCSC. Here, the only difference between the normal line power flow equations and the line power flow equation with TCSC is the controllable reactance xc. TCSC can be incorporated in mathematical model by replacing Equations (42) to (45) with the Equations (19) to (22).
are conductance and succeptance of the line in the presence of TCSC. Here, the only difference between the normal line power flow equations and the line power flow equation with TCSC is the controllable reactance xc. TCSC can be incorporated in mathematical model by replacing Equations (42) to (45) with the Equations (19) to (22).
4.2.3. Static Model Representation of UPFC [36]
The unified power flow controller consists of two voltage source converters called as VSC 1 and VSC 2 operated from a common dc link provided by a dc storage capacitor. The real power can freely flow in either direction between the ac terminals of the two VSCs and can independently generate or absorb reactive power at its own ac output terminal. VSC 2 provides major function of the UPFC by injecting an ac voltage VT with controllable magnitude VT (0 < VT < VTmax) and phase angle (0 < 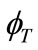 < 360) at the power frequency in series with line via an insertion transformer. This injected voltage can be considered essentially as a synchronous ac voltage source.
< 360) at the power frequency in series with line via an insertion transformer. This injected voltage can be considered essentially as a synchronous ac voltage source.
Based on the principle of UPFC and the vector diagram [36], the basic mathematical relations can be given as:
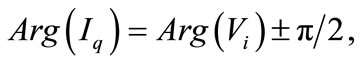
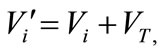 (23)
(23)
 ,
,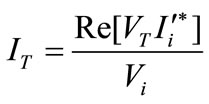 (24)
(24)
The Power flow equations from bus-i to bus-j and from bus-j to bus-i can be written as
 (25)
(25)
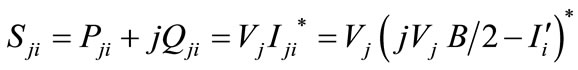 (26)
(26)
Active and reactive power flows in the line having UPFC can be written, with above equations as,
 (27)
(27)
 (28)
(28)
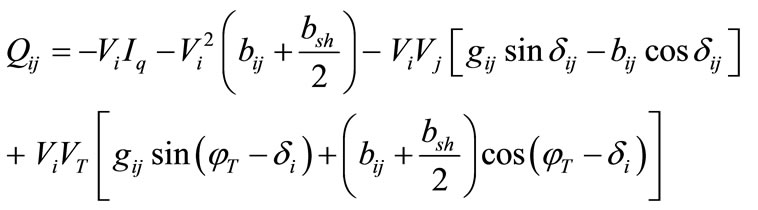 (29)
(29)
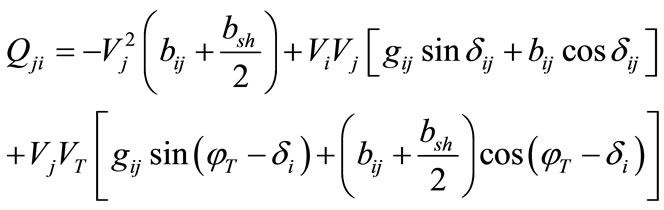 (30)
(30)
The power flow Equations (42) to (45) in the model can be replaced with the Equations (27) to (30) to incorporate the impact of UPFC.
5. Nodal Price determination with Reactive Power and FACTS Cost Models for Bilateral Market Model
The real and reactive power nodal prices, fuel cost, cost components of reactive power with different cost models and FACTS devices have been obtained solving an optimization problem of minimizing total cost subject to equality and inequality constraints for hybrid electricity market model. The generalized mathematical model can be represented as:
Min 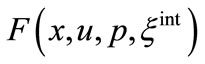 (31)
(31)
Subject to equality and inequality constraints defined as
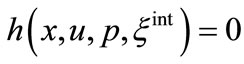 (32)
(32)
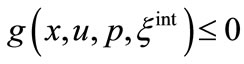 (33)
(33)
wherex is state vector of variables V, δ;
u are the control parameters, Pgi,Qgi, PGB, PGP, ;
p are the fixed parameters PDi, PDB, PDP, QDi, GDij;
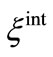 is an integer variable with values {0,1}. The zero value represents absence and one value represents presence of FACTS controllers in the network.
is an integer variable with values {0,1}. The zero value represents absence and one value represents presence of FACTS controllers in the network.
The objective function can be represented as:
1) Objective function
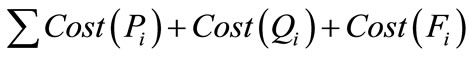 (34)
(34)
The objective function consist three cost components as cost of real power, cost of reactive power, and cost of FACTS devices. These can be represented as:
Cost (PGi) = Cost function of real power The Equations for the cost of reactive power for different reactive power cost models and FACTS cost models are explained in section III and IV.
Cost (Qi) = Cost function of reactive power Cost (Fi) = Cost function of FACTS devices.
where:
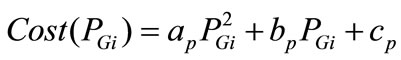 $/h(35)
$/h(35)
An objective function is subject to following set of constraints.
2) Power Injection at buses Nb is given as:
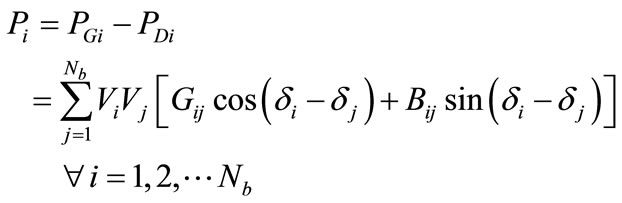 (36)
(36)
 (37)
(37)
With SVC, the reactive power injection at a bus can be represented with (18):
3) Power generating limits
 (38)
(38)
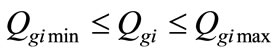 (39)
(39)
4) Power Balance equation at each bus
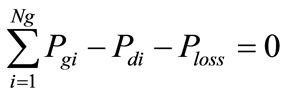 (40)
(40)
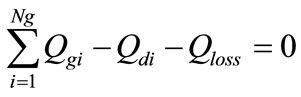 (41)
(41)
5) Transmission limits The real and reactive power flow equations from bus-i to bus-j can be written as:
 (42)
(42)
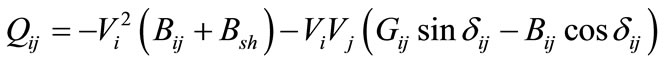 (43)
(43)
The real and reactive power flow equations from bus-j to bus-i can be written as:
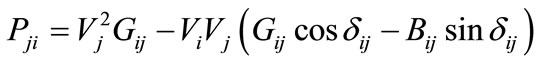 (44)
(44)
 (45)
(45)
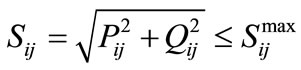 (46)
(46)
6) Voltage limits
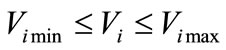 (47)
(47)
7) Phase angle limits
 (48)
(48)
8) Reactive Power Capability Curves limit for generators:
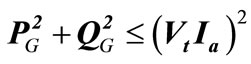 (49)
(49)
For hybrid market model, additional constraints to be satisfied are:
9) Equality constraints for bilateral transactions using transaction matrix GD are:
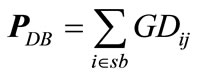 (50)
(50)
 (51)
(51)
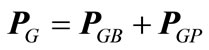 (52)
(52)
 (53)
(53)
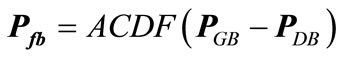 (54)
(54)
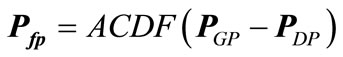 (55)
(55)
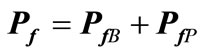 (56)
(56)
 (57)
(57)
where GD = bilateral transaction matrix PDB = vector of bilateral demand PDP = vector of pool demand PGB = vector of bilateral generation PGP = vector of pool generation ACDF are the distribution factors based on AC load flow approach [36].
s and b are the sets of the seller and buyer buses, respectively.
10) Limit on FACTS controllers:
SVC:
 (58)
(58)
where uri = {0,1} is a binary variable defining presence or absence of SVC.
TCSC:
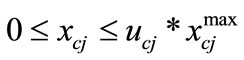 (59)
(59)
where ucj = {0,1} is a binary variable defining presence or absence of TCSC in a branch.
UPFC:
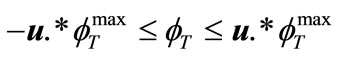 (60)
(60)
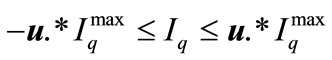 (61)
(61)
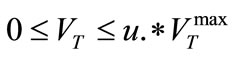 (62)
(62)
u is the vector of binary variable (‘0’s and ‘1’s) representing the presence or absence of UPFC with ‘1’s represent presence and ‘0’s represent absence of FACTS devices.
In the present work, impact of only one FACTS controller present in the system has been studied. However, more than one FACTS controller can be incorporated in the problem using the constraint on number of FACTS devices and can be represented as:
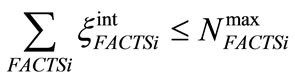 (63)
(63)
The optimization problem is solved using the GAMS 21.3/DICOPT solver and utilizing interfacing with MATLAB 6.5 [28,29]. The flow chart for nodal price determination with reactive and FACTS cost model is show in the Figure 3. The DICOPT model is based on the algorithm of outer approximation, equality relaxation, and augmented penalty approach [28].
6. Results and Discussions
The results have been determined for IEEE-24 bus system for hybrid market model. The impact of three different reactive cost models of generators’ reactive power cost estimation have been incorporated along with FACTS devices. The results have been obtained for different cases for pool model also. The results obtained have been categorized as follows:
Case 1: Results without FACTS devices for all methods
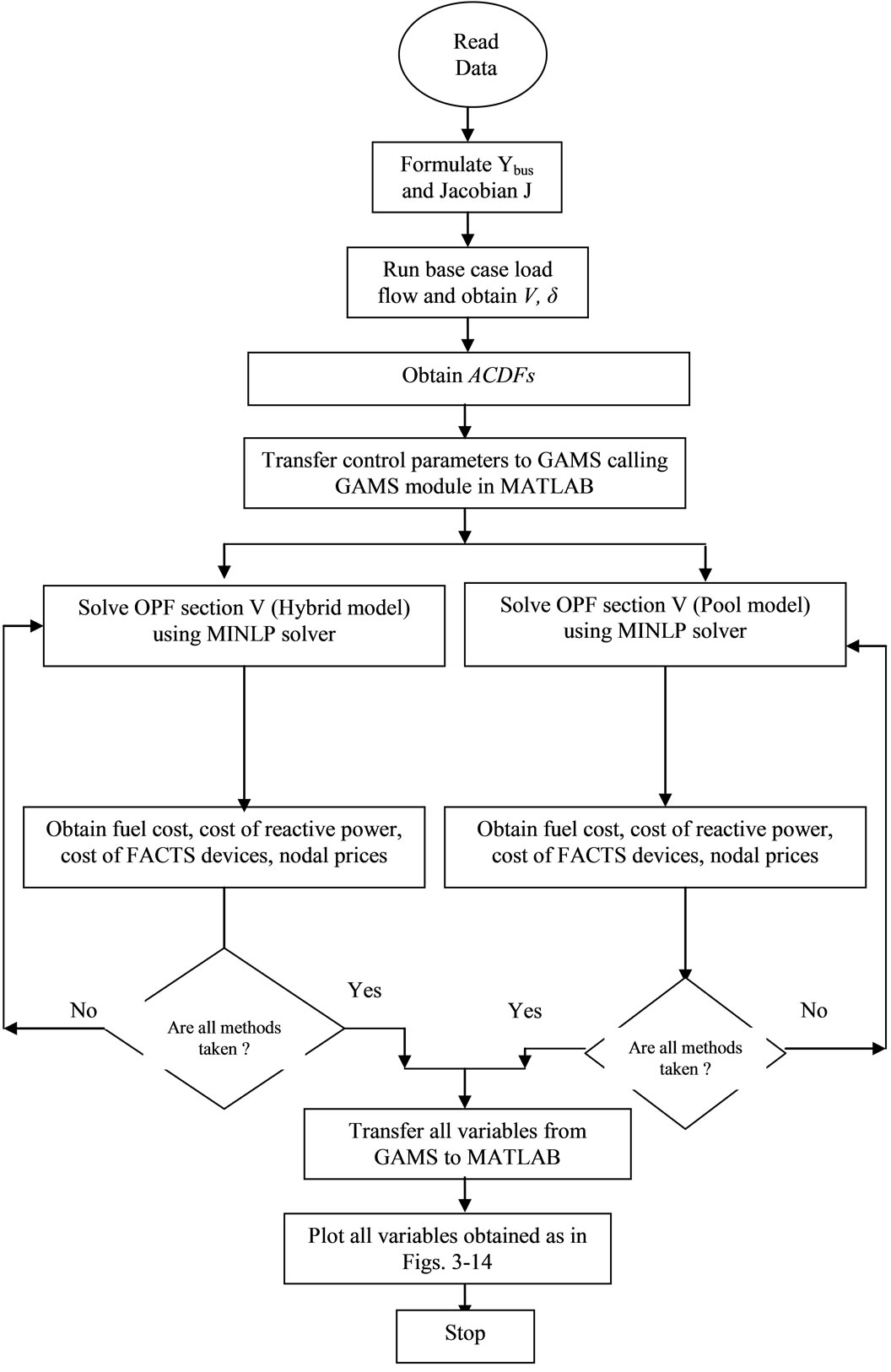
Figure 3. Flow chart.
Case 2: Results with FACTS device (SVC) for all methods Case 3: Results with FACTS device (TCSC) for all methods Case 4: Results with FACTS device (UPFC) for all methods
(a) Results for IEEE 24-bus test system (Bilateral Model)
The plots of the marginal cost for real and reactive power for Case 1 to case 4 using different methods (Method-1, Method-2, Method-3) of reactive power cost model is shown in Figures 4 to 7.
It is observed from Figure 4 that the marginal cost of real power is minimum at bus 22 is 34.86 $/MWh with a maximum value of 52.49 $/MWh. The nodal price for Case 1 with Method-2 is observed lower at almost all buses compared to Method-1 and Method-3. The marginal cost of reactive is both positive and negative. The negative reactive power marginal cost represents that the Lagrange multiplier is negative corresponding to that bus.
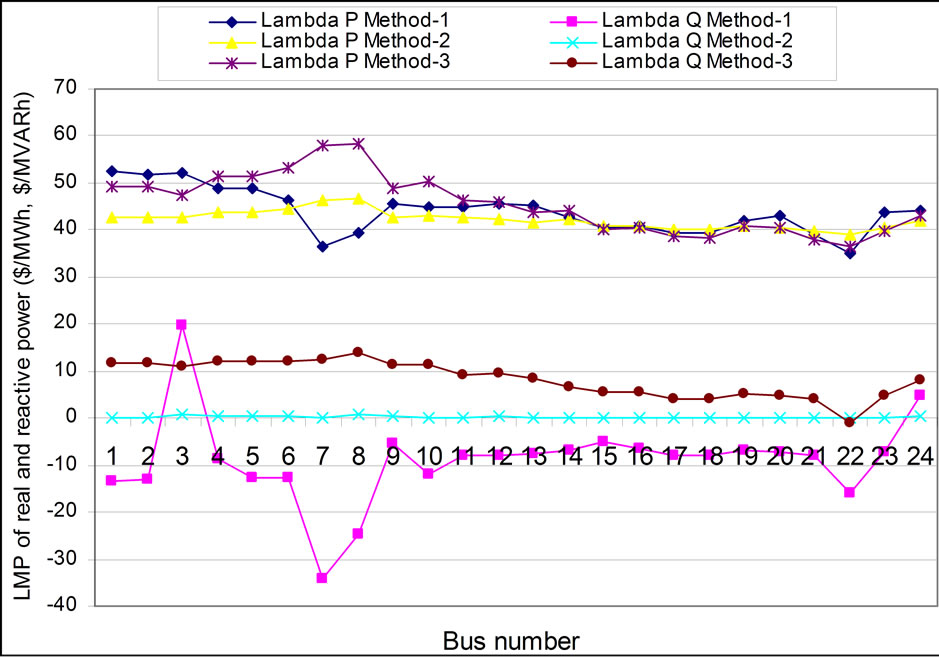
Figure 4. LMP of real and reactive power without any FACTS device for all methods (Case 1).
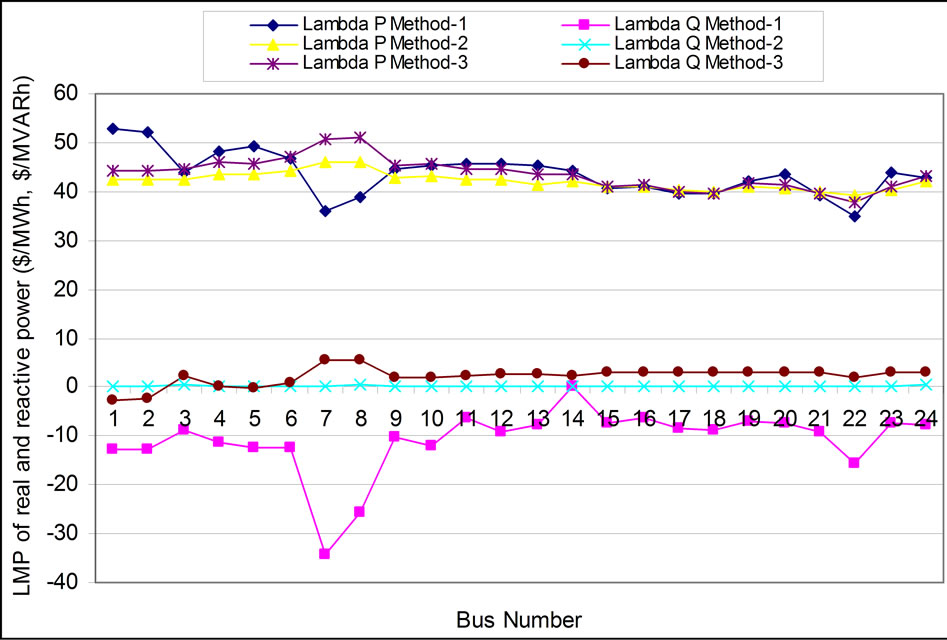
Figure 5. LMP of real and reactive power with SVC device for all methods (Case 2).

Figure 6. LMP of real and reactive power with TCSC for all methods (Case 3).
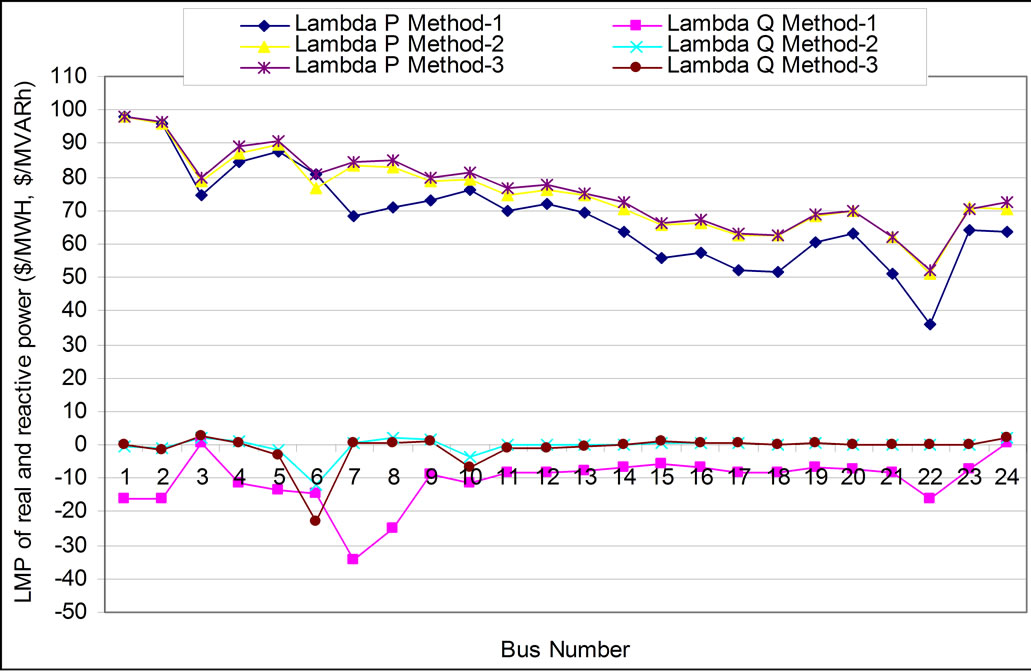
Figure 7. LMP of real and reactive power with UPFC for all methods (Case 4).
The reactive power nodal price is very small for method-2 and for method-3 it is found higher and positive at all buses. Cost component of generators’ reactive power is obtained minimum using method-3. The fuel cost is obtained minimum for method-3 as observed from Figure 8.
It is observed from Figure 5 that the marginal cost of real power is minimum at bus 22 with 34.74 $/MWh and with a maximum value of 53.85 $/MWh. The real power nodal price is observed to be lower for method-3 compared to method 1 and 2 with SVC. The nodal prices of both real and reactive power reduce for all methods with SVC. There is considerable reduction in reactive power nodal price with SVC. It is due to a support of reactive power to improve voltage profile and reducing losses in a system. The minimum fuel cost is obtained for method 3 as shown in Figure 8. SVC is optimally located at bus 3. Cost component of SVC is obtained minimum for method 1 as reactive power support is obtained minimum for this case. From Figure 6 (Case 3) with TCSC, it is found that the nodal prices for real power is lower for method 2 as compared to method 1 and 3. The nodal prices for real power are observed to increase with TCSC due to change in power flow patterns through lines. The nodal reactive power prices are observed to be higher with method-1 compared to method-2 and 3. The fuel cost is found lower using method-3. The reactive cost component is found lower for method-3 due to lower reactive support provided by TCSC. The cost component of TCSC is found minimum for method-1 due to lower reactive support provided by TCSC for this case.
With UPFC (Case 4), It is observed from Figure 7 that the marginal cost of real power is minimum at bus 22 and is 40.88 $/MWh using Method-1 and is found with a maximum value of 109.78 $/MWh for method-2. The real power nodal price is observed lower for method-1 compared to method-2 and 3. The cost component for reactive power is observed minimum for method-3. The fuel cost is found lower for method-3 as given in Figure 8. The fuel cost is observed higher than for Case-3 and lower for Case-1 and Case-2.
The cost component for UPFC is lower for method-3 due to its lower reactive power support compared to other methods. The UPFC is optimally located on line between buses 3 and 24. The cost component of UPFC is much larger than TCSC and SVC as UPFC is costlier than SVC and TCSC and reactive support obtained from UPFC is also higher compared to other FACTS devices. The fuel cost is observed to be lower with FACTS devices for all methods compared to the case without FACTS controller. It is observed from Figure 9 that the cost component of FACTS devices is found lower for method 1 and UPFC cost component is higher compared to SVC and TCSC for all the methods.
The results obtained for nodal prices of real and reactive power for Case 1 to 4 using different methods of reactive power model is shown in Figures 10 to 13 for pool market model.
It is observed from Figure 10 (Case 1) that the marginal cost of real power is minimum at bus 22 and the value is 32.927 $/MWh and with a maximum value 96.705 $/MWh. The marginal cost of reactive power is both positive and negative. The negative reactive power marginal cost represent that the Lagrange multiplier is negative corresponding to that bus. The nodal prices of real power are observed lower for method-3 compared to method-1 and 2. Nodal prices for reactive power are found higher for method-3. Fuel cost is found lower us-
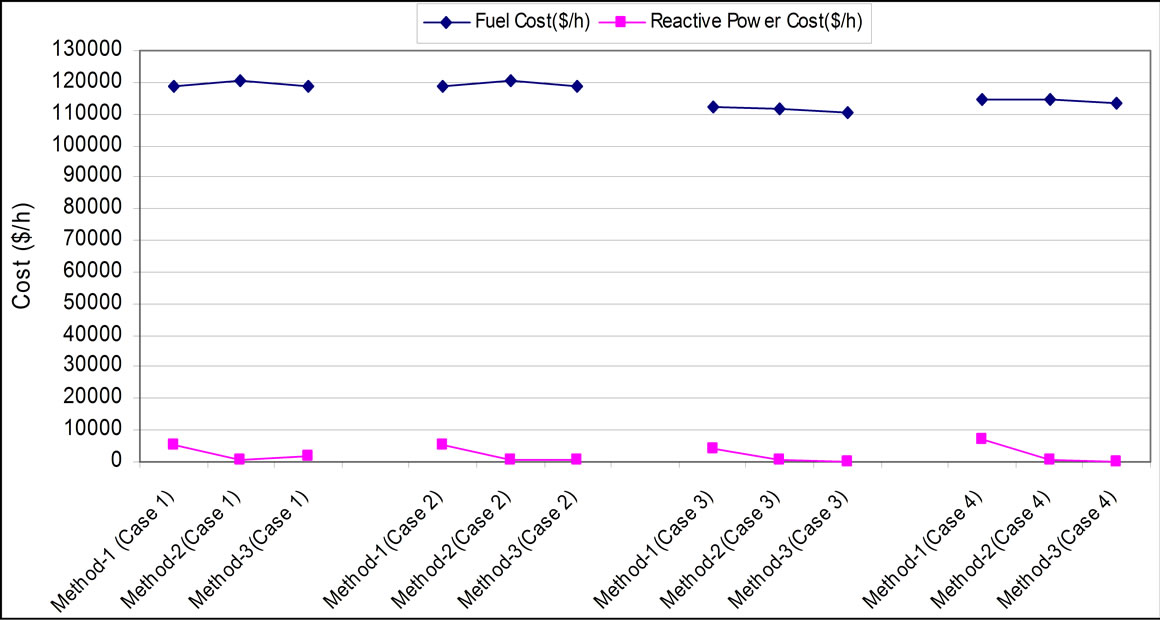
Figure 8. The fuel and reactive power cost ($/h) for all cases and all methods.
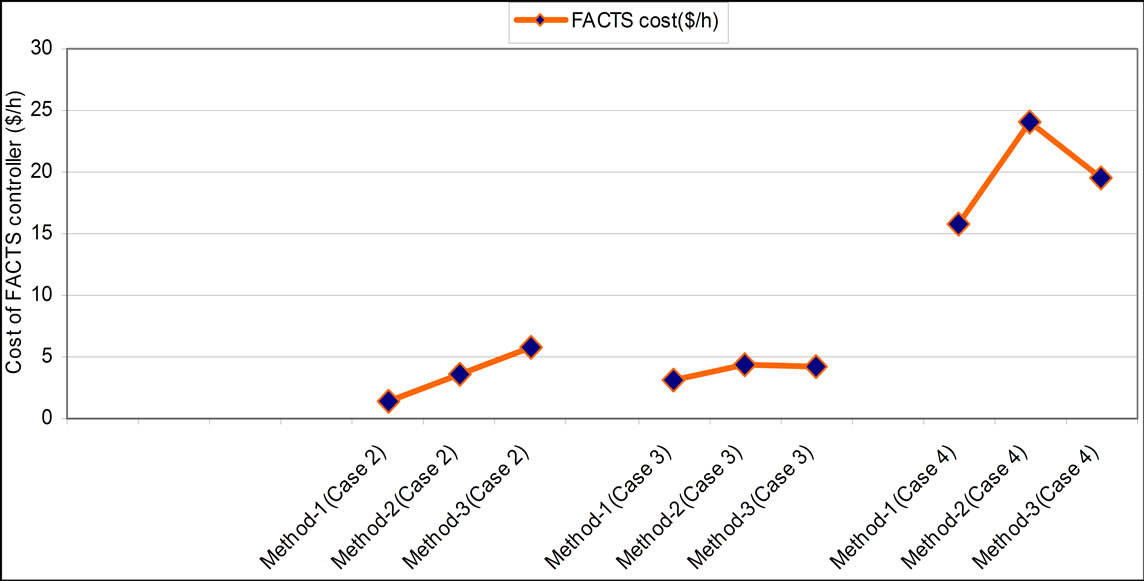
Figure 9. The cost component for FACTS controllers ($/h) for all cases with all methods.
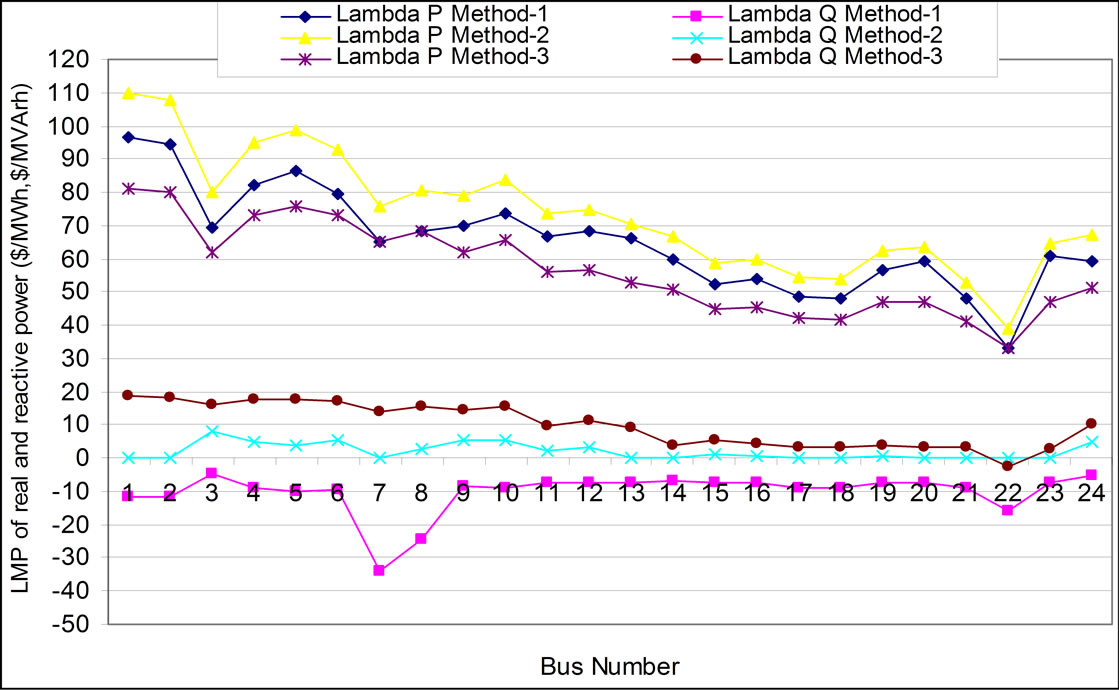
Figure 10. LMP of real and reactive power without any FACTS device for all methods (Case 1).
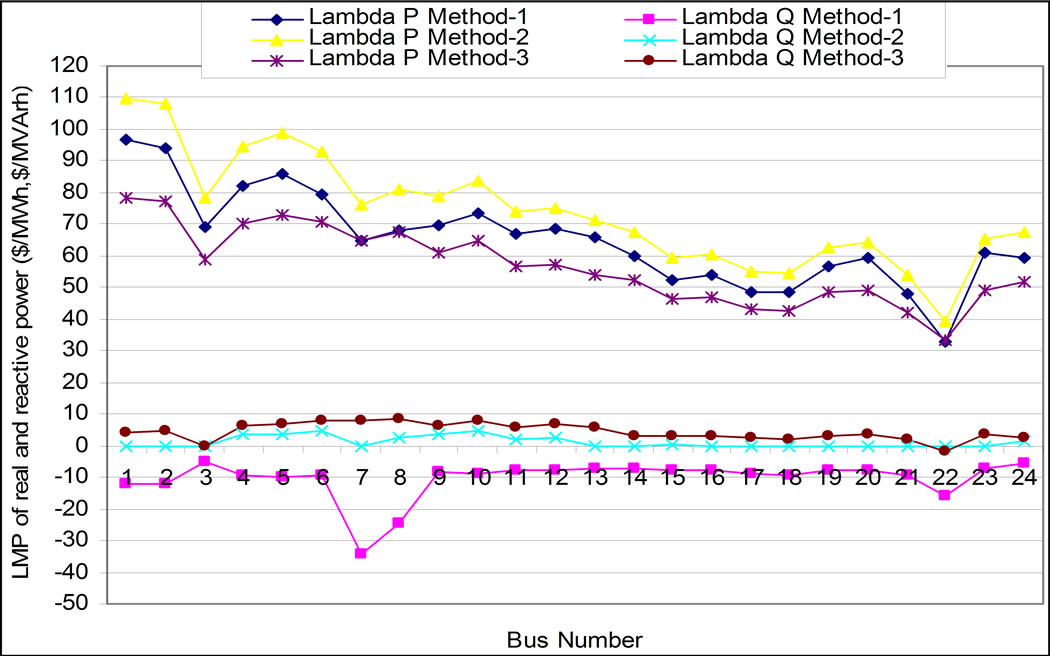
Figure 11. LMP of real and reactive power withSVC for all methods (Case 2).

Figure 12. LMP of real and reactive power with TCSC for all methods (Case 3).

Figure 13. LMP of real and reactive power with UPFC for all methods (Case 4).
ing method-3 as shown in Figure 14. The reactive power cost component is lower for method 3.
From Figure 11 it is observed that the marginal cost of real power is minimum at bus 22 and the values is 32.89 $/MWh and with a maximum value of 109.78 $/MWh for method 2. It is observed that marginal cost reduces at each bus with SVC. The impact on reactive power nodal prices is more prominent due to reactive support of SVC. We observe that marginal cost of reactive power is obtained minimum for method 2 however for method 3 it is found higher and positive at all buses. The upper and lower limits of QSVC have been considered as: 0.5 to 2.0 MVAR and SVC is optimally located at bus 3. The cost component of reactive power is lower for method-3. The cost component of SVC is found higher for method-3 as reactive support for this case is obtained higher compared to other cases. With SVC, the fuel cost is slightly lower compared to the case without SVC.
The results of the marginal cost for real and reactive power for Case-3 using different methods of reactive power model is shown in Figure 12. The TCSC is optimally connected at line 7 between bus 3 and bus 24. For TCSC, the limit of Xc is selected between 0.2 XL to 0.5 XL p.u. It is observed from Figure 12 that the marginal cost of real power is minimum at bus 22 and is 55.60 $/MWh with Method-1 and with a maximum value 113.68 $/MWh for Method-2. Nodal prices for real power are found higher with TCSC due to change in power flow pattern at all lines and are comparatively higher for method-2. The fuel cost is found lower for method-3 and slightly higher compared to Case 1 and 2 as given in the Figure 14. The cost component of TCSC is lower for method-1 as reactive support obtained from TCSC is lower for this case. The reactive cost component is obtained lower for method-3.
For Case 4 (with UPFC) is optimally connected between bus 3 and 24. It is observed that the marginal cost of real power is minimum at bus 22 and is 42.006 $/MWh using Method 1 and with a maximum value 109.78 $/MWh using Method-2. The nodal prices are obtained lower for method-1. The reactive power cost component is lower for method-3. The cost component for UPFC is lower for method-1 due to lower reactive support obtained for this case. With UPFC, fuel cost is found to be more compared to fuel costs obtained with SVC and TCSC in all the methods as given in Figure 14. In comparison to TCSC, the nodal prices of real power are found lower at each bus. Reactive cost component is found lower for method 3 in all the cases. Cost component for UPFC is found higher compared to SVC and TCSC as shown in Figure 15.
From all the four cases above, it is observed that with the FACTS devices cost models and with consideration of reactive cost models, the nodal prices are observed to be different showing the effect of cost models on the marginal prices.
7. Conclusions
In this work, impact of reactive power cost model on nodal price for real and reactive power have been obtained. The cost model of FACTS devices have been incorporated to find their impact on real and reactive nodal price at each node. Based on the results, the following conclusions are:
1) The nodal prices are found different with different methods and are found lower for method-2 in bilateral model for Case 1 and Case 2, however for Case 3 and 4, the nodal prices are found lower for method-1. For pool
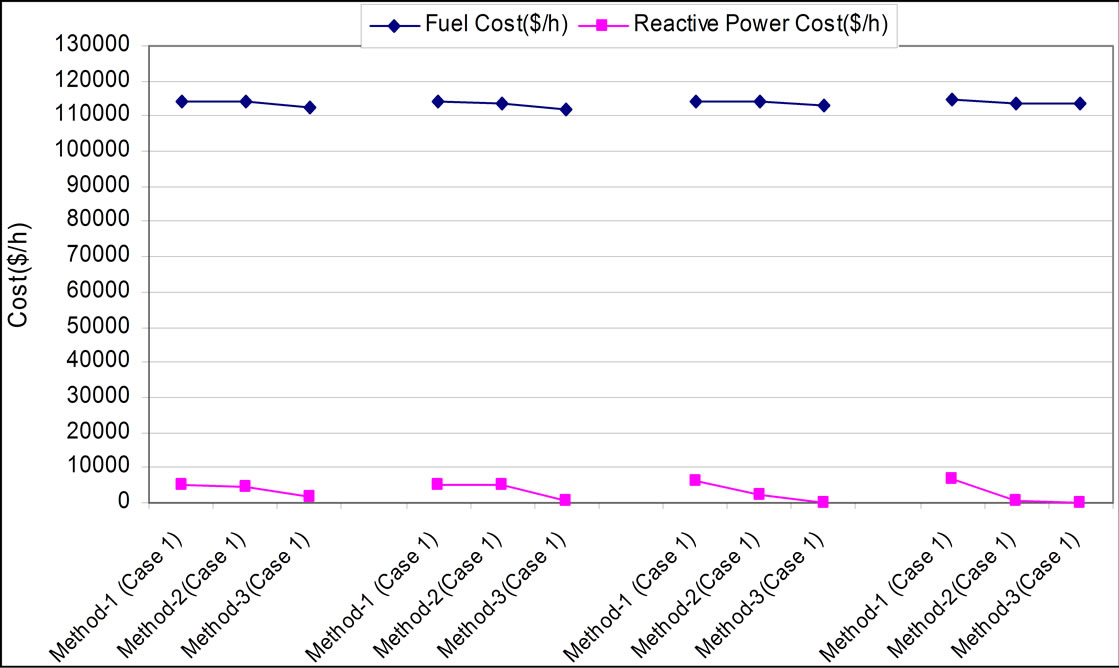
Figure 14. The fuel and reactive power cost ($/h) for all cases and all methods.
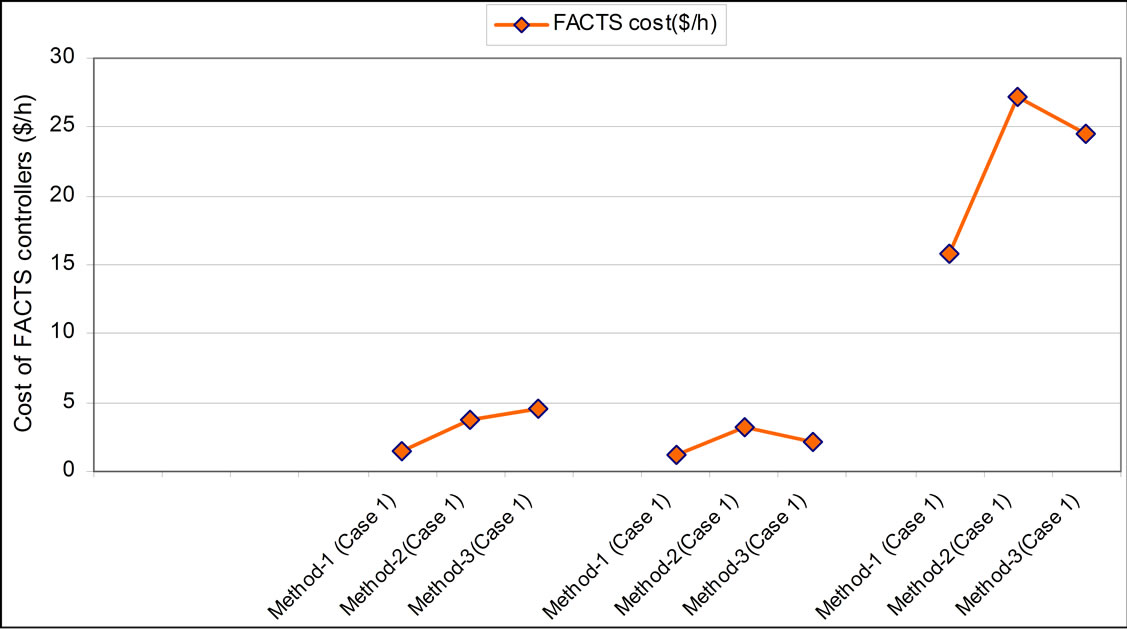
Figure 15. The cost component for FACTS controllers ($/h) for all cases with all methods.
model, the nodal prices for real power are found lower with method 3 for Case 1 and Case 2 and lower with method 1 for case 3 and case 4.
2) The reactive power nodal prices are both positive and negative at buses and with SVC are found lower due to its reactive support. With SVC the nodal prices for real power also reduces at all buses for all methods.
3) With UPFC, nodal prices are found lower compared to TCSC.
4) Cost components for reactive power are found lower for method-3 for all cases.
5) Cost component of UPFC is high compared to TCSC and SVC being costly device compared to SVC and TCSC.
6) Fuel cost is obtained minimum for method-3 for all the cases. With FACTS controllers, fuel costs are found to be lower compared to the case without FACTS controllers.
7) The nodal prices varies with the reactive cost models considered for study and cost model of FACTS devices also plays an important role for variation in nodal prices.
Based on the results, it is concluded that reactive cost models have considerable impact on LMPs of real and reactive power at each bus. Cost model of FACTS devices also have noticeable impact on LMPs. Therefore, the ISO must consider the appropriate reactive cost models for accurate transmission pricing and wheeling cost determination for better market operation. FACTS cost component can not be ignored in the model for accurate transmission pricing due to their impact on LMPs.
REFERENCES
- M. L. Baughman and S. N. Siddiqi, “Real Time Pricing of Reactive Power: Theory and Case Study Results,” IEEE Transactions on Power Systems, Vol. 6, No. 1, 1991, pp. 23-29. doi:org/10.1109/59.131043
- N. Dandachi, M. Rawlins, O. Alsac, M. Paris and B. Stott, “OPF for Reactive Power Transmission Pricing on The NGC System,” IEEE Transactions on Power Systems, Vol. 11, No. 1, 1996, pp. 226-232. doi:org/10.1109/59.486099
- M. Einborn and R. Siddiqi, “Electricity Transmission Pricing and Technology,” Kluwer Academic Publishers, Dordrecht, 1996.
- F. C. Schweppe, M. C. Caramanis, R. D. Tabors and R. E. Bohn, “Locational Based Pricing of Electricity,” Kluwer Academic Publishers, Dordrecht, 1988.
- M. Rivier and I. Perez-Ariaga, “Computation and Decomposition of Location Based Price for Transmission Pricing,” Proceedings of 11th Power Systems Computation Conference, Avignon, France, 30 August-3 September, 1993.
- D. Ray and F. Alvarado, “Use of Engineering Model for Economic Analysis in the Electric Utility Industry,” Presented at the Advanced Workshop on Regulation and Public Utility Economics, Rutgers University, 25-27 May, 1988.
- A. A. El-Keib and X. Ma, “Calculating the Short-Run Marginal Costs of Active and Reactive Power Production,” IEEE Transactions on Power Systems, Vol. 12, No. 2, 1997, pp. 559-565. doi:org/10.1109/59.486099
- Y. Z. Li and A. K. David, “Wheeling Rates of Reactive Flow under Marginal Cost Theory,” IEEE Transactions on Power Systems, Vol. 10, No. 3, 1993.
- A. Zobian and M. Ilic, “Unbundling of Transmission and Ancillary Services,” IEEE Transactions on Power Systems, Vol. 12, No. 1, 1997, pp. 539-548.
- M. C. Caramanis, R. E. Bohn and F. C. Schweppe, “System Security Control and Optimal Pricing of Electricity”, Electric Power and Energy Systems, Vol. 9, No. 4, 1987, pp. 217-224.
- M. L. Baughman, S. N. Siddiqi and J. W. Jarnikau, “Advanced Pricing in Electrical Systems-Part II,” IEEE Transactions on Power Systems, Vol. 12, No. 1, 1997, pp. 496-502. doi:org/10.1109/59.575803
- K. Xie, Y. H. Song, J. Stonham, E. Yu and G. Liu, “Decomposition Model and Interior Point Methods for Optimal Spot Pricing of Electricity in Deregulated Environments,” IEEE Transactions on Power Systems, Vol. 15, No. 1, 2000, pp. 39-50. doi:org/10.1109/59.852099
- D. Chattopadhyaya, K. Bhattacharya and J. Parikh, “Optimal Reactive Power Planning and Its Spot Pricing: An Integrated Approach,” IEEE Transactions on Power Systems, Vol. 10, No. 4, 1995, pp. 2014-2019. doi:org/10.1109/59.476070
- J. Y. Choi, S. Rim and J. Park, “Optimal Real Time Pricing of Real and Reactive Powers,” IEEE Transactions on Power Systems, Vol. 13, No. 4, 1998, pp. 1226-1231. doi:org/10.1109/59.736234
- S. Hao and A. Pepalexopolous, “A Reactive Power Pricing and Management,” IEEE Transactions on Power Systems, Vol. 12, No. 1, 1997, pp. 95-104. doi:org/10.1109/59.574928
- J. W. Lamont and R. Fu, “Cost Analysis of Reactive Power Support,” IEEE Transactions on Power Systems, Vol. 13, No. 3, 1999, pp. 890-898. doi:org/10.1109/59.780900
- M. Muchayi and M. E. El-Hawary, “A Summary of Algorithms in Reactive Power Pricing,” Electric Power and System Research, Vol. 21, 1999, pp. 119-124. doi:org/10.1016/S0142-0615(98)00039-8
- V. M. Dona and A. N. Paredes, “Reactive Power Pricing in Competitive Electric Markets Using Transmission Losses Function,” IEEE Porto Power Tech Conference, Porto, 10-13 September 2001.
- J. B. Gill, T. G. S. Roman, J. J. A. Rioa and P. S. Martin, “Reactive Power Pricing: A Conceptual Framework for Remuneration and Charging Procedures,” IEEE Transactions on Power Systems, Vol. 15, No. 2, 2000, pp. 483- 489. doi:org/10.1109/59.867129
- V. L. Paucar and M. J. Rider, “Reactive Power Pricing in Deregulated Electrical Markets Using Methodology Based on Theory of Marginal Costs,” Proceedings of IEEE PES General Meeting, Vancouver, 2001.
- M. J. Rider and M. L. Paucar, “Application of Nonlinear Reactive Power Pricing Model for Competitive Electric Markets,” IEE Proceedings—Generation, Transmission, Distribution, Vol. 151, No. 3, 2004, pp. 407-414. doi:org/10.1049/ip-gtd:20040385
- Y. Zhao, M. R. Irving and Y. Song “A Cost Allocation and Pricing Method for Reactive Power Services in the New Deregulated Electricity Market Environment,” Proceedings of IEEE Transmission and Distribution Conference, Dalian, August 2005.
- L. J. Cai and István Erlich, “Optimal Choice and Allocation of FACTS Devices using Genetic Algorithms,” Proceedings of ISAP, Intelligent Systems Application to Power Systems, 2003, Lemnos, 31 August-3 September, 2003.
- E. J. de Olivera, J. W. M. Lima and J. L. R. Pereira, “Flexible AC Transmission Devices: Allocation and Transmission Pricing,” Electric Power and Energy Systems, Vol. 21, No. 2, 1999, pp. 111-118.
- S. C. Srivastava and R. K. Verma, “Impact of FACTS Devices on Transmission Pricing in a Deregulated Market,” International Conference on Electric Utility Deregulation and Restructuring and Power Technologies, DRPT, London, 4-7 April 2000, pp. 642-648.
- G. B. Shrestha and W. Feng, “Effects of Series Compensation on Spot Price Markets,” Electric Power and Energy Systems, Vol. 27, No. 5-6, 2005, pp. 428-436. doi:org/10.1016/j.ijepes.2005.03.001
- S. Chanana and A. Kumar, “Effect of Optimally Located FACTS Devices on Active and Reactive Power Price in Deregulated Electricity Markets,” IEEE Power India Conference, New Delhi, 10-12 April 2006.
- G. Hamoud, “Feasibility Assessment of Simultaneous Bilateral Transactions in a Deregulated Environment,” IEEE Transactions on Power systems, Vol. 15, No. 1, 2000, pp. 22-26. doi:org/10.1109/59.852096
- J. W. M. Cheng, F. D. Galiana and D. T. McGills, “Studies of Bilateral Contracts with Respect to Steady State Security in a Deregulated Environment,” IEEE Transactions on Power Systems, Vol. 13, No. 3, 1998, pp. 1020- 1025. http://dx.doi.org/10.1109/59.709092
- J. W. M. Cheng, D. T. McGills and F. D. Galiana, “Probabilistic Security Analysis of Bilateral Transactions in a Deregulated Environment,” IEEE Transactions on Power Systems, Vol. 14, No. 3, 1999, pp. 1153-1159. doi:org/10.1109/59.780948
- F. D. Galiana and M. Ilic, “A Mathematical Framework for the Analysis and Management of Power Transactions under Open Access,” IEEE Transactions on Power Systems, Vol. 13, No. 2, 1998, pp. 681-687. doi:org/10.1109/59.667400
- GAMS—The Solver Manuals, GAMS Development Corporation, March 2001.
- M. C. Ferris, “MATLAB and GAMS: Interfacing Optimization and Visualization Software,” 10 August 1999.
- “IEEE Reliability Test System, A report prepared by the Reliability Test System Task Force of the Applications of Probability Methods Subcommittee,” IEEE Transactions on Power Apparatus and Systems, Vol. PAS-98, 1979, pp. 2047-2054.
- A. K. Sharma and S. Chanana, “New Multiobjective Optimization Problem for Secure Bilateral Transaction Determination with UPFC in Hybrid Electricity Markets,” Electric Power Components and Systems, Vol. 36, No. 6, 2008, pp. 555-574. doi:org/10.1080/15325000701801561
- G. Shaoyun, “Optimal Power System Operation and Control Incorporating FACTS Devices,” Ph.D. Thesis, The Hong Kong University, August 1998.

