Smart Grid and Renewable Energy
Vol.1 No.1(2010), Article ID:1946,7 pages DOI:10.4236/sgre.2010.11006
A Qualitative Perstective on Idempotency Defect of Two Level System Interacting with Laser and Quantized Field
![]()
1Mathematics Department, Faculty of Science, Taif University, Taif, Saudi Arabia; 2Department of Mathematics, Faculty of Science, Sohag University, Sohag, Egypt; 3Mathematics Department, Physics Division, National Research Centre, Cairo, Egypt; 4Mathematics Department, Faculty of Science, Al-Azher University, Nassr City, Cairo, Egypt.
Email: abotalb2010@yahoo.com
Received March 22nd, 2010; revised May 13th, 2010; accepted May 13th, 2010.
Keywords: Entanglement, Idempotency Defect, Two-Level System, Quantized
ABSTRACT
Entanglement due to the interaction of a two level atom with a laser and quantized field is investigated. The role of the nonlinearity due to these interactions is discussed. It is found that the nonlinearity changes strongly the behavior of the entanglement also the detuning parameters have important role in the structure of the measure of entanglement.
1. Introduction
Quantum information processing provides different way for manipulating information other than the classical one. This is related to entanglement, which plays an essential role in the quantum information such as quantum computing [1], teleportation [2], cryptography [3], dense coding [4] and entanglement swapping [5]. Thus intensive efforts have been done to understand theoretically and experimentally the entanglement in quantum systems. For instance, the entanglement between two qubits in an arbitrary pure state has been quantified by the concurrence [6] and Peres-Horodecki measure [7]. However, that of the mixed states is quantified by the average concurrence over all possible pure state ensemble decomposition. Additionally, the entropic relations are used in investigating the entanglement in quantum system. In this regard von Neumann entropy (NE) [8], linear entropy (LE) and the Shannon information entropy (SE) [9] have been frequently used in treating entanglement in the quantum systems. The NE [10] and the LE [11] have been applied to the JCM. It is worth mentioning that the SE involves only the diagonal elements of the density matrix and in some cases it can give information similar to that obtained from the NE and LE.
The paper is prepared in the following order: In section 2 we define the system Hamiltonian. In section 3, we derive the time evolution operator and density matrix. In section 4 we investigate the atomic inversion and idempotency defect (ID). In section 5 we summarize the main results.
2. The System Hamiltonian
The scheme, we are going to discuss exploits the passage of a single atom through a quantized cavity [12]. We wish to underline the relevance of this aspect from an experimental point of view. Preparing and controlling a single atom is certainly much easier to achieve with respect to the case when the manipulation of many atoms is required. In addition, taking into consideration the low efficiency of the atomic state detectors today used in laboratory, conditional measurement procedures involving one atom only instead of many ones, have to be preferred. The dynamics of several Hamiltonian models describing such systems is exactly treatable and, in most cases, testable in the laboratory. The point to be appreciated is indeed that, studying such systems, one has the opportunity to induce entanglement and control its evolution in a multipartite physical system. In this paper: we study a two-level atom injected into a cavity field, where the dipole-allowed transitions between the lower level and the upper levels are nonresonant with the cavity mode. Furthermore, we assume that the interaction including an arbitrary form of nonlinearity of the intensity-dependent coupling. In the rotating wave approximation (RWA), the interaction of the cavity mode with the injected atom is described by the Hamiltonian (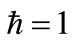 ):
):
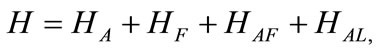 (1)
(1)
where 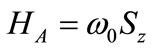 is the atom Hamiltonian,
is the atom Hamiltonian, 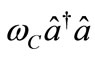
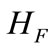 is the field Hamiltonian,
is the field Hamiltonian, 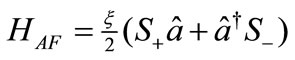 is the atom-field Hamiltonian, and
is the atom-field Hamiltonian, and
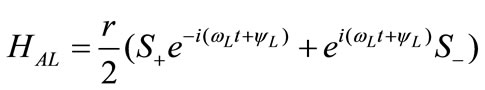
is the atom-laser Hamiltonian.
The atomic transition frequency is denoted by wo, the frequencies of the cavity and laser fields are denoted by wc and wL receptivity, and the laser field is assigned by the phase yL, the operator 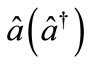 is the annihilation (creation) operator of the cavity field and obey the commutation relation
is the annihilation (creation) operator of the cavity field and obey the commutation relation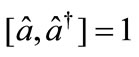 , x and r are the coupling constants associated with the cavity field and the classically described laser field respectively which are assumed real. The
, x and r are the coupling constants associated with the cavity field and the classically described laser field respectively which are assumed real. The 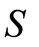 operators are the coherence operators for the atom, satisfying the following angular momentum commutation relations
operators are the coherence operators for the atom, satisfying the following angular momentum commutation relations 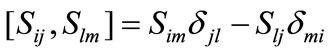 where
where 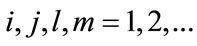
3. Time Evolution Operator and Density Matrix
To obtain the time evolution operator, we must eliminate the explicit time dependence of the previous Hamiltonian 1), we use the following unitary operator [13]
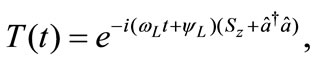 (2)
(2)
we redefine the Hamiltonian as :
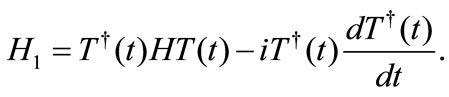 (3)
(3)
Then the Hamiltonian 1) will be in the following form:
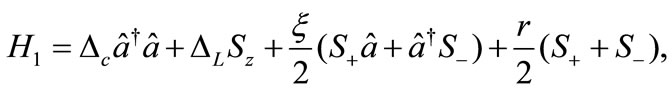 (4)
(4)
where 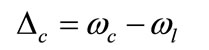 and
and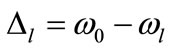 , if we consider the resonant pumping case
, if we consider the resonant pumping case 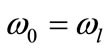 and rearrange the Hamiltonian terms, the Hamiltonian (4) becomes.
and rearrange the Hamiltonian terms, the Hamiltonian (4) becomes.
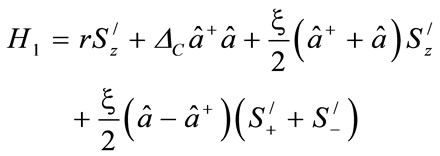 (5)
(5)
The new atomic operators set
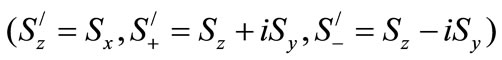
which obey the angular momentum commutation relations among themselves. The eigenvector of 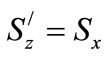 is the dressed states of the atom in the laser field alone and the operators
is the dressed states of the atom in the laser field alone and the operators 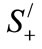 and
and 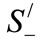 are the corresponding raising and lowering operators.
are the corresponding raising and lowering operators.
To associate the third and the fourth terms of 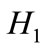 we use the following unitary transformation:
we use the following unitary transformation:
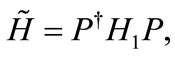 (6)
(6)
where P is an atomic state dependent displacement operator of the cavity field state which is defined as :
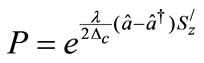 (7)
(7)
Then the Hamiltonian 4) takes the following form:
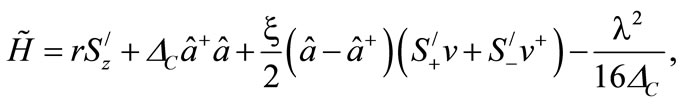 (8)
(8)
where
 (9)
(9)
We can drop  which has no effect in the dynamics of the system.
which has no effect in the dynamics of the system.
This Hamiltonian describes a two level system with energy levels separated by r coupled to a single quantized mode of radiation frequency ![]() and there is an infinite sequence of probe resonance zones in the neighborhood of the Rabi sub harmonic resonances at
and there is an infinite sequence of probe resonance zones in the neighborhood of the Rabi sub harmonic resonances at
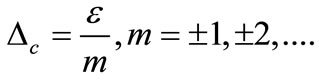
If we consider of the RWA, the slowly varying terms are identified and retained, in the m th resonance zone 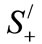 has the zero order time dependence
has the zero order time dependence ![]() that is approximately canceled by the zero order time dependence
that is approximately canceled by the zero order time dependence 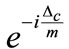 of all field operators of the form
of all field operators of the form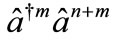 , for any n.
, for any n.
The Hamiltonian for the 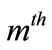 resonance zone is:
resonance zone is:
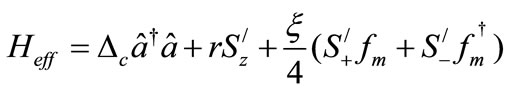 (10)
(10)
In this case, we recognize as the 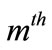 -order multiphoton Jaynes Cumming Hamiltonian where we consider
-order multiphoton Jaynes Cumming Hamiltonian where we consider
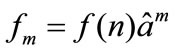 ,
, 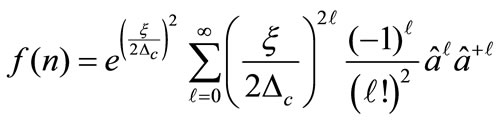
destroys m photons of frequency Dc where ![]() can be further simplified by means of another rotating wave approximation (RWA),( as discussed in detail in [12-14]).
can be further simplified by means of another rotating wave approximation (RWA),( as discussed in detail in [12-14]).
The time evolution operator is given by:
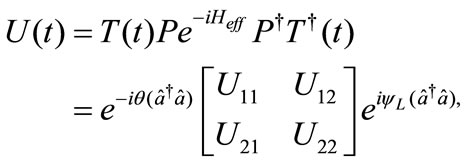 (11)
(11)
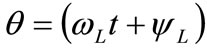
where
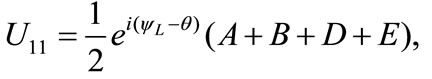
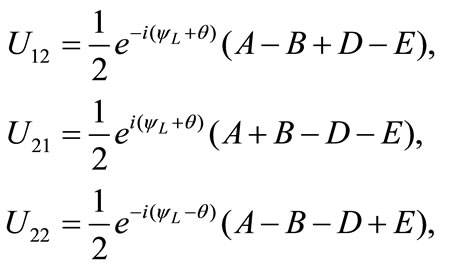 (12)
(12)
and
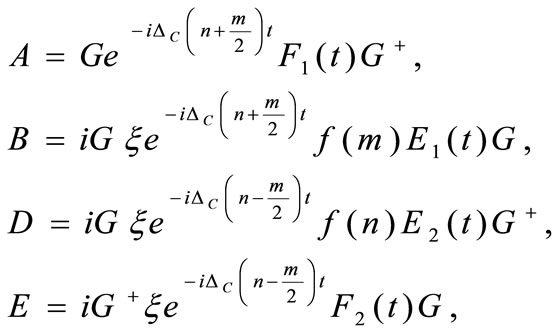 (13)
(13)
where
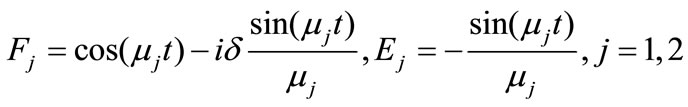 .
.
Also,
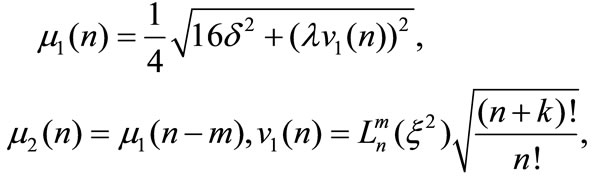
where,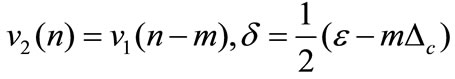 ,
,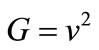 and
and 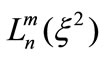 is the Laguerre function. At
is the Laguerre function. At 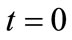 the wave function of the system can be written as:
the wave function of the system can be written as:
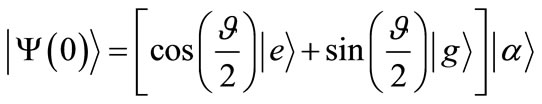 (14)
(14)
where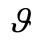 is the superposition state parameter
is the superposition state parameter
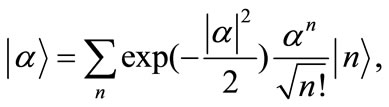 (15)
(15)
with the mean photon number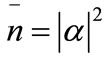 , then the wave function at any time
, then the wave function at any time 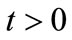 is given by
is given by
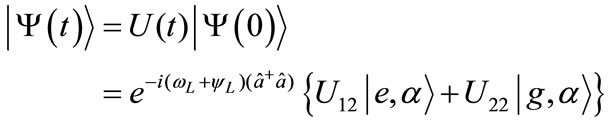 (16)
(16)
In the pure state case it is well known that the density matrix of the atom-field interaction can be written as:
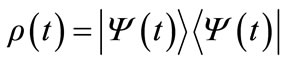 (17)
(17)
In order to analyze what happens to the two level systems interacting with laser and quantized field, we trace out field variables from the state ![]() and get the reduced atomic density matrix of the system given by
and get the reduced atomic density matrix of the system given by
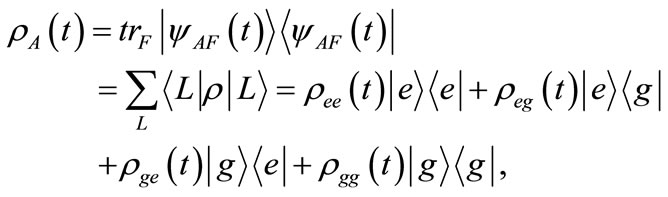 (18)
(18)
where
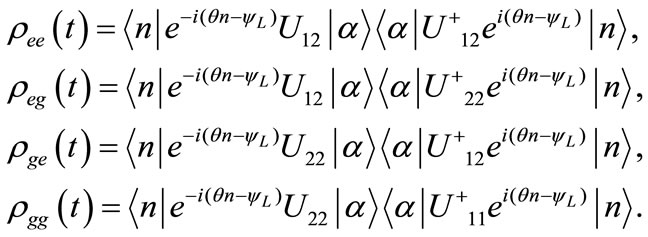 (19)
(19)
4. Atomic Inversion and Idempotency Defect
Atomic inversion can be considered as the simplest important quantity. It is defined as the difference between the probability of finding the atom in the exited state and in the ground state, the time dependent atomic inversion in the 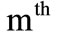 resonance
resonance 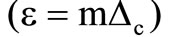 is given by:
is given by:
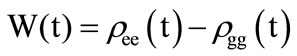 (20)
(20)
Finally the idempotency defect as a measure of entanglement is written as:
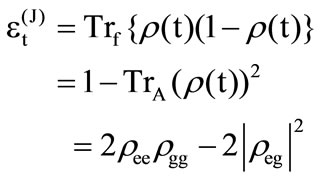 (21)
(21)
In many cases of quantum information processing, one requires a state with high purity and large amount of entanglement. Therefore, it is necessary to consider the purity of the state and its relation with entanglement.
Here we use the idempotency defect, defined by linear entropy, as a measure of the degree of purity for a state , in analogy to what is done for the calculation of the entanglement in terms of von Neumann entropy [15] which has similar behavior in the same cases.
, in analogy to what is done for the calculation of the entanglement in terms of von Neumann entropy [15] which has similar behavior in the same cases.
[In all our figures we have plotted the atomic inversion W(t) and the entanglement ID  as a function of the scaled time x t for the case of two-photon processes]. In figure 1, we plot the atomic inversion and ID as a function of the scaled time. It is seen that, when we neglect the Laguerre function term, the atomic inversion shows fast Rabi oscillations, and the periodic behavior of the ID is seen. In this case the usual two-photon features are observed. Once the Laguerre term is considered the general
as a function of the scaled time x t for the case of two-photon processes]. In figure 1, we plot the atomic inversion and ID as a function of the scaled time. It is seen that, when we neglect the Laguerre function term, the atomic inversion shows fast Rabi oscillations, and the periodic behavior of the ID is seen. In this case the usual two-photon features are observed. Once the Laguerre term is considered the general
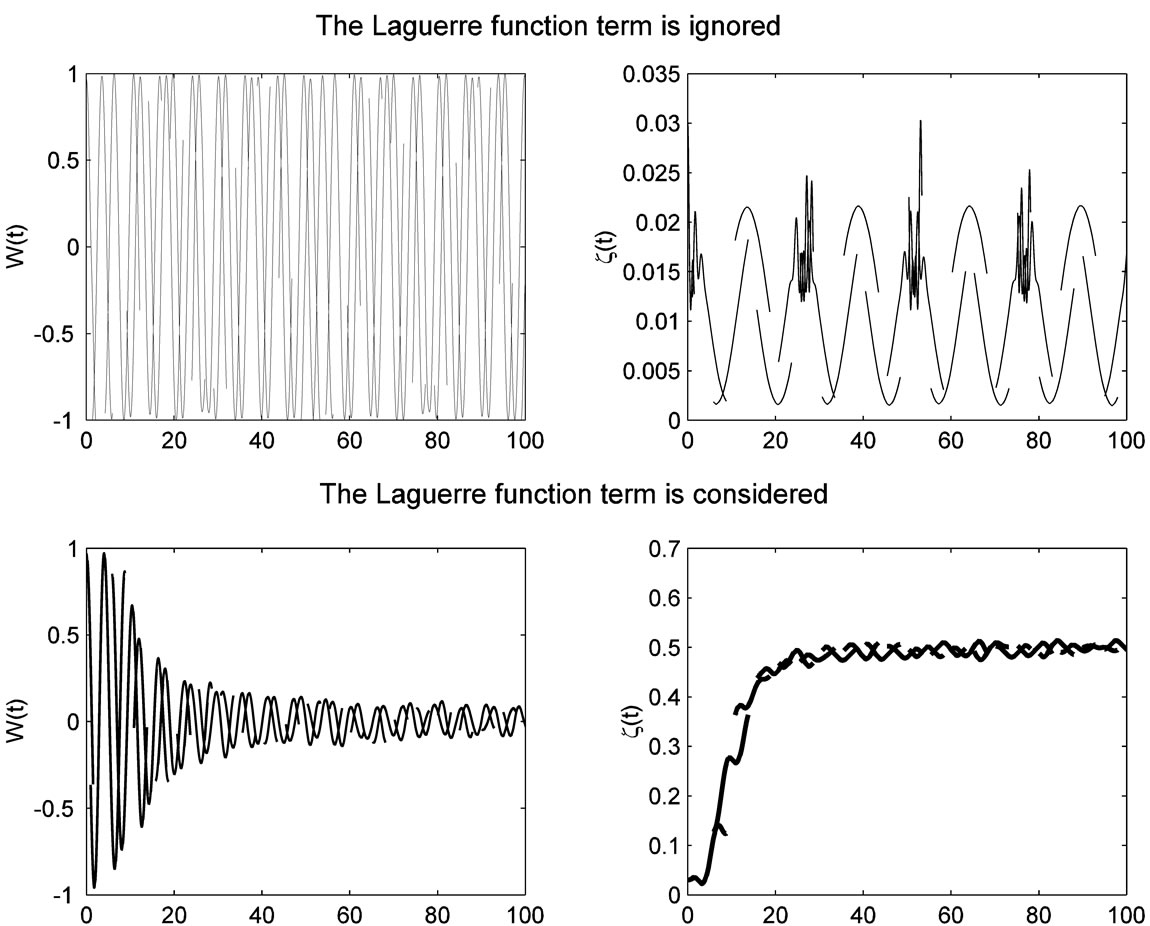
Figure 1. The evolution of the (a) atomic inversion and idempotency defect against the scaled time ![]() for the parameters
for the parameters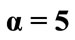 ,
, 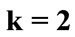
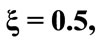 the laser detuning parameter
the laser detuning parameter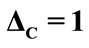 ,
, 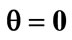 and
and 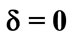
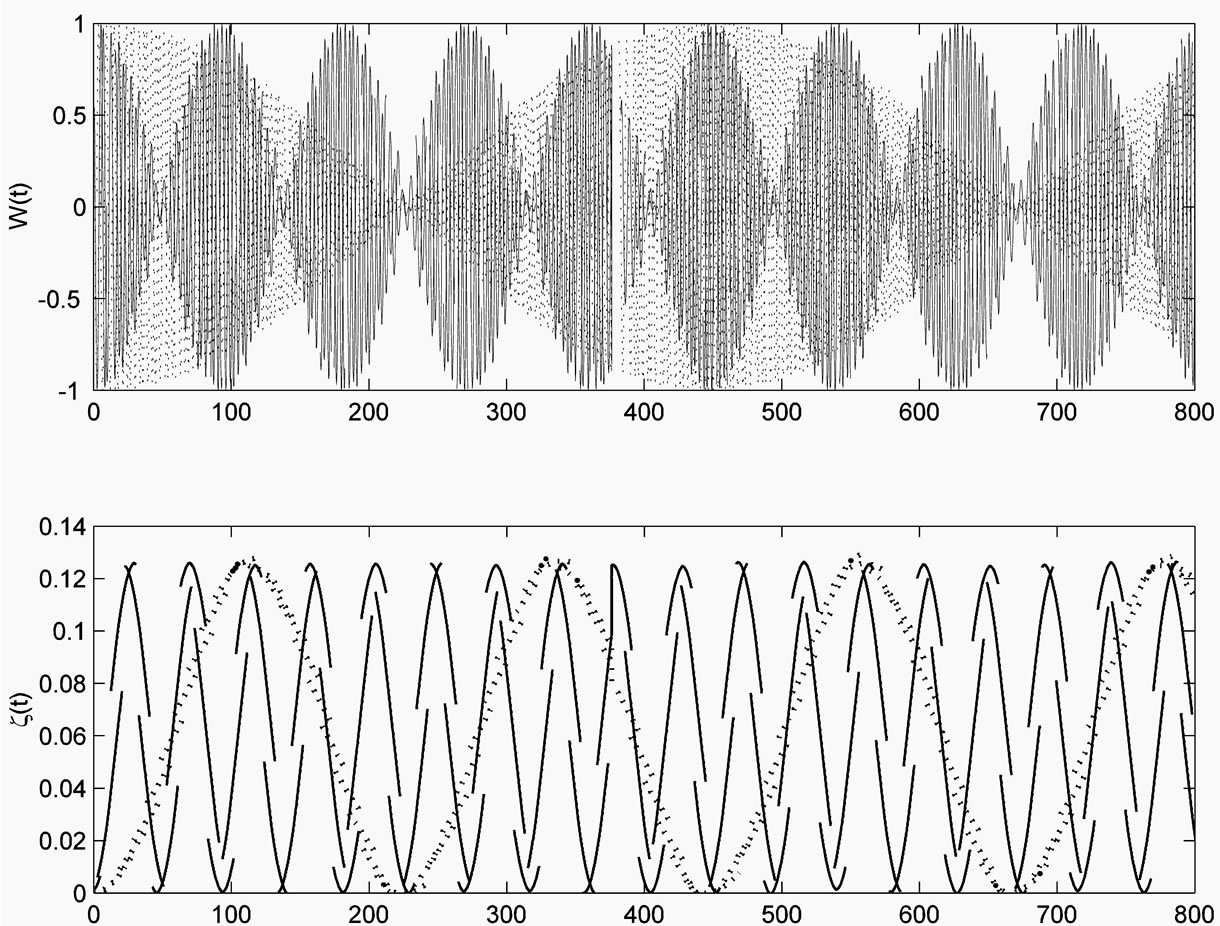
Figure 2. The evolution of the (a) atomic inversion and (b) idempotency defect against the scaled time ![]() for the parameters
for the parameters![]() ,
, 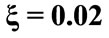 (dotted line),
(dotted line), 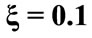 (solid line),
(solid line), 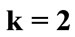 the laser detuning parameter
the laser detuning parameter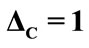 ,
, 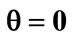 and
and 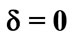
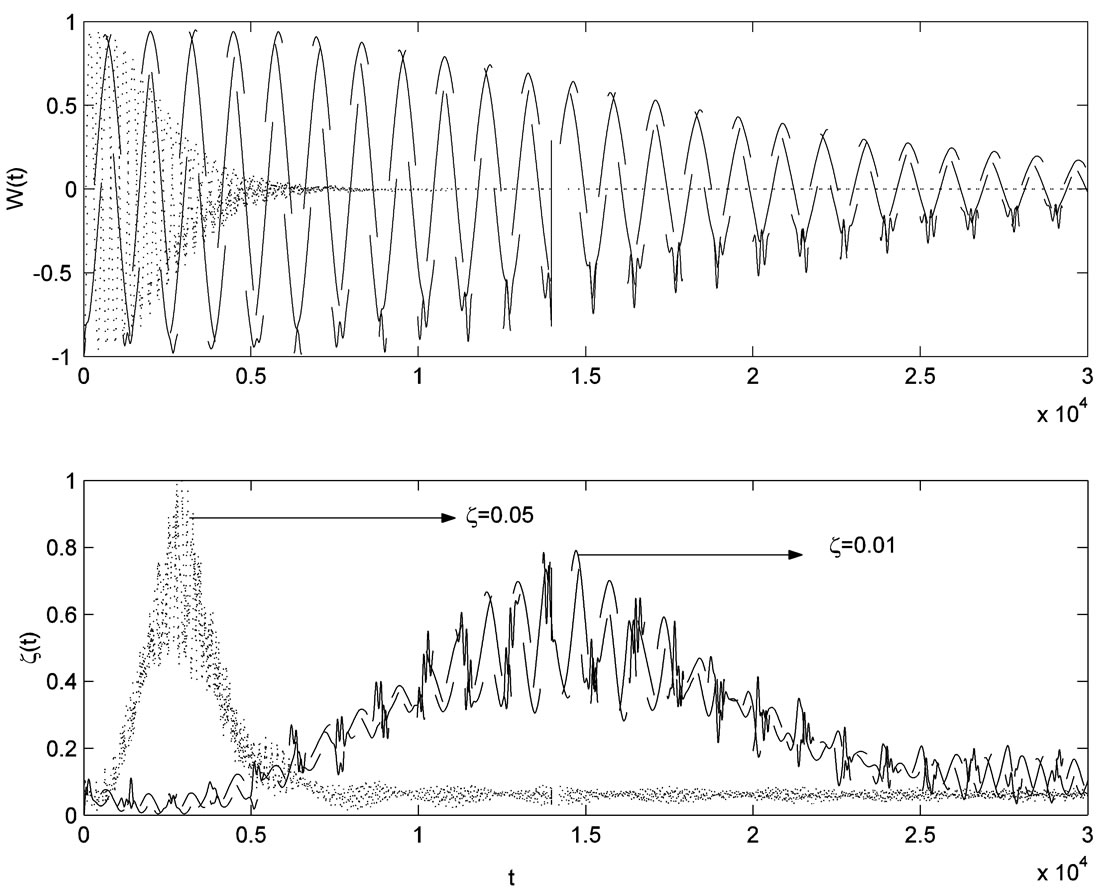
Figure 3. The evolution of the (a) atomic inversion and (b) idempotency defect against the scaled time for the parameters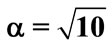 ,
, 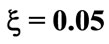 (dotted line),
(dotted line), 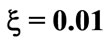 (solid line),
(solid line), 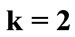 the laser detuning parameter
the laser detuning parameter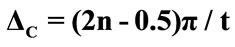 ,
, 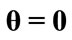 and
and 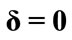
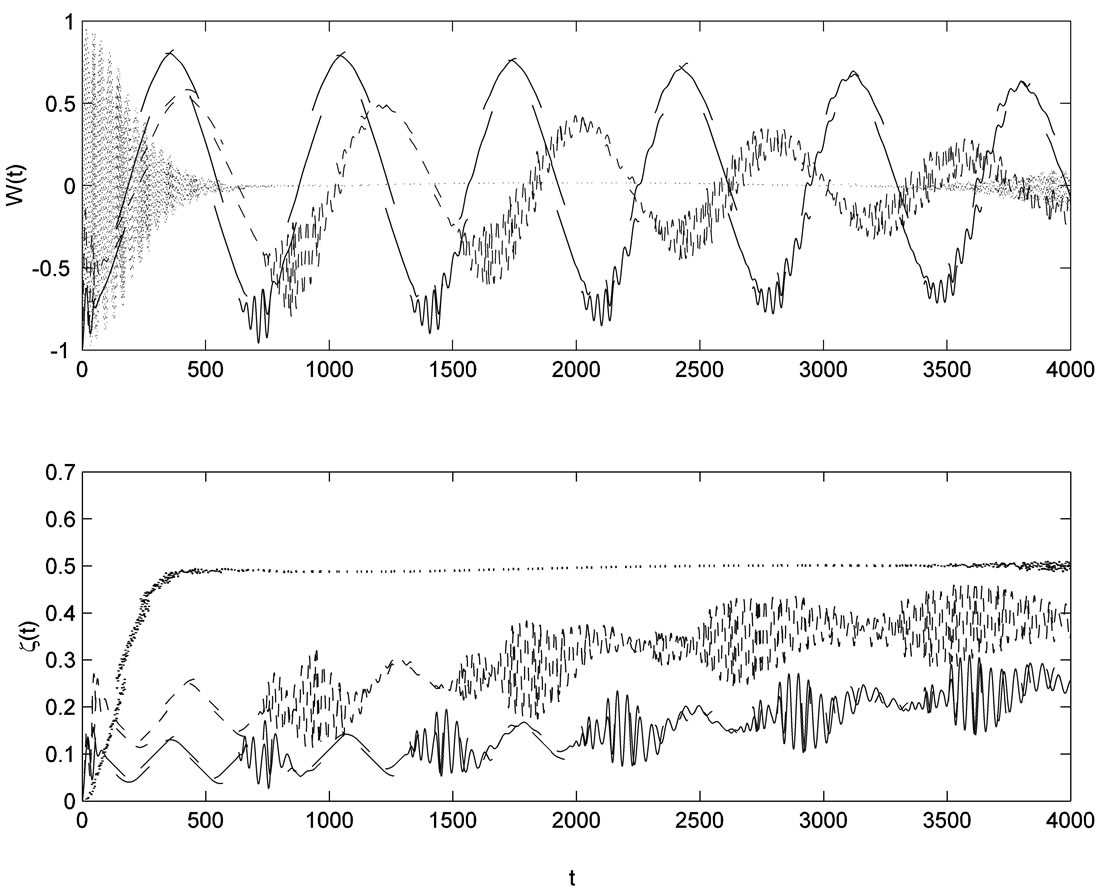
Figure 4. The evolution of the (a) atomic inversion and (b) idempotency defect against the scaled time ![]() for the parameters
for the parameters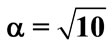 , k = 2 the laser detuning parameter
, k = 2 the laser detuning parameter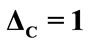 ,
, 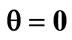 and with different values of the detuning
and with different values of the detuning 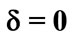 (solid line),
(solid line), 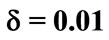 (dashed line),
(dashed line), 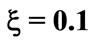 (dotted line)
(dotted line)
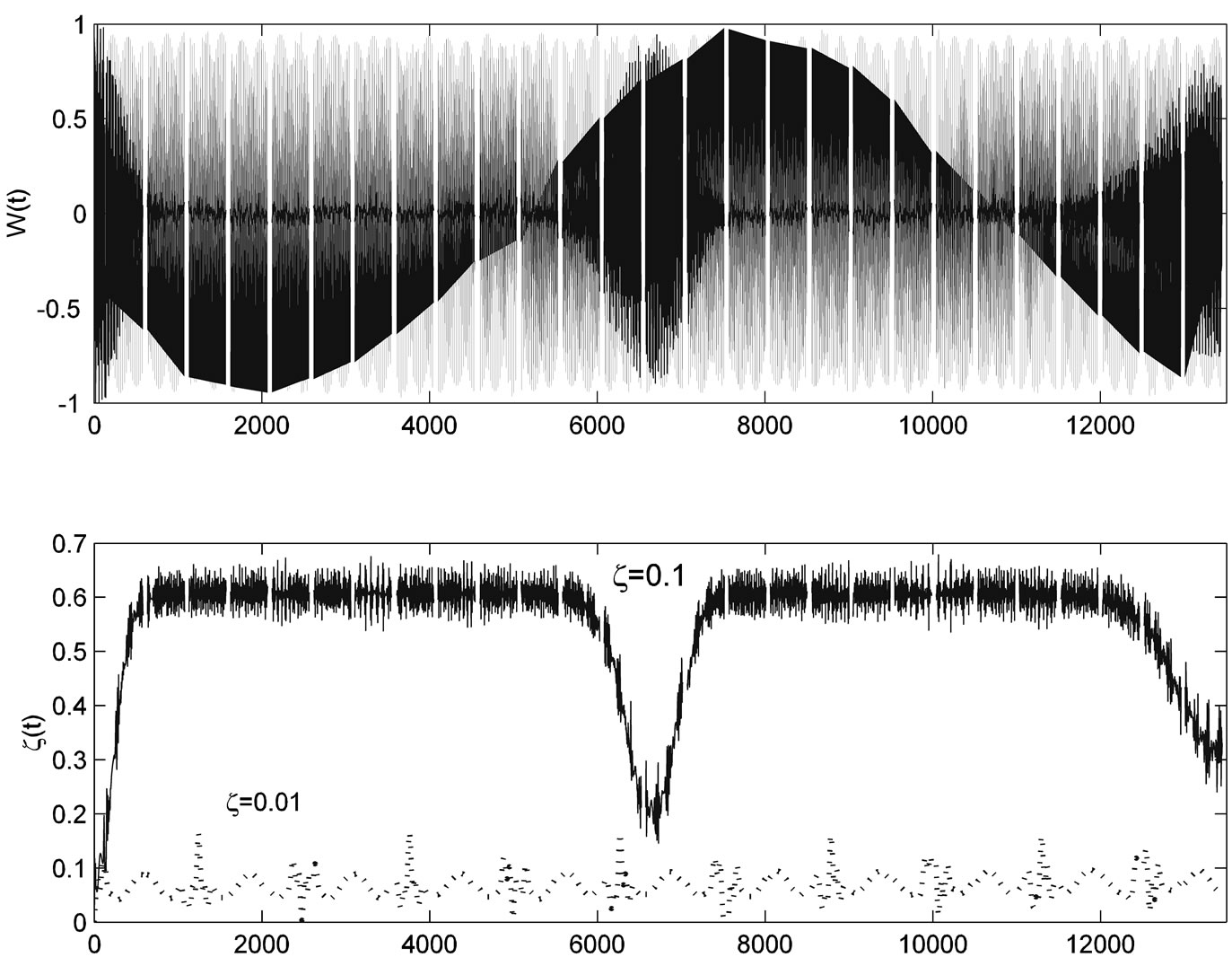
Figure 5. The evolution of the (a) Atomic inversion and (b) Idempotency defect against the scaled time,  for the parameters
for the parameters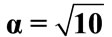 ,
, ![]() (dotted line),
(dotted line), 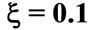 (solid line),
(solid line), 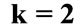 the laser detuning parameter
the laser detuning parameter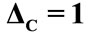 ,
, 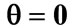 and
and 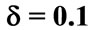
features of both the atomic inversion and ID are washed out, where as the time goes on the atomic inversion shows small amplitude of the oscillations and steady state of the ID (see figure 1). As the time increases further the maximum entangled state can be obtained, where ![]()
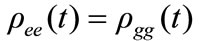 At this moment the entanglement reaches its maximum value. An interesting case is seemed in figure 2, where we have considered small values of the parameter
At this moment the entanglement reaches its maximum value. An interesting case is seemed in figure 2, where we have considered small values of the parameter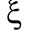 . In this case the collapse-revival phenomenon is shown. Also, the periodic oscillation occurs each
. In this case the collapse-revival phenomenon is shown. Also, the periodic oscillation occurs each 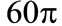 for atomic inversion and the zero ID at
for atomic inversion and the zero ID at ![]() for x = 0.1.
for x = 0.1.
Now we shed the some light on the affect of the different parameters on the both of the atomic inversion and the corresponding ID. For example the effect of the detuning ![]() is considered in figure 3. In this case we see that the amplitude of the value of the detuning increased as the value of the detuning increased. The ID decreases and reaches steady state as
is considered in figure 3. In this case we see that the amplitude of the value of the detuning increased as the value of the detuning increased. The ID decreases and reaches steady state as 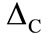 increases further.
increases further.
On the other hand, the detuning of the quantized field d, plays the opposite role, where the ID shows steady state at maximum instead of lowring its value due to the detuning of the laser field.
As d increases further (say d = 0.5) we obtain a long lived entanglement, as to show the fixed value of the ID (x = 0.5). In figure 5, we see that the collapse-revival phenomenon is clearly seen. Also, a perfect correspondence between the atomic inversion revival and the local maxima corresponds to the collapse periods. Also, we see that the collapse-revival phenomenon is clearly seen. Also, a perfect correspondence between the atomic inversion revival and the local maxima corresponds to the collapse periods. we have plotted the atomic inversion and the corresponding field Idempotency for a state of mean photon number of the coherent field as![]() , fixed the detuning parameter
, fixed the detuning parameter 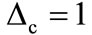 and the parameter d = 0 and changed the parameter
and the parameter d = 0 and changed the parameter 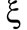 with values (0.01 and 0.1), when x = 0.01, oscillated with period equal
with values (0.01 and 0.1), when x = 0.01, oscillated with period equal 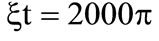 and W(t) oscillated with same interval and
and W(t) oscillated with same interval and 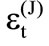 has a long-lived entanglement in each interval. When x = 0.01, then
has a long-lived entanglement in each interval. When x = 0.01, then 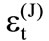 has a weak oscillation and W(t) oscillated with a very small interval between maximum and minimum values .
has a weak oscillation and W(t) oscillated with a very small interval between maximum and minimum values .
5. Conclusions
In the present paper we show that the on idempotency defect can be used to quantify entanglement of a two level system interacting with laser and quantized field. We obtain the long living entanglement due to the idempotency defects of the field. Our results show that the nonlinearity changes strongly the behavior of the entanglement also the detuning parameters have important role in the structure of the measure of entanglement. Also, all the interaction parameters play an important role on the behavior of idempotency defect.
REFERENCES
- G. Benenti, G. Casati and G. Strini “Principles of Quantum Computation and Information, Vol. 1,” World Scientific, 2004.
- C. Bennet, G. Brassard, C. Crepeau, R. Jozsa, A. Peres and W. K. Wootersm, “Teleporting an Unknown Quantum State via Dual Classical and Einstein-PodolskyRosen Channels,” Physical Review Letter, Vol. 70, No. 1895, 1993.
- A. Ekert, “Quantum Cryptography Based on Bell’s Theorem,” Physical Review Letter, Vol. 67, No. 6, 1991, pp. 661-663.
- L. Ye and G.-C. Guo, “Scheme for Implementing Quantum Dense Coding in Cavity QED,” Physical Review Letter A, Vol. 346, No. 5-6, 2005, pp. 330-336.
- O. Glöckl, S. Lorenz, C. Marquardt, J. Heersink, M. Brownnutt, C. Silberhorn, Q. Pan, N. V. Loock, N. Korolkova and G. Leuchs, “Experiment towards Continuous-Variable Entanglement Swapping: Highly Correlated Four-Partite Quantum State,” Physical Review Letter A, Vol. 68, 2003.
- W. K. Wootters, “Entanglement of Formation of an Arbitrary State of Two Qubits,” Physical Review Letter, Vol. 80, No. 2245, 1998.
- A. Peres, “Separability Criterion for Density Matrices,” Physical Review Letter, Vol. 77, No. 1413, 1996.
- J. von Neumann, “Mathematical Foundations of Quantum Mechanics,” Princeton University Press, Princeton, 1955.
- C. E. Shannon and W. Weaver, “The Mathematical Theory of Communication,” Urbana University Press, Chicago, 1949.
- S. J. D. Phoenix and P. L. Knight, “Fluctuations and Entropy in Models of Quantum Optical Resonance,” Annals of Physics, Vol. 186, No. 381, 1988.
- F. A. A. El-Orany and A.-S. Obada, “On the Evolution of Superposition of Squeezed Displaced Number States with the Multiphoton Jaynes–Cummings Model,” Jounal of Optics B: Quantum Semiclass Optics, Vol. 5, No. 60, 2003.
- M. Lewenstein and T. W. Mossberg, “Spectral and Statistical Properties of Strongly Driven Atoms Coupled to Frequency-Dependent Photon Reservoirs,” Physical Review Letter A, Vol. 37, No. 2048, 1988.
- C. K. Law and J. H. Eberly, “Response of a Two-Level Atom to a Classical Field and a Quantized Cavity Field of Different Frequencies,” Physical Review Letter A, Vol. 43, No. 6337, 1991.
- J. H. Eberly and V. D. Popov, “Phase-Dependent Pump-Probe Line-Shape Formulas,” Physical Review Letter A, Vol. 37, No. 2012, 1988.
- G. M. A. Al-Kader and M. M. A. Ahmad, “On the Interaction of Two-Level Atoms with Squeezed Coherent State,” Chinese Jounal of Physical, Vol. 39, No. 1, 2001.
- A. Ekert and P. L. Knight, “Entangled Quantum Systems and the Schmidt Decomposition,” American Journal of Physics, Vol. 63, No. 415, 1994.

