Received 11 March 2016; accepted 26 April 2016; published 29 April 2016

ABSTRACT

According to the structural characteristics of the automobile engine bracket, the finite element model of the bracket is established. As the connecting part between the engine and the body, the performance requirements of the automobile engine bracket affect the comfort and the safety of the vehicle directly. Using the RADIOSS solver, the dangerous point of the bracket is analyzed. Under the premise of ensuring its reliability, with the help of OptiStruct software to carry out the topology optimization design, to get the optimal material distribution of the bracket and the final design will meet the performance requirements.

Keywords:

Engine Bracket, Optimal Material Distribution, Topology Optimization

1. Introduction

Engine bracket is an important component in the powertrain system. It can support the engine and transmission assembly on the body frame. On the one hand, it supports power assembly device; on the other hand, it isolates vibration between power assembly and body frame. Therefore, it has very high requirements of strength properties. In engineering, the design of engine bracket is based on experience, so it is inevitable to be blind, thus producing the waste of human and financial resources. With the development of finite element technology and design concept, by using the method of numerical simulation on the structure, optimization design has been widely used in the field of engineering. This can not only reduce the cost of production, but also shorten the design cycle, with high economic benefits.

At present, there are a lot of researches about topology optimization. Tang Yingying [1] is based on the latest research results from the domestic and abroad, to explore and study the mathematical basis of structural topology optimization method and the basic theory, but on the aspect of ensuring the accuracy of calculation and improving the efficiency, it needs to further deepen the research and discussion; Lindan Yi [2] based on ANSYS software, takes topology optimization design of automobile engine bracket, and makes the strength analysis, fatigue analysis and model analysis of the new optimized bracket. The new bracket is less stress concentration and its fatigue analysis is not based on real road load spectrum. Wen Shijie [3] uses TOSCA, by the results of topology optimization model of bracket structure, forms the series of structural analysis and gets the results of uniform method based on the engineering requirements, but the uniform method in accuracy and number of iterations is inadequate. Yuanchun Kang [4] made multi-objective topology optimization of the suspension control arm and used the method of the inertia of the release. Finally, although the quality is reduced, the stiffness and the low order frequency still do not meet the requirements. In this paper, the 3D model is established in CATIA. HyperMesh is used to mesh the model, and then use the corresponding solver in HyperWorks to calculate related subcase.

2. Topology Optimization Method Based on Variable Density

2.1. Basic Theory

There are three kinds of structure optimization, they are: size optimization, shape optimization and topology optimization. Three optimization methods correspond to the three stages of the product design process, namely the detailed design, basic design and conceptual design, as shown in Figure 1.

Size optimization keeps the structural shape and topology structure invariant, to optimize the various parameters of structure, such as thickness, section size of beam, materials’ properties; shape optimization maintains the topology structure, to change the boundary of structure and shape, seek the most suitable structure boundary situation and shape; topology optimization is to find the optimal path of materials’ distribution in a continuous domain which meet the displacement and stress conditions in structure, make a certain performance optimal. Thus, compared to size and shape optimization, topology optimization with more freedom degree and greater design space, its greatest feature is under uncertain structural shape, according to the known boundary condition and a given load to determine the reasonable structure, both for the conceptual design of new products and improvement design for existing products, it is the most promising aspect of structural optimization [5] .

For continuous structure topology optimization, there are some mature methods like: uniform method, evolutionary structural optimization method, variable density method .etc. Uniform method introduced cell structure of micro structure (unit cell) in the elements of the structure, each unit cell has three forms, namely non-material voids (size = 1), isotropic-material entity medium (size = 0) and orthotropic-material opening-hole medium (0 < size < 1). Wherein the distribution of each form will be able to describe the form of topology and the shape of structure; evolutionary structural optimization method believe that stress in any parts of the structure should under the same level in an ideal structure [6] . That means the local material with a low stress state is not fully utilized, so you can delete the material artificially. So gradually remove material which in a low stress state, and then delete the update rate, so optimized structure becomes more uniform.

Variable density method is used to conduct optimization in this paper. The basic idea is to introduce a hypothetical material which density is variable and range from 0 to 1. After changing the continuous structure to finite element model, then making per units’ density as the design variables, to convert topology optimization

problem into the optimal distribution of material, while in order to suppress the intermediate density of the material (material between void and entities), the introduction of a interpolation penalty factor used to describe the relationship between Young’s modulus and density of the material which shown as the following formula:

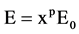(1)

where: p―interpolation penalty factor (p > 1); E₀―Young’s modulus of densified material unit; E―Young’s modulus after interpolation. So that the original model with intermediate density will be eliminated or replaced by densified material and will achieve optimal results which close to the entity [7] .

Therefore, during topology optimization, variable is relative density of units, then structural topology optimization problem is converted into the optimal distribution of the material.

2.2. Process of Topology Optimization

Based on HyperWorks platform topology optimization holder, first, according to the engine mounting position, we establish the three-dimensional geometric model of engine bracket, and then pretreated in HyperMesh, define design area, objective function and constraints under the optimization panel, finally operate topology optimization which design process is as Figure 2.

3. Analysis

To establish the geometry model by CATIA, then input the geometry to the HyperMesh to carry out pre-treat- ment operations like geometry cleanup, meshing, loads, constraints, etc., the maximum of displacement should lower than 0.5 mm; local maximum of stress can’t over 247 Mpa, and under these two requirements, the mass should be lightest.

3.1. Abbreviations and Acronyms

To simplify FE model in software then a high quality mesh can be got. Ignore some of the features which have very small impact on analysis such as holes and fillets. The material is aluminum, the related parameters are shown in Table 1.

Mesh the model with four-node tetrahedral element which the size is 3 mm. The total number of element is 90,847 and using the bar element to simplify screw connection. The final FE model is as Figure 3.

3.2. Static Analysis

We complete pre-treatment in HyperMesh and transfer the user profile to RADIOSS solver. The most dangerous condition of bracket is resonance with the engine when start the car. The car is under the horizontal force 12,000 N, vertical force 10,000 N. 6 degrees of freedom constraint is applied to the area between engine and engine bracket. We calculate the distribution of stress finally.

From the displacement contour, as shown in Figure 4, maximum displacement 0.4 mm occurs in the upper right ligament; from the stress contour, maximum stress 331 Mpa occurs in the upper right connection. Both of them exceed the design requirements, so the bracket needs to optimize.

4. Topology Optimization

On the basis of static analysis, we use OptiStruct to carry out structure topology optimization which means that finding the premise material distribution scheme under the design requirements. Topology optimization model needs to specify the design area where elastic modulus is variable. As shown in Figure 5, both ends of the bolt holes are non-design area, while the rest are set to the design area, calculated in OptiStruct.

The result of topology optimization is shown in Figure 6. Density cloud shows structure of some parts. Optimized geometric module is exported by OSSmooth profile.

To carry out static analysis about the optimized model again, the results are shown in Figure 7.

Comparative analysis is shown in Table 2.

5. Conclusion

In this paper, an in-depth research about technology optimization is carried out with introducing basic theory, mathematical models and solution methods. After the optimization, the stiffness has been greatly improved and

the bracket has a greater carrying capacity. The mass is reduced about 40%, which fully meets the requirements of static characteristics.

Acknowledgements

This research is supported by Shanghai University of Engineering Science Innovation Fund for Graduate Students (Project No. E1-0903-15-01075).

Cite this paper

Po Wu,Qihua Ma,Yiping Luo,Chao Tao, (2016) Topology Optimization Design of Automotive Engine Bracket. Energy and Power Engineering,08,230-235. doi: 10.4236/epe.2016.84021

References