Energy and Power Engineering
Vol.07 No.04(2015), Article ID:56000,5 pages
10.4236/epe.2015.74015
Experimental Determination of Local Resistance Coefficient of Sudden Expansion Tube
Yinpeng Li, Changjin Wang, Mingda Ha
Northeast Petroleum University at Qinhuangdao, Qinhuangdao, China
Email: 214351651@qq.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 15 April 2015; accepted 27 April 2015; published 28 April 2015
ABSTRACT
Theoretical derivation of local resistance coefficient of sudden expansion tube is presented. Several assumptions are analyzed in the theoretical derivation. That the head loss shall be neglected is affirmed. Experimental data proves that the pressure before and after sudden expansion section is basically the same. That the friction force on the side face of control body is neglected is denied and it is pointed out that such neglect is the main cause for error between theoretical calculation and actual measurement. Experimental device for measuring local resistance coefficient is designed in combination with theoretical derivation process. Optimal gradually varied flow section is selected after sudden expansion pipe in Bernoulli equation based on variation of piezometer tube head. It is pointed out in accordance with experimental data analysis that the value of local resistance coefficient of sudden expansion tube determined through experimental data is closer to the actual situation during pipeline design.
Keywords:
Sudden Expansion Pipe, Frictional Head Loss, Loss Head Loss, Local Resistance Coefficient

1. Introduction
Valves, bends and metering devices are installed on pipelines for oil exploitation and transportation to control, adjust and meter the fluid. The flow, direction and even form will be changed when the fluid passes these local parts, which causes the local head loss. Only the calculation of local head loss of sudden expansion tube when fluid passes is studied in this paper. When the fluid flows into pipeline with bigger diameter, it does not expand suddenly but expand gradually after leaving the pipeline of smaller diameter and forms eddy between corner of pipe wall and main stream. The eddy is driven by the main stream to turn and there is energy consumption dur- ing the turning. Besides, the fluid impact and collision produced due to sudden change of pipeline section all lead to loss of mechanical energy.
The calculation of local head loss is the essence of calculation of local resistance coefficient. The local resistance coefficient of sudden expansion pipe is the only one that can be got by the pure theory, the others are experimentally determined. But the current calculation formula shows that local resistance coefficient is only related to the expansion ratio of pipe diameter and it doesn’t matter with dynamic viscosity, flow rate, et al. The conclusion is questionable. In this paper, the determination of local resistance coefficient of sudden expansion tube is discussed on the basis of the experimental phenomena and data. This can provide some help for actual engineering calculation.
2. Theoretical Derivation of Local Resistance Coefficient of Sudden Expansion Pipe
In Figure 1, take the space enclosed by internal wall of pipe, starting end of whirlpool and terminal end of whirl- pool as control body, and apply Bernoulli equation between Section 1 and sections, obtaining
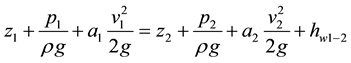 (1)
(1)
where, 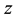 is statical head,
is statical head,  is pressure head,
is pressure head,  is velocity head,
is velocity head, 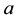 is kinetic energy correction factor, and
is kinetic energy correction factor, and  is water head loss of liquid of unit gravity from Section 1 and Section 2.
is water head loss of liquid of unit gravity from Section 1 and Section 2.
Since distance between the two sections is short, frictional head loss can be neglected, i.e. head loss only includes local head loss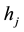 . Take
. Take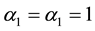 , obtaining
, obtaining
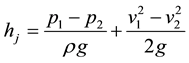 (2)
(2)
Apply momentum equation on control body. Since it is difficult to determine the pressure at Section 1, it can only be assumed equal to pressure before the section. Therefore, total pressure on Section 1 is 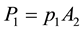 and total pressure on Section 2 is
and total pressure on Section 2 is . Neglecting side friction of control body, the join force on liquid in the control body on flow direction is
. Neglecting side friction of control body, the join force on liquid in the control body on flow direction is
 (3)
(3)
Therefore the momentum equation is
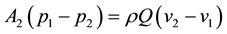 (4)
(4)
Two sides both divided by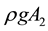 , obtaining
, obtaining
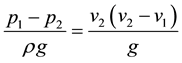 (5)
(5)
Figure 1. Scheme of local resistance of sudden expansion joint and control body selection.
Substitute it into formula (2), obtaining

Sort it and obtain

It can be obtained from continuity equation that 
Formula (7) can be converted to

or

Further obtaining


3. Discussion of Several Assumptions in Theoretical Derivation
In 2009, Zhao Haiyan et al. concluded through numerical simulation analysis that the backflow zone expands with the increase of expansion ratio, so does the eddy size. The existence of eddy necessarily consumes the energy of mainstream. The bigger the eddy size and strength, the more the energy consumption of the main- stream, and the bigger the energy loss through sudden expansion [2] . This conclusion conforms to the results of theoretical derivation above.
Zhao Haiyan et al. also pointed out that the backflow in the backflow zone becomes increasingly obvious with the increase of the Reynolds number, and backflow length continues to increase. The conclusion is consistent with the conclusion of Bedakes D., et al. [3] . In 2012, Zhou Zaidong et al. also concluded through numerical simulation analysis that the bigger Reynolds number leads to more violent eddy, larger effect zone, longer time to reach mainstream and bigger speed at the middle position of the pipeline, and the range affected by the maximum speed is even further from the pipe opening, which conforms to the actual situation [4] . This conclusion is not consistent with results of theoretical derivation above, which indicates that the local resistance loss is not only related to expansion ratio of the pipe diameter, but also to the kinestate of fluid.
To this end, several assumptions in above theoretical derivation are discussed in this paper.
3.1. Neglect of Frictional Head Loss
It is impossible to calculate accurately yet how long the eddy is which is formed after the flow passes the sudden expansion pipe. Currently, it is generally considered that the backflow length should be five to eight times of diameter of sudden expansion pipe. Normally the eddy length can be basically neglected when compared with length of transportation pipeline, so the frictional head loss can be neglected too. Meanwhile, when the energy loss of whole transportation pipeline system is calculated, the frictional head loss and local head loss of sudden expansion section are necessarily calculated. There would be repetition of calculation if frictional head loss [5] [6] is calculated here.
3.2. Pressure of Two Sections of the Control Body
The theoretical derivation shows that it is rather difficult to determine the pressure at Section 1, so it is only possible to assume that the value is equal to the pressure at the front end of the section. Therefore, pressure at the front end of this section and Section 1 are measured in this experiment, see Table 1. The experiment shows that the pressure at Section 1 is not stable and there is certain fluctuation. Mean value of fluctuation is obtained approximately for measurements. The experimental data proves that this assumption has certain accuracy.
3.3. Friction on the Side Face of Control Body
When momentum equation is applied to the control body, the friction force on the side face of the control body is neglected so as to conclude that the local friction coefficient is only related to the expansion ratio of pipe diameter. Literature [5] points out that the reason why the eddy area is able to keep moving is that energy supply is obtained through momentum exchange from the mainstream. This part of energy consumption finally becomes heat after friction with the eddy and wall inside the eddy and this loss is called eddy loss. Since the eddy loss is the most important loss in the local head loss of sudden expansion tube, the neglect of friction force between eddy and wall will lead to substantial error.
4. Design of Experimental Solution
The experimental device, as shown in Figure 2 is placed horizontally on the experimental table. The inlet pipeline on the left is connected with the pipeline of constant head water tank and the tail of outlet pipeline on the right is controlled by the throttle valve. The flow is controlled by the outlet valve. The experiment pipeline is transparent organic glass pipe with inner diameter of inlet pipe being 16 mm, pipe diameter of expansion pipe being 20 mm and room temperature being 15 Celsius degrees.
Positions of piezometer tubes: the first piezometer tube is set at the limit position before sudden expansion, and the second one at the limit position at the entry of sudden expansion. The pressure measurements of these two piezometer tubes are used to check the assumption in the theoretical derivation that the pressure of two sections of control body is approximately the same. The eddy length at entry of sudden expansion tube is generally considered to be five to eight times of the diameter of sudden expansion tube, so the third to the sixth piezometer tubes are set at areas of 100 mm, 120 mm, 140 mm, 160 mm after sudden expansion to analyze the variation of energy loss.
Measurement of piezometer tube head: transparent organic glass pipe with 6 mm of inner diameter and 100 mm of height is fixed on the lifting pressure test plate with the minimum scale of mm.
Flow measuring: volumetric method is applied to measure the flow. Graduate cylinder and cup are used to measure the volume and electronic stopwatch is used for timing.
5. Analysis of Experimental Results
There is always head loss which is monotonic decreasing along the flow due to viscosity of the fluid; the head of piezometer tube reflects the potential energy of the flow, so the head line of piezometer tube may rise, drop or stay unchanged. As for sudden expansion tube, the increase of overflow section leads to the decrease of mean flow of the section and the decrease of flow head. With the decrease of the energy loss and flow head of the sudden expansion tube flow, the total head line decreases while the head line of piezometer tube increases when close to the sudden expansion tube [7] . The head line of frictional head loss decreases in the flow direction. Therefore, one optimum pressure is selected from the third to the sixth piezometer tubes, which is the pressure at the starting position of the pipe section where the frictional resistance plays the dominant role after the eddy is finished, i.e. the pressure at the starting position of the section where the streamline completely recovers to the gradually varied flow.
The Bernoulli equation is used for calculation of local head loss of sudden expansion tube based on the actual measurement (Refer to Table 2 for the results).
As shown in above table, the head loss value calculated from theoretical equation is negligible compared with actually measured head loss value. The head loss value calculated from theoretical equation is less than 1 mm in most cases, that is to say, when the value based on the calculation results is reflected in the experiment, the pressure of piezometer tube is basically unchanged with the change of flow. However, it is obviously inconsis-
Table 1. The pressure measurement before sudden expansion and Section 1.
Table 2. The calculation of local head loss and resistance coefficient of sudden expansion.
Figure 2. Experimental device for determination of local resistance coefficient of sudden expansion tube.
tent with the actual experiment. It is because when the momentum equation is applied, the friction force on the side face of control body is neglected.
Since there are many types of local resistance, and most of them are in turbulent status, it is must to conduct experiment to get the accurate results. The local resistance coefficient of sudden expansion tube is also deter- mined by this experiment. The formula is as follows:

where, 
The calculation of local resistance coefficient of sudden expansion tube is shown in Table 2.
The mean value of experimental determination of local resistance coefficient of sudden expansion tube calculated from the table above is 1.43, which is quite larger than theoretical value of 0.32. Therefore, the friction force on the side face of control body cannot be neglected when momentum equation is applied.


The average value of the error between the local head loss calculated in accordance with local resistance coefficient determined by experiment under different flow rates and the actual measurement is only 1.33%. Obviously, the error is in the allowable range of engineering design.
6. Conclusion
The local resistance coefficient derived from theory is only related to the expansion ratio of the pipe diameter, and is always a constant no matter how the flow changes. The experimental data proves that the head loss calculated from theoretical formula has large difference from the actual measurement, which is mainly because of the neglect of friction force of side face during theoretical derivation. The laboratory determination formula for local resistance coefficient is given in this paper, and the error between the local head loss calculated in accordance with local resistance coefficient determined by experiment and the actual measurement is only 1.33%. Therefore, the value of local resistance coefficient of sudden expansion determined only by actually measured section size and the experimental data meets the design requirements during pipeline design.
References
- Yang, S.R., Wang, Z.M., He, G.Y., et al. (2006) Engineering Fluid Mechanics. Petroleum Industry Press, Beijing, 121- 122.
- Zhao, H.Y., Jia, X.S., Yang, S.M., et al. (2009) Numerical Simulation of Separation Flow Filed of Sudden Expansion Tube. Scientific Technology and Engineering, 9, 5238-5240.
- Bedakes, D. and Knight, D.D. (1992) Eddy Correlations for Laminar Axisymmetric Sudden Expansion Flow. Journal of Fluids Engineering, 114, 119-121. http://dx.doi.org/10.1115/1.2909986
- Zhou, Z.D., Wei, C.Z., Sun, M.Y., et al. (2012) Numerical Simulation of Flow Form of Sudden Expansion Tube. Scientific Technology and Engineering, 12, 7983-7985.
- Zhao, B.F., Jin, Y.Z., Lu, Y.B., et al. (1997) Preliminary Investigation of Local Head Loss of Sudden Expansion. Journal of Northeast Agricultural University, 28, 175-178.
- Zhou, A.P. (2000) Measurement and Analysis of Local Resistance during Sudden Expansion and Reduction of Overflow Section. Journal of Jiaozuo Institute of Technology (Science & Technology Edition), 19, 45-49.
- Zhao, J.Y., Zhang, Y.J., Zheng, X.M., et al. (2004) Study on Pressure Measuring Pipe Head Line of Sudden Expansion Pipe. Journal of Beijing Institute of Civil Engineering and Architecture, 20, 1-3.





