Energy and Power Engineering
Vol.5 No.2(2013), Article ID:29438,10 pages DOI:10.4236/epe.2013.52017
Investigating Diesel Engine Performance and Emissions Using CFD
1Department of Mechanical Engineer, Alexandria University, Alexandria, Egypt
2Department of Mechanical Engineering, Umm Al-Qura University, Makka, KSA
Email: tarek.belal@eg.bureauveritas.com, emmarzouk@yahoo.com, mohsen7351@yahoo.com
Received November 23, 2012; revised December 22, 2012; accepted January 7, 2013
Keywords: Numerical Simulation; Unsteady Flow; Combustion; Diesel Engine
ABSTRACT
Fluid flow in an internal combustion engine presents one of the most challenging fluid dynamics problems to model. This is because the flow is associated with large density variations. So, a detailed understanding of the flow and combustion processes is required to improve performance and reduce emissions without compromising fuel economy. The simulation carried out in the present work to model DI diesel engine with bowl in piston for better understanding of the in cylinder gas motion with details of the combustion process that are essential in evaluating the effects of ingesting synthetic atmosphere on engine performance. This is needed for the course of developing a non-air recycle diesel with exhaust management system [1]. A simulation was carried out using computational fluid dynamics (CFD) code FLUENT. The turbulence and combustion processes are modeled with sufficient generality to include spray formation, delay period, chemical kinetics and on set of ignition. Results from the simulation compared well with that of experimental results. The model proved invaluable in obtaining details of the in cylinder flow patterns, combustion process and combustion species during the engine cycle. The results show that the model over predicting the maximum pressure peak by 6%, (p-θ), (p-v) diagrams for different engine loads are predicted. Also the study shows other engine parameters captured by the simulation such as engine emissions, fuel mass fraction, indicated gross work, ignition delay period and heat release rate.
1. Introduction
The requirement to meet the challenge of producing cleaner and more efficient power plants will intensify further over the next few years. This challenge requires an increased commitment to research by the transportation industry. The internal combustion engine represents one of the more challenging fluid mechanics problems to model because the flow is compressible with large density variations, relatively high Mach number, turbulent, unsteady, cyclic, and non-stationary, both spatially and temporally. Much progress has been made in CFD model development for engines in recent years.
Clean diesel engines are one of the fuel efficient and low emission engines of interest in the automotive Industry. The combustion chamber flow field and its effect on fuel spray characteristics plays an important role in improving the efficiency and reducing the pollutant emission in a direct injection diesel engine, in terms of influencing processes of breakup, evaporation mixture formation, ignition, combustion and pollutant formation. CFD modeling is a valuable tool to acquire detailed information about these important processes. In this context [2], the characteristics of ultra-high injection pressure diesel fuel sprays are simulated and validated in a quiescent constant volume chamber. A profile function is utilized in order to apply variable velocity and mass flow rate at the nozzle exit. The CFD model is also applied to an open cycle engine model to study the effects of engine flow field features such as swirl and tumble motions on the spray behavior [2].
A multi-zone direct-injection (DI) diesel combustion model has been implemented for full cycle simulation of a turbocharged diesel engine [3]. The above combustion model takes into account the following features of the spray dynamics:
• the detailed evolution process of fuel sprays;
• interaction of sprays with the in-cylinder swirl and the walls of the combustion chamber;
• the evolution of a Near-Wall Flow (NWF) formed as a result of a spray-wall impingement as a function of the impingement angle and the local swirl velocity;
• interaction of Near-Wall Flows formed by adjacent sprays;
• the effect of gas and wall temperatures on the evaporation rate in the spray and NWF zones.
A NOx calculation sub-model uses detailed chemistry analysis which considers 199 reactions of 33 species. A soot formation calculation sub-model used is the phenomenological one and takes into account the distribution of the Sauter Mean Diameter in injection process. The ignition delay sub-model implements two concepts. The first concept is based on calculations using the conventional empirical equations. In the second approach the ignition delay period is estimated using relevant data in the calculated comprehensive 4-D map of ignition delays. The model has been validated using published experimental data obtained on highand medium-speed engines. Comparison of results demonstrates a good agreement between theoretical and experimental sets of data [3].
By separating the fluid dynamic calculation from that of the chemistry, the unsteady flamelet model allows the use of comprehensive chemical mechanisms, which include several hundred reactions. This is necessary to describe the different processes that occur in a DI Diesel engine such as auto ignition, the burnout in the partially premixed phase, the transition to diffusive burning, and formation of pollutants like NOx and soot. The experimental results show good agreement for the whole combustion cycle (ignition delay, maximum pressures, torque and pollutant formation) between the two-component reference fuel and Diesel. The simulations are performed for both reference fuels and are compared to the experimental data. Pollutant formation (NOx and soot) is predicted for both reference fuels. The contributions of the different reaction paths (thermal, prompt, nitrous, and reburn) to the NO formation are shown. Finally, the importance of the mixing process for the prediction of soot emissions is discussed [4].
The KIVA code is widely used for model development in academia due to the availability of the source. However, its capability for resolving complex geometries is limited.
The KIVA engine simulation developed by Los Alamos National Laboratory was used to characterize the combustion of alternative fuels in a direct injection diesel engine. Rapeseed oil, its methyl ester and hexadecane were used in engines run at 3000 rev/min and 50% maximum torque. Approximately 40 consecutive cycles were phase averaged to derive the pressure traces for comparison to KIVA predictions. The engine parameters and the fuel properties used in the simulations are described. Simulation results were good for the methyl ester and for hexadecane which was used as a reference fuel. The model predicted lower pressures for the rape oil than those which were experimentally observed [5].
A modified CFD code based on the KIVA family of codes incorporating several strategies for reducing the computational time required for diesel engine simulations is presented. The improved code and coarse meshes are used together to simulate combustion in a heavy-duty Mitsubishi Heavy Industries diesel engine operated over a range of loads, speeds, and injection strategies. The average simulation time from IVC to EVO is reduced from around 60 hours to 1 hour through the use of 12 processors and the new strategies [6].
On the other hand, other commercial CFD codes such as STAR-CD, FIRE, VECTIS and FLUENT are frequently used by industry due to their superior mesh generation interfaces and because of their available user support. Some scientists combined STAR-CD and KIVA code for the engine simulations but they concluded that, it would be preferable to implement the advanced sub models directly into one commercial code for engine simulations [7].
The gas motion inside the engine cylinder plays a very important role in determining the thermal efficiency of an internal combustion engine. A better understanding of in cylinder gas motion will be helpful in optimizing engine design parameters. An attempt has been made to study the combustion processes in a compression ignition engine and simulation was done using computational fluid dynamic (CFD) code FLUENT, Turbulent flow modeling and combustion modeling was analyzed in formulating and developing a model for combustion process [8].
This paper describes the development and use of sub models for combustion analysis in direct injection (DI) diesel engine. In the present study the Computational Fluid dynamics (CFD) code FLUENT is used to model complex combustion phenomenon in compression ignition (CI) engine. The results obtained from modeling were compared with experimental investigation. Consequences in terms of pressure, rate of pressure rise and rate of heat release are presented. The rate of pressure rise and heat release rate were calculated from pressure based statistics. The modeling outcome is discussed in detail with combustion parameters. The results presented in this paper demonstrate that, the CFD modeling can be the reliable tool for modeling combustion of internal combustion engine [9].
2. Scope of Present Work
It is evident from the foregoing discussion that multidimensional calculations for the in cylinder flows are proved to be powerful tool for diesel engines simulation. A three dimensional model has been chosen for this investigation. The turbulence model and combustion model has been taken for analysis. The turbulence and combustion processes are modeled with sufficient generality to include spray formation, delay period, chemical kinetics and on set of ignition. Also the model predicts NO and soot emissions over a wide range of operating conditions in a diesel engine.
3. Mathematical Description
3.1. Mesh and Boundaries
The mathematical models in CFD start with combustion chamber geometry approximation representation (engine mesh) and boundaries types. The geometry can be made using the pre-processor as shown in Figure 1. The gambit software (pre-processor is used to build and meshing a model [10]. Table 1 shows engine data [11,12].
3.2. Numerical Modeling
The physical phenomena of combustion flows in internal combustion engines are very complex, this study uses Eulerian and Lagrangian equations in Fluent code to solve the gas and liquid phase’s governing equations [10]. The gas governing equations consist of mass, momentum,

Figure 1. Engine combustion chamber mesh.
Table 1. F1L511 Engine Data.

energy, species, turbulent equation, and chemical reaction. The liquid fuel governing equations contain the equation of motion, the droplet energy, and spray equations. Regarding the physical boundary conditions, velocity at wall is approximated by turbulent law-of-the-wall velocity and temperature at wall prescribed by fixed temperature (cylinder head = 490 K, cylinder wall = 473 K and piston and piston bowl = 550 K. The program starts at CA = 239˚ CA at inlet valve close with inlet charge already fill the cylinder and ends at CA = 469˚ CA at exhaust valve opening. That means the simulation is counting for the indicated gross work and associated combustion parameters. The simulation is based on the experimental work using the DI diesel engine F1L511 [13]. The present model uses standard k-ε model for solving Navier stokes equations employing the eddy dissipation concept.
3.2.1. Modeling Basic Fluid Flow
It is often required to model a region of the engine as an open thermodynamic system. Such model is appropriate when the gas inside the open system boundary can be assumed uniform in composition and state at each point in time, and when that state and composition vary with time due to heat transfer, work transfer, mass flow across the boundary, and boundary displacement. Governing equations are mass, momentum equations and energy equations. These equations for open system, with time or crank angle as the independent variable, are the building blocks for thermodynamic based models.
Continuity equation:
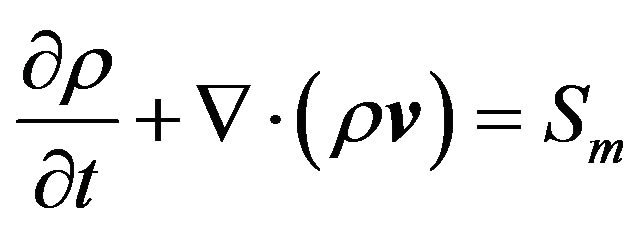 (1)
(1)
Momentum equation:
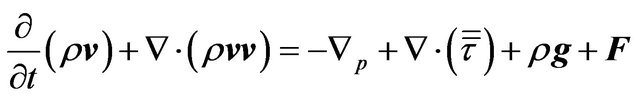 (2)
(2)
3.2.2. Heat Transfer Modeling
The energy equation solved is taking the following form:
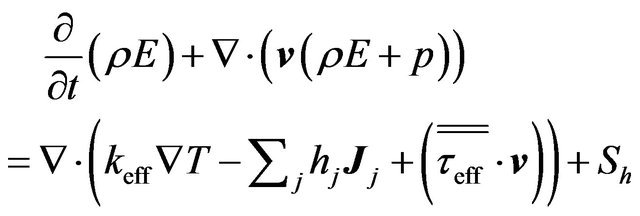 (3)
(3)
The first three terms on the right-hand side of Equation (3) represent energy transfer due to conduction, species diffusion, and viscous dissipation, respectively. Sh includes the heat of chemical reaction, and any other volumetric heat sources may be defined.
3.2.3. k-ε Model
The k-e model is the simplest “complete model” of turbulence consists of two-equation model. It is a semiempirical model, and the derivation of the model equations rely on phenomenological considerations and empiricism [14].
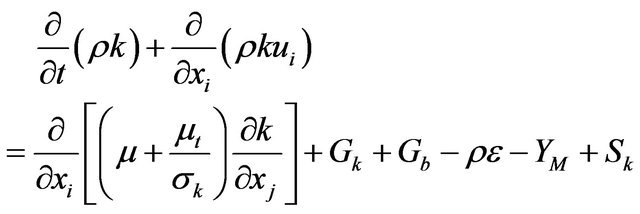 (4)
(4)
and
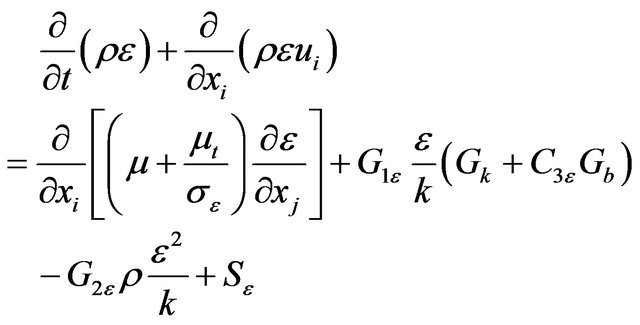 (5)
(5)
3.2.4. Combustion Modeling
The ignition/combustion model is based on a modified eddy dissipation concept (EDC) which has been implemented into the CFD code. Multiple simultaneous chemical reactions can be modeled, with reactions occurring in the bulk phase (volumetric reactions) and/or on wall surfaces. The conservation equation takes the following general form:
 (6)
(6)
It is assumed that reaction occurs in small turbulent structures, called the fine scales [15]. The bulk reaction is assumed to be:

Zeldovich mechanisms [8]:

The equilibrium reactions are:

3.2.5. Engine Ignition Modeling
For the present study the Auto-ignition model (Hardenburg model) [16] is the most suitable one for simulating direct injection Diesel engine. The transport equation for an ignition species, Yig is given by:
 (7)
(7)
The ignition delay period is calculated using the Hardenburg and Hase correlation [9] which is given by:
 (8)
(8)
3.2.6. Discrete Phase Modeling
The Lagrangian discrete phase’s model in the CFD code follows the Euler-Lagrange approach. For x-direction it takes the following form
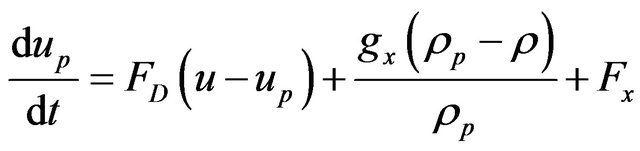 (9)
(9)
3.2.7. Spray Modeling
In the present study the collision model along with the TAB breakup model are used [17-19].
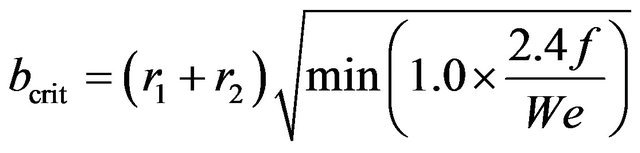 (10)
(10)
 (11)
(11)
3.2.8. Emissions Modeling
In the present study the mass transport equation for the NO species is solved, taking into account convection, diffusion, production and consumption of NO and related species.
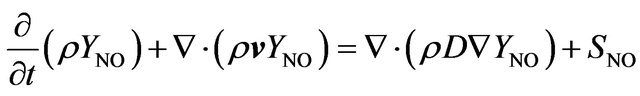 (12)
(12)
For soot formation the two-step Tesner model is used [20]. The model predicts the generation of radical nuclei and then computes the formation of soot on these nuclei.
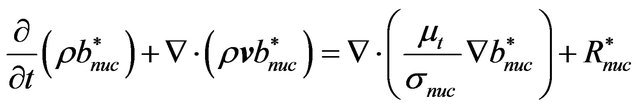 (13)
(13)
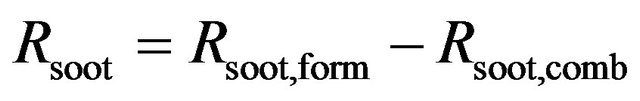 (14)
(14)
4. Results and Analysis
4.1. Grid Analysis
The computational grids of the DI diesel engine are showed in Figure 1. The present study model is build using approximate 200,000 unstructured mixed cells types (hexagonal and tetrahedral) the grid is divided into two zones. The first zone is the cylinder zone and the second is the bowl zone. The first zone uses the hexagonal cells and the second zone uses tetrahedral cells as shown in Figure 1. In engine operation, valves and the piston move, so the mesh should move according to the real engine in order to simulate the charge of valve and piston position with crank angle. Piston and piston bowl movement are decided by the stroke, connecting rod and crank angle. Simulation starts at 239˚ CA and ends at 469˚ CA. This is the period from the inlet valve closing till exhaust valve opening. That means thermodynamically; the compression stroke and power stroke only accounted in this study (indicated gross work). The simulation time step is 0.5 crank angles. Each computer run spends about 12 hours on IBM compatible computer using quad duo processor with 2 GHz and 4 MB cache and 6 GB RAM. The simulation uses fixed temperature boundary conditions [21] and the initial conditions driven from the experimental work [13].
4.2. Model Validation
Figure 2 shows the comparison of the measured and predicted cylinder pressures. The ignition model scaling factor tuned for the first case (maximum load simulation) and kept constant in all cases (other load simulated). The ignition point in most cases is nearly captured. The peak pressure and the pressure gradient over the combustion period produced by CFD simulation match closely with measurements. The peak cylinder pressure is over predicated by about 6%. Figures 3-6 demonstrate the in-cylinder processes reproduced by CFD simulation using a series of distribution plots illustrating temperature, pressure, fuel mass fraction and gas velocity across the cylinder center plan respectively.
4.3. Engine Performances
The engine performance at different loads is shown in Figure 7. The figure shows the predicted performance from maximum load till the no load. From the pressurecrank angle diagram the peaks pressure at different loads are determined, also the start of injection, start of ignition is observed. Figure 8 shows p-v diagram which is not closed, because the simulation period did not reach to the end of expansion stroke at exhaust valve opening.
Figure 9 shows predicted rate of heat release. The curve accurately and clearly determined the different combustion zones and delay time period.
The start of injection crank angle is determined from [13] and the injection period is determined from [11,12]. The delay time period is determined to be from the start of injection till the p-θ change its slope as identified in Figure 9. This period is nearly 11 crank angles vary according to the φ (equivalence ratio) or load. Figure 10
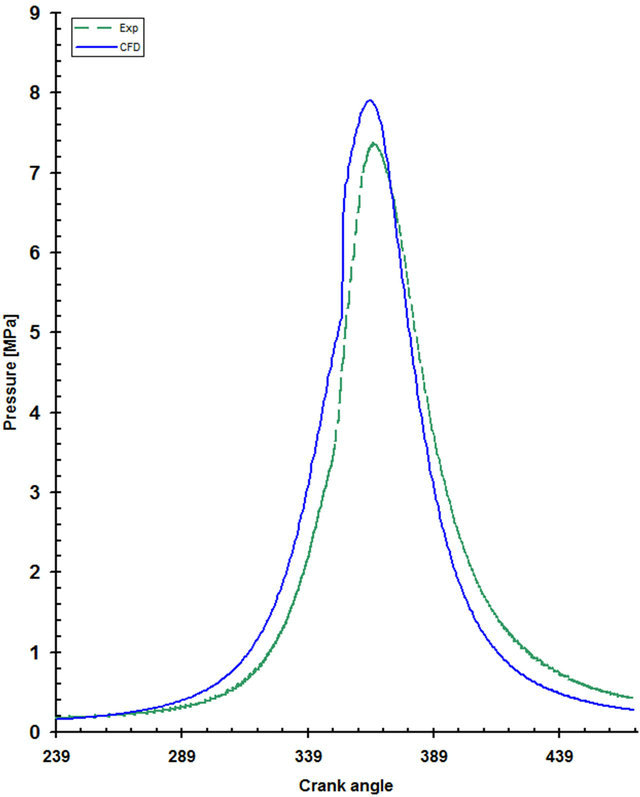
Figure 2. Comparison of the measured and predicted incylinder pressures.
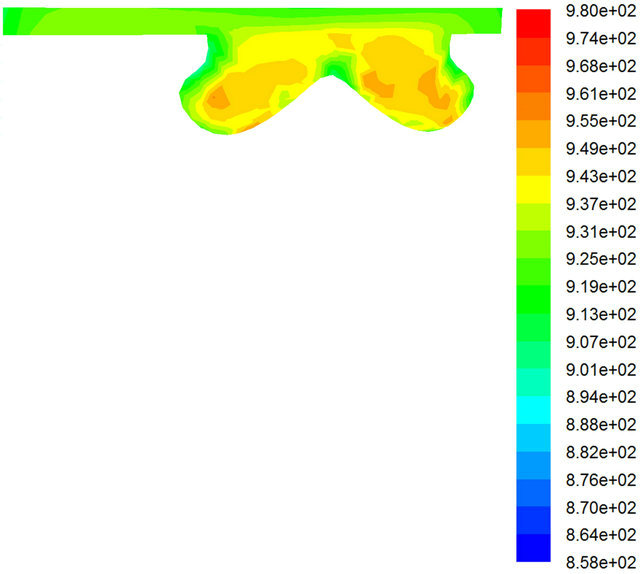
Figure 3. Temperature distribution in (K) at φ = 0.556, CA = 339 (maximum load).
shows the predicted heat release along with the predicted engine pressure at maximum load. From Figure 10 we can get that the total burning period is much longer than the injection period, also the magnitude of the initial peak of the burning rate depends on the ignition delay period; that means increasing delay period will increase burning rate peak [22]. Figure 11 illustrates the relative

Figure 4. Pressure distribution in (Bar) at φ = 0.556, CA = 339 (maximum load).
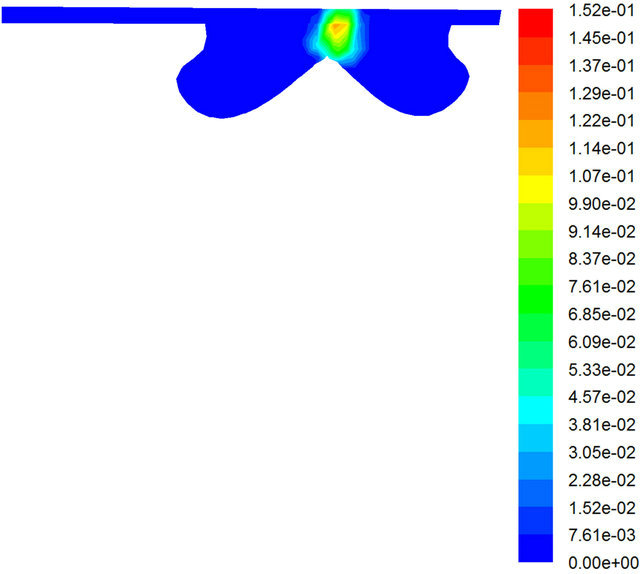
Figure 5. C10H22 mass fraction at φ = 0.556, CA = 345 (maximum load).
magnitude of the gross and net heat release, heat transfer and heat of vaporization and heating up of the fuel at 1500 RPM for the base line engine. The heat release analysis method [23] is used to obtain the combustion information from the pressure data. The net heat release is the gross heat release due to combustion extracts from it, the heat transfer to the walls (omitting the crevice effect) and the effect of fuel vaporization and heat up. The energy change associated with heating up fuel vapor from injection temperature to typical compression air temperature is about 6% of the fuel heating value. The heat transfer integrated over the duration of the combustion period is about 35% of the total heat release. The small kink in the lower part of the curve shows the heat of vaporization
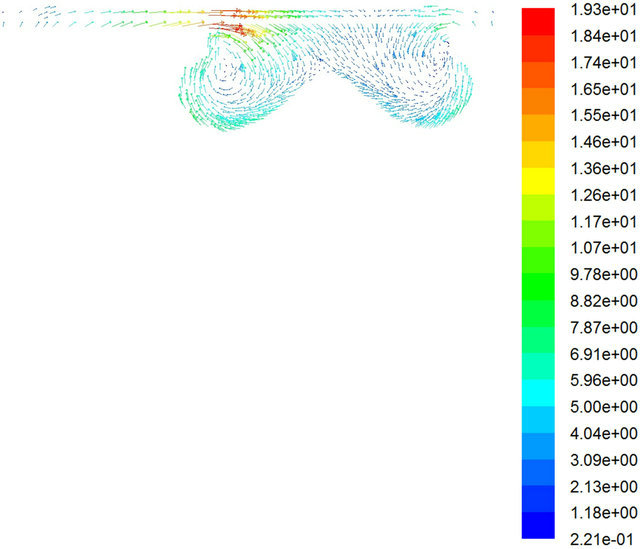
Figure 6. Gas velocity magnitude (m/s) at φ = 0.556, CA = 339 (maximum load).

Figure 7. Pressure-crank angle at different engine loads.
and heating up fuel.
Figure 12 shows the predicted temperature-crank angle diagram at different loads. The curve shows that increasing the load which corresponding to increasing the fuel mass flow rate results in increasing the combustion temperature. Figure 12 shows that the temperature of the air at the end of compression is sufficiently high for the droplets of fuel to vaporize and ignite as they enter the cylinder. Very small downward kinks found near fuel in-

Figure 8. Pressure-volume diagram at different loads.
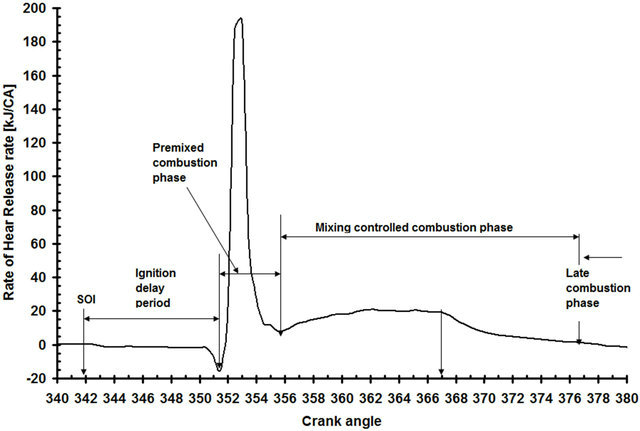
Figure 9. Predicted rate of heat release diagram identifying different diesel combustion phases at maximum load.
jection crank angle represent the interaction between the liquid fuel (heated up) and the air in the cylinder (cooled).
4.4. Emissions
Engine emissions due to combustion of hydrocarbon fuel depend on the combustion equations and the emission model solved to calculate engine pollutant. In the present study the combustion emissions CO, CO2, NO and Soot are calculated. Figure 13 shows NO concentrations rise from the residual gas value following the start of combustion, to a peak at the point where the burned gas equi-
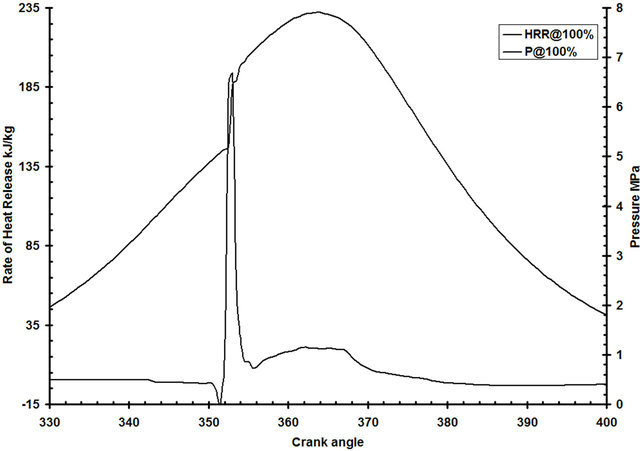
Figure 10. Predicted rate of heat release and engine cylinder pressure at full load.

Figure 11. Predicted grows and net heat Release profile during combustion at 1500 RPM.

Figure 12. Temperature-crank angle diagram.
valence ratio changes from rich to lean (where the CO and CO2 concentration has its maximum value).
As the burned gas equivalence ratio becomes leaner due to mixing with excess air, NO concentrations decrease since formation becomes much slower as dilution occurs.

Figure 13. Concentration of Soot, NO and CO for different loads as a function of crank angle.
5. Conclusions
From the present study the main conclusions are:
• The fluid flow in DI diesel having bowel in piston with turbulence and combustion processes modeled with sufficient generality to include spray formation, delay period, chemical kinetics and onset of ignition; adequately simulated the engine cycle.
• The model is validated through the comparison of the predicted p-θ curve with the experimental p-θ curve.
• Some important engine characteristics are predicted such as heat release rate, gross and net heat release. In addition the T-θ diagrams for different loads are shown.
• Detailed CFD model predictions are obtained as incylinder temperature and pressure distributions, gas velocity and fuel mass fraction on the piston bowl.
REFERENCES
- G. T. R. Reader, M. Zheng, I. J. Potter and J. G. Hawley, “Investigation of Non-Air Diesel Engine Systems,” 28th Inter-Socity Energy Conversion Engineering Conference, San Diego, 1992.
- K. Fukuda, A. Ghasemi, R. Barron and R. Balachandar, “An Open Cycle Simulation of DI Diesel Engine Flow Field Effect on Spray Processes,” SAE Technical Paper 2012-01-0696, 2012. doi:10.4271/2012-01-0696
- A. S. Kuleshov, “Multi-Zone DI Diesel Spray Combustion Model for Thermodynamic Simulation of Engine with PCCI and High EGR Level,” SAE Paper No 2009- 01-1956, 2009.
- H. Barths, H. Pitsch and N. Peters, “3d Simulation of Di Diesel Combustion and Pollutant Formation Using a TwoComponent Reference Fuel,” Oil & Gas Science and Technology, Vol. 54, No. 2, 1999.
- L. V. Griend, M. E. Feldman and C. L. Peterson, “Modeling Combustion of Alternate Fuels in a DI Diesel Engine Using KIVA,” ASAE, Vol. 33, No. 2, 1990, pp. 342-350.
- B. A. Cantrell, R. D. Reitz, C. J. Rutland and Y. Immamori, “Strategies for Reducing the Computational Time of Diesel Engine CFD Simulations,” International Multidimensional Engine Modeling User’s Group Meeting, SAE Congress, 23 April 2012
- S. A. Basha and K. R. Gopal, “In-Cylinder Fluid Flow Turbulence and Spray Models,” Renewable and Sustainable Energy Reviews, Vol. 13, No. 6-7, 2008, pp. 1620-1627.
- S. M. Jameel Basha, P. Issac Prasad and K. Rajagopal, “Simulation of In-Cylinder Processes in a DI Diesel Engine with Various Injection Timings,” ARPN Journal of Engineering and Applied Sciences, Vol. 4, No. 1, 2009.
- U. V. Kongre and V. K. Sunnapwar, “CFD Modeling and Experimental Validation of Combustion in Direct Ignition Engine Fueled with Diesel,” International Journal of Applied Engineering Research, Vol. 1, No. 3, 2010.
- Fluent-ANSYI, “FLUENT 6.3.26. 2006. User’s Manual and Tutorial Guide,” Fluent Inc., 2006.
- KHD Deutz, “FL 511/W Instruction Manual,” 2973544D/ E, 2000.
- Oruva Motor, “F1L511 Diesel Engine Technical Data,” Licensed from Dutez, 2000.
- A. M. Nour, E. M. Marzouk, A. A. Abel Rahman and W. A. Abdel Ghafar, “Effect of Carbon Dioxide in Non-Air Inlet Mixture on Combustion performance in Diesel Engine,” IREME, 2009
- B. E. Launder and D. B. Spalding, “Lectures in Mathematical Models of Turbulence,” Academic Press, London, 1972.
- B. F. Magnussen, “On the Structure of Turbulence and a Generalized Eddy Dissipation Concept for Chemical Reaction in Turbulent Flow,” Nineteenth AIAA Meeting, St. Louis, 1981.
- H. O. Hardenburg and F. W. Hase, “An Empirical Formula for Computing the Pressure Rise Delay of a Fuel from Its Cetane Number and from the Relevant Parameters of Direct Injection Diesel Engines,” SAE Technical Paper 790493, SAE, 1979.
- P. J. O’Rourke and A. A. Amsden, “The TAB Method for Numerical Calculation of Spray Droplet Breakup,” SAE Technical Paper 872089, SAE, 1987.
- R. D. Reitz, “Mechanisms of Atomization Processes in High-Pressure Vaporizing Sprays,” Atomization and Spray Technology, Vol. 3, No. 4, 1987, pp. 309-337.
- R. D. Reitz and F. V. Bracco, “Mechanisms of Breakup of Round Liquid Jets,” The Encyclopedia of Fluid Mechanics, Vol. 3, 1986, pp. 223-249.
- P. A. Tesner, T. D. Snegiriova and V. G. Knorre, “Kinetics of Dispersed Carbon Formation,” Combustion and Flame, Vol. 17, No. 2, 1971, pp. 253-260. doi:10.1016/S0010-2180(71)80168-2
- J. F. Wiedenhoefer and R. D. Reitz, “Multidimensional Modeling of the Effects of Radiation and Soot Deposition in Heavy-Duty Diesel Engines,” SP-1740 SAE 2003-01- 0560, 2003, pp. 251-271.
- G. L. Borman and K. W. Ragland, “Combustion Engineering,” WCB, McGraw-Hill, 1998.
- J. B. Heywood, “Internal Combustion Engine Fundamentals,” McGraw Hill, New York, 1988.
Nomenclature

Continued


