Energy and Power Engineering
Vol. 4 No. 6 (2012) , Article ID: 25027 , 10 pages DOI:10.4236/epe.2012.46056
Hydrokinetic Assessment of the Kvichak River near Igiugig, Alaska, Using a Two-Dimensional Hydrodynamic Model
Civil and Environmental Engineering Department, University of Alaska Fairbanks, Fairbanks, USA
Email: hatoniolo@alaska.edu
Received August 23, 2012; revised September 27, 2012; accepted October 8, 2012
Keywords: Stream; Resource Assessment; Numerical Modeling; Power Density
ABSTRACT
Two-dimensional hydrodynamic simulations were performed on a monthly basis along 2.5 km of the Kvichak River near Igiugig in southwest Alaska, USA, to estimate flow conditions and to assess the hydrokinetic potential of the river reach. Instantaneous power density function along the computational domain was calculated. Study results indicate that two areas may be suitable for deploying turbines. The best option is located near the town, where the channel is relatively straight. A second possible site is located near the end of the study reach (approximately 2.3 km, along the river, from Lake Illiamna). Monthly-averaged velocities along the thalweg ranged from 1.7 to 2.7 m/s; and from 1.1 to 2 m/s at the upstream and downstream sites, respectively. Similarly, averaged values for the instantaneous power density, reduced by an extraction coefficient, were approximately 1500 and 5500 W/m2 during April and September, respectively, at the upstream site, as well as 400 and 2500 W/m2 for the same months at the downstream site. It was found that a previous resource assessment, which considered cross-sectionally averaged velocities, substantially underestimated the available power density along the river reach. Finally, the importance of having adequate bathymetric data is demonstrated by comparing field measurements with model simulations.
1. Introduction
The growth of worldwide energy demand and the need to reduce dependence on fossil resources to avoid undesirable environmental consequences have led to new investigations of renewable energy sources. Extensive research efforts have been carried out in recent years on tidal and in-stream energy resources. Studies have involved many direct and indirect topics related to these sources of renewable energy, such as resource assessments, technology reviews, energy extraction, and fish/ turbine interactions. Resource assessments have been done at different spatial scales, including national [1-3], regional [4,5], state [6,7], and site-specific scales [8-10]. Technology reviews [11,12] and energy extraction mechanisms [13-15] have been also published. Literature on fish and its interactions with hydrokinetic devices is somewhat limited [16,17].
Numerical models with different levels of complexity were used in resource characterization efforts. For instance, one-dimensional models were used to estimate water depths and velocities [18,19]; two-dimensional hydrodynamic models were used to estimate vertically averaged velocity distributions on river cross sections [10]. Finally, three-dimensional models were used to study the effects of turbines on the entire flow field [14,20,21].
In Alaska, initial work on hydrokinetic resource assessment was done considering cross-sectionally averaged velocity [18]. A probable consequence of this approach, which considered a single velocity along the river cross section, was that existing resources could be considerably underestimated.
This paper presents the first resource assessment, on a monthly basis, of the Kvichak River near Igiugig using an existing two-dimensional hydrodynamic model. Instantaneous power density, reduced by an energy extraction coefficient, along the computational domain is also calculated. In addition, suitable sites for deploying turbines are presented, and the importance of adequate bathymetric surveys and methodology used in resource assessment is discussed. The effect of turbine(s) blockage on flow conditions and detailed analysis of macroturbulence (i.e., to estimate off-directional stresses along river cross sections) are beyond the scope of this paper. Analyses of these topics constitute, without a doubt, stand-alone articles.
2. Study Site and Available Data
The study reach is located in southwest Alaska along the Kvichak River near Igiugig, a small village situated at 59˚19′ N, 155˚54′ W. This rural community has no access road [22]. Figure 1 shows the study area.
The mouth of the Kvichak River is at Iliamna Lake, which constitutes the primary source of water for the river [22]. The stream in the area is ice-free during winter months, but has some moving ice, that originates at Iliamna Lake, during spring breakup [18]. In general, the water in the stream is clear, which indicates low or negligible sediment transport [22]. Bed sediment along the reach consists of cobbles, coarse and medium gravel, with insignificant amounts of finer sediment [22].
The United States Geological Survey (USGS) installed and operated a gauging station (ID 15300500) from 1967 to 1987. Historical data can be found at: http://waterdata.usgs.gov/nwis/nwisman/?site_no=15300500&agency_cd=USGS. Table 1 provides the average monthly discharge for the period of record.
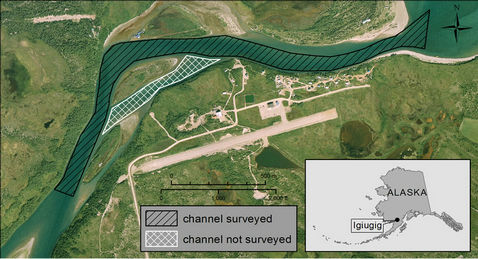
Figure 1. Aerial view of the study reach. Main (surveyed) and secondary (not surveyed) river channels are indicated in the image. Flow direction is from right to left.

Table 1. Historical monthly averaged discharge.
The study reach was intensively investigated by Terrasond (http://www.terrasond.com/) during 2011 as part of a resource reconnaissance and physical-characterization study. Fieldwork activities involved velocity measurements using an Acoustic Doppler Current Profiler (ADCP), water slope measurements, and river reach bathymetry [22].
3. Methods
The approach followed to estimate annual power density along the Kvichak River comprised three main tasks: 1) two-dimensional hydrodynamic model setup; 2) model calibration; and 3) power density calculation. Specific details for each task are described in the following paragraphs.
3.1. Hydrodynamic Model Setup
An existing numerical model, the CCHE2D developed at the National Center for Computational Hydroscience and Engineering (NCCHE), University of Mississippi (http://www.ncche.olemiss.edu/), was used in this work. The model is free but is not an open source. The CCHE2D Model Package is composed of two different applications: CCHE_GUI, the two-dimensional flow and sediment transport model, and CCHE_MESH, the mesh generator [23].
The CCHE2D is a depth-integrated two-dimensional model, which was successfully validated in different river settings [24,25]. The model was also used on the Tanana River at Nenana, Alaska, to assess the in-stream hydrokinetic resource [10].
Mesh generation: The mesh represents the computational domain where the governing equations are discretized and solved; it is generated by CCHE_MESH software [23]. The software does not allow the inclusion of structures to simulate turbines in the domain. Figure 2(a) shows the mesh built with the bathymetric data collected by Terrasond in August 2011 [22]. A comparison between Figures 1 and 2(a) reveals that bathymetric data for the secondary channel near the river bend located in the center of the figure were not collected. The lack of information on this channel poses a serious restriction to any modeling effort because water flow is divided into the main and the secondary channels in that area. To palliate this limitation, a rough rectilinear channel was added to the original bathymetry (Figure 2(b)). The bathymetry along this secondary channel was linearly interpolated from the upstream to the downstream end. This issue is further discussed in the results and discussions section. The final mesh consisted of 10,000 nodes, distributed along a domain defined by 50 by 200 lines.
Boundary conditions: The CCHE2D requires inlet and
 (a)
(a)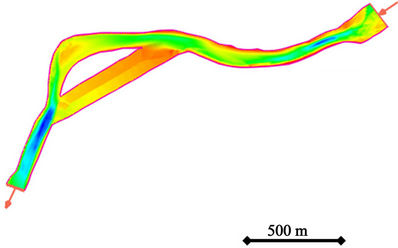 (b)
(b)
Figure 2. (a) Computational bathymetry generated with the model using field data. (b) Secondary channel, using linear interpolation along the bed, added to the numerical domain. Flow direction is from right to left.
outlet boundary conditions [23]. The upstream boundary conditions were defined in terms of average monthly river discharge, Q, given in Table 1. The downstream boundary conditions during the monthly simulations were set in terms of water surface level. Specifically, some water surface levels were measured at different river conditions [22]; others (corresponding to any particular monthly simulation) were calculated using a linear function defined by measured discharge and water level values.
3.2. Model Calibration
Initial work was done to back-calculate the Manning’s roughness coefficient, n, using data gathered in the field by Terrasond during June 2011 [22]. Following the methodology described by Toniolo et al., [26], the ADCPgenerated measurements of channel area, width, and velocity along one river cross section were used, along with the water-surface slope measurement to calculate the roughness coefficient given by
 (1)
(1)
where U denotes the cross-sectional average velocity, H denotes the average depth, and S denotes the water-surface slope. The average cross-sectional depth is obtained as
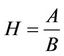 (2)
(2)
where A denotes the cross-sectional area, and B denotes the channel width.
Table 2 shows data gathered on 21 June 2011 on a cross section located approximately 750 m from the river mouth. Water slope at the river cross section was measured on 18 June 2011 [22]. The calculated n value was 0.026. Table 3 shows ADCP data collected on the same river cross section in subsequent field measurements. The n value previously calculated (Table 2) was used to estimate the water slope for different flow conditions. Results indicate a slight increment in S with increasing discharge.
The roughness coefficient was applied to the entire numerical domain, which included the secondary channel near the river bend, and used in preliminary model runs. The objective was to match the modeled water slope with the measured water slope (on 18 June 2011) along the entire reach, which was 0.0005. The agreement between measured and modeled slopes was reached using n = 0.032, which is in the range of reported values for sediments found in the study area. Thus, the calibration process was finished.
Additional model parameters, such as time step and total simulation time, were 10 seconds and 20,000 seconds, respectively. Steady-state solutions were reached with the selected simulation time. A parabolic eddy viscosity model was used to close the momentum equations.
3.3. Power Density Calculation
The HYDOKAL model [27] was used to estimate instantaneous power density along the entire river reach. Specifically, the instantaneous power density of a parcel of fluid [8,9] is defined as
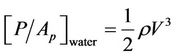 (3)
(3)
where P denotes power, Ap denotes cross-sectional area

Table 2. Calculation of manning’s coefficient.

Table 3. Variation of slope as function of discharge.
of a parcel of fluid, r denotes water density, and V denotes velocity magnitude.
Equation (3) was applied to the velocity field produced by the numerical model. HYDROKAL includes a userdefined energy extraction coefficient, which is fundamental for estimating the energy that could be harvested from the river [27]. This value was set to 0.59, which corresponds to the maximum power limit for wind turbines [28]. The wind/channel analogy is valid if the ratio of the turbine cross section over the channel cross section is small [29]. However, recent research in tidal environments considering ideal turbine models [29] reported values slightly larger than 59%.
As a first approximation, it is assumed here that the wind/channel analogy is valid. Thus, the values reported in the following section constitute the maximum energy that could be extracted from the current. Note that turbine efficiency and blockage are not considered in the calculation.
4. Results and Discussions
Figure 3 shows velocity distributions generated by the model, with and without the secondary channel, and the
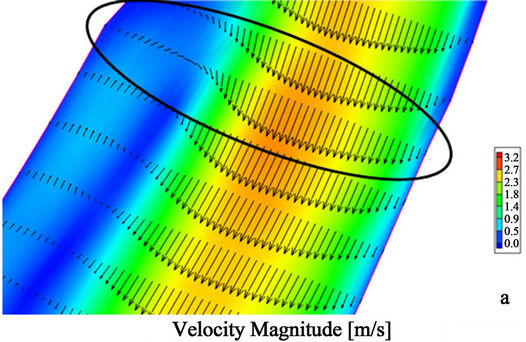
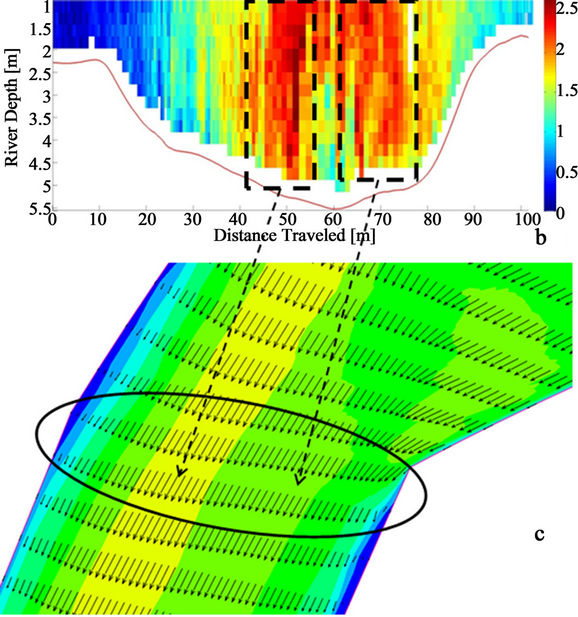
Figure 3. (a) Velocity distribution generated by the numerical model considering a single channel; (b) Velocity distribution measured in the field using ADCP; (c) Velocity distribution generated by the numerical model considering water flow along the main and secondary channels. Velocity is in m/s.
cross-sectional ADCP velocity measurement performed in the same location on 29 August 2011 [22]. The discharge used in both numerical simulations was 544 m3/s, which corresponds to the discharge measured in the river on 29 August 2011. An inspection of graph (b) in Figure 3 reveals the presence of two major areas (or velocity cells), with high velocities separated by a relatively low velocity area between them. Due to the location of this cross-section, it is evident that one of the cells is coming from the main channel and the other cell is coming from the secondary channel. This fact provides a clear indication that the secondary channel was active and moving considerable flow during the survey. A comparison of graphs depicted in (a) and (c) of Figure 3 shows significant differences in velocity magnitude and relative location along the river cross section. A comparison of graphs (b) and (c) in the figure indicates that the model successfully captured the main flow characteristics (i.e., two sectors with high velocity across the river) in that area.
The issue posed by the lack of information on the secondary channel that was not surveyed was introduced in this paper previously, in the sub-section on Mesh Generation. The significant differences in model results, considering a single or a two-channel configuration, were described in Figure 3. Thus, it is important to note that data collection efforts in the field must include both main and secondary channels. Note also that model results could be misleading if no consideration is given to secondary channels, especially in simulations corresponding to high river discharge.
Figure 4 shows velocity plots along the entire computational domain generated by the two-dimensional hydrodynamic model. Note that model results only represent natural river conditions. The eventual deployment of turbine(s) in the stream will modify the flow conditions, which will need to be simulated by a more complex numerical model (for instance, a 3D model capable of representing turbines in the numerical domain). Monthly discharge values used in the simulations are reported in Table 1. For comparison purposes, graphs in the figure have the same color scale from month to month. Several plots in the figure indicate areas in the central channel with velocities close to 3 m/s, which agrees with velocities reported by Terrasond [22]. To improve the color contrast, and thus the visualization of the plot, new graphs were generated using specific color scales for each month. These graphs can be found at http://www.uaf.edu/acep/facilities/alaska-hydrokinetic-energ/Igiugig/velocity/.
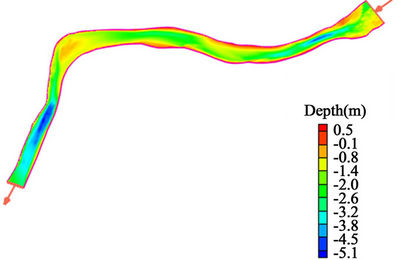
Figure 5 shows power density plots along the computational domain generated by HYDROKAL, considering an extraction coefficient of 0.59. Similar to previous plots, a single scale was used to facilitate the comparison between graphs. The plots reveal a plausible area near the town for deploying hydrokinetic devices (see Figures 1 and 6 for additional details). Maximum power density ranges from 2000 W/m2 (April/May) to 7200 W/m2 (September/October), with average values ranging from 1500 to 5500 W/m2.
It is worthwhile to note here that a previous resource assessment, which considered averaged velocity values across the river in the same reach [18], reported a maximum power density of around 2500 W/m2. An extraction coefficient was not included in the calculation of that maximum value. Thus, it is clear that any methodology that only considers cross-sectionally averaged velocity values considerably underestimates the available resource. In this particular case, the new estimated value (calculated from two-dimensional modeling and even reduced by a 0.59 factor) is approximately 2.2 times greater than the original resource assessment.
A second probable area for installing turbines in the river during high flows, is located downstream of the joining point between main and secondary channels, approximately 2300 m downstream of the lake outlet (Figure 7). The average power density in this secondary region ranges from 400 W/m2 (April) to 2500 W/m2 (September). Note that other factors such as turbulence, navigation, and proximity to infrastructure need to be considered during the site-selection process. Specifically, it is expected that turbulence will be a limiting factor for the installation of devices in the secondary site.
Note that the amount of kinetic energy that could be harvested from the stream is a function of the design of commercial turbines. Explicitly, different companies have different technologies in terms of turbine size, orientation, efficiency, and deployment alternatives. Thus, the turbine/flow interaction and energy extracted from the river are directly related to specific companies and are outside the scope of this work.
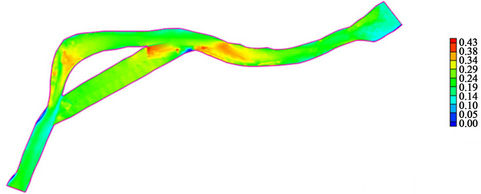
Figure 8 shows another parameter calculated by CCHE2D [23]—the Froude number, Fr, which is the ratio of inertial to gravity forces and is defined as
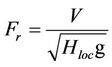 (4)
(4)
where Hloc denotes the local water depth, and g denotes gravity. Figure 8 illustrates the minimum (April) and maximum (September) monthly values. The graphs indicate subcritical flow (i.e., Fr < 1) along the numerical domain. The Froude number remains around 0.25 and 0.30 for most of the domain in April and September, respectively. In general, this situation could be problematic when deciding the location of devices in the river, as the waves and bedforms can be out-of-phase. However, in the case of the Kvichak River, it is not important because sediment transport is very limited or negligible in the area [22].
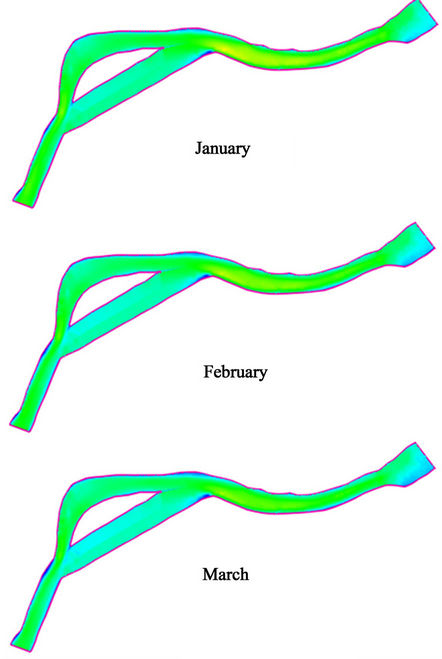

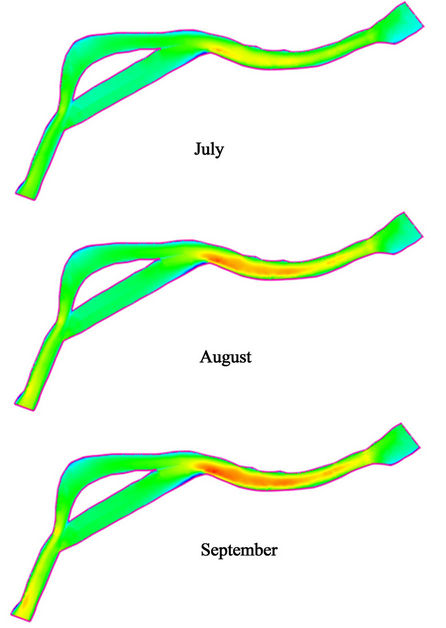

Figure 4. Monthly averaged velocity distributions. Flow is from right to left. Velocity is in m/s.
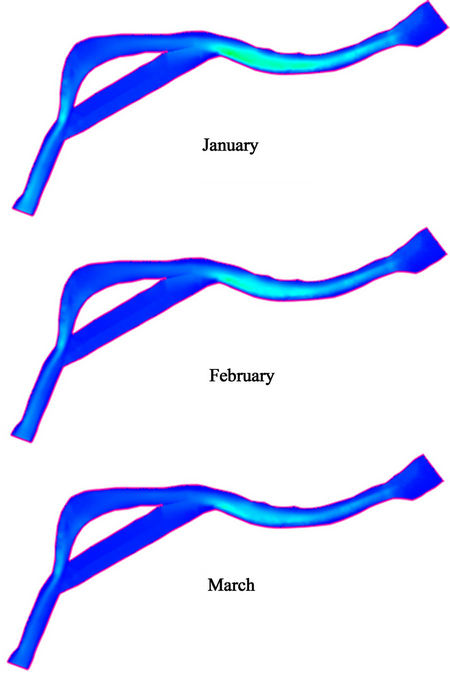
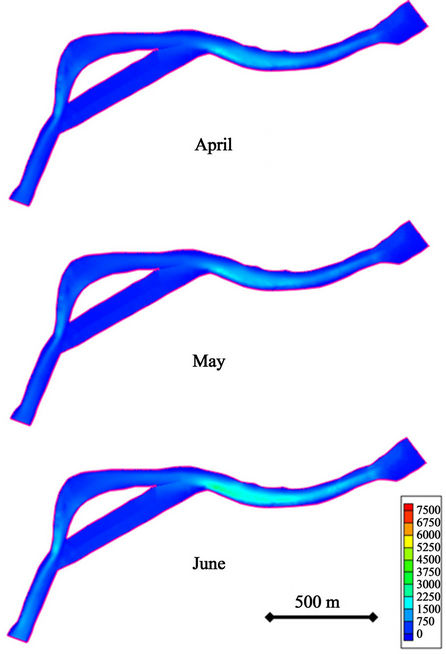

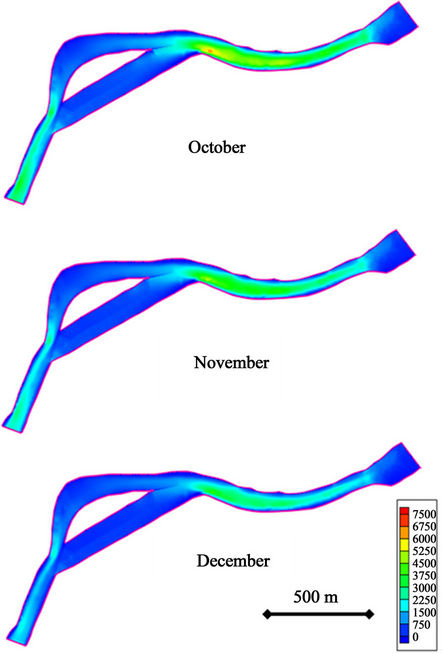
Figure 5. Monthly averaged power density plots considering an extraction factor of 0.59. Power density is in W/m2.

Figure 6. River bathymetry in the most probable area for deploying hydrokinetic devices. Flow is from right to left.
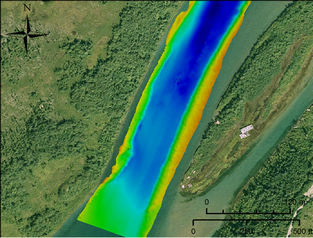
Figure 7. River bathymetry in the secondary area for deploying hydrokinetic turbines (high flow condition). Flow is from top to bottom.
5. Conclusions
This article presents the first, year-round, hydrokinetic resource assessment for the Kvichak River, near Igiugig,
 (a)
(a) (b)
(b)
Figure 8. Froude number along the study reach. (a) minimum (April) and (b) maximum (September) monthly values.
Alaska, using two-dimensional hydrodynamic modeling. The article also presents continuous power density along the study reach, which is the main parameter in estimating the hydrokinetic potential of the river.
Two-dimensional hydrodynamic simulations were performed along the Kvichak River to generate continuous depth-averaged velocity and Froude number through-out the river reach. The model was successfully calibrated against a water slope measurement along the study reach, which covers approximately 2.5 km, starting from the outlet of Iliamna Lake. These model-generated velocity values were used to calculate instantaneous power density along the study reach.
Two probable areas suitable for installing turbines were detected along the domain. The first, and best, site is located near the town of Igiugig, where the flow is confined in a relatively straight channel. The second site is situated approximately 2300 m downstream of the lake outlet, though it is expected that turbulence will be high in this sector due to the spatially changing flow configuration in the upstream region. Instantaneous power density, reduced by an efficiency extraction coefficient, ranged from 1500 to 5500 W/m2 and from 400 to 2500 W/m2 for primary and secondary sites, respectively. The Froude number along the entire domain was always less than one, with values ranging from 0.25 to 0.30 during the year-round simulations, indicating subcritical flow.
Finally, resource assessment using only cross-sectional average velocities should be avoided in the future.
6. Acknowledgements
Data used in this work was obtained from the Igiugig project, which was supported by the Alaska Energy Authority.
REFERENCES
- M. Previsic, A. Moreno, R. Bedard, B. Polagye, C. Collar, D. Lockard, W. Toman, S. Skemp, S. Thornton, R. Paasch, R. Rocheleau, W. Musial and G. Hagerman, “Hydrokinetic Energy in the United States—Resources, Challenges and Opportunities,” Proceedings of the 8th European Wave and Tidal Energy Conference, Uppsala, 7-10 September 2009, pp. 76-84.
- R. E. Taylor, “Non-Conventional Energy Sources,” International Journal of Earth Sciences and Engineering, Vol. 3, 2010, pp. 125-141.
- Z. Defne, K. Hass, H. Fritz, L. Jiang, S. French, X. Shi, B. Smith, V. Neary and K. Sterwart, “National Geodatabase of Tidal Stream Power Resource in USA,” Renewable and Sustainable Energy Reviews, Vol. 16, No. 5, 2012, pp. 3326-3338. doi:10.1016/j.rser.2012.02.061
- A. Botto, P. Claps, D. Ganora and F. Laio, “RegionalScale Assessment of Energy Potential from Hydrokinetic Turbines Used in Irrigation Channels,” SEEP 2010 Conference Proceedings, Bari, 29 June-2 July 2010, 7 p.
- V. Miller, E. Ramde, R. Gradoville and L. Schaefer, “Hydrokinetic Power for Energy Access in Rural Ghana,” Renewable Energy, Vol. 36, No. 2, 2011, pp. 671-675. doi:10.1016/j.renene.2010.08.014
- M. Previsic and R. Bedard, “River In-Stream Energy Conversion (RISEC): Characterization of Alaska Sites,” 29 February 2008, EPRI PP-003-AK.
- M. El-Hawary, “Marine Energy Activities in Nova Scotia: A Status Update,” IEEE Meeting on Power and Energy Society General, San Diego, 24-29 July 2011, 4 p.
- I. Bryden, S. Couch, A. Owen and G. Melville, “Tidal Current Resource Assessment,” Journal of Power and Energy, Vol. 221, No. 2, 2007, pp. 125-135. doi:10.1243/09576509JPE238
- B. Polagye, M. Kawase and P. Malte, “In-Stream Tidal Energy Potential of Puget Sound, Washington,” Journal of Power and Energy, Vol. 223, No. 5, 2009, pp. 571-587. doi:10.1243/09576509JPE748
- H. Toniolo, P. Duvoy, S. Vanlesberg and J. Johnson, “Modeling and Field Measurements in Support of the Hydrokinetic Resource Assessment for the Tanana River at Nenana, Alaska,” Journal of Power and Energy, Vol. 224, No. 8, 2010, pp. 1127-1139. doi:10.1243/09576509JPE1017
- S. Ortega-Achury, W. McAnally, T. Davis and J. Martin, “Hydrokinetic Power Review,” Mississippi State University, Starkville, 2010.
- M. Guney and K. Kaygusuz, “Hydrokinetic Energy Conversion Systems: A Technology Status Review,” Renewable and Sustainable Energy Reviews, Vol. 14, No. 9, 2010, pp. 2996-3004. doi:10.1016/j.rser.2010.06.016
- M. Guney, “Evaluation and Measures to Increase Performance Coefficient of Hydrokinetic Turbines,” Renewable and Sustainable Energy Reviews, Vol. 15, No. 8, 2011, pp. 3669-3675. doi:10.1016/j.rser.2011.07.009
- E. Lalander and M. Leijon, “In-Stream Energy Converters in a River—Effects on Upstream Hydropower Station,” Renewable Energy, Vol. 36, No. 1, 2011, pp. 399-404. doi:10.1016/j.renene.2010.05.019
- B. Polagye and P. Malte, “Far-Field Dynamics of Tidal Energy Extraction in Channel Networks,” Renewable Energy, Vol. 36, No. 1, 2011, pp. 222-234. doi:10.1016/j.renene.2010.06.025
- A. Seitz, K. Moerlein, M. Evans and A. Rosenberger, “Ecology of Fishes in a High-latitude, Turbid River with Implications for the Impacts of Hydrokinetic Devices,” Reviews in Fish Biology and Fisheries, Vol. 21, No. 3, 2011, pp. 481-496. doi:10.1007/s11160-011-9200-3
- P. Schweizer, G. Cada and M. Bevelhimer, “Estimation of the Risks of Collision or Strike to Freshwater Aquatic Organisms Resulting from Operation of In-Stream Hydrokinetic Turbines,” Oak Ridge National Laboratory Report, Vol. 133, 2011, 69 p.
- M. Previsic, R. Bedard and B. Polagye, “System Level Design, Performance, Cost and Economic Assessment— Alaska River In-Stream Power Plants,” 31 October 2008, EPRI RP-006-AK.
- I. Bryden, T. Grinstead and G. Melville, “Assessing the Potential of a Simple Tidal Channel to Deliver Useful Energy,” Applied Ocean Research, Vol. 26, No. 5, 2004, pp. 198-204. doi:10.1016/j.apor.2005.04.001
- E. Lalander, “Modeling Hydrokinetic Energy Resource for In-Stream Energy Converters,” Ph.D. Dissertation. University of Uppsala, Uppsala, 2010.
- S. James, S. Lefantzi, J. Barco, E. Johnson and J. Roberts, “Verifying Marine-Hydro-Kinetic Energy Generation Simulations Using SNL-EFDC,” Oceans 2011 Conference Proceedings, Kona, 19-22 September 2011, pp. 1432-1440.
- Terrasond Ltd., “Kvichak River RISEC Project: Resource Reconnaissance and Physical Characterization—Final Report,” 9 December 2011, 90 p.
- Y. Zhang, “CCHE-GUI—Graphical Users Interface for NCCHE Model User’s Manual—Version 3.0,” National Center for Computational Hydroscience and Engineering, Technical Report No. NCCHE-TR-2006-2, October 2006.
- Y. Jia and S. Wang, “CCHE2D Verification and Validation Tests Documentation,” National Center for Computational Hydroscience and Engineering, Technical Report No. NCCHE-TR-2001-2, August 2001.
- Y. Jia, S. Wang and Y. Xu, “Validation and Application of a 2D Model to Channels with Complex Geometry,” International Journal of Computational Engineering Science, Vol. 3, No. 1, 2002, pp. 57-71. doi:10.1142/S146587630200054X
- H. Toniolo, J. Derry, K. Irving and W. Schnabel, “Hydraulic and Sedimentological Characterizations of a Reach on the Anaktuvuk River, Alaska,” Journal of Hydraulic Engineering, Vol. 136, No. 11, 2010, pp. 935-939. doi:10.1061/(ASCE)HY.1943-7900.0000265
- P. Duvoy and H. Toniolo, “HYDROKAL: A Module for In-Stream Resource Assessment,” Computers & Geosciences, Vol. 39, 2012, pp. 171-181. doi:10.1017/S0022112007007781
- A. Betz, “Windenergie und ihre Ausnutzung durch Windmühlen. Göttingen,” Vandenhoeck & Ruprecht, 1926.
- C. Garrett and P. Cummins, “The Efficiency of a Turbine in a Tidal Channel,” Journal of Fluid Mechanics, Vol. 588, 2007, pp. 243-251. doi:10.1017/S0022112007007781
Notation
A: cross-sectional area Ap: cross-sectional area of a parcel of fluid B: channel width Fr: Froude number H: average water depth Hloc: local water depth P: power Q: water discharge S: water slope U: cross-sectional average velocity V: velocity magnitude n: Manning’s roughness coefficient g: gravity r: density of water

