Energy and Power Engineering
Vol. 4 No. 5 (2012) , Article ID: 22842 , 5 pages DOI:10.4236/epe.2012.45046
Numerical Analysis of the Natural Gas Combustion Products
1Researching and Graduate Section, Applied Hydraulics and Thermal Engineering Laboratory, ESIME-IPN, Mexico City, Mexico
2Researching and Graduate Section, ESIME Culhuacan-IPN, Mexico City, Mexico
3Researching and Graduate Section, Pachuca Technological Institute, Pachuca Hidalgo, Mexico
4Researching and Graduate Section, Design Department, ESIME-IPN, Mexico City, Mexico
Email: mtv49@yahoo.com
Received June 5, 2012; revised July 8, 2012; accepted July 22, 2012
Keywords: Combustion Products; Adiabatic Flame; Stoichiometric Mixture
ABSTRACT
The combustion products of fuels containing the elements C, H, O, N and S are calculated. The methodology is based on the equations obtained in the stoichiometric balance of atoms. The adiabatic flame temperature is determined considering that the pressure of the boiler furnace remains constant. The scope of this work is limited to the analysis of natural gas (methane) with molecular formula CH4. The methodology can, however, be employed for the calculation of combustion products of a great variety of hydrocarbons under the established restrictions. In the development of the methodology two cases are contemplated: Φ ≤ 1 (lean and stoichiometric mixture) and Φ > 1 (rich mixture). In the first case it is considered that when the combustion is complete, the combustion products are O2, H2O, CO2, N2, SO2, and the solution follows directly. When the combustion is incomplete, however, the products H, O, N, H2, OH, CO, NO, O2, H2O, CO2, N2 and SO2 can be generated, according to Stephen R. Turns (2000). When balances of atoms are performed, four conservation equations are obtained, one for each of the C, O, H and N elements. An additional restriction requires that the sum of the molar fractions of the products equals one mol. Finally, seven equilibrium constants, corresponding to the seven chemical reactions of combustion, are introduced. All this provides a system of four nonlinear equations which is solved with the Newton-Raphson method.
1. Introduction
It was therefore decided here to develop a specific purpose computational program for the calculation of the combustion products of boilers burning natural gas and fuel oil. Information about computational codes that handle combustion problems are referenced in the literature. There is for example the one developed by Olikara and Borman [1], the CEC76 [2], developed by NASA and the powerful CEC86 [3] also from NASA (CEC stands for Chemical Equilibrium Code). A more recent code reported in the literature is the STANJAN developed by the Stanford University in 1986 [4]. All these codes are, as mentioned above, extensive and difficult to obtain. This motivated the development of the present methodology, implemented as a computational program for the calculation of the combustion products in boilers.
For this specific case the, composition of the natural gas is: H2 = 8.4%; CH4 = 80.2%; CO4 = 0.5%; C2H4 = 2.0%; C2H6 = 4.5%; C3H6 = 0.6%; C3H8 = 0.3%; C4H4 = 3.4% and S = 0.1%. This data corresponds to the power plant named Jorge Luque, located in the State of Mexico, in Mexico. In the course of development of the system of equations the equivalence ratio Φ is taken into account as a variable which can take different values according to the fuel-air ratios of the boiler.
The contaminants (CO, SO2, NO) are calculated. These originate in the complete and incomplete combustion of the fuel-air mixture in chemical equilibrium conditions. Furthermore, the required equilibrium constants are computed as function of the temperature employing least squares polynomial fitting. The data employed for the fitting is taken from the tables of thermo-chemical properties of JANAF (1985). The range of temperatures for the fitting polynomials is from 600 K to 4000 K.
2. Methodology
In the thermodynamics of equilibrium, the mixing of fuel with composition Cn, Hm, Ol, Nk, Sj (according to David R. Lide [5]) with air, in an equivalence ratio of F, releases combustion products in a state of equilibrium at temperature T and pressure P. The numbers “n” and “m” cannot be zero; “l”, “k” and “j”, on the other hand, could or could not be zero. Furthermore, according to Stephen R Turn [6], twelve combustion products are formed when there is dissociation due to high temperature.
The resulting combustion equation for these elements is: (Equation (1), below).
The equivalence ratio F is commonly employed to quantitatively indicate if the fuel-air mixture is rich, lean or stoichiometric. The equivalence ratio is defined as:
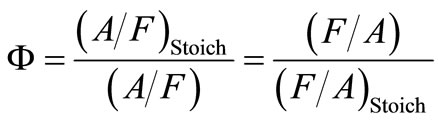 (2)
(2)
This definition shows that for rich fuel mixtures F > 1 while for lean fuel mixtures F < 1; for a stoichiometric mixture F = 1. In many combustion applications, the equivalence ratio is the most important factor for the determination of the system’s efficiency.
The values of  through
through 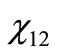 are the molar fractions of the combustion products; the value of
are the molar fractions of the combustion products; the value of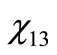 , on the other hand, represents the number of moles of fuel required to obtain one mol of combustion products.
, on the other hand, represents the number of moles of fuel required to obtain one mol of combustion products.
Equation (1) can be simplified to obtain
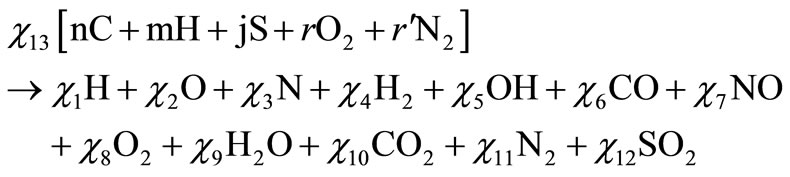 (3)
(3)
where
 .
.
Performing a balance of atoms for each element of the fuel one obtains
 (4)
(4)
 (5)
(5)
 (6)
(6)
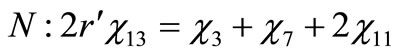 (7)
(7)
 (8)
(8)
An additional condition is imposed to the former system, namely that the sum of all molar fractions of the products must be equal to one mol. That is
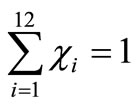 (9)
(9)
Atmospheric air is an Oxygen and Nitrogen mixture with slight quantities of Carbon Anhydrous, Argon and Water Steam. Its composition slightly varies with humidity and altitude. When water steam presence is not considered in atmospheric air composition, it is known as dry air. This work considers the dry air composition as follows 21% Oxygen and 79% Nitrogen. Thus the 79% N2 fraction refers to N2, CO2 and Ar mixture, which is known as atmospheric Nitrogen. That way, there is 0.21 mol of Oxygen and 0.79 mol of Nitrogen in each dry air mol. That is to say: 1DA = 0.21O2 + 0.79N2.
Determining the Adiabatic Flame Temperature (First Law of the Thermodynamics)
The combustion products are determined for a pressure of one atmosphere and at the adiabatic flame temperature. For this reason, the first thing to do is to determine the temperature of the adiabatic flame for complete methane’s combustion.
Assumptions in the application of the first law of the thermodynamics for the boiler furnace (Figure 1):
1) The control volume is fixed to the coordinate system;
2) The fluid properties at each point within the control volume do not change with time;
3) The fluid properties are uniform at all inlet and outlet flows;
4) There is only one inlet and one exit for the fluid in the control volume considered.
Thus, the first law can be written as
 (10)
(10)
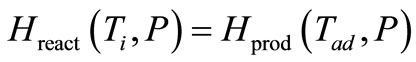 (11)
(11)
The enthalpy of the reactants is
 (12)
(12)


Figure 1. Control volume for the stationary flow in the boiler furnace.
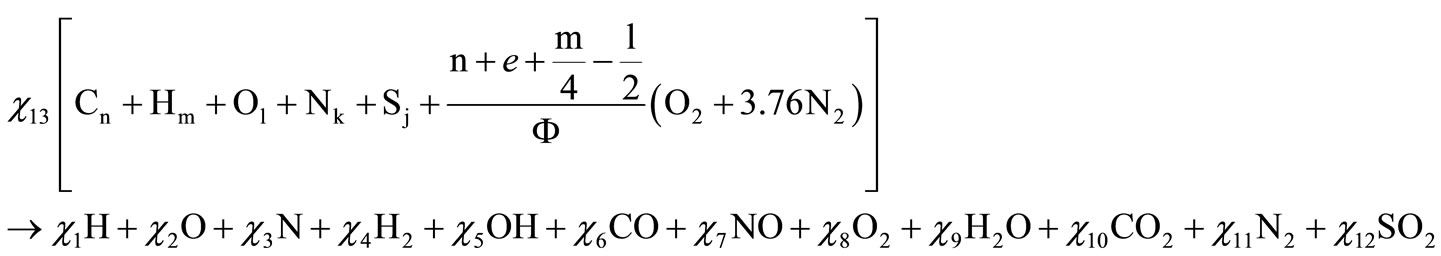 (1)
(1)
The enthalpy of the products is
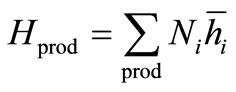 (13)
(13)
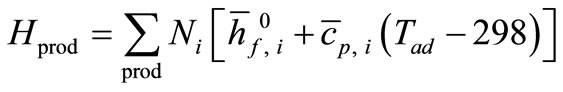

Equating Hreact with Hprod, and solving for Tad gives
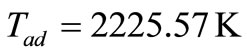 .
.
Once the adiabatic flame temperature is determined the next step is to calculate the combustion products. Below the flow diagram of computational FORTRAN program for complete combustion is presented.

3. Results
Sample solved example 1:
Fuel: CH4;
Equivalence ratio F: 1.0;
Total pressure: 1 atm;
Reactants temperature: 298 K;
Adiabatic flame temperature: 2225.57 K;
Sample solved example 2: numerical solution;
Fuel: CH4;
Equivalence ratio F: 1.10;
Total pressure: 1 atm;
Reactants temperature: 298 K;
Adiabatic flame temperature obtained per iteration: 2195 K.
The results of the numerical solution, Tables 1 and 2 above, were used in order to make some adjustments to the geometry and configuration of a combustion gas turbine, Figure 2, based on some qualitative conclusions and quantitative results obtained from the theoretical study of thermodynamics, fluid mechanics and chemical kinetics applied to turbulent combustion phenomena order to optimize its performance and reduce the gaseous pollutants

Table 1. Results of the combustion products for Φ = 1.

Table 2. Results of the combustion products for Φ = 1.10.
formation rate. The model that was taken as a starting point is the tubular combustion chamber which is located the Applied Thermal and Hydraulics Engineering Laboratory (LABINTHAP) of the Mechanical Engineering School, National Polytechnic Institute.
The specific objective of these amendments is to minimize the concentration of unburned hydrocarbons, carbon monoxide and nitrogen oxides in the combustor exhaust by reaching a uniform temperature distribution within it by adapting the air and fuel flow patterns, Figure 3.
In order to have a reference for comparison, only modifications were made in the flame tube of the chamber, leaving unchanged the case. The geometry of the primary zone inlet section as well as the size and layout of the dilution holes were changed and an annular configuration was used for fuel injection. The proposed geometry for the camera was drawn using the mesh generation software GAMBIT. The simulation of its operation, as well as measurement of its performance parameters were carried out using the computational flow simulation tool FLUENT.
The results of computer simulation show that the geometry of the primary zone, the inlet temperature and

Figure 2. Schematic diagram of a continuous combustion chamber.

Figure 3. Temperature field of the modified primary zone.
location of the fuel injector have a considerable influence on the performance parameters of the camera. With these simple adjustments to the combustion chamber there was an efficiency increase from 76% to 99.99% while the nitric oxide levels were reduced from 105 to 1.2 ppm with respect to the actual model.
4. Conclusions
The development of the equations is based in balances from atom’s conservation, considering that the chemical composition of the fuel contains only the elements C, H, O, N and S. The air is dry, containing only nitrogen and oxygen. Furthermore, for a complete combustion (Φ = 1) it is possible to get in the solution a maximum of five products; for an incomplete combustion (Φ = 1.10), on the other hand, up to twelve products can be present in the solution.
The polynomials for the equilibrium constants as function of the temperature were obtained employing least squares fitting method. The range of temperature for which the polynomials are valid is 600 K through 4000 K in accordance with the data of JANAF tables (1986).
The molar fractions of the combustion products are obtained for the adiabatic flame temperature. In order to compute the products the methodology is divided in two parts: one is for F ≤ 1 and the other for F > 1.
The developed methodology can be employed in the calculation of the combustion products for different values of the equivalence ratio Φ. This can be done for a great variety of hydrocarbons with known molecular formulas and which meet the established restrictions.
This methodology has been applied to engineering in order to make some adjustments to the geometry and configuration of a gas turbine combustion optimizing its performance and reducing the gaseous pollutants formation rate and minimizing the concentration of unburned hydrocarbons, carbon monoxide and nitrogen oxides in the combustor exhaust by reaching a uniform temperature distribution within it by adapting the air and fuel flow patterns.
REFERENCES
- M. J. Moran and H. N. Shapiro, “Fundamentals of Engineering Thermodynamics,” John Wiley and Sons, New York, 2000.
- J. H. Mathews, “Numerical Methods for Mathematics, Science and Engineering,” 2nd Edition, Prentice Hall, Englewood Cliffs, 1992.
- G. Zirkel and E. Berlinger, “Understanding Fortran 77 and 90,” PWS Publishing Company, Boston, 1994.
- J. Warnatz, U. Maas and R. W. Dibble, “Combustion Physical and Chemical Fundamentals, Modeling and Simulation, Experiments, Pollutant Formation,” 3rd Edition, Springer-Verlang, Berlín Heidelberg, 2001.
- D. R. Lide, “CRC Handbook of Chemistry and Physics,” 71st Edition, 1990-1991.
- S. R. Turns, “An Introduction to Combustión. Concepts and Applications,” 2nd Edition, McGraw Hill, New York, 2000.
Nomenclature



