Communications and Network
Vol.6 No.2(2014), Article ID:45796,8 pages DOI:10.4236/cn.2014.62012
A PTS Optimization Scheme with Superimposed Training for PAPR Reduction in OFDM System
Renze Luo1, Rui Li1, Xiaoqiong Wu2, Shuainan Hu1, Na Niu1
1State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation Southwest Petroleum University, Chengdu, Sichuan, China
2Zhongshan Branch China Telecom Co., Ltd., Zhongshan, Guangdong, China
Email: lrzsmith@126.com, 437592751@qq.com, xiaoqiong_wu@163.com, 564738031@qq.com, 690927582@qq.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 10 December 2013; revised 23 January 2014; accepted 20 February 2014
ABSTRACT
Partial Transmit Sequences (PTS) is an efficient scheme for Peak-to-Average Power Ratio (PAPR) reduction in Orthogonal Frequency Division Multiplexing (OFDM) system. It does not bring any signal distortion. However, its remarkable drawback is the high computational complexity. In order to reduce the computational complexity, currently many PTS methods have been proposed but with the cost of the loss of PAPR performance of the system. In this paper, we introduce an improved PTS optimization method with superimposed training. Simulation results show that, compared with conventional PTS, improved PTS scheme can achieve better PAPR performance while be implemented with lower computation complexity of the system.
Keywords:Orthogonal Frequency Division Multiplexing (OFDM), Peak-to-Average Power Ratio (PAPR), Partial Transmit Sequences (PTS), Superimposed Training

1. Introduction
Orthogonal Frequency Division Multiplexing (OFDM) technology has been considered as the core technology for the fourth generation mobile communication system for its high spectral efficiency, good anti-multipath fading capability and anti-interference performance features [1] . However, one of the inherent drawbacks of OFDM signal is that it would have high peak to average power ratio (PAPR), which requires the power amplifier transmitter to have great dynamic range, or else they will have a linear distortion. The power device with larger dynamic range will increase the cost of the transmitter equipment. Besides, when OFDM signals that beyond linear dynamic range transit linear power amplifier devices, they would bring high bit error rate and affect system performance.
Therefore, how to effectively reduce the OFDM system PAPR has become a hot research issue. It has proposed lots of valuable methods to reduce PAPR [2] , which can be summarized as signal distortion method, code method and based on scrambling sequence method. However, these methods have shortcomings varying degrees. Clipping is the most simple method of signal distortion method; it would make signal distortion in-band distortion and out of band radiation. The effect of Coding method to reduce PAPR is good, but the encoding patterns and number that can be used availably are very small. The coding efficiency is very low especially when there are a large number of subcarriers. The method based on scrambling sequence mainly uses different scrambling sequences to process the weighted OFDM signal, thus chooses the smallest PAPR value for OFDM signal transmission. Partial Transmit Sequences (PTS) is an effective method among them for PAPR reduction of OFDM system. However, PTS method has very large computational complexity. Many scholars have proposed some PTS methods with computational complexity reduction [3] , but these methods would bring about PAPR losses varying degrees for the system performance.
Bases on the traditional PTS, this paper proposes an improved PTS optimization scheme by combination with superimposed training sequence method to improve PAPR performance in system with low computational complexity effectively. The method takes advantage of the superimposed training sequence method on reducing PAPR performance, while taking phase-sequence optimization approach to simplify the process of computing phase sequence, thus achieving the purpose for reducing the computational complexity. The simulation results show that compared with the traditional PTS method, the proposed method can not only reduce the computational complexity, but also improve the PAPR performance of system, which is also the greatest advantage that this method has other than other PTS methods having reduced the computational complexity.
2. The PAPR of OFDM System
For an OFDM system with N sub-carrier, in a symbol time interval, after IFFT (Inverse Fast Fourier Transform) and calculating its normalized power (assuming the variance to 1), it can get its complex base band signal defined as Equation (1):
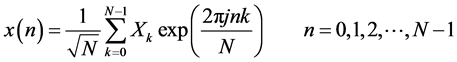 (1)
(1)
where ![]() stands for the
stands for the  sub-carrier modulation signal;
sub-carrier modulation signal; ![]() is the output signal obtained after OFDM modulation.
is the output signal obtained after OFDM modulation.
OFDM signal is the result of superposition by multiple independent sub-carrier signals after modulation, the superimposed signals may have great peak power, thus bring high PAPR. The PAPR in OFDM system is defined as the ratio of the maximum divided by the average power of the signal, expressed as Equation (2):
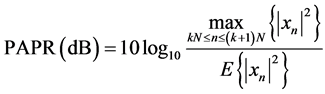 (2)
(2)
where ![]() denotes the expected value.
denotes the expected value.
As it can be seen, it will produce a peak power when the N signals add up with the same phase at the same time. The worst situation can be described as Equations (3) and (4):
 (3)
(3)
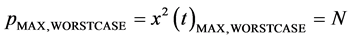 (4)
(4)
Therefore, the maximum value of PAPR as Equation (5):
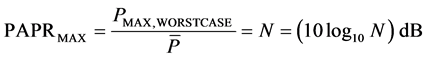 (5)
(5)
The Equation (5) shows that the PAPR of OFDM signal is relevant with the number of sub-carrier. The greater the number of sub-carrier brings higher PAPR, which can make it beyond the linear range of power amplifiers. When signal peak power gets into the nonlinear region of power amplifier, it will cause signal distortion and signal distortion will cause sub-carriers to reconcile and band radiation. As well as a power amplifier with wide range has the shortcomings of low-efficiency and high cost, so it’s necessary to reduce the PAPR value.
3. PTS Scheme
PTS scheme [4] is a common method in the existing technologies to reduce PAPR of OFDM signal. The basic principle of PTS scheme is: an input symbol sequence is presented as Equation (6):
![]() (6)
(6)
Then X is partitioned into V “disjoint” symbol subsequences ![]() shown as Equation (7):
shown as Equation (7):
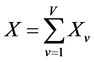 (7)
(7)
It introduces rotating vector: , which is called Side Information (SI), each signal subsequence
, which is called Side Information (SI), each signal subsequence 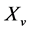 is multiplied by an unit magnitude constant
is multiplied by an unit magnitude constant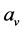 , then it can generate as Equation (8):
, then it can generate as Equation (8):
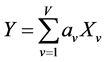 (8)
(8)
Through IFFT, it can get time-domain signal expressed as Equation (9):
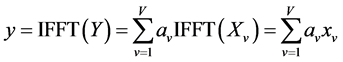 (9)
(9)
Here 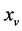 is the IFFT of
is the IFFT of![]() . Then, compare PAPR value by selecting different phase factor, so as to yield the phase factor vector for OFDM signals with the minimum PAPR. When desirable PAPR reduction, the corresponding objective function can be written as Equation (10):
. Then, compare PAPR value by selecting different phase factor, so as to yield the phase factor vector for OFDM signals with the minimum PAPR. When desirable PAPR reduction, the corresponding objective function can be written as Equation (10):
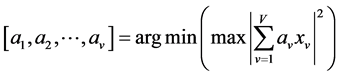 (10)
(10)
where ![]() stands for the decision condition at the minimum value of the function. So that it improves the PAPR performance of OFDM system through finding the best phase factor
stands for the decision condition at the minimum value of the function. So that it improves the PAPR performance of OFDM system through finding the best phase factor 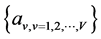 at the cost of
at the cost of 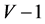 times IFFT. As shown in Figure 1, in a typical OFDM system with traditional PTS.
times IFFT. As shown in Figure 1, in a typical OFDM system with traditional PTS.
PTS method is shown in Figure 1. PTS scheme belongs to the signal scrambler-type techniques which use different scrambling sequences to process the weighted OFDM symbols and optimize the carrier phase for channels, then choose the OFDM symbols and phase combination with smaller PAPR for transmission. Signal scrambler-type techniques have good performance for PAPR reduction, but they obtain good PAPR performance at the cost of higher computational complexity of the system.
4. PTS Optimization Scheme with Superimposed Training
The basic principle of the scheme is making use of superimposed training method, which is used few but has the advantages with inhibiting PAPR of signals and reducing the efficiency of linear power amplifier, as well as further improving band-width utilization in system. At the same time, the paper uses the phase factor with good performance through optimizing phase factor sequence, so as to achieve PAPR reduction for the system more effectively. Where optimizing phase factor sequence makes the computing process of part of the candidate sequence simplified, then reduce the computational complexity.
4.1. Superimposed Training Scheme Method
In order to improve the efficiency of communication, the last century 90’s literatures as in [4] -[7] introduce channel estimation and balanced approaches based on superimposed training sequence, they mainly use supe-

Figure 1. PTS method schematic.
rimposed training sequence method program and first-order statistics for channel estimation and balanced. As information symbols transmit after linear superposition with superimposed training sequence, the receiver can apply only first-order statistics for channel estimation and fast tracking the changes in wireless channel from the principle. For the existing channel estimation methods in communication system, they have advantages of high spectrum efficiency, stable performance, much lower computational complexity and so on. Based on the thinking of researching channel estimation such as in [8] -[11] which mainly use different training sequences for channel estimation research. This paper proposes that apply superimposed training sequence method to the study of PAPR reduction, where it also researches the power conversion efficiency of Power Amplifier (PA) that’s the issue of optimizing the distribution between superimposed training sequence and some transmission sequence. How to distribute the superimposed training sequence signal power to ensure the transmission signals power optimization so as to reduce the PAPR in system more effectively is one of the key technologies in the paper; Further, it can effectively guarantee the system has low computational complexity, band radiation and good system performance.
The paper proposes an improved PTS optimization scheme with superimposed training sequence scheme, its main flow chart for achieving the principle as Figure 2, the main processes for achievement as follows:
Step 1, the sending port deals the input signal sequences with S/P transform, then partitioned into V “disjoint” symbol subsequences;
Step 2, process each partitioned sub-block with reverse Fast Fourier Transform respectively;
Step 3, for the transformed sub-block signals, select some to be processed the following steps: weighted superimposition training sequence 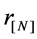 according to a certain power distribution factor to the part of the selected signal sequences
according to a certain power distribution factor to the part of the selected signal sequences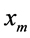 ; In order to ensure the influence that superposition training sequence for system performance as small as possible, generally we value the power ratio factor b between 0 - 0.1, the specific processes that are shown in Figure 3;
; In order to ensure the influence that superposition training sequence for system performance as small as possible, generally we value the power ratio factor b between 0 - 0.1, the specific processes that are shown in Figure 3;
Step 4, weighted all sub-block signals after above-mentioned procession with the optimized phase factor by one-to-one, where the specific process for phase factor optimization is shown below in B in this part;
Step 5, the sending port calculates the peak power and average power ratio for the output of all the signals after the previous processing, then according to calculation results, it selects the smallest result of PAPR to send.
Among them, the main process dealing with the transmission sequence are shown in Figure 3, which is making use of the superimposed training method that has the advantages of inhibiting PAPR for signals and reducing the efficiency of linear power amplifier, as well as further improving band-width utilization for the system.
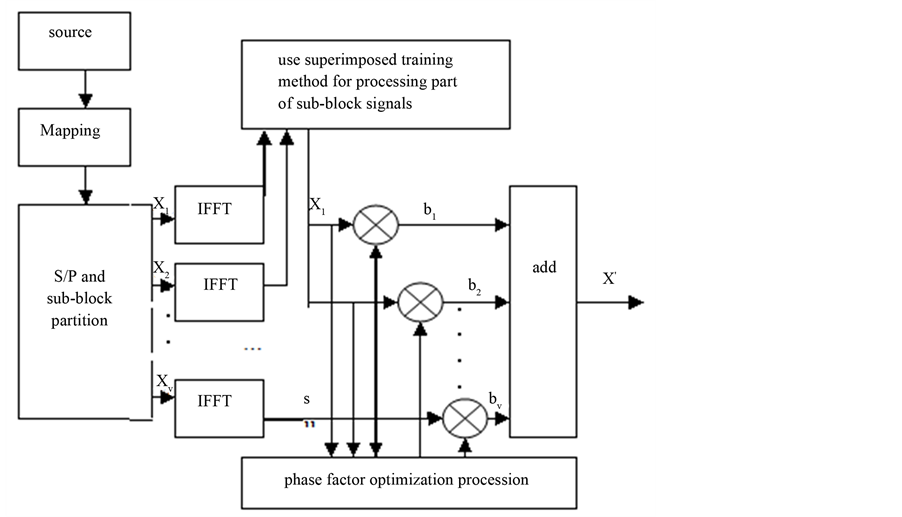
Figure 2. The flow chart of the PTS optimization scheme with superimposed training sequence.
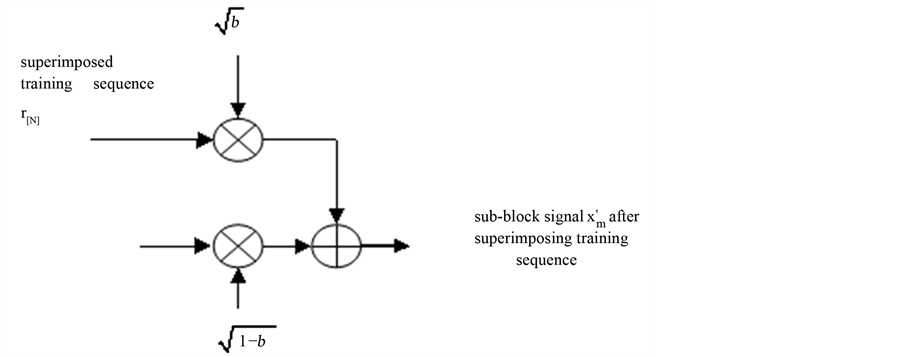
Figure 3. The procession of part signals with superimposed training sequence method.
4.2. Phase Factor Phase Optimization Procession
The processions to optimize phase factor used in PTS method in the paper as follows: implement traditional PTS method to the transmission signals, and the phase factor of the method has only two values 1 and −1. Then it searches the phase factor sequence in accordance with the following steps:
1) Set the initial value for phase factor sequence as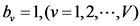 , then calculate its
, then calculate its  that corresponding to the time-domain sequence through IFFT transform, recorded as
that corresponding to the time-domain sequence through IFFT transform, recorded as , and give assignment
, and give assignment 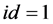 at the same time.
at the same time.
2) Assign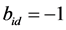 , re-calculate
, re-calculate  of the obtained sequence;
of the obtained sequence;
3) Compare the size between 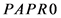 and
and 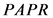 value, if
value, if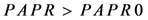 ,
,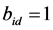 ; Otherwise, assign the
; Otherwise, assign the 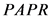 value to
value to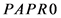 , that is
, that is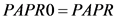 , and then set
, and then set ;
;
4) If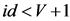 , then return to step 2); Otherwise, execute step 5);
, then return to step 2); Otherwise, execute step 5);
After such a round search, the obtained phase factor 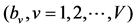 is the optimization phase factor which used in the improved PTS scheme of this paper, the distribution of the PAPR is
is the optimization phase factor which used in the improved PTS scheme of this paper, the distribution of the PAPR is  in this condition.
in this condition.
5. System Simulation and Results Analysis
All simulation results in this paper are achieved in MATLAB simulation platform, we simulate the improved scheme to validate its performance in an OFDM system simulation platform which has been set up.
In the process of simulation, the simulation parameters for the proposed scheme as follows: in OFDM system, an OFDM signal contains 128 sub-carriers, uses QPSK modulation, takes the constant sequence with length 16 as superimposed training sequence, where the phase factor 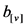 for PTS scheme is obtained from optimization process, the whole system is simulating under the Rayleigh fading channel with multi-path number 20.
for PTS scheme is obtained from optimization process, the whole system is simulating under the Rayleigh fading channel with multi-path number 20.
5.1. The Analysis of Computational Complexity for the System
As shown in Figure 4, it gives the PAPR simulation curve of the paper proposed scheme which is PTS optimization scheme with superimposed training sequence; From CCDF curve that the figure given, it can be seen that the proposed PTS scheme can reduce the PAPR performance of system more effectively comparing with the traditional PTS scheme, while the improved PTS scheme greatly reduces the computational complexity of the system.
5.2. The Analysis for the Algorithm Performance
As shown in Figure 5, it gives the PAPR simulation curve of the paper proposed scheme that’s PTS optimization scheme with superimposed training sequence under different power distribution factor b; b stands for the power distribution factor that superposition training sequence possesses in Figure 5. For some sub-block signals after IFFT transform, they are processed with superimposed training sequence method then corresponding set power distribution factor b that superposition training sequence possesses; Where the selection of the power distribution factor b that superposition training sequence possesses depends on the influence that superposition training sequence for system performance and the actual request for the system’s performance, generally we value the power distribution factor b between 0 - 0.1. As can be seen from the figure, for different power distribution factor b, the proposed scheme in this paper has small difference on improving the PAPR performance.

Figure 4. The PAPR simulation curve of the PTS optimization scheme with superimposed training sequence.
Therefore, in the respect of PAPR performance, the proposed PTS scheme in this paper could reduce computational complexity in the system, as well as it obtains good PAPR performance and the result shows it can more effectively reduce the PAPR performance comparing with the conventional PTS method.
5.3. The Analysis of the Impact That Superimposed Training Sequence on the System Performance
As shown in Figure 6, it gives the bit error rate (BER) simulation curve of the paper proposed scheme that’s PTS
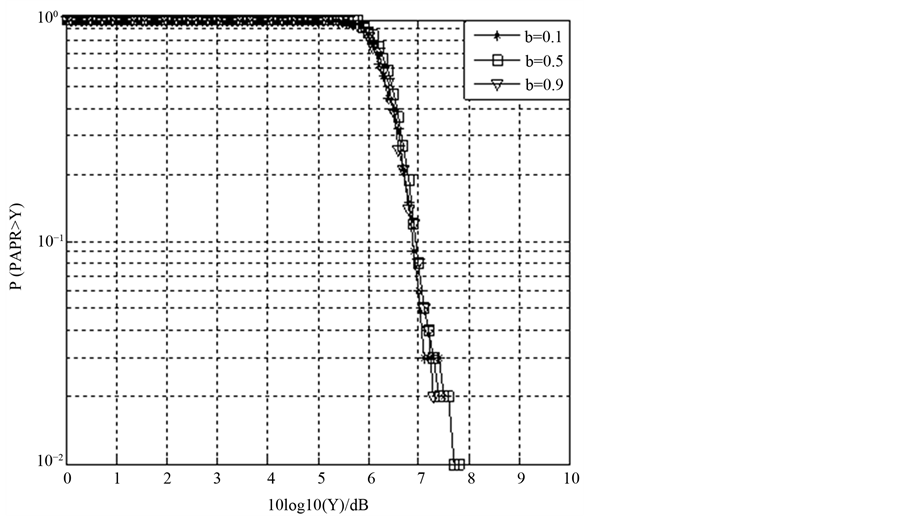
Figure 5. The PAPR simulation curve of the PTS optimization scheme with superimposed training sequence under different power distribution factor.

Figure 6. The BER simulation curve of the PTS optimization scheme with superimposed training sequence under different power distribution factor.
optimization scheme with superimposed training sequence under different power distribution factor b; b stands for the power distribution factor that superposition training sequence possesses. From the figure given by simulation curves, we can see that different power distribution factor b that superposition training sequence possesses would share different impacts on the system BER performance after using superimposed training sequence method. When value 0.1 for the power distribution factor b, the BER for the system that the proposed PTS.
Improved optimization scheme brings about is closer to the original signals’ comparing with b value respectively 0.5, 0.9. In other words, when values the power distribution factor of superimposed training sequence near 0.1, the proposed scheme in this paper has less influence on system performance relatively.
6. Conclusion
The paper introduces a new scheme using superimposed training sequence method to reduce PAPR in OFDM system. Through the simulation, it proves that the scheme can reduce the peak power of the system, thereby achieving the purpose of PAPR reduction. While the paper analyzes the influence of the power distribution factor b that superposition training sequence possesses for PAPR reduction in the OFDM system, and its effect for PAPR reduction is relatively better when we value the power distribution factor b between 0 - 0.1. Where the phase factor which is obtained from optimization process search used for the new scheme has good performance, the scheme has the advantages of much lower computational complexity and small amount of calculation comparing with a variety of methods. From the preceding discussion, we can see that the improved PTS scheme obtains better effects on both PAPR reduction and computation complexity of system than the traditional PTS method.
Acknowledgements
The authors would like to thank the National Natural Science Foundation of China (No.61310306022 and No.61072073), “1000-elite program” foundation of Sichuan Province and Signal Processing Scientific Research and Innovation Team in Southwest Petroleum University (No. 2013XJZT007), and the Science and Technology Support Foundation of Sichuan Province (No.2012FZ0021).
References
- Wu, Y.Y. and Zou, W.Y. (1995) Orthogonal Frequency Division Multiplexing: A Multi-Carrier Modulation Scheme. IEEE Transactions on Consumer Electronics, 41, 392-399. http://dx.doi.org/10.1109/30.468055
- Han, S.H. and Lee, J.H. (2005) An Overview of Peak-to-Average Power Ratio Reduction Techniques for Multicarrier Transmission. IEEE Wireless Community, 12, 56-65. http://dx.doi.org/10.1109/MWC.2005.1421929
- Wang, L. and Cao, Y. (2008) Sub-Optimum PTS for PAPR Reduction of OFDM Signals. IEEE Xplore: Electronics Letters, 44, 921-922.
- Tugnai, J.K. and Luo, W. (2003) On Channel Estimation Using Superimposed Training and First-Order Statistics. IEEE Signal Processing Letters, 7, 413-415.
- Telado, J. (2000) Multicarrier Modulation with Low PAR Applications to DSL and Wireless. Kluver Academic Publishers, Berlin.
- Zhou, G.T., Viberg, M. and Mckelvey, T. (2003) A First-Order Statistical Method for Channel Estimation. IEEE Signal Processing Letters, 10, 57-60.
- Orozco-Lugo, A.G., Lara, M.M. and Mclernon, D.C. (2004) Channel Estimation Using Implicit Trainging. IEEE Transactions on Signal Processing, 52, 240-254. http://dx.doi.org/10.1109/TSP.2003.819993
- Nair, J.P., and Raja Kumar, R.V. (2006) Channel Estimation and Equalization Based on Implicit Training in OFDM Systems. IEEE Wireless and Optical Communications Networks, Bangalore.
- Tugnait, J.K. and Meng, X.H. (2006) On Superimposed Training for Channel Estimation: Performance Analysis, Training Power Allocation, and Frame Synchronization. IEEE Transactions on Signal Processing, 54, 752-763. http://dx.doi.org/10.1109/TSP.2005.861749
- He, S.C. and Tugnait, J.K. (2008) On Doubly Selective Channel Estimation Using Superimposed Training and Discrete Prolate Spheroidal Sequence. IEEE Transactions on Signal Processing, 56, 3214-3228.
- Nair, J.P. and Raja Kumar, R.V (2008) An Iterative Channel Estimation Method Using Superimposed Training in OFDM Systems. IEEE VTC conference, Calgary, 21-24 September 2008, 1-5.

