Communications and Network
Vol. 4 No. 4 (2012) , Article ID: 25020 , 16 pages DOI:10.4236/cn.2012.44036
A Novel Offline PLI-RWA and Hybrid Node Architecture for Zero Blocking and Time Delay Reduction in Translucent Optical WDM Networks
Division of ECE, Netaji Subhas Institute of Technology, New Delhi, India
Email: sridhar@nmsu.edu, sps_nsit@yahoo.co.uk
Received August 17, 2012; revised September 16, 2012; accepted October 19, 2012
Keywords: Translucent WDM Network; Signal Quality Aware Routing; Regenerator Placement; Wavelength Converter Placement; PLI-RWA
ABSTRACT
In this paper, we contrive a model that underpins the offline Physical Layer Impairment-Routing and Wavelength Assignment (PLI-RWA) issue in translucent networks. We introduce an innovative PLI-Signal Quality Aware RWA (PLI-SQARWA) algorithm that a) guarantees zero blocking due to signal degradation and wavelength contention and b) aims at minimizing the total required number of network components i.e. regenerators and all-optical wavelength converters (AOWCs). Further, in view of reducing the time delay due to optical-electrical-optical (OEO) conversions, we propose a novel electro-optical hybrid translucent node architecture. We show that PLI-SQARWA outperforms a recent heuristic for RWA and regenerator placement (RP) in terms of capital expenditure (CapEx) and time delay; while demonstrating superior blocking performance at all traffic loads. In addition, at high traffic loads, PLI-SQARWA also starts to provision savings on operational expenditure (OpEx). We proceed to the performance comparison of network equipped with the proposed hybrid node and existing translucent and transparent node architectures. The results clearly show that use of the hybrid node incurs less time delay at a similar blocking performance shown by nodes which use OEO conversion for both, regeneration and/or wavelength conversion. The results presented also highlight the significance of equipping the PLI-RWA routing phase with signal quality awareness in order to reduce the network component count and the use of AOWCs to minimize time delay due to OEO conversions.
1. Introduction
Routing and wavelength assignment (RWA) is vital for efficient wavelength division multiplexed (WDM) network design [1]. In recent years, realizing that, de-facto, signal transmission is significantly affected by physical layer impairments (PLIs) inherent in the fiber and that a cross-layer design is requisite in both, a transparent and a translucent WDM network, extensive research has been conducted on the issue of physical layer impairment-RWA (PLI-RWA) [2].
The PLI-RWA approaches delineate rules and strategies for lightpath establishment and primarily aim at minimizing the number of rejected requests due to either capacity or QoT limitations. Existing PLI-RWA algorithms are faced with two cases wherein; a) traffic demands are known a-priori and hence, decisions are taken offline using static PLI-RWA or b) traffic demands arrive in a dynamic fashion and decisions are made online using dynamic PLI-RWA [3]. In literature, investigations on PLI-RWA mainly focus on a) selecting regeneration sites and number of regenerators to be deployed on these sites (regenerator placement (RP) problem) and/or b) given sparse placement of regenerators, selecting which of these regenerators to use (regenerator allocation (RA) problem) [4].
The authors in [5] proposed a RP and constraint-based routing (RP-CBR) approach which aims at limiting regeneration to some network nodes while considering the impact of PLIs on quality of transmission (QoT). The proposed algorithm relies on a topology driven strategy and the result clearly show that RP-CBR is suitable for on-the-fly network operations and significantly decreases the blocking probability.
Authors in [6] proposed an improved version of the RP-CBR algorithm [5]. In the amended algorithm, termed as RP-CBR+, different RP combinations are investigated and the first QoT admissible combination providing least number of regenerators is retained as the solution. Results show that for all traffic load values, RP-CBR+ presents non-zero blocking while using the same number of regenerators as RP-CBR algorithm.
The Lightpath Establishment with RP (LERP) algorithm [7] finds k-alternate shortest paths (k-SPs) in its first phase and performs RP in the second phase, after estimating bit error rate (BER) of lightpaths comprising of solution of the first phase. LERP simultaneously minimizes the amount of rejected traffic demands and required regenerators. The results clearly underline efficiency of LERP and indicate that the benefits obtained in terms of demand rejection and number of regenerators is due to a larger combinatoric in lightpath RWA and RP.
Authors in [8] proposed the Cross-Optimization for RWA and RP (COR2P) heuristic which minimizes both, the number of required regenerators and regeneration sites. The authors also introduced an original cost function contributing to capital and operational expenditures (CapEx/OpEx) optimization and further, compared COR2P to RP-CBR+ [6] and LERP [7]. The results show that for low traffic loads, COR2P does not reject any demands while RP-CBR+ presents non-zero blocking; whereas for high traffic loads, COR2P presents a blocking which is 100 times lower than that shown by RP-CBR+. Further, for identical scenarios at low or moderate traffic loads, in comparison to LERP, COR2P reduces both, the total number of regenerators and regeneration sites. The results also reveal the major drawbacks of COR2P viz., at high traffic loads, blocking performance maintained by COR2P is at the expense of increased number of required regenerators and at such loads, COR2P’s methodology of QoT-dependent ordering of demands is not very effective.
The aforementioned translucent network design studies are founded on traditional shortest path (SP) routing protocols since, in general, among all the routes, between a pair of nodes, SP algorithm sufficiently achieves the desired performance. However, since traffic characteristics and resource availability are not a part of its routing decisions, SP approach contributes significantly to network congestion due to its single-path routing, and also comes short of provisioning efficient network utilization that may lead to resource blocking, which as opposed to physical-layer blocking, occurs due to rejection of a connection owing to the unavailability of wavelengths. Further, owing to the heterogeneity of real networks and existence of non-uniform PLIs within such networks, SP may not always demonstrate the best signal quality. Hence, it may occur that any other route(s), apart from SP, exhibits better signal quality, thus requiring fewer intermediate regenerators and in turn lowering the overall network cost.
This can be justified by considering the simple topology shown in Figure 1 wherein; a request originates at the source node (N1) demanding connection till the destination node (N6). The weight on each link corresponds to the transmission delay and hence, among the different possible routes between N1 and N6, route N1-N2-N3-N6 is the SP. Let all-optical wavelength converters (AOWCs) be provisioned for wavelength contention resolutions and let the signal quality threshold (i.e. Q-factor threshold (Qth)) be defined as the value below which the signal quality is unacceptable hence, necessitating regeneration. We assume that each link supports three wavelengths denoted as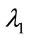 ,
,  and
and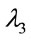 , with the wavelengths indicated on each link corresponding to a free (available) wavelength.
, with the wavelengths indicated on each link corresponding to a free (available) wavelength.
It can be observed from the figure that, if the SP is used for serving the request, then the demand will be blocked since wavelength continuity is not possible on link N3-N6 due to the unavailability of wavelength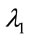 . Deploying an AOWC at node N3 for wavelength conver-
. Deploying an AOWC at node N3 for wavelength conver-

Figure 1. A simple optical network.
sion (WC) to 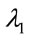 on one hand will relax the wavelength continuity constraint but on the other hand, will increase the network cost. Further, owing to the PLIs, signal quality falls below the pre-defined threshold value on links N2-N3 and N3-N6 which necessitates regenerator deployment at nodes N2 and N3 respectively, further increasing the network cost. On the other hand, if route N1-N4- N3-N6 is used, it can be observed that in order to serve the request, the path requires same amount of network components (i.e. two regenerators at nodes N4 and N3 respectively and an AOWC for WC to
on one hand will relax the wavelength continuity constraint but on the other hand, will increase the network cost. Further, owing to the PLIs, signal quality falls below the pre-defined threshold value on links N2-N3 and N3-N6 which necessitates regenerator deployment at nodes N2 and N3 respectively, further increasing the network cost. On the other hand, if route N1-N4- N3-N6 is used, it can be observed that in order to serve the request, the path requires same amount of network components (i.e. two regenerators at nodes N4 and N3 respectively and an AOWC for WC to 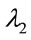 at node N3) and demonstrates a similar cost as the SP. Further, paths N1-N2-N5-N6 and N1-N4-N5-N6 are observed to require lesser number of network components (i.e. one regenerator at nodes N2 and N4 respectively and an AOWC for WC to
at node N3) and demonstrates a similar cost as the SP. Further, paths N1-N2-N5-N6 and N1-N4-N5-N6 are observed to require lesser number of network components (i.e. one regenerator at nodes N2 and N4 respectively and an AOWC for WC to  and
and  at nodes N5 and N4 respectively) compared to the SP. Hence, these routes are the least cost paths as they demonstrate better signal quality among all other network routes thus, requiring fewer intermediate regenerators. Among the two least cost paths, if SP strategy is now applied in order to choose the candidate route, then path N1-N4-N5-N6 will be chosen since its total link weight is lower than that of the route N1-N2- N5-N6. Therefore, outcome of such a routing strategy, which is summarized in Table 1, is a candidate path that requires fewest amounts of regenerators and hence demonstrates least cost. Thus, in addition to simple SP routing, it is judicious to formulate an algorithm that selects candidate routes based on best signal quality.
at nodes N5 and N4 respectively) compared to the SP. Hence, these routes are the least cost paths as they demonstrate better signal quality among all other network routes thus, requiring fewer intermediate regenerators. Among the two least cost paths, if SP strategy is now applied in order to choose the candidate route, then path N1-N4-N5-N6 will be chosen since its total link weight is lower than that of the route N1-N2- N5-N6. Therefore, outcome of such a routing strategy, which is summarized in Table 1, is a candidate path that requires fewest amounts of regenerators and hence demonstrates least cost. Thus, in addition to simple SP routing, it is judicious to formulate an algorithm that selects candidate routes based on best signal quality.
In this paper, we formulate a framework that corroborates the offline version of PLI-RWA problem in translucent networks where, given a network topology and the estimate of traffic demands, both, the static PLI-RWA and the RP problems are solved jointly.
The contributions of this paper are twofold:
• An innovative PLI-Signal Quality Aware RWA (PLISQARWA) algorithm is introduced that 1) guarantees zero blocking due to signal degradation and wavelength contention, and 2) minimizes the total required network components by a) considering signal quality to route connections over paths requiring fewest numbers of regenerators, and b) maximally using placed regenerators for wavelength conversion (WC) before resorting to AOWCs, which in recent years have been demonstrated to be practical [9].
• An electro-optical hybrid translucent node architecture [10] is proposed in view of a latency efficient technology capable of delivering a cost effective implementation suitable for large scale deployment. The proposal is motivated from the fact that for next generation optical networks, a) OEO conversions will be the primary bottleneck [11], and b) provisioning demands with the least possible network latency will be necessitated [12].
The rest of the paper is organized as follows. In Section 2, we describe the network model and the performance evaluation metric used in our study. Section 3, describes details of the PLI-SQARWA algorithm for translucent network design and further, presents performance comparison results of PLI-SQARWA and COR2P. In Section 4, we present details of the proposed hybrid translucent node architecture. We then proceed to performance comparison of the network equipped with the hybrid node and node architectures existing in literature. Finally, Section 5 presents the conclusion of this study.
2. Network Model
Considering the typical configuration of a translucent network, Figure 2 describes within such a network, the architecture of a generic node equipped with a pool of 3R regenerators. In such architecture, the switching node consists of an optical cross connect (OXC) connected to a regenerator pool linked via transponders. Signals which fulfill the QoT requirements and do not require WC, transit through the node optically without undergoing any OEO conversions. On the other hand, if signal quality does not meet the QoT requirements and/or wavelength continuity constraint is not satisfied, the signal is regenerated and/or wavelength converted (assuming that regenerators also have WC capability) and is then re-injected into the switching fabric to join the next node along its route. We assume fiber links to be deployed using standard non-zero dispersion shifted fibers and erbium-doped fiber amplifiers (EDFAs) to be deployed every span (typically every 80 Km) in order to recover from fiber losses.
Existing studies use BER as the metric to evaluate the

Table 1. Summary of the routing strategy.
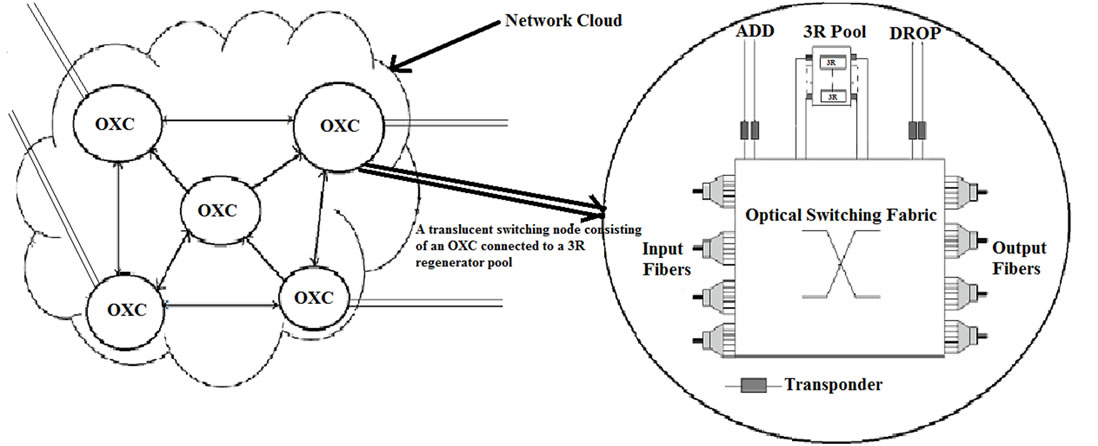
Figure 2. Configuration of a translucent WDM network.
quality of a lightpath as it captures the effects of all impairments. The BER is given as [13]
 (1)
(1)
where Q represents the Quality-factor (Q-factor) which is given as [13]
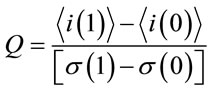 (2)
(2)
In Equation (2), 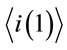 and
and 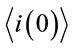 representing the mean values of current
representing the mean values of current  and
and , and
, and  and
and  representing the variance values for bit “1” and bit “0” respectively are given as [14]
representing the variance values for bit “1” and bit “0” respectively are given as [14]
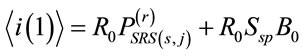 (3)
(3)
 (4)
(4)
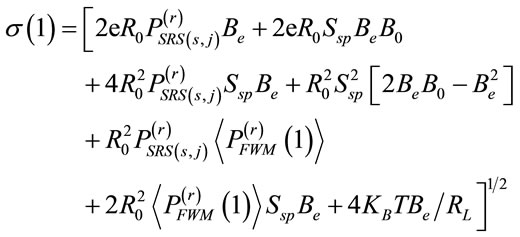 (5)
(5)
and
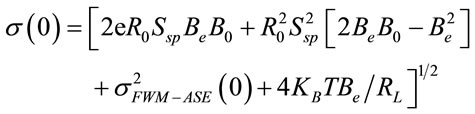 (6)
(6)
where  represents the signal power at the jth (center) receiver at frequency fj, Ssp the power spectral density of ASE noise, B0 the optical filter bandwidth, R0 the responsivity, e the electron charge, KB the Boltzmann constant, Be the electrical bandwidth of the receiver, T the receiver temperature and RL the load resistance.
represents the signal power at the jth (center) receiver at frequency fj, Ssp the power spectral density of ASE noise, B0 the optical filter bandwidth, R0 the responsivity, e the electron charge, KB the Boltzmann constant, Be the electrical bandwidth of the receiver, T the receiver temperature and RL the load resistance.
In the current study, we consider an Intensity Modulation/Direct Detection (IM/DD) system based on on-off keying (OOK) modulation and the lightpath QoT evaluation is based on the realistic estimation of signal quality considering the simultaneous impact of three effects viz. stimulated Raman scattering (SRS), four wave mixing (FWM) and amplified spontaneous emission (ASE) noise. We use the Q-factor model from our previous work [14] in order to evaluate blocking probability (BP), which is the performance metric used in our study. BP is defined as the probability that a connection cannot be accepted and is given as
 (7)
(7)
When the receiver Q-factor associated with a connection request is below the threshold, the connection is blocked.
3. Translucent Network Design
In this section we describe the translucent network design problem statement which can be stated as follows:
Given
a) A network topology;
b) A set of available wavelengths per fiber link;
c) The offered traffic comprising of a set of static demands;
d) An admissible Q-factor threshold value i.e. Qth.
Objective
Find a candidate route that uses fewest numbers of regenerators and assign wavelength(s) on each of the links along the found lightpath route. For wavelength contention resolutions, ensure the maximal use of WC capability of placed regenerators, before deploying AOWCs, in effect, minimizing the required number of total network components. Consequently, the aim of translucent network design is to satisfy maximum number of connection requests (i.e. obtaining lowest possible blocking) simultaneously reducing the overall network cost.
Subject to
i) Signal quality constraint: For any network lightpath, at its destination node, the corresponding Q-factor value must not fall below the threshold value.
ii) Delay constraint: For any network lightpath, the latency incurred must not exceed a given timeout Tmax, which is assumed to be user adjustable.
iii) Minimum cost constraint: For any network lightpath, minimum number of components must be deployed along the route i.e. minimum overall cost must be incurred along the route.
3.1. PLI-Signal Quality Aware RWA (PLI-SQARWA) Algorithm
In this sub-section, we present details of the PLISQARWA algorithm that comprises of three phases. In order to improve the scalability of our approach, we decompose the problem into the RWA and wavelength converter placement (WCP) and the RP sub-problems. The PLI-SQARWA flow-chart is described by diagram in Figure 3.
Phase I. Signal Quality Aware Routing (SQAR) Algorithm
In Phase I, PLI-SQARWA employs the signal quality aware routing (SQAR) algorithm that selects a candidate route requiring fewest numbers of regenerators. The SQAR algorithm comprises of the following three steps:
Step 1. Consider the Q-factor values of individual links and summate them to find the total Q-factor as follows
 (8)
(8)
where N represents the total number of links between the source and destination,  the total Q-factor of a lightpath and Qx the Q-factor value on xth link of the lightpath. Using evaluated total Q-factors of all the lightpath routes, find a route termed as “Best Path” that has the “best (highest)” Q-factor and go to Step 2.
the total Q-factor of a lightpath and Qx the Q-factor value on xth link of the lightpath. Using evaluated total Q-factors of all the lightpath routes, find a route termed as “Best Path” that has the “best (highest)” Q-factor and go to Step 2.
Step 2. Evaluate the SPs, considering that apart from finding Best Paths, aim of SQAR algorithm like any other routing algorithm is also to find a route which demonstrates the least distance and go to Step 3.
Step 3. Compare Best Paths with SPs in terms of number of regenerators required for each path by using the RP algorithm detailed in phase III and select the path that uses fewest numbers of regenerators as the candidate route. In case when both, Best Path and SP use the same number of regenerators, prefer SP over the Best path and go to Phase II.
Phase II. Wavelength Assignment (WA) and Wavelength Converter Placement (WCP) Algorithm
In Phase II, the carried lightpaths from phase I are sequentially processed. For each lightpath, the first-fit WA (FF-WA) technique [1] is used to assign wavelengths and when wavelength continuity is not possible, we resort to wavelength converters. It must be noted that in view of reducing the total number of required network components and hence minimizing the overall network cost, in this phase, before deploying any AOWCs to resolve wavelength contentions, our aim is to maximally use the WC capability of regenerators that will be required to be appropriately placed along lightpaths which demonstrate non-admissible QoT. Based on the number of placed regenerator(s), such non-admissible QoT lightpaths will be divided into section(s) and between any two consecutive sections, the existence of a regenerator with WC capability will imply that wavelength continuity for such lightpaths will have to be ensured only on each section. On the other hand, for lightpaths demonstrating admissible QoT, regenerators will not be required to be placed along the lightpath and thus, such lightpaths will consist of only one section (i.e. from source node to destination node).
We assume that all the wavelengths (λ) and nodes (ni) are numbered consecutively in the order λ1, λ2, ···, λW and n1, ···, ni, ···, nn for 1 < i < n, respectively, where W is the same maximum available wavelength numbers on each link, n1 and ni represent the source and destination nodes of a lightpath route respectively. The WA and WCP process comprises of the following seven steps:
Step 1. Initially, consider 1st node (n1) of the candidate route as the source node and go to Step 2.
Step 2. Starting from source node, scan all the fiber links along the path and check if any common wavelength is available along all the links of the route. If any such wavelength exists, assign one with the smallest index (say for e.g. λ1) to the lightpath. Starting from the source node, check Q-factor of the route and if the route demonstrates Q-factor below the pre-defined threshold value, go to Phase III in order to place regenerators along the route appropriately, otherwise terminate. Else, go to Step 3.
Step 3. If no common wavelength exists along the lightpath route, find the node from where a common wavelength is not available, considering that a common wavelength could be available on all the links up to an intermediate node ni, for 1 < i < n, along the route or starting from the source node itself, no common wavelength could be available along the route. Assign current node as the source node and go to Step 4.
Step 4. Evaluate Q-factor at the next node. If Q-factor value at next node is below the threshold value, place a regenerator at the current node (i.e. source node) and in addition to regeneration, use the placed regenerator for WC to λ1 and go to Step 6. Else, go to Step 5.
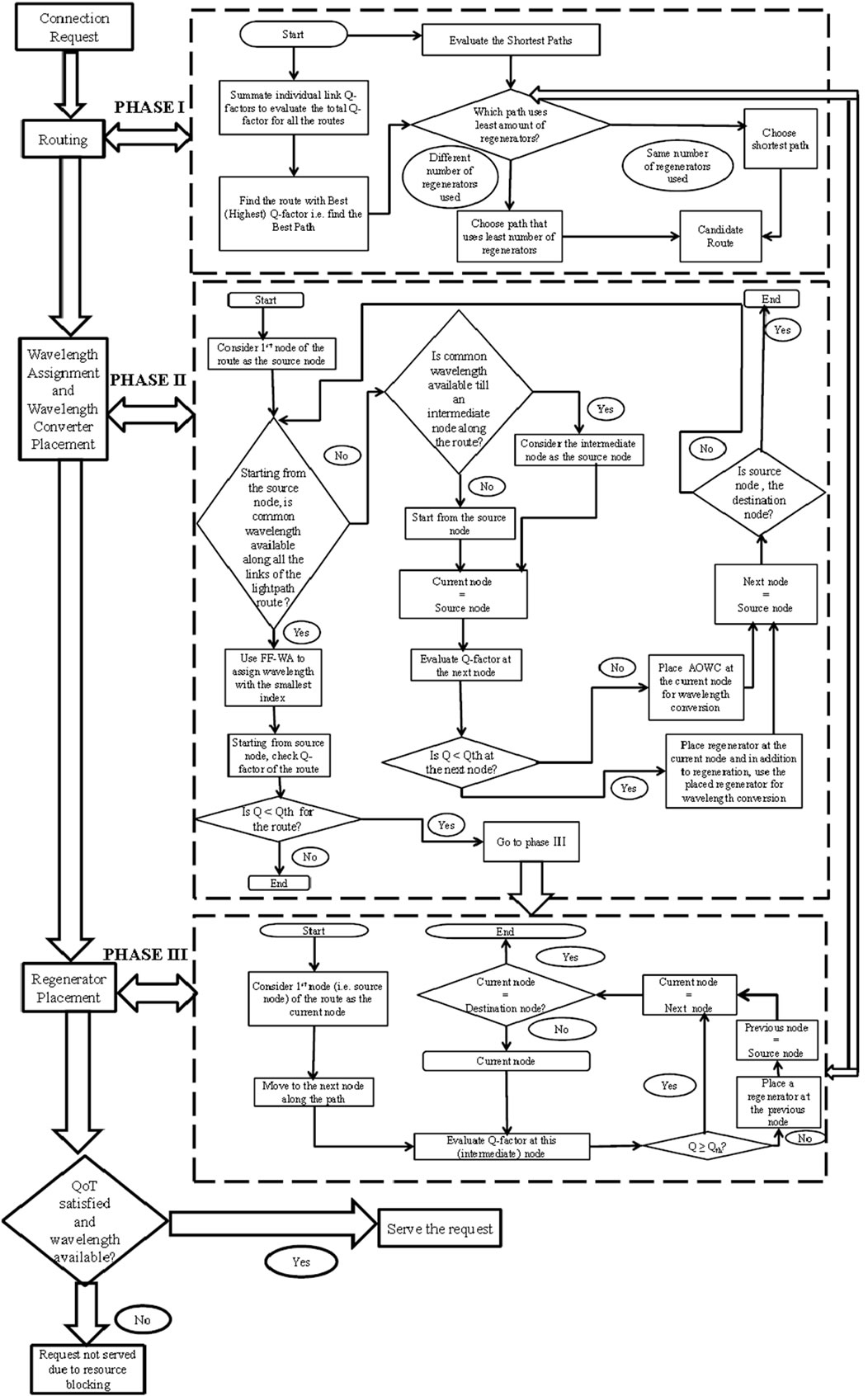
Figure 3. PLI-SQARWA synopsis.
Step 5. If Q-factor value at next node is above the threshold value, a regenerator is not required at the current node (i.e. source node). Hence, in order to satisfy the WC requirement, deploy an AOWC at the current node for WC to λ1 and go to Step 6.
Step 6. Assign next node along the lightpath route as the source node and go to Step 7.
Step 7. Check if the source node is the destination node. If yes, then terminate, else go to Step 2.
Phase III. Regenerator Placement (RP) Algorithm
In this phase, PLI-SQARWA applies an efficient RP algorithm that minimizes number of placed regenerators over a lightpath. The RP algorithm comprises of the following seven steps:
Step 1. Initially, consider source node i.e. 1st node (n1) of the candidate route as current node and go to Step 2.
Step 2. Move to next node along the route and evaluate Q-factor at this node. Continue and go to Step 3.
Step 3. If evaluated Q-factor at the current node is higher than or equal to the pre-defined threshold value i.e. if a regenerator is not required, then go to Step 6. Else go to Step 4.
Step 4. If current node demonstrates Q-factor less than the pre-defined threshold value, place a regenerator at the preceding node and go to Step 5.
Step 5. Assign the node where the regenerator is placed as the source node and go to Step 6.
Step 6. Assign next node as current node. Check if current node is the destination node and go to Step 7.
Step 7. If current node is the destination node, then terminate, else, evaluate Q-factor at this node and go to Step 3.
3.2. Performance Comparison of PLI-SQARWA and COR2P
In this sub-section, we first precise our simulation environment and characteristics and then present the performance comparison results between the two algorithms: PLI-SQARWA and COR2P.
3.2.1. Simulation Assumptions
We investigate the 18 node NSFNET network as depicted in Figure 4. The network is assumed to have 16 wavelengths per fiber link with 50 GHz channel spacing and each carrying a capacity of 10 Gbps.
In the current study, Q-factor threshold takes the value of 6 which corresponds to a BER of 10–9. We consider permanent lightpath demands (PLDs) which are offline requests that consist of pre-known connection demands with data rate equal to full capacity of the wavelength channel and are thus established through a full lightpath. For the simulations, other transmission system parameters are adopted from our previous studies [10,14].
3.2.2. Simulation Results
This sub-section analyses the performance of PLISQARWA by means of comparison with COR2P algorithm. The COR2P algorithm has been executed for range of different values of a set of specific parameters that adjust in order to determine how the solution space is explored heuristically. The results shown in this paper correspond to those parameters which provided the best performances and their values are reproduced so as to allow the results to be repeatable: 1) for computation of k-SPs associated to each demand, the value of k is set to 5; 2) COR2P cost function is simplified by setting the ratio CC/CO to 1, where CO is the unitary OpEx cost corresponding to the cost for managing a single active regenerator at a node and CC is the unitary CapEx cost corresponding to carrier’s investment for installing a regeneration pool at a node; and 3) simulations cover 6 traffic loads that range from 100 to 600 connection demands and for each load, 10 static traffic matrices are generated stochastically according to uniform distribution. Thus, the presented results are average values of ten simulation runs.
In order to appropriate the investigation of number of non-accepted requests by both algorithms, for all traffic load values and comparison of the two algorithms, we chose simulation parameters such that cases admitting a solu-
Figure 4. 18 node NSFNET network.
tion did not guarantee 0% of resource blocking. In Figure 5, variation of BP with traffic load has been plotted for both algorithms. It can be observed from the figure that:
1) For low traffic loads, both, COR2P and proposed PLI-SQARWA show zero BP. This can be attributed to the fact that for both the algorithms:
i) Regeneration and WC is provisioned which eradicates blocking due to signal degradation and wavelength contention respectively, and
ii) Owing to low loads, the network is not overloaded and ample resources are available.
2) For intermediate and high traffic loads, resource blocking starts to occur for both the algorithms. It can be observed that COR2P shows higher resource blocking compared to the proposed PLI-SQARWA algorithm. This can be attributed to the fact that:
i) For COR2P, as the load increases, owing to the use of k-SP routing, higher network overloading occurs which results in higher resource blocking, and
ii) For PLI-SQARWA, rather than the SPs, majority of the Best Paths are selected as the candidate routes which leads to larger resources being available even at higher traffic loads. The low resource blocking observed in the case of PLISQARWA is due to the selection of few SP routes as candidate routes. It can also be observed from the figure that if only Best Paths are used for routing, then zero resource blocking is achieved.
It can also be deduced from Figure 5 that for low loads, both the algorithms accept all demands whereas, between moderate and high loads, both the algorithms are able to maintain acceptable blocking.
Table 2 presents the average total number of required components (i.e., regenerators + wavelength converters) for both the algorithms at different load values. In the
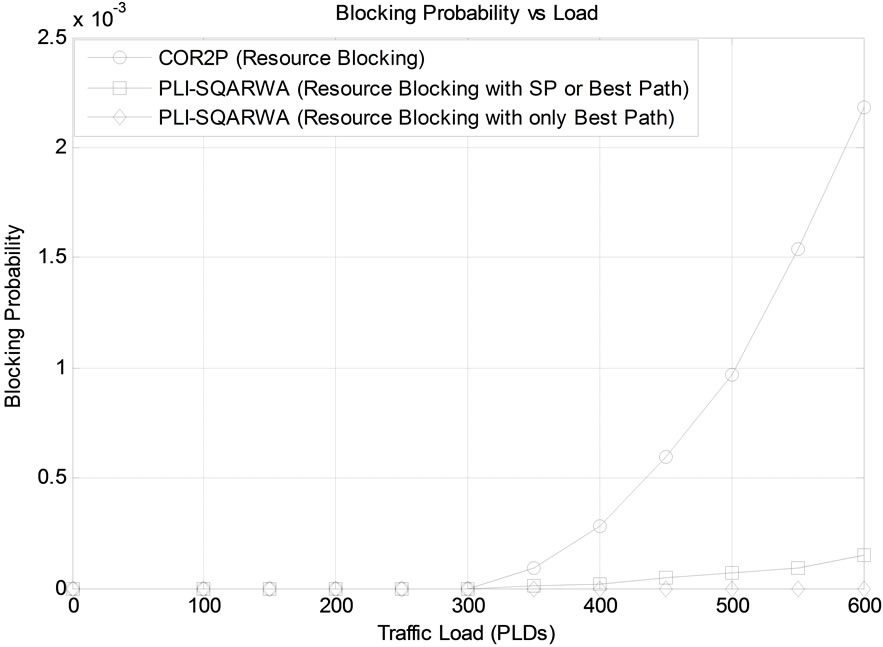
Figure 5. PLI-SQARWA versus COR2P: blocking probability versus traffic load.
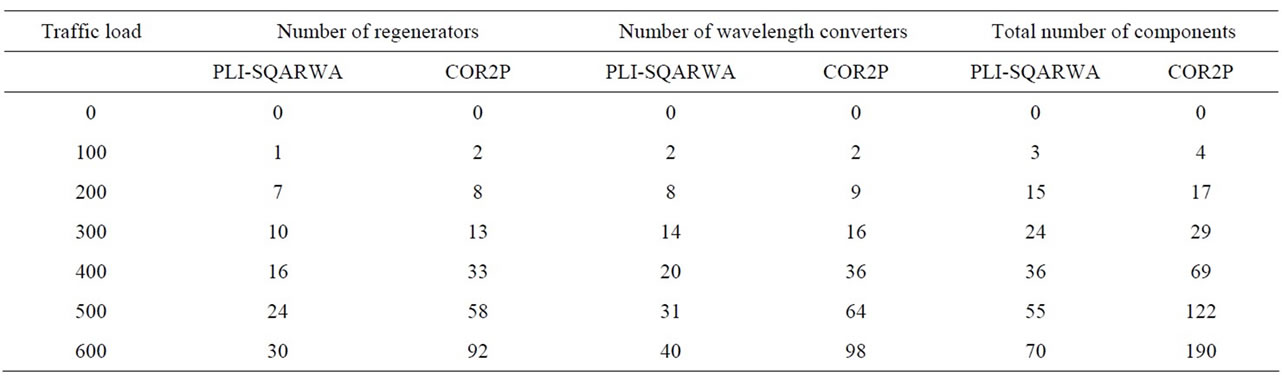
Table 2. Average total number of components for PLI-SQARWA and COR2P.
table, the column corresponding to the number of wavelength converters implies that for COR2P, regenerators have been used for WC whereas for PLI-SQARWA, AOWCs have been used for WC. It can be observed from the table that
1) For low traffic loads, both the algorithms require approximately the same number of components;
2) For moderate to high values of load, COR2P requires larger number of components (i.e., regenerators) compared to PLI-SQARWA (regenerator + wavelength converter). Thus, blocking performance shown by COR2P at moderate and high loads (as shown in Figure 5), compared to PLI-SQARWA, is at the price of increased number of required components. The increase in number of total components is by a factor of:
i) 1.9 when the load is 400
ii) 2.2 when the load is 500 and
iii) 2.7 when the load is 600.
Hence, as the traffic load increases, PLI-SQARWA shows larger benefits in terms of CapEx compared to COR2P.
In view of saving on OpEx, it must be noted that in addition to minimizing the number of regenerators, aim of COR2P is also to concentrate the regenerators at the sites and, if required, allow more freedom for RP at new sites [8]. On the other hand, PLI-SQARWA does not target regenerator concentration but aims at utilizing fewest number of network components simultaneously restricting RP to the sites that it determines in phase III. In order to investigate the variation of OpEx with load, we plotted the component distribution for both the algorithms at 400, 500 and 600 demands as shown in Figures 6-8 respectively. From Figure 6, it is worth noting that under COR2P for 400 demands, the effective regeneration sites remain the same as pre-defined sites initially evaluated by the COR2P algorithm [6,8]. On the other hand, as shown in Figures 7 and 8, for 500 and 600 demands respectively, COR2P begins to deploy regenerators outside the a-priori sites i.e. it adds isolated regenerators at certain sites (see nodes 8 and 10 in Figure 7 and nodes and 1, 5, 9 and 15 in Figure 8). In other words, as the load increases, COR2P provisions the addition of components at certain sites, thus increasing both, CapEx and OpEx. It can also be observed from the plots that for every increase in the load value, PLI-SQARWA introduces lesser number of new sites for component deployment. Specifically, for every increase in the load value between 400 and 600 demands, over the ten matrices and simulation runs, PLI-SQARWA adds only one average number of effective sites whereas, COR2P increases the effective sites in the order of power of 2. Hence, it can be inferred that as the traffic load increases, difference in OpEx cost of the two algorithms decreases.
Keeping in view that both, CapEx and OpEx govern the overall network cost, in order to perform a cost comparison between both algorithms, we adopted a linear capital cost (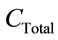 ) that comprises of two different sources of cost: a unique CapEx (
) that comprises of two different sources of cost: a unique CapEx ( ) arising due to hardware cost of network components (i.e. regenerators and AOWCs) and an OpEx (
) arising due to hardware cost of network components (i.e. regenerators and AOWCs) and an OpEx (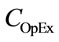 ) arising due to operation and supervision cost of the installed components. Hence, the total cost in terms of CapEx and OpEx is given as
) arising due to operation and supervision cost of the installed components. Hence, the total cost in terms of CapEx and OpEx is given as
 (9)
(9)
Let set  denote the total number of network nodes and further, assuming that (a) finite set
denote the total number of network nodes and further, assuming that (a) finite set  de
de

Figure 6. PLI-SQARWA versus COR2P: component distribution at 400 demands.
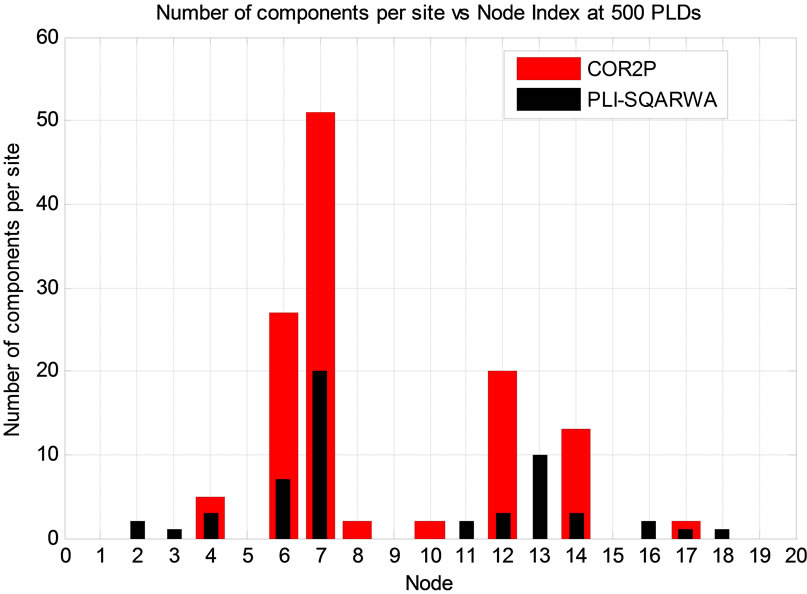
Figure 7. PLI-SQARWA versus COR2P: component distribution at 500 demands.
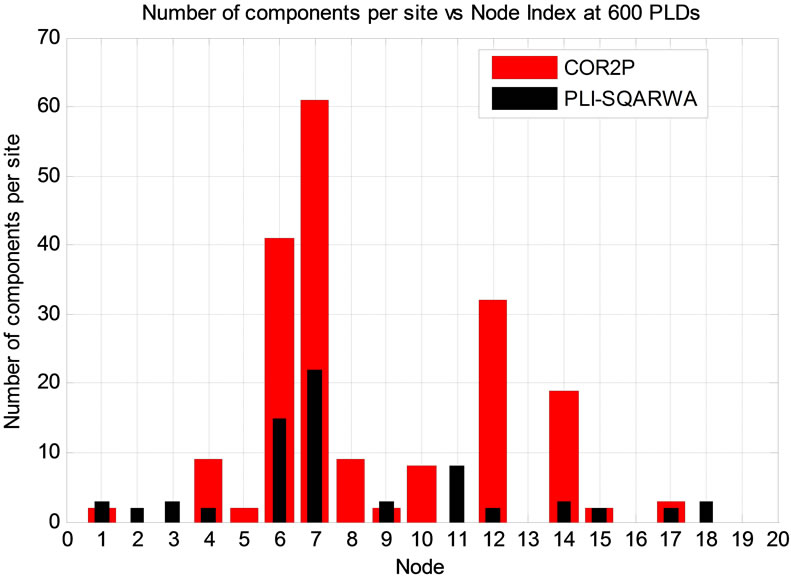
Figure 8. PLI-SQARWA versus COR2P: component distribution at 600 demands.
fines all the wavelength converters and for each wavelength converter,  at any node,
at any node, 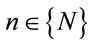 there is a hardware cost,
there is a hardware cost, 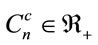 where
where 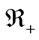 denotes the set of all positive real numbers and (b) finite set
denotes the set of all positive real numbers and (b) finite set  defines all the regenerators and for each regenerator,
defines all the regenerators and for each regenerator,  at any node,
at any node, 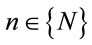 there is a hardware cost,
there is a hardware cost,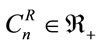 ; the CapEx cost is given as
; the CapEx cost is given as
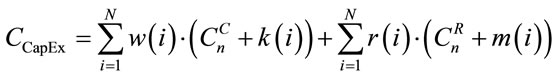 (10)
(10)
where 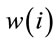 and
and  are number of wavelength converters and regenerators placed at node i respectively, while
are number of wavelength converters and regenerators placed at node i respectively, while  and
and 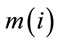 are the installation costs of an AOWC and a regenerator at node i respectively. In Equation (10),
are the installation costs of an AOWC and a regenerator at node i respectively. In Equation (10),
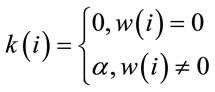 (11)
(11)
and
 (12)
(12)
where 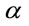 and
and  represent a fixed installation cost of an AOWC and a regenerator respectively.
represent a fixed installation cost of an AOWC and a regenerator respectively.
In the simulation, we have assumed that cost of an OEO regenerator is five times the cost of an AOWC since an optical port is five times less expensive than an electrical port [15]. The capital cost is evaluated in terms of monetary unit (m.u.) which is defined as the cost of a single AOWC and it is assumed that the installation of an AOWC and a regenerator incurs the same cost of half m.u. Further, we consider a supervision staff per component site and that maintenance/supervision required for both, a regenerator and an AOWC incurs the same cost of 1 m.u. The capital cost has been evaluated for a fixed value of Q = 6 i.e., the obtained results correspond to the cost values required to maintain the minimum acceptable QoT. It must be noted that for both algorithms, costs required in the evaluation of capital cost form the input parameters for simulation and hence, the cost evaluation approach in the current study does not depend on the prices of any specific manufacturer/provider or cost model. The capital cost for COR2P has been evaluated using the CapEx and OpEx cost functions presented in [8].
Figure 9 plots, for both algorithms, the variation of capital cost, CapEx and OpEx with traffic load. It can be observed from the figure that
1) At low traffic loads, capital cost of COR2P is lower compared to that of PLI-SQARWA. This can be attributed to the fact that at such loads CapEx cost of both algorithms is approximately the same whereas, owing to the concentration of regenerators at the sites, OpEx cost of COR2P is lower than that of PLISQARWA. Hence, difference in OpEx cost of the two algorithms, dictates the nature of capital cost deviation.
2) At moderate loads, compared to PLI-SQARWA, capital and CapEx costs corresponding to COR2P start to increase rapidly. This is due to the fact that
i) As the load increases, COR2P starts to deploy components outside the a-priori sites i.e., it provisions the use of increased number of components. Specifically, at 405 PLDs, the CapEx cost curves for both algorithms crossover and beyond this load, compared to PLI-SQARWA, CapEx cost due to COR2P increases at a much higher rate owing to the use of larger number of components.
ii) With increase in load, the difference in OpEx cost of both algorithms decreases till at approximately 450 PLDs, the OpEx curves for both algorithms also crossover. Hence, the rapid increase in CapEx and decline in OpEx difference between the two algorithms leads to much higher increase in capital cost of COR2P compared to PLI-SQARWA. Specifically, at 408 PLDs, the capital cost curves of both algorithms crosses over, beyond which the capital cost of COR2P increases rapidly compared to that of PLI-SQARWA.
iii) At higher values of traffic, it is observed that PLI-SQARWA saves on both, CapEx and OpEx and hence, the capital cost. This is due to the fact that at such loads, unlike COR2P, PLI-SQARWA does not provision the deployment of components outside the a-priori sites i.e., PLI-SQARWA is able to maintain the desired QoT while using lesser number of components. The largest capital cost saving shown by PLI-SQARWA in comparison to COR2P is approximately 89 m.u. at 600 PLDs.
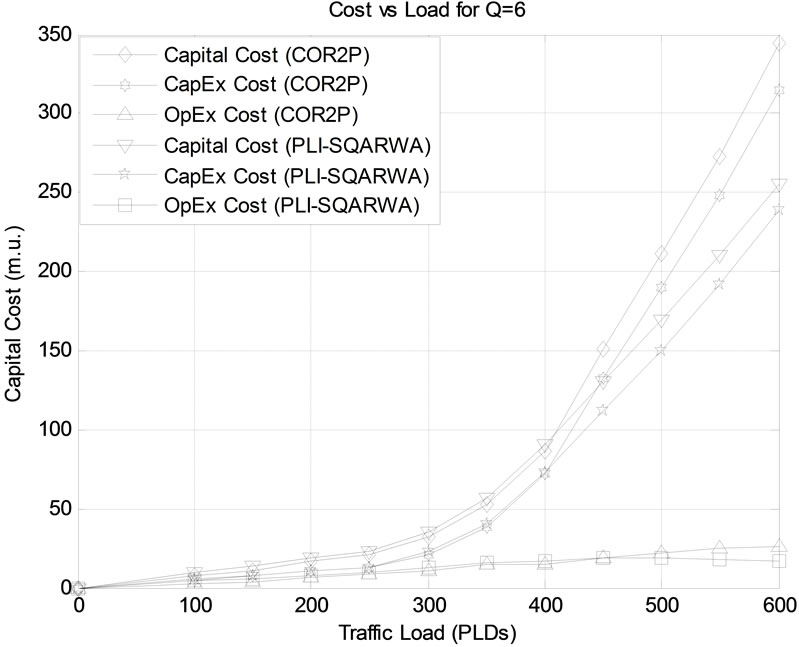
Figure 9. PLI-SQARWA versus COR2P: cost versus traffic load.
In order to compare the two algorithms in terms of latency, we evaluate the delay incurred by the network when either PLI-SQARWA or COR2P algorithm is employed. For network latency evaluation, we make use of the following delay analysis: A call 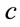 is assumed to incur a total delay
is assumed to incur a total delay 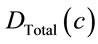 and is blocked if latency incurred in call processing exceeds
and is blocked if latency incurred in call processing exceeds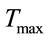 . Let
. Let  denote the processing delay which includes the time required to find a candidate lightpath (
denote the processing delay which includes the time required to find a candidate lightpath ( ), time to run the BER (Q-factor) estimation (
), time to run the BER (Q-factor) estimation ( ) and delay introduced by the OEO conversion (
) and delay introduced by the OEO conversion ( ), if applicable to a lightpath. Hence, the delay in processing a request c without requiring OEO conversion and within the timeout threshold is given as
), if applicable to a lightpath. Hence, the delay in processing a request c without requiring OEO conversion and within the timeout threshold is given as
 (13)
(13)
where n denotes the number of trials before which a lightpath with BER less than threshold value is calculated or below which check for all candidate lightpaths is finished. The processing delay for a request c requiring OEO conversion and within timeout threshold is given as
 (14)
(14)
The propagation delay denoted by  is the delay involved in carrying the lightpath along the link between two nodes of the network. Thus, the total latency for call c is estimated as the sum of processing and propagation delay and is given as
is the delay involved in carrying the lightpath along the link between two nodes of the network. Thus, the total latency for call c is estimated as the sum of processing and propagation delay and is given as
 (15)
(15)
Other delays apart from processing and propagation delays have been ignored in the latency analysis. Also, since optical WC does not involve any OEO conversions, delay introduced by AOWCs is assumed to be zero.
Figure 10 shows delay encountered by the network when COR2P and proposed PLI-SQARWA algorithms are used. Since COR2P deploys more number of regenerators compared to PLI-SQARWA, time delay is higher for the network when COR2P is used. For every traffic load value, corresponding delay value is higher for COR2P compared to proposed PLI-SQARWA which suggests that regenerators should be used only when regeneration or simultaneous regeneration and WC is required and to resolve only wavelength contention, AOWCs should be used as in the case of proposed PLISQARWA.
It can be observed from the figure that for moderate to high traffic loads (i.e. between 300 and 600 PLDs); difference in delay for both algorithms is higher compared to when lower traffic loads are considered. For instance at 200 and 400 demands respectively, for COR2P, network delay is 11.833 ms and 35.832 ms compared to the delay of 9.649 ms and 24.1542 ms shown by PLISQARWA which results in delay difference of 2.184 ms and 11.6778 ms respectively.
The results in this section demonstrating PLI-SQARWA’s
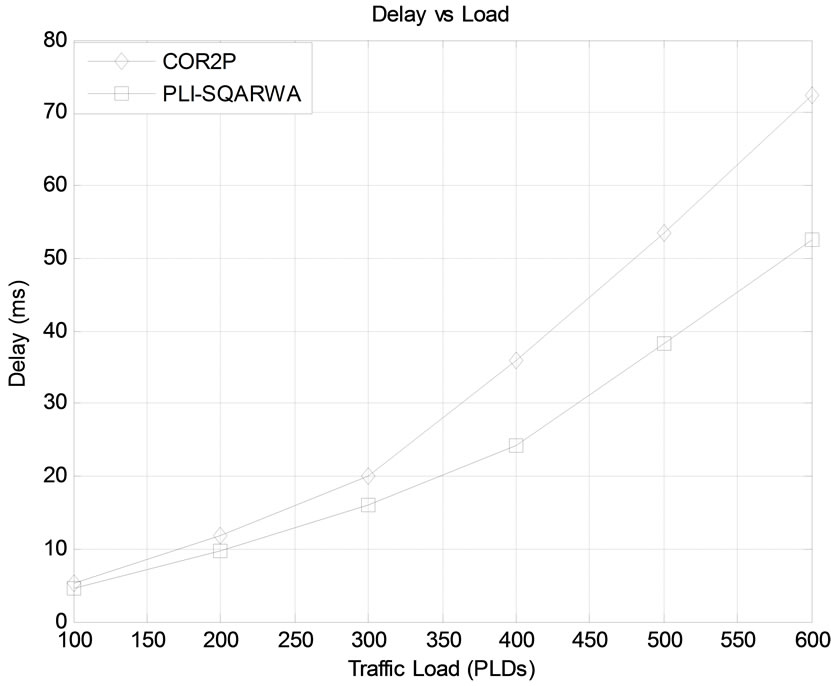
Figure 10. PLI-SQARWA versus COR2P: delay versus traffic load.
lower cost and delay compared to COR2P are obtained under the assumption of static requests. For real time applications, connection requests arrive randomly and according to the available network resources, these demands have to be served on a one-by-one basis. During the last decade a lot of work has been conducted on optical switching and even though many solutions have appeared, a break-through technology capable of delivering a cost and latency effective implementation suitable for large scale deployment has not yet been identified. Under the current circumstances, in order to provision dynamic requests for real-time applications, the idea of hybrid electro-optical solution becomes feasible. In this regard, the next section presents details of the proposed novel hybrid translucent node architecture.
4. Hybrid Node Architecture
In view of an electro-optical solution, we propose a hybrid translucent node architecture as shown in Figure 11. In such a hybrid node, regenerators perform three operations: optical-electrical (O-E) conversion, bit regeneration, and electrical-optical (E-O) conversion and are used if 1) the signal to noise ratio (SNR) at any node falls below the threshold or 2) the SNR at any node falls below the threshold and simultaneously there is also wavelength contention. In the latter case, a regenerator is used for both, regeneration and WC. However, if only wavelength contention is to be resolved at a node, AOWC will be used instead of a regenerator. A lightpath transiting such a node may be switched transparently (L1) or directed to the regenerator pool (L2) if 1) it requires only regeneration or; 2) it simultaneously requires both regeneration and WC. If only wavelength contention is to be resolved, the lightpath is directed to the wavelength converter (L3). It must be noted that deployment of the hybrid node in the network necessitates intelligent switching technology with switches having the ability to direct lightpaths as per the requirement of 1) only regeneration; or 2) simultaneous regeneration and WC; or 3) only WC. In the current study, we assume that AOWC used in hybrid node is equipped with full range wavelength conversion (FRWC) capability i.e., it can convert any input wavelength to any output wavelength [3].
In the next sub-section we present the comparison results of network performance with different node architectures in terms of BP and latency. Performance of the network equipped with hybrid node, named as H-OEOWC, is compared with a) Transparent network with sparse WCP, named as S-WC and b) Translucent network with sparse OEO RP, named as S-OEO [10].
Network Performance with Different Node Architectures
In the current study, since our interest lies in determining the blocking due to only signal degradation and wavelength contention, for comparing performance of the H-OEO-WC node with S-OEO and S-WC nodes, parameters used in our simulation imply that all instances intromit a solution with 0% of resource blocking. Figure 12 shows the variation of BP with offered load for various node architectures. It can be seen from the figure that S-WC nodes show worst blocking since they are equipped with only wavelength converters and no regenerators to account for PLI degradation. On the other hand, S-OEO and H-OEO-WC nodes show zero blocking as they are capable of provisioning both, WC and regeneration as per the requirement. This emphasizes the significance of regeneration and PLI consideration within the RWA.
In the case of S-WC nodes, WC is performed at nodes 5, 8, 7, 11 and 15. This is shown in Figure 12 following S-WC in the legend (i.e. in round brackets). On the other hand, in case of S-OEO and H-OEO-WC nodes, WC is performed at nodes 5, 8, 7, 11 and 15 while regeneration is performed at nodes 3, 4, 9 and 14. This is shown in

Figure 11. Hybrid translucent node architecture within the typical configuration of a translucent WDM network.
Figure 12 following S-OEO and H-OEO-WC in the legend (i.e. in round brackets). It can also be seen from Figure 12 that, both, S-OEO and H-OEO-WC nodes show zero total blocking owing to the use of regenerators, wavelength converters and simulation parameters which result in zero signal, wavelength and resource blocking respectively. The higher blocking shown by S-WC nodes is attributed to the fact that wavelength converters do not alter the overall BP since their presence only decreases wavelength related blocking but increases BER related blocking owing to increase in PLI effects.
In order to compare the different node architectures in terms of latency, we make use of the latency analysis explicated in Section 3 (Sub-section 3.2) comprising of Equations (13)-(15). Figure 13 shows the variation of delay with traffic load for various node architectures.
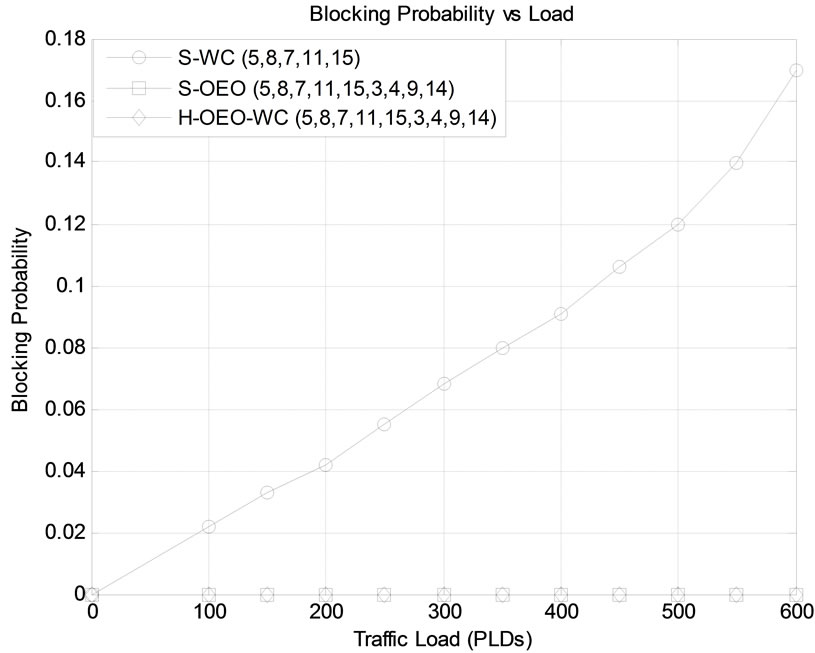
Figure 12. Blocking probability versus load for various node architectures.

Figure 13. Delay versus traffic load for various node architectures.
It can be clearly seen that the delay using S-WC nodes is least as these nodes are not equipped with regenerators and hence do not involve OEO conversions. On the other hand, the delay for S-OEO and H-OEO-WC nodes is high as OEO conversion is used to compensate for PLI degradation. Comparison of S-OEO and H-OEO-WC nodes shows that, H-OEO-WC nodes have lesser delay as such nodes use wavelength converters for WC whereas S-OEO nodes use OEO conversion to resolve both, regeneration and WC which leads to a larger delay. This can be explained as follows: Out of the nine nodes where regeneration and WC is required, only five nodes require WC and the other four need regeneration. Using H-OEO-WC nodes results in OEO conversion at only four nodes as wavelength contention at the other five nodes is resolved using AOWC. Use of S-OEO nodes on the other hand, results in OEO conversion at all nine nodes since regenerators are also used as wavelength converters leading to higher delay. The delay difference between H-OEO-WC and S-OEO nodes is approximately 20 ms.
5. Conclusions
We introduced the PLI-SQARWA algorithm that guarantees zero blocking due to signal degradation and wavelength contention. Deviating from existing studies, PLI-SQARWA uses the SQAR algorithm to evaluate candidate routes which use fewest amounts of regenerators and maximally uses placed regenerators for WC, before resorting to AOWCs; thus, being able to minimize the total network components. Further, in view of large scale deployment of a cost and latency effective implementation, we proposed a novel electro-optical hybrid translucent node architecture suitable for provisioning dynamic requests for real-time applications. In order to reduce OEO conversion time delay, the hybrid node resorts to regenerators only when regeneration or simultaneous regeneration and WC is required whereas, uses AOWCs for only wavelength contention resolutions.
We demonstrated that compared to COR2P, PLISQARWA utilizes fewer number of network components thus, saving on CapEx and further, as the load increases, it also starts to save on OpEx by introducing only a small number of new sites for component deployment. Further, opposed to COR2P’s assumption that regenerators are equipped with WC capability, PLI-SQARWA uses AOWCs to resolve only wavelength contentions hence, introducing lesser delay. The aforementioned benefits by preferring PLI-SQARWA over COR2P are obtained at superior blocking performance shown by PLI-SQARWA. Further, we compared performance of the network consisting of the proposed hybrid node with the network equipped with translucent and transparent node architectures present in literature. The obtained results demonstrated that the use of hybrid node incurs lesser time delay at a similar blocking performance shown by nodes which use OEO conversion for both, regeneration and/or WC.
Finally, the results suggest that for reducing the network component count, it is wiser to equip the routing phase of a PLI-RWA algorithm with signal quality awareness as opposed to using the traditional SP routing and in view of minimizing the time delay due to OEO conversions, using AOWCs for only wavelength contention resolution is a judicious choice rather than resorting to regenerators.
6. Acknowledgements
The authors would like to thank AICTE for funding this work under research promotion scheme (RPS-11/2008- 09).
REFERENCES
- H. Zang, P. Jue and B. Mukherjee, “A Review of RWA Approaches for Wavelength-Routed Optical WDM Networks,” Optical Networks Magazine, Vol. 1, No. 1, 2000, pp. 47-60.
- S. P. Singh, S. Iyer, S. Kar and V. K. Jain, “Study on Mitigation of Transmission Impairments and Issues and Challenges with PLIA-RWA in Optical WDM Networks,” Journal of Optical Communications, De-Gruyter, Vol. 33, No. 2, 2012, pp. 83-101. doi:10.1515/joc-2012-0015
- S. Azodolmolky, M. Klinkowski, E. Marin-Tordera, D. Careglio, J. Sole-Pareta and I. Tomkos, “A Survey on Physical Layer Impairments Aware Routing and Wavelength Assignment Algorithms in Optical Networks,” Computer Networks, Vol. 53, No. 7, 2009, pp. 926-944. doi:10.1016/j.comnet.2008.11.014
- G. Shen and R. S. Tucker, “Translucent Optical Networks: The Way Forward,” IEEE Communications Magazine, Vol. 45, No. 2, 2007, pp. 48-54. doi: 10.1109/MCOM.2007.313394
- S. Pachnicke, T. Paschenda and P. Krummrich, “Assessment of a Constraint-Based Routing Algorithm for Translucent 10 Gbits/s DWDM Networks Considering Fiber Nonlinearities,” Journal of Optical Networking, Vol. 7, No. 4, 2008, pp. 365-377. doi: 10.1364/JON.7.000365
- M. Youssef, S. Al Zahr and M. Gagnaire, “Traffic-Driven vs. Topology-Driven Strategies for Regeneration Sites Placement,” Proceedings of International Conference on Communications (ICC), Cape Town, 2010, pp. 1-6. doi:10.1109/ICC.2010.5501793
- M. A. Ezzahdi, S. Al Zahr, M. Koubaa, N. Puech and M. Gagnaire, “LERP: A Quality of Transmission Dependent Heuristic for Routing and Wavelength Assignment in Hybrid WDM Networks,” Proceedings of International Conference on Computer Communications and Networks (ICCCN), Arlington, 2006, pp. 125-136. doi:10.1109/ICCCN.2006.286257
- M. Youssef, S. Al Zahr and M. Gagnaire, “Translucent Network Design from a CapEx/OpEx Perspective,” Photonic Network Communications, Vol. 22, No. 1, 2011, pp. 85-97. doi:10.1007/s11107-011-0310-6
- P. Runge, C. A. Bunge and K. Petermann, “All-Optical Wavelength Conversion with Extinction Ratio Improvement of 100 Gb/s RZ-Signals in Ultra-Long Bulk Semiconductor Optical Amplifiers,” IEEE Journal of Quantum Electronics, Vol. 46, No. 6, 2010, pp. 937-944. doi:10.1109/JQE.2010.2041430
- S. Iyer and S. P. Singh, “A Novel Hybrid Node Architecture for Reducing Time Delay in Wavelength Division Multiplexed Translucent Network,” Proceedings of IEEE National Conference on Communication (NCC), Indian Institute of Technology-Kharagpur (IIT-K), Kharagpur, 2012, pp. 1-5. doi:10.1109/NCC.2012.6176843
- A. Viglienzoni and W. Mohr, “Next Generation Optical Networks Enabler for Future Wireless and Wireline Applications,” White Paper on NGON, 2011. http://www.photonics21.org/download/Internetversion_P21NetWorks_WhitePaperOnNGON_2011-11-07.pdf
- S. Hardy, “Breaking Barriers to Low Latency,” Lightwave Magazine, 2010. http://online.qmags.com/LW0610/
- G. P. Agrawal, “Fiber-Optic Communication Systems,” 3rd Edition, John Wiley & Sons, Hoboken, 2002.
- S. Iyer and S. P. Singh, “Impact of Combined Non-Linearities and ASE Noise on Performance of 10 Gbps All Optical Star WDM Networks,” Scientific Research, Communications and Network, Vol. 3, No. 4, 2011, pp. 235- 249. doi:10.4236/cn.2011.34028
- M. Gagnaire and S. Al Zahr, “Impairment-Aware Routing and Wavelength Assignment in Translucent Networks: State of the Art,” IEEE Communications Magazine, Vol. 47, No. 5, 2009, pp. 55-61. doi:10.1109/MCOM.2009.4939277

