Advances in Pure Mathematics
Vol.08 No.01(2018), Article ID:82163,64 pages
10.4236/apm.2018.81006
Co-Periodicity Isomorphisms between Forests of Finite p-Groups
Daniel C. Mayer
Naglergasse 53, Graz, Austria

Copyright © 2018 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: December 1, 2017; Accepted: January 28, 2018; Published: January 31, 2018
ABSTRACT
Based on a general theory of descendant trees of finite p-groups and the virtual periodicity isomorphisms between the branches of a coclass subtree, the behavior of algebraic invariants of the tree vertices and their automorphism groups under these isomorphisms is described with simple transformation laws. For the tree of finite 3-groups with elementary bicyclic commutator quotient, the information content of each coclass subtree with metabelian mainline is shown to be finite. As a striking novelty in this paper, evidence is provided of co-periodicity isomorphisms between coclass forests which reduce the information content of the entire metabelian skeleton and a significant part of non-metabelian vertices to a finite amount of data.
Keywords:
Finite p-Groups, Descendant Trees, Pro-p Groups, Coclass Forests, Generator Rank, Relation Rank, Nuclear Rank, Parametrized Polycyclic Pc-Presentations, Automorphism Groups, Central Series, Two-Step Centralizers, Commutator Calculus, Transfer Kernels, Abelian Quotient Invariants, p-Group Generation Algorithm

1. Introduction
Denote by 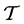 the rooted tree of all finite 3-groups G with elementary bicyclic commutator quotient
the rooted tree of all finite 3-groups G with elementary bicyclic commutator quotient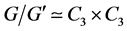 , and let
, and let 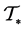 be the infinite pruned subtree of
be the infinite pruned subtree of , where all descendants of capable non-metabelian vertices are eliminated. The main intention of this paper is to prove that the information content of the tree
, where all descendants of capable non-metabelian vertices are eliminated. The main intention of this paper is to prove that the information content of the tree 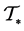 can be reduced to a finite set of representatives with the aid of two kinds of periodicity.
can be reduced to a finite set of representatives with the aid of two kinds of periodicity.
• Firstly, the well-known virtual periodicity isomorphisms 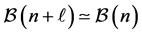 between the finite depth-pruned branches
between the finite depth-pruned branches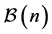 ,
, 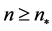 , of a coclass subtree
, of a coclass subtree 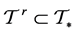 are refined to strict periodicity isomorphisms between complete branches which reduce the information content of the infinite coclass subtree to the finite union of pre-period
are refined to strict periodicity isomorphisms between complete branches which reduce the information content of the infinite coclass subtree to the finite union of pre-period 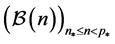 and first primitive period
and first primitive period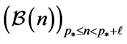 . The virtual periodicity was proved by du Sautoy [1] and independently by Eick and Leedham-Green [2] for groups of any prime power order. The strict periodicity for
. The virtual periodicity was proved by du Sautoy [1] and independently by Eick and Leedham-Green [2] for groups of any prime power order. The strict periodicity for 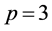 and type
and type 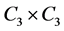 is proved in the present paper.
is proved in the present paper.
• Secondly, evidence is provided of co-periodicity isomorphisms  between the infinite coclass forests
between the infinite coclass forests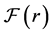 ,
, 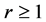 , which reduce the information content of the pruned tree
, which reduce the information content of the pruned tree  to the union of pre-period
to the union of pre-period  and first primitive period
and first primitive period![]() , consisting of the leading six coclass forests only. The discovery of this co-periodicity is the progressive innovation in the present paper.
, consisting of the leading six coclass forests only. The discovery of this co-periodicity is the progressive innovation in the present paper.
Together with the coclass theorems of Leedham-Green [3] and Shalev [4] , which imply that each coclass forest ![]() consists of a finite sporadic part
consists of a finite sporadic part ![]() and a finite number of coclass trees
and a finite number of coclass trees![]() ,
, ![]() , each having a finite information content due to the strict periodicity, this shows that the pruned infinite subtree
, each having a finite information content due to the strict periodicity, this shows that the pruned infinite subtree ![]() of the tree
of the tree ![]() is described by finitely many representatives only.
is described by finitely many representatives only.
We begin with a general theory of descendant trees of finite p-groups with arbitrary prime p in §2 and we explain the conceptual foundations of the virtual periodicity isomorphisms between the finite branches of coclass subtrees [1] [2] [5] and the recently discovered co-periodicity isomorphisms between infinite coclass forests in §3. The behavior of algebraic invariants of the tree vertices and their automorphism groups is described with simple transformation laws in §4. The graph theoretic preliminaries are supplemented by connections between depth, width, information content and numbers of immediate descendants in §5, identifiers of groups in §6, and precise definitions of mainlines and sporadic parts in §7. The main theorems are presented in §8.
Then we focus on the tree ![]() of finite 3-groups G with abelianization
of finite 3-groups G with abelianization![]() . The flow of our investigations is guided by §10 concerning the remarkable infinite main trunk
. The flow of our investigations is guided by §10 concerning the remarkable infinite main trunk ![]() of certain metabelian vertices in
of certain metabelian vertices in ![]() which gives rise to the top vertices of all coclass forests
which gives rise to the top vertices of all coclass forests![]() ,
, ![]() , by periodic bifurcations and constitutes the germ of the newly discovered co-periodicity
, by periodic bifurcations and constitutes the germ of the newly discovered co-periodicity ![]() of length two. To start with a beautiful highlight, we immediately celebrate the simple structure of the first primitive period
of length two. To start with a beautiful highlight, we immediately celebrate the simple structure of the first primitive period ![]() in §§11 and 12 and defer the somewhat arduous task of describing the exceptional pre-period
in §§11 and 12 and defer the somewhat arduous task of describing the exceptional pre-period ![]() to the concluding §§13 and 14.
to the concluding §§13 and 14.
Finally, we point out that our theory, together with the investigations of Eick [6] , provides an independent verification and confirmation of all results about the metabelian skeleton ![]() of the tree
of the tree ![]() in the dissertation of Nebelung [7] , since
in the dissertation of Nebelung [7] , since ![]() is a subtree of the pruned tree
is a subtree of the pruned tree![]() . The present paper shows the co-periodicity of the sporadic parts
. The present paper shows the co-periodicity of the sporadic parts ![]() and coclass trees
and coclass trees![]() ,
, ![]() , of the coclass forests
, of the coclass forests![]() , and ( [6] , §5.2, pp. 114-116) establishes the connection between the coclass trees
, and ( [6] , §5.2, pp. 114-116) establishes the connection between the coclass trees ![]() and infinite metabelian pro-3 groups of coclass r.
and infinite metabelian pro-3 groups of coclass r.
2. Descendant Trees and Coclass Forests
Let p be a prime number. In the mathematical theory of finite groups of order a power of p, so-called p-groups, the introduction of the parent-child relation by Leedham-Green and Newman ( [8] , pp. 194-195) has simplified the classification of such groups considerably. The relation is defined in terms of the lower central series ![]() of a p-group G, where
of a p-group G, where
![]() (2.1)
(2.1)
in particular, ![]() is the commutator subgroup of G. Since the series becomes stationary,
is the commutator subgroup of G. Since the series becomes stationary,
![]() (2.2)
(2.2)
a non-trivial p-group ![]() is nilpotent of class
is nilpotent of class![]() .
.
Definition 2.1. If G is non-abelian, then the class-![]() quotient
quotient
![]() (2.3)
(2.3)
is called the parent of G, and G is a child (or immediate descendant) of![]() .
.
Parent and child share a common class-1 quotient (or derived quotient or abelianization), since
![]() (2.4)
(2.4)
according to the isomorphism theorem. The lower central series of ![]() is shorter by one term:
is shorter by one term:
![]() (2.5)
(2.5)
and thus![]() .
.
Definition 2.2. For an assigned finite p-group![]() , the descendant tree
, the descendant tree ![]() with root R is defined as the digraph
with root R is defined as the digraph ![]() whose set of vertices V consists of all isomorphism classes of p-groups G with
whose set of vertices V consists of all isomorphism classes of p-groups G with![]() , for some
, for some![]() , and whose set of directed edges E consists of all child-parent pairs
, and whose set of directed edges E consists of all child-parent pairs
![]() (2.6)
(2.6)
The mapping ![]() is called the parent operator.
is called the parent operator.
If the root R is abelian, then all vertices of the tree ![]() share the common abelianization
share the common abelianization![]() . Since a nilpotent group with cyclic abelianization is abelian, the descendant tree
. Since a nilpotent group with cyclic abelianization is abelian, the descendant tree ![]() of a cyclic root
of a cyclic root ![]() consists of the single isolated vertex R. The classification of p-groups by their abelianization is refined further, if directed edges are restricted to starting vertices G with cyclic last non-trivial lower central
consists of the single isolated vertex R. The classification of p-groups by their abelianization is refined further, if directed edges are restricted to starting vertices G with cyclic last non-trivial lower central ![]() of order p. Then the descendant tree of R splits into a countably infinite disjoint union
of order p. Then the descendant tree of R splits into a countably infinite disjoint union
![]() (2.7)
(2.7)
of directed subgraphs, where ![]() and the vertices of the component
and the vertices of the component ![]() with fixed
with fixed ![]() share the same coclass,
share the same coclass, ![]() , as a common invariant, since the logarithmic order
, as a common invariant, since the logarithmic order ![]() and the nilpotency class
and the nilpotency class ![]() of the parent
of the parent ![]() and child G satisfy the rule
and child G satisfy the rule
![]() (2.8)
(2.8)
Definition 2.3. Thus, the components ![]() with
with ![]() are called the coclass subgraphs of the descendant tree
are called the coclass subgraphs of the descendant tree![]() .
.
According to the coclass theorems by Leedham-Green [3] and Shalev [4] , a coclass graph ![]() is the disjoint union of a finite sporadic part
is the disjoint union of a finite sporadic part ![]() and finitely many coclass trees
and finitely many coclass trees ![]() (with infinite mainlines), that is, a forest for which there exist integers
(with infinite mainlines), that is, a forest for which there exist integers ![]() such that
such that
![]() (2.9)
(2.9)
Definition 2.4. In the present paper, the focus will lie on finite p-groups with fixed prime ![]() arising as descendants of the fixed elementary bicyclic 3-group
arising as descendants of the fixed elementary bicyclic 3-group ![]() of order
of order ![]() with
with![]() , where
, where ![]() denotes the cyclic group of order n. This assumption permits a simplified notation by omitting the explicit mention of p and R. Further, we shall slightly reduce the complexity of the forests
denotes the cyclic group of order n. This assumption permits a simplified notation by omitting the explicit mention of p and R. Further, we shall slightly reduce the complexity of the forests![]() ,
, ![]() , by eliminating the descendants of capable (i.e., non-terminal) non-metabelian vertices. This pruned light-weight version of
, by eliminating the descendants of capable (i.e., non-terminal) non-metabelian vertices. This pruned light-weight version of ![]() will be denoted by
will be denoted by![]() , called the coclass-r forest, and Formula (2.9) becomes
, called the coclass-r forest, and Formula (2.9) becomes
![]() (2.10)
(2.10)
and possibly different integers ![]() and
and![]() .
.
Remark 2.1. In §§11 and 12 it will turn out that the coclass trees ![]() with metabelian mainlines do not contain any capable non-metabelian vertices. So the pruning process from
with metabelian mainlines do not contain any capable non-metabelian vertices. So the pruning process from ![]() to
to ![]() concerns the sporadic part
concerns the sporadic part![]() , and reduces the number
, and reduces the number ![]() of coclass trees by eliminating those with non-metabelian mainlines entirely, but does not affect the coclass trees with metabelian mainlines, which remain complete in spite of pruning.
of coclass trees by eliminating those with non-metabelian mainlines entirely, but does not affect the coclass trees with metabelian mainlines, which remain complete in spite of pruning.
3. Isomorphic Digraphs and Trees
In general, we denote a graph ![]() as a pair
as a pair ![]() with set of vertices V and set of edges E.
with set of vertices V and set of edges E.
Definition 3.1. Let ![]() and
and ![]() be two digraphs with directed edges in
be two digraphs with directed edges in![]() , respectively
, respectively![]() . If there exists a bijection
. If there exists a bijection ![]() such that
such that
![]() (3.1)
(3.1)
then ![]() and
and ![]() are called isomorphic digraphs, and
are called isomorphic digraphs, and ![]() is an isomorphism of digraphs.
is an isomorphism of digraphs.
When ![]() is a finite digraph with vertex cardinality
is a finite digraph with vertex cardinality![]() , we can identify V with the set
, we can identify V with the set![]() . Then the set of directed edges
. Then the set of directed edges ![]() is characterized uniquely by the characteristic function
is characterized uniquely by the characteristic function ![]() of E in
of E in![]() , which is called the
, which is called the ![]() adjacency matrix
adjacency matrix ![]() of
of![]() . Its entries are defined, for all
. Its entries are defined, for all![]() , by
, by
![]() (3.2)
(3.2)
Proposition 3.1. Let ![]() and
and ![]() be two finite digraphs with n vertices. Then
be two finite digraphs with n vertices. Then ![]() and
and ![]() are isomorphic if and only if there exists a bijection
are isomorphic if and only if there exists a bijection ![]() such that the entries of the adjacency matrices
such that the entries of the adjacency matrices ![]() coincide for all
coincide for all![]() .
.
Proof. The bijection ![]() satisfies the condition in Formula (3.1) if and only if
satisfies the condition in Formula (3.1) if and only if ![]() ⇔
⇔![]() ⇔
⇔![]() ⇔
⇔![]() .
.
The in-resp. out-degree of a vertex ![]() in a finite digraph can be expressed in terms of the vth column-resp. row-sum of the adjacency matrix:
in a finite digraph can be expressed in terms of the vth column-resp. row-sum of the adjacency matrix:
![]() (3.3)
(3.3)
In particular, if ![]() is a finite directed in-tree with root R, then each row of the adjacency matrix A corresponding to a vertex
is a finite directed in-tree with root R, then each row of the adjacency matrix A corresponding to a vertex ![]() contains a unique 1 and
contains a unique 1 and
![]() (3.4)
(3.4)
Proposition 3.2. Let ![]() and
and ![]() be two rooted directed in-trees, and denote by
be two rooted directed in-trees, and denote by ![]() and
and ![]() their parent operators. Then a bijection
their parent operators. Then a bijection ![]() with
with ![]() is an isomorphism of rooted directed in-trees if and only if
is an isomorphism of rooted directed in-trees if and only if ![]() for all
for all![]() , that is,
, that is, ![]() (briefly:
(briefly: ![]() commutes with the parent operator), as shown in Figure 1.
commutes with the parent operator), as shown in Figure 1.
Proof. Recall that each row of the adjacency matrix A of the tree ![]() corresponding to a vertex
corresponding to a vertex![]() ,
, ![]() , contains a unique 1. This fact can be used to define the parent operator
, contains a unique 1. This fact can be used to define the parent operator ![]() of
of ![]() by
by ![]() ⇔
⇔![]() . Consequently, if
. Consequently, if ![]() has the claimed property to commute with the parent operator, then
has the claimed property to commute with the parent operator, then ![]() ⇔
⇔ ![]() ⇔
⇔ ![]() ⇔
⇔ ![]() ⇔
⇔ ![]() ⇔
⇔ ![]() ⇔
⇔![]() . For infinite trees, the steps concerning adjacency matrices must be omitted. The proof of the converse statement is similar.
. For infinite trees, the steps concerning adjacency matrices must be omitted. The proof of the converse statement is similar.
4. Algebraically Structured Digraphs
4.1. General Invariants and Their Transformation Laws
Since the vertices of all trees and branches in this paper are realized by isomorphism classes of finite p-groups, the abstract intrinsic graph theoretic structure of the trees and branches can be extended by additional concrete structures defined with the aid of algebraic invariants of p-groups.
Not all algebraic structures are strict invariants under graph isomorphisms. Some of them change in a well defined way, described by a mapping![]() , the transformation law, when a graph isomorphism is applied. This behaviour is made precise in the following definitions.
, the transformation law, when a graph isomorphism is applied. This behaviour is made precise in the following definitions.
Definition 4.1. Let ![]() be a graph. Suppose that
be a graph. Suppose that ![]() is a set, and each vertex
is a set, and each vertex ![]() is associated with some kind of information
is associated with some kind of information![]() . Then
. Then ![]() is called a structured graph with respect to the mapping
is called a structured graph with respect to the mapping![]() ,
,![]() .
.
If ![]() and
and ![]() are two structured digraphs with respect to mappings
are two structured digraphs with respect to mappings![]() ,
, ![]() , and
, and![]() ,
, ![]() , and
, and ![]() is a mapping, then an isomorphism of digraphs
is a mapping, then an isomorphism of digraphs ![]() is called a
is called a ![]() -iso- morphism of structured digraphs
-iso- morphism of structured digraphs ![]() and
and![]() , if
, if ![]() for all
for all![]() , that is,
, that is, ![]() , as visualized in Figure 2.
, as visualized in Figure 2.
In particular, if the sets ![]() coincide and
coincide and ![]() is the identity mapping of the set X, then
is the identity mapping of the set X, then ![]() is called a strict isomorphism of structured digraphs, and it satisfies the relation
is called a strict isomorphism of structured digraphs, and it satisfies the relation![]() .
.
Definition 4.2. Let ![]() and
and ![]() be two structured digraphs with structure mappings
be two structured digraphs with structure mappings ![]() and
and![]() , and let
, and let ![]() be a
be a ![]() -isomorphism of the two structured digraphs with respect to a mapping
-isomorphism of the two structured digraphs with respect to a mapping![]() , that is,
, that is,![]() . Then
. Then ![]() is called a
is called a ![]() -invariant under
-invariant under ![]() (or invariant under the isomorphism
(or invariant under the isomorphism ![]() and transformation law
and transformation law![]() ). In particular, if
). In particular, if![]() ,
, ![]() and
and![]() , then
, then ![]() is called a strict invariant under
is called a strict invariant under![]() .
.
4.2. Algebraic Invariants Considered in This Paper
With respect to applications in other mathematical theories, in particular, algebraic number theory and class field theory, certain properties of the
automorphism group ![]() of a finite 3-group G are crucial. The general frame of these aspects is the following.
of a finite 3-group G are crucial. The general frame of these aspects is the following.
Definition 4.3. Let p be an odd prime number and let G be a pro-p group. We call G a group with GI-action or a ![]() -group, if there exists a generator inverting automorphism
-group, if there exists a generator inverting automorphism ![]() such that
such that![]() , for all
, for all![]() , or equivalently
, or equivalently![]() , for all
, for all![]() . If additionally
. If additionally![]() , for all
, for all![]() , then G is called a group with RI-action or group with relator inverting automorphism. If
, then G is called a group with RI-action or group with relator inverting automorphism. If ![]() contains a bicyclic subgroup
contains a bicyclic subgroup![]() , then we call G a group with
, then we call G a group with ![]() -action. It is convenient to define the action flag of G by
-action. It is convenient to define the action flag of G by
![]() (4.1)
(4.1)
Remark 4.1. Suppose that G is a finite p-group with odd prime p. We point out that 2 divides the order![]() , if G is a group with GI-action, but the converse claim may be false. If G is a group with
, if G is a group with GI-action, but the converse claim may be false. If G is a group with ![]() -action, then 4 divides
-action, then 4 divides![]() , but we emphasize that the converse statement, even in the case that 8 divides
, but we emphasize that the converse statement, even in the case that 8 divides![]() , may be false, when
, may be false, when ![]() contains a cyclic group
contains a cyclic group ![]() or a (generalized) quaternion group
or a (generalized) quaternion group ![]() of order
of order ![]() with
with![]() .
.
For a brief description of abelian quotient invariants in logarithmic form, we need the concept of nearly homocyclic p-groups. With an arbitrary prime ![]() these groups appear in ( [9] , p. 68, Thm. 3.4) and they are treated systematically in ( [7] , 2.4). For our purpose, it suffices to consider the special case
these groups appear in ( [9] , p. 68, Thm. 3.4) and they are treated systematically in ( [7] , 2.4). For our purpose, it suffices to consider the special case![]() .
.
Definition 4.4. By the nearly homocyclic abelian 3-group ![]() of order
of order![]() , for an integer
, for an integer![]() , we understand the abelian group with logarithmic type invariants
, we understand the abelian group with logarithmic type invariants![]() , where
, where ![]() with integers
with integers ![]() and
and![]() , by Euclidean division with remainder. Additionally, including two degenerate cases, we define that
, by Euclidean division with remainder. Additionally, including two degenerate cases, we define that ![]() denotes the cyclic group
denotes the cyclic group ![]() of order 3, and
of order 3, and ![]() denotes the trivial group 1.
denotes the trivial group 1.
The following invariants ![]() of finite 3-groups
of finite 3-groups ![]() with abeliani- zation
with abeliani- zation ![]() will be of particular interest in the whole paper:
will be of particular interest in the whole paper:
• The logarithmic order![]() ,
, ![]() ,
,
• The nilpotency class![]() , connected with the index of nilpotency m by the relation
, connected with the index of nilpotency m by the relation![]() , where the lower central series stops with
, where the lower central series stops with![]() ,
,
• The coclass![]() , defined by
, defined by![]() ,
,
• The order of the automorphism group![]() ,
, ![]() ,
,
• The action flag![]() , defined by Formula (4.1),
, defined by Formula (4.1),
• The transfer kernel type (TKT)![]() ,
, ![]() , where
, where ![]() denote the transfer homomorphisms from v to the maximal subgroups
denote the transfer homomorphisms from v to the maximal subgroups![]() , for
, for![]() ,
,
• The transfer target type (TTT)![]() ,
, ![]() , viewed as abelian quotient invariants, where
, viewed as abelian quotient invariants, where ![]() denote the maximal subgroups of v ( [10] , Dfn. 5.3, p. 83),
denote the maximal subgroups of v ( [10] , Dfn. 5.3, p. 83),
• The abelian quotient invariants of the first TTT component![]() ,
, ![]() , where k denotes the defect of commutativity of v ( [11] , 2, p. 469),
, where k denotes the defect of commutativity of v ( [11] , 2, p. 469),
• The abelian quotient invariants of the commutator subgroup![]() ,
, ![]() (or
(or ![]() in irregular cases) ( [7] , Satz 4.2.4, p. 131),
in irregular cases) ( [7] , Satz 4.2.4, p. 131),
• The relation rank![]() ,
, ![]() , which coincides with the rank of the p-multiplicator of v ( [13] , Thm. 2.4),
, which coincides with the rank of the p-multiplicator of v ( [13] , Thm. 2.4),
• The nuclear rank![]() , i.e. the rank of the nucleus of
, i.e. the rank of the nucleus of ![]() ( [13] , Thm. 2.4). For a coclass tree, the nuclear rank is given by
( [13] , Thm. 2.4). For a coclass tree, the nuclear rank is given by ![]() .
.
Remark 4.2. Abelian quotient invariants are given in logarithmic notation. The transfer kernel type ![]() is simplified by a family of non-negative integers, in the following way: for
is simplified by a family of non-negative integers, in the following way: for![]() ,
,
![]() (4.2)
(4.2)
5. The Graph Theoretic Structure of a Tree
Cardinality of Branches and Layers, Depth and Width of a Tree
The graph theoretic structure of a coclass tree ![]() with unique infinite mainline and finite branches, consisting of isomorphism classes of finite p-groups, is described by the following concepts.
with unique infinite mainline and finite branches, consisting of isomorphism classes of finite p-groups, is described by the following concepts.
Definition 5.1. Let ![]() be a coclass tree. Suppose that the tree root R is of logarithmic order
be a coclass tree. Suppose that the tree root R is of logarithmic order![]() , and denote by
, and denote by ![]() the unique mainline vertex with
the unique mainline vertex with![]() . In particular,
. In particular,![]() .
.
For![]() , the difference set
, the difference set ![]() is called the eth branch of
is called the eth branch of![]() .
.
Let ![]() be one of the branches of
be one of the branches of![]() . For any integer
. For any integer![]() , we let
, we let
![]() (5.1)
(5.1)
denote the nth layer of![]() , respectively
, respectively![]() .
.
The width of the tree is the maximal cardinality of its layers,
![]() (5.2)
(5.2)
Each vertex v of the branch ![]() is connected with the mainline by a unique finite path of directed edges from v to the branch root
is connected with the mainline by a unique finite path of directed edges from v to the branch root![]() , formed by the iterated parents
, formed by the iterated parents ![]() of v,
of v,
![]() (5.3)
(5.3)
The length ![]() of this path is called the depth
of this path is called the depth ![]() of v.
of v.
The depth of a branch ![]() is the maximal depth of its vertices,
is the maximal depth of its vertices,
![]() (5.4)
(5.4)
Definition 5.2. Let ![]() be a coclass tree. The depth of the tree is the maximal depth of its branches,
be a coclass tree. The depth of the tree is the maximal depth of its branches,
![]() (5.5)
(5.5)
Throughout this paper, we assume that both, the depth ![]() and the width
and the width ![]() of the tree, are bounded. This assumption is satisfied by all trees of finite 3-groups under investigation in the sequel. However, we point out that that tree
of the tree, are bounded. This assumption is satisfied by all trees of finite 3-groups under investigation in the sequel. However, we point out that that tree ![]() of finite 5-groups with coclass one has unbounded depth, and the tree
of finite 5-groups with coclass one has unbounded depth, and the tree ![]() of finite 7-groups with coclass one even has unbounded width and depth. (Compare [6] , 5.1, pp. 113-114)
of finite 7-groups with coclass one even has unbounded width and depth. (Compare [6] , 5.1, pp. 113-114)
Lemma 5.1. Let![]() ,
, ![]() and
and![]() . Then
. Then
![]() (5.6)
(5.6)
Proof. Since ![]() is the root of the branch
is the root of the branch![]() , we have
, we have![]() , but
, but ![]()
![]() . Since
. Since![]() , there exists a vertex
, there exists a vertex![]() , necessarily terminal if
, necessarily terminal if![]() , such that
, such that![]() . The iterated parents
. The iterated parents ![]() of t form the unique finite path from t to the branch root
of t form the unique finite path from t to the branch root ![]() (see Figure 3),
(see Figure 3),
![]()
and we have ![]()
![]() but
but ![]()
![]() .
.
Lemma 5.2. Let ![]() and
and![]() . Then
. Then
![]() (5.7)
(5.7)
Proof. Since![]() , we have
, we have ![]() for each
for each![]() . A branch
. A branch ![]() with
with ![]() cannot contribute to
cannot contribute to![]() . On the other hand, if
. On the other hand, if![]() , then a branch
, then a branch ![]() with
with ![]() cannot contribute to
cannot contribute to ![]() either, since
either, since![]() , according to Lemma 5.1, and we obtain
, according to Lemma 5.1, and we obtain ![]() (see Figure 3). Consequently,
(see Figure 3). Consequently,
![]()
Figure 3. Schematic coclass tree ![]() with ultimately periodic branches and layers.
with ultimately periodic branches and layers.
![]() (5.8)
(5.8)
Since the implementation of the p-group generation algorithm [12] [13] [14] in the computational algebra system MAGMA [15] [16] [17] is able to give the number of all, respectively only the capable, immediate descendants (children) of an assigned finite p-group, we express the cardinalities of the branches of a coclass tree, which were given in a preliminary form in Lemma 5.1, in terms of these numbers![]() , respectively
, respectively![]() .
.
Theorem 5.1. Let ![]() be a coclass tree with tree root R of logarithmic order
be a coclass tree with tree root R of logarithmic order![]() , pre-period of length
, pre-period of length![]() , and period of primitive length
, and period of primitive length![]() . For each vertex
. For each vertex![]() , denote by
, denote by ![]() the number of all children (of step size
the number of all children (of step size![]() ) and by
) and by ![]() the number of capable children of v. When
the number of capable children of v. When ![]() is the vertex with
is the vertex with ![]() on the mainline of
on the mainline of![]() , let
, let ![]() with
with ![]() be the capable children of
be the capable children of![]() , in particular, let
, in particular, let ![]() be the next mainline vertex. Finally, let
be the next mainline vertex. Finally, let ![]() with
with ![]() denote the capable children of
denote the capable children of![]() , for each
, for each![]() .
.
1) If the tree is of depth![]() , then
, then
![]() (5.9)
(5.9)
2) If the tree is of depth![]() , then
, then
![]() (5.10)
(5.10)
3) If the tree is of depth![]() , then
, then
![]() (5.11)
(5.11)
Proof. Put![]() . Generally, we have
. Generally, we have ![]() with
with![]() , according to Lemma 5.1.
, according to Lemma 5.1.
If![]() , then
, then ![]() and
and![]() . We have
. We have ![]() and
and![]() , since the next mainline vertex
, since the next mainline vertex ![]() is one of the
is one of the ![]() children of
children of ![]() but does not belong to
but does not belong to![]() . Thus, we obtain
. Thus, we obtain ![]() .
.
If![]() , then
, then ![]() and
and![]() , where
, where ![]() and
and ![]() as before, and
as before, and![]() . Therefore,
. Therefore,![]() .
.
If![]() , then
, then ![]() and
and![]() , where
, where![]() ,
, ![]() ,
, ![]() as before, and
as before, and ![]() . Thus,
. Thus,
![]()
Remark 5.1. In Theorem 5.1, item (1) is included in item (2), since ![]() implies
implies![]() , and item (2) is included in item (3), since
, and item (2) is included in item (3), since ![]() implies
implies![]() , for all
, for all![]() .
.
Corollary 5.1. Under the same assumptions as in Theorem 5.1, the width of the coclass tree![]() , in dependence on the depth
, in dependence on the depth ![]() and the periodicity
and the periodicity![]() , is generally given by
, is generally given by
![]() (5.12)
(5.12)
For assigned small values of the depth![]() , the width can be expressed in terms of descendant numbers in the following manner:
, the width can be expressed in terms of descendant numbers in the following manner:
1) If the tree is of depth![]() , then
, then
![]() (5.13)
(5.13)
2) If the tree is of depth![]() , then
, then ![]() is the maximum among the number
is the maximum among the number ![]() and all expressions
and all expressions
![]() (5.14)
(5.14)
where n runs from ![]() to
to![]() .
.
3) If the tree is of depth![]() , then
, then ![]() is the maximum among the numbers
is the maximum among the numbers![]() ,
, ![]() , and all expressions
, and all expressions
![]() (5.15)
(5.15)
where n runs from ![]() to
to![]() .
.
Proof. According to [1] [2] [5] , the periodicity of the branches of a coclass tree ![]() with root
with root ![]() and bounded depth
and bounded depth ![]() and width
and width ![]() can be expressed by means of isomorphisms between branches, starting from the periodic root
can be expressed by means of isomorphisms between branches, starting from the periodic root![]() :
:
![]() (5.16)
(5.16)
where ![]() denotes the length of the pre-period and
denotes the length of the pre-period and ![]() is the primitive period length. With Lemma 5.1, an immediate consequence is the periodicity of branch layer cardinalities:
is the primitive period length. With Lemma 5.1, an immediate consequence is the periodicity of branch layer cardinalities:
![]()
According to Lemma 5.2, we have![]() , and thus
, and thus
![]()
For finding the maximal layer cardinality, the root term ![]() can be omitted, since each layer contains a mainline vertex. Beginning with
can be omitted, since each layer contains a mainline vertex. Beginning with![]() , the expression for the tree layer cardinality
, the expression for the tree layer cardinality ![]() is a sum of
is a sum of ![]() terms and we must find the logarithmic order
terms and we must find the logarithmic order ![]() where periodicity of all terms sets in. This leads to the inequality
where periodicity of all terms sets in. This leads to the inequality ![]() with solution
with solution![]() . Consequently,
. Consequently, ![]() is the biggest logarithmic order for which a new value of the tree layer cardinality
is the biggest logarithmic order for which a new value of the tree layer cardinality ![]() may occur (see Figure 3). At the logarithmic order
may occur (see Figure 3). At the logarithmic order![]() , periodic repetitions of the values of tree layer cardinalities begin.
, periodic repetitions of the values of tree layer cardinalities begin.
In the special case of![]() , Theorem 5.1 yields an expression in terms of descendant numbers:
, Theorem 5.1 yields an expression in terms of descendant numbers:
![]()
The following concept provides a quantitative measure for the finite infor- mation content of an infinite tree with periodic branches.
Definition 5.3. By the information content of a coclass tree ![]() we understand the sum of the cardinalities of all branches belonging to the pre-period and to the primitive period of
we understand the sum of the cardinalities of all branches belonging to the pre-period and to the primitive period of![]() ,
,
![]() (5.17)
(5.17)
where ![]() denotes the logarithmic order of the periodic root P of
denotes the logarithmic order of the periodic root P of ![]() (see Figure 3).
(see Figure 3).
6. Identifiers of the SmallGroups Library
Independently of being metabelian or non-metabelian, a finite 3-group G of order up to ![]() will be characterized by its absolute identifier
will be characterized by its absolute identifier ![]() , according to the SmallGroups Database [18] [19] . Starting with order
, according to the SmallGroups Database [18] [19] . Starting with order![]() , a group G is characterized by the absolute identifier of the parent
, a group G is characterized by the absolute identifier of the parent ![]() in the SmallGroups Database [19] together with a relative identifier
in the SmallGroups Database [19] together with a relative identifier ![]() generated by the ANUPQ package [20] of MAGMA [17] . Here, s denotes the step size of the directed edge
generated by the ANUPQ package [20] of MAGMA [17] . Here, s denotes the step size of the directed edge![]() . Occasionally, certain groups of order
. Occasionally, certain groups of order ![]() and coclass 2 are identified by single capital letters
and coclass 2 are identified by single capital letters ![]() similarly as in [21] [22] [23] .
similarly as in [21] [22] [23] .
7. Mainlines of Coclass Trees and Sporadic Parts of Coclass Forests
If we define a mainline as a maximal path of infinitely many directed edges of step size![]() , then there arises the ambiguity that a vertex could be root of several coclass trees. The metabelian 3-group
, then there arises the ambiguity that a vertex could be root of several coclass trees. The metabelian 3-group![]() , for instance, would be the end vertex of more then one mainline, namely on the one hand of the metabelian mainline
, for instance, would be the end vertex of more then one mainline, namely on the one hand of the metabelian mainline
![]()
and on the other hand of non-metabelian mainlines, one which ends with
![]()
and three which end with![]() ,
,![]() .
.
Therefore, an additional condition is required in the precise definition of a mainline.
Definition 7.1. A mainline is a maximal path of infinitely many equally oriented edges of step size![]() , in none of whose vertices other infinite paths of step size
, in none of whose vertices other infinite paths of step size ![]() are ending.
are ending.
The end vertex of a mainline is called the root of a coclass tree.
Definition 7.1 can be expressed equivalently in terms of infinite pro-p groups ( [6] , 3.1, p. 107).
Example 7.1. The metabelian 3-group ![]() is root of the coclass-2 tree
is root of the coclass-2 tree ![]() with metabelian mainline.
with metabelian mainline.
The metabelian 3-group ![]() is root of the coclass-2 tree
is root of the coclass-2 tree ![]() with non-metabelian mainline. According to our pruning convention that descendants of capable non-metabelian vertices do not belong to the coclass forests
with non-metabelian mainline. According to our pruning convention that descendants of capable non-metabelian vertices do not belong to the coclass forests![]() , this tree is not an object of examination in the present paper.
, this tree is not an object of examination in the present paper.
Finally, the metabelian 3-group ![]() is not root of a coclass tree.
is not root of a coclass tree.
Based on the precise definition of a mainline and a root of a coclass tree, we are now in the position to give an exact specification of the sporadic part of a coclass forest.
Definition 7.2. The sporadic part of the coclass forest ![]() with
with ![]() is the complement of the union of the (finitely many) coclass trees in the forest,
is the complement of the union of the (finitely many) coclass trees in the forest,
![]() (7.1)
(7.1)
There is no necessity, to restrict the concepts of a mainline, a coclass tree and its root further by stipulating the coclass stability of the root. It is therefore admissible that directed edges of step size ![]() end in vertices (mainline or of depth
end in vertices (mainline or of depth![]() ) of a coclass tree, due to the phenomenon of multifurcation.
) of a coclass tree, due to the phenomenon of multifurcation.
Example 7.2. In the second mainline vertex ![]() of the coclass-2 tree
of the coclass-2 tree ![]() with root
with root![]() , a bifurcation occurs, due to the nuclear rank
, a bifurcation occurs, due to the nuclear rank![]() . In fact, the directed edge of step size
. In fact, the directed edge of step size ![]() which ends in the vertex
which ends in the vertex ![]() is the final edge of an infinite path with alterating step sizes
is the final edge of an infinite path with alterating step sizes ![]() and
and![]() , due to periodic bifurcations. However, this non-meta- belian path is not the topic of investigations in the present paper. For detailed information on these matters see [24] and [25] .
, due to periodic bifurcations. However, this non-meta- belian path is not the topic of investigations in the present paper. For detailed information on these matters see [24] and [25] .
The same is true for the second mainline vertex ![]() of the coclass-2 tree
of the coclass-2 tree ![]() with root
with root![]() .
.
The unnecessary requirement of coclass stability would eliminate the pre-periods of the trees ![]() and
and ![]() and enforce purely periodic subtrees with periodic coclass-settled roots, namely
and enforce purely periodic subtrees with periodic coclass-settled roots, namely ![]() and
and ![]() .
.
8. Two Main Theorems on Periodicity and Co-Periodicity Isomorphisms
An important technique in the theory of descendant trees is to reduce the structure of an infinite tree to a periodically repeating finite pattern. In particular, it is well known [1] [2] [5] that an infinite coclass tree ![]() of finite p-groups with fixed coclass
of finite p-groups with fixed coclass ![]() is the disjoint union of its branches
is the disjoint union of its branches
![]() , which can be partitioned into a single finite pre-period
, which can be partitioned into a single finite pre-period
![]() of length
of length ![]() and infinitely many copies of a finite primitive period
and infinitely many copies of a finite primitive period ![]() of length
of length![]() , where the integer
, where the integer ![]() characterizes the position of the periodic root on the mainline, provided the tree is suitably depth-pruned.
characterizes the position of the periodic root on the mainline, provided the tree is suitably depth-pruned.
The following first main result of this paper establishes the details of the primitive period of branches of five coclass-4 trees![]() , with
, with![]() , respectively of three coclass-5 trees
, respectively of three coclass-5 trees![]() , with
, with![]() , of finite 3-groups with mainline vertices having a single total transfer kernel and roots
, of finite 3-groups with mainline vertices having a single total transfer kernel and roots ![]() with
with![]() , respec- tively
, respec- tively ![]() with
with![]() , writ- ten in the notation of [18] [19] [20] . In fact, we prove more than the virtual periodicity for arbitrary finite p-groups in [1] [2] [5] , since all trees of the particular finite 3-groups in our investigation have bounded depth and therefore reveal strict periodicity.
, writ- ten in the notation of [18] [19] [20] . In fact, we prove more than the virtual periodicity for arbitrary finite p-groups in [1] [2] [5] , since all trees of the particular finite 3-groups in our investigation have bounded depth and therefore reveal strict periodicity.
Theorem 8.1. (Main Theorem on Strict Periodicity Isomorphisms of Branches.)
For each integer![]() , there exists a bijective mapping
, there exists a bijective mapping ![]() which is a strict isomorphism of finite structured in-trees for the strict invariants in-degree
which is a strict isomorphism of finite structured in-trees for the strict invariants in-degree![]() , out-degree
, out-degree![]() , coclass
, coclass![]() , relation rank
, relation rank![]() , nuclear rank
, nuclear rank![]() , action flag
, action flag![]() , and transfer kernel type
, and transfer kernel type![]() . Moreover,
. Moreover, ![]() is a f-isomorphism of finite structured in-trees for the following
is a f-isomorphism of finite structured in-trees for the following ![]() -invariants with their transformation laws
-invariants with their transformation laws![]() :
:
• logarithmic order ![]() with
with![]() ,
,
• nilpotency class ![]() with
with![]() ,
,
• order of the automorphism group ![]() with
with![]() ,
,
• first component of the transfer target type ![]() with
with ![]() , and
, and
• commutator subgroup ![]() with
with ![]() , respectively
, respectively ![]() .
.
Consequently, the branches of each tree ![]()
![]() , respectively
, respectively ![]()
![]() , are purely periodic with primitive length at most
, are purely periodic with primitive length at most![]() .
.
Proof. The ![]() -isomorphisms between the finite branches of a tree describe the first periodicity and reduce an infinite tree to its finite primitive period, provided the periodicity is pure. This will be proved for even coclass
-isomorphisms between the finite branches of a tree describe the first periodicity and reduce an infinite tree to its finite primitive period, provided the periodicity is pure. This will be proved for even coclass ![]() in Theorem 11.3 for
in Theorem 11.3 for![]() , in Thm. 11.4 for
, in Thm. 11.4 for![]() , in Thm. 11.5 for
, in Thm. 11.5 for![]() , in Thm. 11.6 for
, in Thm. 11.6 for![]() , and in Thm. 11.7 for
, and in Thm. 11.7 for![]() . For odd coclass
. For odd coclass![]() , it will be proved in Theorem 12.3 for
, it will be proved in Theorem 12.3 for![]() , in Thm. 12.4 for
, in Thm. 12.4 for![]() , and in Thm. 12.5 for
, and in Thm. 12.5 for![]() .
.
Invariants connected with the nilpotency class are not strict and satisfy the following transformation laws: the shift ![]() for
for ![]() and
and![]() , and the corresponding transformations
, and the corresponding transformations![]() for
for![]() ,and
,and![]() for
for![]() , with fixed coclass r. For
, with fixed coclass r. For![]() , the transformation law is described by the homothety
, the transformation law is described by the homothety![]() .
.
Theorems 11.3, 11.4, 11.5, 11.6, 11.7 and 12.3, 12.4, 12.5 will give detailed descriptions of the structure of these trees, in particular they will establish a quantitative measure for the finite information content of each tree.
Remark 8.1. According to Theorem 8.1, the diagrams of coclass-r trees ![]() whose mainline vertices V possess a single total kernel
whose mainline vertices V possess a single total kernel ![]() among the transfers
among the transfers ![]() to the four maximal subgroups
to the four maximal subgroups ![]()
![]() reveal several surprising features: firstly, the branches are purely periodic of primitive length at most 2 without pre-period, secondly, the branches are of uniform depth 2 only, and finally, none of the vertices gives rise to descendants of coclass bigger than r. So the trees are entirely regular and coclass-stable, in contrast to the trees with 3-groups G of coclass
reveal several surprising features: firstly, the branches are purely periodic of primitive length at most 2 without pre-period, secondly, the branches are of uniform depth 2 only, and finally, none of the vertices gives rise to descendants of coclass bigger than r. So the trees are entirely regular and coclass-stable, in contrast to the trees with 3-groups G of coclass ![]() as vertices.
as vertices.
Unfortunately it is much less well known that the entire metabelian skeleton ![]() of the descendant tree
of the descendant tree ![]() of the elementary bicyclic 3-group
of the elementary bicyclic 3-group ![]() is the disjoint union of its coclass subgraphs
is the disjoint union of its coclass subgraphs ![]() , where each component
, where each component ![]() consists of a finite sporadic part
consists of a finite sporadic part ![]() and finitely many metabelian coclass trees
and finitely many metabelian coclass trees![]() , and there is a periodicity
, and there is a periodicity ![]() for each
for each![]() . This was proved by Nebelung [7] and confirmed by Eick ( [6] , Cnj. 14, p. 115).
. This was proved by Nebelung [7] and confirmed by Eick ( [6] , Cnj. 14, p. 115).
The following second main result of this paper extends the periodicity from the metabelian skeleton to the entire descendant tree, including all the non-metabelian vertices, provided the mainline vertices are still metabelian. Here, we include coclass trees of finite 3-groups with mainline vertices having two total transfer kernels and roots ![]() with
with![]() , respectively
, respectively ![]() with
with![]() .
.
Theorem 8.2. (Main Theorem on Co-Periodicity Isomorphisms of Coclass Trees.)
Let the integer ![]() be an upper bound. For each integer
be an upper bound. For each integer![]() , and for each of the six roots
, and for each of the six roots![]() ,
, ![]() , with even coclass
, with even coclass![]() , respectively the four roots
, respectively the four roots![]() ,
, ![]() , with odd coclass
, with odd coclass![]() , there exists a bijective mapping
, there exists a bijective mapping![]() , respectively
, respectively![]() , which is a strict isomorphism of infinite structured in-trees for the strict invariants in-degree
, which is a strict isomorphism of infinite structured in-trees for the strict invariants in-degree![]() , out-degree
, out-degree![]() , relation rank
, relation rank![]() , nuclear rank
, nuclear rank![]() , action flag
, action flag![]() , and transfer kernel type
, and transfer kernel type![]() . Moreover,
. Moreover, ![]() is a f-isomorphism of infinite structured in-trees for the following f-invariants with their transformation laws f:
is a f-isomorphism of infinite structured in-trees for the following f-invariants with their transformation laws f:
• logarithmic order ![]() with
with![]() ,
,
• nilpotency class ![]() with
with![]() ,
,
• coclass ![]() with
with![]() ,
,
• order of the automorphism group ![]() with
with![]() ,
,
• first component of the transfer target type ![]() with
with ![]() , and
, and
• commutator subgroup ![]() with
with ![]() , respectively
, respectively ![]() .
.
Proof. The statement for the metabelian skeletons ![]() of the coclass trees
of the coclass trees ![]() is one of the main results of Nebelung’s thesis [7] . With the aid of Theorem 8.1, the periodicity of the entire coclass trees
is one of the main results of Nebelung’s thesis [7] . With the aid of Theorem 8.1, the periodicity of the entire coclass trees ![]() with
with ![]() and fixed subscript i has been verified by computing the metabelian and non-metabelian vertices of the first four branches
and fixed subscript i has been verified by computing the metabelian and non-metabelian vertices of the first four branches ![]() with
with ![]() of the trees
of the trees![]() . The computations were executed by running our own program scripts for the Computer Algebra System MAGMA [17] , which contains an implementation of the p-group generation algorithm by Newman [12] [26] and O’Brien [13] [14] , the SmallGroups Database [18] [19] , and the ANUPQ package [20] . It turned out that, firstly,
. The computations were executed by running our own program scripts for the Computer Algebra System MAGMA [17] , which contains an implementation of the p-group generation algorithm by Newman [12] [26] and O’Brien [13] [14] , the SmallGroups Database [18] [19] , and the ANUPQ package [20] . It turned out that, firstly, ![]() and
and![]() , for each
, for each![]() , and secondly,
, and secondly, ![]() and
and![]() , for each
, for each![]() .
.
The established ![]() -isomorphisms between the infinite coclass trees
-isomorphisms between the infinite coclass trees ![]() and
and![]() , for
, for![]() , describe the germ of the second periodicity expressed in Conjecture 8.1. Invariants connected with the nilpotency class or coclass are not strict and are subject to the following mappings: the shifts
, describe the germ of the second periodicity expressed in Conjecture 8.1. Invariants connected with the nilpotency class or coclass are not strict and are subject to the following mappings: the shifts ![]() for
for![]() ,
,![]() for
for![]() ,and
,and ![]() for
for![]() ,and the corresponding transformations
,and the corresponding transformations![]() for
for![]() ,and
,and![]() for
for![]() .For
.For![]() ,the transformation law is described by the homothety
,the transformation law is described by the homothety![]() .
.
Thus, the confidence in the validity of the following conjecture is supported extensively by sound numerical data.
Conjecture 8.1. (Co-Periodicity Isomorphisms of All Coclass-r Trees for![]() .)
.)
Theorem 8.2 remains true when the upper bound ![]() is replaced by any upper bound
is replaced by any upper bound![]() .
.
Consequently, all coclass trees ![]() with
with ![]() and fixed subscript i are co-periodic in the variable coclass parameter r with primitive length
and fixed subscript i are co-periodic in the variable coclass parameter r with primitive length![]() . The eight coclass trees
. The eight coclass trees ![]() with
with![]() , and
, and ![]() for
for![]() ,
, ![]() for
for![]() ,
, ![]() for
for![]() , can be viewed as the pre-period of the co-periodicity. (Compare [6] , Cnj. 14, p. 115).
, can be viewed as the pre-period of the co-periodicity. (Compare [6] , Cnj. 14, p. 115).
9. Parametrized Polycyclic Power-Commutator Presentations
The general graph theoretic and algebraic foundations of the coclass forests ![]() with
with ![]() have been developed completely in the preceding Sections 2 - 7. Now we can turn to the main goal of the present paper, that is, the proof of the main theorems in section 8 by the systematic investigation of finite 3-groups G with commutator quotient
have been developed completely in the preceding Sections 2 - 7. Now we can turn to the main goal of the present paper, that is, the proof of the main theorems in section 8 by the systematic investigation of finite 3-groups G with commutator quotient![]() , represented by vertices of the descendant tree
, represented by vertices of the descendant tree![]() , with the single restriction that the parent
, with the single restriction that the parent ![]() of G is metabelian. To this end, we first need parametrized presentations for all metabelian vertices of
of G is metabelian. To this end, we first need parametrized presentations for all metabelian vertices of![]() .
.
9.1. 3-Groups of Coclass r = 1
The identification of 3-groups G with coclass![]() , which are metabelian without exceptions [27] , will be achieved with the aid of parametrized polycyclic power-commutator presentations, as given by Blackburn [9] :
, which are metabelian without exceptions [27] , will be achieved with the aid of parametrized polycyclic power-commutator presentations, as given by Blackburn [9] :
![]() (9.1)
(9.1)
where ![]() and
and ![]() are bounded parameters, and the index of nilpotency
are bounded parameters, and the index of nilpotency ![]() is an unbounded parameter.
is an unbounded parameter.
9.2. 3-Groups of Coclass r ≥ 2
Metabelian 3-groups with coclass ![]() will be identified with the aid of parametrized polycyclic power-commutator presentations, given by Nebelung [7] :
will be identified with the aid of parametrized polycyclic power-commutator presentations, given by Nebelung [7] :
![]() (9.2)
(9.2)
where![]() are bounded parameters, and the index of nilpo- tency
are bounded parameters, and the index of nilpo- tency![]() ,the logarithmic order
,the logarithmic order ![]() ,and the CF-invariant
,and the CF-invariant![]() are unbounded parameters.
are unbounded parameters.
10. The Backbone of the Tree![]() : The Infinite Main Trunk
: The Infinite Main Trunk
The flow of our investigations is guided by the present section concerning the remarkable infinite main trunk ![]() of certain metabelian vertices in
of certain metabelian vertices in ![]() which gives rise to the top vertices of all coclass forests
which gives rise to the top vertices of all coclass forests ![]() by periodic bifurcations and constitutes the germ of the newly discovered co-periodicity
by periodic bifurcations and constitutes the germ of the newly discovered co-periodicity ![]() of length two. Since the minimal possible values of the nilpotency class and logarithmic order of a finite metabelian 3-group with coclass
of length two. Since the minimal possible values of the nilpotency class and logarithmic order of a finite metabelian 3-group with coclass![]() , belonging to the forest
, belonging to the forest![]() , are given by
, are given by ![]() and
and![]() , it follows that G must be an immediate descendant of step size
, it follows that G must be an immediate descendant of step size ![]() of its parent
of its parent![]() . The crucial fact is that this parent is precisely the vertex
. The crucial fact is that this parent is precisely the vertex ![]() with
with ![]() of the main trunk. In the following, we rather use the coclass j of the parent than r of the children.
of the main trunk. In the following, we rather use the coclass j of the parent than r of the children.
Theorem 10.1. (The main trunk.)
1) In the descendant tree ![]() of the abelian root
of the abelian root![]() , there exists a unique infinite path of (reverse) directed edges
, there exists a unique infinite path of (reverse) directed edges ![]() such that, for each fixed coclass
such that, for each fixed coclass![]() , every metabelian 3-group G with
, every metabelian 3-group G with ![]() and
and ![]() is a proper descendant of
is a proper descendant of![]() .
.
2) The trailing vertex ![]() is exactly the extra special Blackburn group
is exactly the extra special Blackburn group ![]() with exceptional transfer kernel type (TKT ) a.1,
with exceptional transfer kernel type (TKT ) a.1,![]() .
.
3) All the other vertices ![]() with
with ![]() share the common TKT b.10,
share the common TKT b.10, ![]() , possess nilpotency class
, possess nilpotency class![]() , coclass
, coclass![]() , logarithmic order
, logarithmic order![]() , abelian commutator subgroup of type
, abelian commutator subgroup of type![]() , and transfer target type
, and transfer target type![]() , where
, where![]() .
.
4) For![]() , periodicity of length 2 sets in,
, periodicity of length 2 sets in, ![]() has nuclear rank
has nuclear rank![]() , relation rank
, relation rank![]() , and immediate descendant numbers (including non-metabelian groups)
, and immediate descendant numbers (including non-metabelian groups)
![]()
Restricted to metabelian groups, the immediate descendant numbers are
![]()
All immediate descendants are ![]() -groups, if
-groups, if ![]() is odd, but only
is odd, but only![]() , if
, if![]() , and
, and![]() , if
, if ![]() is even.
is even.
Proof. See the dissertation of Nebelung ( [7] , p. 192).
Remark 10.1. Although the number of metabelian children of step sizes ![]() of the vertex
of the vertex ![]() with
with ![]() fit into the periodic pattern
fit into the periodic pattern ![]() , the number of all children of step sizes
, the number of all children of step sizes ![]() of
of ![]() is bigger than usual with
is bigger than usual with ![]() instead of
instead of![]() . Therefore, periodicity starts with
. Therefore, periodicity starts with ![]() and not with
and not with![]() .
.
Corollary 10.1. (All coclass trees with metabelian mainlines.)
The coclass trees of 3-groups G with![]() , whose mainlines consist of metabelian vertices, possess the following remarkable periodicity of length 2, drawn impressively in Figure 4.
, whose mainlines consist of metabelian vertices, possess the following remarkable periodicity of length 2, drawn impressively in Figure 4.
1) For even![]() , the vertex
, the vertex ![]() with subscript
with subscript ![]() of the main trunk has exactly 4 immediate descendants of step size
of the main trunk has exactly 4 immediate descendants of step size ![]() giving rise to coclass trees
giving rise to coclass trees ![]() whose mainline vertices are metabelian 3-groups G with odd
whose mainline vertices are metabelian 3-groups G with odd ![]() and fixed TKT, either d.19,
and fixed TKT, either d.19, ![]() , or d.23,
, or d.23, ![]() , or d.25,
, or d.25, ![]() , or b.10,
, or b.10, ![]() , the latter with root
, the latter with root![]() .
.
2) For odd![]() , the vertex
, the vertex ![]() with subscript
with subscript ![]() of the main trunk has exactly 6 immediate descendants of step size
of the main trunk has exactly 6 immediate descendants of step size ![]() giving rise to coclass trees
giving rise to coclass trees ![]() whose mainline vertices are metabelian 3-groups G with even
whose mainline vertices are metabelian 3-groups G with even ![]() and fixed TKT, either d.19,
and fixed TKT, either d.19, ![]() , twice, or d.23,
, twice, or d.23, ![]() , or d.25,
, or d.25, ![]() , twice, or b.10,
, twice, or b.10, ![]() , the latter with root
, the latter with root![]() .
.
3) The unique pre-periodic exception is the vertex ![]() of the main trunk, which has exactly 3 immediate descendants of step size
of the main trunk, which has exactly 3 immediate descendants of step size ![]() giving rise to coclass trees
giving rise to coclass trees ![]() whose mainline vertices are metabelian 3-groups G with even
whose mainline vertices are metabelian 3-groups G with even ![]() and fixed TKT, either c.18,
and fixed TKT, either c.18, ![]() , or c.21,
, or c.21, ![]() , or b.10,
, or b.10, ![]() , the latter with root
, the latter with root![]() .
.
Proof. See the dissertation of Nebelung ( [7] , 5.2, pp. 181-195).
![]()
Figure 4. Metabelian mainline skeleton of the descendant tree![]() .
.
11. Sporadic and Periodic 3-Groups G of Even Coclass ![]()
Although formulated for the particular coclass![]() , all results for periodic groups and most of the results for sporadic groups in this section are valid for any even coclass
, all results for periodic groups and most of the results for sporadic groups in this section are valid for any even coclass![]() . The only exception is the bigger (and thus pre-periodic) sporadic part
. The only exception is the bigger (and thus pre-periodic) sporadic part ![]() of the coclass forest
of the coclass forest![]() , described in Proposition 11.2, whereas the (co-periodic) standard case, the sporadic part
, described in Proposition 11.2, whereas the (co-periodic) standard case, the sporadic part ![]() of the coclass forest
of the coclass forest![]() , is presented in Proposition 11.1.
, is presented in Proposition 11.1.
Figure 5 sketches an outline of the metabelian skeleton of the coclass forest ![]() in its top region. The vertices
in its top region. The vertices ![]() and
and![]() ,
,
![]()
Figure 5. Metabelian interface between the coclass forests ![]() and
and![]() .
.
with the crucial bifucation from ![]() to
to![]() , belong to the infinite main trunk (§10).
, belong to the infinite main trunk (§10).
Proposition 11.1 (Co-periodic standard case.)
The sporadic part ![]() of the coclass-6 forest
of the coclass-6 forest ![]() consists of
consists of
• 13 ![]() isolated metabelian vertices of order 313 with types F.7, F.11, F.12, F.13,
isolated metabelian vertices of order 313 with types F.7, F.11, F.12, F.13,
• 8 ![]() metabelian roots of finite trees with types G.16, G.19, H.4, together with a metabelian child having a GI-action, which is unique for each root, and 22 metabelian and 38 non-metabelian children without GI-action, all with depth
metabelian roots of finite trees with types G.16, G.19, H.4, together with a metabelian child having a GI-action, which is unique for each root, and 22 metabelian and 38 non-metabelian children without GI-action, all with depth ![]() and
and![]() ,
,
• 66 ![]() isolated vertices with
isolated vertices with ![]() and types d.19, d.23, d.25,
and types d.19, d.23, d.25,
• 179 isolated vertices with ![]() and type b.10,
and type b.10,
• 23 capable vertices with ![]() and type b.10,
and type b.10,
Whose children do not belong to![]() , by definition.
, by definition.
The action flag of all metabelian top vertices with depth ![]() is
is![]() . The value
. The value ![]() only occurs for all vertices with type b.10, d.25, G.19, and certain vertices with type G.16, H.4, but never for type d.19, d.23, F.7, F.11, F.12, F.13. Exactly the isolated vertices with depth
only occurs for all vertices with type b.10, d.25, G.19, and certain vertices with type G.16, H.4, but never for type d.19, d.23, F.7, F.11, F.12, F.13. Exactly the isolated vertices with depth ![]() have an RI-action.
have an RI-action.
Together with the 6 metabelian roots![]() ,
, ![]() , of coclass-6 trees, the
, of coclass-6 trees, the ![]() top vertices of depth
top vertices of depth ![]() of
of ![]() are exactly the
are exactly the ![]() children of step size
children of step size ![]() of the main trunk vertex
of the main trunk vertex![]() , and the
, and the ![]() capable vertices among them correspond to the invariant
capable vertices among them correspond to the invariant ![]() of
of![]() .
.
Proposition 11.2. (Pre-periodic exception.)
The constitution of the sporadic part ![]() of the coclass-4 forest
of the coclass-4 forest ![]() with respect to the 21 metabelian top vertices and their 68 children (here with order 39, resp.
with respect to the 21 metabelian top vertices and their 68 children (here with order 39, resp.![]() ) is the same as described for
) is the same as described for ![]() in Proposition 11.1, but the number of non-metabelian top vertices of depth
in Proposition 11.1, but the number of non-metabelian top vertices of depth ![]() is bigger, namely
is bigger, namely
• 88 ![]() isolated vertices with
isolated vertices with ![]() and types d.19, d.23, d.25,
and types d.19, d.23, d.25,
• 12 ![]() capable vertices with
capable vertices with ![]() and types d.19, d.23, d.25,
and types d.19, d.23, d.25,
whose children do not belong to![]() , by definition,
, by definition,
• 268 isolated vertices with ![]() and type b.10,
and type b.10,
• 58 capable vertices with ![]() and type b.10,
and type b.10,
whose children do not belong to![]() , by definition.
, by definition.
The distribution of the action flags ![]() is the same as in Proposition 11.1, but the total census of top vertices is considerably bigger:
is the same as in Proposition 11.1, but the total census of top vertices is considerably bigger:
Together with the 6 metabelian roots![]() ,
, ![]() , of coclass-4 trees, the
, of coclass-4 trees, the ![]() top vertices of depth
top vertices of depth ![]() of
of ![]() are exactly the
are exactly the ![]() children of step size
children of step size ![]() of the main trunk vertex
of the main trunk vertex![]() , and the
, and the ![]() capable vertices among them corres- pond to the invariant
capable vertices among them corres- pond to the invariant ![]() of
of![]() .
.
Theorem 11.1. The coclass-r forest ![]() with any even
with any even ![]() is the disjoint union of its finite sporadic part
is the disjoint union of its finite sporadic part ![]() with total information content
with total information content
![]() (11.1)
(11.1)
and ![]() infinite coclass-r trees
infinite coclass-r trees ![]() with roots
with roots![]() , where
, where
![]()
The algebraic invariants for groups with positive action flag![]() , and in cumulative form for
, and in cumulative form for![]() , are given for
, are given for ![]() in Table 1, where the parent vertex
in Table 1, where the parent vertex ![]() on the main trunk is also included, but the 426 non-metabelian top vertices of depth
on the main trunk is also included, but the 426 non-metabelian top vertices of depth ![]() are excluded.
are excluded.
Proof. (of Propositions 11.1, 11.2, and Theorem 11.1) We have computed the sporadic parts ![]() of coclass forests
of coclass forests ![]() with even
with even ![]() up to
up to ![]() by means of MAGMA [17] . Except for the differences pointed out in the
by means of MAGMA [17] . Except for the differences pointed out in the
![]()
Table 1. Data for sporadic 3-groups G with ![]() in the forest
in the forest![]() .
.
Propositions 11.1 and 11.2, they all share a common graph theoretic structure with![]() . The forest
. The forest ![]() contains 6 roots of infinite coclass trees with metabelian mainlines (a unique root
contains 6 roots of infinite coclass trees with metabelian mainlines (a unique root ![]() of type b and five roots
of type b and five roots ![]() of type d), namely
of type d), namely
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
which give rise to the periodic part of![]() , and 51 sporadic metabelian groups of type F, G or H. Among the groups of the sporadic part
, and 51 sporadic metabelian groups of type F, G or H. Among the groups of the sporadic part![]() , there are 13 isolated metabelian vertices with type F, and 8 metabelian roots of finite trees with type G or H and tree depth 1, each with a unique metabelian child having
, there are 13 isolated metabelian vertices with type F, and 8 metabelian roots of finite trees with type G or H and tree depth 1, each with a unique metabelian child having![]() . The other
. The other ![]() children with
children with![]() , of which
, of which ![]() are metabelian and
are metabelian and ![]() have derived length 3, are omitted in the forest diagram, Figure 5. Additionally,
have derived length 3, are omitted in the forest diagram, Figure 5. Additionally, ![]() , respectively
, respectively![]() , contains 426, respectively 268, non-metabelian top vertices, which gives a total information content
, contains 426, respectively 268, non-metabelian top vertices, which gives a total information content ![]() of
of![]() , respectively
, respectively![]() , representatives. The difference is an excess of
, representatives. The difference is an excess of ![]() vertices in
vertices in ![]() .
.
The metabelian skeleton of both, ![]() and
and![]() , consists of
, consists of ![]() vertices. The results for metabelian groups are in accor- dance with the fourth tree diagram
vertices. The results for metabelian groups are in accor- dance with the fourth tree diagram![]() ,
, ![]() , in ( [7] , fourth double page between pp. 191-192). The metabelian groups in Table 1 correpond to the representatives of isomorphism classes in ( [28] , pp. 36-38 and 42-45).
, in ( [7] , fourth double page between pp. 191-192). The metabelian groups in Table 1 correpond to the representatives of isomorphism classes in ( [28] , pp. 36-38 and 42-45).
11.1. The Unique Mainline of Type b.10* for Even Coclass r ≥ 4
Proposition 11.3. (Periodicity and descendant numbers.)
The branches![]() ,
, ![]() , of the coclass-4 tree
, of the coclass-4 tree ![]() with mainline vertices of transfer kernel type b.10*,
with mainline vertices of transfer kernel type b.10*, ![]() , are periodic with pre-period length
, are periodic with pre-period length ![]() and with primitive period length
and with primitive period length![]() , that is,
, that is, ![]() are isomorphic as digraphs, for all
are isomorphic as digraphs, for all![]() .
.
The graph theoretic structure of the tree is determined uniquely by the numbers ![]() of immediate descendants and
of immediate descendants and ![]() of capable immediate descen- dants of the mainline vertices
of capable immediate descen- dants of the mainline vertices ![]() with logarithmic order
with logarithmic order ![]() :
:
![]() for the root
for the root ![]() with
with![]() ,
,
![]() for all mainline vertices
for all mainline vertices ![]() with even logarithmic order
with even logarithmic order ![]() ,
,
![]() for all mainline vertices
for all mainline vertices ![]() with odd logarithmic order
with odd logarithmic order ![]() .
.
Proof. (of Proposition 11.3) The statements concerning the numbers ![]() of immediate descendants of the mainline vertices
of immediate descendants of the mainline vertices ![]() with
with ![]() have been obtained by direct computation with MAGMA [17] , where the p-group generation algorithm by Newman and O'Brien [12] [13] [14] is implemented. In detail, we proved that there are:
have been obtained by direct computation with MAGMA [17] , where the p-group generation algorithm by Newman and O'Brien [12] [13] [14] is implemented. In detail, we proved that there are:
4, resp. 6, metabelian vertices with bicyclic centre![]() , resp. cyclic centre
, resp. cyclic centre![]() , and
, and
5, resp. 6, non-metabelian vertices with![]() , resp.
, resp.![]() ,
,
together 21 vertices (10 of them metabelian) in the pre-periodic branch![]() ,
,
and the primitive period ![]() of length
of length ![]() consists of
consists of
6, resp. 6, metabelian vertices with![]() , resp.
, resp.![]() , and
, and
9, resp. 9, non-metabelian vertices with![]() , resp.
, resp.![]() ,
,
together 30 vertices (12 of them metabelian) in branch![]() , and
, and
4, resp. 8, metabelian vertices with![]() , resp.
, resp.![]() , and
, and
5, resp. 10, non-metabelian vertices with![]() , resp.
, resp.![]() ,
,
together 27 vertices (12 of them metabelian) in branch![]() .
.
The results concerning the metabelian skeleton confirm the corresponding statements in the dissertation of Nebelung ( [7] , Thm. 5.1.16, pp. 178-179, and the fourth Figure, e ≥ 5, e ![]() 1, on the double page between pp. 191-192). The tree
1, on the double page between pp. 191-192). The tree ![]() corresponds to the infinite metabelian pro-3 group
corresponds to the infinite metabelian pro-3 group ![]() in ( [6] , Cnj. 15 (b), p. 116). Although every branch contains 12 metabelian vertices, the primitive period length is
in ( [6] , Cnj. 15 (b), p. 116). Although every branch contains 12 metabelian vertices, the primitive period length is ![]() rather than
rather than![]() , even for the metabelian skeleton, since the constitution
, even for the metabelian skeleton, since the constitution ![]() of branch
of branch ![]() is different from
is different from ![]() for branch
for branch![]() , as proved above.
, as proved above.
The claim of the virtual periodicity of branches has been proved generally for any coclass tree by du Sautoy [1] , and independently by Eick and Leedham- Green [2] . Here, the strict periodicity was confirmed by computation up to branch ![]() and undoubtedly sets in at
and undoubtedly sets in at![]() .
.
Theorem 11.2. (Graph theoretic and algebraic invariants.)
The coclass-4 tree ![]() of finite 3-groups G with coclass
of finite 3-groups G with coclass ![]() which arises from the metabelian root
which arises from the metabelian root ![]() has the fol- lowing graph theoretic properties.
has the fol- lowing graph theoretic properties.
1) The pre-period ![]() of length
of length ![]() is irregular.
is irregular.
2) The cardinality of the irregular branch is![]() .
.
3) The branches![]() ,
, ![]() , are periodic with primitive period
, are periodic with primitive period ![]() of length
of length![]() .
.
4) The cardinalities of the regular branches are ![]() and
and![]() .
.
5) Depth, width, and information content of the tree are given by
![]() (11.2)
(11.2)
The algebraic invariants of the groups represented by vertices forming the pre-period ![]() and the primitive period
and the primitive period ![]() of the tree are given in Table 2. The leading six branches
of the tree are given in Table 2. The leading six branches ![]() are drawn in Figure 6.
are drawn in Figure 6.
Remark 11.1. The algebraic information in Table 2 is visualized in Figure 6. By periodic continuation, the figure shows more branches than the table but less details concerning the exact order ![]() of the automorphism group.
of the automorphism group.
Proof. (of Theorem 11.2) According to Proposition 11.3, the logarithmic order of the tree root, respectively of the periodic root, is ![]() , respectively
, respectively ![]() .
.
Since ![]() for all mainline vertices
for all mainline vertices ![]() with
with ![]() , according to
, according to
![]()
Figure 6. The unique coclass-4 tree ![]() with mainline of type b.10*.
with mainline of type b.10*.
Proposition 11.3, the unique capable child of ![]() is
is ![]() , and each branch has depth
, and each branch has depth ![]() , for
, for ![]() . Consequently, the tree is also of depth
. Consequently, the tree is also of depth ![]() .
.
With the aid of Formula (5.9) in Theorem 5.1, the claims (2) and (4) are consequences of Proposition 11.3:
![]() ,
, ![]() , and
, and ![]() .
.
According to Formula (5.13) in Corollary 5.1, where n runs from ![]() to
to ![]() , the tree width is the maximum
, the tree width is the maximum ![]() of the expressions
of the expressions ![]() ,
, ![]() , and
, and ![]() .
.
![]()
Table 2. Data for 3-groups G with ![]() of the coclass tree
of the coclass tree![]() .
.
The information content of the tree is given by Formula (5.17) in the Definition 5.3:
![]()
The algebraic invariants in Table 2, that is, depth ![]() , derived length
, derived length ![]() , abelian type invariants of the centre
, abelian type invariants of the centre ![]() , relation rank
, relation rank ![]() , nuclear rank
, nuclear rank ![]() , abelian quotient invariants
, abelian quotient invariants ![]() of the first maximal subgroup, respectively
of the first maximal subgroup, respectively ![]() of the commutator subgroup, transfer kernel type
of the commutator subgroup, transfer kernel type ![]() , action flag
, action flag ![]() , and the factorized order
, and the factorized order ![]() of the automorphism group have been computed by means of program scripts written for MAGMA [17] .
of the automorphism group have been computed by means of program scripts written for MAGMA [17] .
Each group is characterized by the parameters of the normalized representative ![]() of its isomorphism class, according to Formula (9.2), and by its identifier
of its isomorphism class, according to Formula (9.2), and by its identifier ![]() in the SmallGroups Database [19] .
in the SmallGroups Database [19] .
The column with header # contains the number of groups with identical invariants (except the presentation), for each row.
Corollary 11.1. (Actions and relation ranks.) The algebraic invariants of the vertices of the structured coclass-4 tree ![]() are listed in Table 2. In particular:
are listed in Table 2. In particular:
1) The groups with ![]() -action are all mainline vertices
-action are all mainline vertices ![]() ,
, ![]() , the two terminal vertices
, the two terminal vertices ![]() with odd
with odd ![]() , the two terminal vertices
, the two terminal vertices ![]() with even
with even ![]() , and two terminal non-metabelian vertices with odd
, and two terminal non-metabelian vertices with odd ![]() .
.
2) With respect to the kernel types, all mainline groups of type b.10*, ![]() , the two leaves of type d.25,
, the two leaves of type d.25, ![]() , with every odd logarithmic order, two distinguished metabelian leaves of type b.10 with every even logarithmic order, and two distinguished non-metabelian leaves of type b.10 with every odd logarithmic order possess a
, with every odd logarithmic order, two distinguished metabelian leaves of type b.10 with every even logarithmic order, and two distinguished non-metabelian leaves of type b.10 with every odd logarithmic order possess a ![]() -action.
-action.
3) The relation rank is given by ![]() for the mainline vertices
for the mainline vertices ![]() ,
, ![]() , and
, and ![]() otherwise. There do not occur any RI-actions.
otherwise. There do not occur any RI-actions.
Proof. (of Corollary 11.1) The existence of an RI-action on G has been checked by means of an algorithm involving the p-covering group of G, written for MAGMA [17] . The other claims follow immediately from Table 2, continued indefinitely with the aid of the periodicity in Prop. 11.3.
11.2. Two Mainlines of Type d.19* for Even Coclass r ≥ 4
Proposition 11.4. (Periodicity and descendant numbers.)
The branches ![]() ,
, ![]() , of the first coclass-4 tree
, of the first coclass-4 tree ![]() with mainline vertices of transfer kernel type d.19*,
with mainline vertices of transfer kernel type d.19*, ![]() , are purely periodic with primitive length
, are purely periodic with primitive length ![]() and without pre-period,
and without pre-period, ![]() , that is,
, that is, ![]() are isomorphic as digraphs, for all
are isomorphic as digraphs, for all ![]() .
.
The graph theoretic structure of the tree is determined uniquely by the numbers ![]() of immediate descendants and
of immediate descendants and ![]() of capable immediate descendants of the mainline vertices
of capable immediate descendants of the mainline vertices ![]() with logarithmic order
with logarithmic order ![]() and of capable vertices v with depth 1 and
and of capable vertices v with depth 1 and ![]() :
:
![]() for mainline vertices
for mainline vertices ![]() with odd logarithmic order
with odd logarithmic order ![]() ,
,
![]() for mainline vertices
for mainline vertices ![]() with even logarithmic order
with even logarithmic order ![]() ,
,
![]() for the capable vertex v of depth 1 and even logarithmic order
for the capable vertex v of depth 1 and even logarithmic order ![]() ,
,
![]() for two capable vertices v of depth 1 and odd logarithmic order
for two capable vertices v of depth 1 and odd logarithmic order ![]() .
.
Proof. (of Proposition 11.4) The statements concerning the numbers ![]() of immediate descendants of the mainline vertices
of immediate descendants of the mainline vertices ![]() with
with ![]() , and
, and ![]() of vertices with depth
of vertices with depth ![]() and logarithmic order
and logarithmic order ![]() , have been obtained by direct computation with the p-group generation algorithm [12] [13] [14] in MAGMA [17] . In detail, we proved that there is no pre-period,
, have been obtained by direct computation with the p-group generation algorithm [12] [13] [14] in MAGMA [17] . In detail, we proved that there is no pre-period, ![]() , and the primitive period
, and the primitive period ![]() of length
of length ![]() consists of
consists of
5, resp. 9, metabelian vertices with ![]() , resp.
, resp. ![]() , and
, and
8, resp. 16, non-metabelian vertices with ![]() , resp.
, resp. ![]() ,
,
(![]() children of
children of ![]() , and
, and ![]() children of
children of ![]() with depth 1)
with depth 1)
together 38 vertices (14 of them metabelian) in branch ![]() , and
, and
9, resp. 10, metabelian vertices with ![]() , resp.
, resp. ![]() , and
, and
16, resp. 16, non-metabelian vertices with ![]() , resp.
, resp. ![]() ,
,
(![]() children of
children of ![]() , and
, and ![]() children of
children of ![]() , both with depth 1)
, both with depth 1)
together 51 vertices (19 of them metabelian) in branch ![]() .
.
The results concerning the metabelian skeleton confirm the corresponding statements in the dissertation of Nebelung ( [7] , Thm. 5.1.16, pp. 178-179, and the fourth Figure, e ≥ 5, ![]() , on the double page between pp. 191-192). The tree
, on the double page between pp. 191-192). The tree ![]() corresponds to the infinite metabelian pro-3 group
corresponds to the infinite metabelian pro-3 group ![]() in ( [6] , Cnj. 15 (b), p. 116).
in ( [6] , Cnj. 15 (b), p. 116).
The claim of the virtual periodicity of branches has been proved generally for any coclass tree in [1] and [2] . Here, the strict periodicity was confirmed by computation up to branch ![]() and undoubtedly sets in at
and undoubtedly sets in at ![]() .
.
Theorem 11.3. (Graph theoretic and algebraic invariants.)
The coclass-4 tree ![]() of 3-groups G with coclass
of 3-groups G with coclass ![]() which arises from the metabelian root
which arises from the metabelian root ![]() has the following abstract graph theoretic properties.
has the following abstract graph theoretic properties.
1) The branches ![]() ,
, ![]() , are purely periodic with primitive period
, are purely periodic with primitive period ![]() of length
of length![]() .
.
2) The cardinalities of the periodic branches are ![]() and
and![]() .
.
3) Depth, width, and information content of the tree are given by
![]() (11.3)
(11.3)
The algebraic invariants of the vertices forming the primitive period ![]() of the tree are given in Table 3. The six leading branches
of the tree are given in Table 3. The six leading branches ![]() are drawn in Figure 7.
are drawn in Figure 7.
Proof. (of Theorem 11.3) Since every mainline vertex ![]() of the tree
of the tree ![]() has several capable children,
has several capable children, ![]() , but every capable vertex v of depth 1 has only terminal children,
, but every capable vertex v of depth 1 has only terminal children, ![]() , according to Proposition 11.4, the depth of the tree is
, according to Proposition 11.4, the depth of the tree is![]() . In this case, the cardinality of a branch
. In this case, the cardinality of a branch ![]() is the sum of the number
is the sum of the number ![]() of immediate descendants of the branch root
of immediate descendants of the branch root ![]() and the numbers
and the numbers ![]() of terminal children of capable vertices
of terminal children of capable vertices ![]() of depth 1 with
of depth 1 with ![]() (excluding the next mainline vertex
(excluding the next mainline vertex![]() ), according to Formula (5.10), that is,
), according to Formula (5.10), that is,
![]()
Table 3. Data for 3-groups G with ![]() of the coclass tree
of the coclass tree![]() .
.
![]()
Figure 7. The first coclass-4 tree ![]() with mainline of type d.19*.
with mainline of type d.19*.
![]()
Applied to the primitive period, this yields![]() ,
,![]() .According to Formula (5.14), the width of the tree is the maximum of all sums of the shape
.According to Formula (5.14), the width of the tree is the maximum of all sums of the shape
![]()
taken over all branch roots![]() with logarithmic orders
with logarithmic orders![]() .Applied to
.Applied to![]() ,
,![]() ,and
,and![]() ,this yields
,this yields
![]() .
.
Finally, we have![]() .
.
Corollary 11.2. (Actions and relation ranks.) The algebraic invariants of the vertices of the structured coclass-4 tree ![]() are listed in Table 3. In par- ticular:
are listed in Table 3. In par- ticular:
1) There are no groups with ![]() -action.
-action.
2) Two distinguished terminal metabelian vertices of depth 2 with even class and type H.4, all terminal vertices of depth 1 with odd class, and the mainline vertices with even class, possess an RI-action.
3) The relation rank is given by ![]() for the mainline vertices
for the mainline vertices ![]() with
with![]() , and the capable vertices
, and the capable vertices ![]() of depth 1 with
of depth 1 with![]() , and
, and ![]() otherwise.
otherwise.
Proof. (of Corollary 11.2) The existence of an RI-action on G has been checked by means of an algorithm involving the p-covering group of G, written for MAGMA [17] . The other claims follow immediately from Table 3, continued indefinitely with the aid of the periodicity in Prop. 11.4.
Theorem 11.4. (Strict isomorphism of the two trees.)
Viewed as an algebraically structured infinite digraph, the second coclass-4 tree ![]() with mainline of type d.19* in Figure 8 is strictly isomorphic to the first coclass-4 tree
with mainline of type d.19* in Figure 8 is strictly isomorphic to the first coclass-4 tree ![]() with mainline of type d.19* in Figure 7. Only the presentations of corresponding vertices are different, but they share common algebraic invariants.
with mainline of type d.19* in Figure 7. Only the presentations of corresponding vertices are different, but they share common algebraic invariants.
Proof. (Proof of Theorem 11.3 and Theorem 11.4) The claims have been verified with the aid of MAGMA [17] for all vertices v with logarithmic orders![]() . Pure periodicity of branches with primitive length 2 sets in from the very beginning with
. Pure periodicity of branches with primitive length 2 sets in from the very beginning with![]() . There is no pre-period. Thus, the claims for all vertices v with logarithmic orders
. There is no pre-period. Thus, the claims for all vertices v with logarithmic orders ![]() are a consequence of the virtual periodicity theorems by du Sautoy in ( [1] , Thm. 1.11, p. 68, and Thm. 8.3, p. 103) and by Eick and Leedham-Green in ( [2] , Thm. 6, p. 277, Thm. 9, p. 278, and Thm. 29, p. 287], without the need of pruning the depth, which is bounded uniformly by 2.
are a consequence of the virtual periodicity theorems by du Sautoy in ( [1] , Thm. 1.11, p. 68, and Thm. 8.3, p. 103) and by Eick and Leedham-Green in ( [2] , Thm. 6, p. 277, Thm. 9, p. 278, and Thm. 29, p. 287], without the need of pruning the depth, which is bounded uniformly by 2.
11.3. The Unique Mainline of Type d.23* for Even Coclass r ≥ 4
Proposition 11.5. (A special nearly strict isomorphism.)
Viewed as an algebraically structured infinite digraph, the unique coclass-4 tree ![]() with mainline of type d.23* in Figure 9 is almost strictly isomorphic to the first coclass-4 tree
with mainline of type d.23* in Figure 9 is almost strictly isomorphic to the first coclass-4 tree ![]() with mainline of type d.19* in Figure 7, and thus also to the second coclass-4 tree
with mainline of type d.19* in Figure 7, and thus also to the second coclass-4 tree ![]() with mainline of type d.19* in Figure 8. Only the
with mainline of type d.19* in Figure 8. Only the
![]()
Figure 8. The second coclass-4 tree ![]() with mainline of type d.19*.
with mainline of type d.19*.
presentations of corresponding vertices are different, but they share common algebraic invariants, with the transfer kernel types as single exception: the nearly strict isomorphism of directed trees maps![]() ,
, ![]() ,
, ![]() , and F.12 either remains fixed or
, and F.12 either remains fixed or![]() .
.
Proof. This follows immediately from comparing Table 4 with Table 3, and using periodicity.
Proposition 11.6. (Periodicity and descendant numbers.)
The branches![]() ,
, ![]() , of the unique coclass-4 tree
, of the unique coclass-4 tree
![]() with mainline vertices of transfer kernel type d.23*,
with mainline vertices of transfer kernel type d.23*,
![]()
Figure 9. The unique coclass-4 tree ![]() with mainline of type d.23*.
with mainline of type d.23*.
![]() , are purely periodic with primitive length
, are purely periodic with primitive length ![]() and without pre-period,
and without pre-period, ![]() , that is,
, that is, ![]() are isomorphic as digraphs, for all
are isomorphic as digraphs, for all![]() .
.
The graph theoretic structure of the tree is determined uniquely by the numbers ![]() of immediate descendants and
of immediate descendants and ![]() of capable immediate descendants of the mainline vertices
of capable immediate descendants of the mainline vertices ![]() with logarithmic order
with logarithmic order ![]() and of capable vertices v with depth 1 and
and of capable vertices v with depth 1 and![]() :
:
![]()
Table 4. Data for 3-groups G with ![]() of the coclass tree
of the coclass tree![]() .
.
![]() for mainline vertices
for mainline vertices ![]() with odd logarithmic order
with odd logarithmic order![]() ,
,
![]() for mainline vertices
for mainline vertices ![]() with even logarithmic order
with even logarithmic order![]() ,
,
![]() for the capable vertex v of depth 1 and even logarithmic order
for the capable vertex v of depth 1 and even logarithmic order![]() ,
,
![]() for two capable vertices v of depth 1 and odd logarithmic order
for two capable vertices v of depth 1 and odd logarithmic order![]() .
.
Proof. This is a consequence of Proposition 11.5 together with Proposition 11.4. The tree ![]() corresponds to the infinite metabelian pro-3 group
corresponds to the infinite metabelian pro-3 group ![]() in ( [6] , Cnj. 15 (b), p. 116).
in ( [6] , Cnj. 15 (b), p. 116).
Theorem 11.5. (Graph theoretic and algebraic invariants.)
The coclass-4 tree ![]() of 3-groups G with coclass
of 3-groups G with coclass ![]() which arises from the metabelian root
which arises from the metabelian root ![]() has the following abstract graph theoretic properties.
has the following abstract graph theoretic properties.
1) The branches![]() ,
, ![]() , are purely periodic with primitive period
, are purely periodic with primitive period ![]() of length
of length![]() .
.
2) The cardinalities of the periodic branches are ![]() and
and ![]() .
.
3) Depth, width, and information content of the tree are given by
![]() (11.4)
(11.4)
The algebraic invariants of the vertices forming the primitive period ![]() of the tree are given in Table 4. The six leading branches
of the tree are given in Table 4. The six leading branches ![]() are drawn in Figure 9.
are drawn in Figure 9.
Proof. Since the tree ![]() is isomorphic to the tree
is isomorphic to the tree ![]() as an abstract digraph, the proof literally coincides with the proof of Theorem 11.3.
as an abstract digraph, the proof literally coincides with the proof of Theorem 11.3.
Corollary 11.3. (Actions and relation ranks.) The algebraic invariants of the vertices of the structured coclass-4 tree ![]() are listed in Table 4. In particular:
are listed in Table 4. In particular:
1) There are no groups with ![]() -action.
-action.
2) Two distinguished terminal metabelian vertices of depth 2 with even class and type G.16, all terminal vertices of depth 1 with odd class, and the mainline vertices with even class, possess an RI-action.
3) The relation rank is given by ![]() for the mainline vertices
for the mainline vertices ![]() with
with![]() , and the capable vertices
, and the capable vertices ![]() of depth 1 with
of depth 1 with![]() , and
, and ![]() otherwise.
otherwise.
11.4. Two Mainlines of Type d.25* for Even Coclass r ≥ 4
Proposition 11.7. (Periodicity and descendant numbers.)
The branches![]() ,
, ![]() , of the first coclass-4 tree
, of the first coclass-4 tree ![]() with mainline vertices of transfer kernel type d.25*,
with mainline vertices of transfer kernel type d.25*, ![]() , are purely periodic with primitive length
, are purely periodic with primitive length ![]() and without pre- period,
and without pre- period, ![]() , that is,
, that is, ![]() are isomorphic as graphs, for all
are isomorphic as graphs, for all![]() .
.
The structure of the tree is determined uniquely by the numbers ![]() of immediate descendants and
of immediate descendants and ![]() of capable immediate descendants for mainline vertices and for capable vertices of depth 1:
of capable immediate descendants for mainline vertices and for capable vertices of depth 1:
![]() for mainline vertices
for mainline vertices ![]() of odd logarithmic order
of odd logarithmic order ![]() ,
,
![]() for mainline vertices
for mainline vertices ![]() of even logarithmic order
of even logarithmic order ![]() ,
,
![]() for a capable vertex v of depth 1 and even logarithmic order
for a capable vertex v of depth 1 and even logarithmic order![]() ,
,
![]() for two capable vertices v of depth 1 and odd logarithmic order
for two capable vertices v of depth 1 and odd logarithmic order![]() .
.
Theorem 11.6. (Graph theoretic and algebraic invariants.)
The coclass-4 tree ![]() of 3-groups G with coclass
of 3-groups G with coclass ![]() which arises from the metabelian root
which arises from the metabelian root ![]() has the following abstract graph theoretic properties.
has the following abstract graph theoretic properties.
1) The branches![]() ,
, ![]() , are purely periodic with primitive period
, are purely periodic with primitive period ![]() of length
of length![]() .
.
2) The cardinalities of the periodic branches are ![]() and
and![]() .
.
3) Depth, width, and information content of the tree are given by
![]() (11.5)
(11.5)
The algebraic invariants of the vertices forming the primitive period ![]() of the tree are presented in Table 5. The leading six branches
of the tree are presented in Table 5. The leading six branches ![]() are drawn in Figure 10.
are drawn in Figure 10.
![]()
Table 5. Data for 3-groups G with ![]() of the coclass tree
of the coclass tree![]() .
.
![]()
Figure 10. The first coclass-4 tree ![]() with mainline of type d.25*.
with mainline of type d.25*.
Corollary 11.4. (Actions and relation ranks.)
The algebraic invariants of the vertices of the structured coclass-4 tree ![]() are listed in Table 5. In particular:
are listed in Table 5. In particular:
1) All mainline vertices, two capable metabelian vertices of depth 1 with odd class and type G.19, two distinguished terminal metabelian vertices of depth 2 with even class and type G.19, and two distinguished terminal non-metabelian vertices of depth 1 with odd class and type d.25 possess a ![]() -action.
-action.
2) Two distinguished terminal metabelian vertices of depth 2 with even class and type G.19, all terminal vertices of depth 1 with odd class, and the mainline vertices with even class, possess an RI-action.
3) The relation rank is given by ![]() for the mainline vertices
for the mainline vertices ![]() with
with![]() , and the capable vertices
, and the capable vertices ![]() of depth 1 with
of depth 1 with![]() , and
, and ![]() otherwise.
otherwise.
Proof. (of Proposition 11.7, Theorem 11.6, and Corollary 11.4) The proofs are very similar to those of Proposition 11.4, Theorem 11.3, and Corollary 11.2. The differences are only the concrete numerical values of the invariants involved in the calculations:
![]() ,
, ![]() ,
,
![]() ,
,
and![]() .
.
In detail, we proved that there is no pre-period, ![]() , and the primitive period
, and the primitive period ![]() of length
of length ![]() consists of
consists of
4, resp. 6, metabelian vertices with![]() , resp.
, resp.![]() , and
, and
5, resp. 9, non-metabelian vertices with![]() , resp.
, resp.![]() ,
,
(![]() children of
children of![]() , and
, and ![]() children of
children of ![]() with depth 1)
with depth 1)
together 24 vertices (10 of them metabelian) in branch![]() , and
, and
6, resp. 8, metabelian vertices with![]() , resp.
, resp.![]() , and
, and
9, resp. 10, non-metabelian vertices with![]() , resp.
, resp.![]() ,
,
(![]() children of
children of![]() , and
, and ![]() children of
children of![]() , both with depth 1)
, both with depth 1)
together 33 vertices (14 of them metabelian) in branch![]() .
.
The tree ![]() corresponds to the infinite metabelian pro-3 group
corresponds to the infinite metabelian pro-3 group ![]() in ( [6] , Cnj. 15 (b), p. 116).
in ( [6] , Cnj. 15 (b), p. 116).
Theorem 11.7. (Strict isomorphism of the two trees.)
Viewed as an algebraically structured infinite digraph, the second coclass-4 tree ![]() with mainline of type d.25* in Figure 11 is strictly isomorphic to the first coclass-4 tree
with mainline of type d.25* in Figure 11 is strictly isomorphic to the first coclass-4 tree ![]() with mainline of type d.25* in Figure 10. Only the presentations of corresponding vertices are different, but they share common algebraic invariants.
with mainline of type d.25* in Figure 10. Only the presentations of corresponding vertices are different, but they share common algebraic invariants.
Proof. (Proof of Thm. 11.6 and Thm 11.7.) The claims have been verified with the aid of MAGMA [17] for all vertices V with logarithmic orders![]() . Pure periodicity of branches sets in with
. Pure periodicity of branches sets in with![]() . Thus, the claims for all vertices V with logarithmic orders
. Thus, the claims for all vertices V with logarithmic orders ![]() are a consequence of the periodicity theorems by du Sautoy in [1] and by Eick and Leedham-Green in [2] , without the need of pruning the depth, which is bounded uniformly by 2.
are a consequence of the periodicity theorems by du Sautoy in [1] and by Eick and Leedham-Green in [2] , without the need of pruning the depth, which is bounded uniformly by 2.
![]()
Figure 11. The second coclass tree ![]() with mainline of type d.25*.
with mainline of type d.25*.
12. Sporadic and Periodic 3-Groups G of Odd Coclass ![]()
Although formulated for the particular coclass![]() , all results on sporadic and periodic groups in this section are valid for any odd coclass
, all results on sporadic and periodic groups in this section are valid for any odd coclass![]() . The exemplary (co-periodic) sporadic part
. The exemplary (co-periodic) sporadic part ![]() of the coclass forest
of the coclass forest ![]() is presented in the following Proposition 12.1.
is presented in the following Proposition 12.1.
Proposition 12.1. The sporadic part ![]() of the coclass-5 forest
of the coclass-5 forest ![]() consists of
consists of
• 7 ![]() isolated metabelian vertices with types F.7, F.11, F.12, F.13,
isolated metabelian vertices with types F.7, F.11, F.12, F.13,
• 4 ![]() metabelian roots of finite trees with types G.16, G.19, H.4, together with their 24 metabelian and 36 non-metabelian children, all with depth
metabelian roots of finite trees with types G.16, G.19, H.4, together with their 24 metabelian and 36 non-metabelian children, all with depth![]() ,
,
• 34 ![]() isolated vertices with
isolated vertices with ![]() and types d.19, d.23, d.25,
and types d.19, d.23, d.25,
• 89 isolated vertices with ![]() and type b.10,
and type b.10,
• 13 capable vertices with ![]() and type b.10,
and type b.10,
whose children do not belong to![]() , by definition.
, by definition.
The action flag of all vertices is![]() , and consequently none of them has an RI- or
, and consequently none of them has an RI- or ![]() -action.
-action.
Together with the 4 metabelian roots of coclass-5 trees, the ![]() vertices of depth
vertices of depth ![]() are exactly the
are exactly the ![]() children of step size
children of step size ![]() of
of![]() , and the
, and the ![]() capable vertices among them correspond to the invariant
capable vertices among them correspond to the invariant ![]() of
of![]() .
.
Figure 12 sketches an outline of the metabelian skeleton of the coclass forest ![]() in its top region. The vertices
in its top region. The vertices ![]() and
and ![]() , with the crucial bifurcation from
, with the crucial bifurcation from ![]() to
to![]() , belong to the infinite main trunk (§10).
, belong to the infinite main trunk (§10).
Theorem 12.1. The coclass-r forest ![]() with any odd
with any odd ![]() is the disjoint union of its finite sporadic part
is the disjoint union of its finite sporadic part ![]() with total information content
with total information content
![]() (12.1)
(12.1)
and ![]() infinite coclass-r trees
infinite coclass-r trees ![]() with roots
with roots![]() , where
, where ![]() for
for![]() . The algebraic invariants for groups with centre
. The algebraic invariants for groups with centre![]() , and in cumulative form for
, and in cumulative form for![]() , are given for
, are given for ![]() in Table 6, where the parent vertex
in Table 6, where the parent vertex ![]() on the maintrunk is also included, but the 136 non-metabelian top vertices of depth
on the maintrunk is also included, but the 136 non-metabelian top vertices of depth ![]() are excluded.
are excluded.
Proof. (of Proposition 12.1 and Theorem 12.1) We have computed the sporadic parts ![]() of coclass forests
of coclass forests ![]() with odd
with odd ![]() up to
up to ![]() by means of MAGMA [17] . They all share a common graph theoretic structure with
by means of MAGMA [17] . They all share a common graph theoretic structure with![]() . The forest
. The forest ![]() contains 4 roots of coclass trees with metabelian mainlines (a unique root
contains 4 roots of coclass trees with metabelian mainlines (a unique root ![]() of type b and three roots
of type b and three roots ![]() of type d), namely
of type d), namely
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
which give rise to the periodic part of![]() , and 35 sporadic metabelian groups of type F, G or H. Among the groups of the sporadic part
, and 35 sporadic metabelian groups of type F, G or H. Among the groups of the sporadic part![]() , there are 7 isolated metabelian vertices with type F, and 4 metabelian roots of finite trees with type G or H and tree depth 1. Among the
, there are 7 isolated metabelian vertices with type F, and 4 metabelian roots of finite trees with type G or H and tree depth 1. Among the ![]()
![]()
Figure 12. Metabelian interface between the coclass forests ![]() and
and![]() .
.
children, there are ![]() metabelian, and
metabelian, and ![]() have derived length 3. The latter are omitted in the forest diagram, Figure 12. Additionally,
have derived length 3. The latter are omitted in the forest diagram, Figure 12. Additionally, ![]() contains 136 non-metabelian top vertices, which gives a total information content
contains 136 non-metabelian top vertices, which gives a total information content ![]() of
of ![]() representatives.
representatives.
The metabelian skeleton consists of ![]() vertices. The results for metabelian groups are in accordance with the third tree diagram
vertices. The results for metabelian groups are in accordance with the third tree diagram![]() ,
, ![]() , in ( [7] , third page between pp. 191-192). The metabelian groups in Table 6 correspond to the representatives of isomorphism classes in ( [28] , pp. 34-35).
, in ( [7] , third page between pp. 191-192). The metabelian groups in Table 6 correspond to the representatives of isomorphism classes in ( [28] , pp. 34-35).
12.1. The Unique Mainline of Type b.10* for Odd Coclass r ≥ 5
Proposition 12.2. (Periodicity and descendant numbers.)
![]()
Table 6. Data for sporadic 3-groups G with ![]() of the forest
of the forest![]() .
.
The branches![]() ,
, ![]() , of the coclass-5 tree
, of the coclass-5 tree ![]() with mainline vertices of transfer kernel type b.10*,
with mainline vertices of transfer kernel type b.10*, ![]() , are periodic with pre-period length
, are periodic with pre-period length ![]() and with primitive period length
and with primitive period length![]() , that is,
, that is, ![]() are isomorphic as digraphs, for all
are isomorphic as digraphs, for all![]() .
.
The graph theoretic structure of the tree is determined uniquely by the numbers ![]() of immediate descendants and
of immediate descendants and ![]() of capable immediate descen- dants of the mainline vertices
of capable immediate descen- dants of the mainline vertices ![]() with logarithmic order
with logarithmic order![]() :
:
![]() for the root
for the root ![]() with
with![]() ,
,
![]() for all mainline vertices
for all mainline vertices ![]() with even logarithmic order
with even logarithmic order![]() ,
,
![]() for all mainline vertices
for all mainline vertices ![]() with odd logarithmic order
with odd logarithmic order![]() .
.
Proof. (of Proposition 12.2) The statements concerning the numbers ![]() of immediate descendants of the mainline vertices
of immediate descendants of the mainline vertices ![]() with
with ![]() have been obtained by direct computation with the p-group generation algorithm [12] [13] [14] in MAGMA [17] . In detail, we proved that there are
have been obtained by direct computation with the p-group generation algorithm [12] [13] [14] in MAGMA [17] . In detail, we proved that there are
6, resp. 6, metabelian vertices with bicyclic centre![]() , resp. cyclic centre
, resp. cyclic centre![]() , and
, and
9, resp. 9, non-metabelian vertices with![]() , resp.
, resp.![]() ,
,
together 30 vertices (12 of them metabelian) in the pre-periodic branch![]() ,
,
and the primitive period ![]() of length
of length ![]() consists of
consists of
4, resp. 6, metabelian vertices with![]() , resp.
, resp.![]() , and
, and
5, resp. 9, non-metabelian vertices with![]() , resp.
, resp.![]() ,
,
together 24 vertices (10 of them metabelian) in branch![]() , and
, and
6, resp. 9, metabelian vertices with![]() , resp.
, resp.![]() , and
, and
9, resp. 16, non-metabelian vertices with![]() , resp.
, resp.![]() ,
,
together 40 vertices (15 of them metabelian) in branch![]() .
.
The results concerning the metabelian skeleton confirm the corresponding statements in the dissertation of Nebelung ( [7] , Thm. 5.1.16, pp. 178-179, and the third Figure, e ≥ 4, e ![]() 0 (mod 2), on the third page between pp. 191-192]). The tree
0 (mod 2), on the third page between pp. 191-192]). The tree ![]() corresponds to the infinite metabelian pro-3 group
corresponds to the infinite metabelian pro-3 group ![]() in ( [6] , Cnj. 15 (a), p. 116).
in ( [6] , Cnj. 15 (a), p. 116).
The claim of the virtual periodicity of branches has been proved generally for any coclass tree in [1] and [2] . Here, the strict periodicity was confirmed by computation up to branch ![]() and clearly sets in at
and clearly sets in at![]() .
.
Theorem 12.2. (Graph theoretic and algebraic invariants.)
The coclass-5 tree ![]() of finite 3-groups G with coclass
of finite 3-groups G with coclass ![]() which arises from the metabelian root
which arises from the metabelian root ![]() has the following graph theoretic properties.
has the following graph theoretic properties.
1) The pre-period ![]() of length
of length ![]() is irregular.
is irregular.
2) The cardinality of the irregular branch is![]() .
.
3) The branches![]() ,
, ![]() , are periodic with primitive period
, are periodic with primitive period ![]() of length
of length![]() .
.
4) The cardinalities of the regular branches are ![]() and
and ![]() .
.
5) Depth, width, and information content of the tree are given by
![]() (12.2)
(12.2)
The algebraic invariants of the groups represented by vertices forming the pre-period ![]() and the primitive period
and the primitive period ![]() of the tree are given in Table 7. The six leading branches
of the tree are given in Table 7. The six leading branches ![]() are drawn in Figure 13.
are drawn in Figure 13.
Remark 12.1. The algebraic information in Table 7 is visualized in Figure 13. By periodic continuation, the figure shows more branches than the table but less details concerning the exact order ![]() of the automorphism group.
of the automorphism group.
Proof. (of Theorem 12.2) According to Proposition 12.2, the logarithmic order of the tree root, respectively of the periodic root, is![]() , respectively
, respectively![]() .
.
Since ![]() for all mainline vertices
for all mainline vertices ![]() with
with![]() , according to Proposition 12.2, the unique capable child of
, according to Proposition 12.2, the unique capable child of ![]() is
is![]() , and each branch has
, and each branch has
![]()
Table 7. Data for 3-groups G with ![]() of the coclass tree
of the coclass tree![]() .
.
![]()
Figure 13. The unique coclass-5 tree ![]() with mainline of type b.10*.
with mainline of type b.10*.
depth![]() , for
, for![]() . Consequently, the tree is also of depth
. Consequently, the tree is also of depth![]() .
.
With the aid of Formula (5.9) in Theorem 5.1, the claims (2) and (4) are consequences of Proposition 12.2:
![]() ,
, ![]() ,
,
and![]() .
.
According to Formula (5.13) in Corollary 5.1, where n runs from ![]() to
to ![]() , the tree width is the maximum
, the tree width is the maximum ![]() of the expressions
of the expressions ![]() ,
, ![]() , and
, and ![]() .
.
The information content of the tree is given by Formula (5.17) in the Definition 5.3:
![]() .
.
The algebraic invariants in Table 7, that is, depth ![]() , derived length
, derived length ![]() , abelian type invariants of the centre
, abelian type invariants of the centre ![]() , relation rank
, relation rank ![]() , nuclear rank
, nuclear rank ![]() , abelian quotient invariants
, abelian quotient invariants ![]() of the first maximal subgroup, respectively
of the first maximal subgroup, respectively ![]() of the commutator subgroup, transfer kernel type
of the commutator subgroup, transfer kernel type ![]() , action flag
, action flag ![]() , and the factorized order
, and the factorized order ![]() of the automorphism group have been computed by means of program scripts written for MAGMA [17] .
of the automorphism group have been computed by means of program scripts written for MAGMA [17] .
Each group is characterized by the parameters of the normalized repre- sentative ![]() of its isomorphism class, according to Formula (9.2), and by its identifier
of its isomorphism class, according to Formula (9.2), and by its identifier ![]() in the SmallGroups Database [19] .
in the SmallGroups Database [19] .
The column with header # contains the number of groups with identical invariants (except the presentation), for each row.
Corollary 12.1. (Actions and relation ranks.) The algebraic invariants of the vertices of the structured coclass-5 tree ![]() are listed in Table 7. In par- ticular:
are listed in Table 7. In par- ticular:
1) The groups with ![]() -action are all mainline vertices
-action are all mainline vertices ![]() ,
, ![]() , the two terminal vertices
, the two terminal vertices ![]() with even
with even ![]() , two terminal non-metabelian vertices with
, two terminal non-metabelian vertices with ![]() and even
and even ![]() , three pre-periodic terminal vertices
, three pre-periodic terminal vertices ![]() , and two pre-periodic terminal non-metabelian vertices with
, and two pre-periodic terminal non-metabelian vertices with ![]() and
and ![]() .
.
2) With respect to the kernel types, all mainline groups of type b.10*, ![]() , the two leaves of type d.25,
, the two leaves of type d.25, ![]() , with every even logari- thmic order, two distinguished non-metabelian leaves of type b.10 with every even logarithmic order, and five pre-periodic leaves of type b.10 with
, with every even logari- thmic order, two distinguished non-metabelian leaves of type b.10 with every even logarithmic order, and five pre-periodic leaves of type b.10 with ![]() possess a
possess a ![]() -action.
-action.
3) All terminal vertices of depth 1 with odd class and the mainline vertices with even class possess an RI-action.
4) The relation rank is given by ![]() for the mainline vertices
for the mainline vertices ![]() ,
, ![]() , and
, and ![]() otherwise.
otherwise.
Proof. (of Corollary 12.1) The existence of an RI-action on G has been checked by means of an algorithm involving the p-covering group of G, written for MAGMA [17] . The other claims follow immediately from Table 7, continued indefinitely with the aid of the periodicity in Proposition 12.2.
12.2. The Unique Mainline of Type d.19* for Odd Coclass r ≥ 5
Proposition 12.3. (Periodicity and descendant numbers.)
The branches ![]() ,
, ![]() , of the unique coclass-5 tree
, of the unique coclass-5 tree ![]() with mainline vertices of transfer kernel type d.19*,
with mainline vertices of transfer kernel type d.19*, ![]() , are purely periodic with primitive length
, are purely periodic with primitive length ![]() and without pre-period,
and without pre-period, ![]() , that is,
, that is, ![]() are isomorphic as structured digraphs, for all
are isomorphic as structured digraphs, for all ![]() .
.
The graph theoretic structure of the tree is determined uniquely by the numbers ![]() of immediate descendants and
of immediate descendants and ![]() of capable immediate descendants for mainline vertices
of capable immediate descendants for mainline vertices ![]() with logarithmic order
with logarithmic order ![]() and for capable vertices v with depth 1 and
and for capable vertices v with depth 1 and ![]() :
:
![]() for all mainline vertices
for all mainline vertices ![]() of any logarithmic order
of any logarithmic order ![]() ,
,
![]() for two capable vertices v of depth 1 and any logarithmic order
for two capable vertices v of depth 1 and any logarithmic order ![]() .
.
Proof. (of Proposition 12.3) The statements concerning the numbers ![]() of immediate descendants of the mainline vertices
of immediate descendants of the mainline vertices ![]() with
with ![]() , and
, and ![]() of vertices with depth
of vertices with depth ![]() and logarithmic order
and logarithmic order ![]() , have been obtained by direct computation with the p-group generation algorithm [12] [13] [14] in MAGMA [17] . In detail, we proved that there is no pre-period,
, have been obtained by direct computation with the p-group generation algorithm [12] [13] [14] in MAGMA [17] . In detail, we proved that there is no pre-period, ![]() , and the primitive period
, and the primitive period ![]() of length
of length ![]() consists of:
consists of:
9, resp. 18, metabelian vertices with ![]() , resp.
, resp. ![]() , and
, and
16, resp. 32, non-metabelian vertices with ![]() , resp.
, resp. ![]() ,
,
(i.e. ![]() children of
children of ![]() , and
, and ![]() children of
children of ![]() , both with depth 1)
, both with depth 1)
together 75 vertices (27 of them metabelian) in branch ![]() .
.
The results concerning the metabelian skeleton confirm the corresponding statements in the dissertation of Nebelung ( [7] , Thm. 5.1.16, pp. 178-179, and the third Figure, e ≥ 4, ![]() , on the third page between pp. 191-192) The tree
, on the third page between pp. 191-192) The tree ![]() corresponds to the infinite metabelian pro-3 group
corresponds to the infinite metabelian pro-3 group ![]() in ( [6] , Cnj. 15 (a), p. 116).
in ( [6] , Cnj. 15 (a), p. 116).
The claim of the virtual periodicity of branches has been proved generally for any coclass tree in [1] and [2] . Here, the strict periodicity was confirmed by computation up to branch ![]() and certainly sets in at
and certainly sets in at ![]() .
.
Theorem 12.3. (Graph theoretic and algebraic invariants.)
The coclass-5 tree ![]() of 3-groups G with coclass
of 3-groups G with coclass ![]() which arises from the metabelian root
which arises from the metabelian root ![]() has the following abstract graph theoretic properties.
has the following abstract graph theoretic properties.
1) The branches ![]() ,
, ![]() , are purely periodic with primitive period
, are purely periodic with primitive period ![]() of length
of length ![]() .
.
2) The cardinality of the periodic branch is ![]() .
.
3) Depth, width, and information content of the tree are given by
![]() (12.3)
(12.3)
The algebraic invariants of the vertices forming the root and the primitive period ![]() of the tree are presented in Table 8. The leading six branches
of the tree are presented in Table 8. The leading six branches ![]() are drawn in Figure 14.
are drawn in Figure 14.
Proof. (Proof of Theorem 12.3) Since every mainline vertex ![]() of the tree
of the tree ![]() has three capable children,
has three capable children, ![]() , but every capable vertex v of depth 1 has only terminal children,
, but every capable vertex v of depth 1 has only terminal children, ![]() , according to Proposition 12.3, the depth of the tree is
, according to Proposition 12.3, the depth of the tree is ![]() . In this case, the cardinality of a branch
. In this case, the cardinality of a branch ![]() is
is
![]()
Figure 14. The unique coclass-5 tree ![]() with mainline of type d.19*.
with mainline of type d.19*.
![]()
Table 8. Data for 3-groups G with ![]() of the coclass tree
of the coclass tree ![]() .
.
the sum of the number ![]() of immediate descendants of the branch root
of immediate descendants of the branch root ![]() and the numbers
and the numbers ![]() of terminal children of capable vertices
of terminal children of capable vertices ![]() of depth 1 with
of depth 1 with ![]() (excluding the next mainline vertex
(excluding the next mainline vertex ![]() ), according to Formula (5.10), that is,
), according to Formula (5.10), that is,
![]()
Applied to the primitive period, this yields ![]() . According to Formula (30), the width of the tree is the maximum of all sums of the shape
. According to Formula (30), the width of the tree is the maximum of all sums of the shape
![]()
taken over all branch roots ![]() with logarithmic orders
with logarithmic orders ![]() . Applied to
. Applied to ![]() ,
, ![]() , and
, and ![]() , this yields
, this yields ![]() .
.
Finally, we have ![]() .
.
Corollary 12.2. (Actions and relation ranks.)
The algebraic invariants of the vertices of the structured coclass-5 tree ![]() are listed in Table 8. In particular:
are listed in Table 8. In particular:
1) There are no groups with GI-action, let alone with RI- or ![]() -action.
-action.
2) The relation rank is given by ![]() for the mainline vertices
for the mainline vertices ![]() with
with ![]() , and the capable vertices
, and the capable vertices ![]() of depth 1 with
of depth 1 with ![]() , and
, and ![]() otherwise.
otherwise.
Proof. (of Corollary 12.2) The existence of an RI-action on G has been checked by means of an algorithm involving the p-covering group of G, written for MAGMA [17] . The other claims follow immediately from Table 8, continued indefinitely with the aid of the periodicity in Proposition 12.3.
12.3. The Unique Mainline of Type d.23* for Odd Coclass r ≥ 5
Proposition 12.4. (Periodicity and descendant numbers.)
The branches ![]() ,
, ![]() , of the unique coclass-5 tree
, of the unique coclass-5 tree ![]() with mainline vertices of transfer kernel type d.23*,
with mainline vertices of transfer kernel type d.23*, ![]() , are purely periodic with primitive length
, are purely periodic with primitive length ![]() and without pre-period,
and without pre-period, ![]() , that is,
, that is, ![]() are isomorphic as structured digraphs, for all
are isomorphic as structured digraphs, for all ![]() .
.
The graph theoretic structure of the tree is determined uniquely by the numbers ![]() of immediate descendants and
of immediate descendants and ![]() of capable immediate descendants for mainline vertices
of capable immediate descendants for mainline vertices ![]() with logarithmic order
with logarithmic order ![]() and for capable vertices v with depth 1 and
and for capable vertices v with depth 1 and ![]() :
:
![]() for all mainline vertices
for all mainline vertices ![]() of any logarithmic order
of any logarithmic order ![]() ,
,
![]() for the capable vertex v of depth 1 and any logarithmic order
for the capable vertex v of depth 1 and any logarithmic order ![]() .
.
Proof. (of Proposition 12.4) The statements concerning the numbers ![]() of immediate descendants of the mainline vertices
of immediate descendants of the mainline vertices ![]() with
with ![]() , and
, and ![]() of vertices with depth
of vertices with depth ![]() and logarithmic order
and logarithmic order ![]() , have been obtained by direct computation with the p-group generation algorithm [12] [13] [14] in MAGMA [17] . In detail, we proved that there is no pre-period,
, have been obtained by direct computation with the p-group generation algorithm [12] [13] [14] in MAGMA [17] . In detail, we proved that there is no pre-period, ![]() , and the primitive period
, and the primitive period ![]() of length
of length ![]() consists of
consists of
6, resp. 9, metabelian vertices with ![]() , resp.
, resp. ![]() , and
, and
9, resp. 16, non-metabelian vertices with ![]() , resp.
, resp. ![]() ,
,
(i.e. ![]() children of
children of ![]() , and
, and ![]() ) children of
) children of ![]() with depth 1)
with depth 1)
together 40 vertices (15 of them metabelian) in branch ![]() .
.
The results concerning the metabelian skeleton confirm the corresponding statements in the dissertation of Nebelung ( [7] , Thm. 5.1.16, pp. 178-179, and the third Figure, e ≥ 4, ![]() , on the third page between pp. 191-192). The tree
, on the third page between pp. 191-192). The tree ![]() corresponds to the infinite metabelian pro-3 group
corresponds to the infinite metabelian pro-3 group ![]() in ( [6] , Cnj. 15 (a), p. 116).
in ( [6] , Cnj. 15 (a), p. 116).
The claim of the virtual periodicity of branches has been proved generally for any coclass tree in [1] and [2] . Here, the strict periodicity was confirmed by computation up to branch ![]() and certainly sets in at
and certainly sets in at ![]() .
.
Theorem 12.4. (Graph theoretic and algebraic invariants.)
The coclass-5 tree ![]() of 3-groups G with coclass
of 3-groups G with coclass ![]() arises from the metabelian root
arises from the metabelian root ![]() and has the following abstract graph theoretic properties.
and has the following abstract graph theoretic properties.
1) The branches ![]() ,
, ![]() , are purely periodic with primitive period
, are purely periodic with primitive period ![]() of length
of length ![]() .
.
2) The cardinality of the periodic branch is ![]() .
.
3) Depth, width, and information content of the tree are given by
![]() (12.4)
(12.4)
The algebraic invariants of the vertices forming the root and the primitive period ![]() of the tree are presented in Table 9. The leading six branches
of the tree are presented in Table 9. The leading six branches ![]() are drawn in Figure 15.
are drawn in Figure 15.
![]()
Figure 15. The unique coclass-5 tree ![]() with mainline of type d.23*.
with mainline of type d.23*.
![]()
Table 9. Data for 3-groups G with ![]() of the coclass tree
of the coclass tree ![]() .
.
Proof. (Proof of Theorem 12.4) Since every mainline vertex ![]() of the tree
of the tree ![]() has two capable children,
has two capable children, ![]() , but every capable vertex v of depth 1 has only terminal children,
, but every capable vertex v of depth 1 has only terminal children, ![]() , according to Proposition 12.4, the depth of the tree is
, according to Proposition 12.4, the depth of the tree is ![]() . In this case, the cardinality of a branch
. In this case, the cardinality of a branch ![]() is the sum of the number
is the sum of the number ![]() of immediate descendants of the branch root
of immediate descendants of the branch root ![]() and the numbers
and the numbers ![]() of terminal children of capable vertices
of terminal children of capable vertices ![]() of depth 1,
of depth 1, ![]() (
(![]() the next mainline vertex must be omitted), according to Formula (5.10),
the next mainline vertex must be omitted), according to Formula (5.10),
![]()
Applied to the primitive period, this yields ![]() . According to Formula (5.14), the width of the tree is the maximum of all sums of the shape
. According to Formula (5.14), the width of the tree is the maximum of all sums of the shape
![]()
taken over all branch roots ![]() with logarithmic orders
with logarithmic orders ![]() . Applied to
. Applied to ![]() ,
, ![]() , and
, and ![]() , this yields
, this yields ![]() . Finally, we have
. Finally, we have ![]() .
.
Corollary 12.3. (Actions and relation ranks.) The algebraic invariants of the vertices of the structured coclass-5 tree ![]() are listed in Table 9. In par- ticular:
are listed in Table 9. In par- ticular:
1) There are no groups with GI-action, let alone with RI- or ![]() -action.
-action.
2) The relation rank is given by ![]() for the mainline vertices
for the mainline vertices ![]() with
with ![]() , and the capable vertices
, and the capable vertices ![]() of depth 1 with
of depth 1 with ![]() , and
, and ![]() otherwise.
otherwise.
Proof. (of Corollary 12.3) The existence of an RI-action on G has been checked by means of an algorithm involving the p-covering group of G, written for MAGMA [17] . The other claims follow immediately from Table 9, continued indefinitely with the aid of the periodicity in Prop. 12.4.
12.4. The Unique Mainline of Type d.25* for Odd Coclass r ≥ 5
Proposition 12.5. (Periodicity and descendant numbers.)
The branches ![]() ,
, ![]() , of the unique coclass-5 tree
, of the unique coclass-5 tree ![]() with mainline vertices of transfer kernel type d.25*,
with mainline vertices of transfer kernel type d.25*, ![]() , are purely periodic with primitive length
, are purely periodic with primitive length ![]() and without pre-period,
and without pre-period, ![]() , that is,
, that is, ![]() are isomorphic as structured digraphs, for all
are isomorphic as structured digraphs, for all ![]() .
.
The graph theoretic structure of the tree is determined uniquely by the numbers ![]() of immediate descendants and
of immediate descendants and ![]() of capable immediate descendants for mainline vertices
of capable immediate descendants for mainline vertices ![]() with logarithmic order
with logarithmic order ![]() and for capable vertices v with depth 1 and
and for capable vertices v with depth 1 and ![]() :
:
![]() for all mainline vertices
for all mainline vertices ![]() of odd logarithmic order
of odd logarithmic order ![]() ,
,
![]() for all mainline vertices
for all mainline vertices ![]() of even logarithmic order
of even logarithmic order ![]() ,
,
![]() for two capable vertices v of depth 1 and even logarithmic order
for two capable vertices v of depth 1 and even logarithmic order ![]() ,
,
![]() for the capable vertex v of depth 1 and odd logarithmic order
for the capable vertex v of depth 1 and odd logarithmic order ![]() .
.
Proof. (of Proposition 12.5) The statements concerning the numbers ![]() of immediate descendants of the mainline vertices
of immediate descendants of the mainline vertices ![]() with
with ![]() , and
, and ![]() of vertices with depth
of vertices with depth ![]() and logarithmic order
and logarithmic order ![]() , have been obtained by direct computation with the p-group generation algori- thm [12] [13] [14] in MAGMA [17] . In detail, we proved that there is no pre-period,
, have been obtained by direct computation with the p-group generation algori- thm [12] [13] [14] in MAGMA [17] . In detail, we proved that there is no pre-period, ![]() , and the primitive period
, and the primitive period ![]() of length
of length ![]() consists of
consists of
6, resp. 12, metabelian vertices with ![]() , resp.
, resp. ![]() , and
, and
9, resp. 18, non-metabelian vertices with ![]() , resp.
, resp. ![]() ,
,
(i.e. ![]() children of
children of ![]() , and
, and ![]() children of
children of ![]() , both with depth 1)
, both with depth 1)
together 45 vertices (18 of them metabelian) in branch ![]() , and
, and
6, resp. 9, metabelian vertices with ![]() , resp.
, resp. ![]() , and
, and
9, resp. 16, non-metabelian vertices with ![]() , resp.
, resp. ![]() ,
,
(i.e. ![]() children of
children of ![]() , and
, and ![]() children of
children of ![]() with depth 1)
with depth 1)
together 40 vertices (15 of them metabelian) in branch ![]() .
.
The results concerning the metabelian skeleton confirm the corresponding statements in the dissertation of Nebelung ( [7] , Thm. 5.1.16, pp. 178-179, and the third Figure, e ≥ 4, ![]() , on the third page between pp. 191-192]. The tree
, on the third page between pp. 191-192]. The tree ![]() corresponds to the infinite metabelian pro-3 group
corresponds to the infinite metabelian pro-3 group ![]() in ( [6] , Cnj. 15 (a), p. 116).
in ( [6] , Cnj. 15 (a), p. 116).
The claim of the virtual periodicity of branches has been proved generally for any coclass tree in [1] and [2] . Here, the strict periodicity was confirmed by computation up to branch ![]() and certainly sets in at
and certainly sets in at ![]() .
.
Theorem 12.5. (Graph theoretic and algebraic invariants.)
The coclass-5 tree ![]() of 3-groups G with coclass
of 3-groups G with coclass ![]() which arises from the metabelian root
which arises from the metabelian root ![]() has the following abstract graph theoretic properties.
has the following abstract graph theoretic properties.
1) The branches ![]() ,
, ![]() , are purely periodic with primitive period
, are purely periodic with primitive period ![]() of length
of length ![]() .
.
2) The cardinalities of the periodic branches are ![]() and
and ![]() .
.
3) Depth, width, and information content of the tree are given by
![]() (12.5)
(12.5)
The algebraic invariants of the vertices forming the root and the primitive period ![]() of the tree are presented in Table 10. The leading six branches
of the tree are presented in Table 10. The leading six branches ![]() are drawn in Figure 16.
are drawn in Figure 16.
Proof. (Proof of Theorem 12.5) Since every mainline vertex ![]() of the tree
of the tree ![]() has several capable children,
has several capable children, ![]() , but every capable vertex v of depth 1 has only terminal children,
, but every capable vertex v of depth 1 has only terminal children, ![]() , according to Proposition 12.5, the depth of the tree is
, according to Proposition 12.5, the depth of the tree is ![]() . In this case, the cardinality of a branch
. In this case, the cardinality of a branch ![]() is the sum of the number
is the sum of the number ![]() of immediate descendants of the branch root
of immediate descendants of the branch root ![]() and the numbers
and the numbers ![]() of terminal children of capable vertices
of terminal children of capable vertices ![]() of depth 1,
of depth 1, ![]() (where
(where ![]() is the next mainline vertex and must be discouraged), according to Formula (5.10),
is the next mainline vertex and must be discouraged), according to Formula (5.10),![]() Applied to the primitive period, this yields
Applied to the primitive period, this yields ![]() and
and ![]() . According to Formula (5.14), the width of the tree is the maximum of all sums of the shape
. According to Formula (5.14), the width of the tree is the maximum of all sums of the shape![]() taken over all branch roots
taken over all branch roots ![]() with logarithmic orders
with logarithmic orders ![]() . Applied to
. Applied to ![]() ,
, ![]() , and
, and ![]() , this yields
, this yields ![]() . Finally, we have
. Finally, we have ![]() .Corollary 12.4. (Actions and relation ranks.)
.Corollary 12.4. (Actions and relation ranks.)
![]()
Figure 16. The unique coclass-5 tree ![]() with mainline of type d.25*.
with mainline of type d.25*.
The algebraic invariants of the vertices of the structured coclass-5 tree ![]() are listed in Table 10. In particular:
are listed in Table 10. In particular:
1) There are no groups with GI-action, let alone with RI- or ![]() -action.
-action.
2) The relation rank is given by ![]() for the mainline vertices
for the mainline vertices ![]() with
with ![]() , and the capable vertices
, and the capable vertices ![]() of depth 1 with
of depth 1 with ![]() , and
, and ![]() otherwise.
otherwise.
![]()
Table 10. Data for 3-groups G with ![]() of the coclass tree
of the coclass tree ![]() .
.
Proof. (of Corollary 12.4) The existence of an RI-action on G has been checked by means of an algorithm involving the p-covering group of G, written for MAGMA [17] . The other claims follow immediately from Table 10, continued indefinitely with the aid of the periodicity in Proposition 12.5.
13. The Forest of 3-Groups with Coclass 1
The coclass forests ![]() and
and ![]() , and even their metabelian skeletons, sporadic parts, and individual coclass trees, do not reveal any isomorphism to higher coclass forests
, and even their metabelian skeletons, sporadic parts, and individual coclass trees, do not reveal any isomorphism to higher coclass forests ![]() , with
, with ![]() , or parts of them. The metabelian skeleton of the coclass forest
, or parts of them. The metabelian skeleton of the coclass forest ![]() is isomorphic to the metabelian skeleton of any coclass forest
is isomorphic to the metabelian skeleton of any coclass forest ![]() , with odd
, with odd ![]() , according to Nebelung [7] , but neither its sporadic part nor its coclass trees are isomorphic to the corres- ponding components of other coclass forests.
, according to Nebelung [7] , but neither its sporadic part nor its coclass trees are isomorphic to the corres- ponding components of other coclass forests.
Whereas the complexity of the pre-periodic forests ![]() and
and ![]() is very high, the simplest forest
is very high, the simplest forest ![]() can be described easily. In particular, the coclass-1 forest
can be described easily. In particular, the coclass-1 forest ![]() coincides with its unique coclass tree arising from the abelian root
coincides with its unique coclass tree arising from the abelian root ![]() . Its sporadic part
. Its sporadic part ![]() is void.
is void.
The Unique Mainline of Type a.1* for Coclass r = 1
Proposition 13.1. (Periodicity and descendant numbers.)
The branches ![]() ,
, ![]() , of the coclass-1 tree
, of the coclass-1 tree ![]() with mainline vertices of transfer kernel type a.1*,
with mainline vertices of transfer kernel type a.1*, ![]() , are periodic with pre-period length
, are periodic with pre-period length ![]() and with primitive period length
and with primitive period length ![]() , that is,
, that is, ![]() are isomorphic as digraphs, for all
are isomorphic as digraphs, for all ![]() .
.
The graph theoretic structure of the tree is determined uniquely by the numbers ![]() of immediate descendants and
of immediate descendants and ![]() of capable immediate descendants of the mainline vertices
of capable immediate descendants of the mainline vertices ![]() with logarithmic order
with logarithmic order ![]() :
:
![]() for the root
for the root ![]() with
with ![]() ,
,
![]() for the mainline vertex
for the mainline vertex ![]() with
with ![]() ,
,
![]() for mainline vertices
for mainline vertices ![]() with even logarithmic order
with even logarithmic order ![]() ,
,
![]() for mainline vertices
for mainline vertices ![]() with odd logarithmic order
with odd logarithmic order ![]() .
.
Proof. (of Proposition 13.1) The statements concerning the numbers ![]() of immediate descendants of the mainline vertices
of immediate descendants of the mainline vertices ![]() with
with ![]() are due to Blackburn ( [9] , Thm. 4.2 and Thm 4.3, p. 88), who distinguishes the groups according to their defect of commutativity
are due to Blackburn ( [9] , Thm. 4.2 and Thm 4.3, p. 88), who distinguishes the groups according to their defect of commutativity ![]() , which is defined by
, which is defined by ![]() in terms of the lower central series
in terms of the lower central series ![]() , nilpotency class
, nilpotency class ![]() , and the two-step centralizer
, and the two-step centralizer ![]() of G.
of G.
In detail, Blackburn proved that there are
4 vertices v with defect ![]() in the pre-periodic branch
in the pre-periodic branch ![]() ,
,
and the primitive period ![]() of length
of length ![]() consists of
consists of
3 vertices v with defect ![]() , and 3 vertices v with defect
, and 3 vertices v with defect ![]() ,
,
together 6 vertices in branch ![]() , and
, and
4 vertices v with defect ![]() , and 3 vertices v with defect
, and 3 vertices v with defect ![]() ,
,
together 7 vertices in branch ![]() . All vertices of the tree are metabelian.
. All vertices of the tree are metabelian.
The results were reproduced and supplemented with ![]() by Nebe- lung ( [7] , Thm. 5.1.17, pp. 179-180), and have been verified by ourselves independently by direct computation with MAGMA [17] , where the p-group generation algorithm by Newman and O'Brien [12] [13] [14] is implemented.
by Nebe- lung ( [7] , Thm. 5.1.17, pp. 179-180), and have been verified by ourselves independently by direct computation with MAGMA [17] , where the p-group generation algorithm by Newman and O'Brien [12] [13] [14] is implemented.
Accordingly, the pre-period ![]() of length
of length ![]() consists of
consists of
2 vertices v with defect ![]() in branch
in branch ![]() , and
, and
4 vertices v with defect ![]() in branch
in branch ![]() .
.
The claim of the virtual periodicity of branches has been proved generally for any coclass tree by du Sautoy [1] , and independently by Eick and Leedham-Green [2] . Here, the strict periodicity is also a consequence of Blackburn’s results, and has been tested up to ![]() computationally.
computationally.
Theorem 13.1. (Graph theoretic and algebraic invariants.)
The coclass-1 tree ![]() of all finite 3-groups
of all finite 3-groups ![]() with coclass
with coclass ![]() arises from the abelian root
arises from the abelian root ![]() and has the following graph theoretic properties.
and has the following graph theoretic properties.
1) The pre-period ![]() of length
of length ![]() is irregular.
is irregular.
2) The cardinalities of the irregular branches are ![]() and
and ![]() .
.
3) The branches ![]() ,
, ![]() , are periodic with primitive period
, are periodic with primitive period ![]() of length
of length ![]() .
.
4) The cardinalities of the regular branches are ![]() and
and ![]() .
.
5) Depth, width, and information content of the tree are given by
![]() (13.1)
(13.1)
The algebraic invariants of the groups represented by vertices forming the pre-period ![]() and the primitive period
and the primitive period ![]() of the tree are given in Table 11. The leading eight branches
of the tree are given in Table 11. The leading eight branches ![]() are drawn in Figure 17. All vertices of the tree are metabelian.
are drawn in Figure 17. All vertices of the tree are metabelian.
![]()
Table 11. Data for 3-groups G with ![]() of the coclass tree
of the coclass tree ![]() .
.
![]()
Figure 17. The unique coclass-1 tree ![]() with mainline of type a.1*.
with mainline of type a.1*.
Proof. (of Theorem 13.1) According to Proposition 13.1, the logarithmic order of the tree root, respectively of the periodic root, is ![]() , respectively
, respectively ![]() .
.
Since ![]() for all mainline vertices
for all mainline vertices ![]() with
with ![]() , according to Proposition 13.1, the unique capable child of
, according to Proposition 13.1, the unique capable child of ![]() is
is ![]() , and each branch has depth
, and each branch has depth ![]() , for
, for ![]() . Consequently, the tree is also of depth
. Consequently, the tree is also of depth ![]() .
.
With the aid of Formula (5.9) in Theorem 5.1, the claims (2) and (4) are consequences of Proposition 13.1:
![]() ,
, ![]() ,
,
![]() , and
, and ![]() .
.
According to Formula (5.13) in Corollary 5.1, where n runs from ![]() to
to ![]() , the tree width is the maximum
, the tree width is the maximum ![]() of the expressions
of the expressions ![]() ,
, ![]() ,
, ![]() , and
, and ![]() .
.
The information content of the tree is given by Formula (5.17) in the Definition 5.3:
![]()
The algebraic invariants in Table 11, that is, defect of commutativity k, depth ![]() , derived length
, derived length ![]() , abelian type invariants of the centre
, abelian type invariants of the centre ![]() , relation rank
, relation rank ![]() , nuclear rank
, nuclear rank ![]() , abelian quotient invariants
, abelian quotient invariants ![]() of the first maximal subgroup, respectively
of the first maximal subgroup, respectively ![]() of the commutator subgroup, transfer kernel type
of the commutator subgroup, transfer kernel type ![]() , action flag
, action flag ![]() , and the factorized order
, and the factorized order ![]() of the automorphism group have been computed by means of program scripts written for MAGMA [17] .
of the automorphism group have been computed by means of program scripts written for MAGMA [17] .
Each group is characterized by the parameters of the normalized repre- sentative ![]() of its isomorphism class, according to Formula (9.1), and by its identifier
of its isomorphism class, according to Formula (9.1), and by its identifier ![]() in the SmallGroups Database [19] .
in the SmallGroups Database [19] .
The column with header # contains the number of groups with identical invariants (except the presentation and identifier), for each row.
Corollary 13.1. (Actions and relation ranks.)
The algebraic invariants of the vertices of the structured coclass-1 tree ![]() with abelian root
with abelian root ![]() , which is drawn in Figure 17, are listed in Table 11. In particular:
, which is drawn in Figure 17, are listed in Table 11. In particular:
1) The groups with ![]() -action are the root R, all mainline vertices
-action are the root R, all mainline vertices ![]() ,
, ![]() , and the terminal vertices
, and the terminal vertices ![]() with even logarithmic order
with even logarithmic order ![]() .
.
2) With respect to the transfer kernel types, all mainline groups of type a.1*, ![]() , and the leaves of type a.3,
, and the leaves of type a.3, ![]() , with odd class
, with odd class ![]() , possess a
, possess a ![]() -action.
-action.
3) The relation rank is given by ![]() for the mainline vertices
for the mainline vertices ![]() ,
, ![]() ,
, ![]() for the terminal extraspecial group
for the terminal extraspecial group ![]() , and
, and ![]() otherwise.
otherwise.
4) All terminal vertices with odd class, and the mainline vertices with even class, possess an RI-action. The terminal vertices with odd class are Schur + 1 ![]() -groups [29] [30] .
-groups [29] [30] .
Proof. (of Corollary 13.1) The existence of an RI-action on G has been checked by means of an algorithm involving the p-covering group of G, written for MAGMA [17] . The other claims follow immediately from Table 11, continued indefinitely with the aid of the periodicity in Proposition 13.1. A Schur + 1 ![]() -group has an RI-action and relation rank
-group has an RI-action and relation rank ![]() [29] [30] .
[29] [30] .
14. Conclusions
In the core Sections 11 and 12 of this paper, we have elaborated our long desired proof that the pruned tree of all finite 3-groups with elementary bicyclic commutator quotient, which do not arise as descendants of non-metabelian groups, can be described with a finite amount of data.
Theorem 14.1. (Main Theorem on the Finite Information Content.)
The total information content of the coclass forest ![]() is given by
is given by
![]() (14.1)
(14.1)
Proof. The total information content of a coclass forest is the sum of the cardinality of its sporadic part ![]() and the information contents of its pairwise non-isomorphic coclass trees
and the information contents of its pairwise non-isomorphic coclass trees ![]()
![]()
Due to the exceptional complexity of the pre-periodic forests ![]() and
and ![]() , their information contents are unknown up to now. However, since they are certainly finite, this does not obfuscate our clear and beautiful results concerning the infinitely many co-periodic forests
, their information contents are unknown up to now. However, since they are certainly finite, this does not obfuscate our clear and beautiful results concerning the infinitely many co-periodic forests ![]() with
with ![]() , which can be reduced to the finite information content of the primitive co-period
, which can be reduced to the finite information content of the primitive co-period ![]() .
.
Acknowledgements
We gratefully acknowledge that our research was supported by the Austrian Science Fund (FWF): Project P 26008-N25. Indebtedness is expressed to the anonymous referees for valuable suggestions concerning the readability and, in particular, for drawing our attention to the paper [6] .
Supported
Research supported by the Austrian Science Fund (FWF): P 26008-N25.
Cite this paper
Mayer, D.C. (2018) Co-Periodicity Isomorphisms between Forests of Finite p-Groups. Advances in Pure Mathematics, 8, 77-140. https://doi.org/10.4236/apm.2018.81006
References
- 1. du Sautoy, M. (2001) Counting p-Groups and Nilpotent Groups. Publications Mathématiques de l'Institut des Hautes études Scientifiques, 92, 63-112. https://doi.org/10.1007/BF02698914
- 2. Eick, B. and Leedham-Green, C. (2008) On the Classification of Prime-Power Groups by Coclass. Bulletin of the London Mathematical Society, 40, 274-288. https://doi.org/10.1112/blms/bdn007
- 3. Leedham-Green, C.R. (1994) The Structure of Finite p-Groups. Journal of the London Mathematical Society, 50, 49-67. https://doi.org/10.1112/jlms/50.1.49
- 4. Shalev, A. (1994) The Structure of Finite p-Groups: Effective Proof of the Coclass Conjectures. Inventiones Mathematicae, 115, 315-345.
- 5. du Sautoy, M. and Segal, D. (2000) Zeta Functions of Groups. New Horizons in Pro-p Groups, Progress in Mathematics, Vol. 184, Birkhäuser, Basel, 249-286.
- 6. Eick, B. (2015) Metabelian p-Groups and Coclass Theory. Journal of Algebra, 421, 102-118. https://doi.org/10.1016/j.jalgebra.2014.08.021
- 7. Nebelung, B. (1989) Klassifikation metabelscher 3-Gruppen mit Faktorkommutatorgruppe vom Typ (3, 3) und Anwendung auf das Kapitulationsproblem, Inauguraldissertation (W. Jehne), Band 1, Universität zu Köln.
- 8. Leedham-Green, C.R. and Newman, M.F. (1980) Space Groups and Groups of Prime Power Order I. Archiv der Mathematik, 35, 193-203. https://doi.org/10.1007/BF01235338
- 9. Blackburn, N. (1958) On a Special Class of p-Groups. Acta Mathematica, 100, 45-92. https://doi.org/10.1007/BF02559602
- 10. Mayer, D.C. (2016) Artin Transfer Patterns on Descendant Trees of Finite p-Groups. Advances in Pure Mathematics, 6, 66-104.
- 11. Mayer, D.C. (2012) Transfers of Metabelian p-Groups. Monatshefte für Mathematik, 166, 467-495.
- 12. Newman, M.F. (1975) Determination of Groups of Prime-Power Order. Group Theory, Canberra, Lecture Notes in Math., vol. 573, Springer, Berlin, 73-84. https://doi.org/10.1007/BFb0087814
- 13. O’Brien, E.A. (1990) The p-Group Generation Algorithm. Journal of Symbolic Computation, 9, 677-698. https://doi.org/10.1016/S0747-7171(08)80082-X
- 14. Holt, D.F., Eick, B. and O’Brien, E.A. (2005) Handbook of Computational Group Theory, Discrete Mathematics and Its Applications. Chapman and Hall/CRC Press. https://doi.org/10.1201/9781420035216
- 15. Bosma, W., Cannon, J. and Playoust, C. (1997) The Magma Algebra System. I. The User Language. Journal of Symbolic Computation, 24, 235-265. https://doi.org/10.1006/jsco.1996.0125
- 16. Bosma, W., Cannon, J.J., Fieker, C. and Steels, A., Eds. (2017) Handbook of Magma Functions. Edition 2.23, Sydney.
- 17. MAGMA Developer Group, MAGMA Computational Algebra System, Version 2.23-6, Sydney, 2017. http://magma.maths.usyd.edu.au
- 18. Besche, H.U., Eick, B. and O’Brien, E.A. (2002) A Millennium Project: Constructing Small Groups. International Journal of Algebra and Computation, 12, 623-644. https://doi.org/10.1142/S0218196702001115
- 19. Besche, H.U., Eick, B. and O’Brien, E.A. (2005) The Small Groups Library—A Library of Groups of Small Order, an Accepted and Refereed GAP Package, Available Also in MAGMA.
- 20. Gamble, G., Nickel, W. and O’Brien, E.A. (2006) ANUPQ—p-Quotient and p-Group Generation Algorithms, an Accepted GAP Package, Available Also in MAGMA.
- 21. Ascione, J.A. (1979) On 3-Groups of Second Maximal Class. Ph.D. Thesis, (M. F. Newman), Australian National University, Canberra.
- 22. Ascione, J.A. (1980) On 3-Groups of Second Maximal Class. Bulletin of the Australian Mathematical Society, 21, 473-474. https://doi.org/10.1017/S0004972700006298
- 23. Ascione, J.A., Havas, G. and Leedham-Green, C.R. (1977) A Computer Aided Classification of Certain Groups of Prime Power Order. Bulletin of the Australian Mathematical Society, 17, 257-274, Corrigendum, 317-319, Microfiche Supplement, 320.
- 24. Mayer, D.C. (2015) Periodic Bifurcations in Descendant Trees of Finite p-Groups. Advances in Pure Mathematics, 5, 162-195.
- 25. Mayer, D.C. (2018) Modeling Rooted In-Trees by Finite p-Groups, to Appear in the Open Access Book Graph Theory. In: Sirmacek, B., Ed., InTech. http://www.algebra.at/ModelingInTrees.pdf
- 26. Newman, M.F. (1990) Groups of Prime-Power Order, Groups, Canberra 1989. Lecture Notes in Math., 1456, Springer, 49-62.
- 27. Blackburn, N. (1957) On Prime-Power Groups in Which the Derived Group Has Two Generators. Proceedings of the Cambridge Philosophical Society, 53, 19-27. https://doi.org/10.1017/S0305004100031959
- 28. Nebelung, B. (1989) Anhang zu Klassifikation metabelscher 3-Gruppen mit Faktorkommutatorgruppe vom Typ (3, 3) und Anwendung auf das Kapitulationsproblem, Inauguraldissertation, Band 2, Universität zu Köln.
- 29. Boston, N., Bush, M.R. and Hajir, F. (2017) Heuristics for p-Class Towers of Imaginary Quadratic Fields. Mathematische Annalen, 368, 633-669.
- 30. Boston, N., Bush, M.R. and Hajir, F. (2017) Heuristics for p-Class Towers of Real Quadratic Fields.





 the rooted tree of all finite 3-groups G with elementary bicyclic commutator quotient
the rooted tree of all finite 3-groups G with elementary bicyclic commutator quotient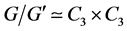 , and let
, and let 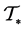 be the infinite pruned subtree of
be the infinite pruned subtree of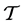 , where all descendants of capable non-metabelian vertices are eliminated. The main intention of this paper is to prove that the information content of the tree
, where all descendants of capable non-metabelian vertices are eliminated. The main intention of this paper is to prove that the information content of the tree 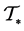 can be reduced to a finite set of representatives with the aid of two kinds of periodicity.
can be reduced to a finite set of representatives with the aid of two kinds of periodicity.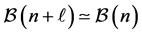 between the finite depth-pruned branches
between the finite depth-pruned branches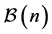 ,
,  , of a coclass subtree
, of a coclass subtree 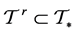 are refined to strict periodicity isomorphisms between complete branches which reduce the information content of the infinite coclass subtree to the finite union of pre-period
are refined to strict periodicity isomorphisms between complete branches which reduce the information content of the infinite coclass subtree to the finite union of pre-period 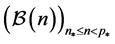 and first primitive period
and first primitive period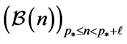 . The virtual periodicity was proved by du Sautoy [1] and independently by Eick and Leedham-Green [2] for groups of any prime power order. The strict periodicity for
. The virtual periodicity was proved by du Sautoy [1] and independently by Eick and Leedham-Green [2] for groups of any prime power order. The strict periodicity for  and type
and type 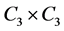 is proved in the present paper.
is proved in the present paper. between the infinite coclass forests
between the infinite coclass forests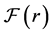 ,
, 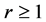 , which reduce the information content of the pruned tree
, which reduce the information content of the pruned tree  to the union of pre-period
to the union of pre-period  and first primitive period
and first primitive period

















































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































