ABSTRACT

In this paper, we establish the dual Orlicz-Minkowski inequality and the dual Orlicz- Brunn-Minkowski inequality for dual Orlicz mixed quermassintegrals.

Keywords:

Star Body, Orlicz Radial Sum, Dual Orlicz Mixed Volume

1. Introduction

Recently, Convex Geometry Analysis has made great achievement in Orlicz space (see [1] - [14] ). Zhu, Zhou and Xu [12] defined the Orlicz radial sum and dual Orlicz mixed volumes. Let 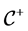be the set of convex and strictly decreasing functions such that, 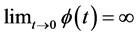and.

Let K and L be two star bodies about the origin in 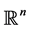and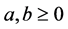; the Orlicz radial sum was defined by [13]

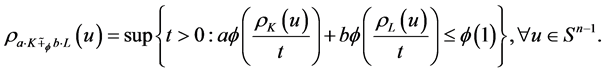(1.1)

The case 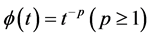of the Orlicz radial sum is the 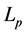harmonic radial sum, which was defined by Lutwak (see [15] ).

Let denote the right derivative of a real-valued function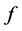. For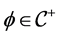, there is because 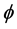is convex and strictly decreasing. The dual Orlicz mixed volume 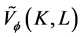is defined by

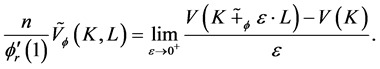(1.2)

In this paper, we will define the dual Orlicz mixed quermassintegral by

(1.3)

The main purpose of this paper is to establish the dual Orlicz-Minkowski inequality and the dual Orlicz-Brunn-Minkowski inequality for dual Orlicz mixed quermassintegrals.

Theorem 1.1 Let K and L be two star bodies about the origin in and. If, then

(1.4)

with equality if and only if K and L are dilates of each other.

Theorem 1.2 Let K and L be two star bodies about the origin in and. If, then

(1.5)

with equality if and only if K and L are dilates of each other.

This paper is organized as follows: In Section 2 we introduce above interrelated notations and their background materials. Section 3 contains the proofs of our main results.

2. Notation and Background Material

The radial function of a compact star-shaped about the origin is defined, for, by

(2.1)

If is positive and continuous, then K is called a star body about the origin. The set of star bodies about the origin in is denoted by. Obviously, for,

(2.2)

If is independent of, then we say star bodies K and L are dilates of

each other.

If and are nonnegative real numbers, then the volume of is a homogeneous polynomial of degree n in given by

where the sum is taken over all n-tuples of positive integers not exceeding m. The coefficient depends only on the bodies, and is uniquely determined by the above identity, it is called the dual mixed volume of. More explicitly, the dual mixed volume has the following integral representation [16] :

(2.3)

where S is the Lebesgue measure on

The coefficients are nonnegative, symmetric and monotone (with respect to set inclusion). They are also multilinear with respect to the radial sum and. Let and, then the dual mixed volume is usually written as. If L = B, then is the dual quermassintegral. For, the dual mixed quermassinte-

gral denotes the dual mixed volume. For,

then.

The dual mixed quermassintegral has the following integral representation:

(2.4)

where S is the Lebesgue measure on.

By using the Minkowski’s integral inequality, we can obtain the dual Minkowski inequality for dual mixed quermassintegrals: If, and, then

(2.5)

equality holds if and only if K and L are dilates of each other.

Suppose that m is a probability measure on a space X and is a m- intergrable function, where I is a possibly infinite interval. Jessen’s inequality states that if is a convex function, then

(2.6)

If is strictly convex, equality holds if and only if is a constant for m-almost all (see [17] ).

3. Main Results

Let and. For, the dual Orlicz mixed quermassintegral is defined by

(3.1)

For, then. The case of the dual Orlicz mixed quermassintegral is the dual Orlicz mixed volume, which was defined by Zhu, Zhou and Xu [12] .

Corollary 3.1 The dual Orlicz mixed quermassintegral is monotone with respect to set inclusion.

Proof. Let and. By (3.1), (2.2) and the fact that is strictly decreasing on, we have

Lemma 3.1 [12] Let and. If, then

if and only if

Lemma 3.2 [12] Let and. Then

(3.2)

uniformly for all.

Theorem 3.1 Let and. For, then

Proof. Suppose, and. Note that as (see [12] ). By Lemma 3.2, it follows that

uniformly on.

Hence

We complete the proof of Theorem 3.1. ,

From (3.1) and Theorem 3.1, we have

(3.3)

For, since, then is a probabil-

ity measure on.

Proof of Theorem 1.1

By (3.1), (2.6), (2.5) and the fact that is decreasing on, we obtain

This gives the desired inequality. Since is strictly decreasing, from the equality condition of the dual Minkowski inequality (2.5), we have that K and L are dilates of each other.

Conversely, when, by (3.1), we have

,

The following uniqueness is a direct consequence of the dual Orlicz-Minkowski inequality (1.4).

Corollary 3.2 Suppose, and such that. For, if

(3.4)

or

(3.5)

then.

Proof. Suppose (3.4) holds. If we take K for M, then from (3.1), we obtain

Hence, from the dual Orlicz-Minkowski inequality (1.4), we have

with equality if and only if K and L are dilates of each other. Since is strictly decreasing on, we have

with equality if and only if K and L are dilates of each other. If we take L for M, we similarly have. Hence, and from the equality condition we can conclude that K and L are dilates of each other. However, since they have the same volume they must be equal.

Next, suppose (3.5) holds. If we take K for M, then from (3.1), we obtain

Then, from the dual Orlicz-Minkowski inequality (1.4), we have

with equality if and only if K and L are dilates of each other. Since is strictly decreasing on, we have

with equality if and only if K and L are dilates of each other. If we take L for M, we similarly have. Hence, and from the equality condition we can conclude that K and L are dilates of each other. However, since they have the same volume they must be equal.

From the dual Orlicz-Minkowski inequality, we will prove the following dual Orlicz-Brunn-Minkowski inequality which is more general than Theorem 1.2.

Theorem 3.2 Let, and. If, then

with equality if and only if K and L are dilates of each other.

Proof. Let. From (2.3), Lemma 3.1 and (1.4), it follows that

By the equality condition of the dual Orlicz-Minkowski inequality (1.4), equality in (3.6) holds if and only if K and L are dilates of each other.

Indeed, we also can prove the dual Orilcz-Minkowski inequality by the dual Orilcz- Brunn-Minkowski inequality.

Proof. For, let. Note that as. By the dual Orlicz-Brunn-Minkowski inequality, the following function

is non-positive. Obviously,. Thus

(3.7)

On the other hand, we have

(3.8)

Let and note that as. Consequently,

(3.9)

By (3.3), we have

(3.10)

From (3.8), (3.9), and (3,10), it follows that

(3.11)

Combing (3.7) and (3.11), we have

(3.12)

Therefore, the equality in (3.12) holds if and only if, this implies that K and L are dilates of each other.

Remark 3.1 The case of Theorem 1.1 and Theorem 1.2 were established by Zhu, Zhou and Xu [12] . The dual forms of Theorem 1.1 and Theorem 1.2 were established by Xiong and Zou [11] .

Cite this paper

Liu, L.J. (2016) Inequalities for Dual Orlicz Mixed Quermassintegrals. Advances in Pure Mathematics, 6, 894-902. http://dx.doi.org/10.4236/apm.2016.612067

References