Advances in Pure Mathematics
Vol.06 No.03(2016), Article ID:63993,12 pages
10.4236/apm.2016.63015
Kummer’s 24 Solutions of the Hypergeometric Differential Equation with the Aid of Fractional Calculus
Tohru Morita1, Ken-ichi Sato2
1Tohoku University, Sendai, Japan
2College of Engineering, Nihon University, Koriyama, Japan

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 30 November 2015; accepted 24 February 2016; published 29 February 2016
ABSTRACT
We know that the hypergeometric function, which is a solution of the hypergeometric differential equation, is expressed in terms of the Riemann-Liouville fractional derivative (fD). The solution of the differential equation obtained by the Euler method takes the form of an integral, which is confirmed to be expressed in terms of the Riemann-Liouville fD of a function. We can rewrite this derivation such that we obtain the solution in the form of the Riemann-Liouville fD of a function. We present a derivation of Kummer’s 24 solutions of the hypergeometric differential equation by this method.
Keywords:
Fractional Derivative, Hypergeometric Differential Equation, Hypergeometric Function

1. Introduction
The hypergeometric function is a solution of the hypergeometric differential equation, and is known to be expressed in terms of the Riemann-Liouville fractional derivative (fD) ([1] , p. 334). By the Euler method ( [2] , Section 3.2), the solution of the hypergeometric differential equation is obtained in the form of an integral, which is confirmed to be expressed in terms of the Riemann-Liouville fD of a function. This shows that we can obtain the solution in the form of the Riemann-Liouville fD of a function. In fact, Nishimoto [3] obtained a solution of the hypergeometric differential equation in terms of the Liouville fD in the first step, and then expressed the obtained fD in terms of the hypergeometric function in the second step. His calculation in the second step is unacceptable. In [4] , he gave a derivation of Kummer’s 24 solutions of the hypergeometric differential equation ( [5] , Formula 15.5.4) ( [6] , Section 2.2) by his method. In the present paper, we show that the desired solutions are obtained by using the Riemann-Liouville fD in place of the Liouville fD.
In a preceding paper [7] , we discussed the Riemann-Liouville fD and the Liouville fD as analytic continuations of the respective fractional integrals (fIs), on the basis of the papers by Lavoie et al [1] [8] , and those by Nishimoto [3] and Campos [9] , respectively. In Section 2, we define these fIs of a function ,
, 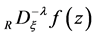 and
and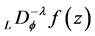 , of order
, of order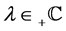 , by (1) and (2), respectively, and give their properties which we use later. The notation
, by (1) and (2), respectively, and give their properties which we use later. The notation  is defined at the end of this section.
is defined at the end of this section.
In Section 3, following [1] [3] [7] -[9] , the Riemann-Liouville fD,  and
and , and the Liouville fD,
, and the Liouville fD, 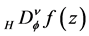 and
and , of order
, of order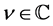 , are defined in the form of a contour integral, for a function
, are defined in the form of a contour integral, for a function 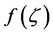 which is analytic on a neighborhood of the path of integration. They are defined such that they are analytic continuations of the corresponding fI as a function of
which is analytic on a neighborhood of the path of integration. They are defined such that they are analytic continuations of the corresponding fI as a function of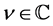 . In the present paper, the fI and fD are operated to a function of the form
. In the present paper, the fI and fD are operated to a function of the form 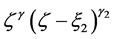 for
for 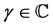 and
and . The analytic continuations of
. The analytic continuations of 




In [1] , the expression of the hypergeometric function: 
In a separate paper [10] , a method of obtaining the asymptotic expansion of the Riemann-Liouville fD is presented by using a relation of its expression via a path integral or a contour integral with the corresponding Liouville fD. It is then applied to obtain the asymptotic expansion of the confluent hypergeometric function which is a solution of Kummer’s differential equation. In that paper, Kummer’s 8 solutions of Kummer’s differential equation are obtained by using the method which is adopted in the present paper to obtain the solutions of the hypergeometric differential equation.
We use notations









2. Riemann-Liouville fD and Liouville fD
Following preceding papers [7] [10] , we adopt the following definitions of the Riemann-Liouville fI, f-dept Liouville fI and the corresponding fDs.
2.1. Riemann-Liouville fI on the Complex Plane
Let 





Definition 1. Let






where 
2.2. Definition of f-Dept Liouville fI
Let 







Definition 2. Let








gence, and denote it by 

We then have 

Lemma 1. Let 



Definition 3. Let 









We call 

Definition 4. When the conditions in Definition 3 are satisfied, we define 

The following lemma was mentioned in [11] .
Lemma 2. Let
Proof. This is confirmed by comparing the second members of (1) and of (2). ,
2.3. Definitions of Riemann-Liouville fD and Liouville fD
Definition 5. The Riemann-Liouville fD: 






when the righthand side exists, where


Here 

2.4. Index Law and Leibniz’s Rule of Riemann-Liouville fI and Liouville fI
We use the following index law and Leibniz’s rule, in Section 4.2. By Lemma 2, the formulas for 
Lemma 3. Let




Proof. Proof for 







Lemma 4. Let








Proof. Proof of (4) for the case (i) is found in ( [7] , Appendix A). In the case (ii), with the aid of this knowledge and formula (3), we prove the first equation in (4) in the following way:

where




Lemma 5. Let


Proof. By using the righthand side of (1), we see that both sides of the equation in this lemma are equal to

This Leibniz’s rule is given in ( [13] , Section 5.5). The following corollary follows from this lemma.
Corollary 1. Let



3. Analytic Continuations of Riemann-Liouville fD and Liouville fD
3.1. Analytic Continuations of Riemann-Liouville fI
In [1] [7] [8] , analytic continuations of the Riemann-Liouville fI via contour integrals are discussed. In [7] , 


Definition 6. Let 





for






Definition 7. Let







for





3.2. Analytic Continuations of Liouville fI
In [3] [7] [9] , the analytic continuation of Liouville fI: 
Definition 8. Let 






where


In [7] , another analytic continuation of Liouville fI: 





Definition 9. Let (i): 


















Figure 1. The contours of integration, (a):

Figure 2. The contour of integration








where




3.3. Analyticity of Riemann-Liouville fD and Liouville fD
In this section, we consider functions 


where



The following Lemmas 6~10 are obtained by modifying the corresponding arguments given in Section 2 for the Riemann-Liouville fD and in Sections 3.1~3.3 for the Liouville fD in [7] , with the aid of ( [14] , Sections 3.1 and 3.2).
Lemma 6. 
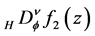





Lemma 7. 




Lemma 8. Let 


Lemma 9. Let 



Lemma 10. Lemmas 8 and 9 with







Remark 1. The statements related with 

In the following sections, we use 

4. The Hypergeometric Function in Terms of Riemann-Liouville fD
Let









where 




The integral representation of 

when

This function is a solution of the hypergeometric differential equation:

which has also another solution given by

see ( [5] , Section 15.5.1) ( [6] , Section 2.2).
4.1. Solution of the Hypergeometric Differential Equation (15) with the Aid of Riemann-Liouville fD
The function 

Proofs of the following two lemmas are presented in the following two sections.
Lemma 11. Let 




where the values al, bl and cl are given in Table 1, and 



Lemma 12. When



Table 1. Values of


Corollary 2. When we put 



Remark 2. The solutions 





4.2. Proof of Lemma 11
Lemma 13 Let








Proof. We assume that a solution of (15) is expressed as 




Putting 



with the aid of Lemma 3. This equation requires that

and 



Remark 3. The proof of Lemma 13 corresponds to the derivation, given in ( [2] , pp. 43-44), of an integral form of the solution of (15), where the method is called the Euler method.
Lemma 14. If 


Proof. We first consider the case of



When we choose











Proof of Lemma 11. The formula (18) for 
4.3. Expressions of 
We now present the expressions of 
Proof of Lemma 12 is given at the first part of the proof of Lemma 15 below.
By using Lemmas 8, 9 and 10 and the middle member of (1), (18) is expressed as

Lemma 15. We choose


Then 



if k, 







Proof. We put 


when



We put 


when



We put 


when



We put 
Table 2. Functions 









Applying this to the formula (28) for 

Remark 4. Let 



























Remark 5. In Lemma 15, we have two expressions of 



Remark 6. When


4.4. Solutions of (15) as a Function of



In the following, there appear




Lemma 16. If 


Proof. When







When





When we choose





Table 3. Fuctions 




When




the same equation with







When
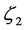




We then obtain the same equation with b, 






When




the same equation with







respectively. ,
By Corollary 2 and Lemma 16, we obtain the following corollary.
Corollary 3. Let 






is a solution of (15).
We note here the following remark, which is used in obtaining Table 4 below.
Table 4. Functions 






Remark 7




5. Kummer’s 24 Solutions of the Hypergeometric Differential Equation
By Corollary 3 and Lemma 7, we obtain the following theorem by the present method.
Theorem 1 We have 24 solutions of (15), which are expressed as

where the functions 





The values for 


Lemma 17. Let





















where 

The following lemma is well known, see ( [5] , Formulas 15.5.3~15.5.14) ([6] , Section 2.2).
Theorem 2. The solutions 


Proof. This is confirmed by using Lemma 16 or Corollary 3 with the aid of Remark 2. ,
Cite this paper
TohruMorita,Ken-ichiSato, (2016) Kummer’s 24 Solutions of the Hypergeometric Differential Equation with the Aid of Fractional Calculus. Advances in Pure Mathematics,06,180-191. doi: 10.4236/apm.2016.63015
References
- 1. Lavoie, J.L., Tremblay, R. and Osler, T.J. (1975) Fundamental Properties of Fractional Derivatives via Pochhammer Integrals. In: Ross, B., Ed., Fractional Calculus and its Applications, Springer-Verlag, Berlin, 327-356.
http://dx.doi.org/10.1007/BFb0067118 - 2. Sneddon, I.N. (1980) Special Functions of Mathematical Physics and Chemistry. Longman Inc., New York.
- 3. Nishimoto, K. (1991) An Essence of Nishimoto’s Fractional Calculus. Descartes Press, Koriyama.
- 4. Nishimoto, K. (1997) Kummer’s Twenty-Four Functions and N-Fractional Calculus. Nonlinear Analysis, Theory, Methods & Applications, 30, 1271-1282.
- 5. Abramowitz, M. and Stegun, I.A. (1972) Handbook of Mathematical Functions with Formulas, Graphs and Mathematical Tables, Chapter 15. Dover Publ., Inc., New York.
- 6. Magnus, W., Oberhettinger, F. and Soni, R.P. (1966) Formulas and Theorems for the Special Fuctions of Mathematical Physics, Chapter II. Springer-Verlag New York Inc., New York.
http://dx.doi.org/10.1007/978-3-662-11761-3 - 7. Morita, T. and Sato, K. (2013) Liouville and Riemann-Liouville Fractional Derivatives via Contour Integrals. Fractional Calculus and Applied Analysis, 16, 630-653.
http://dx.doi.org/10.2478/s13540-013-0040-9 - 8. Lavoie, J.L., Osler, T.J. and Tremblay, R. (1976) Fractional Derivatives and Special Functions. SIAM Review, 18, 240-268.
http://dx.doi.org/10.1137/1018042 - 9. Campos, L.M.B.C. (1984) On a Concept of Derivative of Complex Order with Applications to Special Functions. IMA Journal of Applied Mathematics, 33, 109-133.
http://dx.doi.org/10.1093/imamat/33.2.109 - 10. Morita, T. and Sato, K. (2015) Asymptotic Expansions of Fractional Derivatives and Their Applications. Mathematics 3, 171-189.
http://dx.doi.org/10.3390/math3020171 - 11. Samko, S.G., Kilbas, A.A. and Marichev, O.I. (1993) Fractional Integrals and Derivatives, Theory and Applications. Gordon and Breach Sc. Publ., Amsterdam.
- 12. Podlubny, I. (1999) Fractional Differential Equations. Academic Press, San Diego.
- 13. Oldham, K.B. and Spanier, J. (2006) The Fractional Calculus. Dover Publ. Inc., New York.
- 14. Whittaker, E.T. and Watson, G.N. (1935) A Course of Modern Analysis. Cambridge U.P., Cambridge.










