Advances in Pure Mathematics
Vol.05 No.14(2015), Article ID:62270,9 pages
10.4236/apm.2015.514080
Matrices Associated with Moving Least-Squares Approximation and Corresponding Inequalities
Svetoslav Nenov, Tsvetelin Tsvetkov
Department of Mathematics, University of Chemical Technology and Metallurgy, Sofia, Bulgaria

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 17 November 2015; accepted 25 December 2015; published 28 December 2015
ABSTRACT
In this article, some properties of matrices of moving least-squares approximation have been pro- ven. The used technique is based on known inequalities for singular-values of matrices. Some inequalities for the norm of coefficients-vector of the linear approximation have been proven.
Keywords:
Moving Least-Squares Approximation, Singular-Values

1. Statement
Let us remind the definition of the moving least-squares approximation and a basic result.
Let:
1. 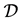 be a bounded domain in
be a bounded domain in ;
;
2.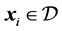 ,
,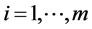 ;
;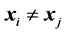 , if
, if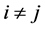 ;
;
3. 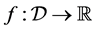 be a continuous function;
be a continuous function;
4. 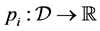 be continuous functions,
be continuous functions,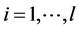 . The functions
. The functions 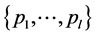 are linearly independent in
are linearly independent in 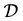 and let
and let 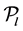 be their linear span;
be their linear span;
5. 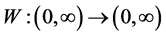 be a strong positive function.
be a strong positive function.
Usually, the basis in 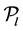 is constructed by monomials. For example:
is constructed by monomials. For example: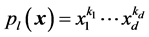 , where
, where




Following [1] -[4] , we will use the following definition. The moving least-squares approximation of order l at a fixed point 


among all
The approximation is “local” if weight function W is fast decreasing as its argument tends to infinity and interpolation is achieved if

Some examples of 


Here and below: 



We introduce the notations:
Through the article, we assume the following conditions (H1):
(H1.1)
(H1.2)
(H1.3)
(H1.4) w is smooth function.
Theorem 1.1. (see [2] ): Let the conditions (H1) hold true.
Then:
1. The matrix 
2. The approximation defined by the moving least-squares method is

where

3. If 

For the approximation order of moving least-squares approximation (see [2] and [5] ), it is not difficult to receive (for convenience we suppose 

and moreover (C =const.)

It follows from (3) and (4) that the error of moving least-squares approximation is upper-bounded from the 2- norm of coefficients of approximation (
Here the constants M and N depend on singular values of matrix


The main result in Section 3 is formulated in the case of exp-moving least-squares approximation, but it is not hard to receive analogous results in the different cases: Backus-Gilbert wight functions, McLain wight functions, etc.
2. Some Auxiliary Lemmas
Definition 2.1. We will call the matrices



Lemma 2.1. Let the conditions (H1) hold true.
Then, the matrices 

Proof. Direct calculation of the corresponding transpose matrices.
Lemma 2.2. Let the conditions (H1) hold true.
Then:
1. All eigenvalues of 

2. All eigenvalues of 

Proof. Part 1: We will prove that the dimension of the null-space 
Using the definition of
Hence,
Using (H1.3), 



over,


Part 2: We will prove that 


has 
Obviously the systems

and

are equivalent. Indeed, if 
i.e. 
On the other hand, if 
i.e. 
Part 3: It follows from parts 1 and 2 of the proof that 0 is an eigenvalue of 



It remains to prove that 1 is eigenvalue of 

The following two results are proven in [6] .
Theorem 2.1 (see [6] , Theorem 2.2): Suppose U, V are 
denote the eigenvalues of U and V, respectively.
Let:
1. 
2. 
3. 
Then:
1. If
2. If
3. If
Corollary 2.1. (see [6] , Corollary 2.4): Suppose U, V are 
Then for any
As a result of Lemma 2.1, Lemma 2.2 and Theorem 2.1, we may prove the following lemma.
Lemma 2.3. Let the conditions (H1) hold true.
1. Then 

2. The following inequality hods true
Proof. (1) We apply Theorem 2.1, where
Obviously, U is a symmetric positive definite matrix (in fact it is a diagonal matrix). Moreover



The matrix V is symmetric (see Lemma 2.1).
From the cited theorem, for any index k 
In particular, if

Let us suppose that there exists index 


It fowollws from (8) and positive definiteness of U, that
Therefore (see (7)),

If we set


(2) From the first statement of Lemma 2.3, 
for all


Therefore
or

In the following, we will need some results related to inequalities for singular values. So, we will list some necessary inequalities in the next lemma.
Lemma 2.4. (see [7] [8] ): Let U be an 

Then:




If 



Lemma 2.5. Let the conditions (H1) hold true and let

Then:



Proof. The matrix 
The inequality (14) follows from (12) (
From (14) and (10), we receive
Therefore, the equality 
Using 
or
The lemma has been proved. □
3. An Inequality for the Norm of Approximation Coefficients
We will use the following hypotheses (H2):
(H2.1) The hypotheses (H1) hold true;
(H2.2)

(H2.3) The map 


(H2.4)

Theorem 3.1. Let the following conditions hold true:
1. Hypotheses (H2);
2. Let 
3. The index 
Then, there exist constants 
Proof. Part 1: Let
then
We have (obviously


Therefore, the function 

Part 2: Obviously
It follows from (15) that
Here


For the norm of diagonal matrix H, we receive
Therefore
We will use Lemma 2.4 to obtain the norm of
Obviously,

i.e.
Therefore, if we set

Let the constant 
and let
Part 3: On the end, we have only to apply Lemma 4.1 form [9] to the Equation (16):
Remark 3.1. Let the hypotheses (H2) hold true and let moreover
In such a case, we may replace the differentiation of vector-fuction
by left-multiplication:
The singular values of the matrix 


That is why, we may chose
Additionally, if we supose
Therefore, in such a case:
If we suppose
Cite this paper
SvetoslavNenov,TsvetelinTsvetkov, (2015) Matrices Associated with Moving Least-Squares Approximation and Corresponding Inequalities. Advances in Pure Mathematics,05,856-864. doi: 10.4236/apm.2015.514080
References
- 1. Alexa, M., Behr, J., Cohen-Or, D., Fleishman, S., Levin, D. and Silva, C.T. Point-Set Surfaces.
http://www.math.tau.ac.il/~levin/ - 2. Levin, D. The Approximation Power of Moving Least-Squares.
http://www.math.tau.ac.il/~levin/ - 3. Levin, D. Mesh-Independent Surface Interpolation.
http://www.math.tau.ac.il/~levin/ - 4. Levin, D. (1999) Stable Integration Rules with Scattered Integration Points. Journal of Computational and Applied Mathematics, 112, 181-187.
http://www.math.tau.ac.il/~levin/
http://dx.doi.org/10.1016/S0377-0427(99)00218-6 - 5. Fasshauer, G. (2003) Multivariate Meshfree Approximation.
http://www.math.iit.edu/~fass/603_ch7.pdf - 6. Lu, L.-Z. and Pearce, C.E.M. (2000) Some New Bounds for Singular Values and Eigenvalues of Matrix Products. Annals of Operations Research, 98, 141-148.
http://dx.doi.org/10.1023/A:1019200322441 - 7. Merikoski, J.K. (2004) Ravinder Kumar, Inequalities for Spreads of Matrix Sums and Products. Applied Mathematics E-Notes, 4, 150-159.
- 8. Jabbari, F. (2015) Linear System Theory II. Chapter 3: Eigenvalue, Singular Values, Pseudo-Inverse. The Henry Samueli School of Engineering, University of California, Irvine.
http://gram.eng.uci.edu/~fjabbari/me270b/me270b.html - 9. Hartman, P. (2002) Ordinary Differential Equations. Second Edition, SIAM, Philadelphia, Pennsylvania, United States.
http://dx.doi.org/10.1137/1.9780898719222.fm






















































