Received 19 August 2015; accepted 27 September 2015; published 30 September 2015

ABSTRACT

In this paper, we proof some properties of the space of bounded p(×)-variation in Wiener’s sense. We show that a functions is of bounded p(×)-variation in Wiener’s sense with variable exponent if and only if it is the composition of a bounded nondecreasing functions and hölderian maps of the variable exponent. We show that the composition operator H, associated with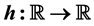, maps the spaces 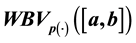into itself if and only if h is locally Lipschitz. Also, we prove that if the composition operator generated by maps this space into itself and is uniformly bounded, then the regularization of h is affine in the second variable.

Keywords:

Generalized Variation, p(×)-Variation in Wiener’s Sense, Variable Exponent, Composition Operator, Matkowski’s Condition

1. Introduction

Since Camile Jordan in 1881 first gave the notion of variation of a function in the paper [1] devoted to the convergence of Fourier series, a number of generalizations and extensions have been given in many directions. Such extensions find many applications in different areas of mathematics. Consequently, the study of notions of generalized bounded variation forms an important direction in the field of mathematical analysis. Two well- known generalizations are the functions of bounded p-variation and the functions of bounded j-variation, due to N. Wiener [2] and L. C. Young [3] respectively. In 1924, N. Wiener [2] generalized the Jordan notion and intro- duced the notion of p-variation (variation in the sense of Wiener). L. Young [3] introduced the notion of j-variation of a function. The p-variation of a function f is the supremum of the sums of the pth powers of absolute increments of f over no overlapping intervals. Wiener mainly focused on the case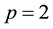, the 2- variation. For p-variations with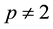, the first major work was done by Young [3] , partly with Love [4] . After a long hiatus following Young’s work, pth-variations were reconsidered in a probabilistic context by R. Dudley [5] [6] . Many basic properties of the variation in the sense of Wiener and a number of important applications of the concept can be found in [7] [8] . Also the paper by V. V. Chistyakov and O. E. Galkin [9] is very important in the context of p-variation. They study properties of maps of bounded p-variation in the sense of Wiener are defined on a subset of the real line and take values in metric or normed spaces.

In recent years, there has been an increasing interest in the study of various mathematical problems with variable exponents. With the emergency of nonlinear problems in applied sciences, standard Lebesgue and Sobolev spaces demonstrated their limitations in applications. The class of nonlinear problems with exponent growth is a new research field and it reflects a new kind of physical phenomena. In 2000, the field began to expand even further. Motivated by problems in the study of electrorheological fluids, Diening [10] raised the question of when the Hardy-Littlewood maximal operator and other classical operators in harmonic analysis were bounded on the variable Lebesgue spaces. These and related problems are the subject of active research to this day. These problems were interesting in applications (see [11] - [14] ) and gave rise to a revival of the interest in Lebesgue and Sobolev spaces with variable exponent, the origins of which could be traced back to the work of Orlicz in the 1930’s [15] . In the 1950’s, this study was carried on by Nakano [16] [17] who made the first systematic study of spaces with variable exponent. Later, Polish and Czechoslovak mathematicians investigated the modular function spaces (see for the example Musielak [18] [19] , Kovacik and Rakosnik [20] ). We refer to books [14] for the detailed information on the theoretical approach to the Lebesgue and Sobolev spaces with variable exponents. In [21] , Castillo, Merentes and Rafeiro studied a new space of functions of generalized bounded variation. There, the authors introduced the notion of bounded variation in the Wiener sense with the exponent p(×)-variable.

The main purpose of this paper is threefold: First, we provide a further develop of the results of the article [21] . We give a detailed description of the new class formed by the functions of bounded variation in the sense of Wiener with the exponent p(×)-variable. Second, in the spirit of some results of Federer ( [22] sec. 2.5.16), Sierpinski [23] , and Chistyakov and Galkin [9] , we provide a characterization of the functions with variable bounded variation in the sense of Wiener. We prove a structural theorem for mappings of bounded variation in the sense of Wiener with the exponent p(×)-variable. Finally, we analyze a necessary and sufficient conditions for the acting of composition operator (Nemystskij) on the space.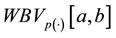

This paper is organized as follows: Section 2 contains definitions, notations, and necessary background about the class of functions of bounded p(×)-variation in Wiener’s sense; Section 3 contains some properties of this space; Section 4 contains a main theorem, which is a characterization of the functions of bounded p(×)-variation in Wiener’s sense of the composition of two functions with certain properties; Section 5 contains another main theorem, in which we prove a result in the case when h is locally Lipschitz if and only if the composition operator maps the space 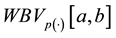into itself; Finally, in section 6 we give the last main theorem, namely, we show that any uniformly bounded composition operator that maps the space 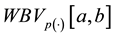into itself necessarily satisfies the so called Matkowski’s weak condition.

2. Preliminaries

Throughout this paper, we use the following notation: we will denote by

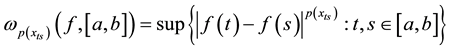the diameter of the image (or the oscillation

of f on) and by a number between.

The concept of functions of bounded variation has been well-known since C. Jordan in 1881 (see [1] ) gave the complete characterization of functions of bounded variation as a difference of two increasing functions. This class of functions exhibit so many interesting properties that it makes them a suitable class of functions in a variety of contexts with wide applications in pure and applied mathematics (see [8] [24] ).

Definition 1 Let be a function. For each partition of, we define

(2.1)

where the supremum is taken over all partitions of the interval. If, we say that f has bounded variation. The collection of all functions of bounded variation on is denoted by.

The notion of bounded variation due to Jordan was generalized in 1924 by Wiener (see [2] ) who introduced the definition of p-variation as follows.

Definition 2 Given a real number, a partition of, and a function. The nonnegative real number

(2.2)

is called the Wiener variation (or p-variation in Wiener’s sense) of f on where the supremum is taken over all partitions of π. In case that, we say that f has bounded Wiener variation (or bounded p-variation in Wiener’s sense) on. The symbol will denote the space of functions of bounded p-variation in Wiener’s sense on.

In 2013 R. Castillo, N. Merentes and H. Rafeiro [21] introduce the notation of bounded variation space in the Wiener sense with variable exponent on and study some of its basic properties.

Definition 3 Given a function, a partition of the interval, and a function. The nonnegative real number

(2.3)

is called Wiener variation with variable exponent (or p(×)-variation in Wiener’s sense) of f on where is a tagged partition of the interval, i.e., a partition of the interval together with a finite sequence of numbers subject to the conditions that for each i,.

In case that, we say that f has bounded Wiener variation with variable exponent (or bounded p(×)-variation in Wiener’s sense) on. The symbol will denote the space of functions of bounded p(×)-variation in Wiener’s sense with variable exponent on.

Remark 1 Given a function

1) If for all x in, then.

2) If for all x in and, then.

3. Properties of the Space

Definition 4 (Norm in)

(3.1)

where.

In [21] is shown that the space endowed with the norm is a Banach space.

Theorem 2 Let be a function, then is a Banach space.

Lemma 1 Let be a function such that then f has the left-hand and right- hand limits in all point on.

Proof. Without loss of generality we can show that f has a left limit on. Assume that the do not exist. Then

Case 1: If, then

so. Since and, then, which is a contradiction.

Case 2: do not converge a any point. That means that the function f oscillates. Let be

a sequence such that when

therefore, which is a contradiction as well. □

Remark 3 Without loss of generality we can take. If then, further, as is bounded

since and we have

So, i.e.,

The following properties of elements of allow us to get characterizations of them.

Lemma 2 (General properties of the p(×)-variation) Let be an arbitrary map. We have

(P1) minimality: if, then

(P2) monotonicity: if and, then,

and.

(P3) semi-additivity: if, then

(P4) change of a variable: if and is a (not necessarily strictly) monotone func- tion, then.

(P5) regularity:.

Proof. (P1) Let,

(P2) Let, and the partition so

the other cases are similarly.

(P3) Let and denote and. We consider the following two cases:

1) if or, then

2) if for some, then

For the case (a) we have

For the case (b) we get

also

Therefore

Taking the supremum over all, we arrive at the left hand side inequality in (P3).

Now we prove the right hand side inequality. Let and. Then for every

there are partitions and of the interval and respectively, such that

It follows that

and take into account the arbitrariness of.

(P4) Let, a (not necessarily strictly) monotone function, a tagged parti-

tion of the interval, and with, then

On the other hand, if a partition of is such that for then there exist such that and, again by the monotonicity of

(P5) By monotonicity of we get

On the other hand, for any number such that there is a partition with. We define a partition of the interval then and

, i.e.,

□

4. Characterization

W. Sierpi?ski in 1933 (See [23] ) showed that a function is regular function if and only if it is the composition of increasing function and continuous function. This is a notable result which links regular functions with continuous functions. In 1969 (see [22] ), H. Federer demostrated that function is of bounded variation if and only if it is the composition of a Lipschitz function with a monotone function. In the year 1998 (see [9] ) V. V. Chistyakov and O. E. Galkin proved similar result for bounded p-variation with, they show that a function is of bounded p-variation if and only if it is the composition of a bounded nondecreasing function with a Hölder function. In this section we show that a function is of bounded p(×)-variation in Wiener’s sense with variable exponent if and only if it is the composition of a bounded nondecreasing function with a

Hölderian function with variable exponent equal to.

We say that, the Hölder space of variable exponent, where is a positive function, , if

for all. The least number C satisfying the above inequality is called the Hölder constant of g.

Theorem 4 The map is of bounded p(×)-variation if and only if there exists a bounded non- decreasing function a Hölderian map of exponent and such that on.

The proof of this theorem is contained in the following two lemmas.

Lemma 4.1 If is bounded monotone, is Hölderian of exponent and, then

Proof. Assume that is nondecreasing. Since

by virtue of change of a variable (P4) we have

If is a partition of

where. Therefore, by boundedness of yield

If is nonincreasing the proof is similarly. □

Lemma 4.2 Let be a map of bounded p(×)-variation. Then, there exist a bounded nondecreas- ing nonnegative function and a Hölderian map of exponent and the Hölder constant such that

1) on.

2) in.

3).

Proof. We define the function by; by (P2) it is well define nonnegative bounded

and nondecreasing. If denote by the inverse image of the one-

point set under the function. Define the map as follows if

(4.1)

By (P1) and (P3),

The representation of f in (1) follows from (5), for if, then and, so that (5) yields.

The assertions in (2) and (3) follows from (1) and (P4). Now we will show that g is Hölderian. We have

Hence, if, then by (P1) and (P3) we get

then

□

In the next section we will be dealing with the composition operator (Nemitskij).

5. Composition Operator between the Space

In any field of nonlinear analysis composition operators (Nemytskij), the superposition operators generated by appropriate functions, play a crucial role in the theory of differential, integral and functional equations. Their analytic properties depend on the postulated properties of the defining function and on the function space in which they are considered. A rich source of related questions are the monograph by J. Appell and P. P. Zabrejko [25] and J. Appell, J. Banas, N. Merentes [8] .

Given a function, the composition operator H, associated to a function f (autonomous case) maps each function into the composition function given by

(5.1)

More generally, given we consider the operator H, defined by

(5.2)

This operator is also called superposition operator or susbtitution operator or Nemytskij operator. In what follows, will refer (5.1) as the autonomus case and to (5.2) as the non-autonomus case.

One of our main goals is to prove a result in the case when h is locally Lipschitz if and only if the composition operator maps the space of functions of bounded p(×)-variation into itself.

Theorem 5 Let H be a composition operator associated to. H maps the space into itself if and only if h is locally Lipschitz.

Proof. We may suppose without loss generality that. First, let be locally Lipschitz on, and let. Then for some. Considering the local Lipschitz condition

(5.3)

for, for any partition we obtain the estimate

This shows that for, , and hence as claimed.

For the converse implication, suppose that h does not satisfy a local Lipschitz condition (5.3), in this way for any increasing sequence of positive real numbers that converges to infinite, that we will be defined

later, we can choose sequences, , with and

(5.4)

Considering subsequences if necessary, we can assume that the sequence is monotone. We supposed without loss of generality the sequence is increasing. Since is compact, from de inequality (5.2)

we have that there exists subsequences of and that we will denote in the same way, and that

converge to. Since the sequence is a Cauchy sequence, we can assume that

such that for all k, and so. Choose.

Pick the sequence defined recursively by

This sequence is strictly increasing and

So to ensure that, it is sufficient to suppose that. We define the continuous zig-zag

functions, as

Put and write each interval, as the union of the family of non-overlapping ones

The function f is defined on as follows:

Let, then the possibilities for the location of s and t on are as follows

Case 1. If and are in the same interval.

Case 2. If and are in two different intervals.

, ,. We get

Case 3. If, ,

Case 4. If.

Case 5. If.

Case 6: If

In this circumstance and the situation is trivial.

So, for each partition of the interval of the form

and using the inequality (5.4) and definition of, we have

Hence series diverges, , which is a contradiction. □

6. Uniformly Continuous Composition Operator

In this section, we give the other main result of this paper, namely, we show that any uniformly bounded com- position operator that maps the space the into itself necessarily satisfies the so called Matkow- ski’s weak condition.

First of all we will give the definition of left regularization of a function.

Definition 5 Let, its left regularization of mapping f is the function given as

We will denote by the subset in which consists of those functions

that are left continuous on.

Lemma 6.1 If, then.

Thus, if a function f has Wiener variation with variable exponent, then its left regularization is a left con- tinuous function.

Theorem 6 Suppose that the composition operator H generated by maps into itself and satisfies the following inequality

(6.1)

for some function. Then, there exist functions such that

(6.2)

where is the left regularization of for all.

Proof. By hypothesis, for fixed the constant function belongs to

. Since H maps into itself, we have. By

Lemma 6.1 the left regularization for every.

From the inequality (6.1) and definition of the norm we obtain for,

(6.3)

From the inequality (6.3) and Lemma 6.1, if then

(6.4)

Let, and let be the equidistant partition defined by

Given with, define by

(6.5)

and

(6.6)

Then, the difference satisfies

Consequently, by the inequality (6.1)

From the inequality (6.4) and the definition of p(×)-variation in Wiener’s sense, we have

However, by definition of the definition of the functions and,

Then

Since for all and passing to the limit as, necessarily

So, we conclude that satisfies the Jensen equation in (see [26] , p. 315). The continuity of with respect of the second variable implies that for every there exist such that

Because, and, for each, we obtain that. □

J. Matkowski [27] introduced the notion of a uniformly bounded operator and proved that any uniformly bounded composition operator acting between general Lipschitz function normed spaces must be of the form (11).

Definition 6 ([27] , Def. 1]) Let and be two metric (or normed) spaces. We say that a mapping is uniformly bounded if, for any there exists a nonnegative real number such that for any nonempty set we have

Remark 6.2 Every uniformly continuous operator or Lipschitzian operator is uniformly bounded.

Theorem 7 Let and H the composition operator associated with h. Suppose that H maps into itself and is uniformly continuous, then, there exist functions such that

where is the left regularization of for all.

Proof. Take any and such that

Since by the uniform boundedness of H, we have

that is,

therefore, by the Theorem 6 we get

Acknowledgements

This research has been partially supported by the Central Bank of Venezuela. We want to give thanks to the library staff of BCV for compiling the references.

Cite this paper

OdalisMejía,NelsonMerentes,José LuisSánchez, (2015) The Space of Bounded p(·)-Variation in Wiener’s Sense with Variable Exponent. Advances in Pure Mathematics,05,703-716. doi: 10.4236/apm.2015.511064

References