Advances in Pure Mathematics
Vol.05 No.08(2015), Article ID:57681,21 pages
10.4236/apm.2015.58046
Analytic Theory of Finite Asymptotic Expansions in the Real Domain. Part II-B: Solutions of Differential Inequalities and Asymptotic Admissibility of Standard Derivatives
Antonio Granata
Department of Mathematics and Computer Science, University of Calabria, Cosenza, Italy
Email: antonio.granata@unical.it
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 30 April 2015; accepted 27 June 2015; published 30 June 2015
ABSTRACT
Part II-B of our work continues the factorizational theory of asymptotic expansions of type (*)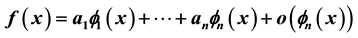 ,
, 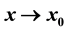 ,
, 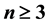 where the asymptotic scale
where the asymptotic scale 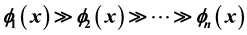 ,
, 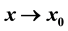 , is assumed to be an extended complete Chebyshev system on a one-sided neighborhood of x0. The main result states that to each scale of this type it remains associated an important class of functions (namely that of generalized convex functions) enjoying the property that the expansion (*), if valid, is automatically formally differentiable n − 1 times in the two special senses characterized in Part II-A. A second result shows that formal applications of ordinary derivatives to an asymptotic expansion are rarely admissible and that they may also yield skew results even for scales of powers.
, is assumed to be an extended complete Chebyshev system on a one-sided neighborhood of x0. The main result states that to each scale of this type it remains associated an important class of functions (namely that of generalized convex functions) enjoying the property that the expansion (*), if valid, is automatically formally differentiable n − 1 times in the two special senses characterized in Part II-A. A second result shows that formal applications of ordinary derivatives to an asymptotic expansion are rarely admissible and that they may also yield skew results even for scales of powers.
Keywords:
Asymptotic Expansions, Formal Differentiation of Asymptotic Expansions, Factorizations of Ordinary Differential Operators, Chebyshev Asymptotic Scales

7. A Brief Introduction
This is a continuation of a previous paper [1] , about the factorizational theory of asymptotic expansions in the real domain.
・ §8 contains the main result in the paper: to each Chebyshev asymptotic scale 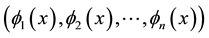 it remains associated an important class of functions enjoying the property that an asymptotic expansion according to this scale, if valid, is automatically formally differentiable
it remains associated an important class of functions enjoying the property that an asymptotic expansion according to this scale, if valid, is automatically formally differentiable 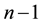 times in the two special senses characterized in §§4,5 in Part II-A. Under the regularity assumptions of the factorizational theory, this class is characterized by an nth-order differential inequality whereas in the yet-to-be-developed geometric theory it will be the class of generalized convex functions as in the special case of polynomial expansions ([2] , §4).
times in the two special senses characterized in §§4,5 in Part II-A. Under the regularity assumptions of the factorizational theory, this class is characterized by an nth-order differential inequality whereas in the yet-to-be-developed geometric theory it will be the class of generalized convex functions as in the special case of polynomial expansions ([2] , §4).
・ In §9, discussing formal application of standard derivatives to an asymptotic expansion, we characterize the existence of certain polynomial expansions at an endpoint where derivatives may fail to exist and such that the growth-order estimates of the remainders of the differentiated expansions follow unexpected algebraic rules.
・ §10 contains the proofs and §11 contains a few remarks about our theory.
Whereas the results in Part II-A show that “formal differentiation of asymptotic expansions” is usually admissible only if suitable operators linked to the given scale are used, the results in this Part II-B shed further light on this classical problem by exhibiting a meaningful and not too special case wherein suitable formal differentiations are automatically admissible and by showing that standard derivatives are admissible in very special cases only and that they may yield formulas algebraically skew from a classical viewpoint.
We continue the numbering of sections and formulas in [1] , but we adopt an independent numbering of the references in the bibliography. In order to agree with some classical terminology about the matter in this paper, it is convenient to specify the signs of certain Wronskians, so we list the fundamental properties of the scale we shall use taken from ([1] , Def. 2.1 and Prop. 2.3):
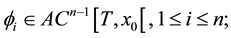 (7.1)
(7.1)
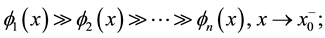 (7.2)
(7.2)
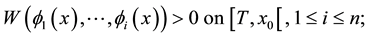 (7.3)
(7.3)
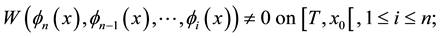 (7.4)
(7.4)
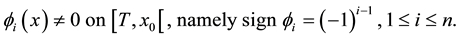 (7.5)
(7.5)
The operator
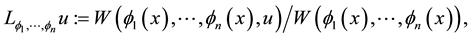 (7.6)
(7.6)
is the unique linear ordinary differential operator of type (2.1)1,2, acting on the space  and such that
and such that 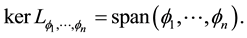 Expansions we are studying are of type
Expansions we are studying are of type
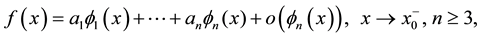 (7.7)
(7.7)
and we are supposing 




8. Absolute Convergence and Solutions of Differential Inequalities
The theory developed in Part II-A becomes particularly simple when the involved improper integrals are absolutely convergent and still more expressive for a function f satisfying the nth-order differential inequality

Under the assumptions (7.1) and (7.3) this is a subclass of the so-called “generalized convex functions with respect to the system

Theorem 8.1 (Complete asymptotic expansions). If 
1) There exist 


2) There exist n real numbers 

3) The following set of asymptotic expansions holds true:

4) The following set of asymptotic expansions holds true:

5) The following integral condition is satisfied:

6) The following integral condition is satisfied:

To this list we may obviously add the other properties in Theorem 5.1 and if this is the case the remainder 

whence it follows that

The above equivalence “1) Û 2)” simply means that, under condition (8.1), a relation “


In addition to the equivalence “3) Û 4)” there is another remarkable circumstance wherein the two types of formal differentiations are simultaneously admissible namely when the convergence of the pertinent improper integrals is absolute.
Theorem 8.2. For 



Hence each of these three conditions implies both sets of asymptotic expansions (4.31) and (5.5)-(5.6) (here the signs of the Wronskians are immaterial).
An indirect brief proof of the equivalence “(8.11) Û (8.12)” can be based on Theorem 8.1, but it also follows from the following remarkable relation valid for any signs of the Wronskians in (7.3), (7.4):

Using Theorems 4.4 and 5.2, we can also get the analogues of Theorems 8.1-8.2 for incomplete asymptotic expansions and here is a concise statement, all asymptotic relations referring to 
Theorem 8.3 (Incomplete asymptotic expansions). Let 




(which last relations are written in (4.28) in an expanded form);




To the foregoing list we may obviously add property 2) or property 5) in Theorem 4.4 and properties 2)-3) in Theorem 5.2. For 

Notice that relation (8.13) and the definition of 

hence (8.18) does not in general imply the convergence, as


Moreover each of the “O”-estimates in (8.17) is meaningful whenever the involved integral diverges as 


one-signedness, it is possible to infer from condition (8.20) sharper estimates not depending on
Theorem 8.4 (Sharper estimates for





Then the estimates in (8.17) for 


In the present context the above estimates are by no means obvious or “natural”: they have been obtained by adapting the standard calculations in the proof of the Abel-Dirichlet’s test for convergence of weighted improper integrals (Lemma 10.1 below). As a simple check of their validity we reobtain classical estimates for the derivatives of nth-order convex functions, and to be consistent with the meaning of n in the present series of papers, namely “n = dimension of the Chebyshev system

Corollary 8.5 (Rates of increase of derivatives of higher-order convex functions). Assume that: 



Then the following asymptotic relations hold true as

Here the asymptotic scale is:








The case 
The estimates in Corollary 8.5 also follow from old results by Landau, Hardy and Littlewood about differentiation of asymptotic relations involving real powers, under assumptions of monotonicity on the derivatives, results that were discussed in [4] and then extended in [5] to asymptotic expansions in real powers. The special case 


An important remark. In Theorem 8.1 the two types of formal differentibility 
lent facts whereas it is not so for a generic f such that 
borhood of


Open problem. For 
We shall not dwell on this marginal aspect of the theory though it leaves unsolved whether or not we may use representation formula (14.38), in alternative to (15.12)-(15.13), under condition (15.10).
9. Asymptotic Admissibility of Standard Derivatives
9.1. Asymptotically-Admissible Operators
Before investigating cases wherein standard derivatives 
Definition 9.1 (Asymptotically-admissible operators). Let 







without any further regularity assumptions.
(I) (A definition valid in special cases but highlighting the concept). 

if its formal application to both sides of (9.2) yields a new asymptotic expansion

This implicitly implies that 


Put in these terms the definition is well-posed if none of the functions 




(II) (A general definition). First, if


and say that 


after suppression of all the zero terms. An alternative locution for an asymptotically-admissible 


A first group of examples clarifies the necessity of specifying “after suppression of all the zero terms”. In each of the following three examples the standard operator of differentiation 



That the standard operator of differentiation does not preserve asymptotic hierarchies is quite elementary but a second group of examples shows that it may not preserve asymptotic hierarchies even when acting on an n-tuple forming a Chebyshev asymptotic scale (signs apart) on a neighborhooh of 

1) Elementary examples showing that if 





2) Examples of Chebyshev asymptotic scales 


3) Example of a Chebyshev asymptotic scale 


The above examples are variations on the examples in Bourbaki ([8] ; Part V, §4, pp. V.22-V.23).
4) Example of a Chebyshev asymptotic scale 


and there exists a function g such that

Just take

with different values of
9.2. Asymptotic Admissibility of Standard Derivatives
Let us ask the question: What are the natural scales granting the asymptotic admissibility of the standard operators



disproved even for the familiar scale at










for some function 



For 



Here the operators 


Lemma 9.1. (I) If 



(II) If 



The reader must not think that we are now filling a few pages with trivialities about Taylor’s formula; as a matter of fact if we apply our theory to the operator 




Theorem 9.2. Let:



whereas the one associated to factorization (9.20) is the standard derivative

Consider now a generic polynomial of order 

(I) (The continuity property of Taylor’s formula). The following are equivalent properties for a fixed 
1) The set of asymptotic expansions as

As concerns the bound 


2) The improper integral (involving n−i iterated integrations)

which for 

On account of the hypothesis

which is equivalent to condition

Hence relations (9.29) are nothing but Taylor’s formula of order i of 



(II) (A polynomial expansion at an endpoint where derivatives may fail to exist). The following are equivalent properties for a fixed
3) The set of aymptotic expansions as

4) The set of aymptotic expansions as

where the two estimates coincide for

The nondifferentiated expansion is written differently in (9.34) than in (9.35) to correctly apply the operators 




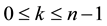
5) The iterated improper integral (involving i+1 integrations)

We must comment on the above claims. Part (I) is a classical elementary property which may be traced back to Walter and Ford ([9] , Lemma II, p. 350), 1911, and a proof is reported in Aumann and Haupt ([10] , Ch. 8, §8.9.2.1, pp. 235-236) valid under weaker regularity assumptions involving only the existence of the highest- order left derivative of the given function and its limit as













then the estimate for 





Examples. The following simple examples involving oscillatory functions will reassure the doubtful readers (and the author himself was in the number). For 


an example being provided by

which is differentiable at 


For 





It is obvious that in both cases f can be extended so as to be of class 


for which

A final comment. The discussion in this section shows that formal applications of ordinary derivatives to an asymptotic expansion is not admissible generally speaking, and even for the very special asymptotic scale (9.22) the first (but not the second) factorizational approach can give seemingly-unnatural results. It is in principle true that each of the two sets of expansions characterized in Part II-A, §§4,5, can provide asymptotic information (not always meaningful and not necessarily expansions) for the ordinary derivatives; however this is easily achieved for the first-order derivative but is practically unmanageable for higher-order derivatives and yields no theoretical result. It is also true that for expansions in arbitrary real powers as 



10. Proofs
Proof of Theorem 8.1. The only thing to be proved is the inference “1) Þ 5) Ù 6)”, the other properties being included in Theorems 4.5 and 5.1. We use a procedure already used in ([2] , p. 193) and in ([5] , p. 213). From representation in (4.15) we get (using the simplified notation

By the assumption (8.2) the left-hand side has a finite limit as

after applying L’Hospital’s rule 



with suitable constants

Here again the left-hand side has a finite limit as 
after applying L’Hospital’s rule 


with suitable constants

with a suitable constant

and (10.6) in turn implies:

By the positivity of the integrand this last relation implies (8.6) and the first representation in (8.8) for



which implies

and (5.1) can be rewritten as

with suitable constants

Evaluating the limit of the right-hand side by L’Hospital’s rule and using formula in (2.31), 
and this last limit, which exists in

and (10.11) can be rewritten as

with suitable constants


for some



exists in
which, by the positivity of the integrand, exists in 




with some constant


and if we try to evaluate the limit of the ratio on the left applying L’Hospital’s rule 


lows the second representation in (8.8) for the remainder in (8.3). The proof is over.
Proof of Theorem 8.2. The equivalence between (8.10) and (8.11) easily follows from Fubini’s theorem by interchanging the order of integrations in (8.10) whereas the equivalence between (8.11) and (8.12) is by no means an obvious fact. A concise proof based on Theorem 8.1 is as follows; putting

we have

hence F satisfies 

and (8.12). Now we prove relation (8.13) recalling that all the involved functions and Wronskians are strictly one-signed on the interval. The symbol of asymptotic equivalence is referred to 

valid for any ordered 




where in the last but one passage we have applied formula (10.22) to the ordered triplet

Now, for a fixed

As in (10.24) we can prove that (10.26) is true for

that is (10.26). Using this relation for 

that is (8.13).
Proof of Theorem 8.3. The only thing to prove is the O-estimates in (8.17). From representation (5.2)

for some constant c, whence the estimate for 
Proof of Theorem 8.4 is contained in the following lemma only valid under the stated one-signedness restrictions.
Lemma 10.1 (Growth-order estimates for iterated improper integrals with nonnegative integrands). Assumptions:





Thesis. The following estimates hold true:

Proof. All functions 



which implies the first relation in (10.33). To estimate 
Now the integral on the left is convergent by hypothesis and the first integral on the right is convergent by (10.34), hence the second integral on the right converges as well and we get the equality

whence, again by (10.34),

The nondecreasingness of 

which yields the estimate for

we want to prove


whence

And now the nondecreasingness of 

Relations (10.39)-(10.40) allow iteration of the procedure to estimate 
Proof of Theorem 9.2. Part (I) is nothing but Theorems 5.1 and 5.2 applied to the present case wherein f is replaced by 





Lemma 10.2. Let f be of class 


For a fixed 


is equivalent to the set of asymptotic relations, as

where the two estimates coincide for

For 




Proof. It is easily proved by induction that the expanded expressions of the

with suitable constants 

whence

Second step. From the second equality in (10.45) we infer

having used (10.47), and from these last estimates we get

Suppose now that the relations in (10.43) for the derivatives have been proved true for



whence

Now for 



For the remaining values of i we must use the second estimate in (10.42) for 


Now inside the sum each 

In the first case the restriction 






Finally from (10.51) we get the sought-for estimates for

The proof of “(10.42) Þ (10.43)” is over. The converse implication is checked at once replacing the estimates in (10.43) into the sum (10.45) expressing

11. Some Remarks on Factorizational Theory
11.1. On the Use of Non-Canonical Factorizations
We show by two examples that the use of non-C.F.’s is unreliable to construct a general theory. Let us refer, e.g., to the characterizations of an asymptotic expansion for a generalized convex function.
First example. For

and that the inference “Þ” can be easily proved when a C.F. of the operator 



and the related representation

Assuming the validity of the expansion in (11.1), we try to find a necessary integral condition involving
and by reasons of constant sign, we infer

a much weaker condition than 
Second example. Let us consider the operator 



We have 

obtained from the results in §8 based on the use of C.F.’s. However, in this case the equivalence in (11.8) can be also obtained using the non C.F. in (11.7) if one starts from the corresponding integral representation for f and reapplies the same procedure used in the proof of Theorem 8.1.
11.2. On the Use of Integral Representations Inferred from Factorizations
We start noticing that the convergence of an iterated integral

where 



Now an integral representation linked to a C.F. of type (I) and more general than (4.15) in Part II-A is

wherein the


If there exists an n-tuple 

then, recalling that

with an appropriate representation of the remainder.
But, by the initial remark, such an integral condition is almost useless for general results as well as for practical applications if the




Moral. Working with the C.F. of type (I) at
The situation is technically different when working with a C.F. of type (II). Referring to an integral representation of type

more general than (5.1) in Part II-A, we see that as soon as we may choose 

does not “whimsically” depend on 


References
- Granata, A. (2015) Analytic Theory of Finite Asymptotic Expansions in the Real Domain. Part II-A: The Factorizational Theory for Chebyshev Asymptotic Scales. Advances in Pure Mathematics, 5, 454-480.
- Granata, A. (2007) Polynomial Asymptotic Expansions in the Real Domain: The Geometric, the Factorizational, and the Stabilization Approaches. Analysis Mathematica, 33, 161-198. http://dx.doi.org/10.1007/s10476-007-0301-0
- Granata, A. (2011) Analytic Theory of Finite Asymptotic Expansions in the Real Domain. Part I: Two-Term Expansions of Differentiable Functions. Analysis Mathematica, 37, 245-287. http://dx.doi.org/10.1007/s10476-011-0402-7
- Granata, A. (2010) The Problem of Differentiating an Asymptotic Expansion in Real Powers. Part I: Unsatisfactory or Partial Results by Classical Approaches. Analysis Mathematica, 36, 85-112. http://dx.doi.org/10.1007/s10476-010-0201-6
- Granata, A. (2010) The Problem of Differentiating an Asymptotic Expansion in Real Powers. Part II: Factorizational Theory. Analysis Mathematica, 36, 173-218. http://dx.doi.org/10.1007/s10476-010-0301-3
- Popoviciu T. (1944) Les Fonctions Convexes. Hermann & C
Éditeurs, Paris.>http://html.scirp.org/file/6-5300896x476.png" class="200" /> Éditeurs, Paris.
- Granata, A. (2015) The Factorizational Theory of Finite Asymptotic Expansions in the Real Domain: A Survey of the Main Results. Advances in Pure Mathematics, 5, 1-20. http://dx.doi.org/10.4236/apm.2015.51001
- Bourbaki, N. (1976) Fonctions d’une Variable Réelle―Théorie élémentaire. Hermann, Paris.
- Walter, M. and Ford, B. (1911) Conditions Suffisantes pour qu’une Fonction Admette un Développement Asymptotique. Bulletin de la Société Mathématique de France, 39, 347-352.
- Aumann, G. and Haupt, O. (1974) Einführung in die reelle Analysis. I: Funktionen einer reellen Veränderlichen. Walter de Gruyter, Berlin. http://dx.doi.org/10.1515/9783110841046














 Éditeurs, Paris.>http://html.scirp.org/file/6-5300896x476.png" class="200" /> Éditeurs, Paris.
Éditeurs, Paris.>http://html.scirp.org/file/6-5300896x476.png" class="200" /> Éditeurs, Paris.