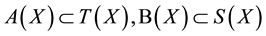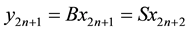Received 17 April 2015; accepted 25 May 2015; published 28 May 2015

ABSTRACT

We establish fixed point theorems in complete fuzzy metric space by using notion of altering distance, initiated by Khan et al. [Bull. Austral. Math. Soc. 30 (1984), 1-9]. Also, we find an affirmative answer in fuzzy metric space to the problem of Sastry [TamkangJ. Math., 31(3) (2000), 243-250].

Keywords:

Fixed Points, Fuzzy Metric Spaces, Altering Distance, Fixed Point Results

1. Introduction

The concept of fuzzy sets was introduced by Zadeh. With the concept of fuzzy sets, the fuzzy metric space was introduced by Kramosil and Michalek [1] . Grabiec [2] proved the contraction principle in the setting of fuzzy metric space. Also, George and Veermani [3] modified the notion of fuzzy metric space with the help of continuous t-norm. Fuzzy set theory has applications in applied sciences such as neural network theory, stability theory, mathematical programming, modelling theory, engineering sciences, medical sciences (medical genetics, nervous system), image processing, control theory and communication.

Boyd and Wong [4] introduced the notion of Φ-contractions. In 1997, Alber and Guerre-Delabriere [5] defined the ϕ-weak contraction which was a generalization of Φ-contractions. Many researchers studied the notion of weak contractions on different settings which generalized the Banach Contraction Mapping Principle. Another interesting and significant fixed point results as a generalization of Banach Contraction Principle have been established by using the notion of alerting distance function, a new notion propounded by Khan et al. [6] . Altering Distance Functions are control functions which alter the distance between two points in a metric space. For more details, we refer to [6] - [12] .

Sastry et al. [13] proved the following:

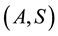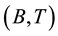Theorem 2.4 [13] Let and be weakly commuting pairs of self mappings of a complete metric space 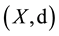satisfying

1)

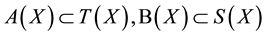
2) There exists 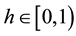such that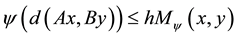, where

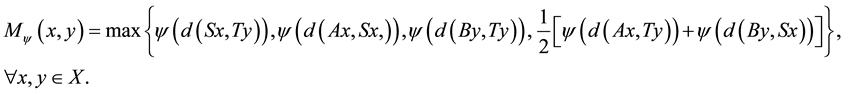
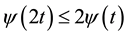and is continuous at zero, monotonically increasing, and 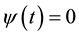if and only if. Suppose that A and S are 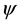-compatible and S is continuous. Then A, B, S and T have a unique common fixed point.

On the basis of theorem 2.4 of [13] , Sastry posed the following open problem:

Is theorem 2.4 of [13] valid if we replace continuity of S by continuity of A?

In this paper, we prove common fixed point theorems which provide an affirmative answer to the above question on existence of fixed point in fuzzy metric spaces.

2. Preliminaries

To set up our results in the next section, we recall some basic definitions.

Definition 2.1 [14] A fuzzy set A in X is a function with domain X and values in [0, 1].

Definition 2.2 [14] A binary operation *: [0, 1] × [0, 1] ® [0, 1] is a continuous t-norm if ([0, 1], *) is a topological abelianmonoid with unit 1 such that. 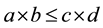whenever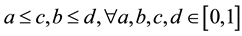

Definition 2.3 [15] The 3-tuple (X, M, *) is called a fuzzy metric space if X is an arbitrary set, * is a continuous t-norm and M is a fuzzy set on X² × [0, ∞) satisfying the following conditions:

(FM-1) M(x, y, t) > 0 and M(x, y, 0) = 0,

(FM-2) M(x, y, t) = 1 if x = y,

(FM-3) M(x, y, t) = M(y, x, t),

(FM-4) M(x, y, t) * M(y, z, s) ≤ M(x, z, t + s),

(FM-5) M(x, y, t): (0, ∞) ® [0,1] is continuous, for all x, y, z ∊ X and s, t > 0.

We note that 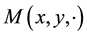is non-decreasing for all x, y ∊ X.

Definition 2.4 Let 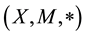be a fuzzy metric space. A sequence is said to be

1) G-Cauchy (i.e., Cauchy sequence in sense of Grabiec [5] ) if for all t > 0 and each p > 0.

2) Convergent to a point x ∊ X if for all t > 0.

Definition 2.5 [16] -[18] A pair of self mappings (f, g) on fuzzy metric space is said to be reciprocally continuous if

whenever is a sequence in X such that

for some z in X.

Definition 2.6 An altering distance function or control function is a function

such that the following axioms hold:

1) is monotonic increasing and continuous;

2) if and only if t = 0.

Lemma 2.1 [5] . Let (X, M, *) be fuzzy metric space and for all, and if for a number,. Then x = y.

Lemma 2.2 [5] . Let (X, M, *) be fuzzy metric space and be a sequence in X. If there exists a number such that for all and n = 1, 2,・・・

Then is a Cauchy sequence in X.

Lemma 2.3 Let is continuous and decreasing if and only if. Then and implies.

Definition 2.7 [13] A pair of self mappings on fuzzy metric space is said to be ψ-com- patible if

whenever is a sequence in X such that

for some z in X.

3. Main Results

Theorem 3.1 Let and be weakly commuting pairs of self mappings of a complete fuzzy metric space satisfying

(3.1)

(3.2) There exists such that, where

Suppose that A and S are -compatible and A is continuous. Then A, B, S and T have a unique common fixed point.

Proof: Let be any fixed point in X. Define sequences and in X given by the rule

(3.3) and

This can be done by virtue of (3.1). Now, we prove that is a Cauchy sequence. For in (3.2), we have

As

If

,

a contradiction and hence

,

but as is decreasing so we have and hence by lemma (2.2), the sequence is a Cauchy sequence in X. Since X is complete, there is a point z in X such that

(3.4) and as.

Now, suppose that A and S are -compatible then we have

(3.5) and implies that

Also, A is continuous, so by (3.3),

(3.6) and as

We claim that. By (3.5), we get

as. By lemma (2.3) as and so.

Also, since for some w in X and corresponding to each, there exists a such that. Thus, we have and. Also, since, corresponding to each, there exists a such that Thus we have and.

Now, we claim that as. Using (3.2) with

.

Letting,

,

as is decreasing, so we have

Thus, we have as.

Also, we claim that. Using (3.2) for

Letting, we get Thus, we have

Again, since, so there exists u in X such that That is. Lastly, we show that. Then by (3.2) with, we have

(3.7) This gives and hence we have

As A and S are weakly commuting, we have and hence

(3.8)

Also, B and T are weakly commuting, we get

(3.9)

Finally, we show that. Again using (3.5), (3.6) and (3.2) with.

which gives that Therefore is a common fixed point of A and S. Similarly, we can show that and since we have, a common fixed point of B and T. Finally, we have as a common fixed point for A, B, S and T. The uniqueness follows from 2) and hence the theorem.

Theorem 3.2 Let and be weakly commuting pairs of self mappings of a complete fuzzy metric space satisfying

(3.10)

(3.11) There exists such that, where

. Suppose that A and S are -compatible pair of reciprocal continuous mappings. Then A, B, S and T have a unique common fixed point.

Proof: Let be any fixed point in X. Define sequences and in X given by the rule and.

As in theorem 3.1, the sequence is a Cauchy sequence in X. Since X is complete, there is a point z in X such that

and as.

Now, suppose that A and S are ψ-compatible pair of reciprocal continuous mappings, so we have and

Also, -compatibility of A and S implies that

(3.12)

By lemma (2.3) as. We claim that.

(3.13).

Since, , there is a point w in X such that. By (3.13),

(3.14)

Now, we show that. Suppose. Using (3.11), we have

A contradiction. Hence. Therefore by (3.14)

(3.15)

As A and S are weakly commuting, we have and hence

(3.16)

Also, B and T are weakly commuting, we get

(3.17)

Finally, we show that Again using (3.11) with.

which gives that. Therefore, is a common fixed point of A and S. Similarly, we can show that and since, we have, a common fixed point of B and T. Finally, , we have as a common fixed point for A, B, S and T. The uniqueness follows from 2) and hence the theorem.

Conflict of Interest

All the authors declare that they have no conflict of interest.

Acknowledgements

The authors wish to acknowledge with thanks the Deanship of Scientific Research, Jazan University, Jazan, K.S.A., for their technical and financial support for this research.

References