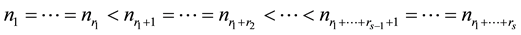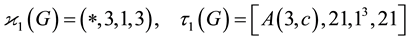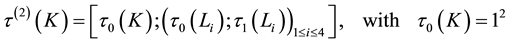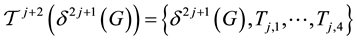Advances in Pure Mathematics
Vol.05 No.05(2015), Article ID:55789,27 pages
10.4236/apm.2015.55029
Index-p Abelianization Data of p-Class Tower Groups
Daniel C. Mayer
Naglergasse 53, 8010 Graz, Austria
Email: algebraic.number.theory@algebra.at
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 18 February 2015; accepted 11 April 2015; published 20 April 2015
ABSTRACT
Given a fixed prime number p, the multiplet of abelian type invariants of the p-class groups of all unramified cyclic degree p extensions of a number field K is called its IPAD (index-p abeliani- zation data). These invariants have proved to be a valuable information for determining the Galois group 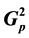 of the second Hilbert p-class field and the p-capitulation type
of the second Hilbert p-class field and the p-capitulation type 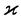 of K. For
of K. For 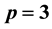 and a number field K with elementary p-class group of rank two, all possible IPADs are given in the complete form of several infinite sequences. Iterated IPADs of second order are used to identify the group
and a number field K with elementary p-class group of rank two, all possible IPADs are given in the complete form of several infinite sequences. Iterated IPADs of second order are used to identify the group 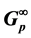 of the maximal unramified pro-p extension of K.
of the maximal unramified pro-p extension of K.
Keywords:
p-Class Groups, p-Principalization Types, p-Class Field Towers, Quadratic Fields, Second p-Class Groups, p-Class Tower Groups, Coclass Graphs

1. Introduction
After a thorough discussion of the terminology used in this article, such as the logarithmic and power form of abelian type invariants in Section 2, and multilayered transfer target types (TTTs), ordered and accumulated index-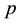 abelianization data (IPADs) up to the third order in Section 3, we state the main results on IPADs of exceptional form in Section 3.1, and on IPADs in parametrized infinite sequences in Section 3.2. These main theorems give all possible IPADs of number fields
abelianization data (IPADs) up to the third order in Section 3, we state the main results on IPADs of exceptional form in Section 3.1, and on IPADs in parametrized infinite sequences in Section 3.2. These main theorems give all possible IPADs of number fields 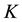 with 3-class group
with 3-class group 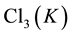 of type
of type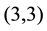 .
.
Before we turn to applications in extreme computing, that is, squeezing the computational algebra systems PARI/GP [1] and MAGMA [2] -[4] to their limits in Section 5, where we show how to detect malformed IPADs in Section 5.1, and how to complete partial 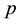 -capitulation types in Section 5.2, we have to establish a com- ponentwise correspondence between transfer kernel types (TKTs) and IPADs in Section 4 by exploiting details of proofs which were given in [5] .
-capitulation types in Section 5.2, we have to establish a com- ponentwise correspondence between transfer kernel types (TKTs) and IPADs in Section 4 by exploiting details of proofs which were given in [5] .
Iterated IPADs of second order are used in Section 6 for the indirect calculation of TKTs in Section 6.1, and for determining the exact length 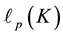 of the
of the 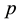 -class tower of a number field K in Section 6.2. These
-class tower of a number field K in Section 6.2. These
sophisticated techniques prove 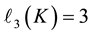 for quadratic number fields
for quadratic number fields 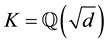 with
with
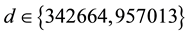 (the first real quadratic fields) and
(the first real quadratic fields) and 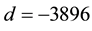 (the first tough complex quadratic field after the easy
(the first tough complex quadratic field after the easy 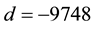 ( [6] , Cor.4.1.1), which resisted all attempts up to now.
( [6] , Cor.4.1.1), which resisted all attempts up to now.
Finally, we emphasize that IPADs of infinite 

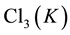
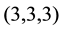
2. Abelian Type Invariants
Let 







The powers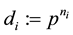






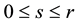
The cumbersome subscripts can be avoided by defining 
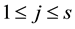

and we can define:
Definition 2.1. The abelian type invariants (ATI) of 

of strictly increasing positive integers 

Remark 2.1. The integers 


1) For abelian type invariants of high complexity, the logarithmic form in Definition 2.1 requires considerably less space (e.g. in Section 7, Table 2) than the usual power form

2) For brevity, we can even omit the commas separating the entries of the logarithmic form of abelian type invariants, provided all the 
3) A further advantage of the brief logarithmic notation is the independence of the prime


4) Finally, since our preference is to select generators of finite 
Example 2.1. For instance, if
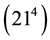
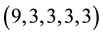


Now let 




Definition 2.2. The abelian type invariants of the commutator quotient group 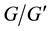


3. Index-p Abelianization Data
Let 





According to the Artin reciprocity law of class field theory [7] , 
quotient group 

extension 



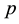







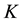


open) subgroup of finite index 


Definition 3.1. For each integer

of intermediate fields 










Now let 


Galois group 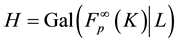



and the quotient 
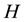

Definition 3.2. For each integer
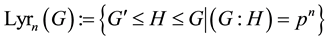
of intermediate groups 






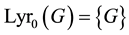


A further application of Artin’s reciprocity law [7] shows that

for every subgroup 


Since the abelianization 

Definition 3.3. For each integer






Similarly, the multiplet

abelian type invariants, is called the 

Remark 3.1.
1) If it is necessary to specify the underlying prime number


2) Suppose that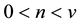




3) In view of the considerations in Equation (7), it is clear that we have the equality

in the sense of componentwise isomorphisms.
Since it is increasingly difficult to compute the structure of the 



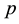
Definition 3.4. The restriction

of the TTT


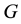

So, the complete TTT is an extension of the IPAD. However, there also exists another extension of the IPAD which is not covered by the TTT. It has also been used already in previous investigations by Boston, Bush and Nover [12] [14] [15] and is constructed from the usual IPAD 



to the IPAD 
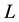
Definition 3.5. The family

is called the iterated IPAD of second order of

The concept of iterated IPADs as given in Dfn. 3.5 is restricted to the second order and first layers, and thus is open for further generalization (higher orders and higher layers). Since it could be useful for 2-power extensions, whose absolute degrees increase moderately and remain manageable by MAGMA [4] or PARI/GP [1] , we briefly indicate how the iterated IPAD of third order could be defined:

3.1. Sporadic IPADs
In the next two central theorems, we present complete specifications of all possible IPADs of pro-

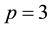




Since the abelian type invariants of the members of TTT layers will depend on the parity of the nilpotency class 

Definition 3.6. For an integer









In the following theorems, we use the identifiers in the SmallGroups Library [17] [18] .
Theorem 3.1. (First Main Theorem on

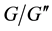
Let 







1) If 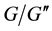


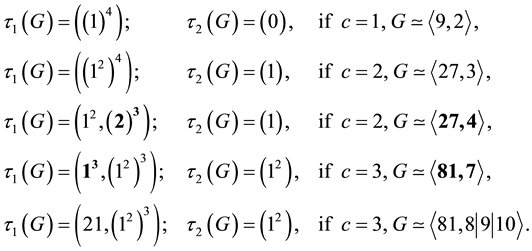
where generally
2) If 



where 

However, if 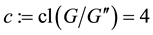

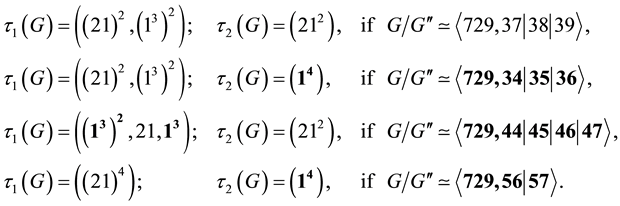
3) If 



However, if

where the irregular case can only occur for even class and coclass
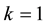

Proof. Since this proof heavily relies on our earlier paper [5] , it should be pointed out that, for a 





1) Using the association between the identifier of 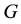
2) For



3) All the regular cases behave completely similar as the general case in Theorem 3.2, item (3), Equation (22). In the irregular case, only the bottom layer
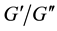

3.2. Infinite IPAD Sequences
Now we come to the IPADs of pro-


Theorem 3.2. (Second Main Theorem on


Let 
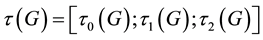






1) If 



2) If 




in dependence on the coclass tree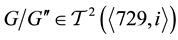


3) If 





The first member 


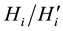



Proof. Again, we make use of [5] , and we point out that, for a 




1) All components of 
2) The first component of 



3) The first two components of 
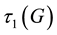




Finally, the bottom layer
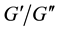
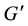
4. Componentwise Correspondence of IPAD and TKT
Within this section, where generally
Definition 4.1. We say a class of a base field 
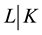
When the 3-class group of 


Our desire is to show that the components of the ordered IPAD and TKT [9] [19] are in a strict corre- spondence to each other. For this purpose, we exploit details of the proofs given in [5] , where generators of metabelian 3-groups G with 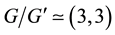
Since we now prefer a more computational aspect, we translate the results into a form which is given by the computational algebra system MAGMA [4] .
To be specific, we choose the vertices of two important coclass trees for illustrating these peculiar techniques. The vertices of depth (distance from the mainline) at most 1 of both coclass trees, with roots 





4.1. The Coclass Tree
Remark 4.1. The first layers of the TTT and TKT of vertices of depth at most 1 of the coclass tree 
1) polarization (dependence on the class
2) Stabilization (independence of the class
3) Rank 3 at the second TTT component (
Using the class

However, to assure the general applicability of the theorems and corollaries in this section, we aim at in- dependency of the selection of generators (and thus invariance under permutations).
Theorem 4.1. (in field theoretic terminology)
1) The class associated with the polarization becomes principal in the extension with rank 3.
2) The class associated with rank 3 becomes principal in both extensions of type
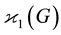
In the sequel, we use designations of special TKTs which were developed in [19] - [21] .
Remark 4.2. Aside from the common properties, there also arise variations due to the polarization, which we first express with respect to Magma’s selection of generators:
1) The TKT is E.6, 
2) The TKT is E.14, 

3) The TKT is H.4, 
4) The TKT is c.18, 
Corollary 4.1. (in field theoretic terminology)
1) For the TKTs E.6 and H.4, both classes associated with type 
2) All extensions satisfy Taussky’s condition (B) [22] , with the single exception of the polarized extension in the case of TKT E.6 or c.18, which satisfies condition (A).
3) TKT E.6 has a single fixed point, E.14 contains a 3-cycle, and H.4 contains a 2-cycle.
Proof. (of Theorem 4.1 and Corollary 4.1)
Observe that in [5] , the index of nilpotency 



with respect to the canonical generators, to the corresponding invariants
with respect to Magma’s generators. □
4.2. The Coclass Tree
Remark 4.3. The first layer TTT and TKT of vertices of depth at most 1 of the coclass tree 
1) polarization (dependence on the class
2) stabilization (independence of the class
3) rank 3 does not occur at any TTT component (
Using the class

Again, we have to ensure the general applicability of the following theorem and corollary, which must be in- dependent of the choice of generators (and thus invariant under permutations).
Theorem 4.2. (in field theoretic terminology)
1) Two extensions of type (21) reveal fixed point principalization satisfying condition (A) [22] .
2) The remaining extension of type (21) satisfies condition (B), since the class associated with the polarization becomes principal there.
Remark 4.4. Next, we come to variations caused by the polarization, which we now express with respect to Magma’s choice of generators:
1) The TKT is E.8, 
2) The TKT is E.9, 
3) The TKT is G.16, 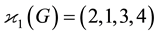
4) The TKT is c.21, 
Corollary 4.2. (in field theoretic terminology)
1) For the TKTs E.8 and E.9, the class associated with type (21), satisfying condition (B), remains resistant.
2) The polarized extension satisfies condition (B) [22] in the case of TKT E.9 or G.16, and it satisfies con- dition (A) in the case of TKT E.8 or c.21.
3) TKT G.16 is a permutation containing a 2-cycle, and TKT E.8 is the unique TKT possessing three fixed points.
Proof. (of Theorem 4.2 and Corollary 4.2)
In our paper [5] , the index of nilpotency 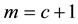



with respect to the canonical generators, to the corresponding invariants
with respect to Magma’s generators. □
5. Applications in Extreme Computing
5.1. Application 1: Sifting Malformed IPADs
Definition 5.1. An IPAD with bottom layer component 
To verify predicted asymptotic densities of maximal unramified pro-3 extensions in the article [10] numeri- cally, the IPADs of all complex quadratic fields 

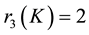



Example 5.1.
A check of all 276375 IPADs for complex quadratic fields with type 


1) For d = −96174803, the erroneous IPAD 
formed component 

2) For

malformed component 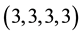
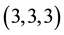
3) For

formed component 

4) For

formed component 

5) For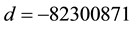

malformed component 

For the last two cases, Magma failed to determine the TKT. Nevertheless, none of the discriminants
is particularly spectacular.
Example 5.2.
We also checked all 122444 IPADs for complex quadratic fields with type 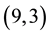


1) For
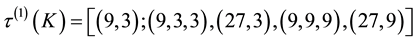
the malformed component 

2) For d = −79749087, the erroneous IPAD 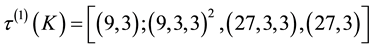
formed component 


3) For

the malformed component 

4) For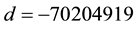

malformed component 

5) For d = −86139199, the erroneous IPAD 
formed component 


Again, none of the corresponding discriminants
is particularly spectacular.
We emphasize that, in both Examples 5.1 and 5.2, the errors of PARI/GP [1] occured in the upper limit range of absolute discriminants above 70 millions. This seems to be a critical region of extreme computing where current computational algebra systems become unstable. MAGMA [4] also often fails to compute the TKT in that range.
Fortunately, there appeared a single discriminant only for each of the 5 erroneous IPADs, in both examples. This indicates that the errors are not systematic but rather stochastic.
5.2. Application 2: Completing Partial Capitulation Types
Example 5.3. For the discriminant 

group of type


puted the IPAD 
According to Equation (20) in Theorem 3.2, the second 3-class group G of K must be of coclass










When we tried to determine the 3-principalization type

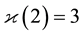









Example 5.4. For the discriminant 
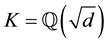
group of type


puted the IPAD 
According to Equation (20) in Theorem 3.2, the second 3-class group 











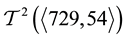
Next, we tried to determine the 3-principalization type

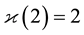



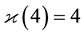









Example 5.5. For the discriminant 

class group of type

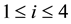
computed the IPAD 
According to Equation (20) in Theorem 3.2, the second 3-class group G of K must be of coclass










Then we tried to determine the 3-principalization type




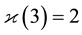







6. Iterated IPADs of Second Order
In this section, where generally
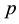

6.1. p-Capitulation Type
By means of the following theorem, the exact 3-principalization type 


of number fields of absolute degree
Theorem 6.1. (Indirect computation of the 
Suppose that 

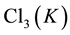


1) If the IPAD of 
then by Equation (14) in Theorem 3.1,
in particular, the length of the 3-class tower of 

2) If the first layer 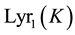
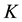

admits a sharp decision about the group 

if and only if


if and only if


if and only if
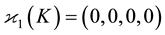
Proof. It suffices to compute the iterated IPADs of the groups 


Example 6.1. A possible future application of Theorem 6.1 could be, for instance, the separation of the capitulation types a.2, 

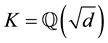




which was outside of our reach in all investigations of ( [23] , Tbl. 2, p. 496), ( [5] , Tbl. 6.1, p. 451) and ( [9] , Figure 3.2, p. 422). The reason why we expect this enterprise to be promising is that our experience with MAGMA [4] shows that computing class groups can become slow but remains sound and stable for huge discriminants
6.2. Length of the p-Class Tower
In this section, we use the iterated IPAD of second order 
indirect computation of the length 





We begin with theorems which permit a decision between finitely many possibilities for the length 






6.2.1. Second p-Class Groups with Finite Cover
In the following theorems, we must use extended identifiers [4] [24] [25] of finite 3-groups with order bigger than
Theorem 6.2. (Length 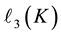

Suppose that 

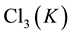


1) If the IPAD of 
and the first layer TKT 


2) If the first layer 
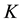

admits a sharp decision about the length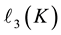

if and only if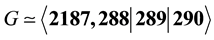


if and only if

Proof. According to Theorem 3.2, an IPAD of the form 
metabelianization of the group 


According to Section 4.1, the lack of a total principalization excludes the TKT c.18 and the absence of a 2-cycle discourages the TKT H.4, whence the group 
By means of the techniques described in ( [6] , Proof of Thm. 4.1), a search in the complete descendant tree
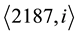




Finally, we have
Theorem 6.3. (Length 

Suppose that 




1) If the IPAD of 
and the first layer TKT 


2) If the first layer 


admits a sharp decision about the length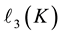

if and only if


if and only if

Proof. According to Theorem 3.2, an IPAD of the form 
lianization of the group 


According to Section 4.2, the lack of a total principalization excludes the TKT c.21 and the absence of a 2-cycle discourages the TKT G.16, whence the group 
As we have shown in detail in [6] , Proof of Thm. 4.1], a search in the complete descendant tree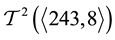





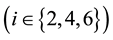
Eventually, the 3-tower length of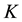


Example 6.2. (The first real quadratic field 

discriminant 


3-tower group 

The complex quadratic analogue 
Taussky [20] . However, it required almost 80 years until M.R. Bush and ourselves ([6] , Cor. 4.1.1) succeeded in providing the first faultless proof that 







For

yield four possible 3-tower groups of K, namely either the two unbalanced groups 






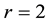

In October 2014, we succeeded in proving that three of the unramified cyclic cubic extensions 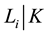
the critical IPAD component 


6.2.2. Another Descendant Tree with Periodic Bifurcations
In ( [16] , Section 21.2), we provided computational evidence of periodic bifurcations in pruned descendant trees with roots





For brevity, we give 3-logarithms of abelian type invariants in the following theorem and we denote iteration
by formal exponents, for instance, 


initial anomalies of generalized identifiers by putting

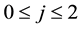


Theorem 6.4. Let 
1) In the descendant tree 
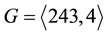


and (reverse) directed edges with alternating step sizes 1 and 2 such that

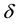



resp. all the vertices with odd superscript 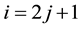

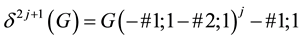
of this path share the following common invariants, respectively:
-the uniform IPAD

-the uniform transfer kernel type

-the 3-multiplicator rank and the nuclear rank [14] [16] ,

resp., giving rise to the bifurcations for odd

-and the counters of immediate descendants [16] [18] ,

resp.

determining the local structure of the descendant tree.
2) A few other invariants of the vertices 
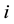
-the 3-logarithm of the order, the nilpotency class and the coclass,

resp.

Theorem 6.4 provides the scaffold of the pruned descendant tree 

With respect to our intended applications, however, the following Corollaries 6.1 and 6.2 are of the greatest importance.
Corollary 6.1. Let 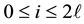
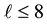
Whereas the vertices with even superscript


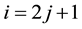


1) The regular component 


2) The irregular component 


and additionally contains the next vertex of the distinguished path
Remark 6.1. We apply a sifting strategy for reducing the entire descendant tree 


1) keeping the unique terminal step size-2 descendant, which is exactly the Schur 





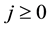
2) eliminating ([16] , Section 20, (F1)) the 3 non-


A finite part at the top of the resulting tree 
Proof. (of Theorem 6.4, and Corollary 6.1)
The 


with the descendants


one of them the Schur 
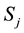



The vertical construction was terminated for 

The extent to which we constructed the pruned descendant tree 
Conjecture 6.1. Theorem 6.4 and Corollary 6.1 remain true for an arbitrarily large positive integer
For the convenience of the reader, we now recall ( [16] , Dfn. 21.2):
Definition 6.1. Let 











Corollary 6.2. The group

For the proof, we have to recall that L. Bartholdi and M.R. Bush ( [13] , Thm. 2.1, p. 160, and Prop. 3.6, p. 165) have constructed an infinite family 

Figure 1. Periodic bifurcations in the pruned descendant tree

such that 

dratic field 


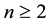
the common IPAD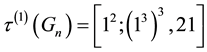
Proof. Several issues must be clarified for the groups 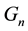

Firstly, according to the Equations (15) and (16) in Theorem 3.1, there are only five possibilities for the metabelianizations




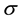
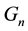




Secondly, we have to make sure that the 


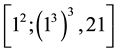

of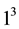






since it gives rise to exactly the seven immediate step size-2 descendants 

Finally, the Schur 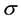





Indeed, since each 
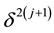


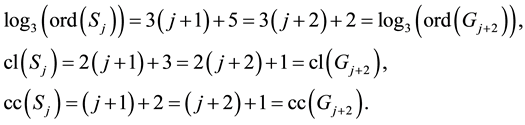
Consequently, the inclusions in Equation (44) can be replaced by equalities, and the claims of Corollary 6.2 are proved. □
Remark 6.2.
1) The claims of Conjecture 6.1 are strongly supported by the proven infinitude of the family 


2) The IPAD 
H.4, 






3) The exact specification of the infinite cover, resp. the infinite and entirely non-metabelian balanced cover, of 

quadratic field 



6.2.3. Second p-Class Groups with Infinite Cover
As a final coronation of this section, we show that our new IPAD strategies are powerful enough to enable the
determination of the length 


solute degree
For this purpose, we extend the concept of iterated IPADs of second order
once more by adding the second layers 



Theorem 6.5. (Length 

Suppose that 




1) If the IPAD of 
then the first layer TKT is 


2) If the first layer 


admits certain partial decisions about the length 
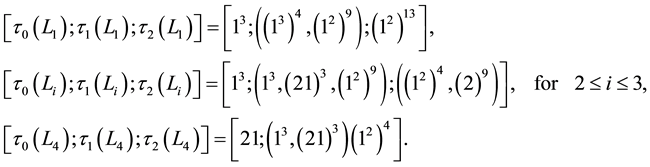
if and only if


if and only if
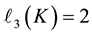

if and only if

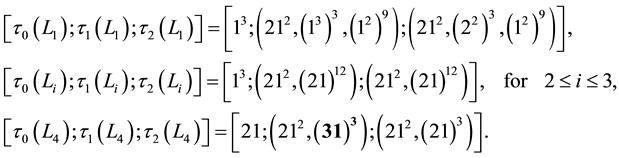
if and only if either 



if and only if


if and only if either 
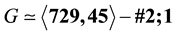


occurs for 



occurs for either
or
or
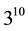


occurs for 



occurs for either




or 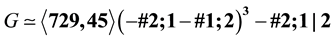

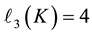
The various groups which occur in Theorem 6.5 are drawn in the tree diagram of Figure 1. This diagram im- pressively visualizes periodically repeating bifurcations in the descendant tree 











Proof. If we restricted the statements to complex quadratic fields it would be sufficient to consider the Schur 









We point out that Equation (56) cannot be used for a conclusive identification.
Example 6.3. (The first quadratic fields with TKT H.4 and
the smallest discriminant 





The complex quadratic analogue 


([21] , p. 84). All these fields share the same IPAD
In February 2015, we succeeded in proving that the unramified cyclic cubic extensions






However, the 3-class tower groups 









The justifications were conducted by computing 3-class groups of number fields of absolute degree 6 × 9 = 54 with the aid of MAGMA [4] on a machine with two XEON 8-core CPUs and 256 GB RAM.
7. Complex Quadratic Fields of 3-Rank Three
In this concluding section we present another intriguing application of IPADs.
Due to Koch and Venkov [32] , it is known that a complex quadratic field 





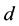











We summarize our results and their obvious conclusion in the following theorem.
Theorem 7.1.
There exist exactly 14 complex quadratic number fields 
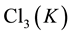


1) second and higher 3-class groups

2) infinite topological 3-class field tower groups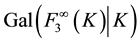
Before we come to the proof of Theorem 7.1 in Section 7.3, we collect basic numerical data concerning fields with 

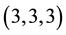


7.1. Discriminants 

Since one of our aims is to investigate tendencies for the coclass of second and higher 




field tower, for an odd prime
possible prime 
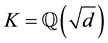

ble 3-class group 
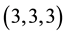
The reason is that Koch and Venkov [32] have improved the lower bound of Golod, Shafarevich [31] [36] and Vinberg [37] for the 



However, quadratic fields with 3-rank 

To provide an independent verification, we used the computational algebra system MAGMA [2] - [4] for compiling a list of all quadratic fundamental discriminants 
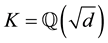




There are 14 discriminants, starting with

Table 1. Data collection for 




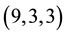


7.2. Arithmetic Invariants of Fields 
After the preliminary data collection in Section 7.1, we restrict ourselves to the 14 cases with elementary abe-
lian 3-class group of type

cubic extensions 






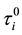



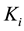
Table 2. Pattern recognition via ordered IPADs.
Table 3. Pattern recognition (continued).
cubic subfield of



In Table 4, we classify each of the 14 complex quadratic fields 

the counters of the abelian type invariants of the 3-class groups 
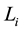
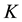

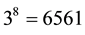


7.3. Proof of Theorem 7.1
Proof. According to ( [9] , Thm.1.1 and Dfn. 1.1, pp. 402-403), the information given in Table 4 consists of iso- morphism invariants of the metabelian Galois group 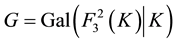
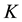






7.4. Final Remark
We would like to emphasize that Theorem 7.1 provides evidence of a wealth of structure in the set of infinite 3-class field towers, which was unknown up to now, since the common practice is to consider a 3-class field tower as done when some criterion in the style of Golod-Shafarevich-Vinberg [31] [36] [37] or Koch-Venkov [32] ensures just its infinity. However, this perspective is very coarse and our result proves that it can be refined considerably.
It would be interesting to extend the range of discriminants 
Table 4. Accumulative (unordered) form of IPADs.
Another very difficult remaining open problem is the actual identification of the metabelianizations of the 3-tower groups 



Acknowledgements
We gratefully acknowledge that our research is supported by the Austrian Science Fund (FWF): P 26008-N25. The results of this paper will be presented during the 29th Journées Arithmeétiques at the University of Debrecen [41] .
Funding
Research supported by the Austrian Science Fund (FWF): P 26008-N25.
References
- The PARI Group (2014) PARI/GP. Version 2.7.2, Bordeaux. http://pari.math.u-bordeaux.fr
- Bosma, W., Cannon, J. and Playoust, C. (1997) The Magma Algebra System I: The User Language. Journal of Symbolic Computation, 24, 235-265. http://dx.doi.org/10.1006/jsco.1996.0125
- Bosma, W., Cannon, J.J., Fieker, C. and Steels, A., Eds. (2015) Handbook of Magma Functions. Edition 2.21, University of Sydney, Sydney.
- The MAGMA Group (2015) MAGMA Computational Algebra System. Version 2.21-2, Sydney. http://magma.maths.usyd.edu.au
- Mayer, D.C. (2014) Principalization Algorithm via Class Group Structure. Journal de Théorie des Nombres de Bordeaux, 26, 415-464.
- Bush, M.R. and Mayer, D.C. (2015) 3-Class Field Towers of Exact Length 3. Journal of Number Theory, 147, 766-777. http://arxiv.org/abs/1312.0251
- Artin, E. (1927) Beweis des allgemeinen Reziprozitätsgesetzes. Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg, 5, 353-363. http://dx.doi.org/10.1007/BF02952531
- Artin, E. (1929) Idealklassen in Oberkörpern und allgemeines Reziprozitätsgesetz. Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg, 7, 46-51. http://dx.doi.org/10.1007/BF02941159
- Mayer, D.C. (2013) The Distribution of Second p-Class Groups on Coclass Graphs. Journal de Théorie des Nombres de Bordeaux, 25, 401-456. http://dx.doi.org/10.5802/jtnb.842
- Boston, N., Bush, M.R. and Hajir, F. (2014) Heuristics for p-Class Towers of Imaginary Quadratic Fields, with an Appendix by Jonathan Blackhurst. Mathematische Annalen, in Press. http://arxiv.org/abs/1111.4679
- Boston, N. and Leedham-Green, C. (2002) Explicit Computation of Galois p-Groups Unramified at p. Journal of Algebra, 256, 402-413. http://dx.doi.org/10.1016/S0021-8693(02)00028-5
- Bush, M.R. (2003) Computation of Galois Groups Associated to the 2-Class Towers of Some Quadratic Fields. Journal of Number Theory, 100, 313-325. http://dx.doi.org/10.1016/S0022-314X(02)00128-2
- Bartholdi, L. and Bush, M.R. (2007) Maximal Unramified 3-Extensions of Imaginary Quadratic Fields and SL2(Z3). Journal of Number Theory, 124, 159-166. http://dx.doi.org/10.1016/j.jnt.2006.08.008
- Boston, N. and Nover, H. (2006) Computing Pro-p Galois Groups. Proceedings of ANTS 2006, Lecture Notes in Computer Science 4076, Springer-Verlag Berlin Heidelberg, Berlin, 1-10.
- Nover, H. (2009) Computation of Galois Groups of 2-Class Towers. Ph.D. Thesis, University of Wisconsin, Madison.
- Mayer, D.C. (2015) Periodic Bifurcations in Descendant Trees of Finite p-Groups. Advances in Pure Mathematics, 5, 162-195. http://dx.doi.org/10.4236/apm.2015.54020
- Besche, H.U., Eick, B. and O’Brien, E.A. (2002) A Millennium Project: Constructing Small Groups. International Journal of Algebra and Computation, 12, 623-644. http://dx.doi.org/10.1142/S0218196702001115
- Besche, H.U., Eick, B. and O’Brien, E.A. (2005) The Small Groups Library―A Library of Groups of Small Order. An Accepted and Refereed GAP 4 Package, Available Also in MAGMA.
- Mayer, D.C. (2012) Transfers of Metabelian p-Groups. Monatshefte für Mathematik, 166, 467-495.
- Scholz, A. and Taussky, O. (1934) Die Hauptideale der kubischen Klassenkörper imaginär quadratischer Zahlkörper: Ihre rechnerische Bestimmung und ihr Einfluß auf den Klassenkörperturm. Journal für die Reine und Angewandte Mathematik, 171, 19-41.
- Mayer, D.C. (1990) Principalization in Complex S3-Fields. Congressus Numerantium, 80, 73-87.
- Taussky, O. (1970) A Remark Concerning Hilbert’s Theorem 94. Journal für die Reine und Angewandte Mathematik, 239/240, 435-438.
- Mayer, D.C. (2012) The Second p-Class Group of a Number Field. International Journal of Number Theory, 8, 471- 505.
- Gamble, G., Nickel, W. and O’Brien, E.A. (2006) ANU p-Quotient―p-Quotient and p-Group Generation Algorithms. An Accepted GAP 4 Package, Available Also in MAGMA.
- The GAP Group (2015) GAP―Groups, Algorithms, and Programming―A System for Computational Discrete Algebra. Version 4.7.7, Aachen, Braunschweig, Fort Collins, St. Andrews. http://www.gap-system.org
- Ascione, J.A., Havas, G. and Leedham-Green, C.R. (1977) A Computer Aided Classification of Certain Groups of Prime Power Order. Bulletin of the Australian Mathematical Society, 17, 257-274, Corrigendum 317-319, Microfiche Supplement, 320.
- Ascione, J.A. (1979) On 3-Groups of Second Maximal Class. Ph.D. Thesis, Australian National University, Canberra.
- O’Brien, E.A. (1990) The p-Group Generation Algorithm. Journal of Symbolic Computation, 9, 677-698. http://dx.doi.org/10.1016/S0747-7171(08)80082-X
- Holt, D.F., Eick, B. and O’Brien, E.A. (2005) Handbook of Computational Group Theory. Discrete Mathematics and Its Applications, Chapman and Hall/CRC Press. http://dx.doi.org/10.1201/9781420035216
- Heider, F.-P. and Schmithals, B. (1982) Zur Kapitulation der Idealklassen in unverzweigten primzyklischen Erweiterungen. Journal für die reine und angewandte Mathematik, 336, 1-25.
- Shafarevich, I.R. (1966) Extensions with Prescribed Ramification Points. Publications mathématiques de l’IHÉS, 18, 71-95.
- Koch, H. and Venkov, B.B. (1975) Über den p-Klassenkörperturm eines imaginär-quadratischen Zahlkörpers. Astérisque, 24-25, 57-67.
- Diaz, F. and Diaz (1973/74) Sur les corps quadratiques imaginaires dont le 3-rang du groupe des classes est supérieur à 1. Séminaire Delange-Pisot-Poitou, No. G15.
- Diaz, F. and Diaz (1978) Sur le 3-rang des corps quadratiques. No. 78-11, Université Paris-Sud, Orsay.
- Buell, D.A. (1976) Class Groups of Quadratic Fields. Mathematics of Computation, 30, 610-623.
- Golod, E.S. and Shafarevich, I.R. (1965) On Class Field Towers. Izvestiya Akademii Nauk SSSR. Seriya Matematicheskaya, 28, 261-272.
- Vinberg, E.B. (1965) On a Theorem Concerning the Infinite-Dimensionality of an Associative Algebra. Izvestiya Akademii Nauk SSSR. Seriya Matematicheskaya, 29, 209-214.
- Shanks, D. (1976) Class Groups of the Quadratic Fields Found by Diaz y Diaz. Mathematics of Computation, 30, 173- 178. http://dx.doi.org/10.1090/S0025-5718-1976-0399039-9
- Sloane, N.J.A. (2014) The On-Line Encyclopedia of Integer Sequences (OEIS). The OEIS Foundation Inc. http://oeis.org/
- Fieker, C. (2001) Computing Class Fields via the Artin Map. Mathematics of Computation, 70, 1293-1303.
- Mayer, D.C. (2015) Index-p Abelianization Data of p-Class Tower Groups. Proceedings of the 29th Journées Arithmé- tiques, Debrecen, 6-10 July 2015, in Preparation.