Received 17 February 2015; accepted 5 March 2015; published 23 March 2015

ABSTRACT

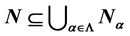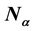Let R be a commutative ring with 1, and M is a (left) R-module. We introduce the concept of coprimarily packed submodules as a proper submodule N of an R-module M which is said to be Coprimarily Packed Submodule. If where is a primary submodule of M for each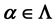, then 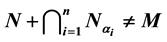for some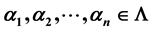. When there exists 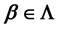such that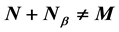; N is called Strongly Coprimarily Packed submodule. In this paper, we list some basic properties of this concept. We end this paper by explaining the relations between p-compactly packed and coprimarily packed submodules, and also the relations between strongly p-compactly packed and strongly coprimarily packed submodules.

Keywords:

Coprimarily Packed Submodule, Strongly Coprimarily Packed Submodule, Bezout Module

1. Introduction

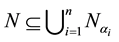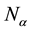Coprimely packed rings were introduced by Erdo˘gdu for the first time in [1] . Al-Ani gave an analogous concept in modules [2] , that is, a proper submodule N of an R-module M which is called Coprimely Packed. If where is a prime submodule of M for each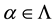, then 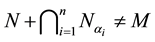for some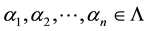. If there exists such that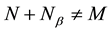, then N is called Strongly Coprimely Packed submodule.

In this paper, we discuss the situation where the union of a family of primary submodules of M is considered.

In [2] , the concept of compactly packed modules was introduced. We generalized this concept to the concept of p-compactly packed modules in [3] , that is, a proper submodule N of an R-module M which is called

P-Compactly Packed. If for each family 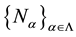of primary submodules of M with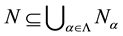, there ex-

ist such that. If for some, then N is called Strongly

P-Compactly Packed. A module M is said to be P-Compactly Packed (Strongly P-Compactly Packed), if every proper submodule of M is p-compactly packed (strongly p-compactly packed).

In this paper, we introduce the definitions of coprimarily packed and strongly coprimarily packed module and discuss some of their properties. We end this paper by explaining the relations between p-compactly packed and coprimarily packed submodules, and also the relations between strongly p-compactly packed and strongly coprimarily packed submodules.

2. Coprimarily Packed and Strongly Coprimarily Packed Submodules

In this section we introduce the definition of coprimarily packed and strongly coprimarily packed module and discuss some of their properties.

2.1. Definition

Let N be a proper submodule of an R-module M. N is said to be Coprimarily Packed Submodule if whenever where is a primary submodule of M for each, then for some. When there exists such that, N is called Strongly Coprimarily Packed submodule.

A module M is called Coprimarily Packed (Strongly Coprimarily Packed) module if every proper submodule of M is coprimarily packed (strongly coprimarily packed) submodule. It is clear that every strongly coprimarily packed submodule is a coprimarily packed submodule.

In the following proposition, we discuss the behavior of strongly coprimarily packed module under homomorphism.

2.2. Proposition

Let be an epimorphism. If M is an R-module such that for every primary submodule N of M, then M is a strongly coprimarily packed module if and only if is a strongly coprimarily packed module.

Proof. Suppose that M is a strongly coprimarily packed module and let where is a proper submodule of and is a primary submodule of for each, so

.

is a primary submodule of M for each there exists such that

.

We must show.

Suppose, let so there exists and such that. Since f is an epimorphism there exists such that

, , and.

Thus, so, this implies. Since,

, and, so, hence

,

this implies

which is a contradiction. So is a strongly coprimarily packed module.

Conversely, suppose is a strongly coprimarily packed module and let, where N is a proper submodule of M and is a primary submodule of M for each. Hence

and since for each, is a primary submodule of, there exists such that.

Suppose and let, since f is an epimorphism, there exists such that and there exists and such that. Then, hence, so). It follows which is a contradiction, thus, so M is a strongly coprimarily packed modul.

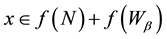
The following proposition gives a characterization of strongly coprimarily packed submodules in a multiplication or finitely generated module.

2.3. Proposition

Let M be a finitely generated or multiplication R-module. A proper submodule N is strongly coprimarily packed if and only if whenever where is a maximal submodule of M for each then there exists such that.

Proof. Suppose N is a strongly coprimarily packed submodule and let where is a maximal submodule of M for each, hence is a primary submodule, so there exists such that. But and is a maximal submodule, hence thus.

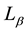
Conversely, let where is a primary submodule for each. There exists a maximal submodule that contains for each, hence. By hypothesis, there ex- ists such that, but so, thus N is a strongly coprimarily packed submodule.

Recall that an R-module M is called Bezout Module if every finitely generated submodule of M is cyclic.

In the following proposition we will give a characterization for strongly coprimarily packed multiplication module.

2.4. Proposition

Let M be a multiplication R-module. If one of the following holds:

1) M is a cyclic module.

2) R is a Bezout ring.

3) M is a Bezout module.

Then M is strongly coprimarily packed module if and only if every primary submodule is strongly coprimarily packed.

Proof. Let N be a proper submodule of a module M such that where is a maximal submodule of M for each, then by proposition (2.3), it is enough to show that there exists such that.

First, if, since N is a submodule of a multiplication module, there exists a primary submodule L that contains N. By hypothesis, L is strongly coprimarily packed submodule and, so there exists such that hence.

Now, if, let and, so is an -closed subset of M. Since, so thus there exists a submodule K that contains N and K is a maximal in [1] , K is prime [1] , so it is primary submodule. Thus by hypothesis K is strongly coprimarily packed and since and by proposition (2.3) there exists such that.

We end this Paper by looking at the relations between the strongly p-compactly packed modules and strongly coprimarily packed modules.

Recall that a proper submodule N of an R-module M is called P-Compactly Packed if for each family

of primary submodules of M with, there exist such that. If

for some, then N is called Strongly P-Compactly Packed. A module M is said to be P-Com- pactly Packed (Strongly P-Compactly Packed) if every proper submodule of M is p-compactly packed (strongly p-compactly packed).

It is easy to show that every strongly p-compactly packed submodule is a strongly coprimarily packed submodule.

2.5. Proposition

If M is a p-compactly packed module, which cannot be written as a finite union of primary submodules, then M is a coprimarily packed module.

Proof. Let where N is a proper submodule and is a primary submodule of M for each. Since M is a p-compactly packed module then there exists such that.

We claim that, let so there exists and such that. Then there exists such that, hence, so, thus

.

By hypothesis therefore.

2.6. Definition

Let M be a non-zero module, M is called Primary Module if the zero-submodule of M is a primary submodule.

2.7. Proposition

If M is a multiplication or finitely generated strongly p-compactly packed module, then M is a strongly coprimarily packed module. The converse holds if M is a primary module such that every primary submodule of M contains no non-trivial primary submodule.

Proof. Suppose M is a primary module such that every primary submodule of M contains no non-trivial primary submodule. Let N be a proper submodule of M such that where is a primary submodule of M for each. Without loss of generality we can suppose that, for each. Then is a maximal submodule of M, for each. Since M is strongly coprimarily packed module, there exists, such that; but is a maximal submodule and. This implies, and hence. Therefore M is a strongly p-compactly packed module.

The other direction is trivial.

Cite this paper

Lamis J. M.Abulebda， (2015) On Co-Primarily Packed Modules。 Advances in Pure Mathematics，05，208-211. doi: 10.4236/apm.2015.54022

References