Advances in Pure Mathematics
Vol.05 No.02(2015), Article ID:54243,6 pages
10.4236/apm.2015.52012
Relation between Two Operator Inequalities
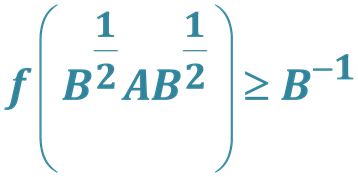 and
and

Mohammad Ilyas1, Reyaz Ahmad2, Shadab Ilyas3
1Department of Mathematics, Gaya College, Gaya, India
2Al-Ain University of Science and Technology, Al Ain, UAE
3Department of Information Technology, Gaya College, Gaya, India
Email: milyas347@gmail.com, reyaz56@hotmail.com, shadabilyas@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 8 February 2015; accepted 22 February 2015; published 26 February 2015

ABSTRACT
We shall show relation between two operator inequalities
 and
and
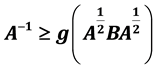 for positive, invertible operators A and B, where f and g are non-negative continuous invertible functions on
for positive, invertible operators A and B, where f and g are non-negative continuous invertible functions on
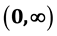 satisfying
satisfying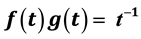 .
.
Keywords:
Operator Inequality, Orthoprojection, Representing Function

1. Introduction
We denote by capital letter A, B et al. the bounded linear operators on a complex Hilbert space H. An operator T on H is said to be positive, denoted by
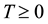 if
if
 for all
for all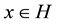 .
.
M. Ito and T. Yamazaki [1] obtained relations between two inequalities
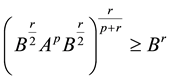 and
and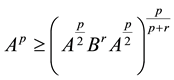 , (1.1)
, (1.1)
and Yamazaki and Yanagida [2] obtained relation between two inequalities
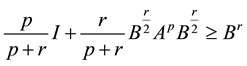 and
and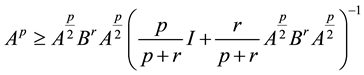 , (1.2)
, (1.2)
for (not necessarily invertible) positive operators A and B and for fixed
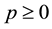 and
and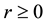 . These results led M. Ito [3] to obtain relation between two operator inequalities
. These results led M. Ito [3] to obtain relation between two operator inequalities
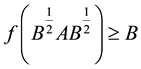 and
and
for (not necessarily invertible) positive operators A and B, where f and g are non-negative continuous functions on


Remarks (1.1): The two inequalities in (1.1) are closely related to Furuta inequalities [4] .
The inequalities in (1.1) and (1.2) are equivalent, respectively, if A and B are invertibles; but they are not always equivalent. Their equivalence for invertible case was shown in [5] .
Motivated by the result (1.3) of M. Ito [3] , we obtain the results taking representing functions f and g as non-negative continuous invertible functions on


2. Main Results
We denote by

Theorem 1: Let A and B be positive invertible operators, and let f and g be non-negative invertible continuous functions on


1)


2)


Here




The following Lemma is helpful in proving our results:
Lemma 2: If




Proof of Lemma: Since


sequence of polynomials on



Hence the result.
Proof of Theorem 1: For



1) We suppose that

Let



We have
Further since



we have

Then

i.e.

2) We suppose that


With



Now as


we have

Then

thus completing the proof of 2.
Corollary 3. Let A and B be positive invertible operators, and let f and g be non-negative continuous invertible functions on


1) If




2) If


Proof 1) This result follows from 1) of Theorem 1 because each of the conditions




2) This result follows from 2) of Theorem (1) because

Hence the proof is complete.
Remark (3.1) 1) If


2) The invertibility of positive operators A and B is necessary condition.
3) We have considered






We have the following results as a consequence of corollary 3.
Theorem 4: Let A and B be positive invertible operators. Then for each


1) If


2) If



In Theorem 4 we consider that





Theorem 5: Let A and B be positive invertible operators. Then for each


1) If

2) If



Proof of Theorem 4: 1) First we consider the case when






if


If


if


i.e., if


i.e., if


i.e., if


or in other words,


But, since







2) Again first we consider the case





Since


If p = 0 and r > 0, (5.2) means that



ensures
which implies that
Hence (5.3) means that




Hence the result.
Proof of Theorem 5: We can prove by the similar way to Theorem 4 for








Corollary 4: Let A and B be positive invertible operators, and let f and g be non-negative continuous invertible functions on




Proof: The proof





Cite this paper
MohammadIlyas,ReyazAhmad,ShadabIlyas, (2015) Relation between Two Operator Inequalities . Advances in Pure Mathematics,05,93-99. doi: 10.4236/apm.2015.52012
References
- 1. Ito, M. and Yamazaki, T. (2002) Relations between Two Inequalities and and Their Applications. Integral Equations and Operator Theory, 44, 442-450.
http://dx.doi.org/10.1007/BF01193670 - 2. Yamazaki, T. and Yanagida, M. (to appear) Relations between Two Operator Inequalities and Their Application to Paranormal Operators. Acta Scientiarum Mathematicarum (Szeged).
- 3. Ito, M. (2005) Relations between Two Operator Inequalities Motivated by the Theory of Operator Means. Integral Equations and Operator Theory, 53, 527-534.
http://dx.doi.org/10.1007/s00020-004-1321-9 - 4. Furuta, T. (1987) Assures for with. Proceedings of the American Mathematical Society, 101, 85-88.
- 5. Furuta, T. (1992) Applications of Order Preserving Operator Inequalities. Operator Theory: Advances and Applications, 59, 180-190.

