Received 25 November 2014; revised 18 December 2014; accepted 22 December 2014

ABSTRACT

In this note, we analyze a few major claims about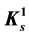. As a consequence, we rewrite a major theorem, nullify its proof and one remark of importance, and offer a valid proof for it. The most important gift of this paper is probably the reasoning involved in all: We observe that a constant, namely t, has been changed into a variable, and we then tell why such a move could not have been made, we observe the discrepancy between the claimed domain and the actual domain of a supposed function that is created and we then explain why such a function could not, or should not, have been created, along with others.

Keywords:

Analysis, Convexity, Definition, S-Convexity, Geometry

1. Introduction

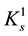is a very interesting component of 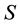-convexity, not to say exotic: It differs substantially from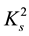, yet, in a certain sense, seems to supplement it.

1.1. Notation

We use the symbols from [1] here:

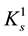・ for the class 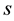-convex functions in the first sense, where;

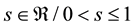・ for the class 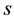-convex functions in the second sense, where;

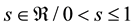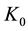・ for the class convex functions;

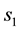・ for the variable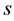, , used for the first type of 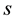-convexity;

・ for the variable, , used for the second type of -convexity.

Remark 1 The class 1-convex functions is simply a subclass of the class convex functions. If we make the domain of the convex functions be inside of the set of the non-negative real numbers, we then have the class 1-convex functions:.

1.2. Definition

We use the definition from [1] here:

Definition 1 A function is said to be -convex if the inequality

holds;;.

Remark 2 If the inequality is obeyed in the reverse¹ situation by, then is told to be -concave.

1.3. Theorems That We Discuss Here

Dragomir and Pearce, in [2] , state that Hudzik and Maligranda, in [3] , told us that:

Theorem 1.1 Let. If, then is nondecreasing on and.

We can infer, from the above theorem, that:

(1) (Claim X) Any function in, with domain contained in, specified, , is non- decreasing;

(2) (Claim Y) for,.

In this paper, we prove that (1) is true but does not yet have an actual proof and (2) is incomplete, con- troversial or unnecessary.

2. Analyzing Claim X

[2] presents the following sequence of implications as a proof for the claim X:

Proof. We have, for and,

(PROBLEM 1)

The function

is continuous on, decreasing on, increasing on and

(PROBLEM 2).

This yields that

(5.147) for all,.

If now, then, and therefore, by the fact that (5.147) holds for all, we get

for² all. By induction, we therefore obtain that

(5.148) (PROBLEM 3) for all,

Hence, by taking and applying (5.148), we get

which means that is non-decreasing on. □

We prove that PROBLEM 1, PROBLEM 2, and PROBLEM 3 will make the proof not be a mathematical proof. There are more problems with the proof, however.

From [4] , we learn that we cannot have in the definition of -convexity (it is all tied to the geo- metric definition of convexity).

This way, PROBLEM 1 should, per se, nullify the proof that we have just presented.

Notwithstanding, notice that goes as close as we wish (PROBLEM 2) to 0 (limit when) and actually assumes the value 1 (when), what then makes the interval be a degenerated interval, or

not be an interval, but just a point instead. Besides, we have different intervals, depending on the value of we choose³ (,). We then know that we cannot generalize this to

. That is a very serious mistake. Besides, t replaces and is what they themselves have called therefore a function, what then would have to mean that is not a constant. That means that we

can replace with numerical values, but those would have to be each and every value of the function

for us to claim that we have.

We do notice that instead of the usual, , in the theorem, so that does not run the risk of being a degenerated interval or an improper interval.

Even if the result were true, and we are obviously entitled to try to get it using the reasoning contained in the above proof, we cannot use the just-exposed lines as a proof.

As for PROBLEM 3: Notice that, when,. This means that instead of what is written there at least when.

With that, we must have, for instance, in the next line, not, when. Notice that this sort of problem will happen with all values of.

In this situation, just like in the original situation, in the proof, v and u cannot be variables for f because whatever be a variable for f spans or its domain set with no discrimination. We select only the values that obey the rule that we have created, which is, after due fixing in what regards,. This way, we are using only a few selected values of the original variable of f. Because of that, we should create

a new variable, which we could call, which is then going to be equal to, with and assuming only

the values that we have selected, what means that the simplification is not valid in the proof. Consequently, the inference is not valid.

On the other hand, notice that is a function that is totally different from

in shape, so that even if the first coordinates of the functions are the same, say varies from 0 to 1, the second

coordinates may be completely different (take and, for instance).

We must respect the original function, the one from the definition, when proving something in Mathematics or replace it with a completely equivalent function, what then means that this step is unacceptable (replacing

with and then applying the rule that should apply when we have for when we have instead).

We have then just proven that there is no actual proof of being nondecreasing on so far.

It is then the case that we either have to find a proper proof for the claim or a suitable counter-example/proof of the contrary.

Notice that all convex functions whose domain is in should be -convex (is supposed to extend, so that this should be valid for any we choose, provided that). When, we should have precisely the class convex functions.

The quadratic function, in the piece of domain, is a convex, and therefore should also be an -convex, function, and it decreases in. Notwithstanding, is part of the exclusions in this theorem, so that this is not a counter-example to their claim.

A suitable proof would be similar to what has been presented in [2] , but not equal.

Notice that and can always be made as similar as we wish.

We can make one differ from the other by the thousandth decimal place, for instance.

We can therefore, in practice, equate to whilst applying the definition of -convex function.

Proof. When we apply the definition of -convexity to a function that satisfy the conditions of this theorem,

will always be inside of the inclusions, so that we can use it in our proof with no loss.

In replacing with in our definition, we get.

In making go really close to, what we can always do because of, which is a condition that we will explain later on in this paper, we can make them differ by the thousandth decimal place, for instance. In this case, in practice, we can equate both.

When we do that, our inequality becomes or.

Because in our theorem, we have and therefore, what implies. Assuming is a nonnegative number (definition of), we get.

In this case, we can only have a nondecreasing function (and).

3. Analyzing Claim Y

must exist because it appears in the theorem. Therefore, 0 is part of the domain of the function and we can replace the domain interval with at least when stating the second part of the theorem.

Because every convex function is continuous (please refer to on page), we know that

for each in the domain of, therefore

when both lateral limits can be calculated. Because the domain interval does not include the left neighbors of zero, we can only have the right lateral limit here.

As a consequence, and are both true.

Since it is never true that or, we should at most write that.

The definition of implies any f that be continuous (simply imagine that it be not. Imagine a discontinuity of first type, right on the vertex of a parabola that has a point of minimum value, which we know is the image of a convex, therefore convex in both senses (as for all we have been told by others), function. Now let, where is the first coordinate of the vertex of the parabola we talk about, be a point that is sufficiently distant from the vertex and assume that. In fact, make this point be fully detached from the rest of the graph and lie miles below it. Make it be the only atypical point in this parabola. Now make, , , be our in the definition inequality for and be our. Notice that we will unavoidably find points in the graph that are above the limiting line, and that will make the function be both not convex and not -convex, what is absurd). Please call this paragraph.

We will also try to find the mistake in the proof presented in [2] .

The proof in [2] is:

Proof. For, we have

(PROBLEM 4)

and making, we obtain

(PROBLEM 5)

Hence,

PROBLEM 4 is that the assertion is only true if and satisfy the conditions of the definition of, that is, if, what, as we know, implies and [5] .

Even if such a piece of information were not relevant to the proof, we can only accept the proof as a proof if such constraints are mentioned.

PROBLEM 5 is that it is missing explaining where the information came from, for instance. Since and their assumption was that the function, in this situation, does not decrease (see ()), what implies that, not the opposite, things are unacceptable from this point onwards in the proof.

4. Supplementary Remarks

Still in [2] , we find a remark that is told to be in [3] :

Remark 3 If, then the function is nondecreasing on but not necessarily on.

From Real Analysis, we know that this remark is absurd. It is not possible that one point, in a continuous function, change the nature of the function from nondecreasing to decreasing. That can only happen to a func- tion with a discontinuity on.

Suppose that is continuous and nondecreasing on but not on.

Then, for, we have and .

We can then find, extremely close to zero but different from it, such that but.

That would mean that such that and,. By assumption of the proposal, however, such a family, of s, could not exist, since its existence would imply that is nondecreasing on, where is greater than zero, instead of on.

This conclusion just makes sense, since saying that functions do not have to be continuous would make sustaining that they extend the class convex functions be a likely-to-be-impossible task (see on page).

Besides, the definition of does not allow us to do that.

5. Conclusions

In this paper, we have rewritten the proof of the theorem

Theorem 5.1 Let. If, then is nondecreasing on and

and the own theorem as well.

This theorem appears in [2] and is there reported to have originated in [3] . We have proved that if

, then as well since for any s-convex func-

tion that be defined on or in one of its subsets and also on zero.

It does not make sense making a theorem to tell the just-written information because we aim objectivity and clarity in Mathematics and the only actual piece of information that we need to know regarding this is contained in the definition in an almost explicit way (continuity).

The new version of the theorem is therefore

Theorem 5.2 Let. If, then is nondecreasing on.

Its new proof is

Proof. When we apply the definition of -convexity to a function that satisfy the conditions of this theorem,

will always be inside of the inclusions, so that we can use it in our proof with no loss.

In replacing with in our definition, we get.

In making go really close to, what we can always do because of, we can make them differ by the thousandth decimal place, for instance. In this case, in practice, we can equate both.

When we do that, our inequality becomes or.

Because in our theorem, we have and therefore, what implies. Assuming is a nonnegative number (definition of), we get.

In this case, we can only have a nondecreasing function (and).

We have also nullified a remark of importance ( [2] ):

Remark 4 If 0 < s < 1, then the function is nondecreasing on but not necessarily on

The remark has been nullified in this paper in what regards continuous functions and, therefore, unless we change the definitions of convex and -convex functions in order not to have only continuous functions inside of our sets, when one could then think of reassessing this remark, this remark has been nullified in full.

References

NOTES

¹Reverse here means, not.

²Notice that the second member of the inequality should have been, not as well.

³0.743 is an approximation. The original value was something like 0.742997.