ABSTRACT

The present paper deals with a subgroup X of a group G is almost normal if the index |G: NG(X)| is finite, while X is nearly normal if it has finite index in the normal closure XG. This paper investigates the structure of groups in which every (infinite) subgroup is either almost normal or nearly normal.

Keywords:Normality, Nearly Normality, Normalizer Subgroup

1. Introduction

A subgroup X of a group G is said to be almost normal if it has only finitely many conjugates, or equivalently if the normalizer NG(X) of X has finite index in G. A famous result of B. H. Neumann [1] states that all subgroups of a group G are almost normal if and only if the centre Z (G) has finite index in G. This theorem was later generalized by I. I. Eremin [2] , who showed that it is enough to impose the almost normality restriction just to abelian subgroups. Another relevant type of generalized normality is the so-called nearly normality: a subgroup X of a group G is nearly normal if it has finite index in its normal closure XG. In the above quoted paper, Neumann also proved that all subgroups of a group G are nearly normal if and only if the commutator subgroup G⁰ of G is finite; also in this case, it is enough to suppose that all abelian subgroups are nearly normal (a result that was obtained by M. J. Tomkinson [3] ). The concepts of almost normal and nearly normal subgroups are in general incomparable. For instance, all subgroups of the base group of the standard wreath product W = Z₀Z² are almost normal in W, but only few of them are nearly normal; moreover, if G is any group containing an infinite minimal normal subgroup N, which is abelian of prime exponent, then each proper subgroup of finite index of N is nearly normal in G but has infinitely many conjugates. On the other hand, it follows from Neumann’s results and from the celebrated theorem of Schur on the finiteness of the commutator subgroup of central-by-finite groups (see for instance [4] Part 1, Theorem 4.12) that if all subgroups of a group G are almost normal, then they must be also nearly normal. It should also be mentioned here that the structure of groups in which every infinite subgroup is almost normal and that of groups in which all infinite subgroups are nearly normal have been described in [5] and [6] , respectively; it turns out that the information that all subgroups of a certain type are almost normal (or that they all are nearly normal) is of some relevance. The aim of this paper is to study groups in which every member of a relevant system of subgroups is either almost normal or nearly normal; in particular, Tomkinson’s theorem quoted above will be generalized to this situation.

A result of Y. D. Polovicki˘ı [7] shows that a group G has finitely many normalizers of abelian subgroups if and only if it is finite over the centre. In recent years, many other papers have appeared on the structure of groups with finitely many normalizers of subgroups with a given property (see for instance [8] -[12] ); here we will also consider groups with finitely many normalizers of subgroups which are neither almost normal nor nearly normal.

Most of our notation is standard and can be found in [4] .

2. Abelian Subgroups

Recall that the F C-centre of a group G is the subgroup consisting of all elements with finitely many conjugates, and G is an F C-group if it coincides with its F C-centre. The theory of F C-groups plays an important role in many questions concerning infinite groups with finiteness conditions; we refer to the monograph [13] for the main properties of F C-groups.

It is easy to show that a cyclic subgroup hxi of a group G is almost normal if and only if it is nearly normal, and both such properties are also equivalent to the fact that the conjugacy class of x in G is finite. Thus a group G is an F C-group if and only if all its cyclic subgroups are almost normal (or nearly normal). It turns out that, within the universe of F C-groups, almost normality is a stronger property than nearly normality.

Lemma 2.1. Let G be an F C-group, and let X be an almost normal subgroup of G. Then X is nearly normal in G.

Proof: As the normalizer NG(X) has finite index in G, there exists a finitely generated subgroup E of G such that G = hE, NG(X)i. Moreover, the subgroup E can be chosen normal in G, since its normal closure EG is likewise finitely generated. Thus G = NG(X)E and so XG = XE . Clearly, E is central-by-finite, so that it satisfies the maximal condition on subgroups, and in particular its subgroup [X, E] is finitely generated. On the other hand, the commutator subgroup G⁰ of G is locally finite, and hence [X, E] is finite. Therefore the subgroup X has finite index in its normal closure XG = X[X, E], and so it is nearly normal in G.

The main result of this section is an extension of Tomkinson’s theorem quoted in the introduction to the case in which every (abelian) subgroup is either almost normal or nearly normal; it will be obtained as a consequence of a theorem on groups with finitely many normalizers of subgroups with a suitable property. For such purpose, we need a result of B. H. Neumann [14] , who holds in the more general situation of groups covered by cosets of subgroups.

Lemma 2.2. Let the group 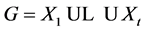be the union of finitely many subgroups. Then all Xi’s of infinite index can be omitted from this decomposition; in particular, at least one of the subgroups 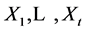has finite index in G.

Theorem 2.3. Let G be a group with finitely many normalizers of abelian subgroups which are neither almost normal nor nearly normal. Then the commutator subgroup G⁰ of G is finite, and so all subgroups of G are nearly normal.

Proof: Let

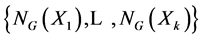
be the set of all normalizers of abelian subgroups of G which are neither almost normal nor nearly normal. If x is any element of G having infinitely many conjugates, we have that NG(hxi) = NG(Xj) for some j ≤ k, so that in particular x belongs to NG(Xj) and hence

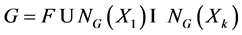
where F is the F C-centre of G. On the other hand, each normalizer NG(Xi) has infinite index in G, and so it follows from Lemma 2.2 that G = F is an F C-group. The same result shows that the set

is properly contained in G, so that we may consider an element g of

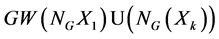
Clearly, g normalizes all subgroups of its centralizer CG(g), so that each abelian subgroup of CG(g) must be either almost normal or nearly normal. Therefore all abelian subgroups of CG(g) are nearly normal by Lemma 2.1, and hence CG(g) has finite commutator subgroup by Tomkinson’s theorem. As the index |G: CG(g)| is finite, the group G is finite-by-abelian-by-finite. On the other hand, any abelian-by-finite F C-group is central-by-finite, and so it follows from Schur’s theorem that the commutator subgroup G⁰ of G is finite. In particular, all subgroups of G are nearly normal.

Corollary 2.4. Let G be a group in which every abelian subgroup is either almost normal or nearly normal. Then the commutator subgroup G⁰ of G is finite, and so all subgroups of G are nearly normal.

3. Infinite Subgroups of Locally Finite Groups

It was remarked in Section 2 that any almost normal subgroup of an F C-group is nearly normal. Our next lemma shows in particular that a converse conclusion holds in the case of groups with finite Prufer rank.

Lemma 3.1. Let G be a group, and let X be a nearly normal subgroup of G. If X has finite Prufer rank, then it is almost normal in G.

Proof: Put |XG: X| = n. Then the subgroup (XG)n! is contained in X and hence the factor group XG/XG has finite exponent. Moreover, XG/XG obviously is residually finite and has finite Prufer rank, so that a relevant result by Mann and Segal (see [15] , Theorem A) can be applied to show that XG/XG is locally finite. On the other hand, any abelian subgroup of XG/XG is finite, and hence it follows from the Hall-Kulatilaka-Kargapolov theorem that XG/XG itself is finite (see for instance [4] Part 1, Theorem 3.43). Therefore X is almost normal in G.

In order to study groups with finitely many normalizers of infinite subgroups which are neither almost normal nor nearly normal we need a series of lemmas.

Lemma 3.2. Let G be a group, and let A be an infinite abelian normal subgroup of finite index of G. If A is the direct product of a collection of subgroups of prime order, then there exists a sequence (an) of elements of A such that

Proof: Let a1 be any non-trivial element of A, and suppose by induction that elements 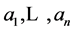of A have been chosen in such a way that

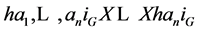
Clearly, the subgroup is finite, and hence A contains an infinite subgroup B such that

Since B has finitely many conjugates in G, its core BG has finite index in A and so it is infinite. If an+1 is any non-trivial element of BG, we have

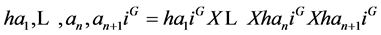
and the lemma is proved.

Lemma 3.3. Let G be a locally finite group, and let g be an element of G such that Xg = X for each infinite subgroup X of G which is neither almost normal nor nearly normal. If g has infinitely many conjugates, then all abelian hgi-invariant subgroups of G satisfy the minimal condition.

Proof: Assume for a contradiction that there exists an abelian hgi-invariant subgroup A of G which does not satisfy the minimal condition. Then the socle of A is infinite, and so by Lemma 3.2 there exist infinite hgi-invariant subgroups A1 and A2 of A such that

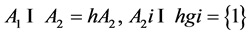
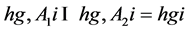
Moreover, by hypothesis each of the infinite subgroups hg, A1i and hg, A2i is either almost normal or nearly normal, but they cannot have the same generalized normality property. Without loss of generality, we suppose that hg, A1i is almost normal and hg, A2i is nearly normal in G. Then the normalizer L = NG(hg, A1i) has finite index in G, and so there exists a finite subgroup E of G such that G = LE. On the other hand, the subgroup hg, A2i ∩L is nearly normal in L, so that

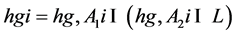
is likewise nearly normal in L, and hence the subgroup hgiL is finite. Thus also the normal closure

is finite. This contradiction proves the lemma.

Corollary 3.4. Let G be a locally finite group, and let g be an element of G such that Xg = X for each infinite subgroup X of G which is neither almost normal nor nearly normal. If g has infinitely many conjugates, then its centralizer CG(g) is a Cernikov group.

Proof: It follows from Lemma 3.3 that all abelian subgroups of the centralizer CG(g) satisfy the minimal condition. Therefore CG(g) satisfies the minimal condition on abelian subgroups, and hence it is a Cernikov group by a relevant result of Sunkov [16] .

In order to prove that locally finite groups in our situations are close to be locally soluble, we need the following result of B. Hartley [17] on locally finite groups admitting an automorphism of prime-power order for which the set of fixed points is small.

Lemma 3.5. Let G be a locally finite group admitting an automorphism α of prime-power order such that the set of all elements of G fixed by α is a Cernikov group. Then G contains a locally soluble subgroup of finite index.

Lemma 3.6. Let G be a locally finite group with finitely many normalizers of infinite subgroups which are neither almost normal nor nearly normal. Then G contains a locally soluble subgroup of finite index.

Proof: Let F be the F C-centre of G, and let

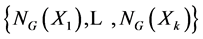
be the set of all normalizers of infinite subgroups of G which are neither almost normal nor nearly normal. Clearly, each NG(Xi) has infinite index in G, and so it follows from Lemma 2.2 that either G is an F C-group or the set

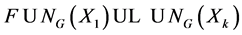
is properly contained in G. If G is an F C-group, then it has finitely many normalizers of subgroups which are neither almost normal nor nearly normal, and hence G is soluble-by-finite by Theorem 2.3. Suppose now that

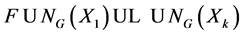
is a proper subset of G, and let g be an element of prime-power order in the set

Then g satisfies the condition of Corollary 3.4, so that its centralizer CG(g) is a Cernikov group, and hence G contains a locally soluble subgroup of finite index by Lemma 3.5.

Lemma 3.7. Let G be a group with finitely many normalizers of infinite subgroups which are neither almost normal nor nearly normal. Then G contains a characteristic subgroup M of finite index such that the normalizer NM(X) is normal in M for each infinite subgroup X of M which is neither almost normal nor nearly normal in G.

Proof: If X is any infinite subgroup of G which is neither almost normal nor nearly normal, the normalizer NG(X) has obviously finitely many images under automorphisms of G; in particular, the subgroup NG(X) has finitely many conjugates in G and so the index |G: NG(NG(X))| is finite. It follows that also the characteristic subgroup

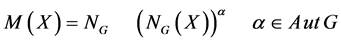
has finite index in G. Let Λ be the set of all infinite subgroups of G which are neither almost normal nor nearly normal. If X and Y are elements of Λ such that NG(X) = NG(Y), then M(X) = M(Y), and hence also

is a characteristic subgroup of finite index of G. Let X be any infinite subgroup of M which is neither almost normal nor nearly normal. Then

and so the normalizer NM(X) = NG (X) ∩ M is a normal subgroup of M .

Finally, we mention the following result of D. I. Zaicev [18] , which is needed in our proofs.

Lemma 3.8. Let G be a locally soluble group, and let Γ be a finite group of automorphisms of G. If all abelian Γ-invariant subgroups of G satisfy the minimal condition, then G is a Cernikov group.

We are now in a position to prove the main result of this section. Of course, it describes in particular the structure of locally finite groups in which every infinite subgroup is either almost normal or nearly normal.

Theorem 3.9. Let G be a locally finite group with finitely many normalizers of infinite subgroups which are neither almost normal nor nearly normal. Then either the commutator subgroup G⁰ of G is finite or G is a Cernikov group whose infinite subgroups are almost normal.

Proof: Suppose first that G is an F C-group. Then G has finitely many normalizers of subgroups which are neither almost normal nor nearly normal, and hence the commutator subgroup G⁰ of G is finite by Theorem 2.3.

Assume now that the F C-centre F of G is a proper subgroup, and let

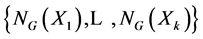
be the set of all normalizers of infinite subgroups of G which are neither almost normal nor nearly normal. It follows from Lemma 2.2 that the subset

is properly contained in G, and so we may consider an element g in the set

Clearly, g satisfies the conditions of Lemma 3.3, and hence all abelian hgi-invariant subgroups of G satisfy the minimal condition. As G contains a locally soluble (normal) subgroup of finite index by Lemma 3.6, it follows from Lemma 3.8 that G is a Cernikov group. Finally, in this case all nearly normal subgroups of G are almost normal by Lemma 3.1, and hence G has only finitely many normalizers of infinite subgroups which are not almost normal. Let X be any infinite subgroup of G, and let J be the finite residual of X. Then J is infinite, and so NG(J)/J has only finitely many normalizers of infinite index; another application of Lemma 2.2 yields now that NG(J)/J is an F C-group, so that it is central-by-finite. Thus X is almost normal in NG(J) and so even in G, as the index |G : NG (J )| is finite. Therefore all infinite subgroups of G are almost normal.

4. Main Results: Now We Prove Our Main Results

Infinite Subgroups of Non-Periodic Groups

As we mentioned in the introduction, the structure of groups in which all infinite subgroups are almost normal has been described by L. A. Kurdachenko, S. S. Levishchenko and N. N. Semko [5] , while that of groups in which all infinite subgroups are nearly normal has been studied by S. Franciosi and F. de Giovanni [6] . We state here as lemmas parts of their results.

Lemma 4.1. Let G be a non-periodic group whose infinite subgroups are almost normal. Then either G is central-by-finite or it contains normal subgroups N and A such that N ≤ A, N is finite, G/A has prime order p and A/N is a free abelian group of rank p − 1 on which G/A acts rationally irreducibly.

Lemma 4.2. Let G be a non-periodic group whose infinite subgroups are nearly normal. Then either G⁰ is finite or G is a finite extension of an infinite cyclic subgroup.

It was observed in the introduction that if all subgroups of a group G are almost normal, then each of them must be nearly normal. The following example shows that the imposition of almost normality just to infinite subgroups does not have similar consequences. Let the group

be the semidirect product of a free abelian group of rank 2 by a cyclic group hxi of order 3, acting by the rules ax = b and bx = a^–1b^–1. Then all infinite subgroups of G are almost normal, but hai has obviously infinite index in its normal closure. On the other hand, Lemma 4.2 shows that if G is a non-periodic group in which every infinite subgroup is nearly normal, then either G⁰ is finite (and so all subgroups are nearly normal) or all infinite subgroups of G are almost normal. Our next result proves that the same conclusion holds in a more general situation.

Theorem 4.3. Let G be a non-periodic group in which every infinite subgroup is either almost normal or nearly normal. Then either the commutator subgroup G⁰ of G is finite or all infinite subgroups of G are almost normal.

Proof: Let a be any element of infinite order of G. Then the cyclic subgroup hai is either almost normal or nearly normal, and hence the conjugacy class of a is finite. In particular, the normal closure haiG is a finitely generated F C-group, and so it is central-by-finite. Moreover, every subgroup of G/haiG is either almost normal or nearly normal, so that the commutator subgroup of G/haiG is finite by Corollary 2.4 and hence G is soluble-by-finite.

Let T be the largest periodic normal subgroup of G, and assume first that T is infinite. Then each subgroup of G/T is either almost normal or nearly normal, and hence the commutator subgroup of G/T is finite by Corollary 2.4. It follows that the commutator subgroup of G is periodic, so that T is the set of all elements of finite order of G and G is generated by its elements of infinite order. Thus G is an F C-group by the first part of the proof, and so each subgroup of G is either almost normal or nearly normal. Again Corollary 2.4 shows that in this case all subgroups of G are nearly normal, and hence G⁰ is finite.

Suppose now that T is finite. If all infinite subgroups of G/T are nearly normal, we have of course that also all infinite subgroups of G are nearly normal; on the other hand, if all infinite subgroups of G/T are almost normal, it follows from Lemma 4.1 that either the commutator subgroup of G/T is finite (and in this case G⁰ is finite, and so again all infinite subgroups of G are nearly normal) or G has finite Prufer rank, and so by Lemma 3.1 all infinite subgroups of G are almost normal. Therefore it is enough to prove that either all infinite subgroups of G/T are almost normal or all infinite subgroups of G/T are nearly normal, and hence by replacing G by the factor group G/T, it can be assumed without loss of generality that G has no periodic non-trivial normal subgroups. In particular, the Hirsch-Plotkin radical H of G is torsion-free, so that each element of H has finitely many conjugates and hence H is abelian. If h is any non-trivial element of H, the index |hhiG: hhi| is finite, so that hhiG is infinite cyclic and then hhi is normal in G. Therefore all cyclic subgroups of H are normal in G, and G/CG(H) is isomorphic to a group of power automorphisms of H; in particular, G/CG (H ) is finite, as any torsion-free abelian group has precisely two power automorphisms. Let S be the largest soluble normal subgroup of G. Then H is contained in S and CS(H) = H, so that S/H is finite and the factor group G/H is likewise finite. Let X be any infinite subgroup of G. Then X ∩ H is a non-trivial normal subgroup of G, and each subgroup of G/X ∩ H is either almost normal or nearly normal. Application of Corollary 2.4 yields that all subgroups of G/X ∩ H are nearly normal, so that X is a nearly normal subgroup of G. Therefore all infinite subgroups of G are nearly normal in this case, and the theorem is proved.

Our last results provide informations on non-periodic groups with finitely many normalizers of infinite subgroups which are neither almost normal nor nearly normal.

Theorem 4.4. Let G be a non-periodic group in which the elements of finite order form a subgroup. If G has finitely many normalizers of infinite subgroups which are neither almost normal nor nearly normal, then either all infinite subgroups of G are almost normal or all infinite subgroups of G are nearly normal.

Proof: Let T be the subgroup consisting of all elements of finite order of G, and consider the F C-centre F of G. Assume for a contradiction that the statement is false, so that by Theorem 4.3 the group G must contain some infinite subgroup which is neither almost normal nor nearly normal. Let

be the set of all normalizers of infinite subgroups of G which are neither almost normal nor nearly normal. Then

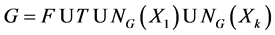
As each of the subgroups T, 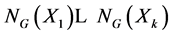has infinite index in G, it follows from Lemma 2.2 that G = F is an F C-group, and hence all its finite subgroups are almost normal. Therefore G has finitely many normalizers of subgroups which are neither almost normal nor nearly normal, and so the commutator subgroup G⁰ of G is finite by Theorem 2.3. This contradiction proves the theorem.

Corollary 4.5. Let G be a non-periodic group in which the elements of finite order form a subgroup. Then G has finitely many normalizers of infinite subgroups which are neither almost normal nor nearly normal if and only if either G is a finite extension of an infinite cyclic group or the commutator subgroup G⁰ of G is finite.

Proof: Suppose that G has finite many normalizers of infinite subgroups which are neither almost normal nor nearly normal. It follows from Theorem 4.4 that either all infinite subgroups are almost normal or all infinite subgroups of G are nearly normal. In the latter case, either G⁰ is finite or G is a finite extension of an infinite cyclic group by Lemma 4.2. Assume now that all infinite subgroups of G are almost normal. Then it follows from Lemma 4.1 either G/Z (G) is finite or G contains normal subgroups E and A such that E ≤ A, E is finite, G/A has prime order p, A/E is free abelian of rank p − 1 and any element of G\A acts rationally irreducibly on A/E. If G/Z (G) is finite, of course we obtain that G⁰ is likewise finite. In the other case, as the elements of finite order in G form a subgroup, we have that G/E must be torsion-free, so that A/E is infinite cyclic and G is a finite extension of an infinite cyclic subgroup. The converse statement is obvious.

Finally, we observe that in our situation the existence of infinite periodic normal subgroups forces the elements of finite order to form a subgroup, and hence allows to apply Theorem 4.4.

Corollary 4.6. Let G be a non-periodic group containing an infinite periodic normal subgroup. If G has finitely many normalizers of infinite subgroups which are neither almost normal nor nearly normal, then the set of all elements of finite order of G is a subgroup.

Proof. Let N be an infinite periodic normal subgroup of G. Then the factor group G/N has finitely many normalizers of subgroups which are neither almost normal nor nearly normal, and hence its commutator subgroup is finite by Theorem 2.3. It follows that the commutator subgroup G⁰ of G is periodic, so that the elements of finite order of G form a subgroup.

5. Conclusion

Thus a subgroup X of a group G is almost normal if the index |G : NG(X)| is finite, while X is nearly normal if it has finite index in the normal closure XG . This paper investigates the structure of groups in which every (infinite) subgroup is either almost normal or nearly normal.

References