Advances in Pure Mathematics
Vol.4 No.2(2014), Article ID:43378,9 pages DOI:10.4236/apm.2014.42010
Applications of Homomorphism on the Structure of Semigroups*
School of Science, Jiangnan University, Wuxi, China
Email: xiangzhikong@jiangnan.edu.cn
Copyright © 2014 Huishu Yuan, Xiangzhi Kong. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Hui shu Yuan, Xiang zhi Kong. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received December 4, 2013; revised January 4, 2014; accepted January 10, 2014
Keywords:Homomorphism; Natural Partial Order; Green’s  -Relation; Semilattice Decomposition
-Relation; Semilattice Decomposition
ABSTRACT
By utilizing homomorphisms and 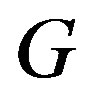 -strong semilattice of semigroups, we show that the Green
-strong semilattice of semigroups, we show that the Green  -relation
-relation 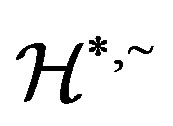 is a regular band congruence on a
is a regular band congruence on a 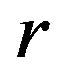 -ample semigroup if and only if it is a
-ample semigroup if and only if it is a  -strong semilattice of completely
-strong semilattice of completely 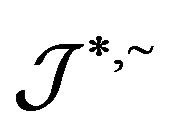 -simple semigroups. The result generalizes Petrich’s result on completely regular semigroups with Green’s relation
-simple semigroups. The result generalizes Petrich’s result on completely regular semigroups with Green’s relation  a normal band congruence or a regular band congruence from the round of regular semigroups to the round of
a normal band congruence or a regular band congruence from the round of regular semigroups to the round of 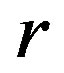 -ample semigroups.
-ample semigroups.
1. Introduction and Preliminaries
It is well known that the usual Green’s relations on a semigroup 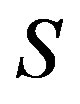 play an important role in the study of the structure of regular semigroups [1-7]. Especially, the well-known theorem of A. H. Clifford states that a semigroup is a completely regular semigroup if and only if it can be expressed as a semilattice of completely simple semigroups (see [1]), where a completely regular semigroup is a semigroup whose
play an important role in the study of the structure of regular semigroups [1-7]. Especially, the well-known theorem of A. H. Clifford states that a semigroup is a completely regular semigroup if and only if it can be expressed as a semilattice of completely simple semigroups (see [1]), where a completely regular semigroup is a semigroup whose 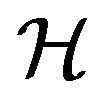 -class contains an idempotent. By using this result, A. H. Clifford, M. Petrich both showed that a completely regular semigroup
-class contains an idempotent. By using this result, A. H. Clifford, M. Petrich both showed that a completely regular semigroup 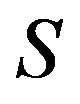 with its Green’s relation
with its Green’s relation 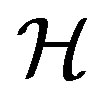 a normal band congruence if and only if
a normal band congruence if and only if  is a strong semilattice of complete simple semigroups [3]. On the other hand, J. B. Fountain generalized the Clifford theorem by showing that an abundant semigroup is a superabundant semigroup, that is, an abundant semigroup
is a strong semilattice of complete simple semigroups [3]. On the other hand, J. B. Fountain generalized the Clifford theorem by showing that an abundant semigroup is a superabundant semigroup, that is, an abundant semigroup 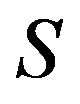 with every
with every 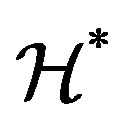 -class of
-class of 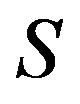 contains an idempotent of
contains an idempotent of 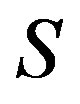 if and only if
if and only if 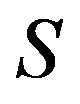 is a semilattice of completely
is a semilattice of completely  -simple semigroups.
-simple semigroups.
We first recall some of the generalized Green’s relations which are frequently used to study the structure of abundant semigroups. The following Green  -relations on a semigroup
-relations on a semigroup  were originally due to F. Pastijn [8] and were extensively used by J. B. Fountain to study the so called abundant semigroups in [9]. Let
were originally due to F. Pastijn [8] and were extensively used by J. B. Fountain to study the so called abundant semigroups in [9]. Let  be an arbitrary semigroup. Then, we define
be an arbitrary semigroup. Then, we define . Dually, we define
. Dually, we define  and define
and define ,
,  while
while
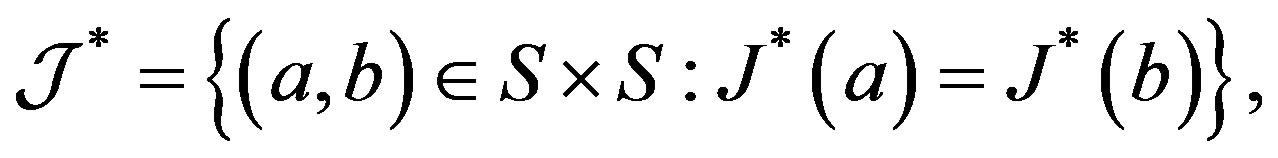 where
where 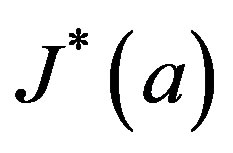 is the smallest ideal containing element
is the smallest ideal containing element  saturated by
saturated by
 and
and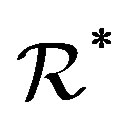 , that is,
, that is, 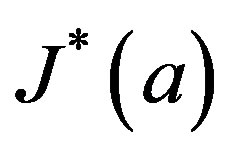 is a union of some
is a union of some 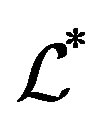 -classes and also a union of some
-classes and also a union of some 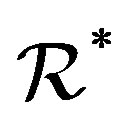 -classes of
-classes of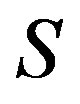 .
.
It was given by M. V. Lawson in [10] the definition of 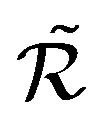 on a semigroup
on a semigroup 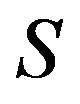 as
as
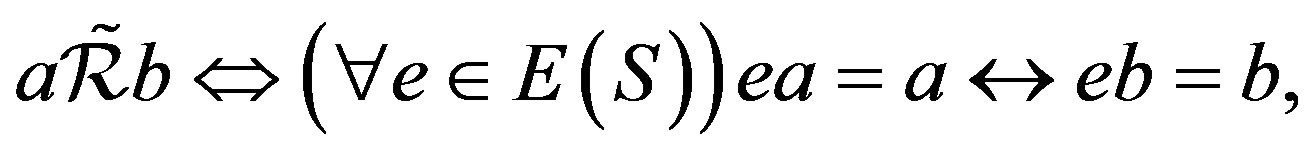 where
where  is the idempotents set of
is the idempotents set of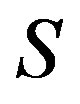 . It can be easily seen that
. It can be easily seen that  and for any regular elements
and for any regular elements 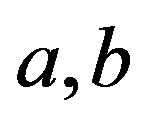 of a semigroup
of a semigroup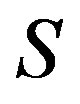 ,
, 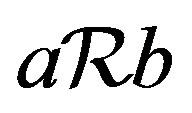 if and only if
if and only if .
.
In order to further investigate the structure of non-regular semigroups, we have to generalize the usual Green’s relations. For this purpose, J. B. Fountain and F. Pastijn both generalized the Green’s relations to the so called Green  -relations in [8] and [9], respectively and by using these Green
-relations in [8] and [9], respectively and by using these Green  -relations, many new results of
-relations, many new results of 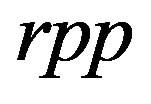 -semigroups and abundant semigroups have been obtained by many authors in [10-18]. For the results of all other generalized Green’s relations and their mutual relationships, the reader is referred to a recent paper of Shum, Du and Guo [17].
-semigroups and abundant semigroups have been obtained by many authors in [10-18]. For the results of all other generalized Green’s relations and their mutual relationships, the reader is referred to a recent paper of Shum, Du and Guo [17].
In this paper, we introduce the concept of the Green  -relations which is a common generalization of the Green
-relations which is a common generalization of the Green  -relations and the
-relations and the  relation. We also introduce the concept of the
relation. We also introduce the concept of the 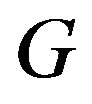 -strong semilattice of semigroups and give the semilattice decomposition of a
-strong semilattice of semigroups and give the semilattice decomposition of a 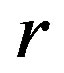 -ample semigroup whose
-ample semigroup whose 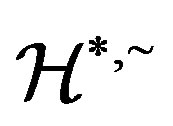 is a congruence. By using this decomposition, we will show that a semigroup
is a congruence. By using this decomposition, we will show that a semigroup  is a
is a 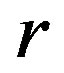 -ample semigroup whose
-ample semigroup whose 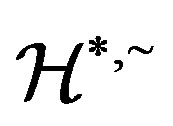 is a regular band congruence if and only if
is a regular band congruence if and only if 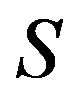 is a
is a  -strong semilattice of completely
-strong semilattice of completely 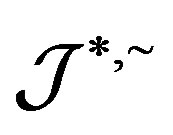 -simple semigroups. Our result extends and enriches the results of A. H. Clifford, M. Petrich and J. B. Fountain in the literature.
-simple semigroups. Our result extends and enriches the results of A. H. Clifford, M. Petrich and J. B. Fountain in the literature.
we first generalize the usual Green’s relations and the Green  -relations to the Green
-relations to the Green  -relations on a semigroup
-relations on a semigroup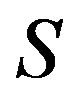 .
.
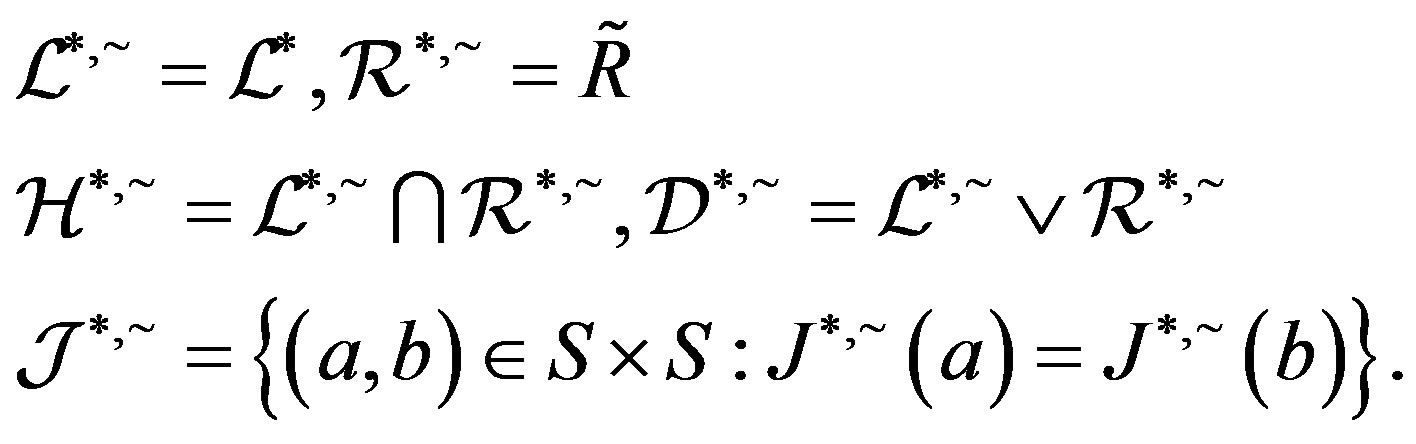
where 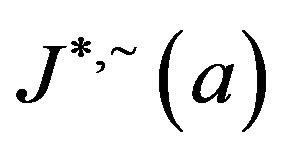 is the smallest ideal containing
is the smallest ideal containing 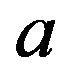 saturated by
saturated by 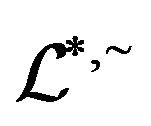 and
and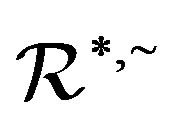 . We can easily see that
. We can easily see that 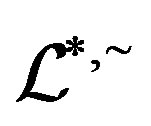 is a right congruence on
is a right congruence on  while
while  is only an equivalence relation on
is only an equivalence relation on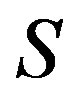 . One can immediately see that there is at most one idempotent contained in each
. One can immediately see that there is at most one idempotent contained in each  -class. If
-class. If , for some
, for some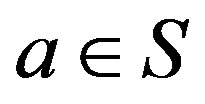 , then we write
, then we write  as
as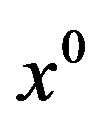 , for any
, for any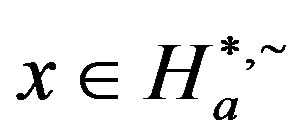 . Clearly, for any
. Clearly, for any 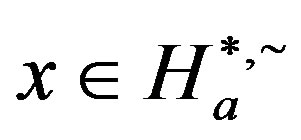 with
with , we have
, we have .
.
If a semigroup  is a regular semigroup, then every
is a regular semigroup, then every 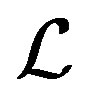 -class of
-class of  contains at least one idempotent, and so does every
contains at least one idempotent, and so does every 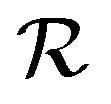 -class of
-class of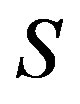 . If
. If  is a completely regular semigroup, then every
is a completely regular semigroup, then every 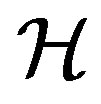 -class of
-class of 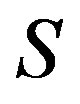 contains an idempotent, in such a case, every
contains an idempotent, in such a case, every 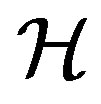 -class is a group. A semigroup
-class is a group. A semigroup 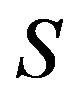 is called an
is called an  semigroup by J. B. Fountain in [9] if every
semigroup by J. B. Fountain in [9] if every  - and
- and 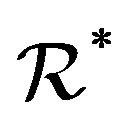 -class of
-class of 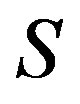 contains an idempotent. One can easily see that
contains an idempotent. One can easily see that 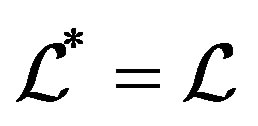 on the regular elements of a semigroup. Therefore, all regular semigroups are obviously abundant semigroups. As an analogy of the orthodox subsemigroup in a regular semigroup, a subsemigroup in an abundant semigroup is called a
on the regular elements of a semigroup. Therefore, all regular semigroups are obviously abundant semigroups. As an analogy of the orthodox subsemigroup in a regular semigroup, a subsemigroup in an abundant semigroup is called a 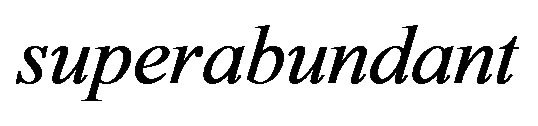 semigroup [9] if each of the
semigroup [9] if each of the 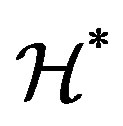 -classes of the abundant semigroup
-classes of the abundant semigroup 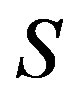 contains an idempotent, in such a case, every
contains an idempotent, in such a case, every 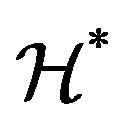 -class of
-class of 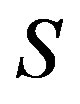 is a cancellative monoid, which is the generalization of completely regular semigroups within the classes of abundant semigroups. The concept of ample semigroups was first mentioned in the paper of G. Gomes and V. Gould [19]. We now call a semigroup
is a cancellative monoid, which is the generalization of completely regular semigroups within the classes of abundant semigroups. The concept of ample semigroups was first mentioned in the paper of G. Gomes and V. Gould [19]. We now call a semigroup  -ample if each
-ample if each 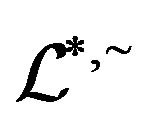 -class and each
-class and each 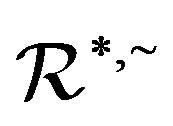 -class contain an idempotent, the concept was first mentioned by Y. Q. Guo, K. P. Shum and C. M. Gong [3]. Certainly, an abundant semigroup is a
-class contain an idempotent, the concept was first mentioned by Y. Q. Guo, K. P. Shum and C. M. Gong [3]. Certainly, an abundant semigroup is a 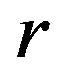 -ample semigroup, but the converse is not true, and an example can be found in [3]. We now call a semigroup
-ample semigroup, but the converse is not true, and an example can be found in [3]. We now call a semigroup  a super
a super  -ample semigroup if each
-ample semigroup if each  -class of
-class of 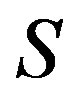 contains an idempotent and
contains an idempotent and  is a congruence. It is clear that every
is a congruence. It is clear that every  -class of such super
-class of such super 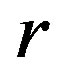 -ample semigroup forms a left cancellative monoid which is a generalization of the completely regular semigroups and the superabundant semigroups in the classes of
-ample semigroup forms a left cancellative monoid which is a generalization of the completely regular semigroups and the superabundant semigroups in the classes of 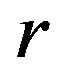 -ample semigroups.
-ample semigroups.
It is recalled that a regular band is a band that satisfies the identity . For further notations and terminology, such as strong semilattice decomposition of semigroups, the readers refer to [2,3]. For some other concepts that have already appeared in the literature, we occasionally use its alternatives, though equivalent definitions.
. For further notations and terminology, such as strong semilattice decomposition of semigroups, the readers refer to [2,3]. For some other concepts that have already appeared in the literature, we occasionally use its alternatives, though equivalent definitions.
2. Properties of r-Ample Semigroups
A completely simple semigroup is a  -simple completely regular semigroup whose Green’s relation
-simple completely regular semigroup whose Green’s relation 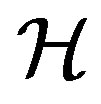 is a congruence on
is a congruence on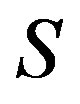 , as a natural generalization of this concept, we call a
, as a natural generalization of this concept, we call a 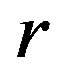 -ample semigroup
-ample semigroup 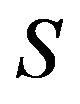 a completely
a completely  -simple semigroup if it is a
-simple semigroup if it is a  -simple semigroup and the Green
-simple semigroup and the Green  -relation
-relation 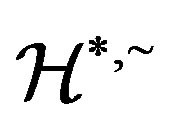 is a congruence on
is a congruence on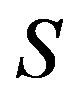 .
.
We first state the following crucial lemma.
Lemma 1 Let  be a
be a 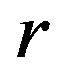 -ample semigroup with each
-ample semigroup with each 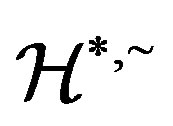 -class contains an idempotent. Then the Green
-class contains an idempotent. Then the Green
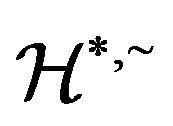 relation on
relation on 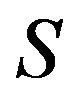 is a congruence on
is a congruence on 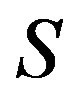 if and only if for any
if and only if for any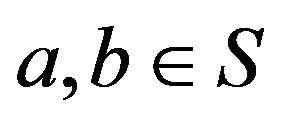 ,
,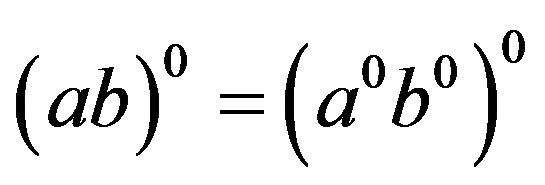 .
.
Proof. Necessity. Let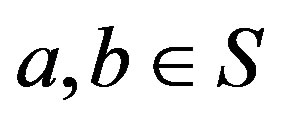 . Then,
. Then, 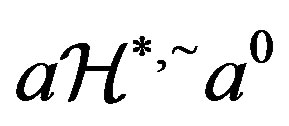 and
and . Since
. Since 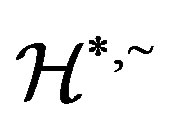 is a congruence on
is a congruence on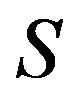 ,
,
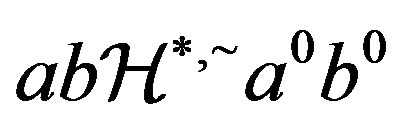 . But
. But 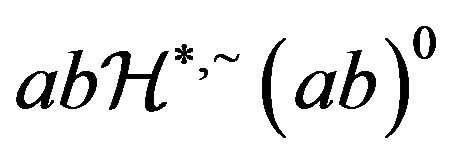 and so,
and so,  since every
since every  -class contains a unique idempotent.
-class contains a unique idempotent.
Sufficiency. Since  is an equivalence on
is an equivalence on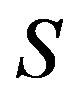 , we only need to show that
, we only need to show that 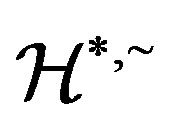 is compatible with the multiplication of
is compatible with the multiplication of . Let
. Let  and
and . Then
. Then 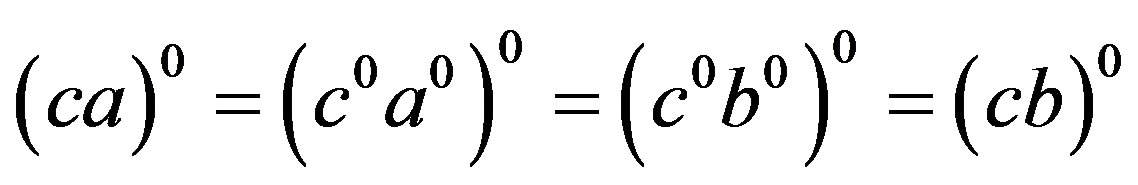 and so that
and so that 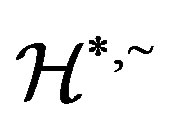
is left compatible with the multiplication on . Similarly,
. Similarly, 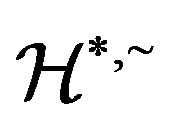 is right compatible wit the multipication on
is right compatible wit the multipication on  and thus
and thus 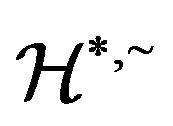 is a congruence on
is a congruence on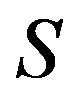 .
.
Lemma 2 If  are
are  -related idempotents of a
-related idempotents of a 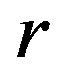 -ample semigroup
-ample semigroup 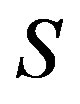 with each
with each 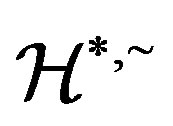 -class contains an idempotent, then
-class contains an idempotent, then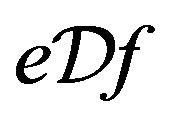 .
.
Proof. Since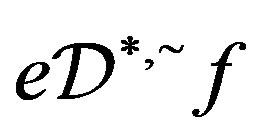 , there are elements
, there are elements 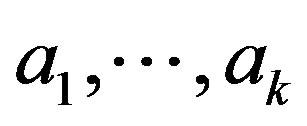 of
of 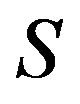 such that
such that
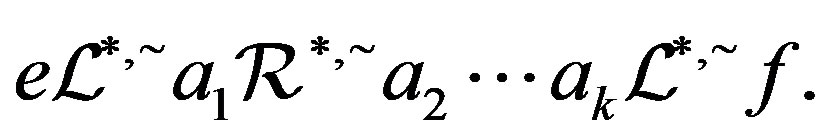
Since 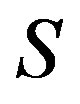 is
is 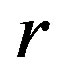 -ample,
-ample,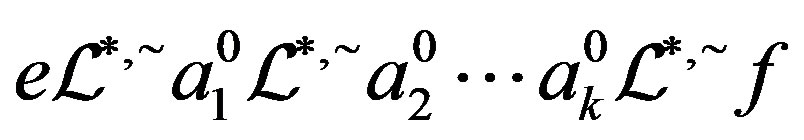 . Thus,
. Thus, 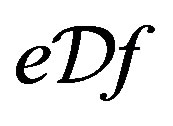 since for regular elements
since for regular elements 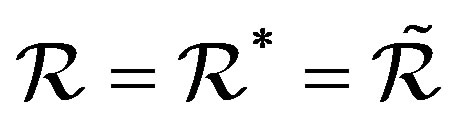 and
and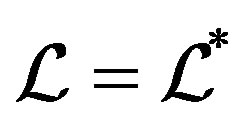 .
.
Corollary 3 If 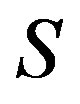 is a
is a 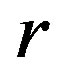 -ample semigroup with each
-ample semigroup with each  -class contains an idempotent, then
-class contains an idempotent, then
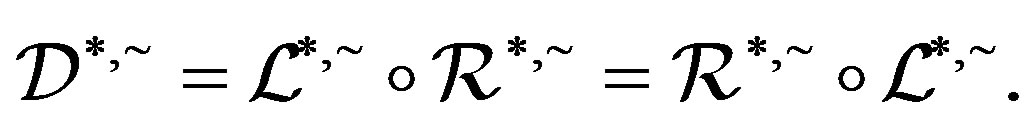
Proof. Let 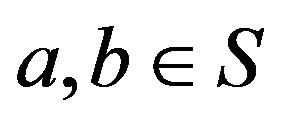 and
and . Then, by Lemma 2,
. Then, by Lemma 2,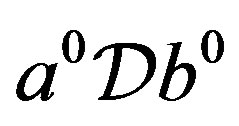 . Thus, there exist elements
. Thus, there exist elements  in
in  with
with  and
and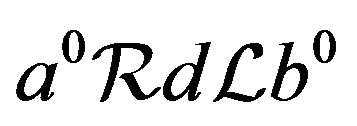 . Then
. Then 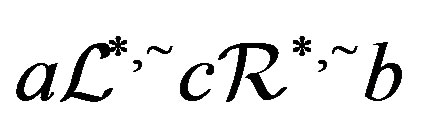 and
and 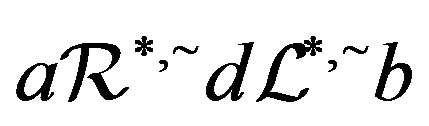 and the result follows.
and the result follows.
Lemma 4 Let 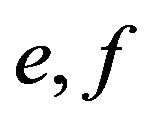 be idempotents in a
be idempotents in a 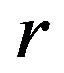 -ample semigroup
-ample semigroup 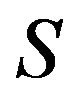 with each
with each 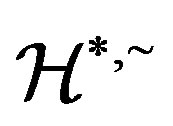 -class contains an idempotent. if
-class contains an idempotent. if , then
, then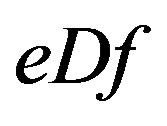 .
.
Proof. Since , there are elements
, there are elements 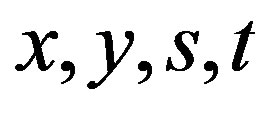 in
in 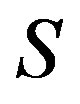 such that
such that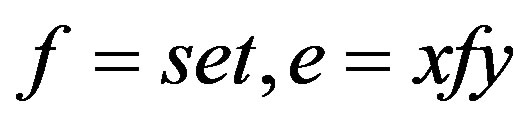 . Let
. Let 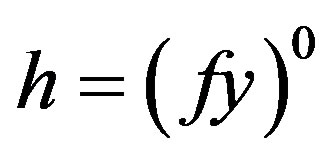 and
and
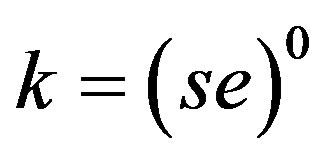 . Then
. Then  so that
so that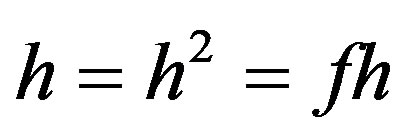 , and
, and 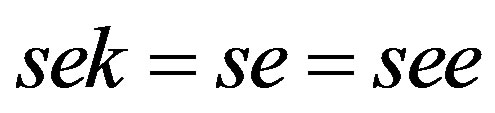 so that
so that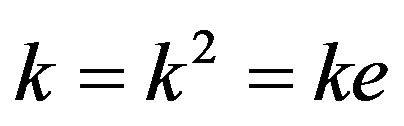 . It follows that
. It follows that  are idempotents with
are idempotents with  and
and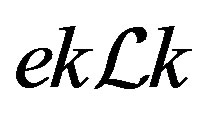 . Hence
. Hence 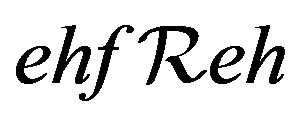 and
and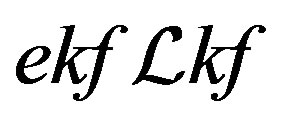 . Now
. Now 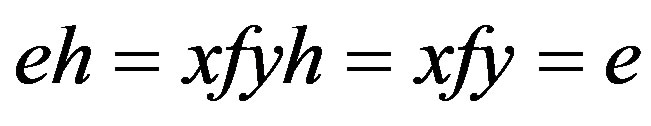 and
and  so that
so that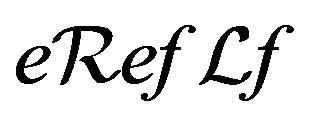 , that is,
, that is, .
.
Proposition 5 If 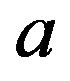 is an element of a
is an element of a  -ample semigroup
-ample semigroup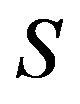 , then
, then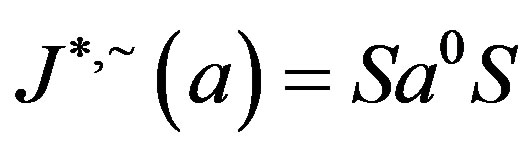 .
.
Proof. Certainly, 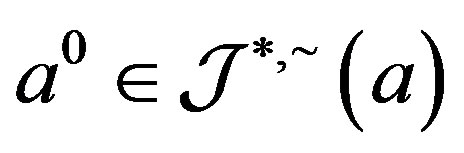 so that
so that . We now show that the ideal
. We now show that the ideal 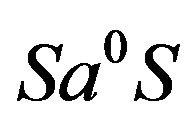 is actually an ideal which is saturated by
is actually an ideal which is saturated by 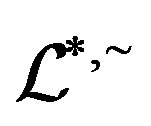 and
and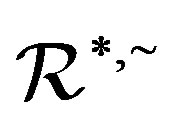 , since
, since , the result follows. Let
, the result follows. Let
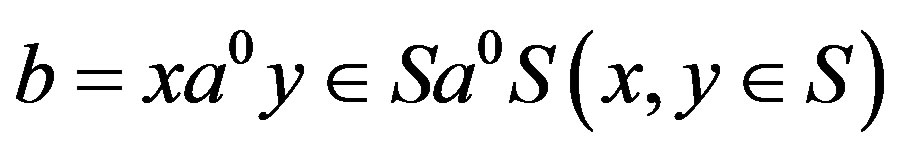 and
and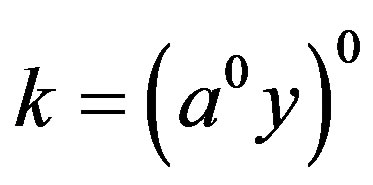 . Then
. Then  so that
so that . Also since
. Also since
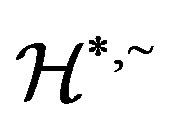 is a congruence on
is a congruence on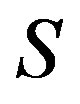 ,
,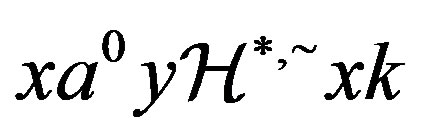 . Now let
. Now let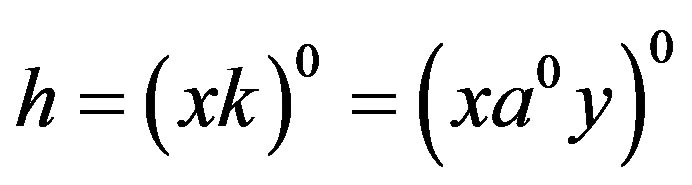 . Then
. Then 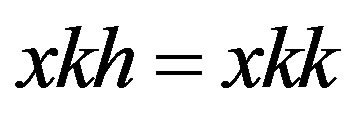 so that
so that
 . Hence if
. Hence if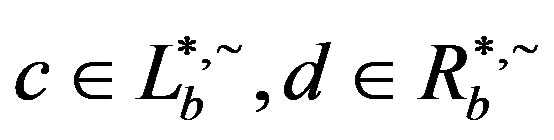 , then
, then  so that
so that 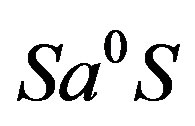 is indeed an ideal saturated by
is indeed an ideal saturated by  and
and , as required.
, as required.
Proposition 6 On a completely  -simple semigroup
-simple semigroup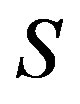 ,
,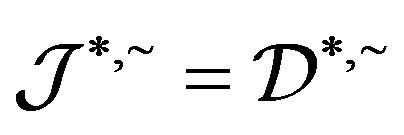 .
.
Proof. Suppose that  with
with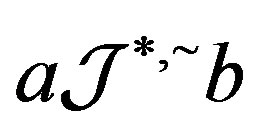 . Then, by Proposition 5,
. Then, by Proposition 5, . By Lemma 4,
. By Lemma 4, 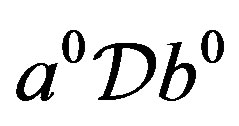
and so , which implies that
, which implies that 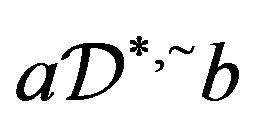 and hence
and hence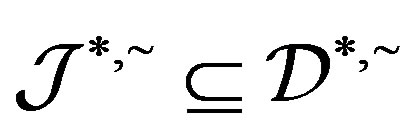 . Conversely, let
. Conversely, let 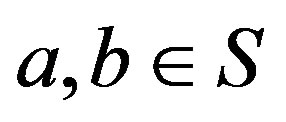 with
with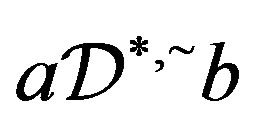 . Now, by Corollary 3, there exists
. Now, by Corollary 3, there exists  such that
such that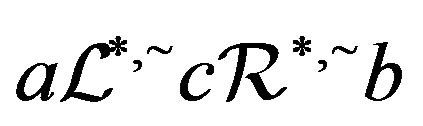 . Thus
. Thus 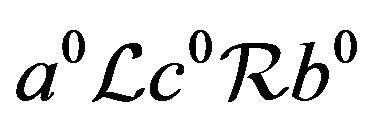 and so
and so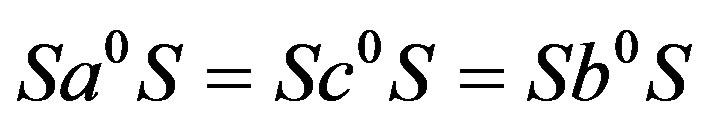 . By Proposition 5,
. By Proposition 5,  and hence
and hence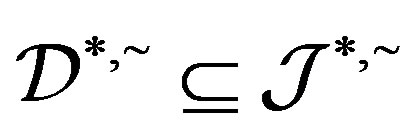 . Now we have
. Now we have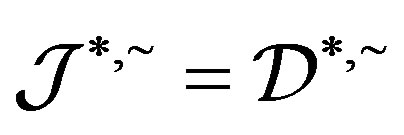 .
.
Proposition 7 A completely  -simple
-simple 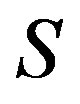 is primitive for idempotents.
is primitive for idempotents.
Proof. Let 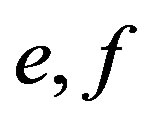 be idempotents in
be idempotents in  with
with . Since
. Since 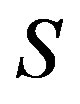 is a completely
is a completely 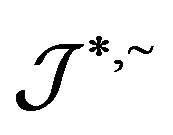 -simple semigroup, it follows from Proposition 5 that
-simple semigroup, it follows from Proposition 5 that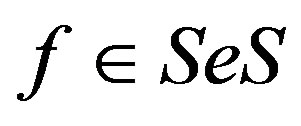 . Now by the first part of Exercise 3 of [1,
. Now by the first part of Exercise 3 of [1,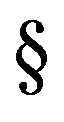 8.4] there is an idempotent
8.4] there is an idempotent 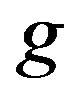 of
of 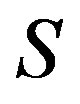 such that
such that 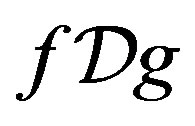 and
and 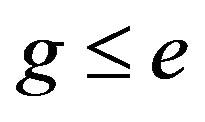 . Let
. Let  be such that
be such that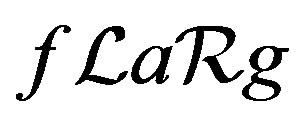 . Then
. Then  and since
and since 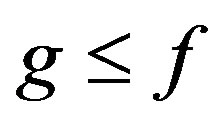 we have
we have

Now we have 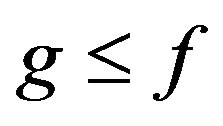 and
and 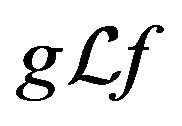 and so
and so 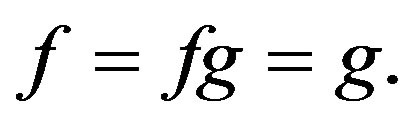 But
But 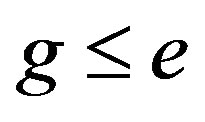 so that
so that 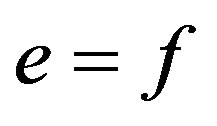 and all idempotent of
and all idempotent of 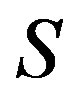 are primitive.
are primitive.
Lemma 8 In a completely 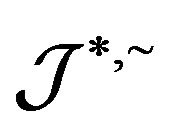 -simple semigroupm
-simple semigroupm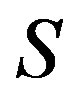 , the regular elements of
, the regular elements of 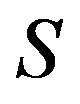 generate a completely simple subsemigroup.
generate a completely simple subsemigroup.
Proof. Let  be regular elements of
be regular elements of . Since
. Since 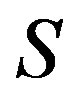 consists of a single
consists of a single  -class(by Proposition 6), it follows from Corollary 3 that there is an element
-class(by Proposition 6), it follows from Corollary 3 that there is an element 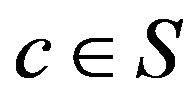 with
with . Hence, we have
. Hence, we have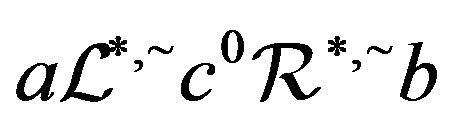 . Thus,
. Thus, 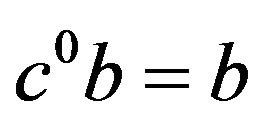 and
and 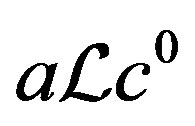 since
since 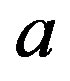 is regular. Now we see that
is regular. Now we see that  and the regularity of
and the regularity of  follows from that of
follows from that of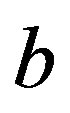 . The property of completely simple of the subsemigroup generated by regular elements follows Proposition 6, lemma 2 and Corollary 3 easily.
. The property of completely simple of the subsemigroup generated by regular elements follows Proposition 6, lemma 2 and Corollary 3 easily.
Theorem 9 Let 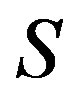 be a
be a  -ample semigroup.Then
-ample semigroup.Then 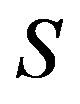 is a semilattice
is a semilattice 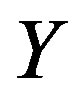 of completely
of completely  -simple semigroups
-simple semigroups 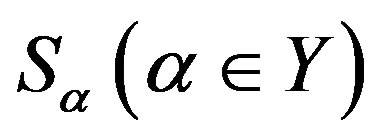 such that for
such that for  and
and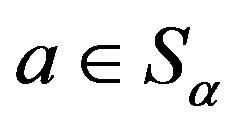 ,
,  ,
,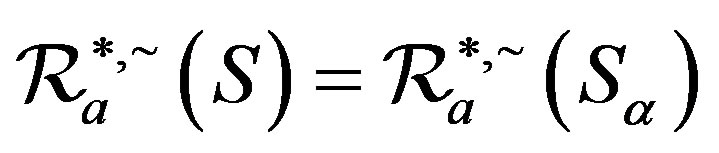 .
.
Proof. If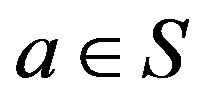 , then
, then 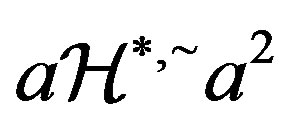 so that by Proposition 5,
so that by Proposition 5,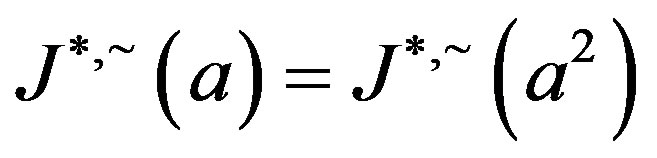 . Now for
. Now for  ,
,
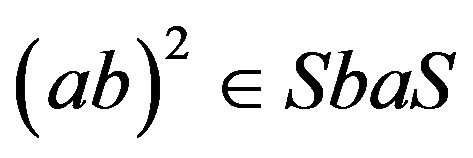 , and so
, and so
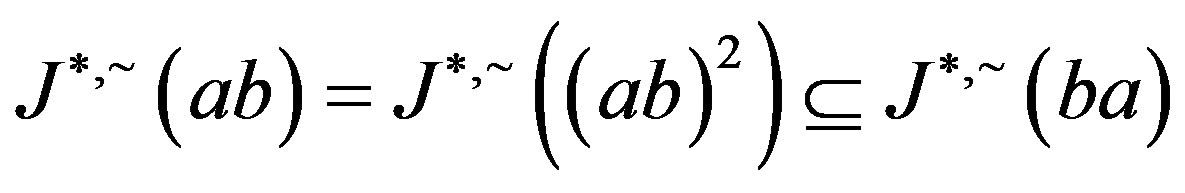
Now, by symmetry, we get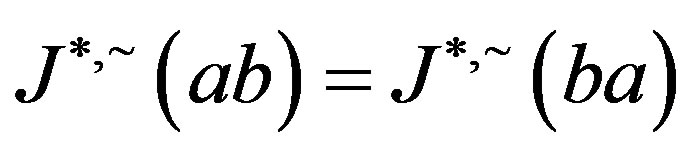 . By Proposition 5,
. By Proposition 5, 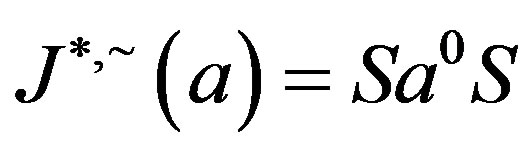 ,
, 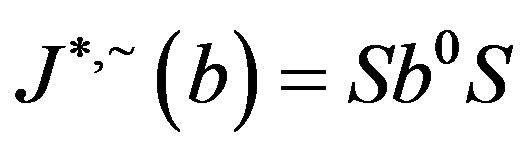 so that if
so that if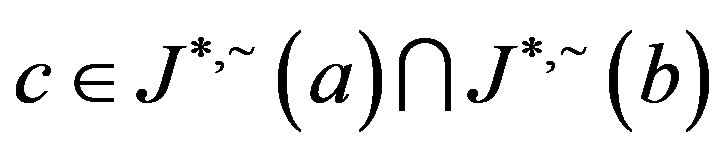 , we have
, we have  for some
for some . Now
. Now
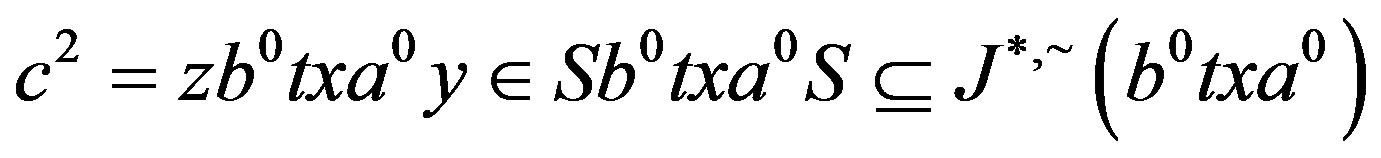 and
and 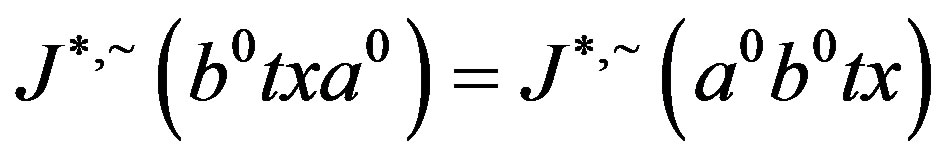 and by the preceding paragraph.
and by the preceding paragraph.
we have 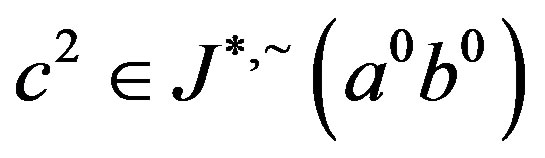 and since
and since ,
, 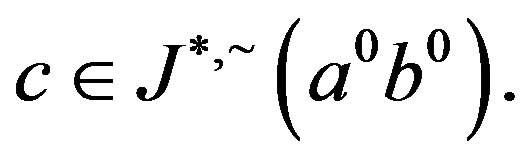 Since
Since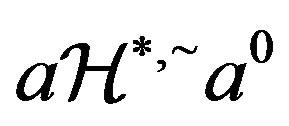 ,
, 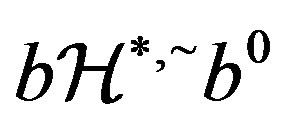 and
and 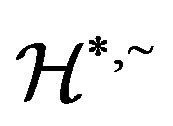 is a congruence on
is a congruence on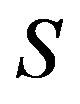 , and so
, and so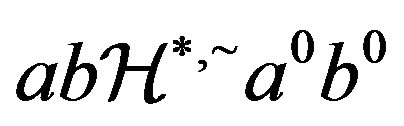 . Now,
. Now, 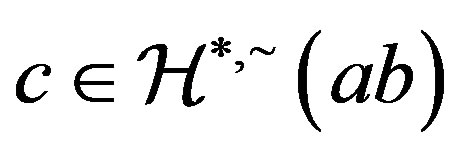 , we have
, we have 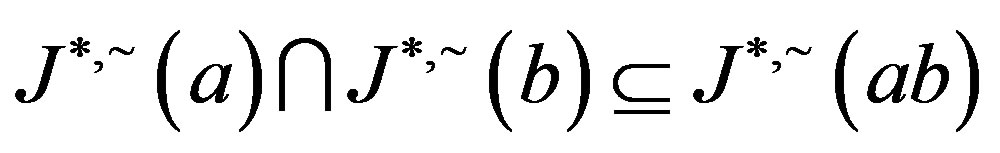 and since the opposite inclusion is clear, we conclude that
and since the opposite inclusion is clear, we conclude that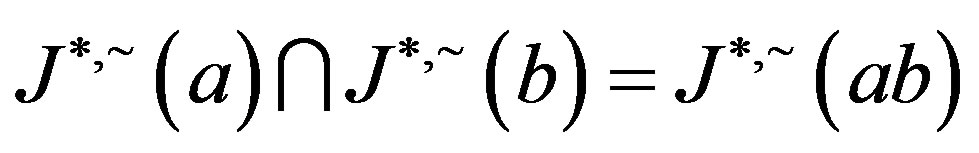 .
.
Because the set 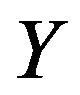 of all ideals
of all ideals 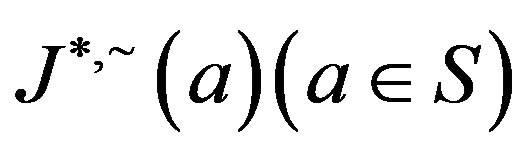 forms a semilattice under the usual set intersection and that the map
forms a semilattice under the usual set intersection and that the map 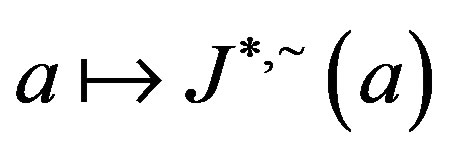 is a homomorphism from
is a homomorphism from 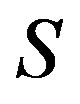 onto
onto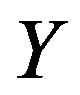 . The inverse image of
. The inverse image of 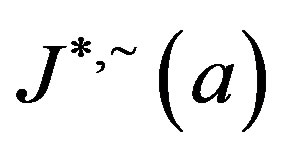 is just the
is just the 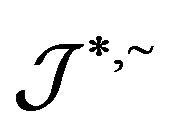 -class
-class 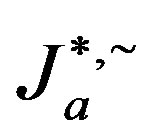 which is thus a subsemigroup of
which is thus a subsemigroup of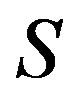 . Hence
. Hence 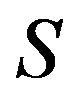 is a semilattice
is a semilattice  of the semigroups
of the semigroups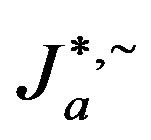 .
.
Now let 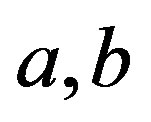 be elements of
be elements of 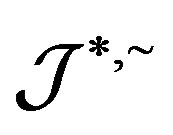 -class
-class  and suppose that
and suppose that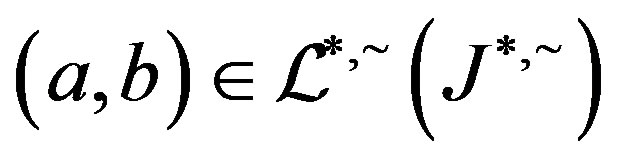 . Certainly
. Certainly 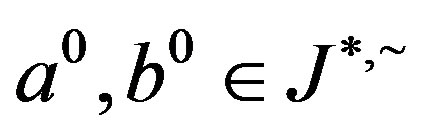
so that we have , that is,
, that is, 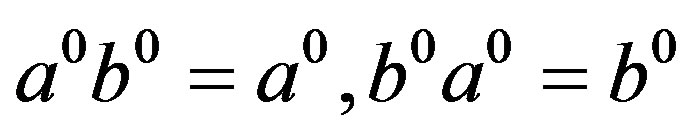 and
and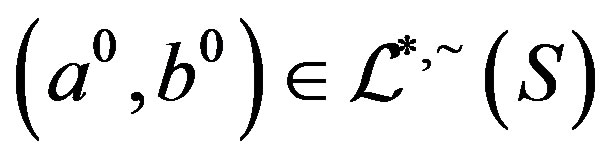 . It follows that
. It follows that
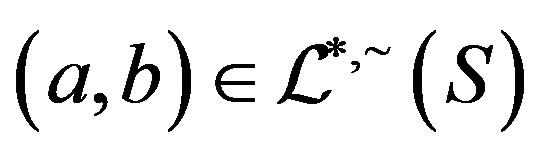 and consequently, since
and consequently, since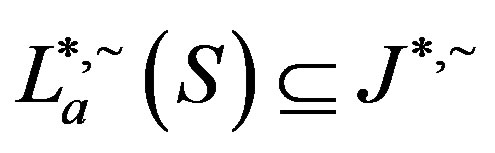 , we have
, we have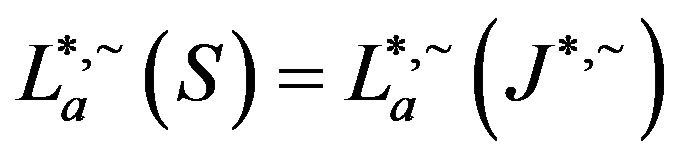 . A similar argument shows that
. A similar argument shows that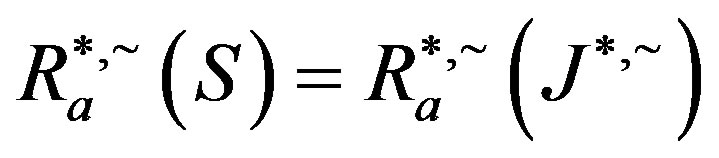 .
.
From the last paragraph, we have 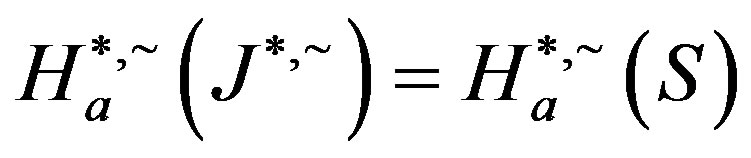 so that
so that  is a
is a 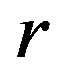 -ample semigroup.
-ample semigroup.
Furthermore, if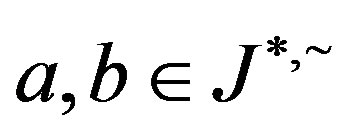 , then by Proposition 6,
, then by Proposition 6, 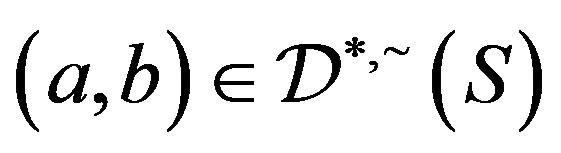 so that, by Corollary 3, there is an element
so that, by Corollary 3, there is an element
 in
in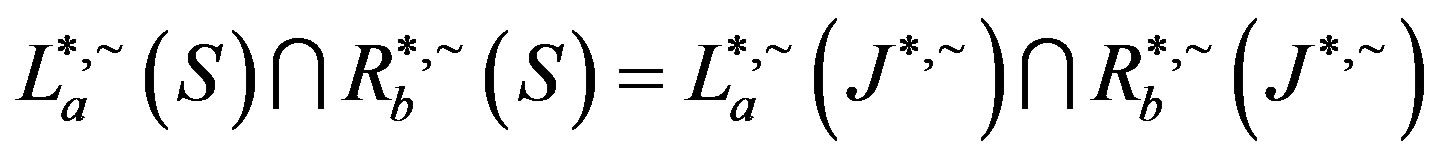 . Thus,
. Thus,  are
are 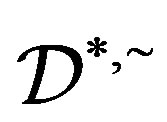 -related in
-related in  so that
so that  is a
is a
 -simple semigroup.
-simple semigroup.
We need the following crucial lemma.
Lemma 10 Let  be a
be a 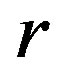 -ample semigroup.
-ample semigroup.
1) Let 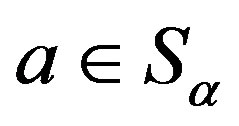 and
and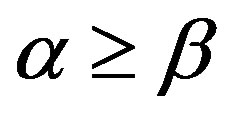 . Then, there exists
. Then, there exists 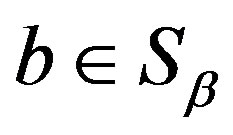 with
with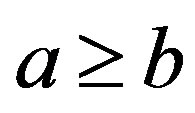 ;
;
2) Let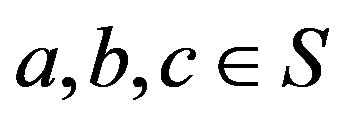 ,
,  and
and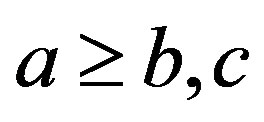 . Then,
. Then,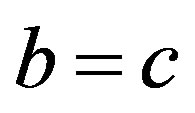 ;
;
3) Let 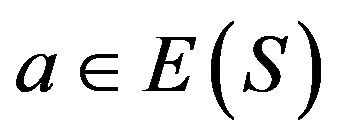 and
and  be such that
be such that . Then,
. Then, .
.
Proof. 1) Let . Then, by Lemma 1,
. Then, by Lemma 1, 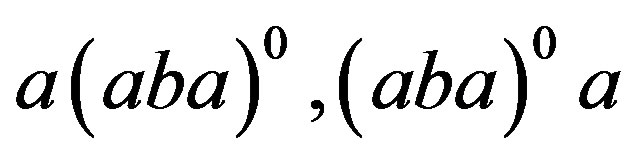 and
and 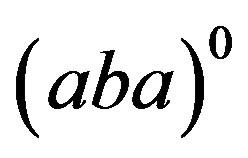 are in the same
are in the same 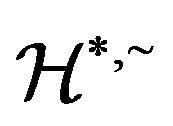 -class and so
-class and so . Let
. Let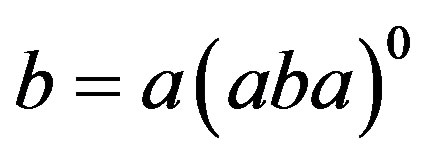 . Then
. Then 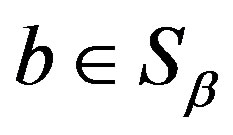 and
and .
.
2) By the definition of “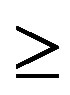 ”, there exist
”, there exist  such that
such that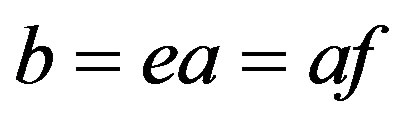 ,
,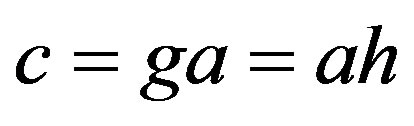 . From
. From  and
and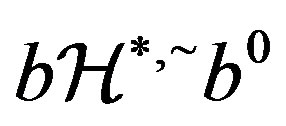 , we have
, we have . Similarly,
. Similarly,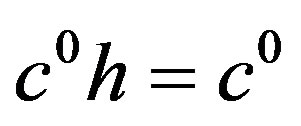 . Thus,
. Thus, . Similarly,
. Similarly,  and so
and so 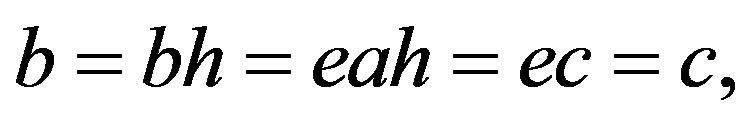 as required.
as required.
3) We have 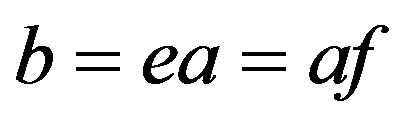 for some
for some 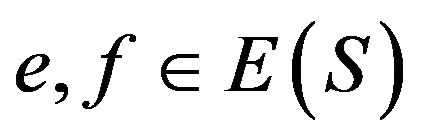 whence
whence
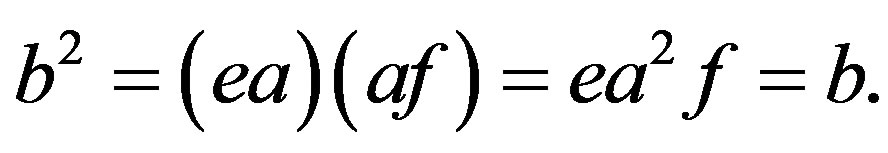
Following Proposition 7, we can easily prove the following lemma Lemma 11 Let 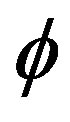 be a homomorphism from a completely
be a homomorphism from a completely 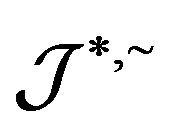 -simple semigroup
-simple semigroup 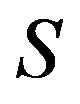 into another completely
into another completely 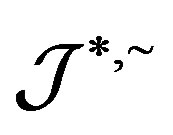 -simple semigroup
-simple semigroup . Then
. Then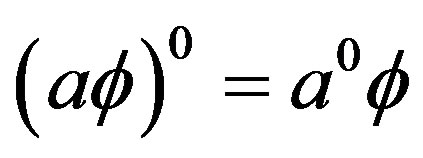 .
.
If 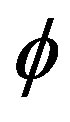 is a homomorphism between two completely
is a homomorphism between two completely  -simple semigroups. Then the Green
-simple semigroups. Then the Green  -relations
-relations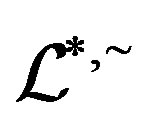 ,
, 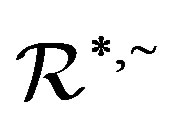 are preserved, so that
are preserved, so that 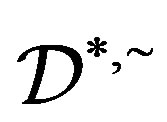 is preserved. We call a homomorphism preserving
is preserved. We call a homomorphism preserving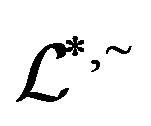 ,
, 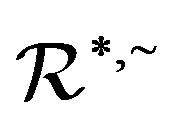 are good. By Proposition 7 and Lemma 10, we can show that a completely
are good. By Proposition 7 and Lemma 10, we can show that a completely 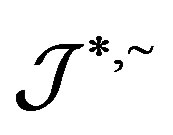 -simple semigroup is primitive.
-simple semigroup is primitive.
3. G-Strong Semilattice Structure of r-Ample Semigroups
In this section, we introduce the  -strong semilattice of semigroups which is a generalization of the well known strong semilattice of semigroups.
-strong semilattice of semigroups which is a generalization of the well known strong semilattice of semigroups.
Definition 12 Let 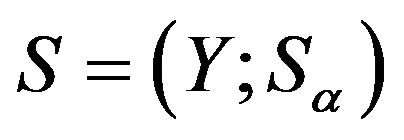 be a semilattice
be a semilattice 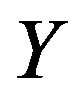 decomposition of semigroup
decomposition of semigroup 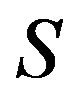 into subsemigroups
into subsemigroups
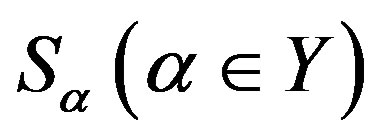 . Suppose that the following conditions hold in the semigroup
. Suppose that the following conditions hold in the semigroup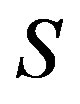 .
.
(C1) for any , there is a band congruence
, there is a band congruence 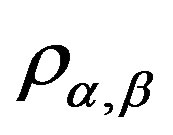 on
on 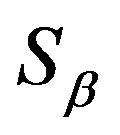 with congruence classes
with congruence classes
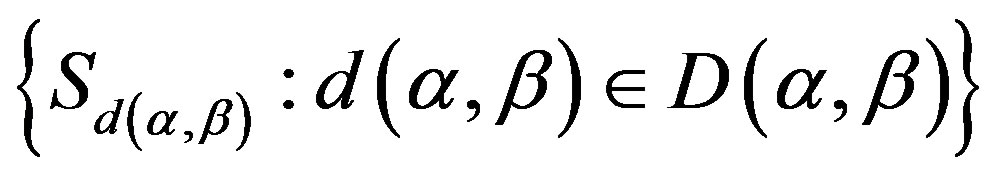 , where
, where 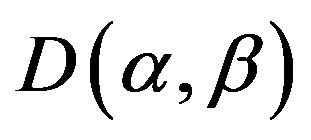 is the index set and for
is the index set and for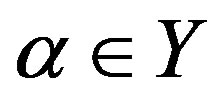 ,
, 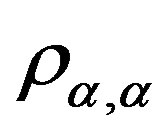 is the universal relation
is the universal relation
 ;
;
(C2) for  on
on 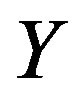 and any
and any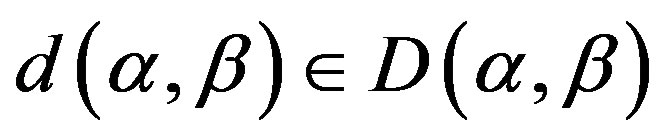 , there is a homomorphism
, there is a homomorphism 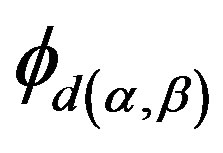 from
from 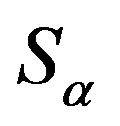 into
into
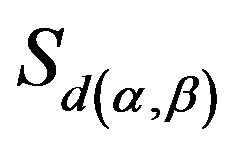 . Let
. Let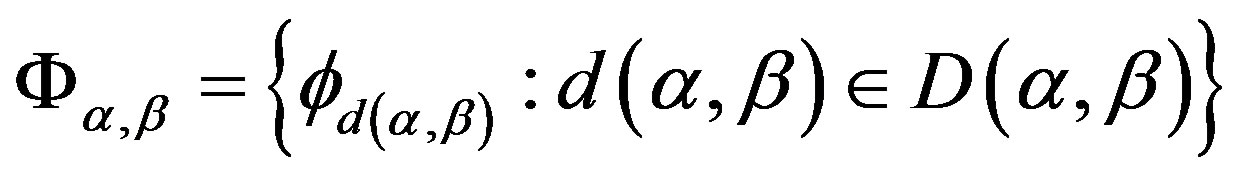 . Then 1) for
. Then 1) for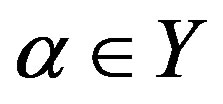 , the homomorphism
, the homomorphism 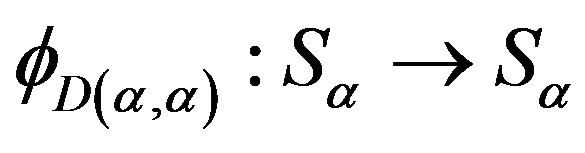 is the identity automorphism of the semigroup
is the identity automorphism of the semigroup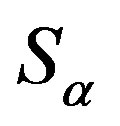 .
.
2) for  on
on ,
, 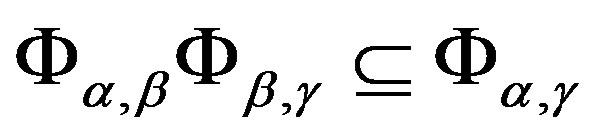 , where
, where 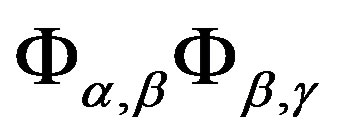 is the set
is the set
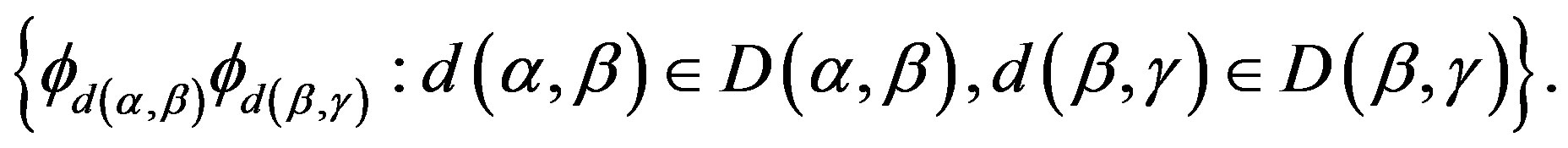
3) for , there exists
, there exists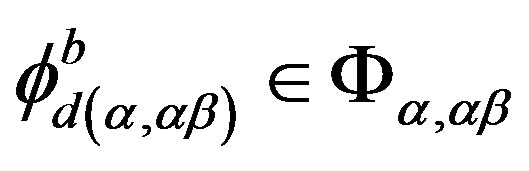 , for all
, for all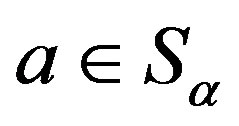 ,
,

If the semigroup  satisfies the above conditions, then we call
satisfies the above conditions, then we call  a
a 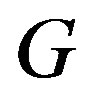 -strong semilattice of subsemigroups
-strong semilattice of subsemigroups 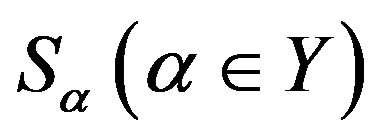 and write
and write . One can easily see that a
. One can easily see that a  -strong semilattice
-strong semilattice 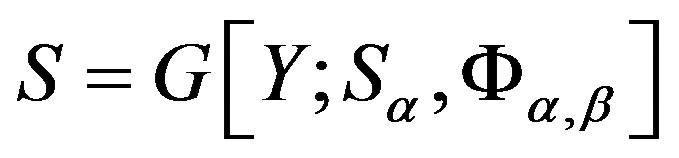 is the ural strong semilattice if and only if all
is the ural strong semilattice if and only if all 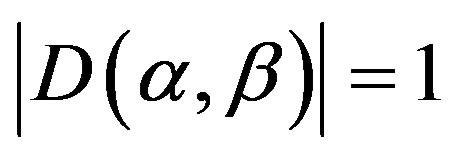 for all
for all 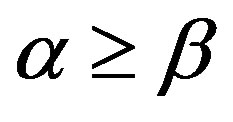 on
on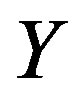 .
.
Following Theorem 9, we can easily see that a 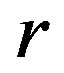 -ample semigroup
-ample semigroup 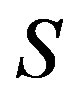 is a semilattice of completely
is a semilattice of completely  simple semigroups
simple semigroups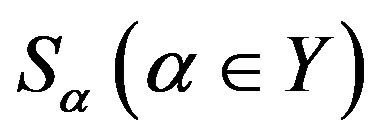 . In this section, we introduce the band congruence
. In this section, we introduce the band congruence  on a regular
on a regular 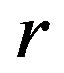 -ample semigroup
-ample semigroup 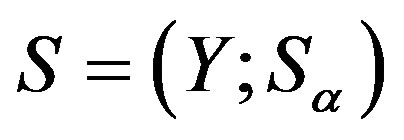 and the structure homomorphisms set
and the structure homomorphisms set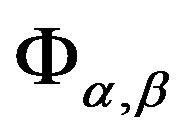 . Finally, we will show the main result of the paper, that is, a
. Finally, we will show the main result of the paper, that is, a 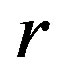 -ample semigroup is a regular
-ample semigroup is a regular 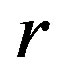 -ample semigroup if and only if it is a
-ample semigroup if and only if it is a 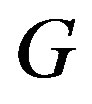 -strong semilattice of completely
-strong semilattice of completely 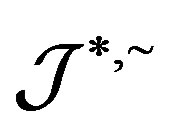 -simple semigroups.
-simple semigroups.
Lemma 13 Let 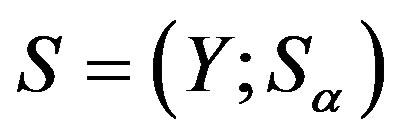 be a regular
be a regular 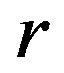 -ample semigroup, that is,
-ample semigroup, that is, 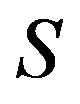 is a
is a 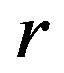 -ample semigroup with the Green
-ample semigroup with the Green  -relation
-relation  as a regular band congruence on
as a regular band congruence on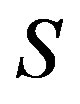 . Then, for any element
. Then, for any element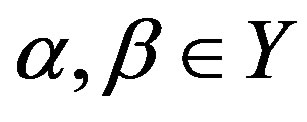 , we define
, we define 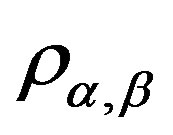 on
on 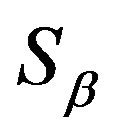 as the following:
as the following:
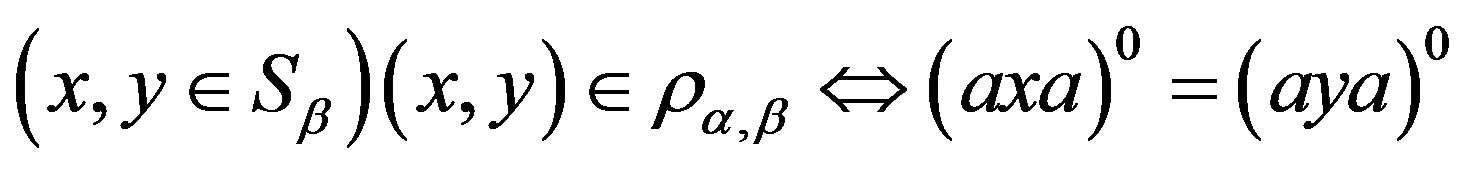
for some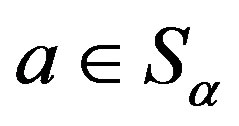 . Then 1)
. Then 1) 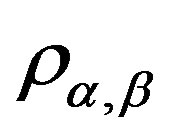 is a band congruence on
is a band congruence on  and for
and for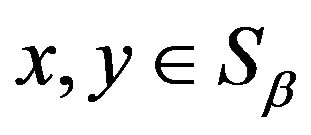 ,
, 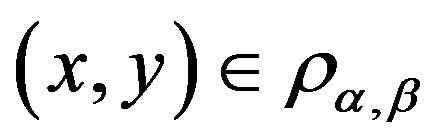 if and only if for any
if and only if for any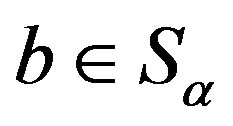 ,
,
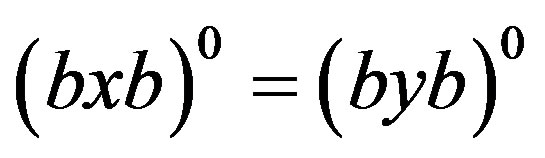 .
.
2) for  on
on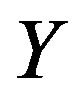 ,
,  and
and  is the universal relation
is the universal relation 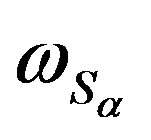 on
on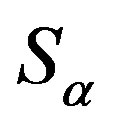 .
.
3) for 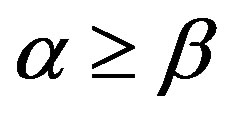 on
on  and
and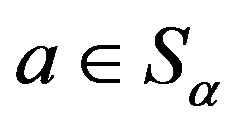 ,
, 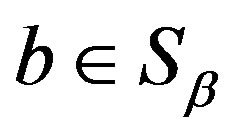 ,
,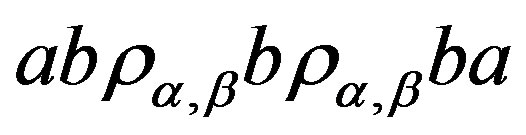 .
.
Proof. We only prove 1), 2) and 3) can be proved similarly. Let  with
with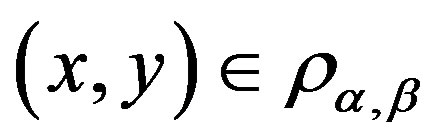 , then there exists
, then there exists 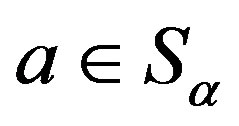 such that
such that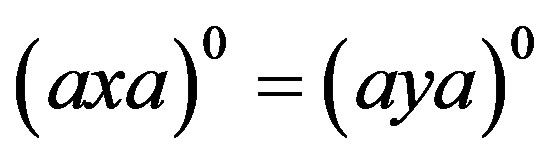 . For any element
. For any element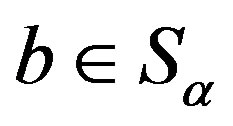 , we have
, we have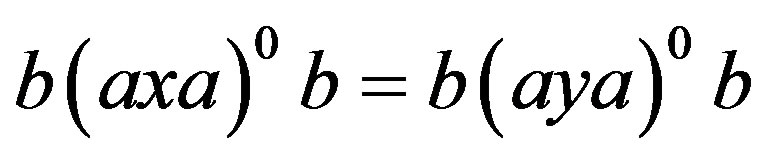 . Thus
. Thus
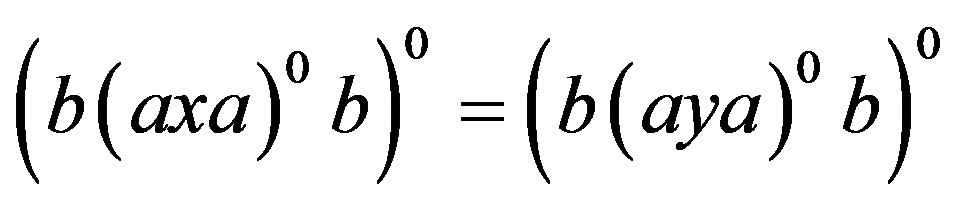 . By the property of regular bands and Lemma 1 and Lemma 8, we easily have
. By the property of regular bands and Lemma 1 and Lemma 8, we easily have
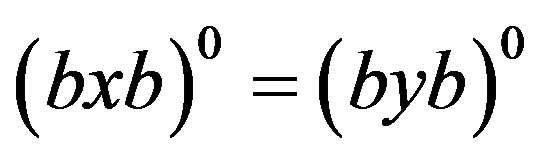 . Now the proof is completed.
. Now the proof is completed.
We denote the 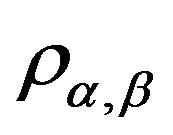 -congruence classes by
-congruence classes by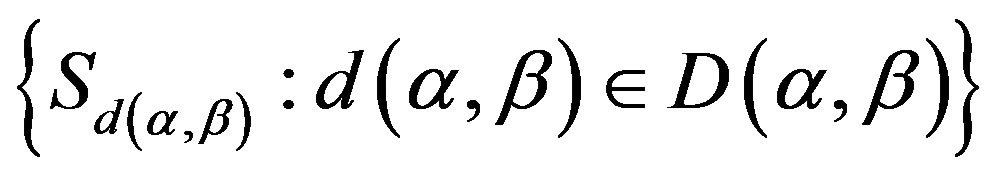 , following Lemma 13,
, following Lemma 13, 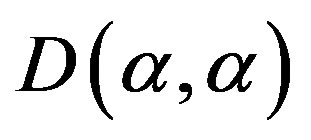
is a singleton.
Lemma 14 Let 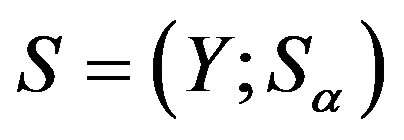 be a regular
be a regular 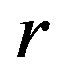 -ample semigroup.
-ample semigroup.
1) For any  on
on  and
and . Let
. Let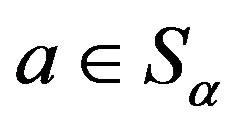 , there exists a unique element
, there exists a unique element
 such that
such that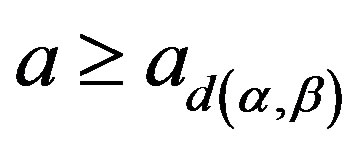 .
.
2) For any 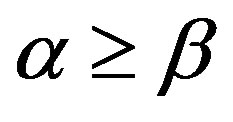 on
on  and
and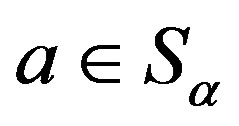 ,
, 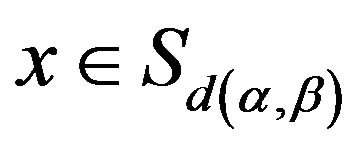 , if
, if 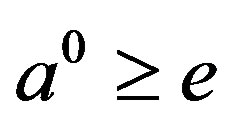 for some idempotent
for some idempotent , then
, then
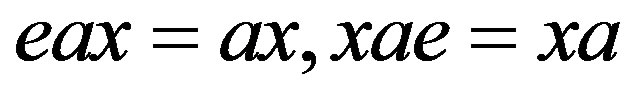 ,
, 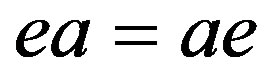 and
and .
.
Proof. 1) By Lemma 13 2) and Lemma 10 1), for any , the element
, the element
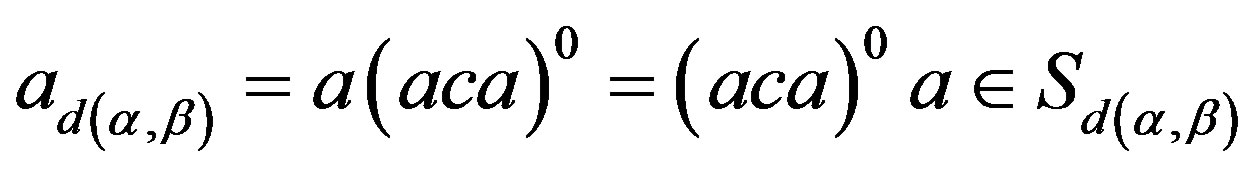 such that
such that . Easily see
. Easily see . If there is another
. If there is another
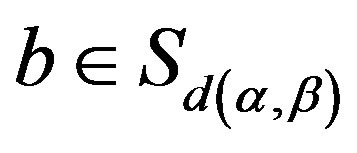 such that
such that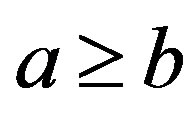 , then there are idempotents
, then there are idempotents 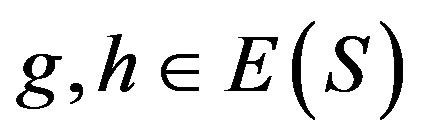 such that
such that 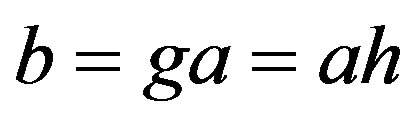 and so
and so
 , thus
, thus 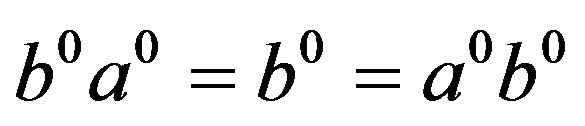 since
since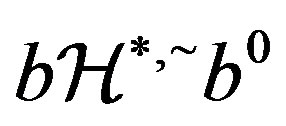 , which implies
, which implies 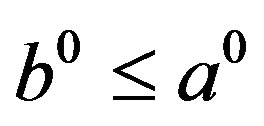 and hence
and hence
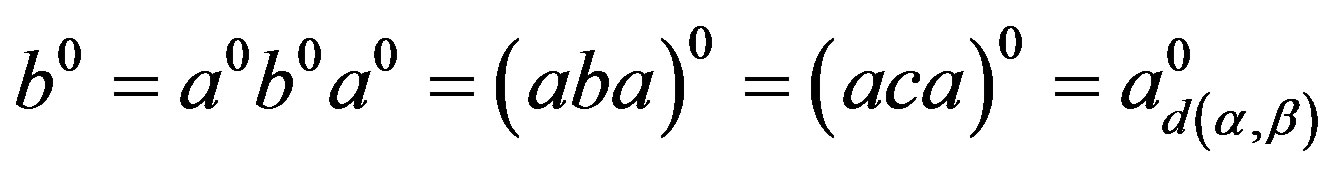 , that is,
, that is,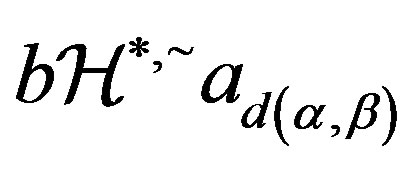 . Thus by Lemma 10 (ii),
. Thus by Lemma 10 (ii), 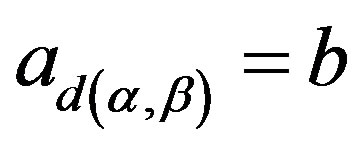 is required.
is required.
2) Since
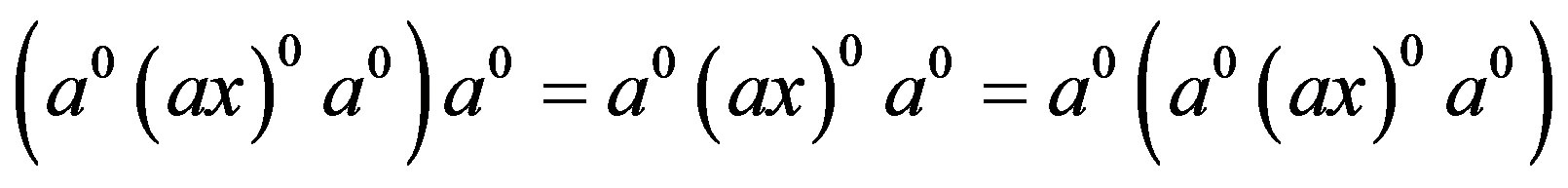
and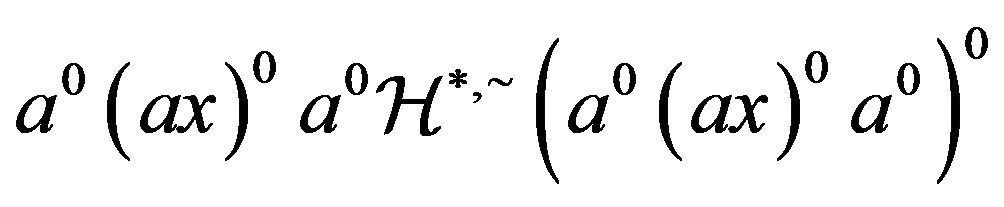 , we have
, we have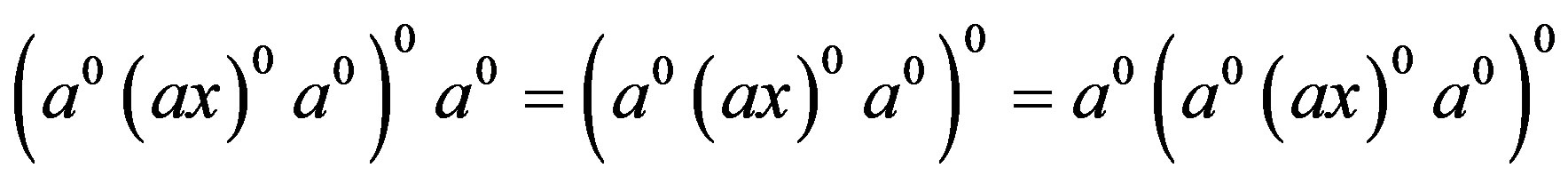 , that is,
, that is,
 . Also, since
. Also, since 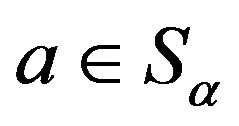 and
and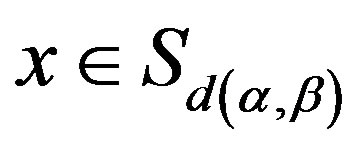 , we have
, we have 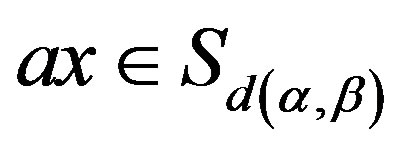 and so that
and so that 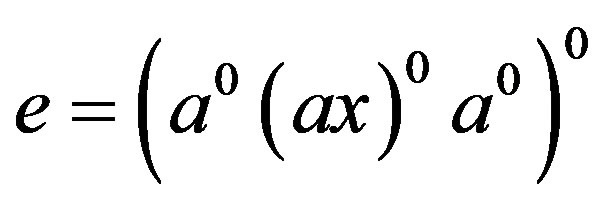
by (i). Thereby, we have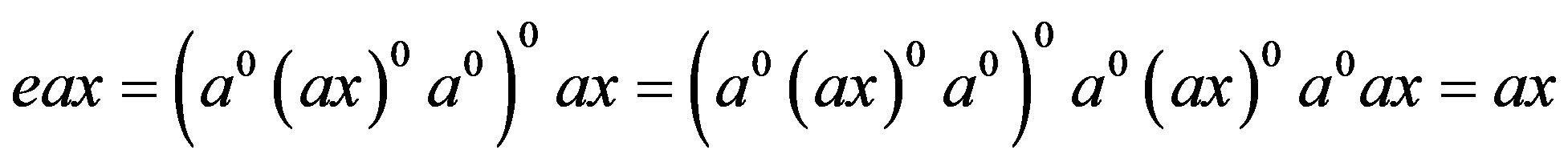 . Similarly, we have
. Similarly, we have
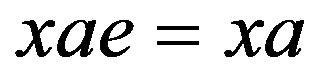 . Since
. Since 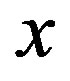 is arbitrarily chosen element in
is arbitrarily chosen element in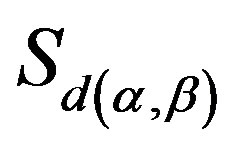 , we can particularly choose
, we can particularly choose . In this way, we obtain that
. In this way, we obtain that 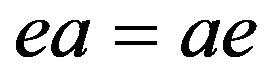 and consequently, by Lemma 1, we have
and consequently, by Lemma 1, we have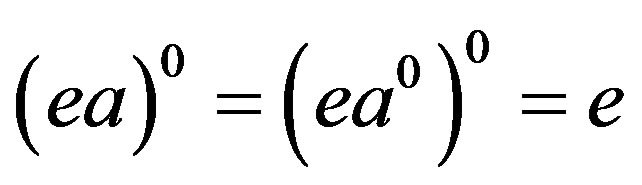 .
.
Lemma 15 Let  be a regular
be a regular 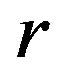 -ample semigroup. For any
-ample semigroup. For any  on
on  and
and
 , define a mapping
, define a mapping  from
from 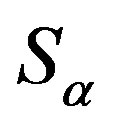 into
into 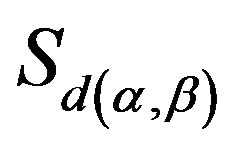 with
with , where
, where 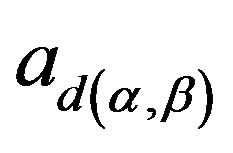
is defined in Lemma 14. Write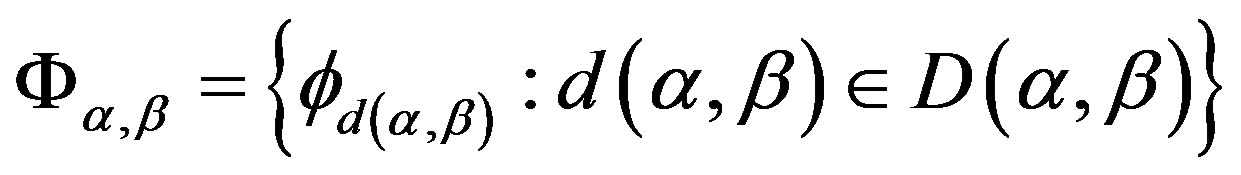 . Then 1)
. Then 1) 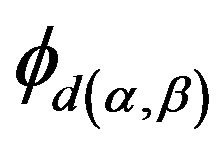 is a homomorphism.
is a homomorphism.
2) for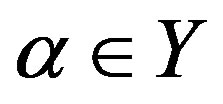 ,
, 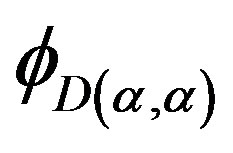 is the identity homomorphism of
is the identity homomorphism of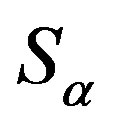 .
.
3) for 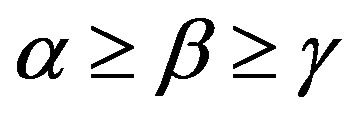 on
on ,
,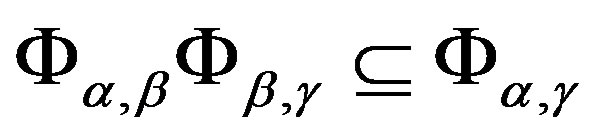 .
.
4) for , there exists
, there exists , for all
, for all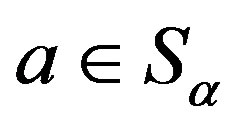 ,
,
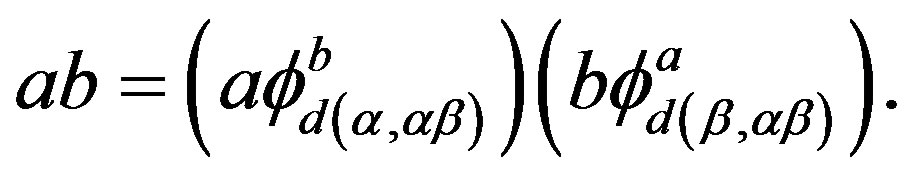
Proof. 1) Following Lemma 14, 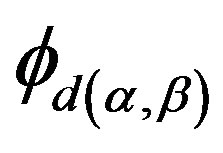 is well defined. For
is well defined. For 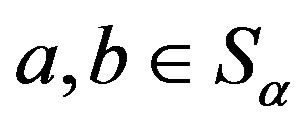 and
and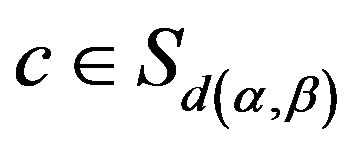 , by Lemma 14 again,
, by Lemma 14 again,
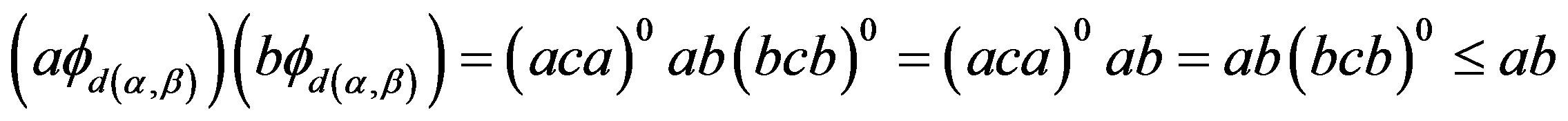 and so
and so

2) It follows easily since  is primitive.
is primitive.
3) We only need to show that for any 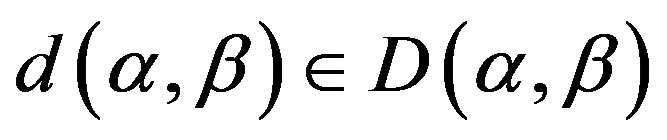
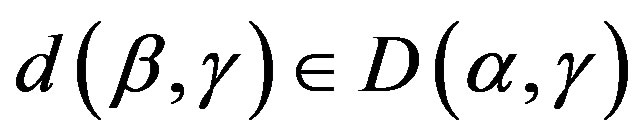 ,
, 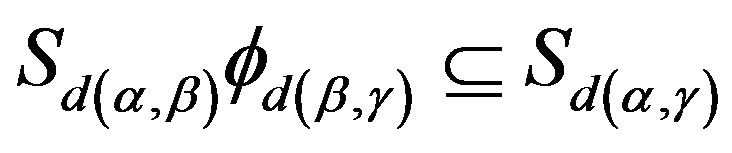 for some
for some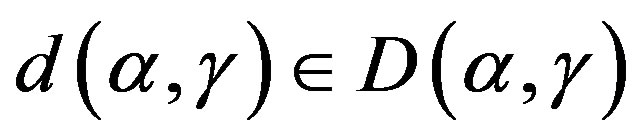 . Let
. Let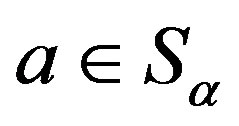 ,
,  and
and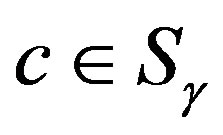 , we have
, we have  and
and
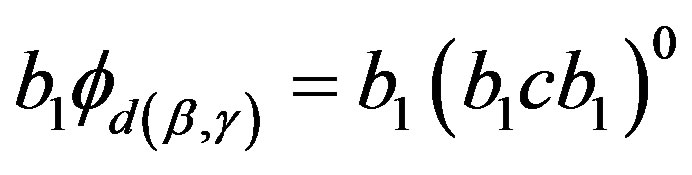 ,
, 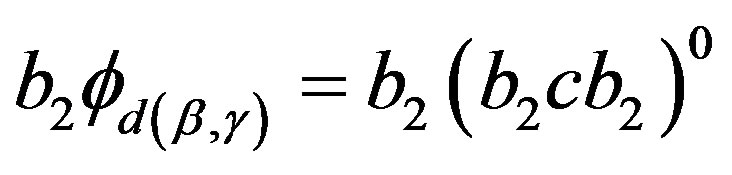 and so
and so
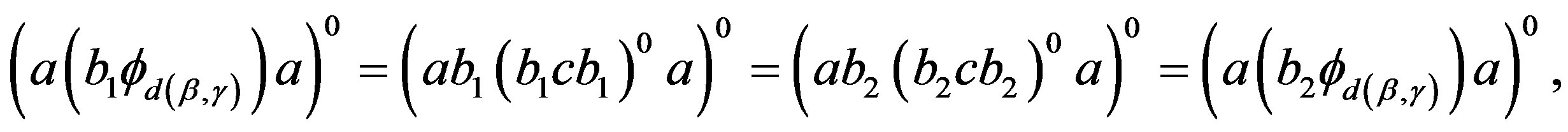
which implies 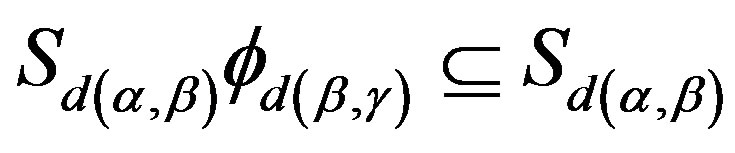 for some
for some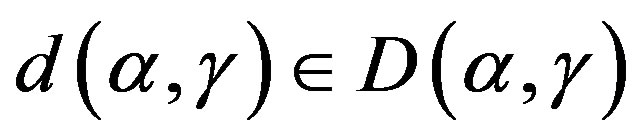 .
.
4) For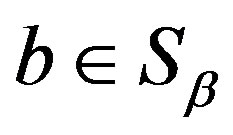 , we need to prove that
, we need to prove that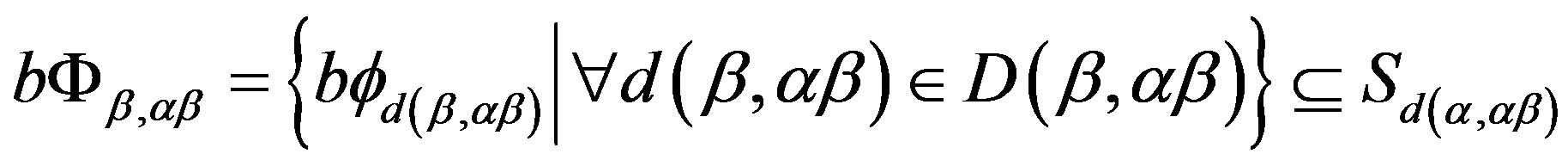 . In fact, it suffices to show that for any
. In fact, it suffices to show that for any 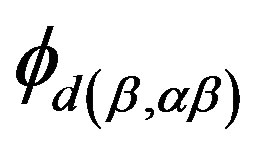 and
and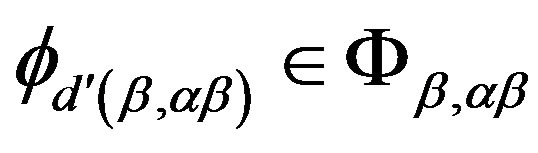 , we have
, we have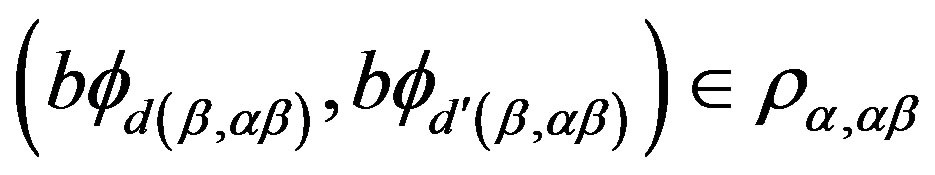 . For this purpose, we let
. For this purpose, we let 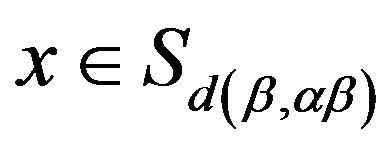 and
and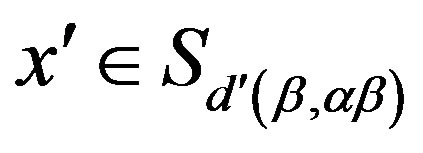 . Then, by (i), we have
. Then, by (i), we have 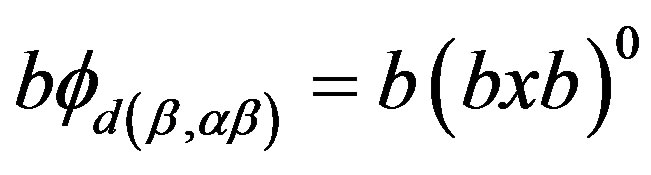 and
and
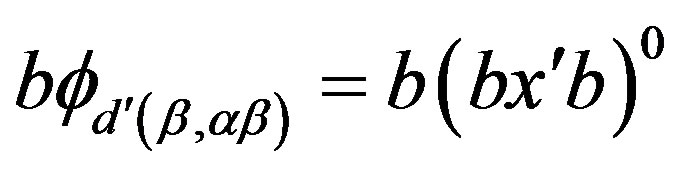 . Let
. Let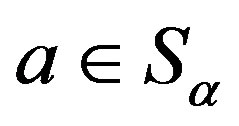 , then, because
, then, because 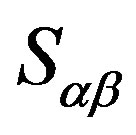 is a completely
is a completely  -simple semigroup, and
-simple semigroup, and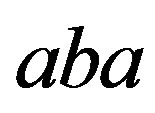 ,
,
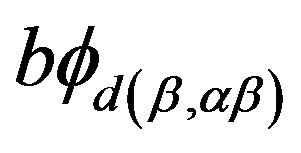 ,
, 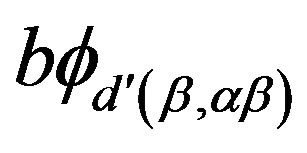 are elements in
are elements in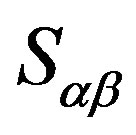 . We obtain that
. We obtain that 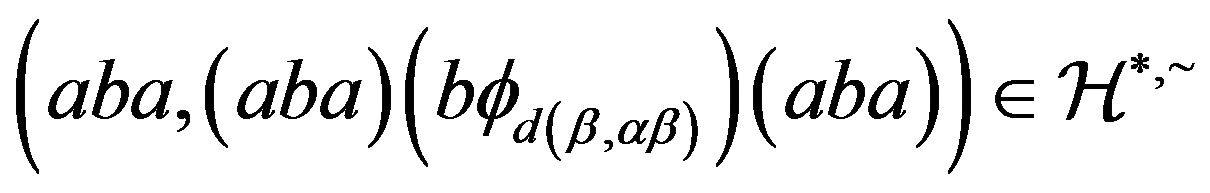 and
and
 . By Lemma 1, we conclude that
. By Lemma 1, we conclude that
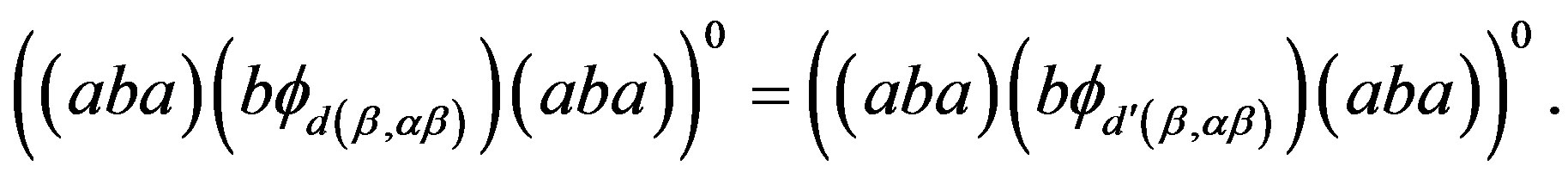
In other words,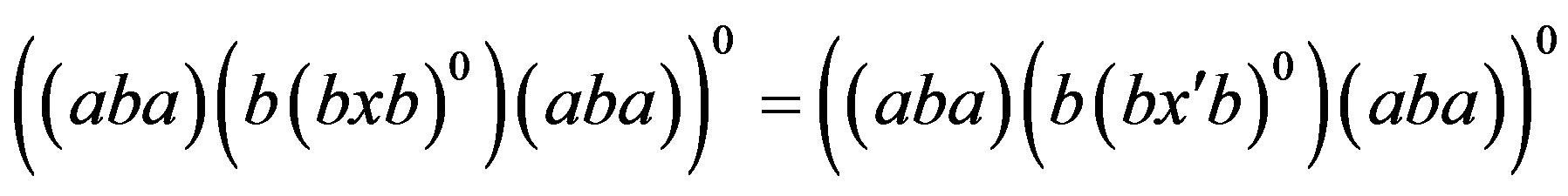 . Thus, by the regularity of the band
. Thus, by the regularity of the band
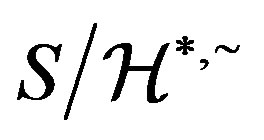 , we can further simplify the above equality to
, we can further simplify the above equality to , that is,
, that is,
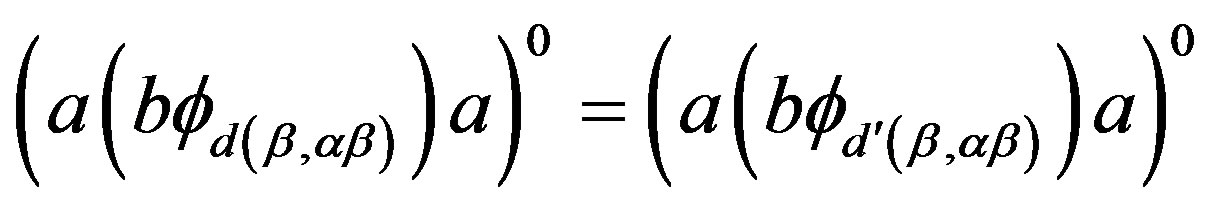 . It hence follows, by the definition of
. It hence follows, by the definition of , that is
, that is
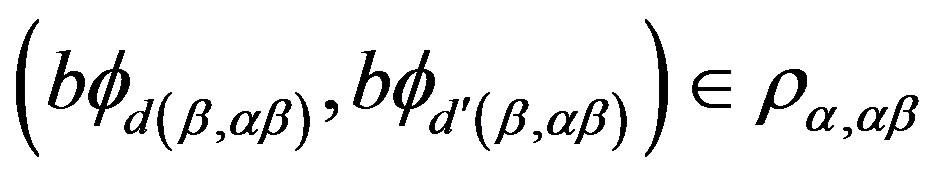 .
.
Now let ,
,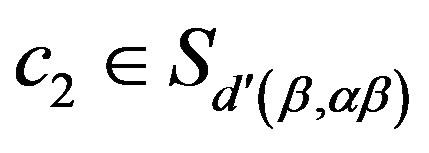 . Then
. Then 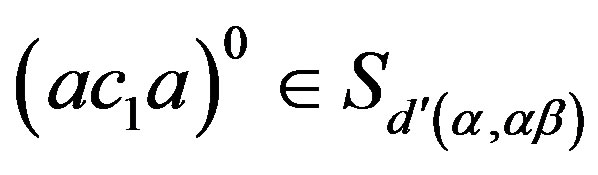 because
because 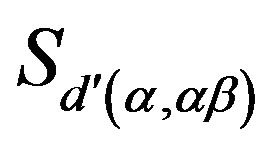 is a
is a  -equivalence class of
-equivalence class of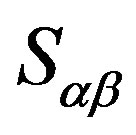 . Now, by (i),
. Now, by (i), 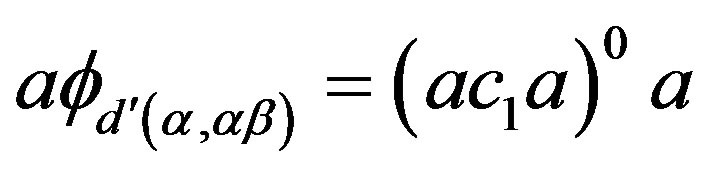 and
and 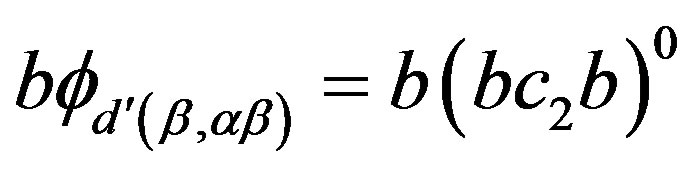 for
for  and
and
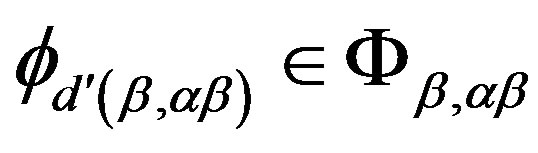 . Since we assume that
. Since we assume that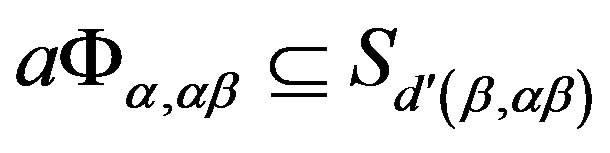 , we have
, we have . Similarlywe have
. Similarlywe have . Thus, we have
. Thus, we have
 and also
and also
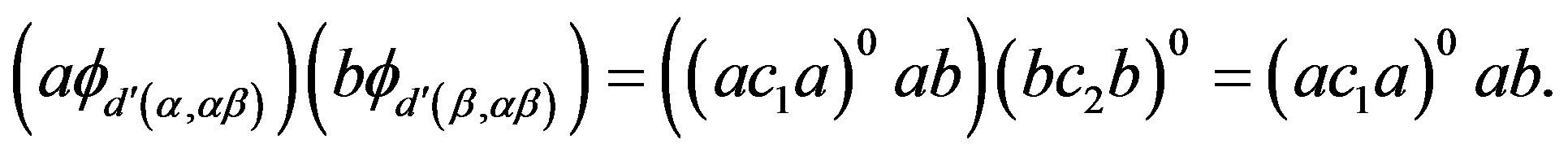
However, by the definition of the natural partial order “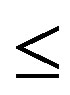 ” on semigroup
” on semigroup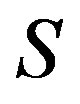 , we have
, we have
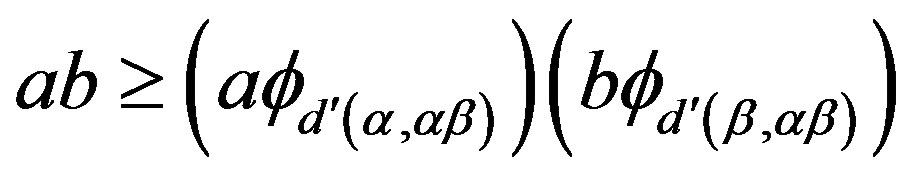 . On the other hand, because every
. On the other hand, because every 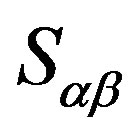 is a completely
is a completely 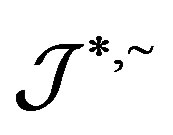 -simple semigroup,
-simple semigroup,
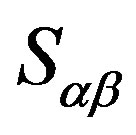 is a primitive semigroup. Hence, we obtain that
is a primitive semigroup. Hence, we obtain that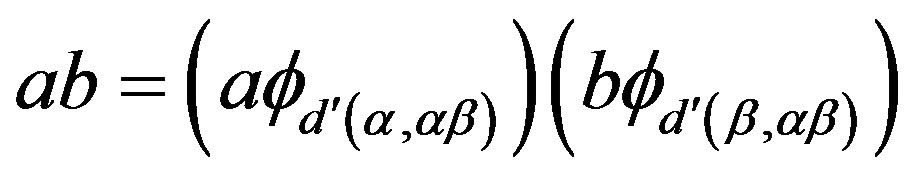 .
.
Finally, we can easily see that for any 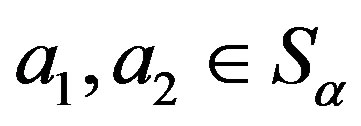 and
and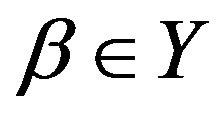 , if
, if  and
and  are all subsets of the same
are all subsets of the same 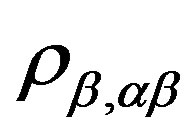 -class
-class , then
, then 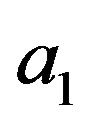 and
and 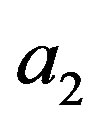 determine the same mapping
determine the same mapping 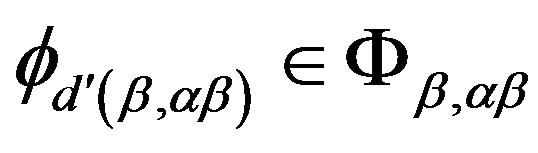 and hence for any
and hence for any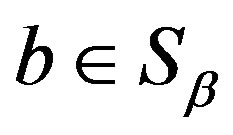 , we have
, we have 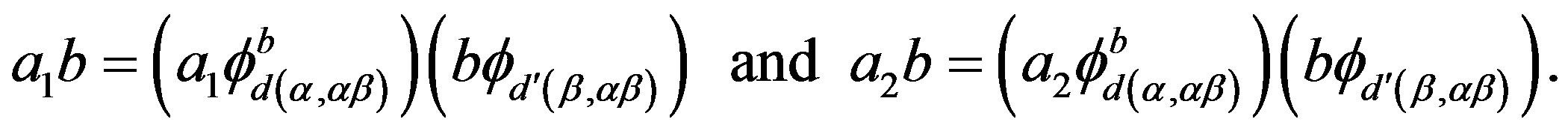
Theorem 16 A  -ample semigroup
-ample semigroup 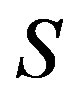 is a regular
is a regular 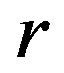 -ample semigroup if and only if it is a
-ample semigroup if and only if it is a 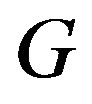 -strong semilattice of completely
-strong semilattice of completely  -simple semigroups.
-simple semigroups.
Proof. We have already proved the necessity from Lemma 14 and Lemma 15. We now prove the sufficiency part of the theorem. We first show that the Green’s  -relation
-relation 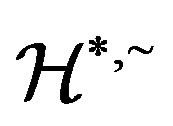 is a congruence on
is a congruence on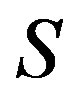 . In fact, if
. In fact, if ,
, 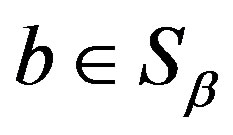 then by the definition of
then by the definition of 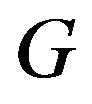 -strong semilattice and that each
-strong semilattice and that each 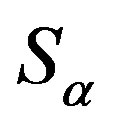 is a completely
is a completely 
simple semigroup, we see that there exist 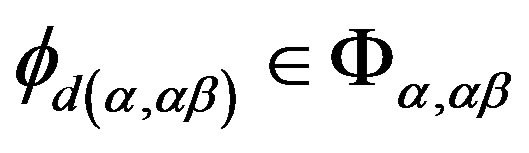 and
and 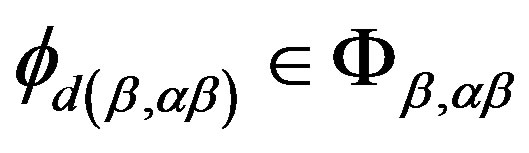 satisfying the following equalities
satisfying the following equalities
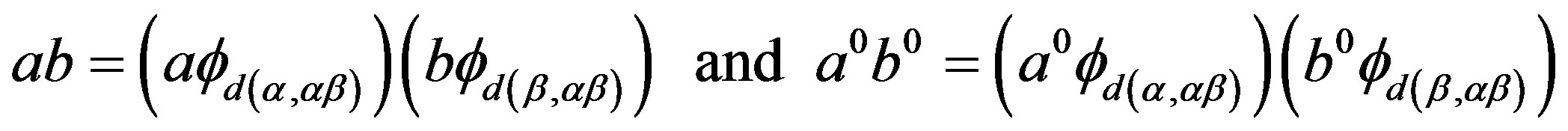
since  is a band congruence on
is a band congruence on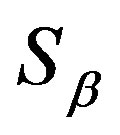 . Hence, we deduce that
. Hence, we deduce that

Now by Lemma 1, 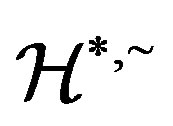 is a congruence on
is a congruence on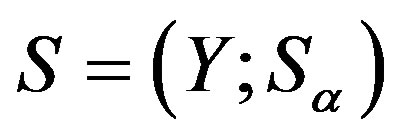 .
.
To see that  is a regular band, by a result of [18], we only need to show that the Green’s relations
is a regular band, by a result of [18], we only need to show that the Green’s relations 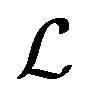 and
and 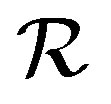 are both congruences on
are both congruences on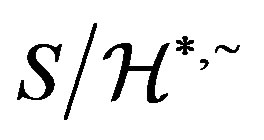 . We only show that
. We only show that  is a congruence in
is a congruence in 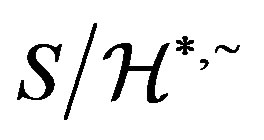 as
as 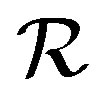 is a congruence in
is a congruence in 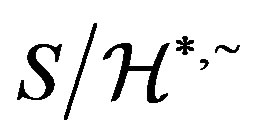 which can be proved in a similar fashion. Since
which can be proved in a similar fashion. Since  is a
is a  -ample semigroup, we can let
-ample semigroup, we can let  and
and , where
, where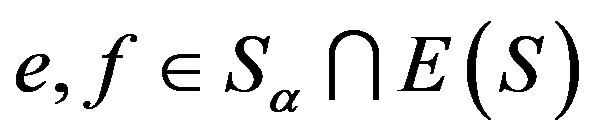 ,
, 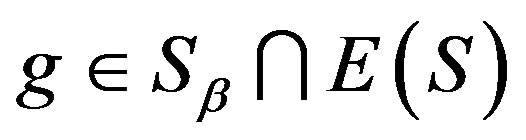 with
with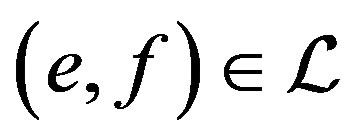 . Thenwe have
. Thenwe have 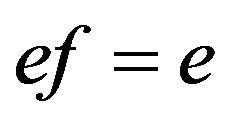 and
and . By the definition of
. By the definition of  -strong semilattice, we can find homomorphisms
-strong semilattice, we can find homomorphisms 
and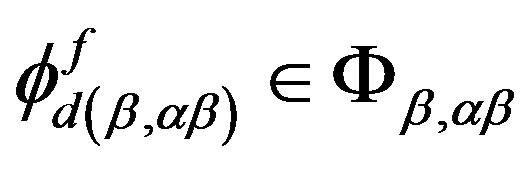 ,
, 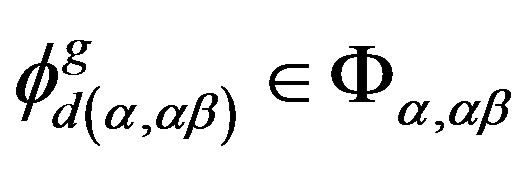 such that
such that
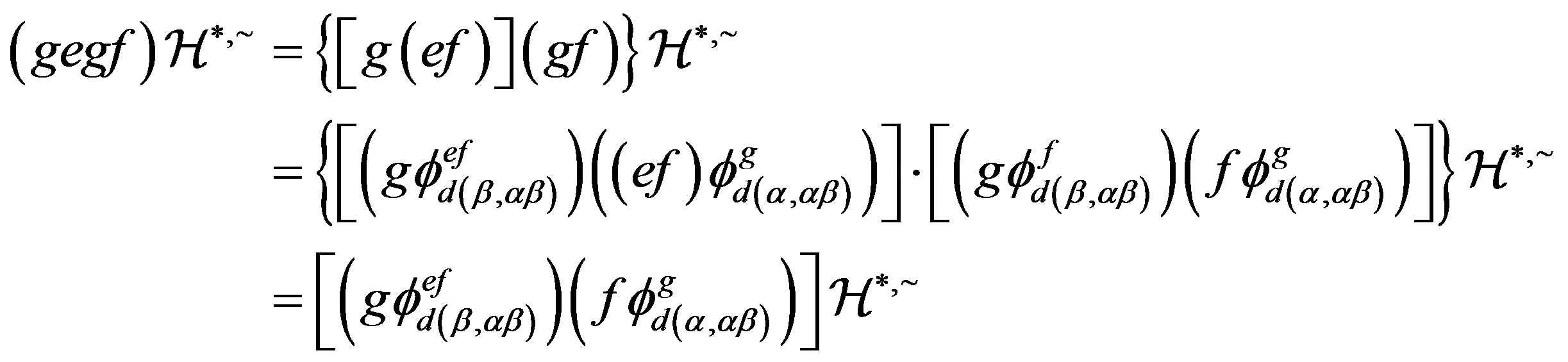
and

Thereby,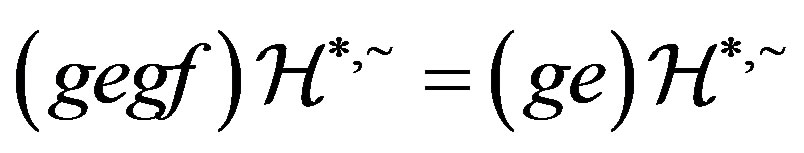 . Analogously, we can also prove that
. Analogously, we can also prove that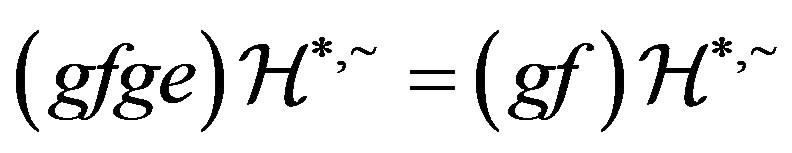 . This proves that
. This proves that 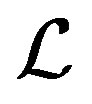 is left compatible on
is left compatible on . Since
. Since 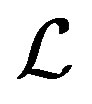 is always right compatible, we see that
is always right compatible, we see that 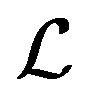 is a congruence on
is a congruence on , as required. Dually,
, as required. Dually, 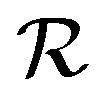 is also a congruence on
is also a congruence on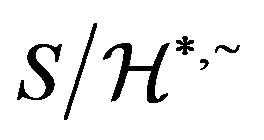 . Thus by [18] (see II. 3.6 Proposition),
. Thus by [18] (see II. 3.6 Proposition), 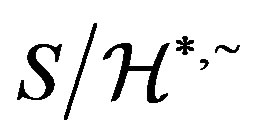 is a regular band and hence
is a regular band and hence 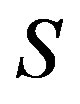 is a regular cryptic
is a regular cryptic  -ample semigroup. Our proof is completed.
-ample semigroup. Our proof is completed.
REFERENCES
[1] A. H. Clifford and G. B. Preston, “The Algebraic Theory of Semigroups,” American Mathematical Society, New York, 1967, pp. 98-120.
[2] A. H. Clifford, “Semigroups Admitting Relative Inverses,” Annals of Mathematics, Vol. 42, 1941, pp. 1037-1049. http://dx.doi.org/10.2307/1968781
[3] Y. Q. Guo, K. P. Shum and C. M. Gong, “On  -Green’s Relations and Ortho-Lc-Monoids,” Communications in Algebra, Vol. 39, No. 1, 2011, pp. 5-31. http://dx.doi.org/10.1080/00927870903428247
-Green’s Relations and Ortho-Lc-Monoids,” Communications in Algebra, Vol. 39, No. 1, 2011, pp. 5-31. http://dx.doi.org/10.1080/00927870903428247
[4] J. M. Howie, “Fundamental of Semigroup Theory,” Clarendon Press, Oxford, 1995, pp. 56-73.
[5] M. Petrich and N. R. Reilly, “Completely Regular Semigroups,” John Wiley & Sons, New York, 1999, pp. 162-197.
[6] M. Petrich, “The Structure of Completely Regular Semigroups,” Transactions of the American Mathematical Society, Vol. 189, 1974, pp. 211-236. http://dx.doi.org/10.1090/S0002-9947-1974-0330331-4
[7] M. Petrich, “Lectures in Semigroups,” Wiley & Sons Inc., London, 1976, pp. 124-156.
[8] F. Pastijn, “A Representation of a Semigroup by a Semigroup of Matrices over a Group with Zero,” Semigroup Forum, Vol. 10, 1975, pp. 238-249.
[9] J. B. Fountain, “Abundant Semigroups,” Proceedings London Mathematical Society, Vol. 43, No. 3, 1982, pp. 103-129. http://dx.doi.org/10.1112/plms/s3-44.1.103
[10] M. V. Lawson, “Rees Matrix Semigroups,” Proceedings of the Edinburgh Mathematical Society, Vol. 33, 1990, pp. 23-39.
[11] X. M. Ren, K. P. Shum and Y. Q. Guo, “A Generalized Clifford Theorem of Semigroups,” Science China Mathematics, Vol. 53, No. 4, 2010, pp. 1097-1101. http://dx.doi.org/10.1007/s11425-009-0150-3
[12] X. Z. Kong and K. P. Shum, “On the Structure of Regular Crypto Semigroups,” Communications in Algebra, Vol. 29, No. 6, 2001, pp. 2461-2479. http://dx.doi.org/10.1007/s00233-006-0614-5
[13] X. Z. Kong and Z. L. Yuan, “Normal Crypto  -Abundant Semigroups,” Advances in Mathematics (in Chinese), Vol. 36, No. 5, 2007, pp. 539-545.
-Abundant Semigroups,” Advances in Mathematics (in Chinese), Vol. 36, No. 5, 2007, pp. 539-545.
[14] X. Z. Kong and Z. L. Yuan, “KG-Strong Semilattice Structure of Regular Orthocryptosemigroups,” Semigroup Fourm, Vol. 73, No. 1, 2006, pp. 95-108. http://dx.doi.org/10.1007/s00233-006-0614-5
[15] X. Z. Kong and K. P. Shum, “A Structure Theorem of Normal 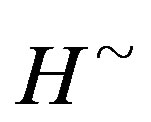 -Cryptographs,” Publicationes Mathematicae, Vol. 72, No. 3-4, 2008, pp. 335-346.
-Cryptographs,” Publicationes Mathematicae, Vol. 72, No. 3-4, 2008, pp. 335-346.
[16] X. Z. Kong, Z. L. Yuan and K. P. Shum, “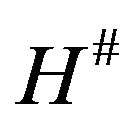 -Abundant Semigroups and
-Abundant Semigroups and  -Cryptographs,” Algebra Collections, Vol. 15, No. 4, 2008, pp. 653-666.
-Cryptographs,” Algebra Collections, Vol. 15, No. 4, 2008, pp. 653-666.
[17] K. P. Shum, L. Du and Y. Q. Guo, “Green’s Relations and Their Generalizations on Semigroups,” Discussiones Mathematicae —General Algebra and Applications, Vol. 30, No. 1, 2010, pp. 71-89. http://dx.doi.org/10.7151/dmgaa.1163
[18] X. D. Tang, “On a Theorem of C-Wrpp Semigroups,” Communications in Algebra, Vol. 25, No. 5, 1997, pp. 1499-1504. http://dx.doi.org/10.1080/00927879708825931
[19] G. M. S. Gomes and V. Gould, “Proper Weakly Left Ample Semigroups,” International Journal of Algebra and Computation, Vol. 9, No. 6, 1999, pp. 721-739. http://dx.doi.org/10.1142/S0218196799000412
NOTES

*The research is supported by the national natural science foundation of China (11371174, 11301227) and natural science foundation of Jiansu (BK20130119).

