Advances in Pure Mathematics
Vol.3 No.9A(2013), Article ID:41499,6 pages DOI:10.4236/apm.2013.39A1006
Time-Optimal Control Problem for n × n Co-Operative Parabolic Systems with Control in Initial Conditions
Department of Mathematics, Faculty of Science, Jazan University, Jazan, KSA
Email: mashehata_math@yahoo.com
Copyright © 2013 Mohammed A. Shehata. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2013 are reserved for SCIRP and the owner of the intellectual property Mohammed A. Shehata. All Copyright © 2013 are guarded by law and by SCIRP as a guardian.
Received November 5, 2013; revised December 15, 2013; accepted December 21, 2013
Keywords: Time-optimal control problems; bang-bang controls; parabolic system; co-operative systems
ABSTRACT
In this paper, time-optimal control problem for a liner  co-operative parabolic system involving Laplace operator is considered. This problem is, steering an initial state
co-operative parabolic system involving Laplace operator is considered. This problem is, steering an initial state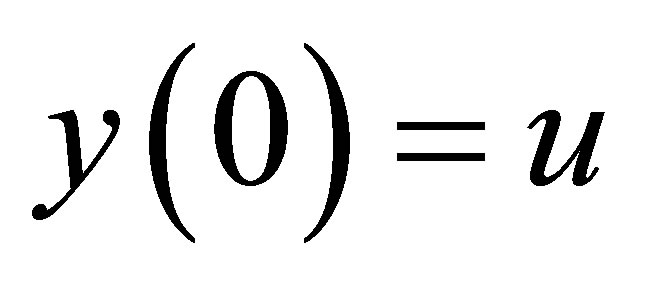 , with control
, with control 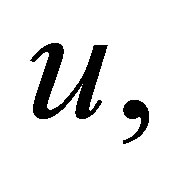 so that an observation
so that an observation 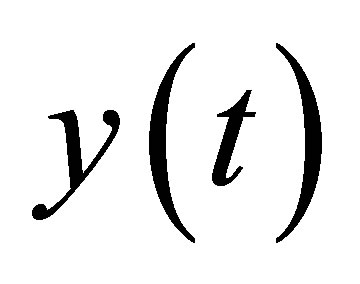 hits a given target set in minimum time. First, the existence and uniqueness of solutions of such system under conditions on the coefficients are proved. Afterwards necessary and sufficient conditions of optimality are obtained. Finally a scaler case is given.
hits a given target set in minimum time. First, the existence and uniqueness of solutions of such system under conditions on the coefficients are proved. Afterwards necessary and sufficient conditions of optimality are obtained. Finally a scaler case is given.
1. Introduction
The “time optimal” control problem is one of the most important problems in the field of control theory. The simple version is that steering the initial state 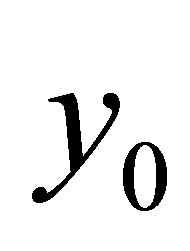 in a Hilbert space
in a Hilbert space  to hit a target set
to hit a target set  in minimum time, with control subject to constraints
in minimum time, with control subject to constraints .
.
In this paper, we will focus our attention on some special aspects of minimum time problems for co-operative parabolic system involving Laplace operator with control acts in the initial conditions. In order to explain the results we have in mind, it is convenient to consider the abstract form.
Let  and
and  be two real Hilbert spaces such that
be two real Hilbert spaces such that 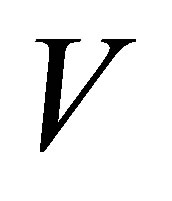 is a dense subspace of
is a dense subspace of  Identifying the dual of
Identifying the dual of  with
with 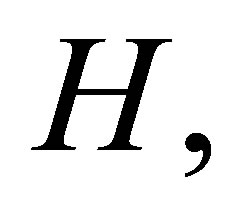 we may consider
we may consider  where the embedding is dense in the following space. Let
where the embedding is dense in the following space. Let 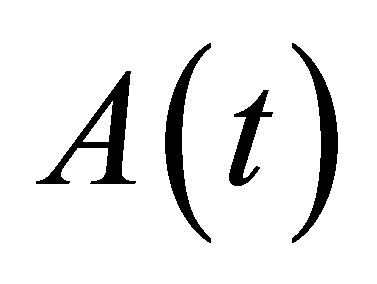
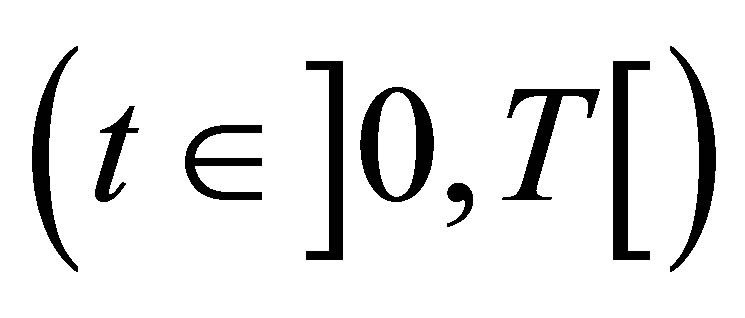 be a family of continuous operators associated with a bilinear forms
be a family of continuous operators associated with a bilinear forms 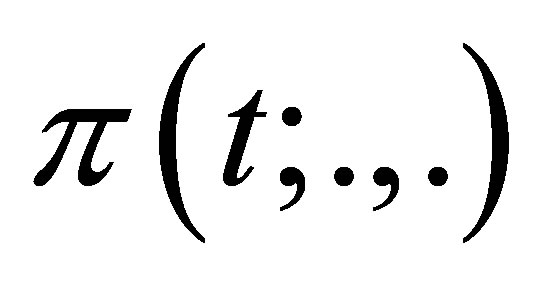 defined on
defined on 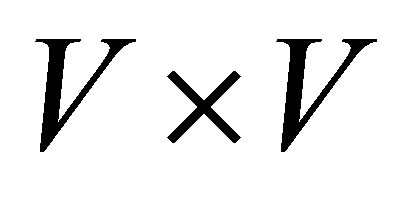 which are satisfied with Gårding’s inequality
which are satisfied with Gårding’s inequality
 (1)
(1)
for  and
and 
Then, from [1] and [2], for  and
and 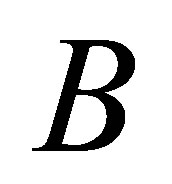 being a bounded linear operator on
being a bounded linear operator on  the following abstract systems:
the following abstract systems:
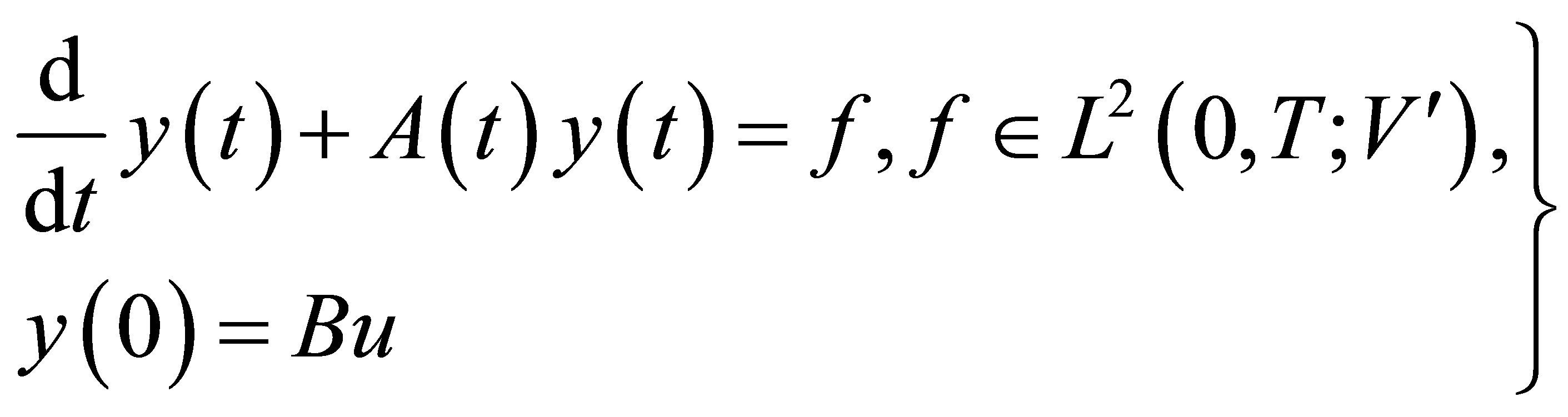 (2)
(2)
have a unique weak solution 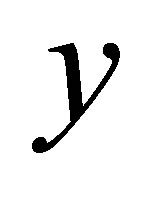 such that
such that 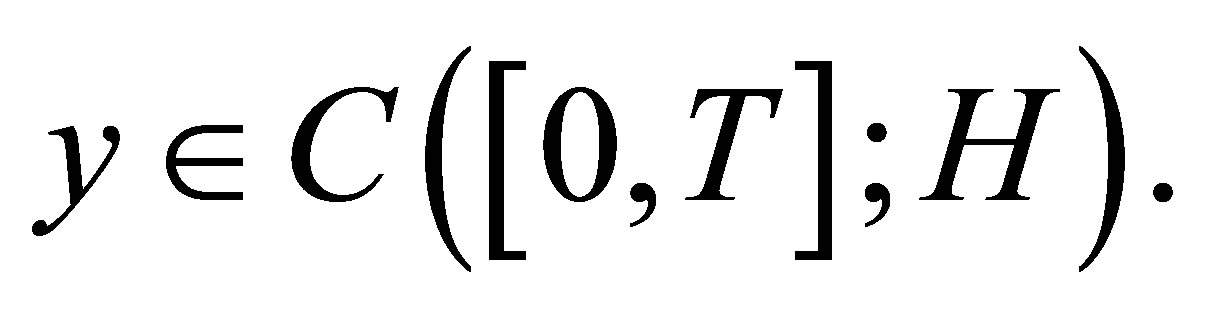 We shall denote by
We shall denote by 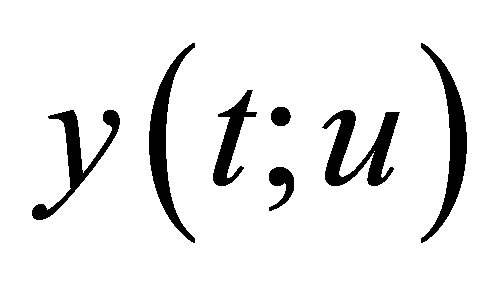 the unique solution of the Equation (2) corresponding to the control u. The time optimal control problem that we shall concern reads:
the unique solution of the Equation (2) corresponding to the control u. The time optimal control problem that we shall concern reads:
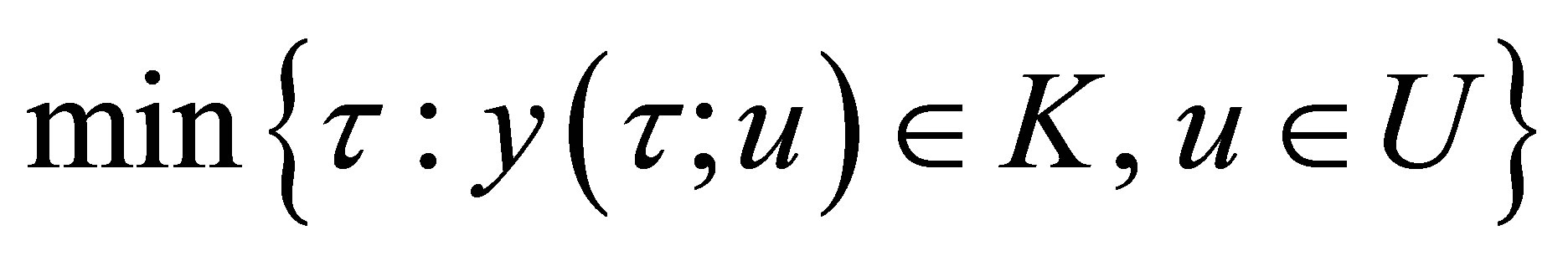 (3)
(3)
where  is a given subset of
is a given subset of 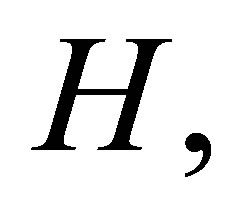 which is called the target set of the Problem (3). A control
which is called the target set of the Problem (3). A control 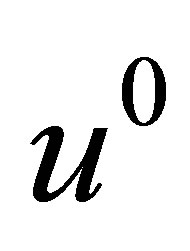 is called a time optimal control if
is called a time optimal control if 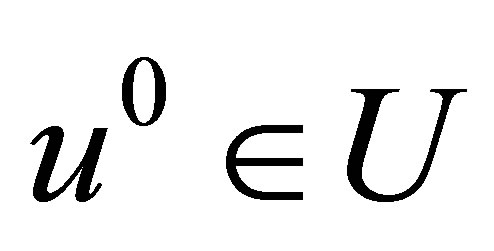 and if there is a number
and if there is a number 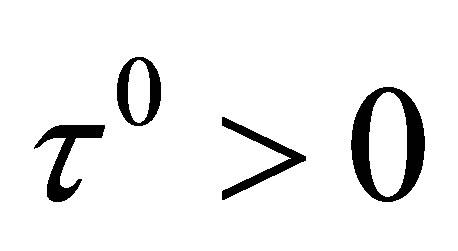 such that
such that 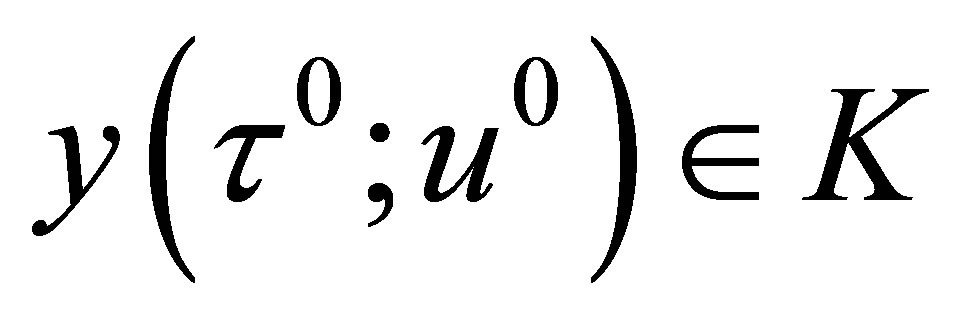 and
and
 (4)
(4)
We call the number 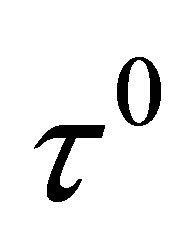 as the optimal time for the time optimal control Problem (3).
as the optimal time for the time optimal control Problem (3).
Three questions (problems) arise naturally in connection with this problem:
1) Is there a control 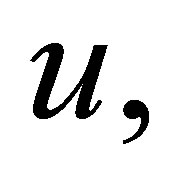 and
and 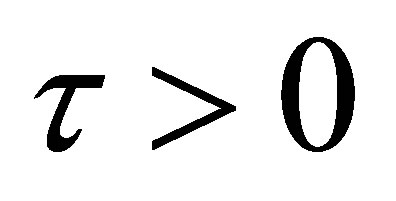 such that
such that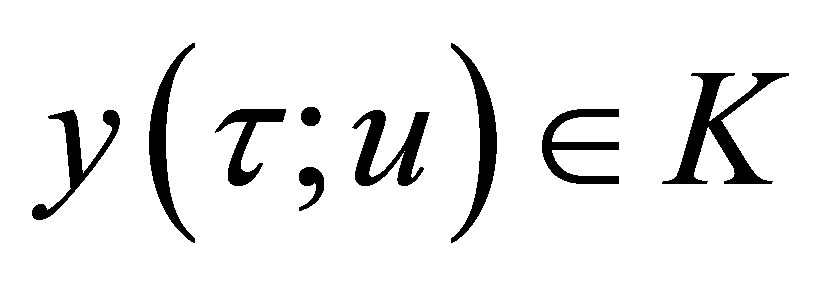 ? (this is an approximate controllability problem).
? (this is an approximate controllability problem).
2) Assume that the answer to 1) is in the affirmative and
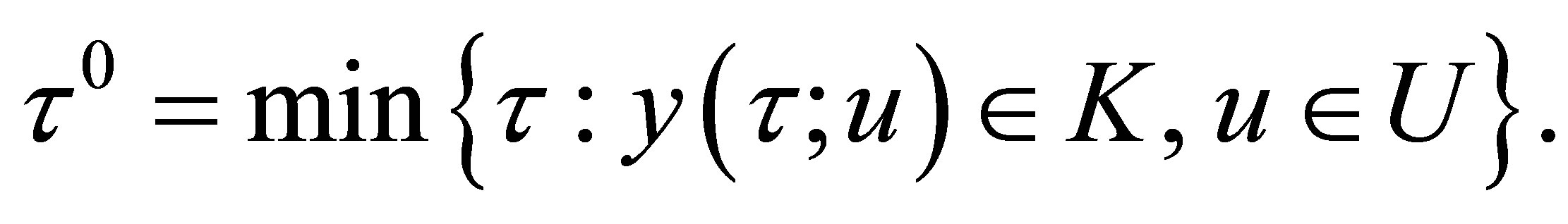
Is there a control 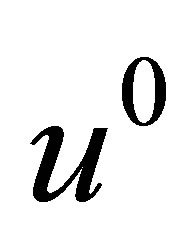 which steers
which steers  to hit a target set
to hit a target set 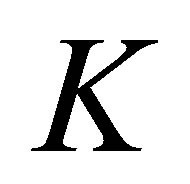 in minimum time?
in minimum time?
3) If 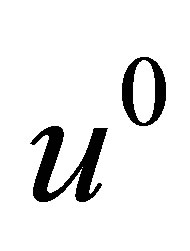 exists, is it unique? What additional properties does it have?
exists, is it unique? What additional properties does it have?
Let 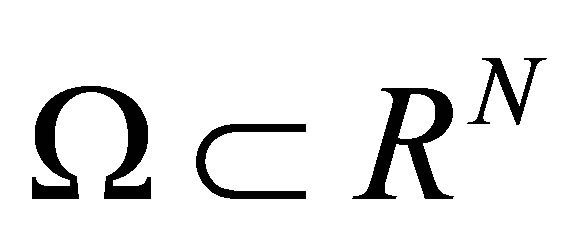 be a bounded open domain with smooth boundary
be a bounded open domain with smooth boundary 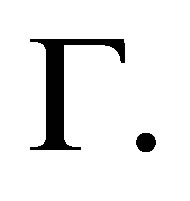 and set
and set 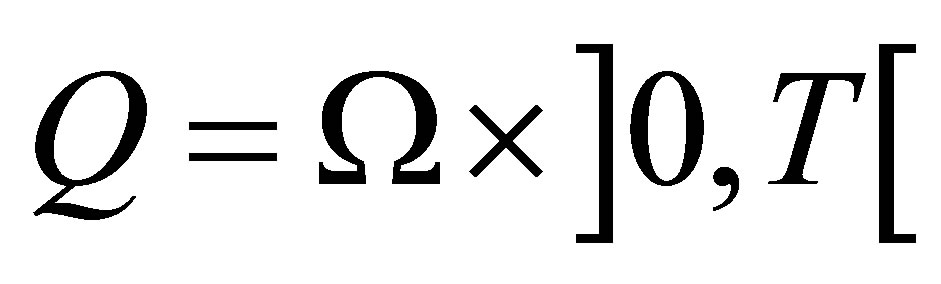
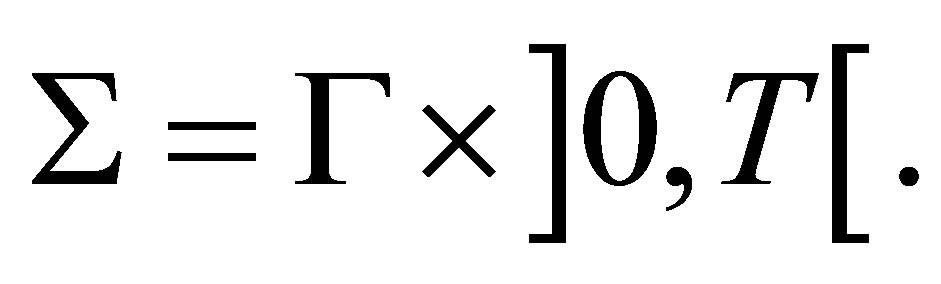 In the works [1] and [3], the existence of time optimal controls of the following controlled linear parabolic equations with distributed control
In the works [1] and [3], the existence of time optimal controls of the following controlled linear parabolic equations with distributed control  was obtained:
was obtained:
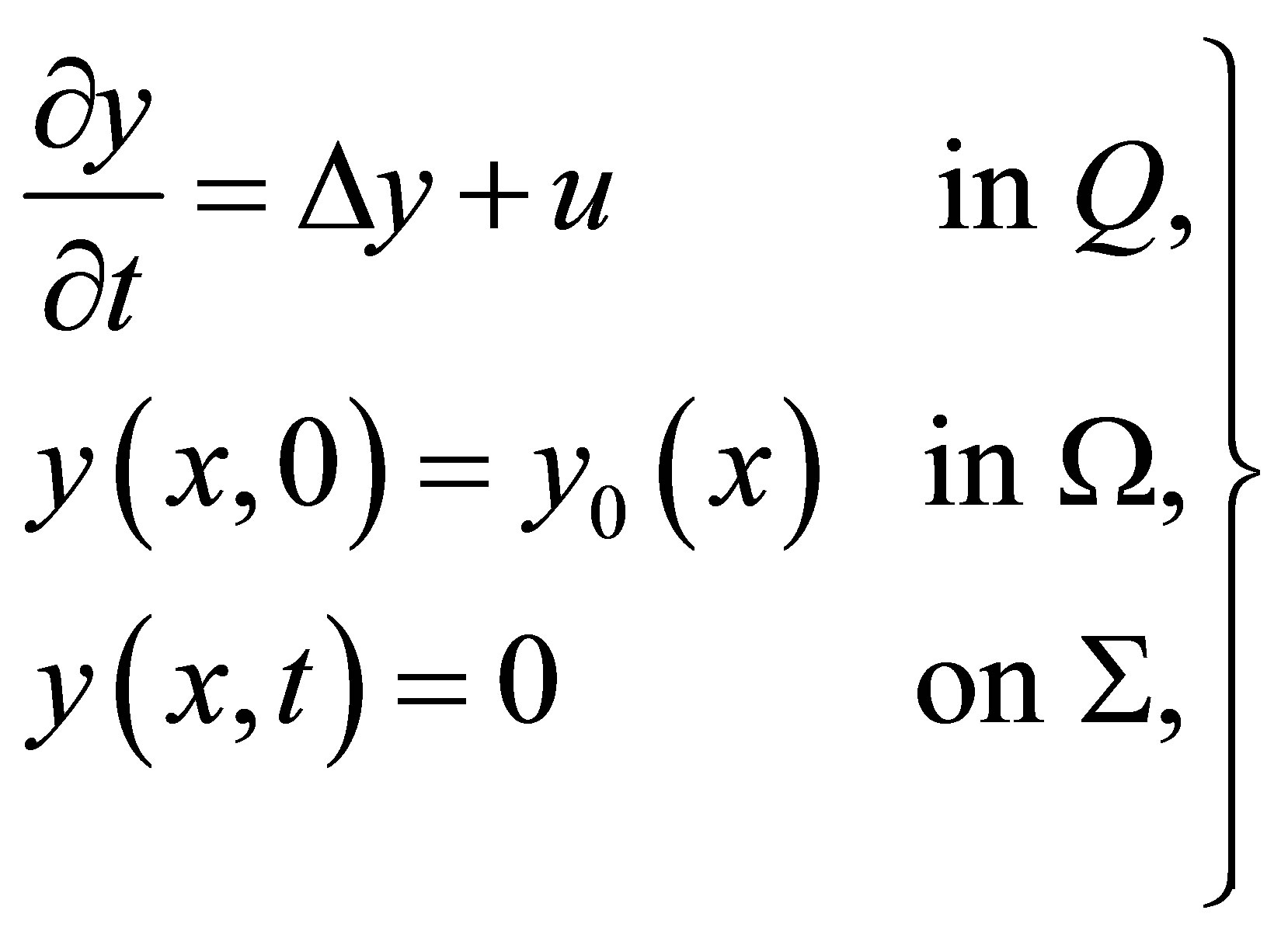 (5)
(5)
where 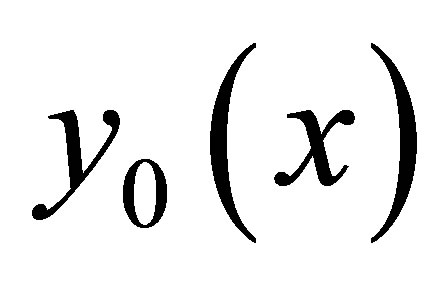 is a given function in
is a given function in 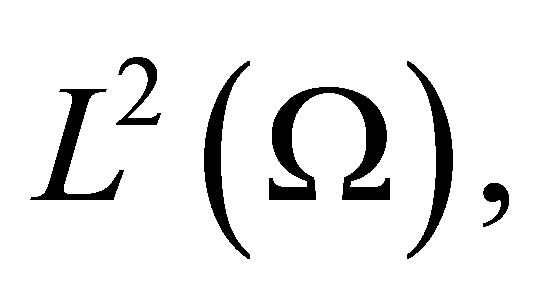
 and
and 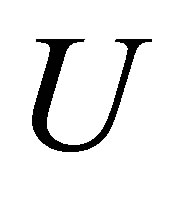 is a closed bounded set in
is a closed bounded set in 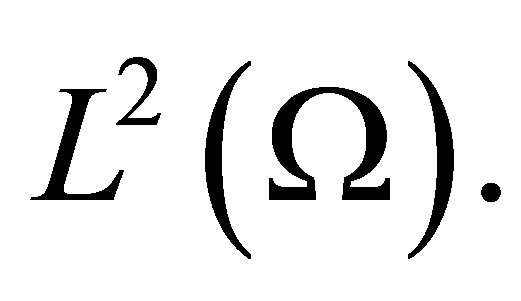 The results in [3] partly overlap with results in [1] and they were shown that if the system (5) is controllable and if
The results in [3] partly overlap with results in [1] and they were shown that if the system (5) is controllable and if 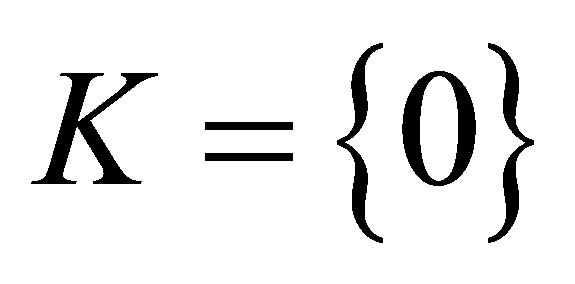 then the corresponding time optimal control problem has at least one solution and it is bangbang.
then the corresponding time optimal control problem has at least one solution and it is bangbang.
In the work [4], the authors gave a sufficient and necessary condition for the existence of time optimal control for the problem with the target set  and certain controlled systems. These results will be stated as follows. Consider the following controlled system
and certain controlled systems. These results will be stated as follows. Consider the following controlled system
 (6)
(6)
where  is a real number. Let
is a real number. Let 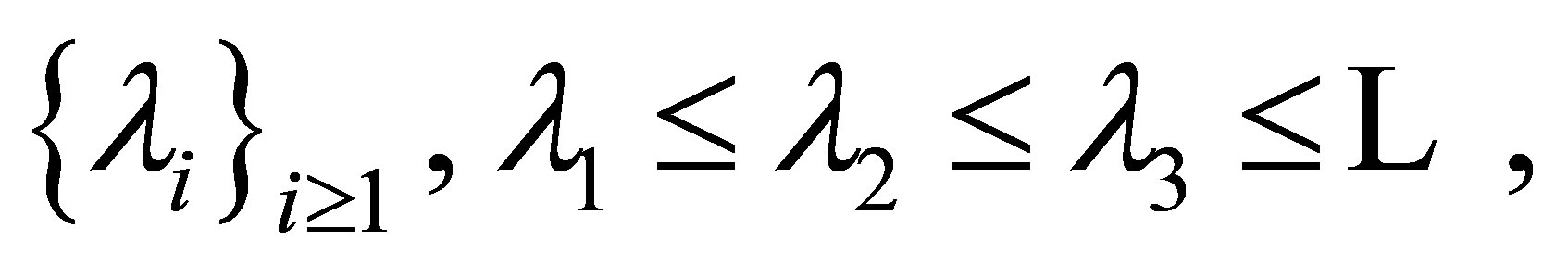 be the eigenvalues of
be the eigenvalues of 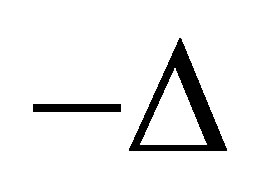 with the Dirichlet boundary condition and
with the Dirichlet boundary condition and  be the corresponding eigenfunctions, which forms an orthogonal basis of
be the corresponding eigenfunctions, which forms an orthogonal basis of 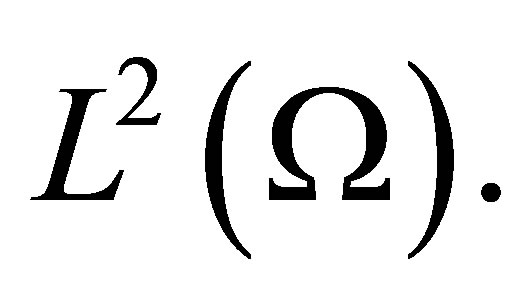 We take the target set
We take the target set  to be the origin
to be the origin  in
in 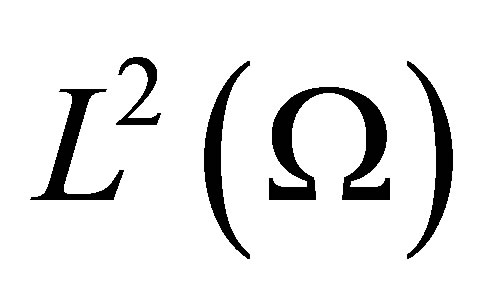 and the control set
and the control set  to be the set
to be the set
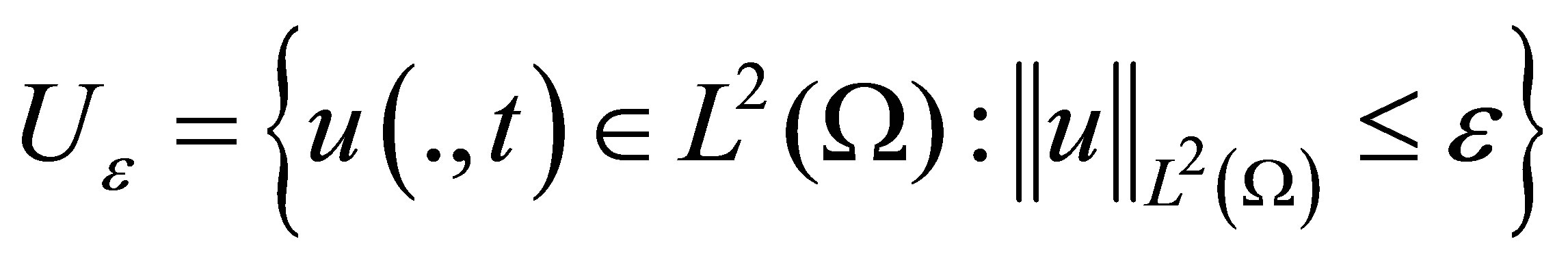
where  is a positive number, namely,
is a positive number, namely, 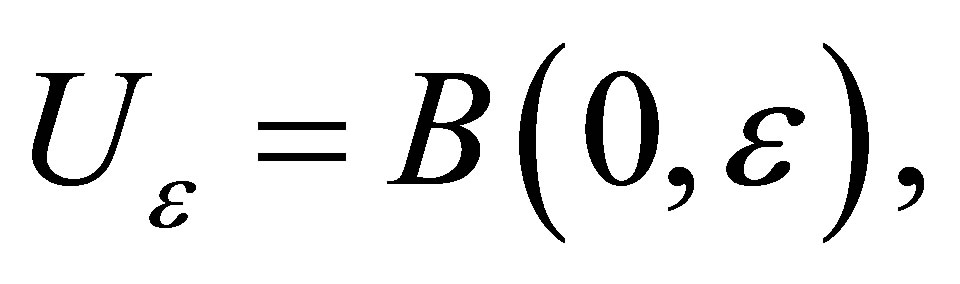 the closed ball in
the closed ball in 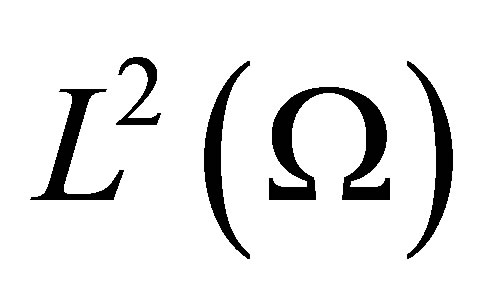 centered at 0 and of radius
centered at 0 and of radius  It was proved that if
It was proved that if  and
and 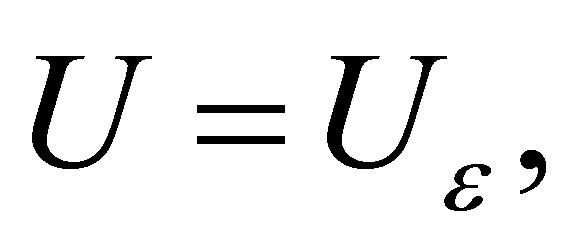 then the corresponding time optimal control problem has at least one solution if and only if
then the corresponding time optimal control problem has at least one solution if and only if 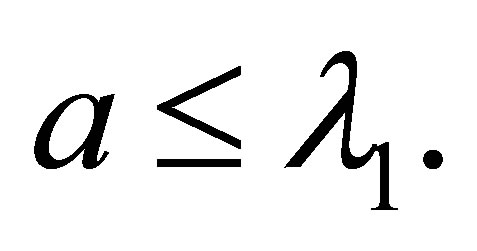
More early, in the works [5-7], the time optimal controls problem for globally controlled linear and semilinear parabolic equations was considered.
In our papers [8,9], the time optimal control problem of  co-operative hyperbolic systems with different cases of the observation and distributed or boundary controls constraints was considered.
co-operative hyperbolic systems with different cases of the observation and distributed or boundary controls constraints was considered.
In [10], optimal control of infinite order hyperbolic equation with control via initial conditions was considered.
In the present paper, the above results for the time optimal control of systems governed by parabolic equations are extended to the case of  co-operative parabolic systems as well as control via initial conditions. First, the existence and uniqueness of solutions for
co-operative parabolic systems as well as control via initial conditions. First, the existence and uniqueness of solutions for 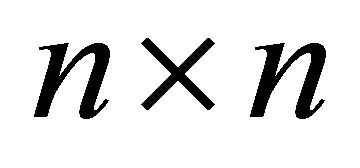 co-operative parabolic system are proved under conditions on the coefficients stated by the principal eigenvalue of the Laplace eigenvalue problem, then the time optimal control problem is formulated and the existence of a time optimal control is proved. Then the necessary and sufficient conditions which the optimal controls must satisfy are derived in terms of the adjoint. Finally, the scaler case is given.
co-operative parabolic system are proved under conditions on the coefficients stated by the principal eigenvalue of the Laplace eigenvalue problem, then the time optimal control problem is formulated and the existence of a time optimal control is proved. Then the necessary and sufficient conditions which the optimal controls must satisfy are derived in terms of the adjoint. Finally, the scaler case is given.
2. n × n Co-Operative Parabolic Systems
Let  be the usual Sobolev space of order one which consists of all
be the usual Sobolev space of order one which consists of all 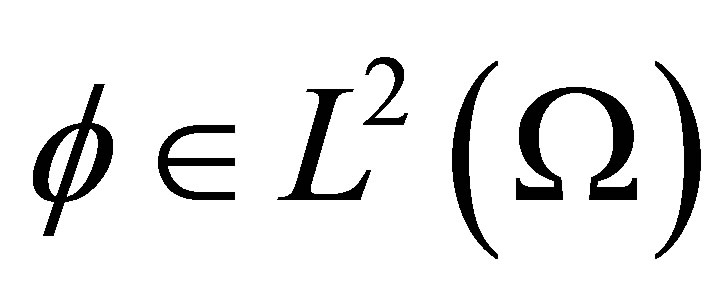 whose distributional derivatives
whose distributional derivatives 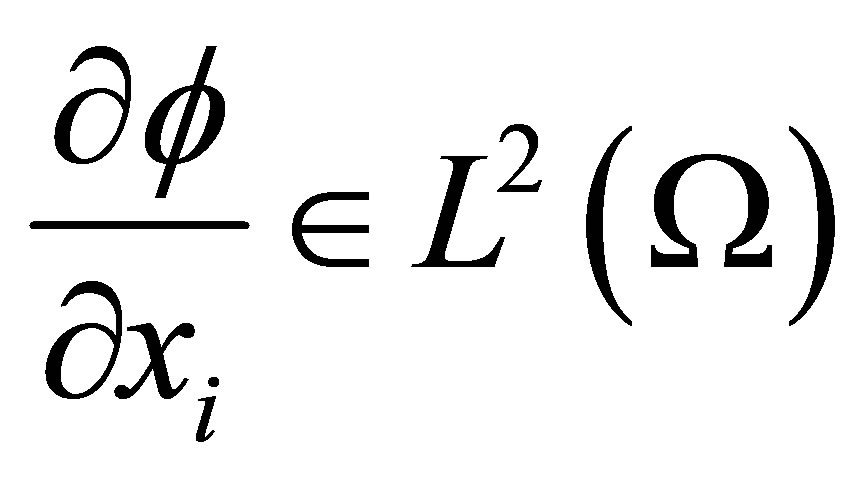 and
and  with the scalar product norm
with the scalar product norm
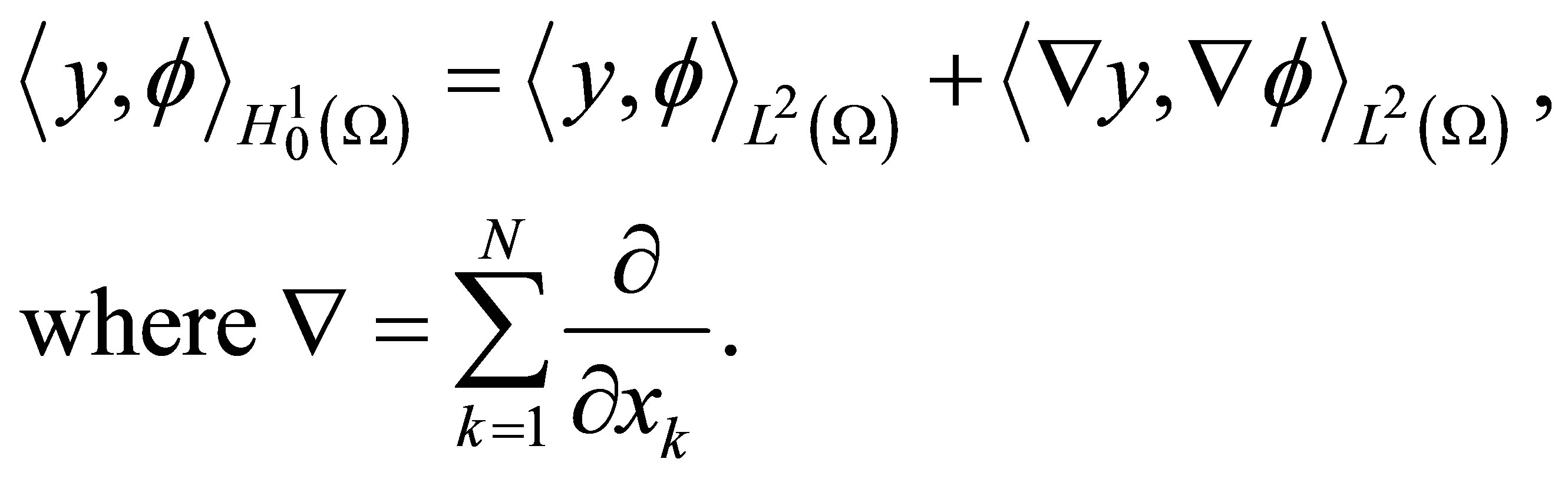
We have the following dense embedding chain [11]
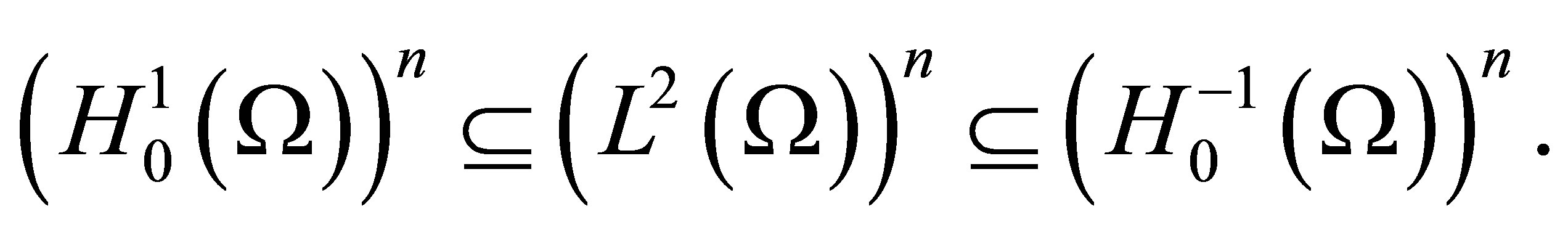
where 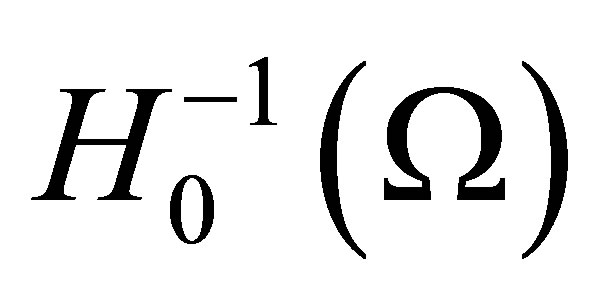 is the dual of
is the dual of 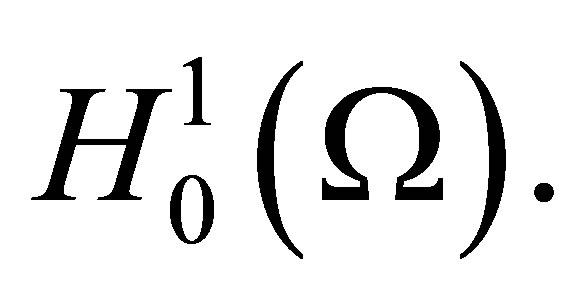
Here and everywhere below the vectors are denoted by bold letters. For 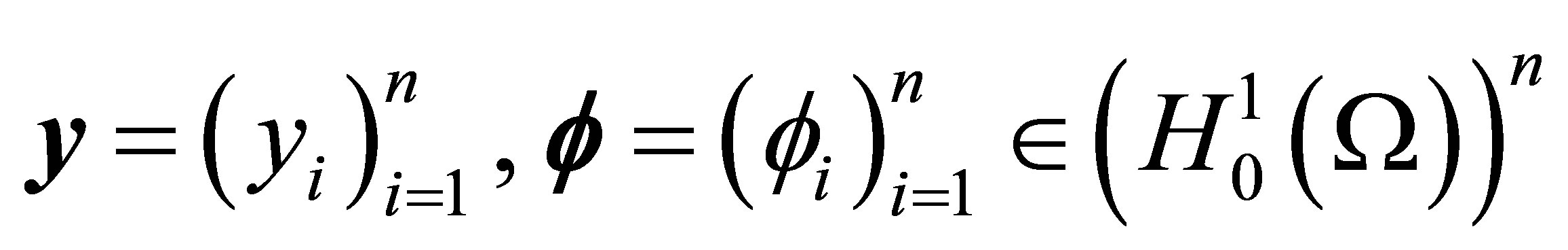 and
and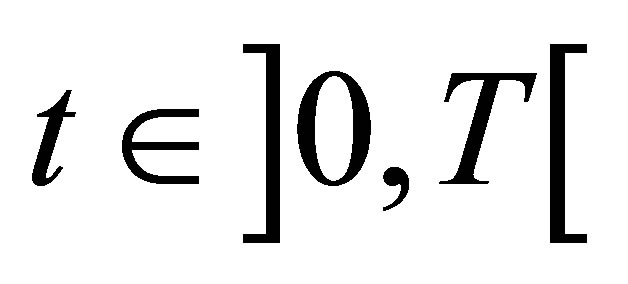 , let us define a family of continues bilinear forms
, let us define a family of continues bilinear forms
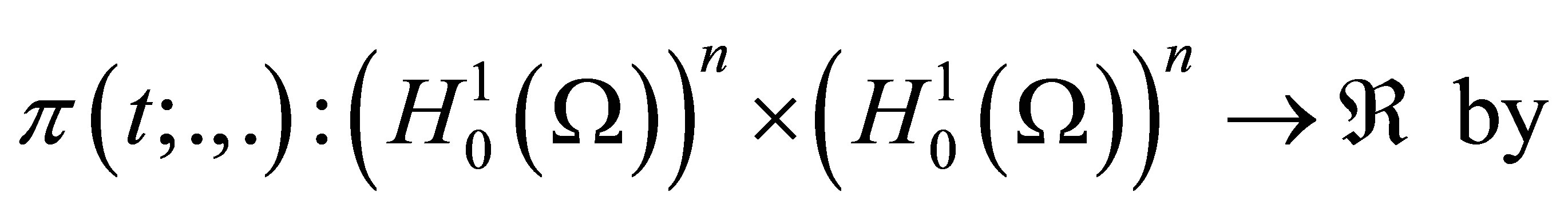
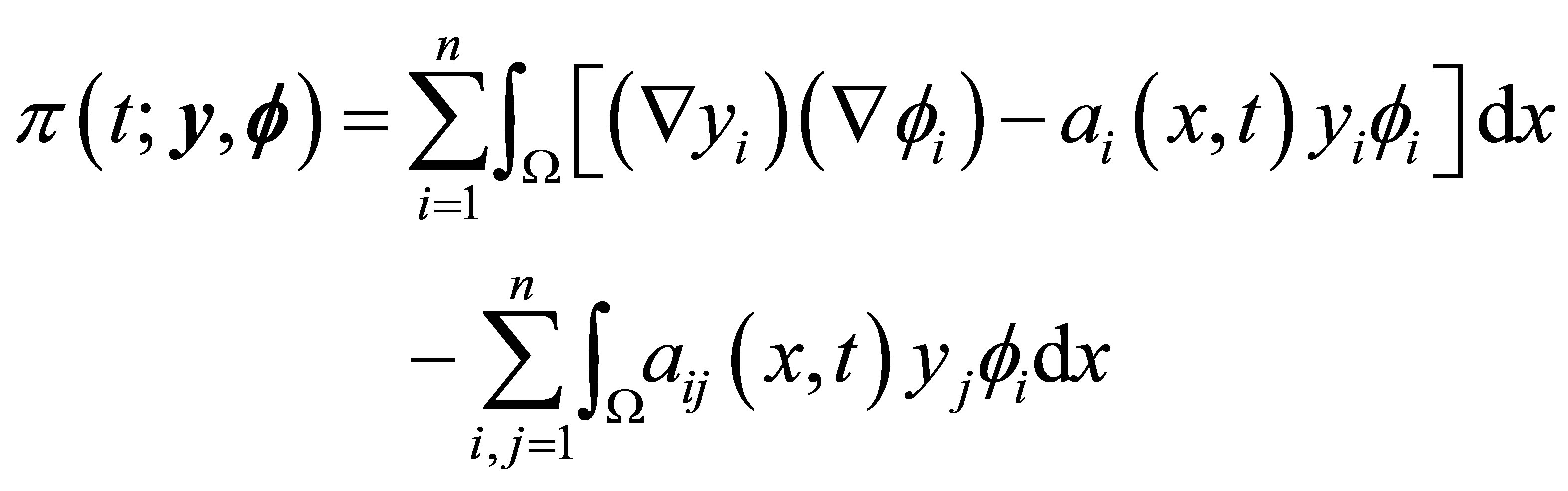 (7)
(7)
where
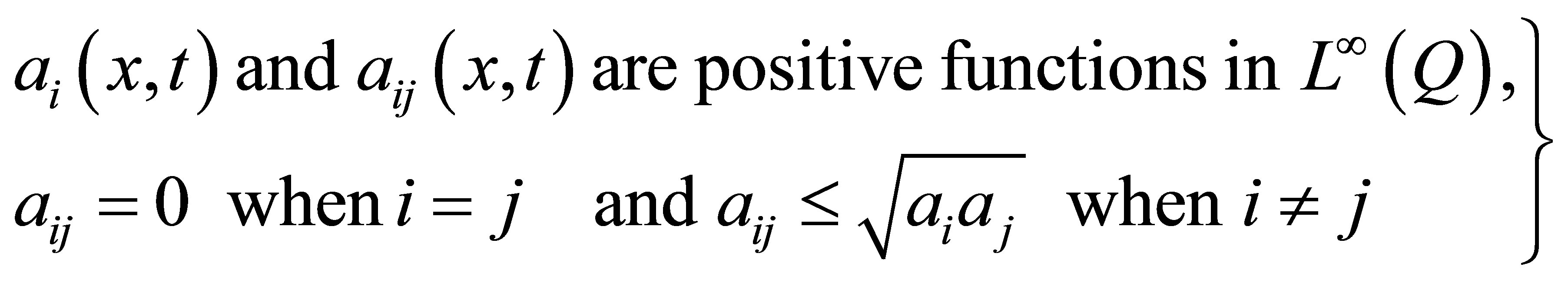 (8)
(8)
The bilinear form (7) can be but in the operator form:

where 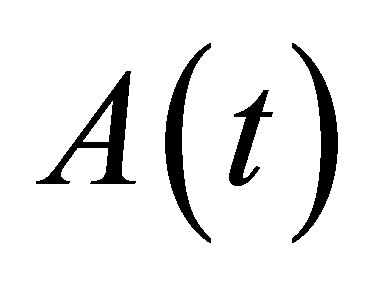 is
is  matrix operator which maps
matrix operator which maps  onto
onto  and takes the form
and takes the form
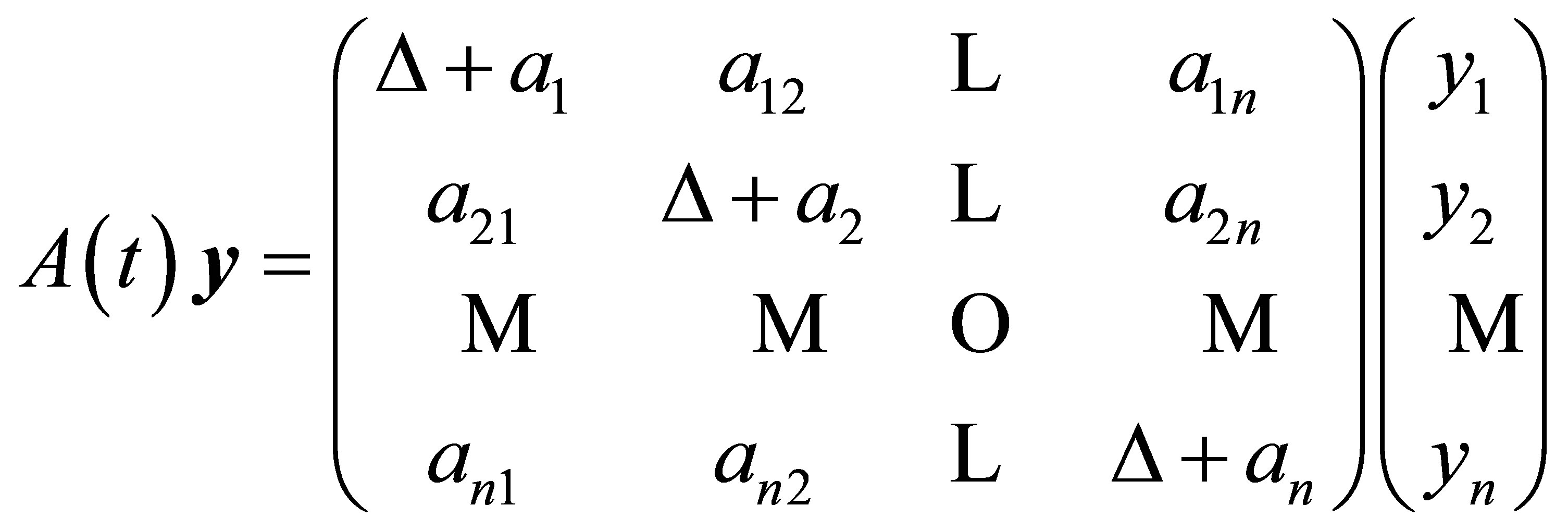 .
.
Lemma 2.1. If  is a regular bounded domain in
is a regular bounded domain in 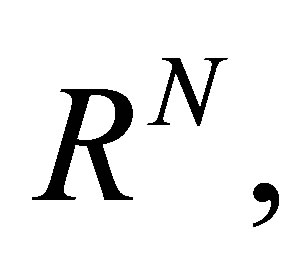 with boundary
with boundary  and if
and if 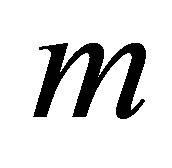 is positive on
is positive on  and smooth enough ( in particular
and smooth enough ( in particular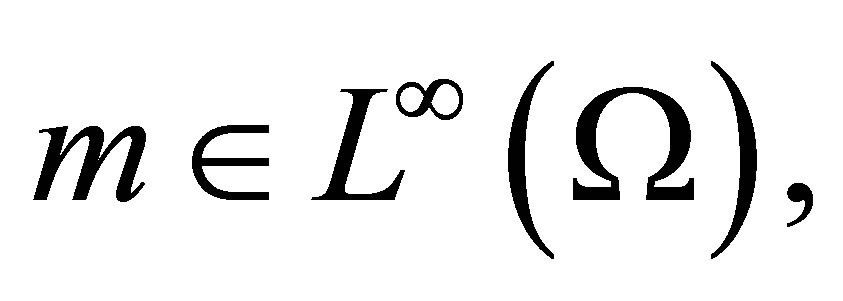 ) then the eigenvalue problem:
) then the eigenvalue problem:
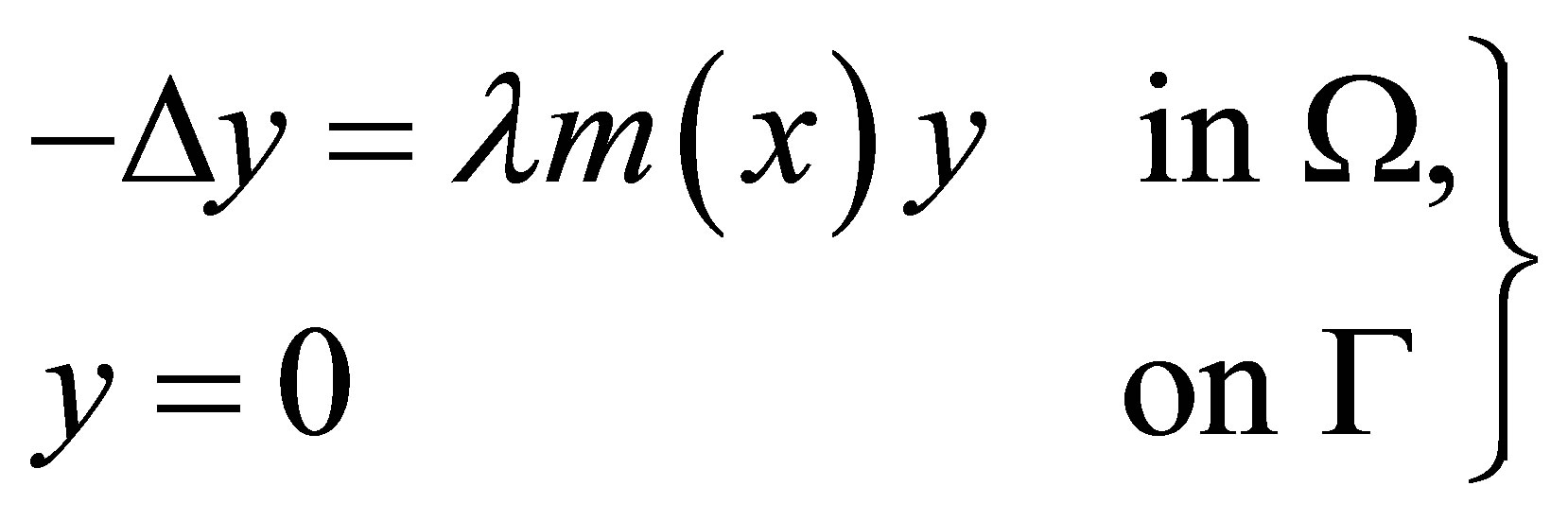
possesses an infinite sequence of positive eigenvalues:
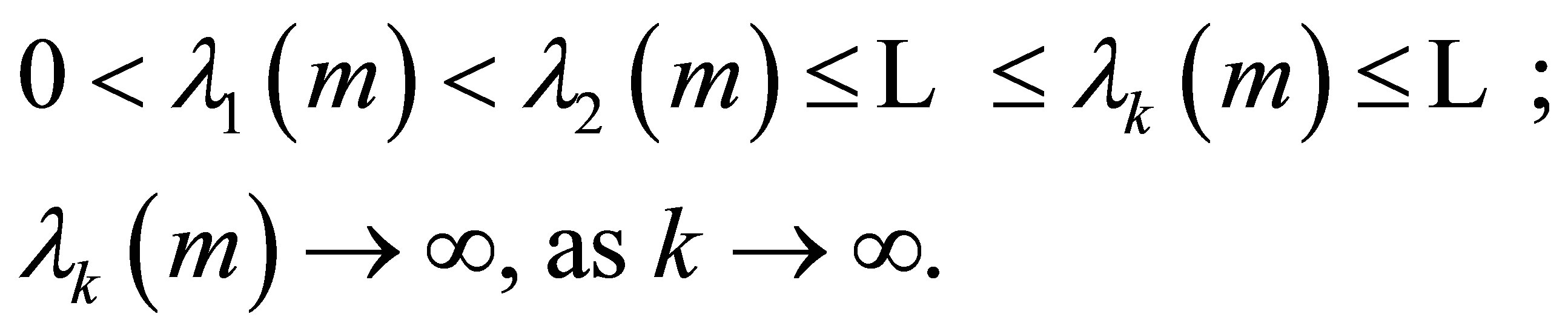
Moreover 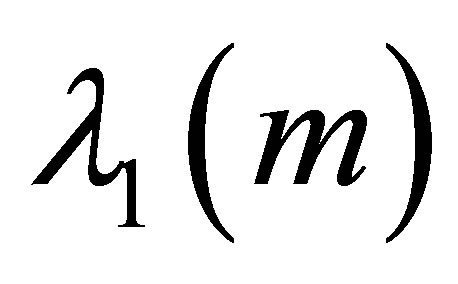 is simple, its associate eigenfunction
is simple, its associate eigenfunction 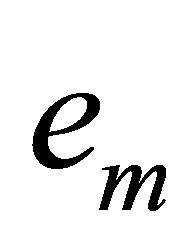 is positive, and
is positive, and 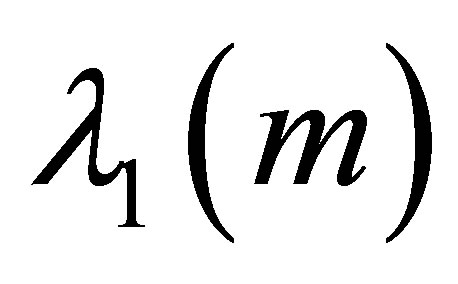 is characterized by:
is characterized by:
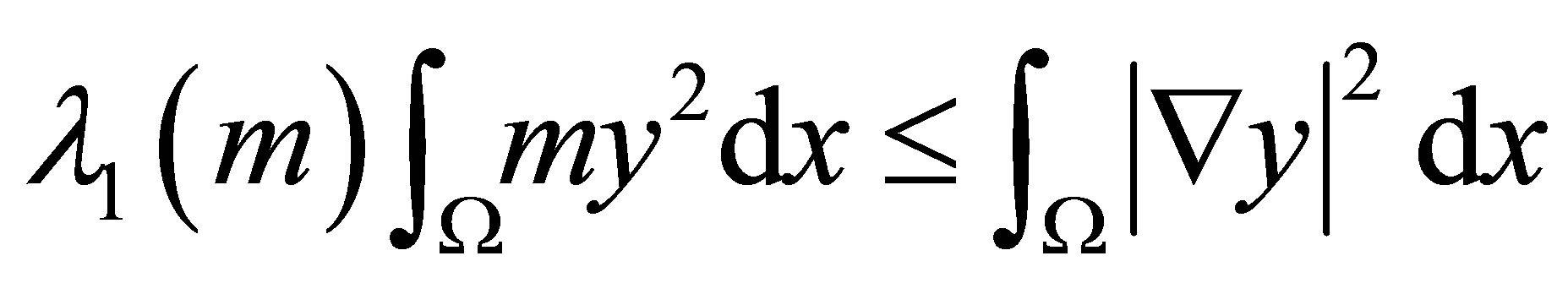 (9)
(9)
Proof. See [12]. ,.
Now, let
 (10)
(10)
Lemma 2.2. If (8) and (10) hold then, the bilinear form (7) satisfy the Gårding inequality
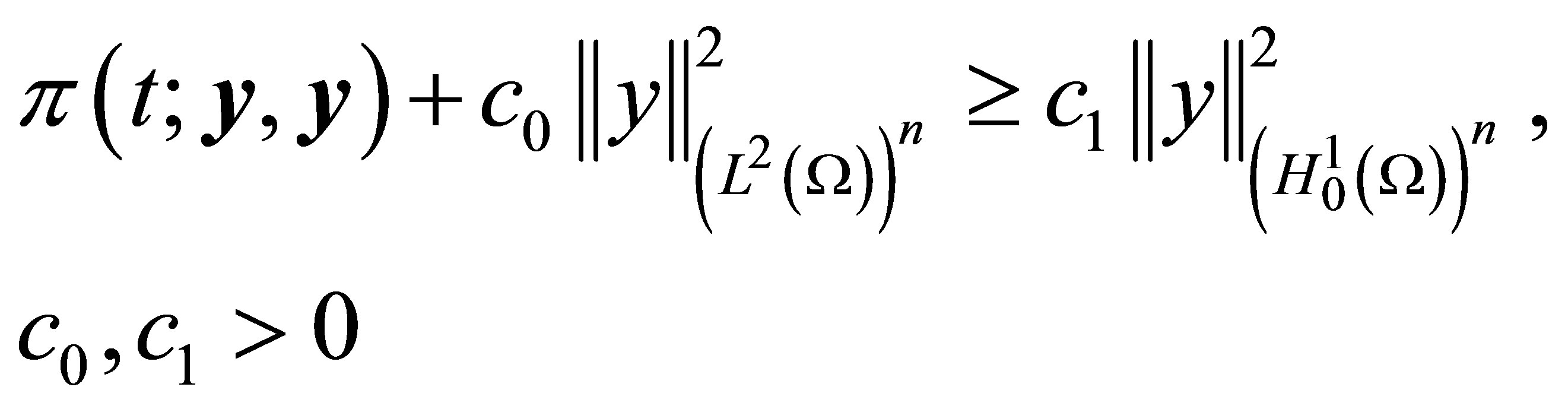
Proof. In fact

By Cauchy Schwarz inequality and (9), we obtain
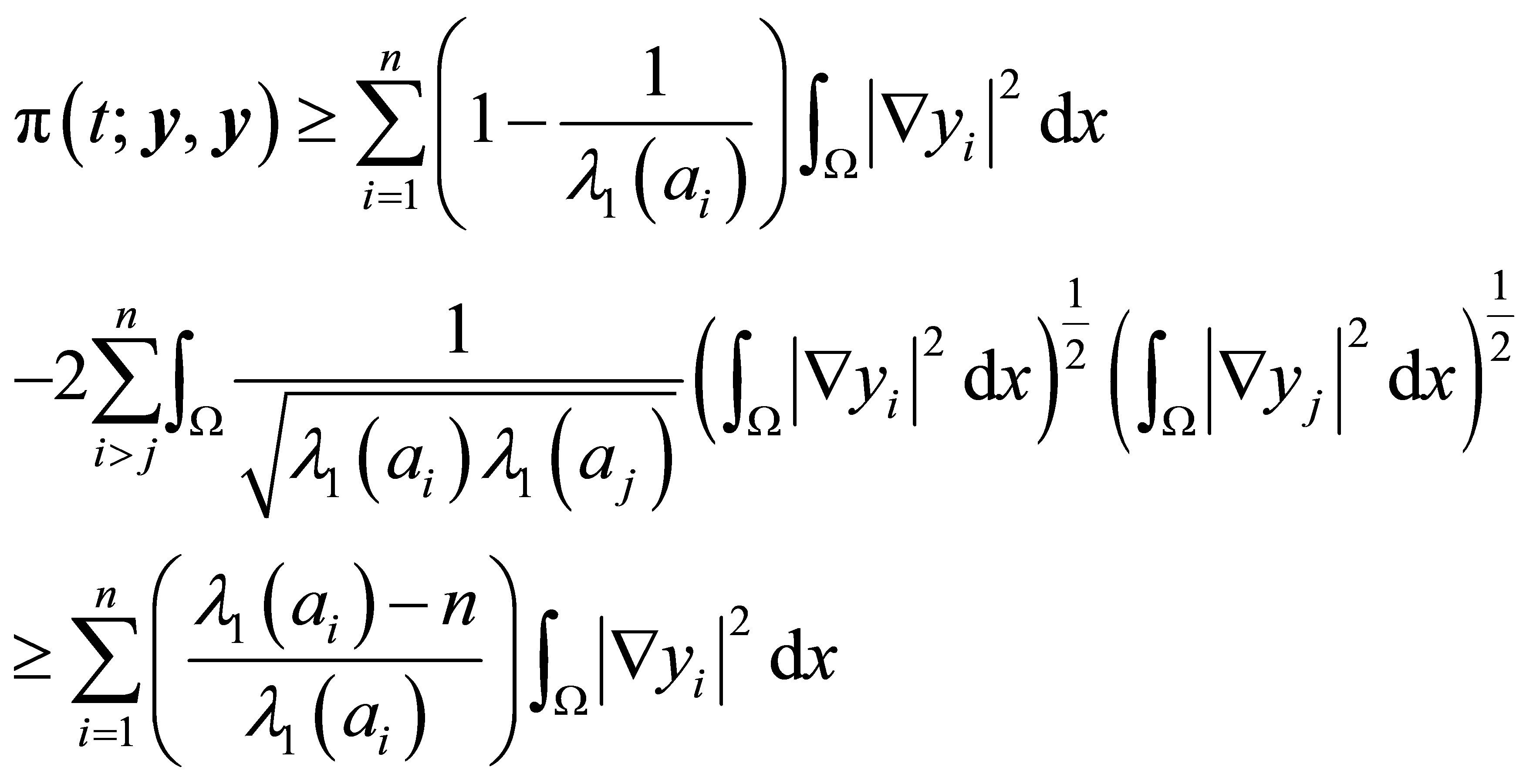
From (10) we have
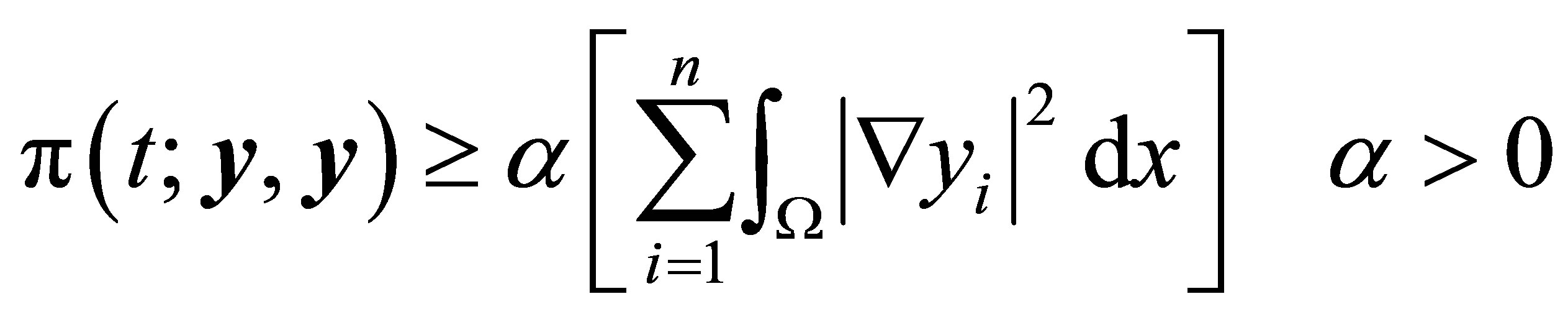
Add 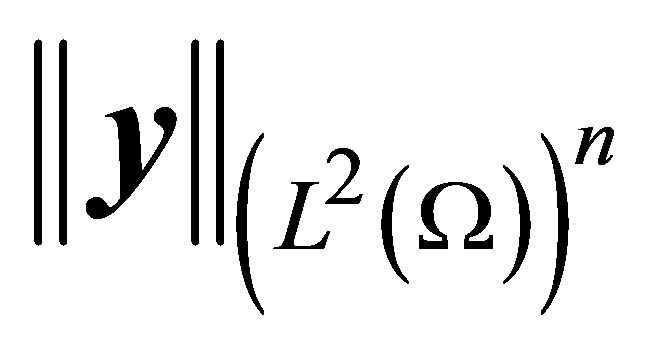 to two sides, then we have the result. ,.
to two sides, then we have the result. ,.
We can now apply Theorem 1.1 and Theorem 1.2 Chapter 3 in [1] (with 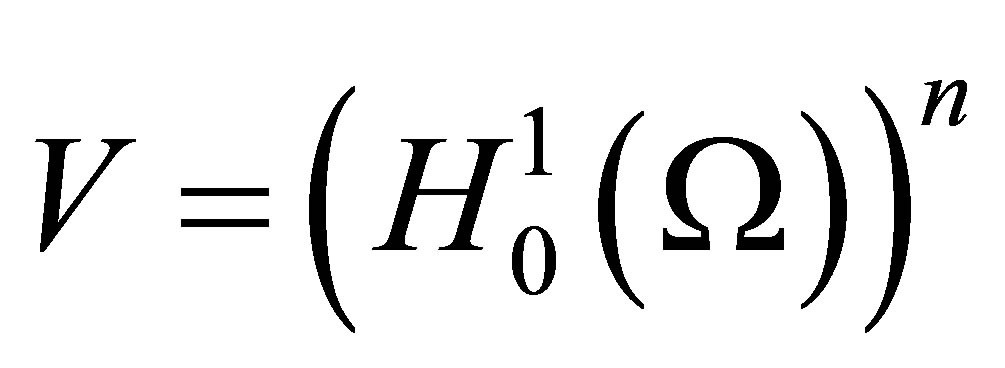 and
and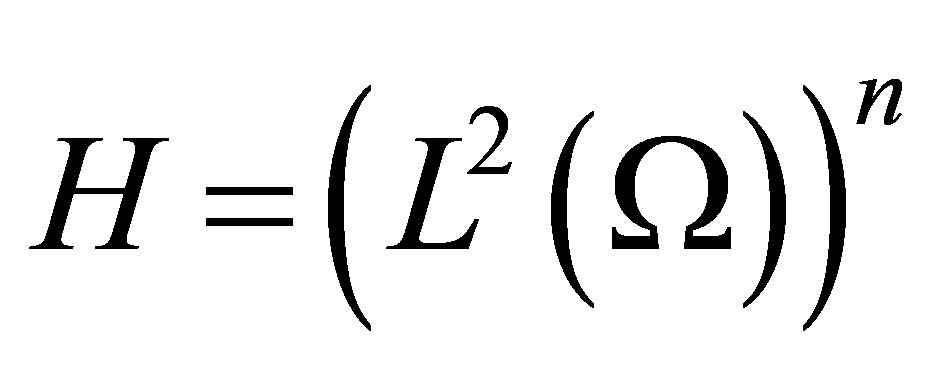 ) to obtain the following theorem:
) to obtain the following theorem:
Theorem 2.3. If (8) and (10) hold, then there exist a unique solution
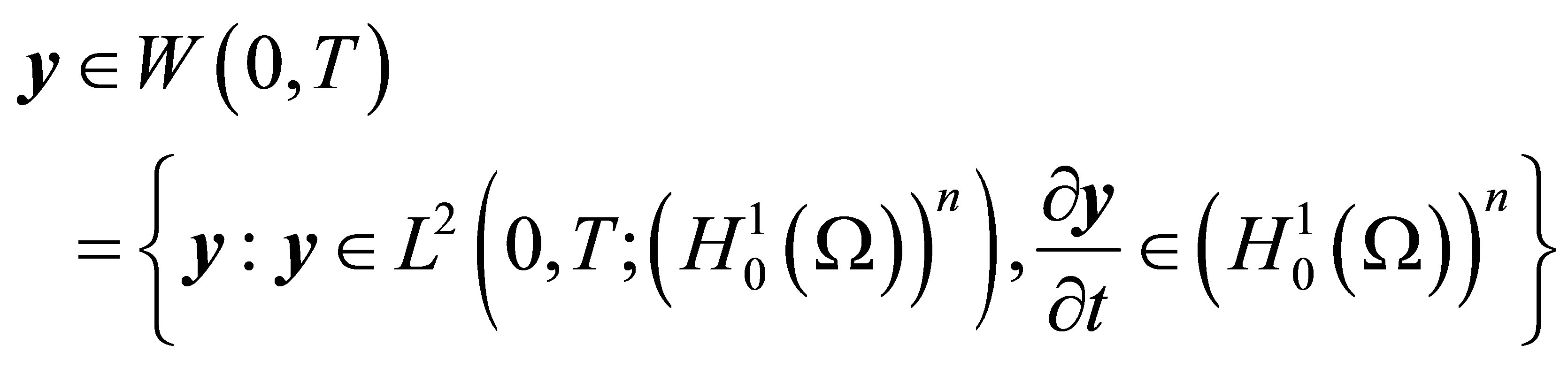
satisfying the following 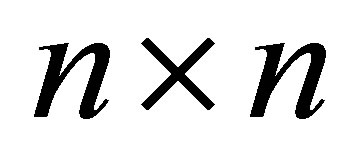 system:
system: 
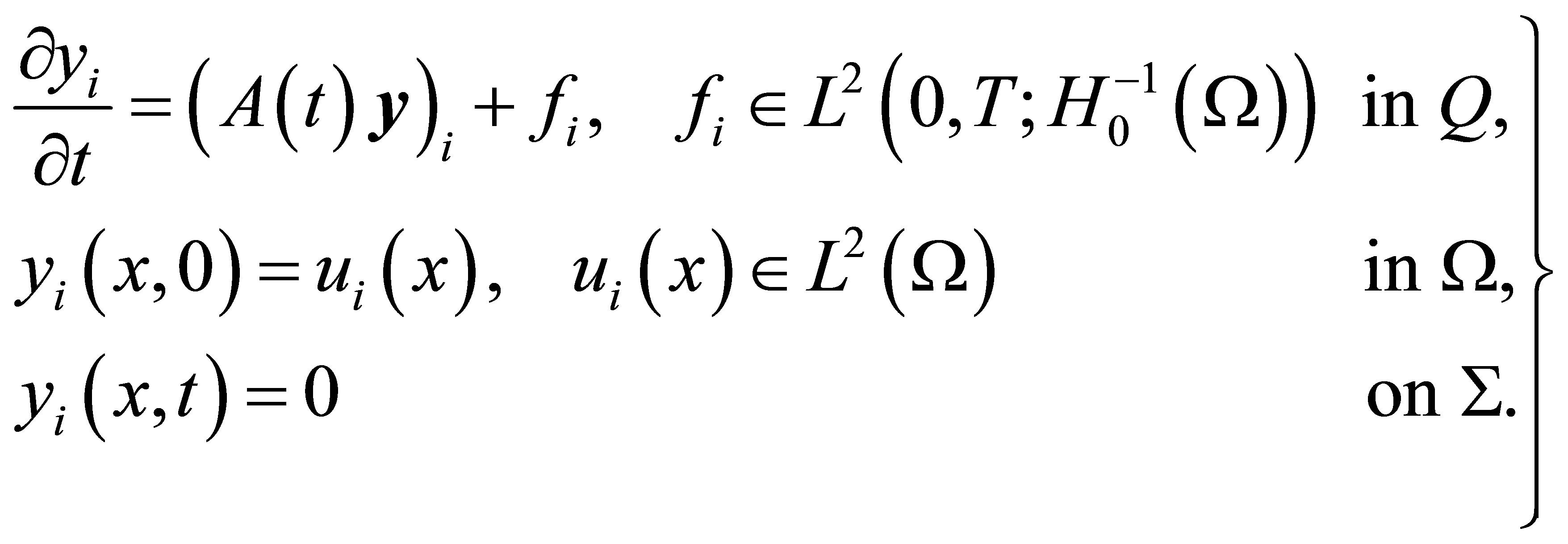 (11)
(11)
Moreover  is continuous from
is continuous from 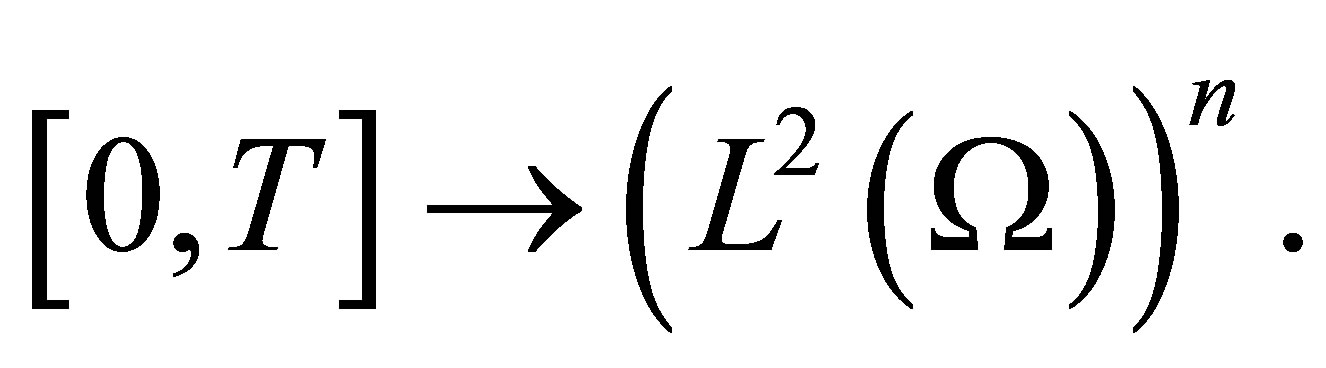
3. Minimum Time and Controllability
We denote the unique solution of (11), at time  for each control
for each control 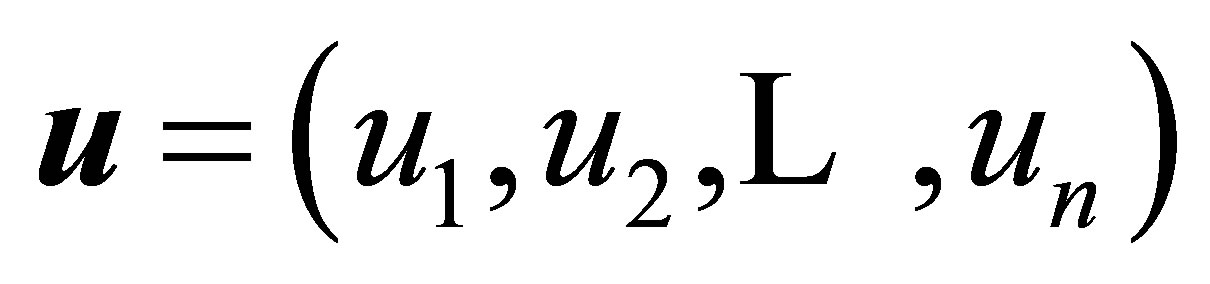 by
by 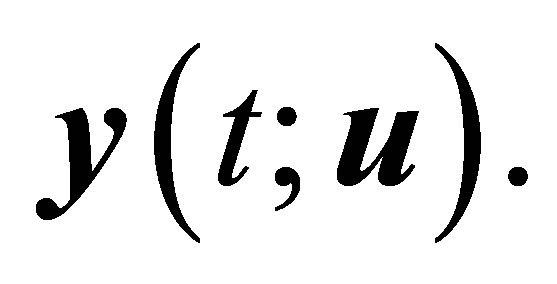 Occasionally, we write
Occasionally, we write  when the explicit dependence on
when the explicit dependence on 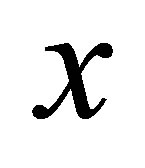 is required. We can now formulate the time optimal control problem corresponding to the
is required. We can now formulate the time optimal control problem corresponding to the 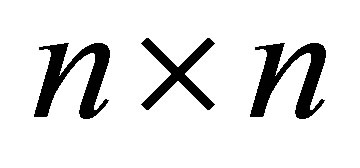 cooperative parabolic system (11):
cooperative parabolic system (11):
 (12)
(12)
with constraints
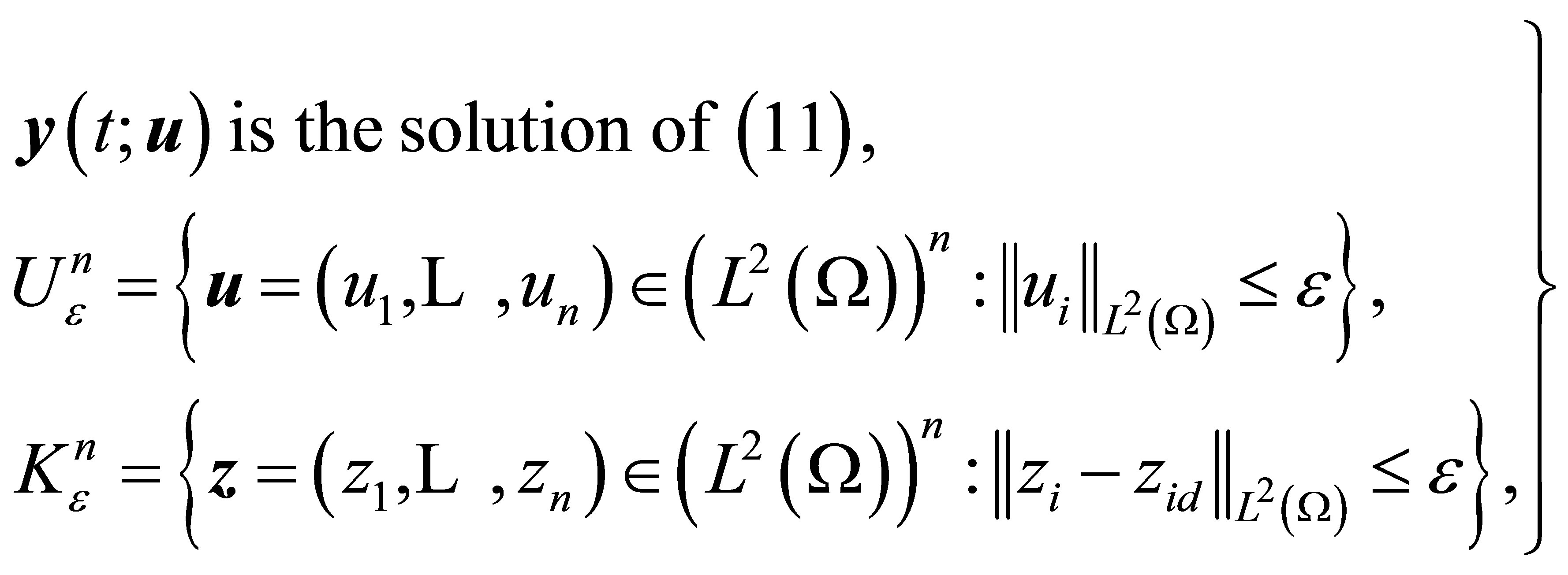 (13)
(13)
and 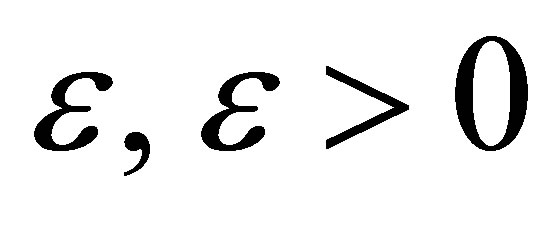 and
and 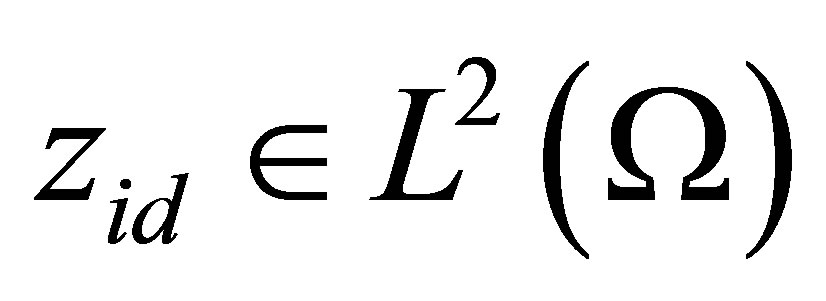 are given.
are given.
Theorem 3.1. If (8) and (10) are hold, then the system whose state is given by (11) is controllable, i.e.,
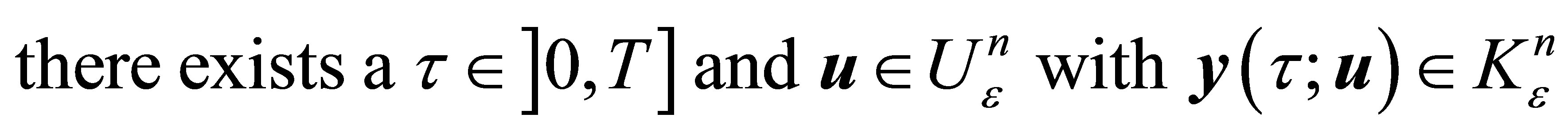 (14)
(14)
Proof. Let us first remark that by translation we may always reduce the problem of controllability to the case were the system (11) with 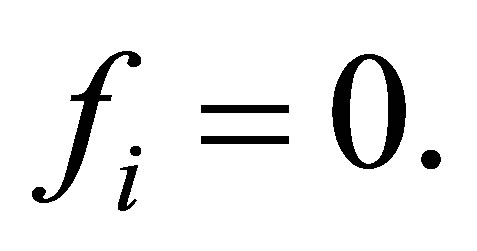 We can show quit easily that (11) is approximately controllable in
We can show quit easily that (11) is approximately controllable in 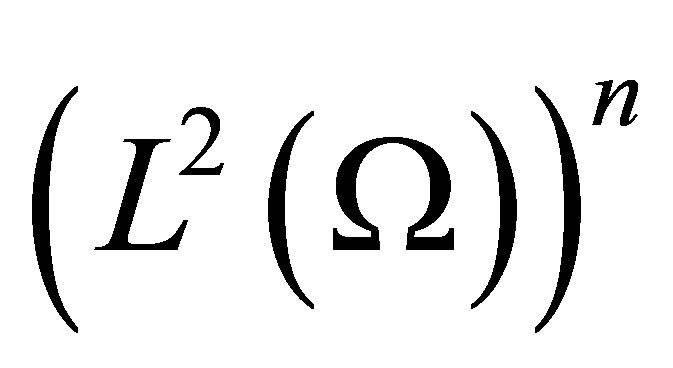 in any finite time
in any finite time 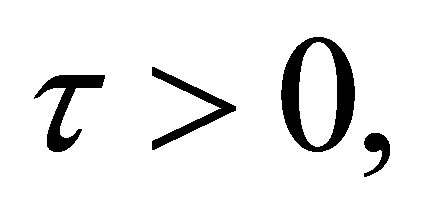 if and only if,
if and only if, 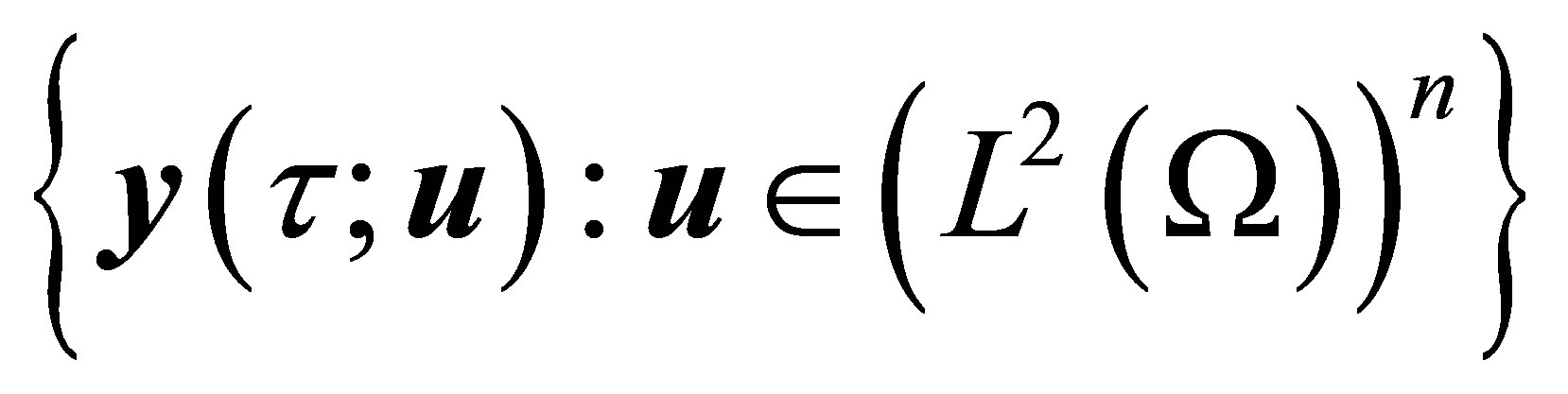 is dense in
is dense in 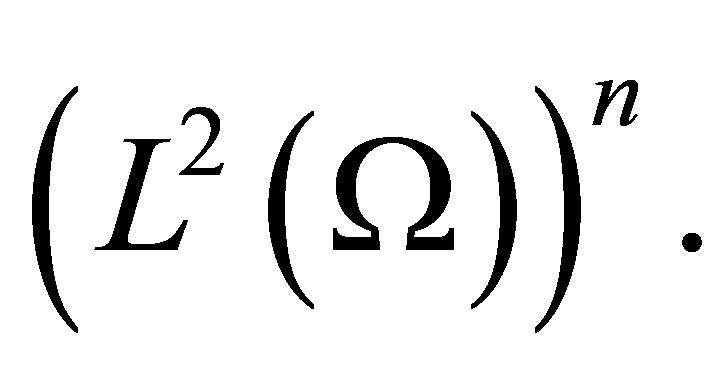 By the Hahn-Banach theorem, this will be the case if
By the Hahn-Banach theorem, this will be the case if
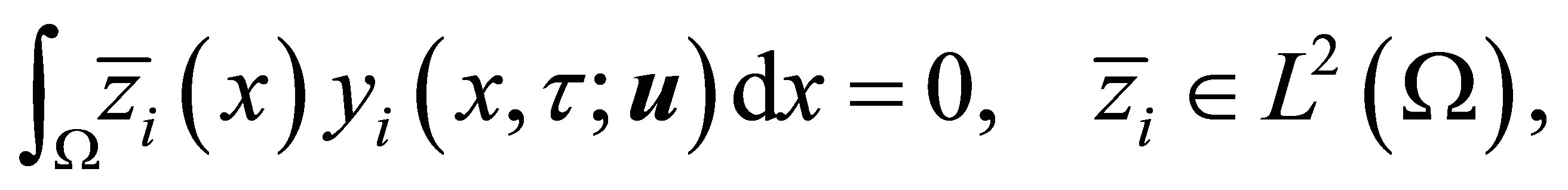 (15)
(15)
for all 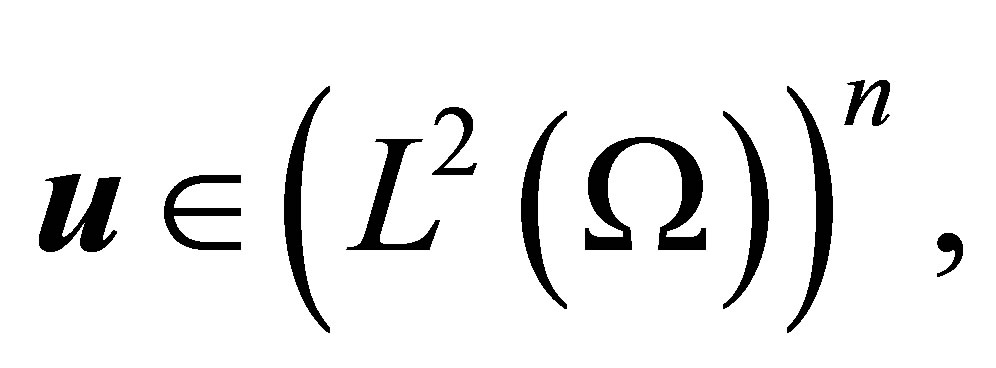 implies that
implies that 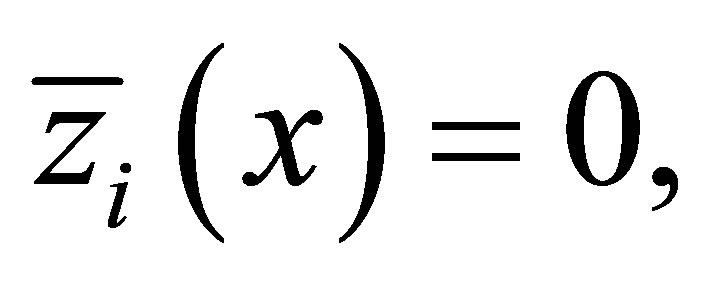
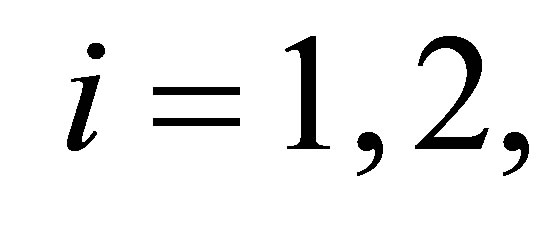
Let us introduce the adjoint state 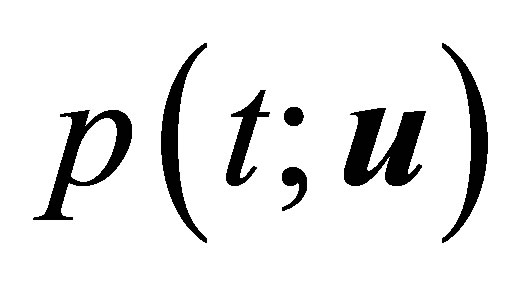 by the solution of the following system
by the solution of the following system
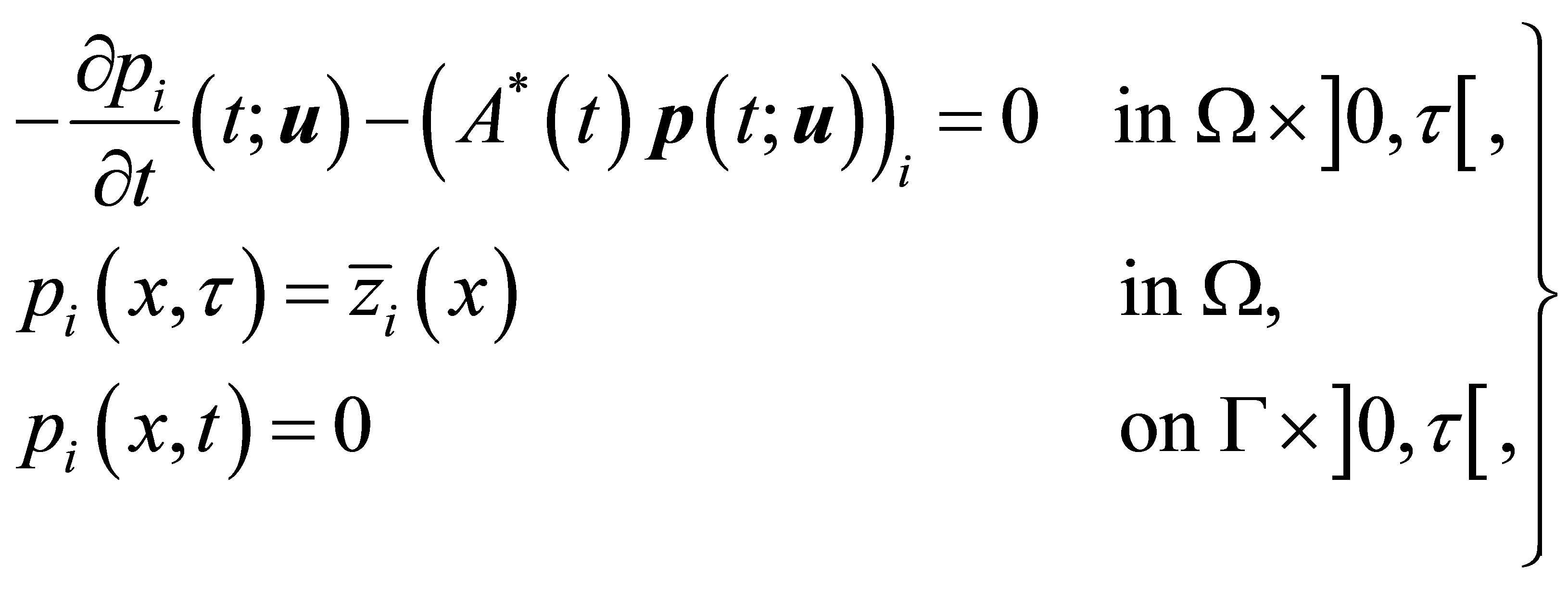 (16)
(16)
where 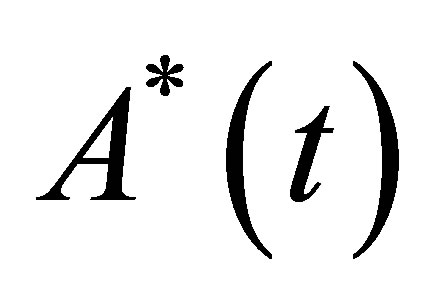 is the adjoint of
is the adjoint of 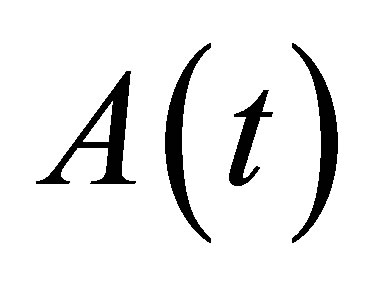 which is defined by
which is defined by
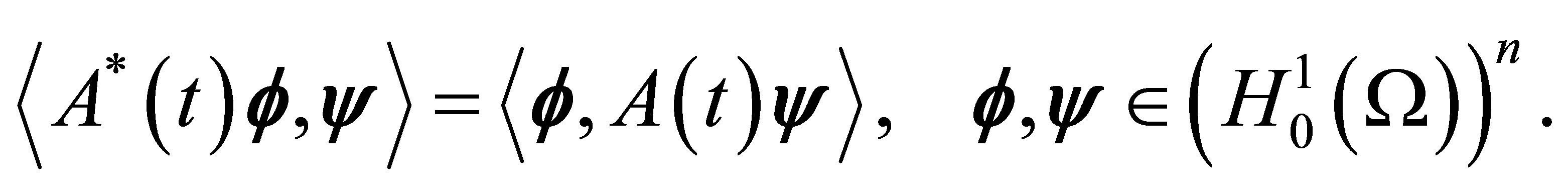
The existence of a unique solution for the Problem (16) can be proved using Theorem 2.3, with an obvious change of variables.
Multiply the first equation in (16) by 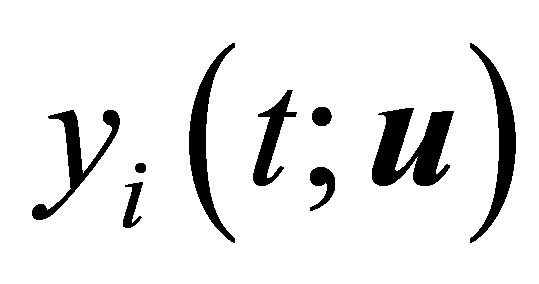 and integrate by parts from 0 to
and integrate by parts from 0 to 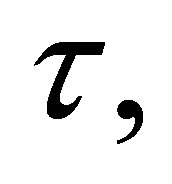 we obtain the following identity:
we obtain the following identity:
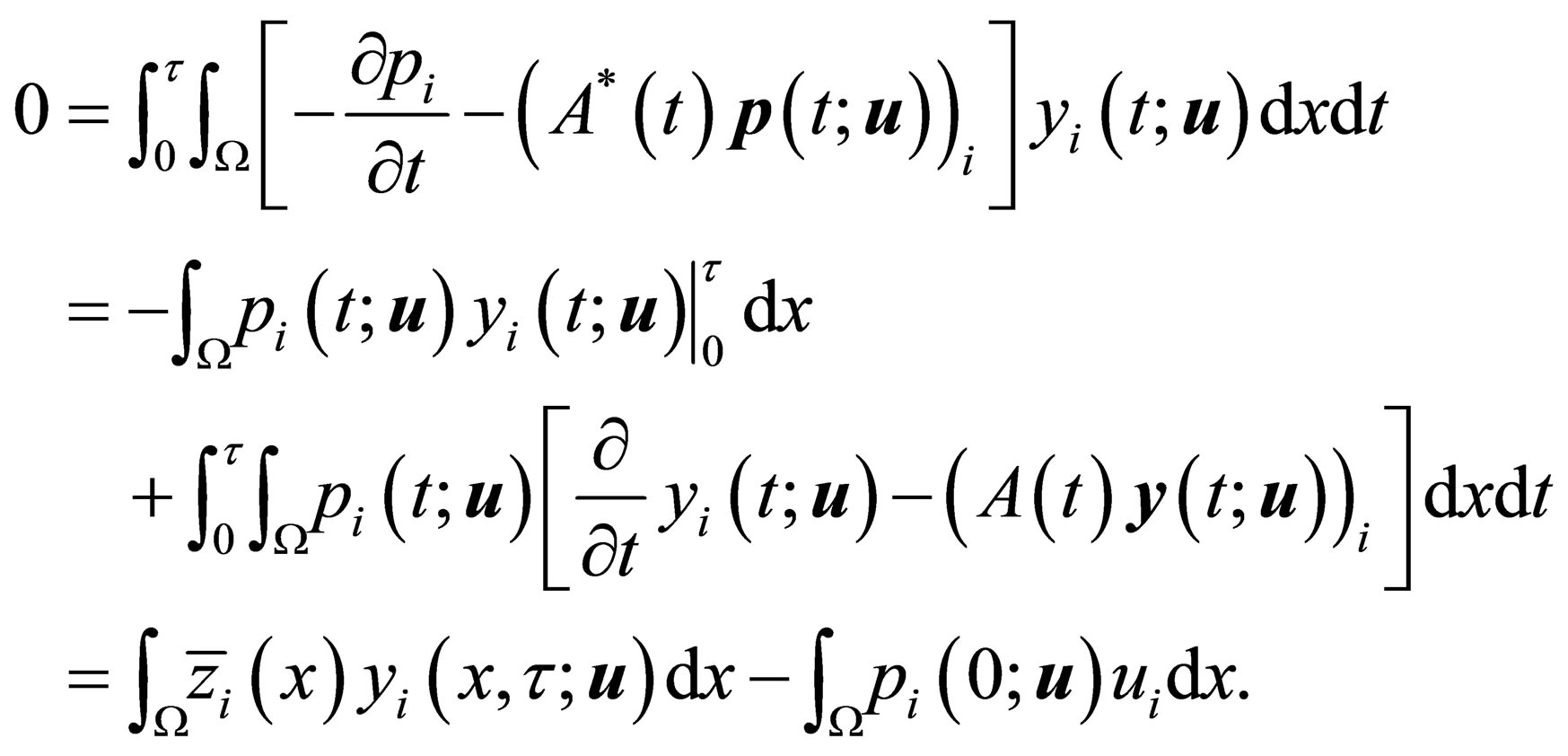
and so, if (15) holds, then
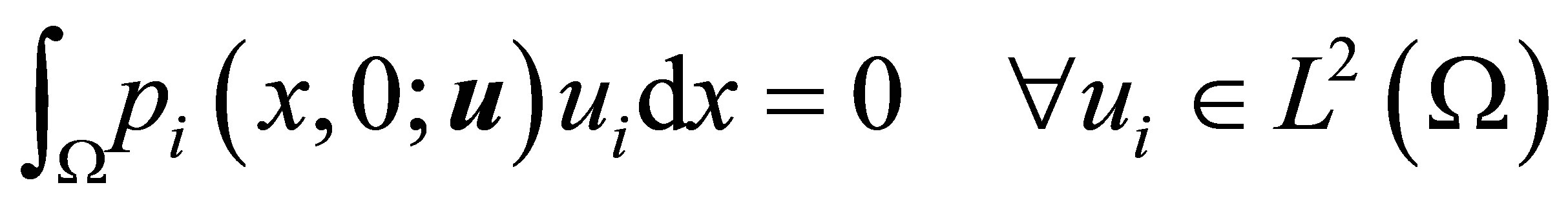
hence 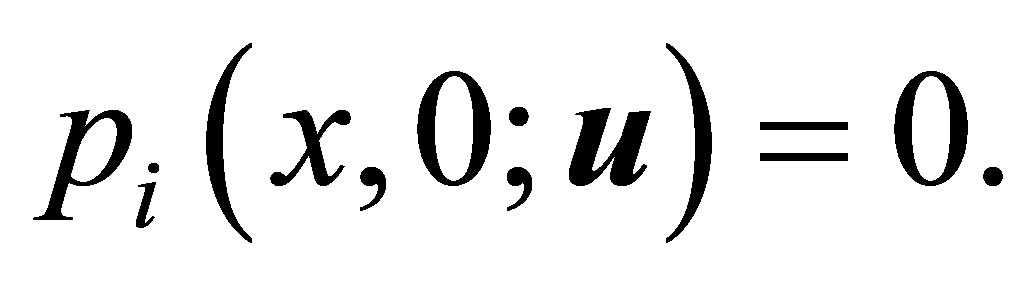 But from the backward uniqueness property,
But from the backward uniqueness property,  and hence
and hence  ,.
,.
Now set
 (17)
(17)
Then , the following result holds.
Theorem 3.2. If (8) and (10) are hold, then there exist an admissible control  to the problem (12)-(17), which steering
to the problem (12)-(17), which steering 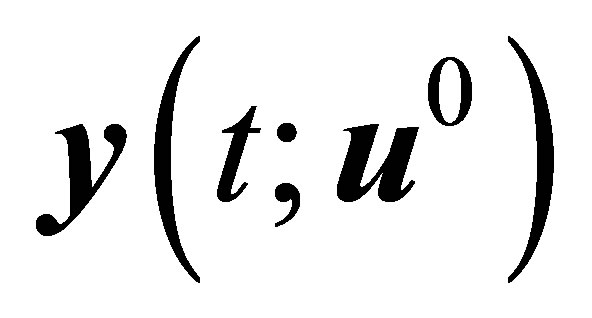 to hitting a target set
to hitting a target set 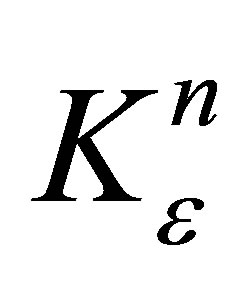 in minimum time
in minimum time 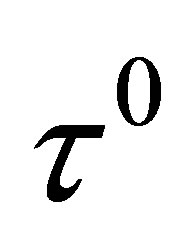 (defined by (17)). Moreover
(defined by (17)). Moreover
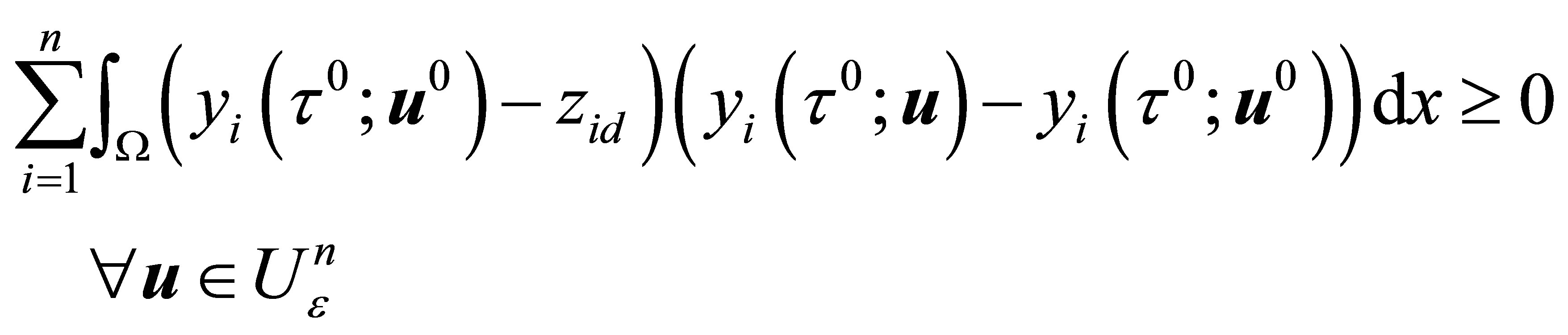 (18)
(18)
Proof. Fixe  we can choose
we can choose  and admissible controls
and admissible controls  such that
such that
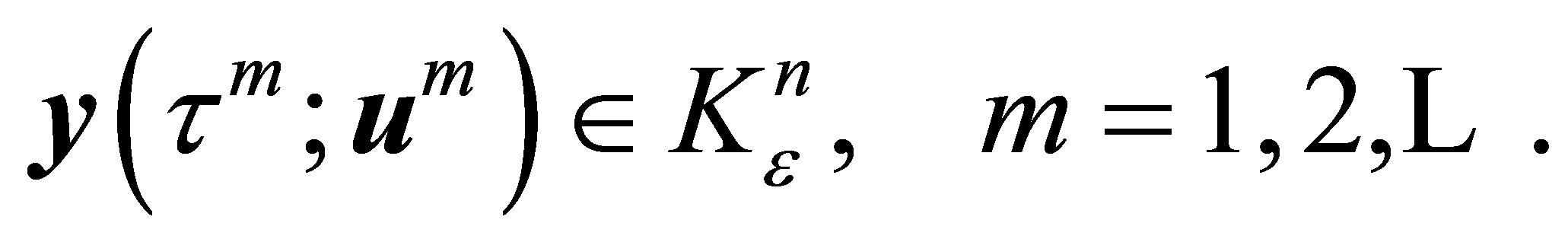
Set 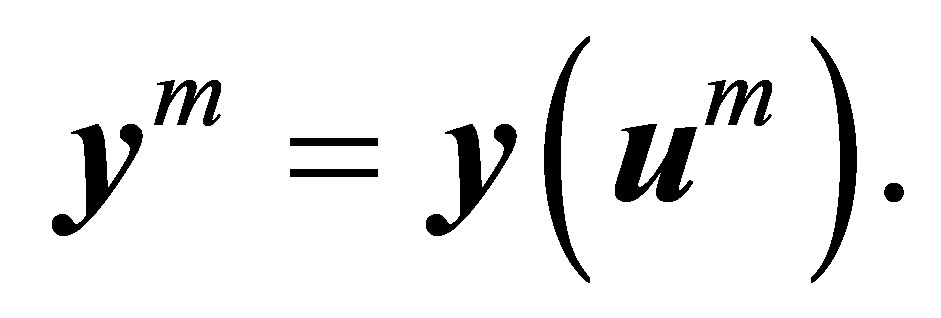 Since
Since  is bounded, we may verify that
is bounded, we may verify that 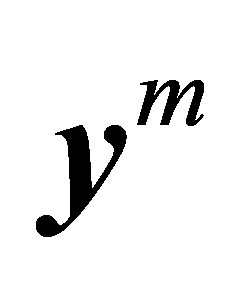 ranges in a bounded set in
ranges in a bounded set in
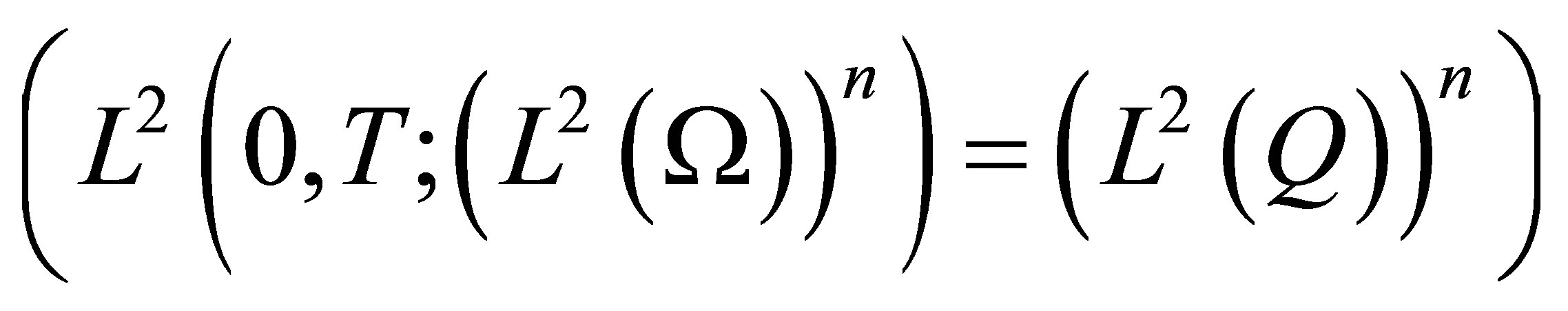 .
.
We may then extract a subsequence, again denoted by 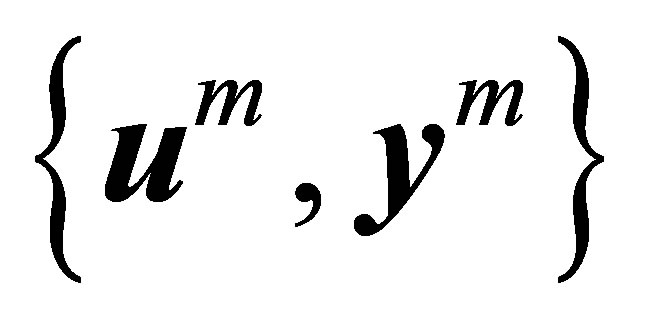 such that
such that
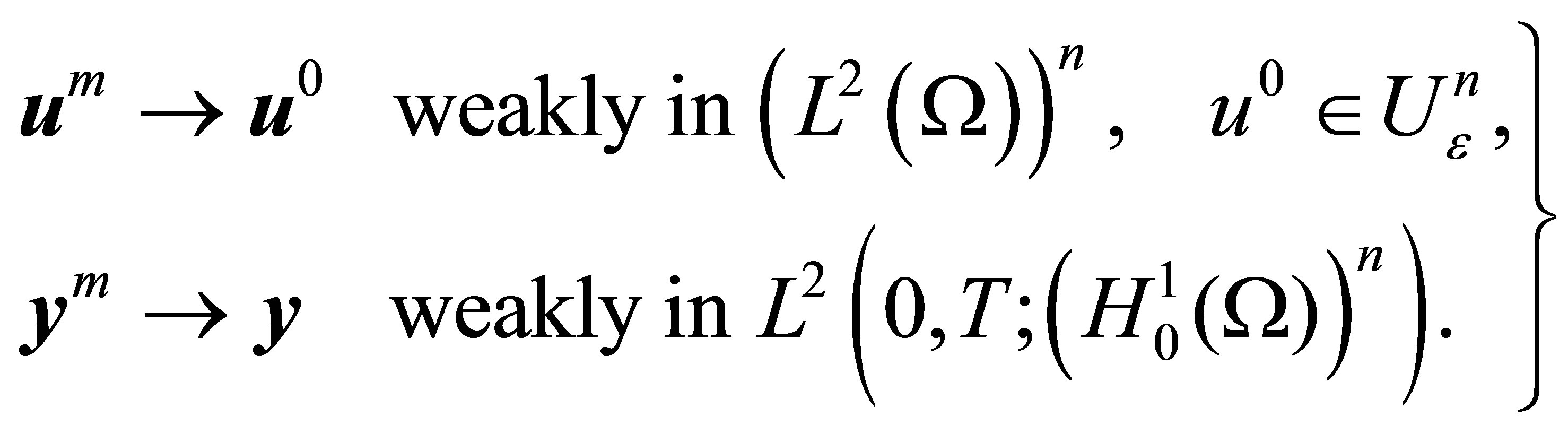 (19)
(19)
We deduce from the equality
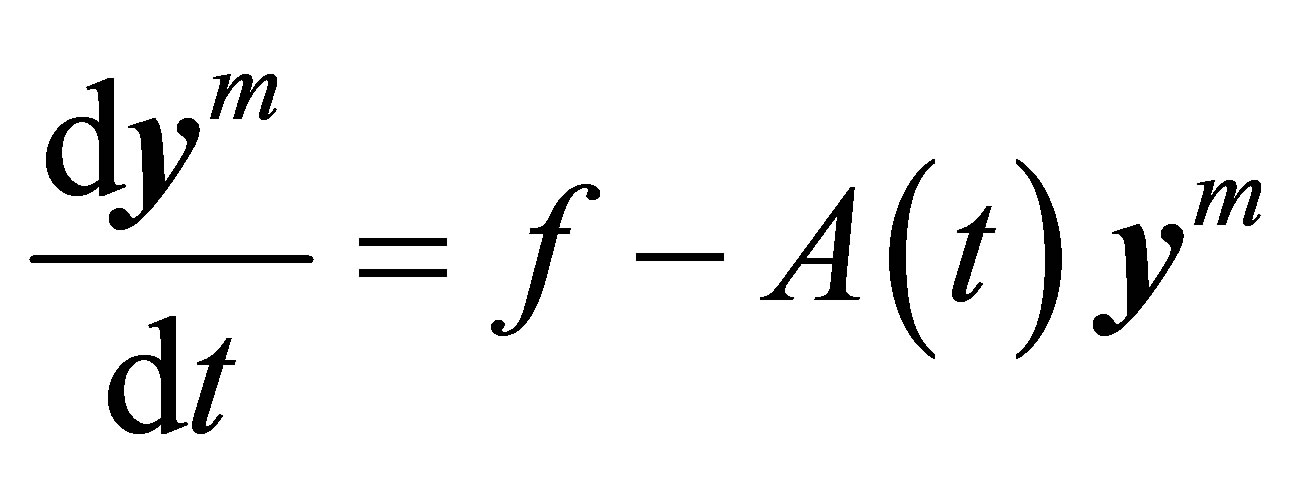
that
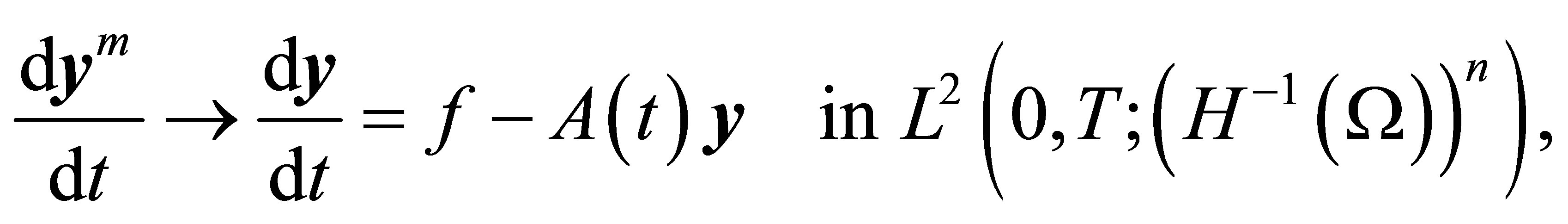
and
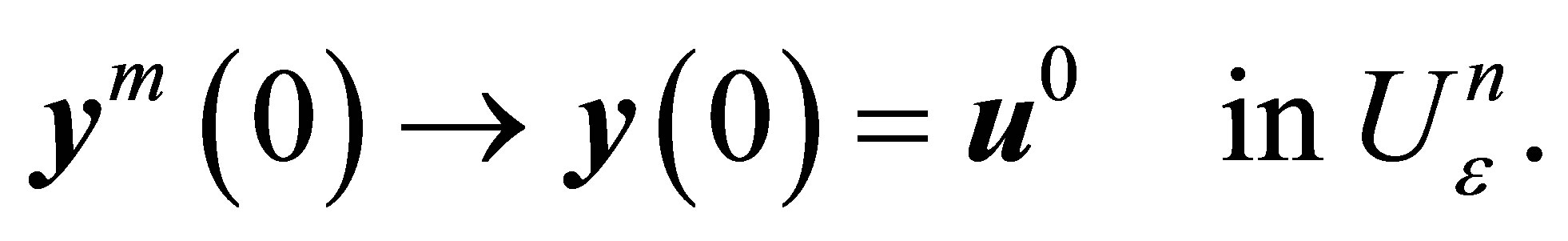
But
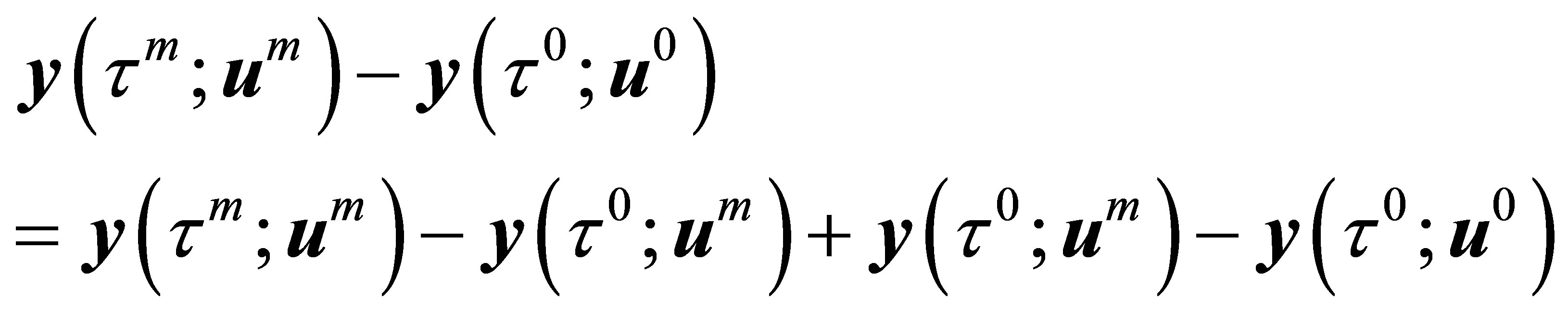
Now from (19)
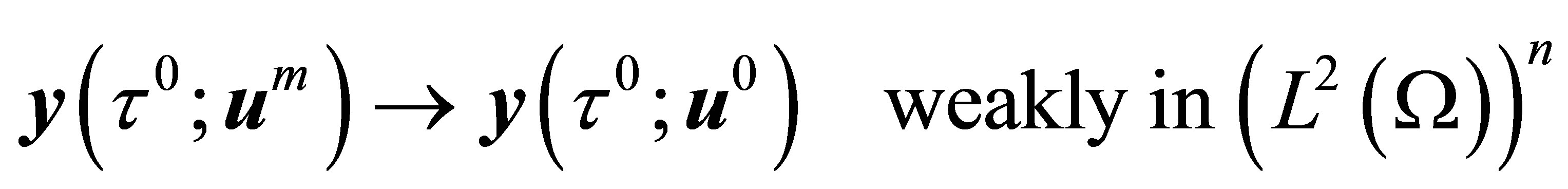 (20)
(20)
and
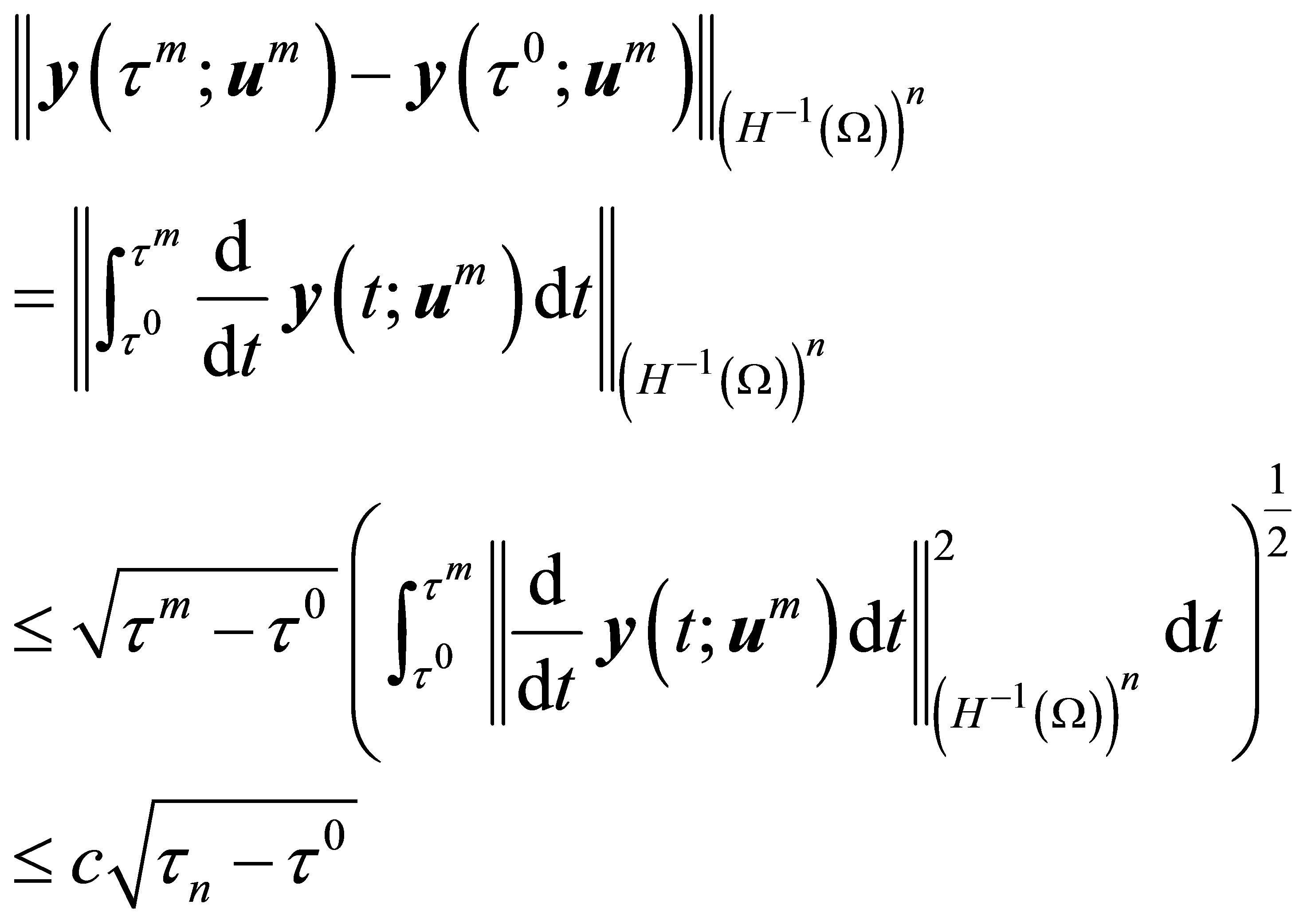 (21)
(21)
Combine (20) and (21) show that
 (22)
(22)
and so,  as
as 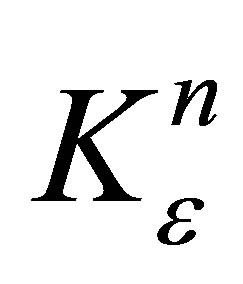 is closed and convex, hence weakly closed. This shows that
is closed and convex, hence weakly closed. This shows that  is reached in time
is reached in time 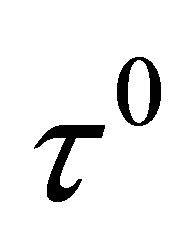 by admissible control
by admissible control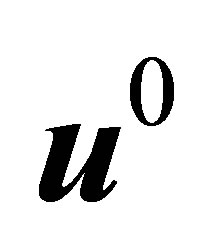 .
.
For the second part of the theorem, really, from Theorem 2.3, the mapping 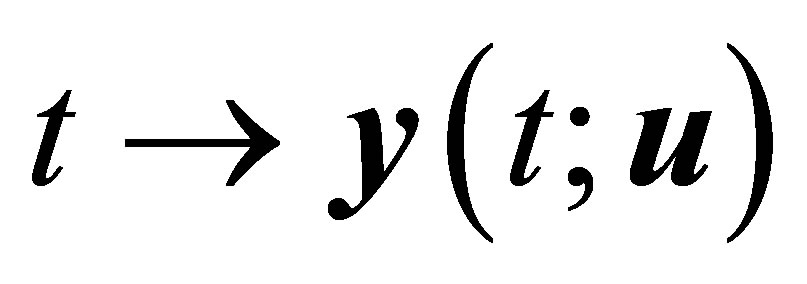 from
from  is continuous for each fixed
is continuous for each fixed  and so
and so 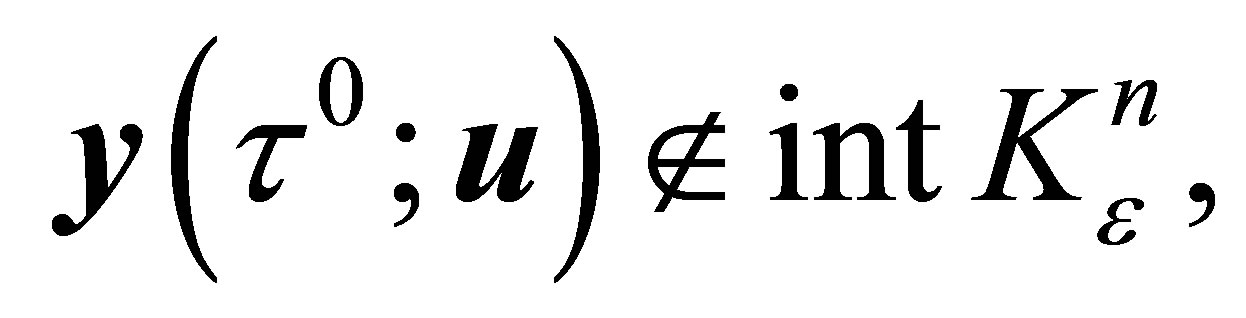 for any
for any 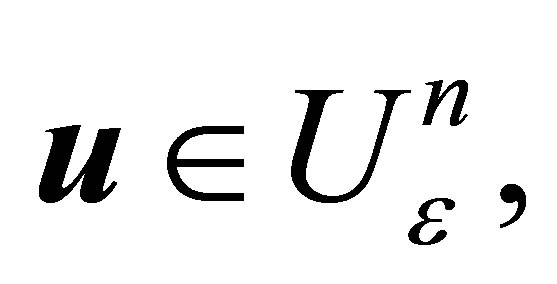 by minimality of
by minimality of 
Using Theorem 2.3, it is easy to verify that the mapping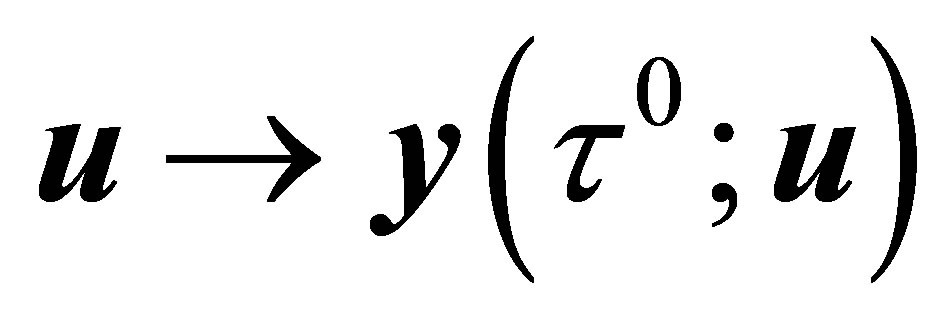 , from
, from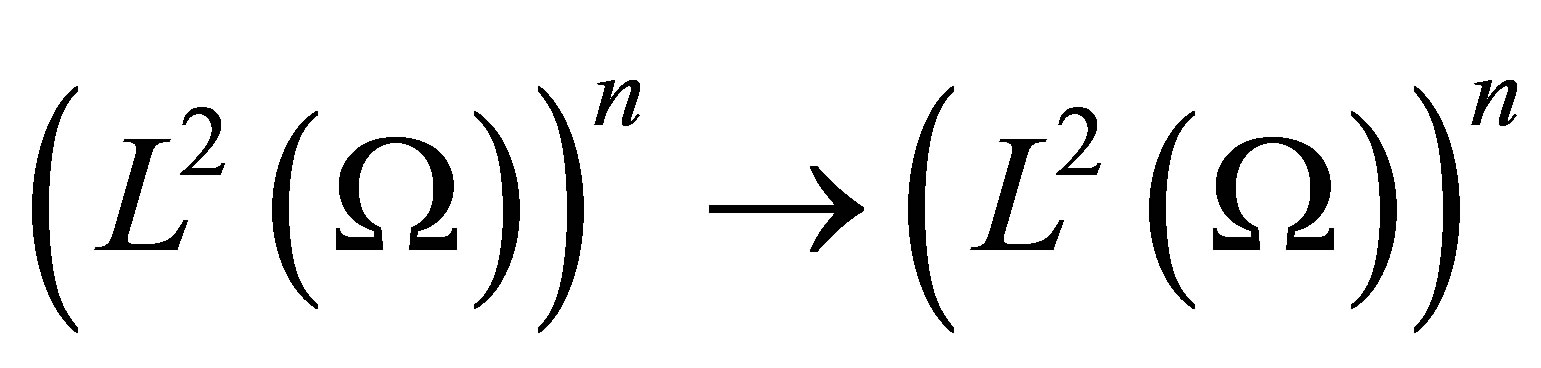 , is continuous and linear. then, the set
, is continuous and linear. then, the set
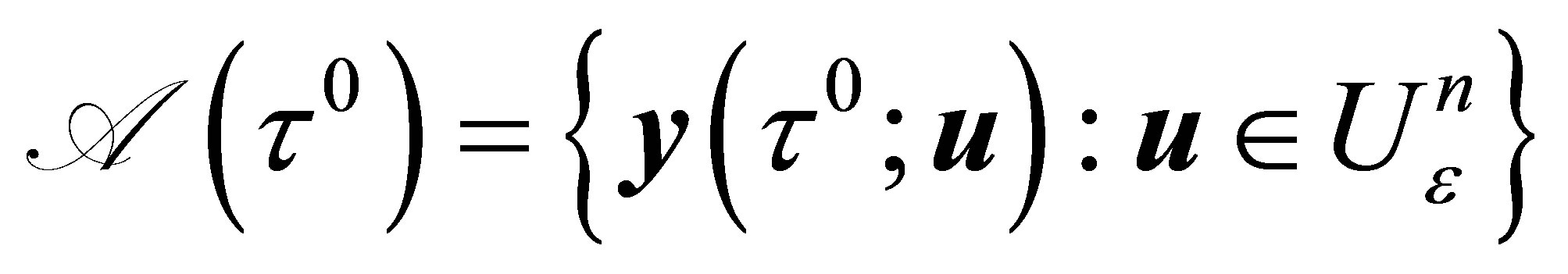
is the image under a linear mapping of a convex set hence 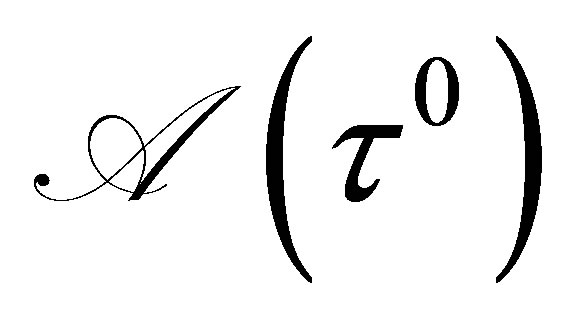 is convex. Thus we have
is convex. Thus we have
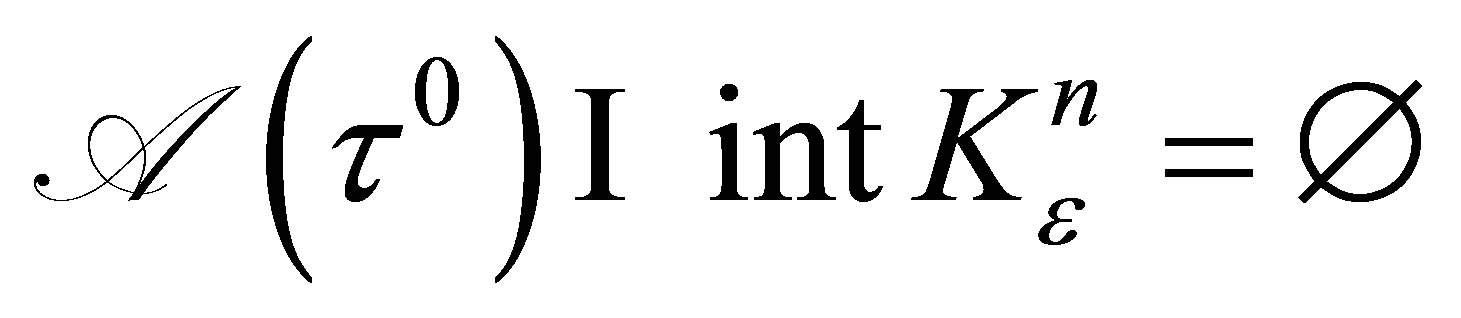 and
and 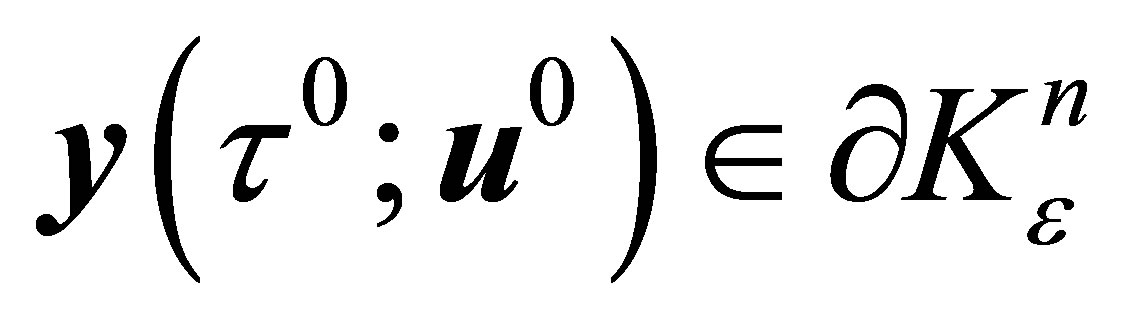 (boundary of
(boundary of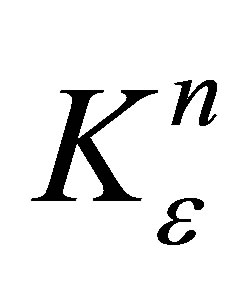 ) . Since
) . Since 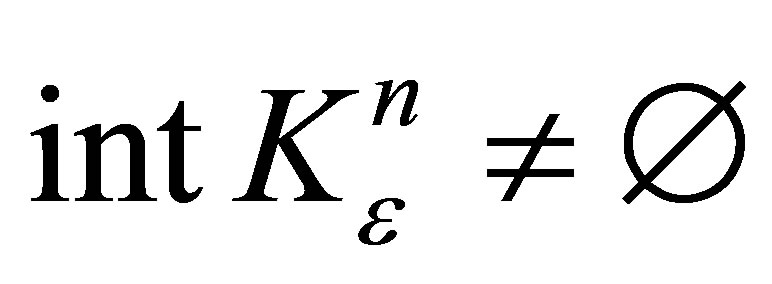 (from (14)) so there exists a closed hyperplane separating
(from (14)) so there exists a closed hyperplane separating 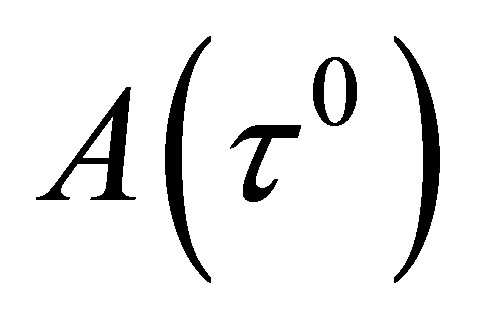 and
and  containing
containing , i.e. there is a nonzero
, i.e. there is a nonzero 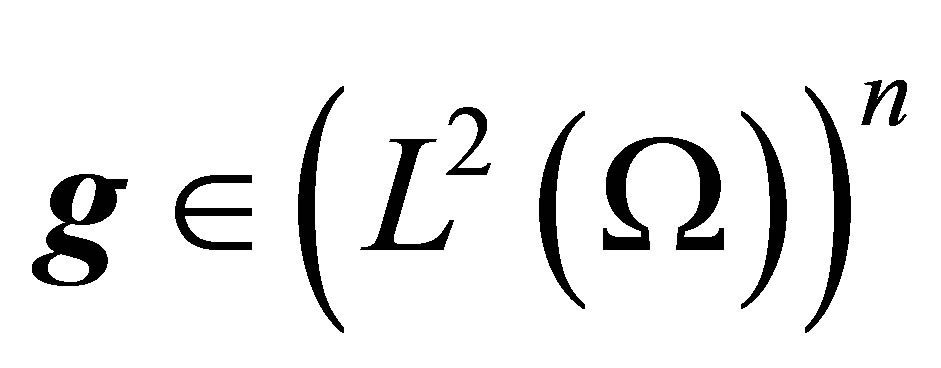 such as
such as
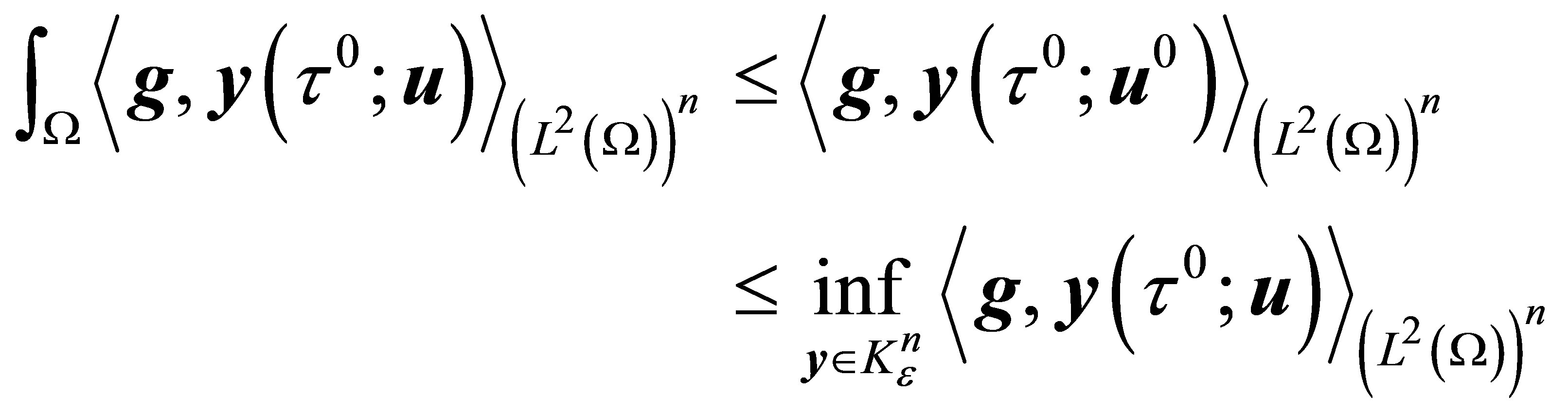 (23)
(23)
From the second inequality in (23), 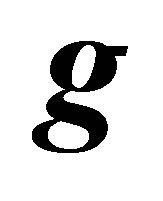 must support the set
must support the set 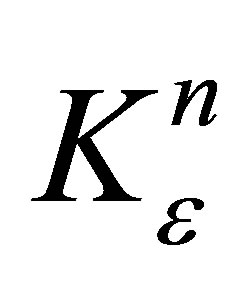 at
at  i.e.
i.e.
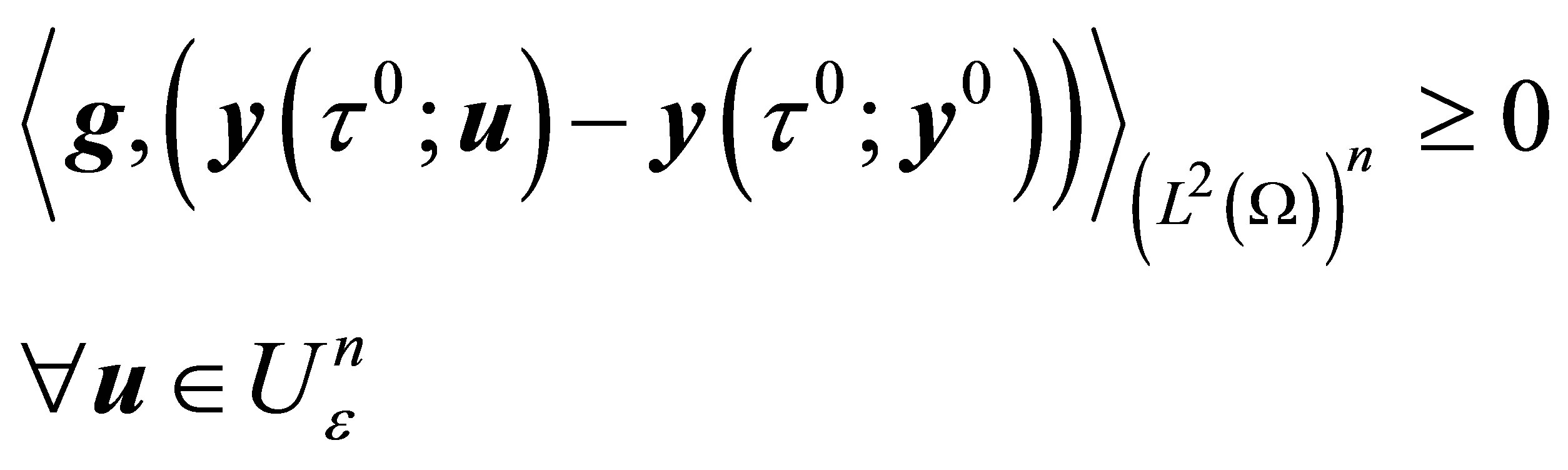
and since  is a Hilbert space,
is a Hilbert space, 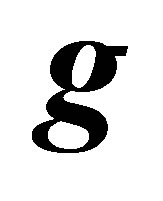 must be of the form
must be of the form

Dividing the inequality (23) by 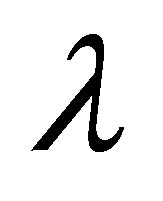 gives the desired result. ,.
gives the desired result. ,.
Now Inequality (18) can be interpreted as follows: let us introduce the adjoint state 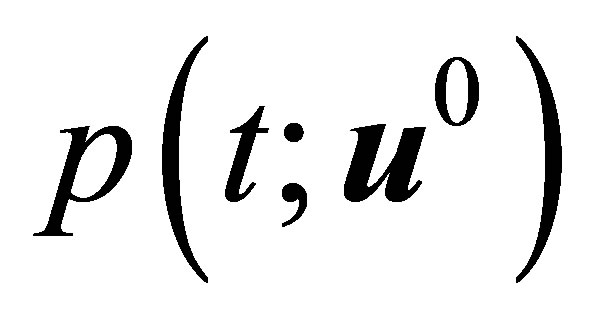 by the solution of the following system
by the solution of the following system
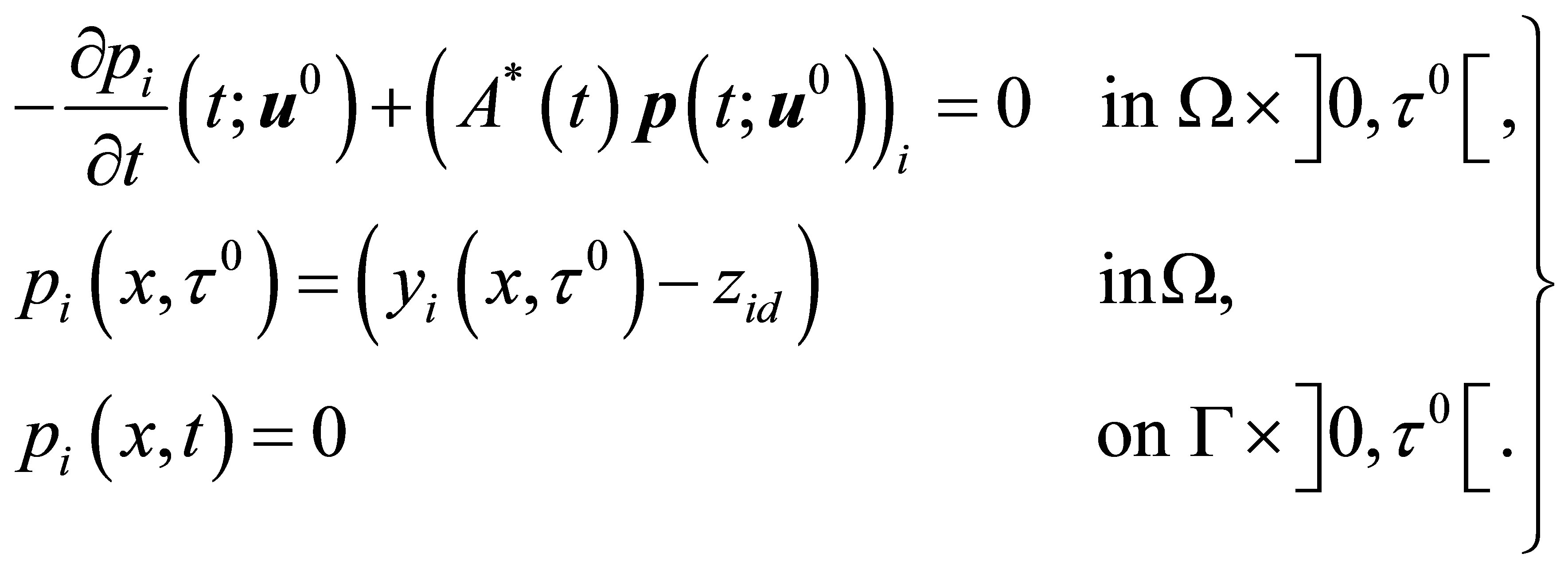 (24)
(24)
As the proof of Theorem 3.1, we multiply the first equation int (24) by 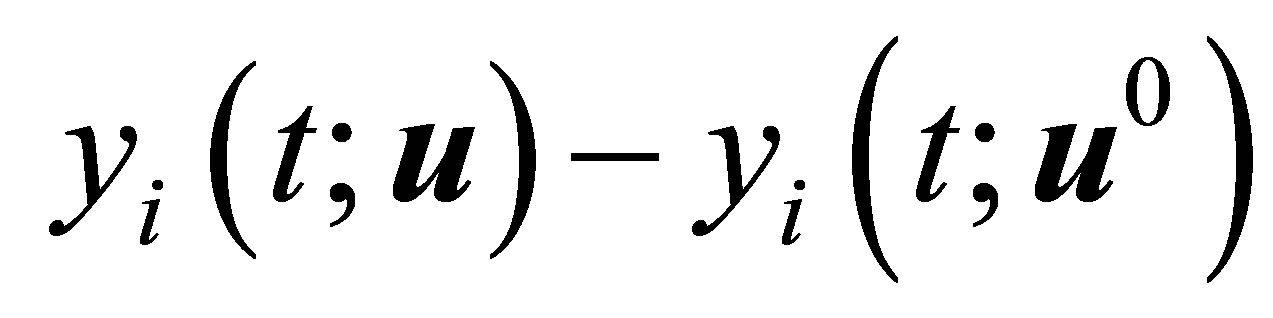 and integrate by parts from
and integrate by parts from  to
to 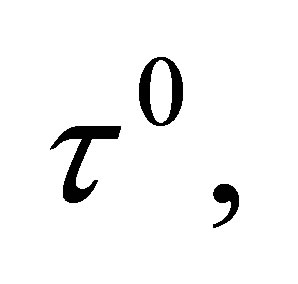 we obtain the following identity:
we obtain the following identity:

hence condition (18) becomes
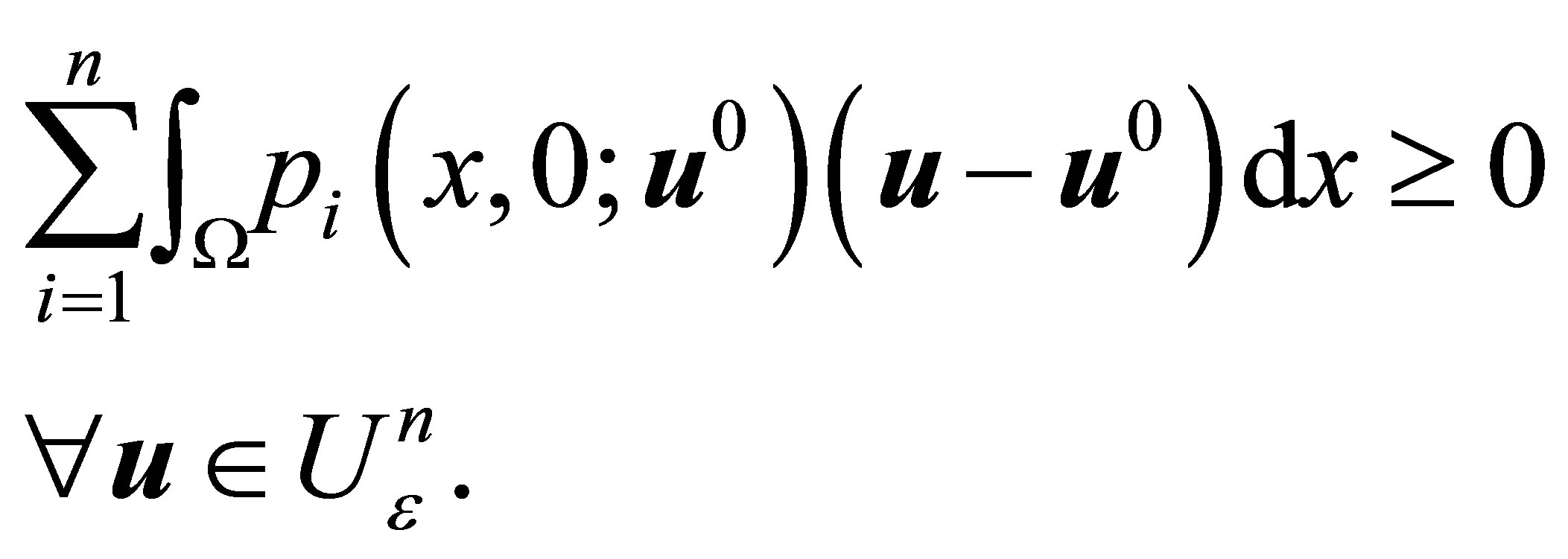 (25)
(25)
Using controllability condition (14), the backward uniqueness property implies 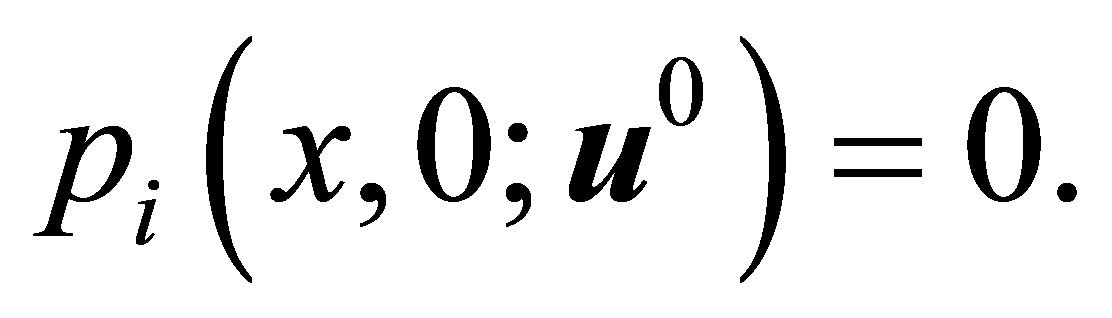 then the optimal control is bang-bang, i.e.,
then the optimal control is bang-bang, i.e.,  and since
and since
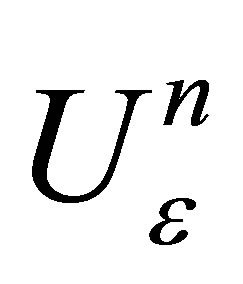 is strictly convex, then the optimal control is unique. We have thus proved:
is strictly convex, then the optimal control is unique. We have thus proved:
Theorem 3.3. If (8) and (10) are hold, then there exist the adjoint state
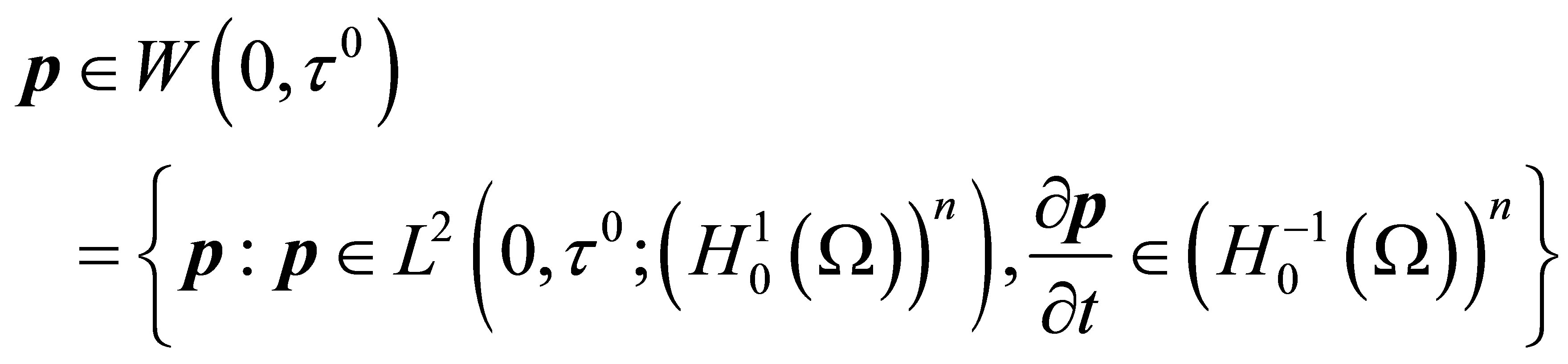
such that the optimal control  of problem (12)-(17) is bang-bang unique and it is determined by (24), (25) together with (11) (with
of problem (12)-(17) is bang-bang unique and it is determined by (24), (25) together with (11) (with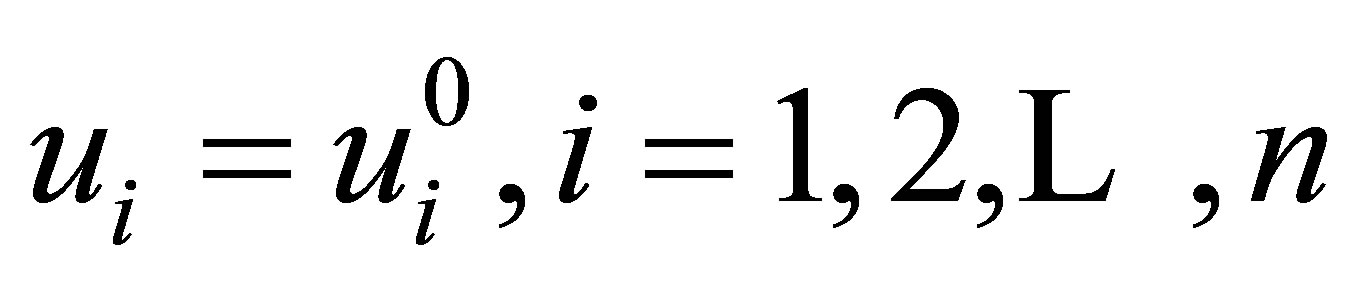 ).
).
4. Scaler Case
Here, we take the case where 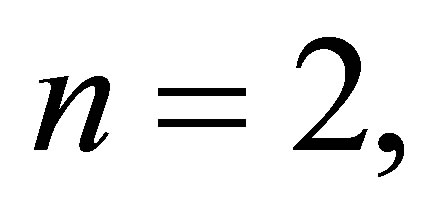 in this case, the time optimal problem therefore is
in this case, the time optimal problem therefore is
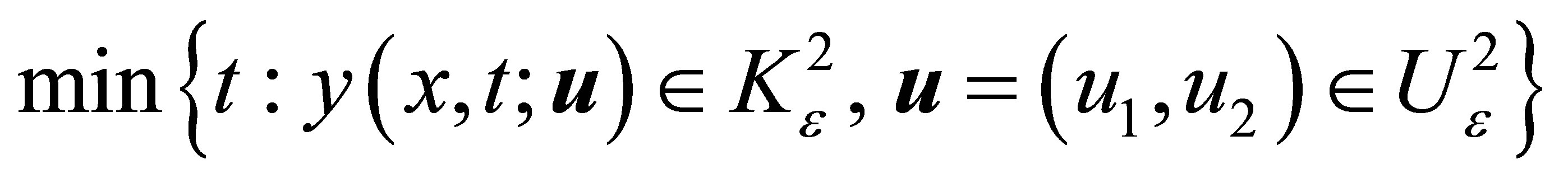
The state 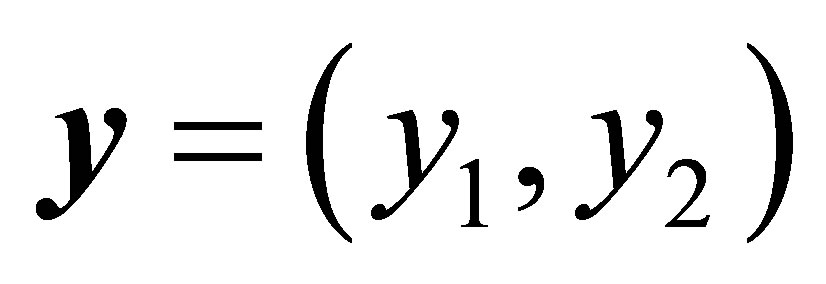 is solution of the following equations
is solution of the following equations
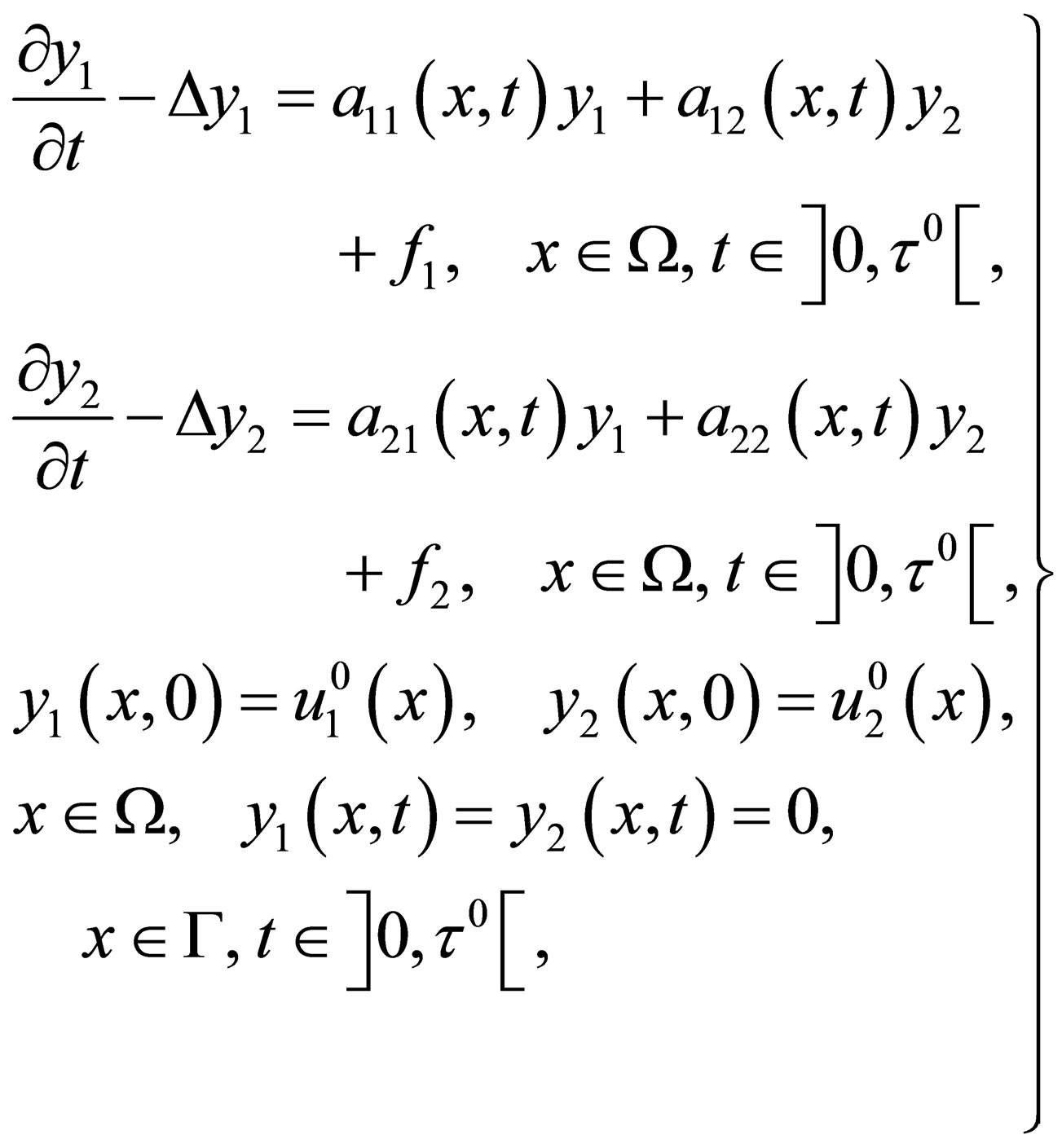
with
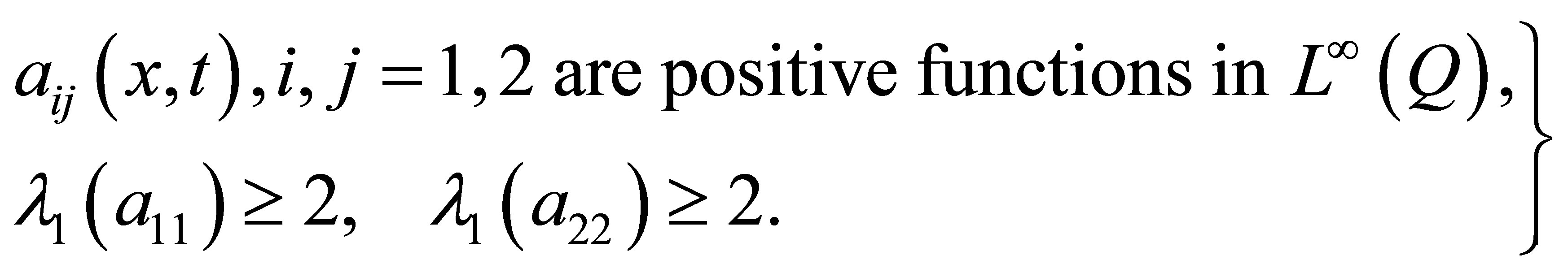
The adjoint is solution of the following equations
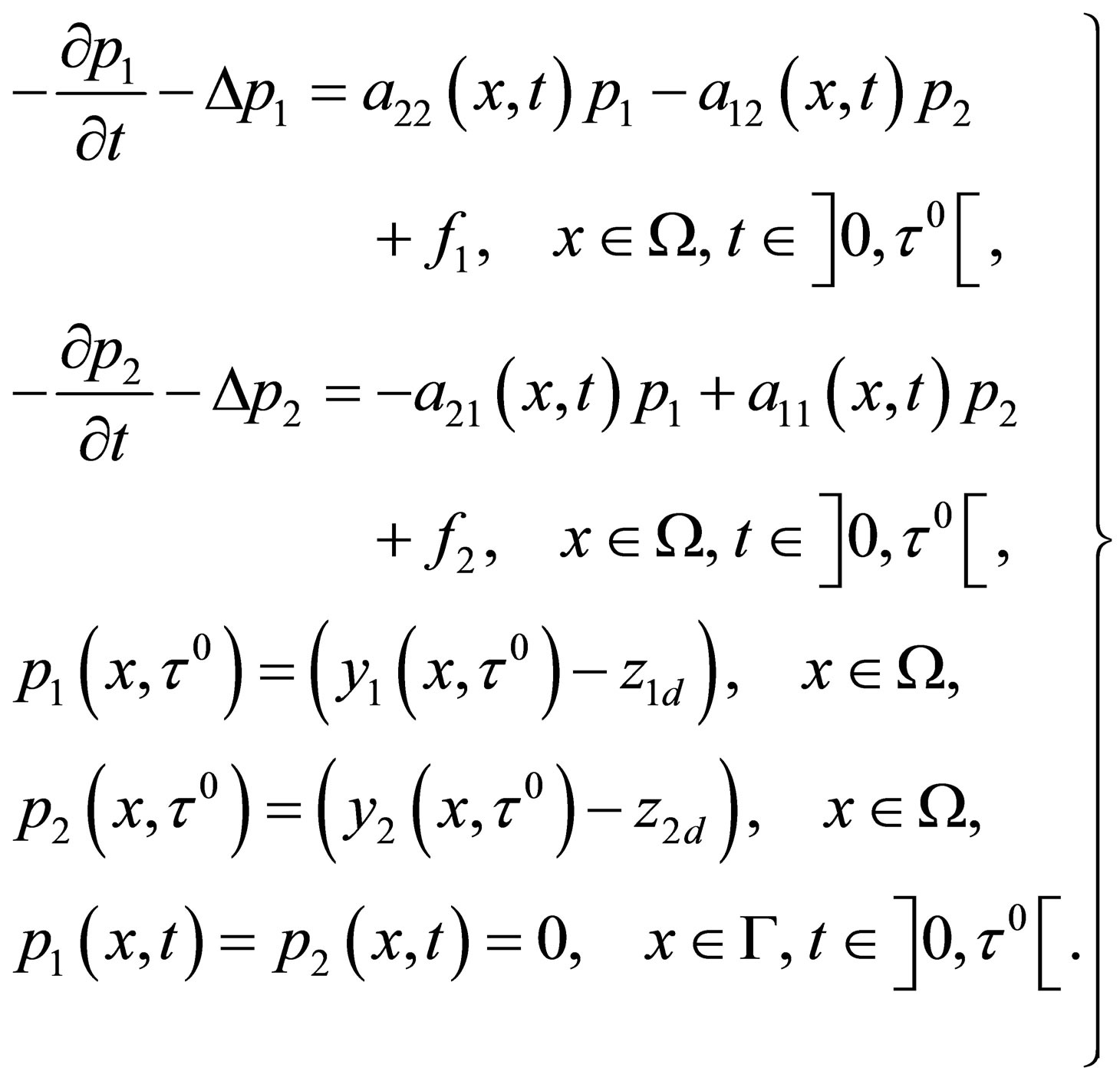
The maximum condition is
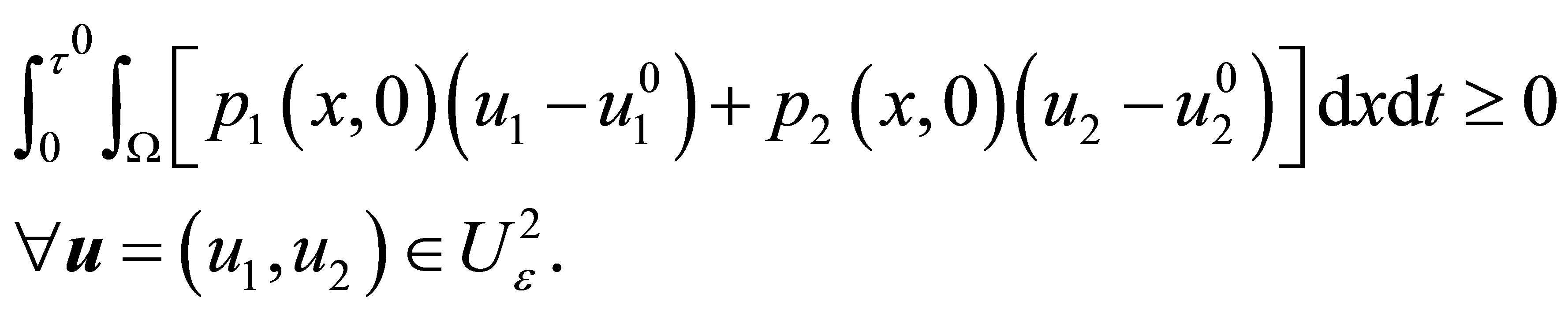
5. Comments
We note that, in this paper, we have chosen to treat a special systems involving Laplace operator just for simplicity. Most of the results we described in this paper apply without any change on the results to more general parabolic systems involving the following second order operator:
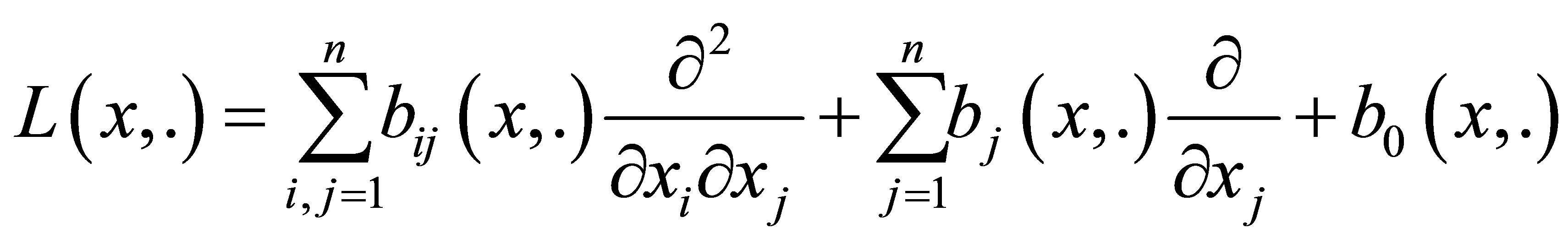
with sufficiently smooth coefficients (in particular,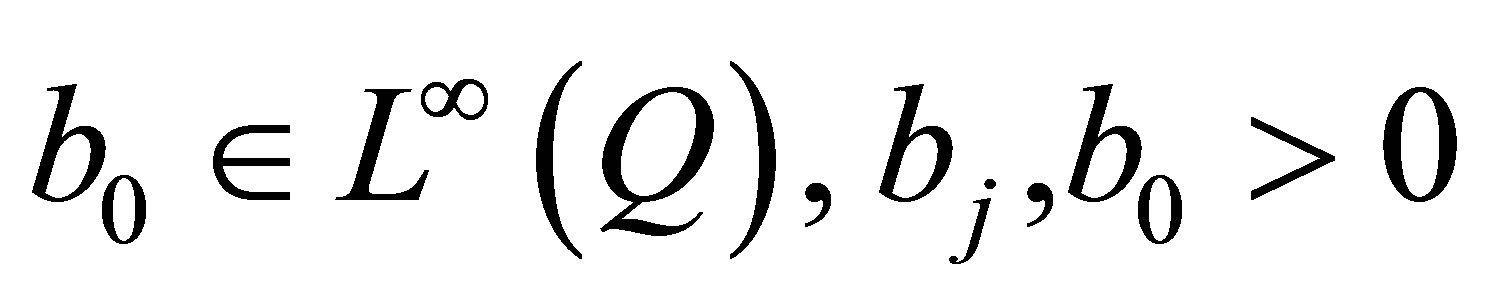

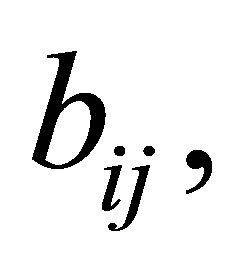 ) and under the LegendreHadamard ellipticity condition
) and under the LegendreHadamard ellipticity condition
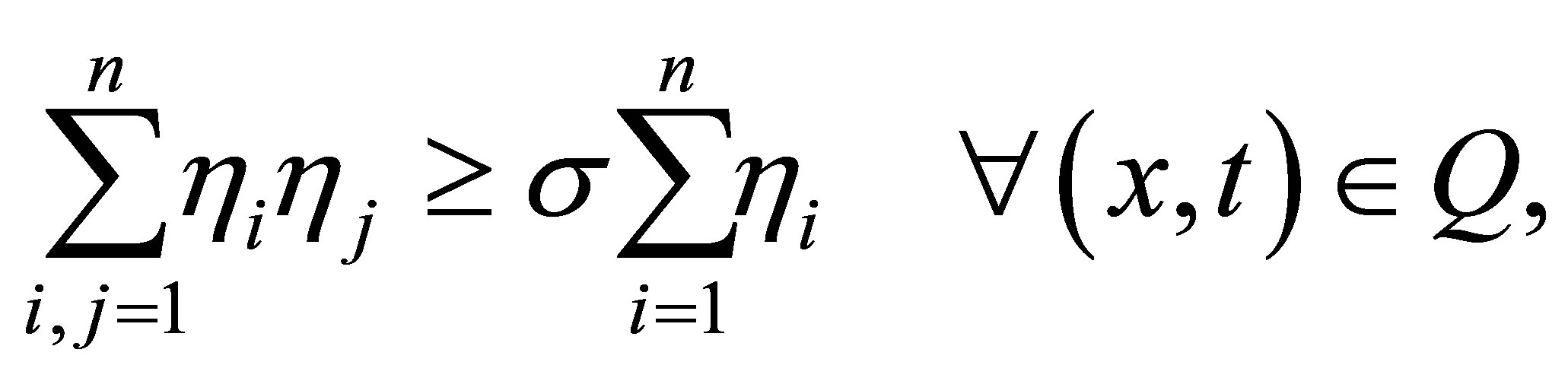
for all 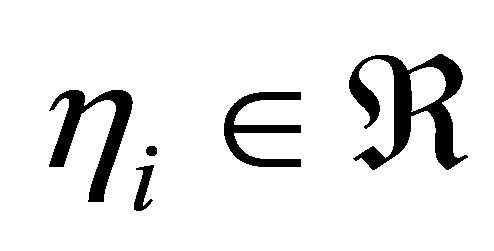 and some constants
and some constants 
In this case, we replace the first eigenvalue of the Laplace operator by the first eigenvalue of the operator 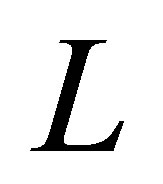 (see [12]).
(see [12]).
In this paper, we have chosen to treat a co-operative parabolic system with Dirichlet boundary conditions. The results can be extended to the case of 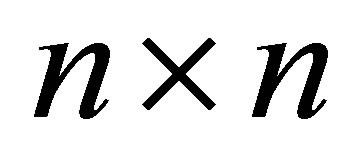 cooperative parabolic system with Neumann boundary conditions: if we take
cooperative parabolic system with Neumann boundary conditions: if we take 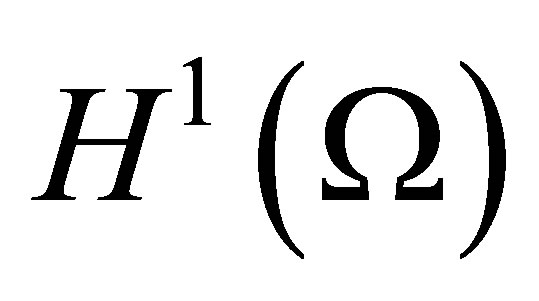 instead of
instead of 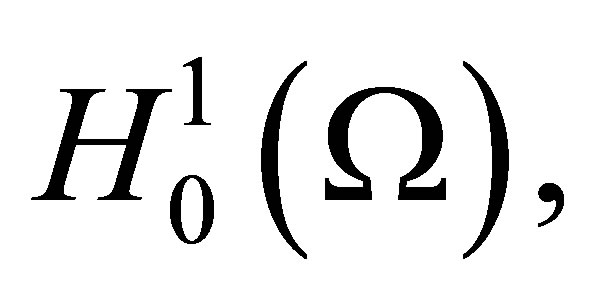 we have to replace the Dirichlet boundary conditions
we have to replace the Dirichlet boundary conditions 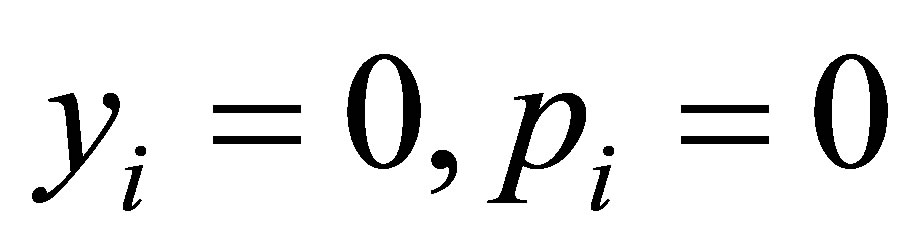 on the boundary by Neumann boundary conditions
on the boundary by Neumann boundary conditions 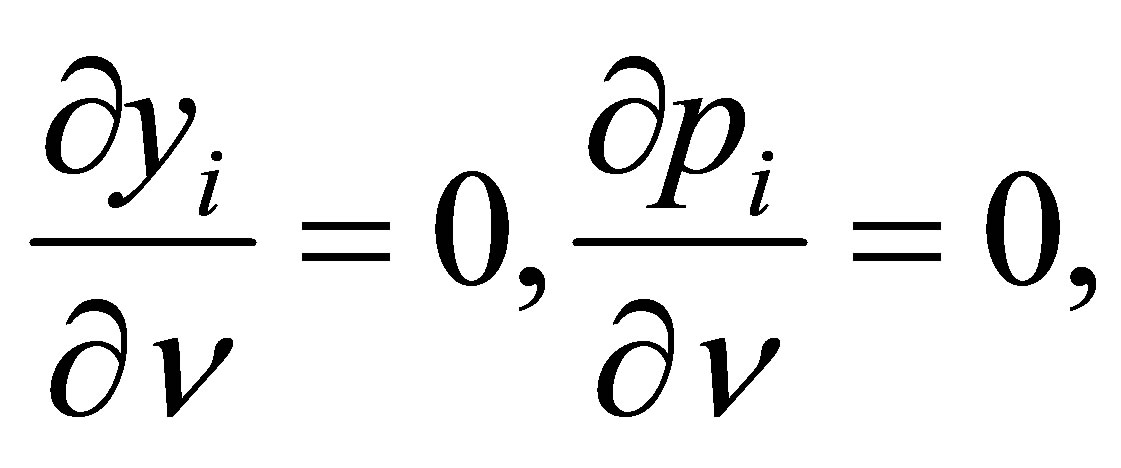 where
where 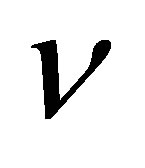 is the outward normal.
is the outward normal.
The results in this paper carry over to the fixed-time problem ([1] chapter 3).
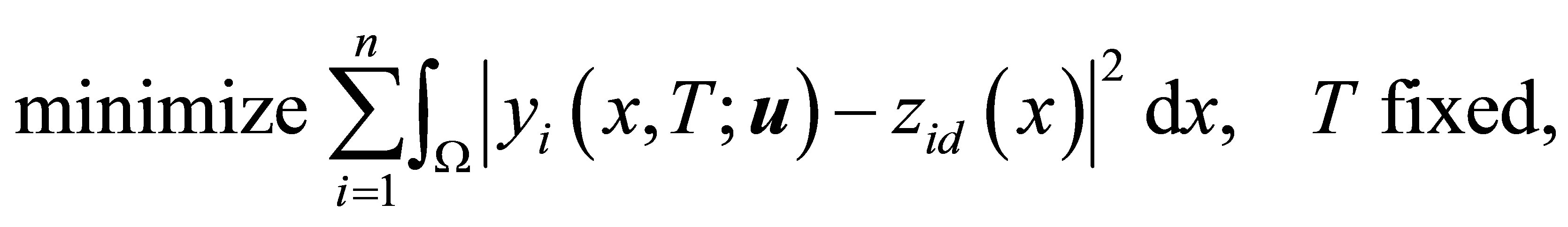
subject to (11) [except in the trivial case where 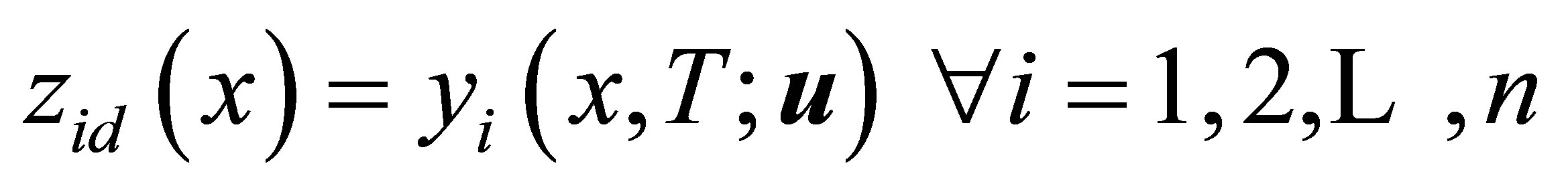 for some admissible control
for some admissible control ]. This can be proven in an analogous manner, as the necessary and sufficient conditions for optimality for this problem coincide with (11), (16) and (25) (with
]. This can be proven in an analogous manner, as the necessary and sufficient conditions for optimality for this problem coincide with (11), (16) and (25) (with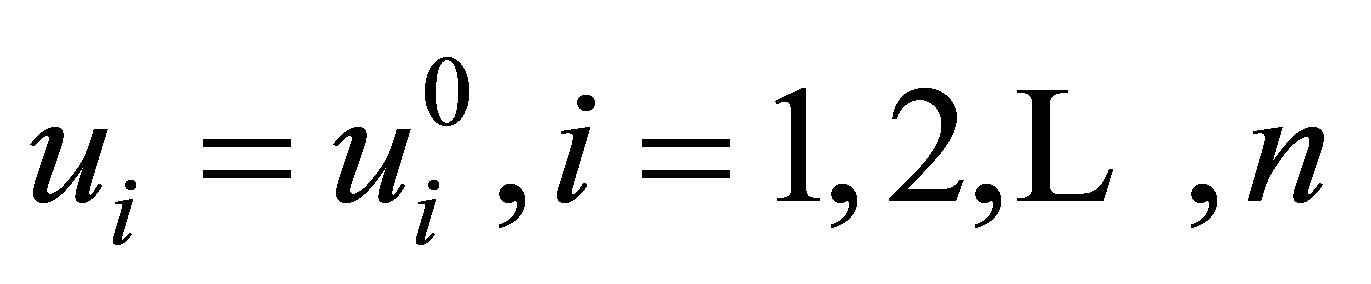 ).
).
REFERENCES
- J. L. Lions, “Optimal Control of Systems Governed by Partial Differential Equations,” Springer-Verlag, New York, 1971. http://dx.doi.org/10.1007/978-3-642-65024-6
- J. L. Lions and E. Magenes, “Non-Homogeneous Boundary Value Problem and Applications, I, II,” Spring-Verlage, New York, 1972.
- H. O. Fattorini, “Infinite Dimensional Optimization Theory and Opotimal Control,” Cambridge University Press, Cambridge, 1998.
- K. D. Phung, G. Wang and X. Zhang, “On the Existence of Time Optimal Controls for Linear Evolution Equations,” Discrete and Continuous Dynamical Systems, Series B, Vol. 8, No. 4, 2007, pp. 925-941. http://dx.doi.org/10.3934/dcdsb.2007.8.925
- G. Knowles, “Time Optimal Control of Parabolic Systems with Boundary Condition Involving Time Delays,” Journal of Optimization Theory and Applications, Vol. 25, No. 1, 1978, pp. 563-574. http://dx.doi.org/10.1007/BF00933521
- H. O. Fattorini, “Infinite Dimensional Linear Control Systems: The Time Optimal and Norm Optimal Problems,” North-Holland Mathematics Studies, Vol. 201, Elsevier, Amsterdam, 2005.
- X. Li and J. Yong, “Optimal Control Theory for Infinite Dimensional Systems,” Birkhauser, Boston, 1995. http://dx.doi.org/10.1007/978-1-4612-4260-4
- H. A. El-Saify, H. M. Serag and M. A. Shehata, “TimeOptimal Control for Co-Operative Hyperbolic Systems Involving Laplace Operator,” Journal of Dynamical and Control Systems, Vol. 15, No. 3, 2009, pp. 405-423. http://dx.doi.org/10.1007/s10883-009-9067-y
- M. A. Shehata, “Some Time-Optimal Control Problems for n × n Co-Operative Hyperbolic Systems with Distributed or Boundary Controls,” Journal of Mathematical Sciences: Advances and Applications, Vol. 18, No. 1-2, 2012, pp. 63-83.
- A. Kowalewski, “Optimal Control via Initial State of an Infinite Order Time Delay Hyperbolic System,” 15th International Conference on Methods and Models in Automation and Robotics (MMAR), 23-26 August 2010, pp. 275-277.
- R. A. Adams, “Sobolev Spaces,” Academic Press, New York, 1975.
- J. Fleckinger, J. Hernández and F. de Thélin, “On the Existence of Multiple Principal Eigenvalues for Some Indefinite Linear Eigenvalue Problems,” Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A: Matemáticas, Vol. 97, No. 2, 2003, pp. 461-466.

