Advances in Pure Mathematics
Vol. 3 No. 6 (2013) , Article ID: 37447 , 11 pages DOI:10.4236/apm.2013.36077
Optimality of Distributed Control for n ( n Hyperbolic Systems with an Infinite Number of Variables
Department of Mathematics, Faculty of Applied sciences, Umm AL-Qura University, Makkah, Saudi Arabia
Email: drahqamlo@yahoo.com
Copyright © 2013 Ahlam Hasan Qamlo. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received June 10, 2013; revised July 13, 2013, accepted August 11, 2013
Keywords: Hyperbolic Operators; Cooperative Systems; Spaces With an Infinite Number of Variables; Existence and Uniqueness of Solutions; Distributed Control Problems; Control Constraints; Variable Coefficients
ABSTRACT
In this paper, we study the existence of solutions for 2l order (n ´ n) cooperative systems governed by Dirichlet and Neumann problems involving hyperbolic operators with an infinite number of variables and with variable coefficients. The necessary and sufficient conditions for optimality of the distributed control with constraints are obtained and the set of inequalities that defining the optimal control of these systems are also obtained.
1. Introduction
The optimality conditions for systems consisting of only one equation and for n × n systems governed by different types of partial differential equations defined on spaces of functions of infinitely many variables have been discussed for example in [1-11].
In addition, optimal control problems for systems involving operators with an infinite number of variables for non-standard functional and time delay have been introduced in [12,13].
Furthermore, time-optimal control of systems with an infinite number of variables has been studied in [14-18].
Some applications of optimal control problem for systems involving Schrodinger operators are introduced for example in [19-21].
Making use of the theory of Lions [22] and Berezanskiĭ [23], we consider the optimal control problem of distributed type for 2l order (n × n) cooperative systems governed by Dirichlet and Neumann problems involving hyperbolic operators with an infinite number of variables and with variable coefficients. We first prove the existence and uniqueness of the state for these systems, then we find the set of equations and inequalities that characterize the optimal control of these systems. Finally, we impose some constraints on the control. Necessary and sufficient conditions for optimality with control constraints are derived.
This paper is organized as follows. In Section 1, we introduce spaces of functions of an infinite number of variables. In Section 2, we discuss the distributed control problem for these systems with Dirichlet conditions. In Section 3, we consider the problem with Neumann conditions.
2. Sobolev Spaces with an Infinite Number of Variables
This section covers the basic notations, definitions, and properties, which are necessary to present this work [24]. Let  be a sequence of continuous positive probability weights such that
be a sequence of continuous positive probability weights such that

with respect to it we introduce on the region  , the measure dr(x) by:
, the measure dr(x) by:
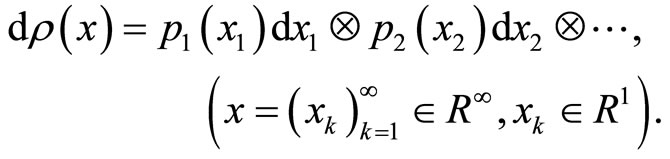
On  we construct the space
we construct the space  with respect to this measure such that
with respect to this measure such that 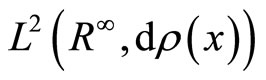 is the space of all square integrable functions on
is the space of all square integrable functions on 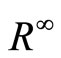 i.e.
i.e.
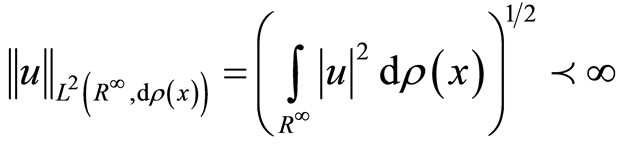 .
.
We shall set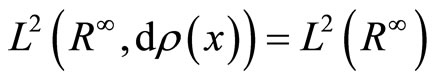 .
.
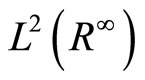 is a Hilbert space for the scalar product
is a Hilbert space for the scalar product
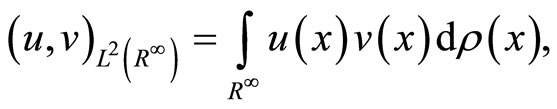
associated to the above norm.
We consider a Sobolev space in the case of an unbounded region. For functions which are continuously differentiable l times up to the boundary G of 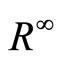 and which vanish in a neighborhood of ¥, we introduce the scalar product
and which vanish in a neighborhood of ¥, we introduce the scalar product
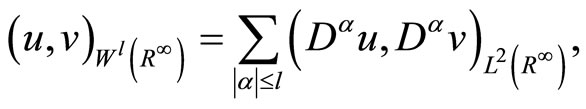
where 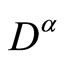 is defined by
is defined by
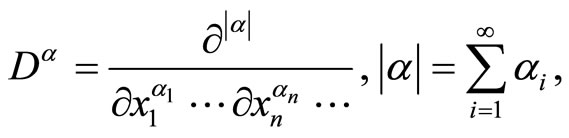
and the differentiation is taken in the sense of generalized function on , and after the completion, we obtain the Sobolev space
, and after the completion, we obtain the Sobolev space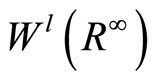 , which is a Hilbert space and dense in
, which is a Hilbert space and dense in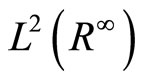 . The space
. The space 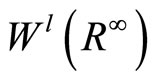 forms a positive space. We can construct the negative space
forms a positive space. We can construct the negative space 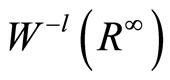 with respect to the zero space
with respect to the zero space 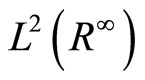 and then we have the following imbedding
and then we have the following imbedding
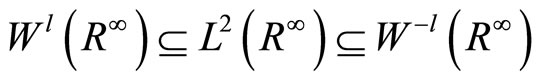 ,
,
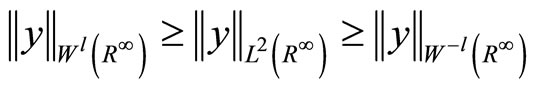 .
.
Analogous to the above chain we have a chain of the form
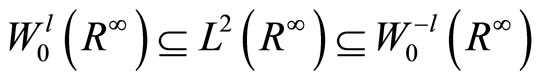 ,
,
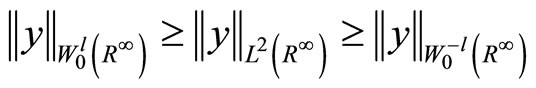 where
where
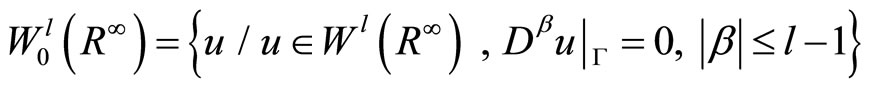
with the scalar product
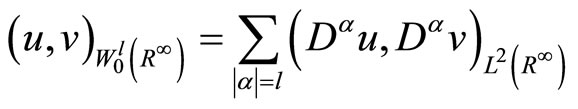
and 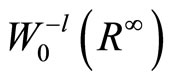 is its dual.
is its dual.
 denotes the space of measurable function t ® f(t) on open interval (0,T) for the Lebesgue measure dt and such that
denotes the space of measurable function t ® f(t) on open interval (0,T) for the Lebesgue measure dt and such that
 endowed with the scalar product
endowed with the scalar product
 which is a Hilbert space.
which is a Hilbert space.
Analogously, we can define the spaces
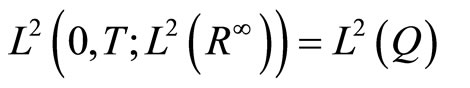 and
and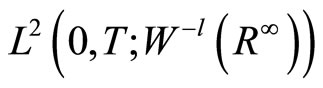 then we have a chain in the form
then we have a chain in the form
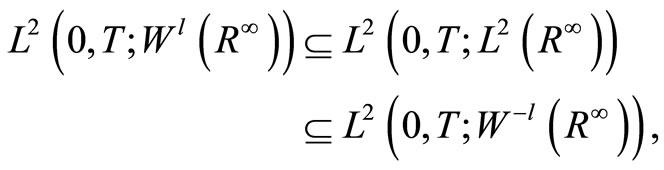
where  with boundary
with boundary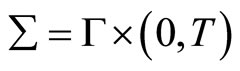 .
.
By the Cartesian product, it is easy to construct the following Sobolev spaces 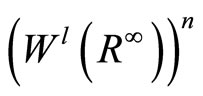 with the norm defined by
with the norm defined by
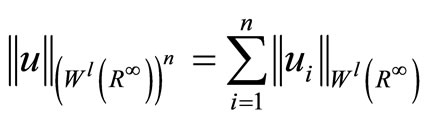 where
where  is a vector function and
is a vector function and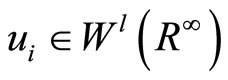 , also we can construct the Cartesian product for the above Hilbert spaces. Finally we have the following chain:
, also we can construct the Cartesian product for the above Hilbert spaces. Finally we have the following chain:


where
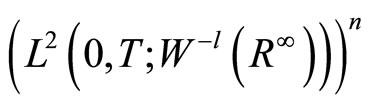 and
and 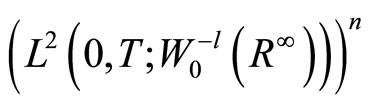
are the dual spaces of 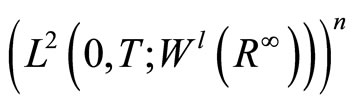 and
and 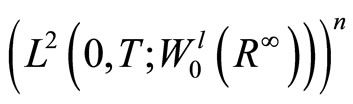 resp.
resp.
3. Dirichlet Problem for 2l Order (n × n) Cooperative Hyperbolic System with an Infinite Number of Variables and with Variable Coefficients
In this section, we study the existence and uniqueness of solutions for 2l order 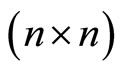 cooperative systems governed by Dirichlet problems involving hyperbolic operators with an infinite number of variables and with variable coefficients, then we find the necessary and sufficient conditions of the optimal control of distributed type.
cooperative systems governed by Dirichlet problems involving hyperbolic operators with an infinite number of variables and with variable coefficients, then we find the necessary and sufficient conditions of the optimal control of distributed type.
For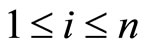 , we have the following system:
, we have the following system:
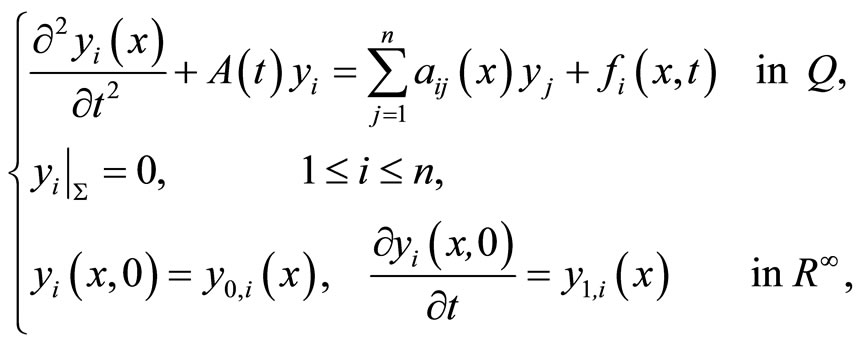 (1)
(1)
where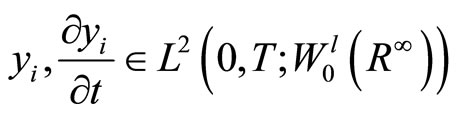 ,
, 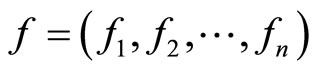
is a given function, and 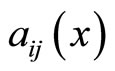 are bounded functions such that
are bounded functions such that
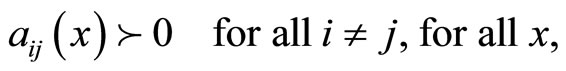 (2)
(2)
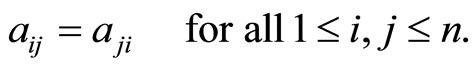 (3)
(3)
System (1) is called cooperative if (2) holds.
The operator 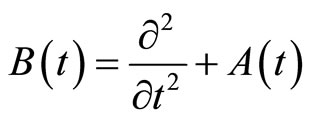 in system (1) is 2l order hyperbolic operator with an infinite number of variables with
in system (1) is 2l order hyperbolic operator with an infinite number of variables with
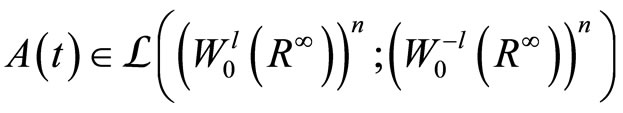 [23] is given by:
[23] is given by:
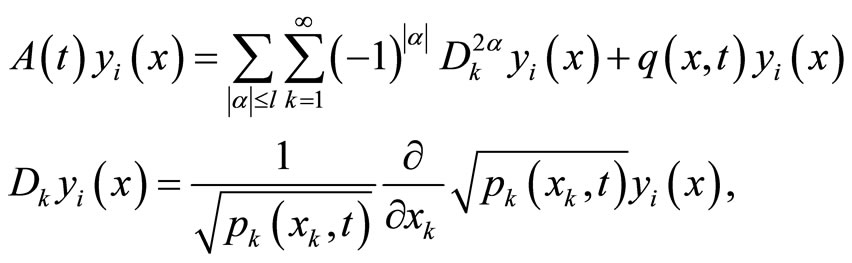 (4)
(4)
since q(x,t) is a real valued function in x which is bounded and measurable on , such that
, such that
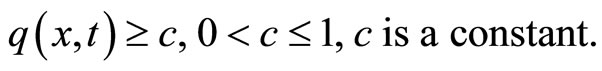 (5)
(5)
Definition 1:
For each t Î (0,T), we define a bilinear form
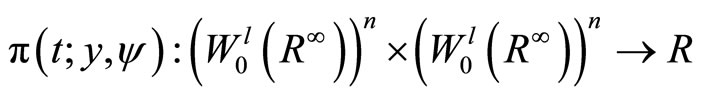 by
by
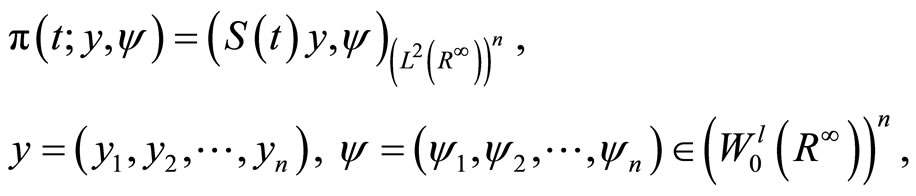
where
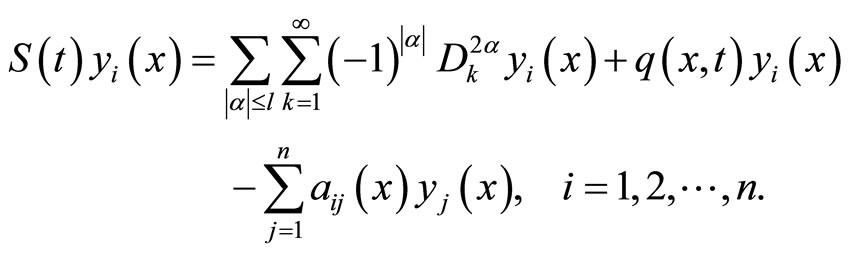
Then,
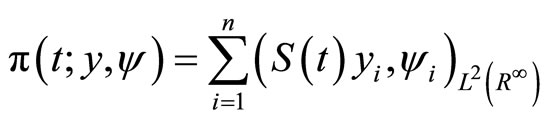 ,
,
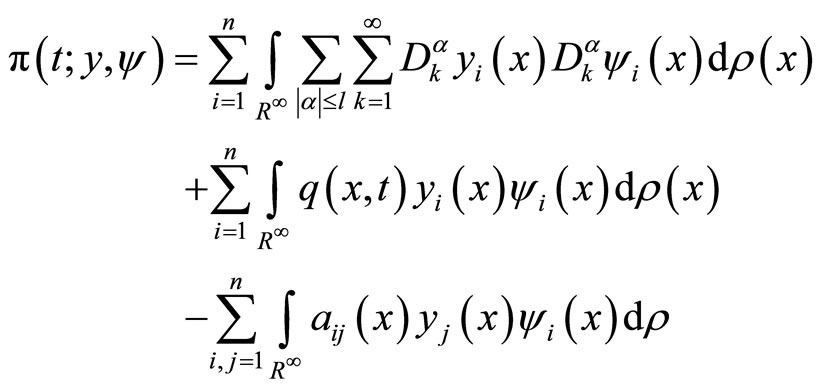 (6)
(6)
3.1. The Existence and Uniqueness of Solution
Lemma 1:
The bilinear form (6) is coercive on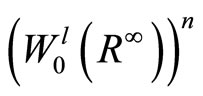 , that is, there exists c, c1 Î R, such that:
, that is, there exists c, c1 Î R, such that:
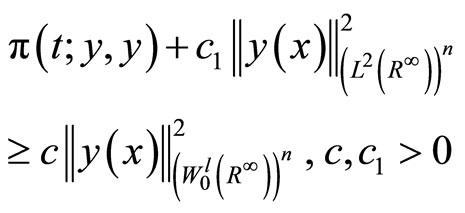 (7)
(7)
Proof:
We have,
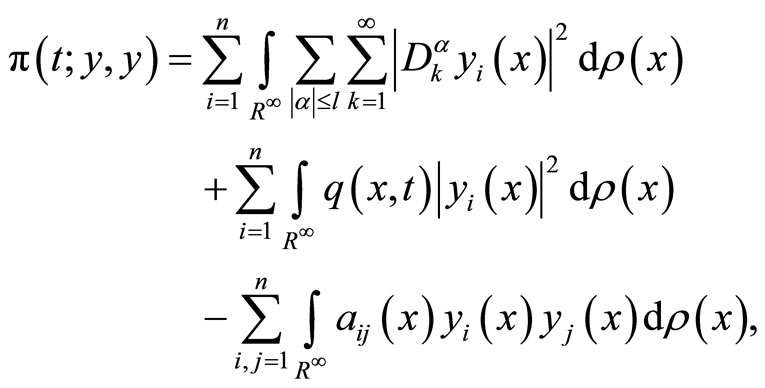
thus,

From (2), (3), and (5), we deduce
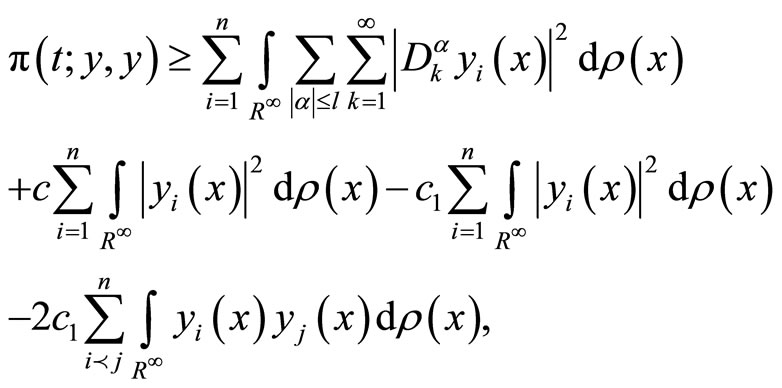
then,
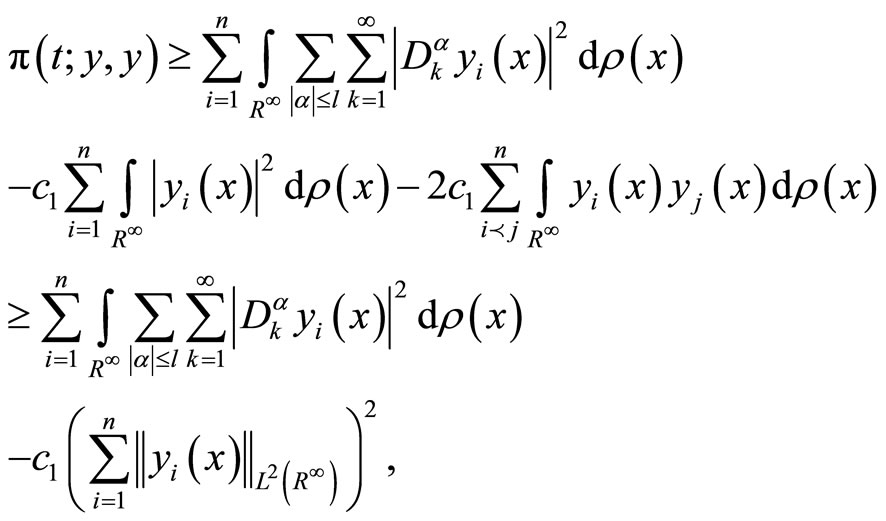

then,

since 0 < c £ 1, we have,
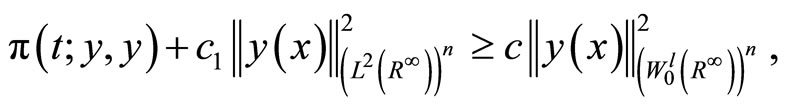
which proves the coerciveness condition on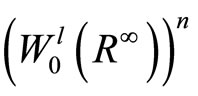 .
.
Under all the a bove consideration, theorems of Lions [22] and using the Lax-Milgram lemma we have proved the following theorem.
Theorem 1:
Under the hypotheses (2), (3) and (7), if
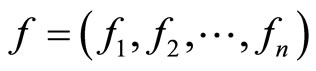 ,
,  and
and 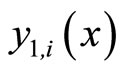 are given in
are given in
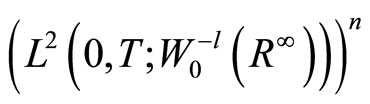 ,
, 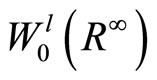 and
and 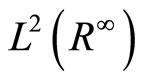 resp., then there exists a unique solution
resp., then there exists a unique solution
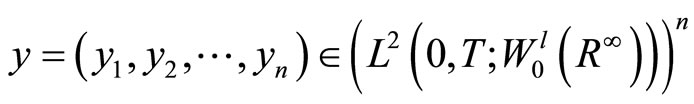
for system (1).
Proof:
Let  be a continuous linear form defined on
be a continuous linear form defined on 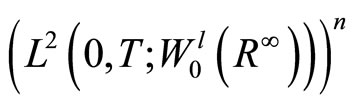 by
by
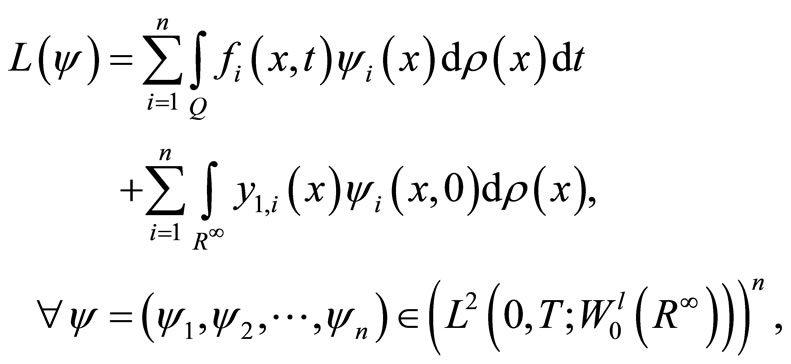
then by Lax-Milgram lemma, there exists a unique element  such that
such that
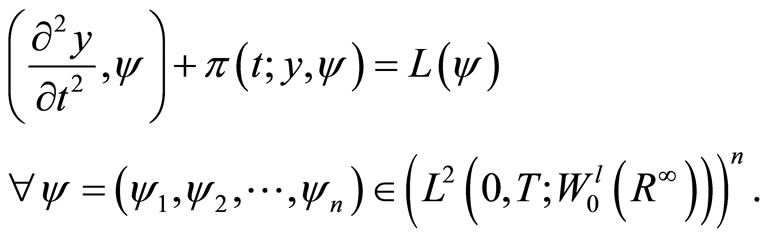 (9)
(9)
Now, let us multiply both sides of first equation of system (1) by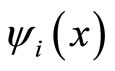 , then integration over Q, we have:
, then integration over Q, we have:
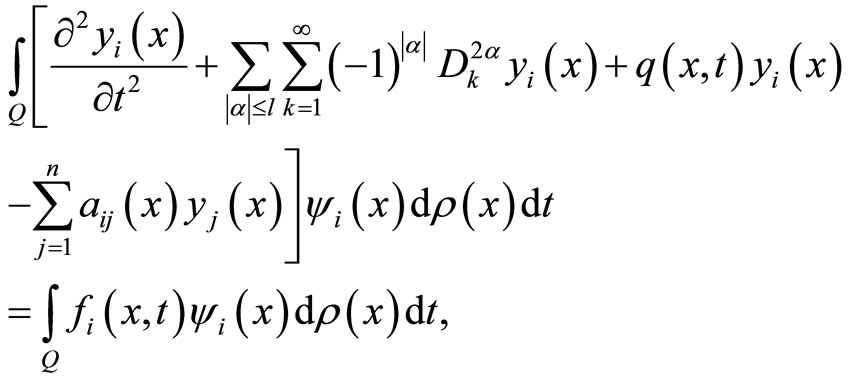
by applying Green’s formula
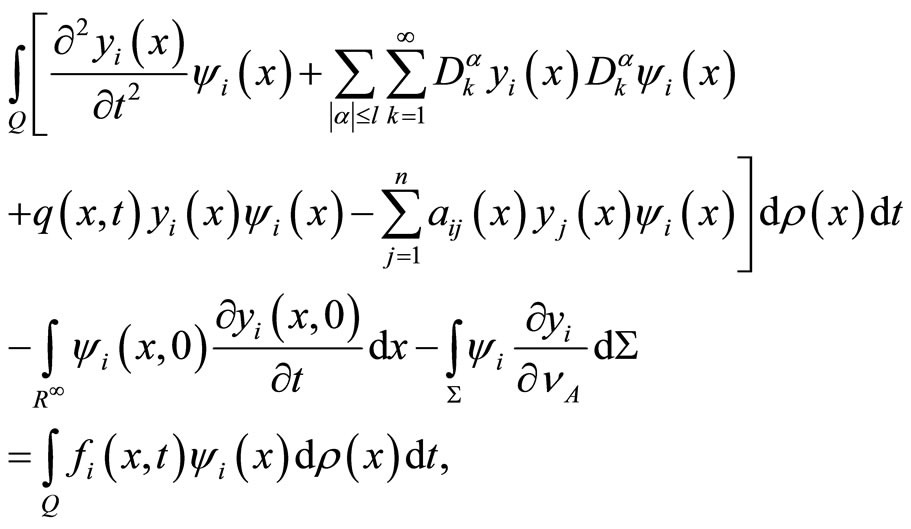
by entering the summation on the both sides, we have

by comparing the summation with (6), (8) and (9) we obtain:
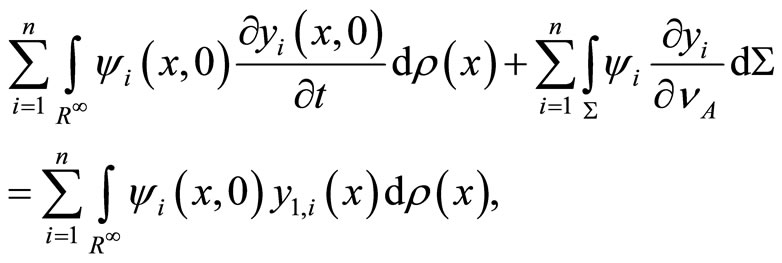
then we deduce that:

which completes the proof.
3.2. Formulation of Dirichlet Problem
The space 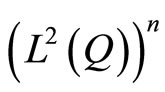 being the space of controls. For a control
being the space of controls. For a control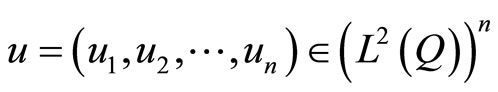 , the state
, the state
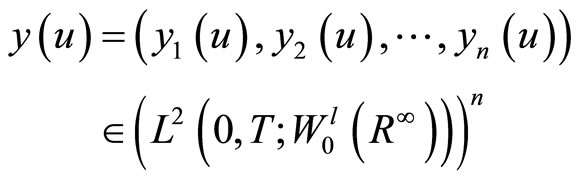
of system (1) is given by the solution of
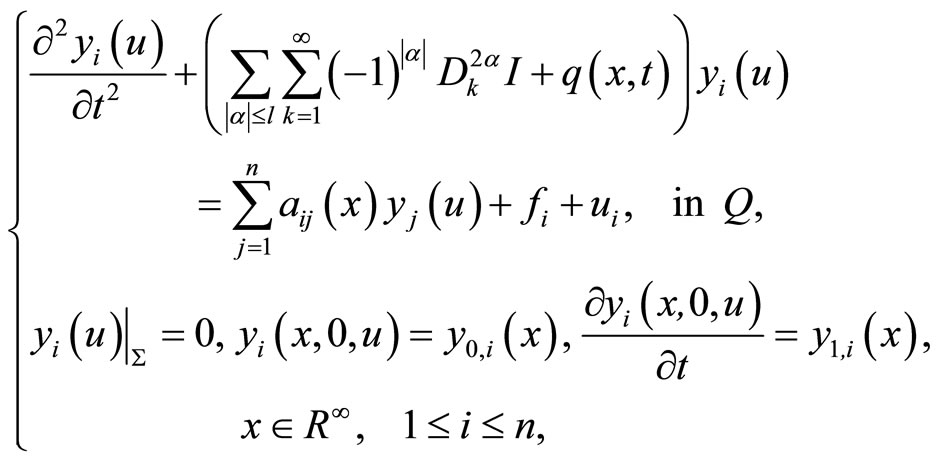 (10)
(10)
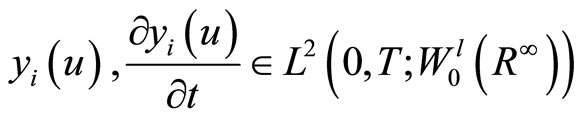 .
.
The observation equation is given by
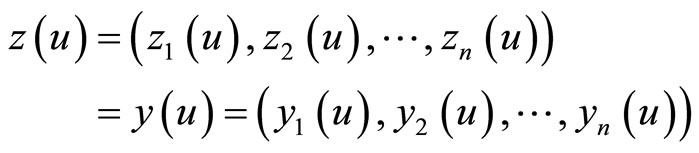 .
.
N is given as
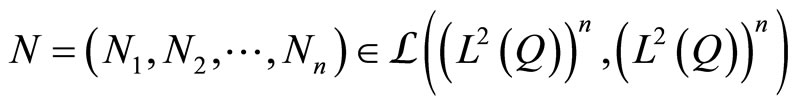
such that,
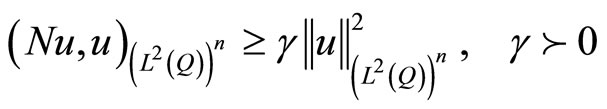 .
.
For a given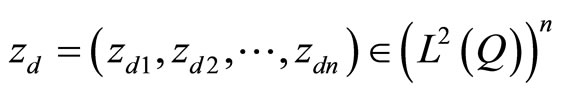 , the cost function is given by
, the cost function is given by
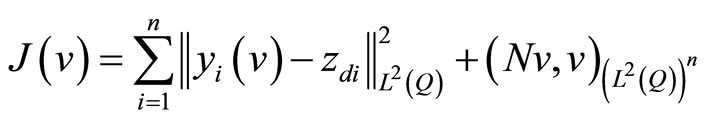 . (11)
. (11)
4. Control Constraints
The set of admissible controls Uad is a closed convex subset of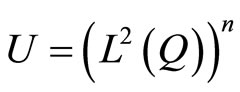 , Then the control problem is to find inf J(v) over Uad.
, Then the control problem is to find inf J(v) over Uad.
Then using the general theory of Lions [22], there exists a unique optimal control u Î Uad such that J(u) = inf J(v) for all v Î Uad. Moreover, we have the following theorem which gives the necessary and sufficient conditions of optimality.
Theorem 2:
Assume that (7) holds and the cost function is given by (11). The necessary and sufficient conditions for
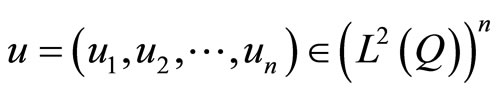
to be an optimal control are the following equations and inequalities:
 (12)
(12)
with
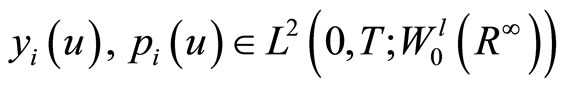 ,
,
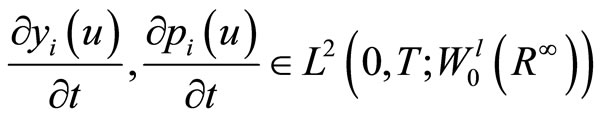 ,
,
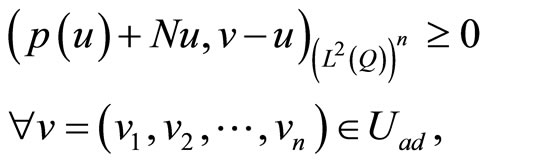 (13)
(13)
together with (10), where
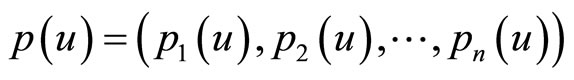
is the adjoint state.
Proof:
The optimal control  is characterized by [23]:
is characterized by [23]:

that is
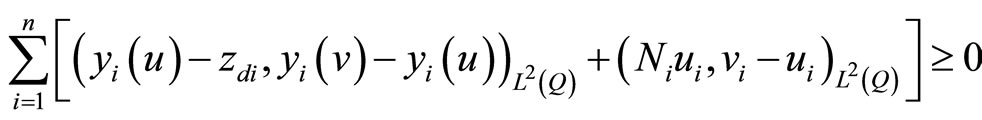
this inequality can be written as
 (14)
(14)
Now, since
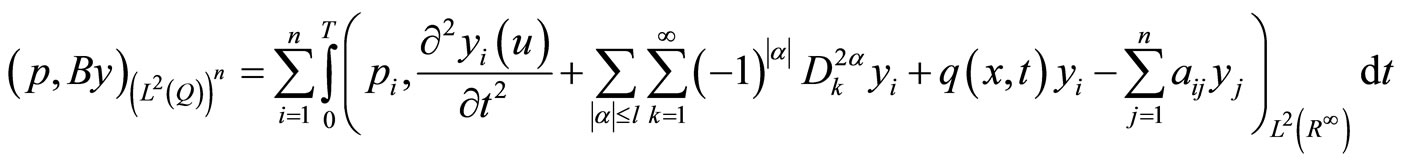
by using Green’s formula, (3) and (10), we have

Then
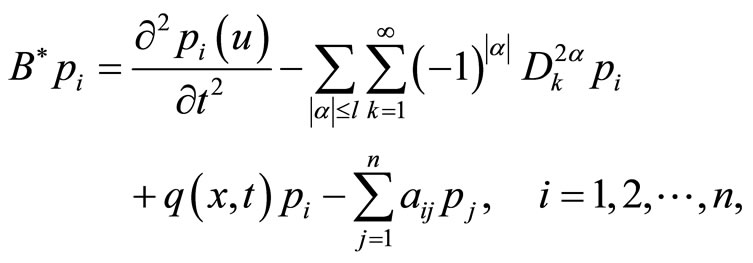
and
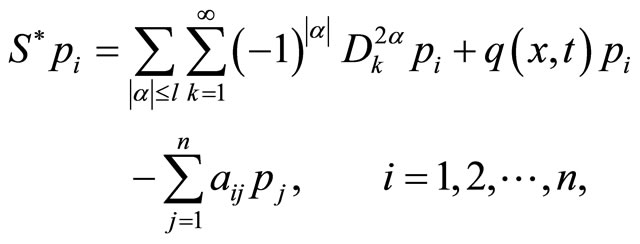 (15)
(15)
Since the adjoint equation for hyperbolic systems in Lions [22] takes the following form:
 then, from (15) we obtain the first equation in (12), and from theorem1, system (12) admits a unique solution which satisfies
then, from (15) we obtain the first equation in (12), and from theorem1, system (12) admits a unique solution which satisfies
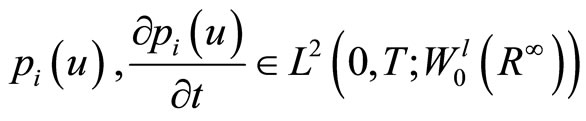 .
.
Now, we transform (14) by using (12) as follows:

using Green’s formula, (10) and (12), we obtain
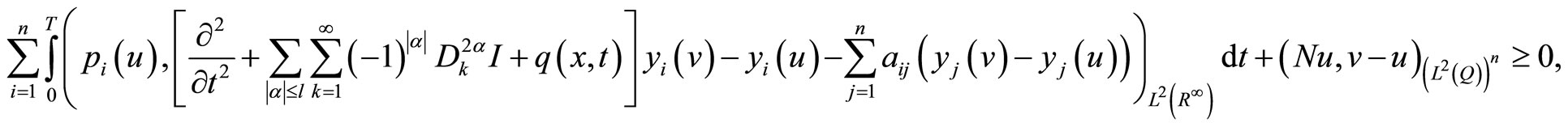
using (10), we have
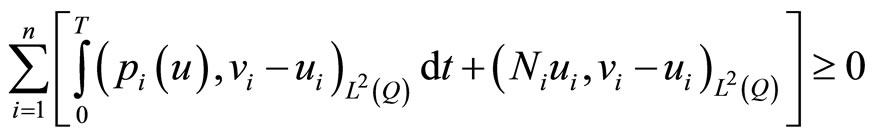 which is equivalent to
which is equivalent to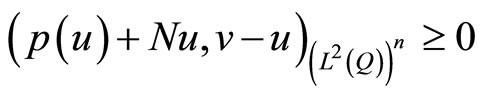 .
.
Thus the proof is complete.
5. Neumann Problem for 2l Order (n × n) Cooperative Hyperbolic System with an Infinite Number of Variables and with Variable Coefficients
In this section, we discuss the optimal control for 2l order 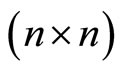 cooperative non-homogenous Neumann systems involving hyperbolic operators with an infinite number of variables and with variable coefficients.
cooperative non-homogenous Neumann systems involving hyperbolic operators with an infinite number of variables and with variable coefficients.
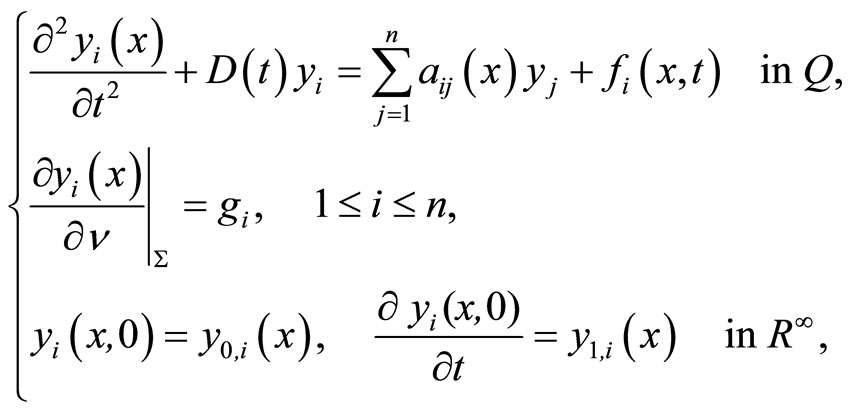 (16)
(16)
where , for all 1 £ i £ n,
, for all 1 £ i £ n,
 is a given function in
is a given function in
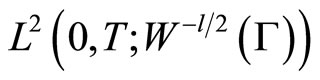 and the operator
and the operator 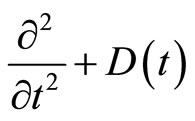 in system (16) is 2l order hyperbolic operator with an infinite number of variables with
in system (16) is 2l order hyperbolic operator with an infinite number of variables with
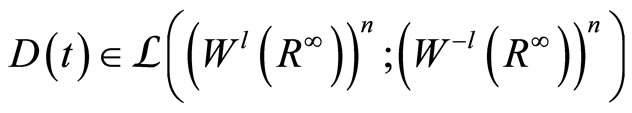
is given by:
 since q(x,t) is defined as in (5).
since q(x,t) is defined as in (5).
For each t Î (0,T), we define a bilinear form
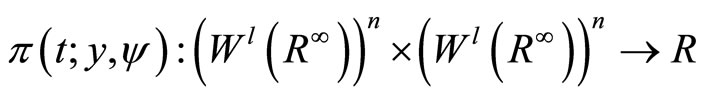
as in (6).
5.1. The Existence and Uniqueness of Solution
Lemma 2:
The bilinear form  is also coercive on
is also coercive on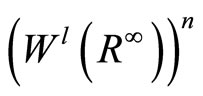 , that is, there exists c, c1Î R, such that:
, that is, there exists c, c1Î R, such that:
 (17)
(17)
Proof:
Since  is everywhere dense in
is everywhere dense in 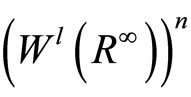 with topological inclusion, then we have
with topological inclusion, then we have
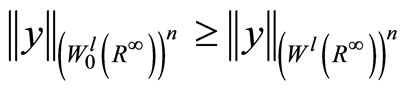 . (18)
. (18)
By using (18) in (7), we obtain
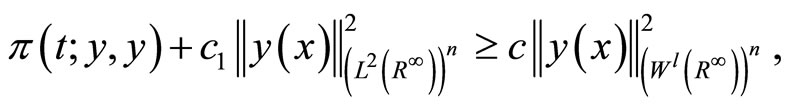
which proves the coerciveness condition on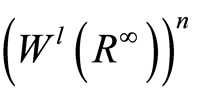 .
.
By the Lax-Milgram lemma, we shall introduce the following theorem which gives the existence and uniqueness of the state for system (16).
Theorem 3:
Under the hypotheses (2), (3) and (17), if
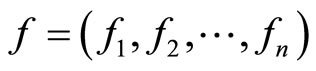 ,
, 
and 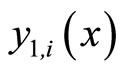 are given in
are given in ,
,
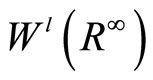 and
and 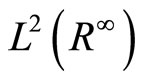 resp., then there exists a unique solution
resp., then there exists a unique solution
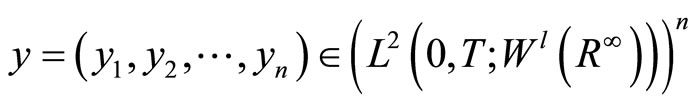
for system (16).
Proof:
Let 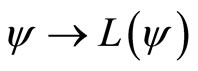 be a continuous linear form defined on
be a continuous linear form defined on 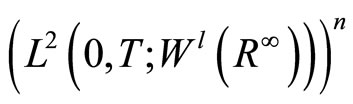 by
by
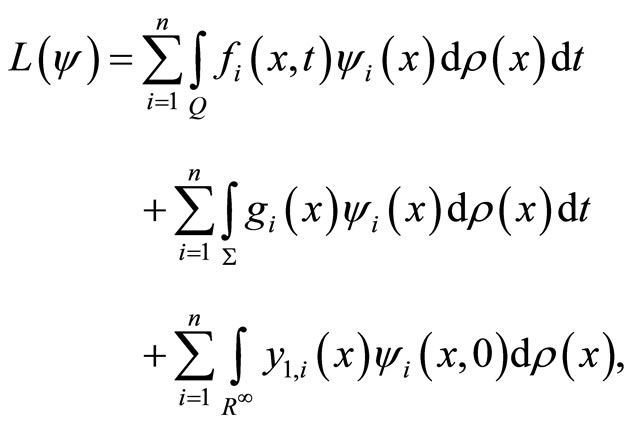 (19)
(19)
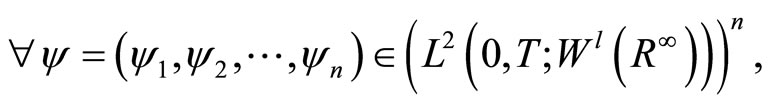
then by Lax-Milgram lemma, there exists a unique element
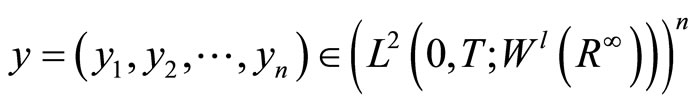
such that (9) is satisfied.

by applying Green’s formula
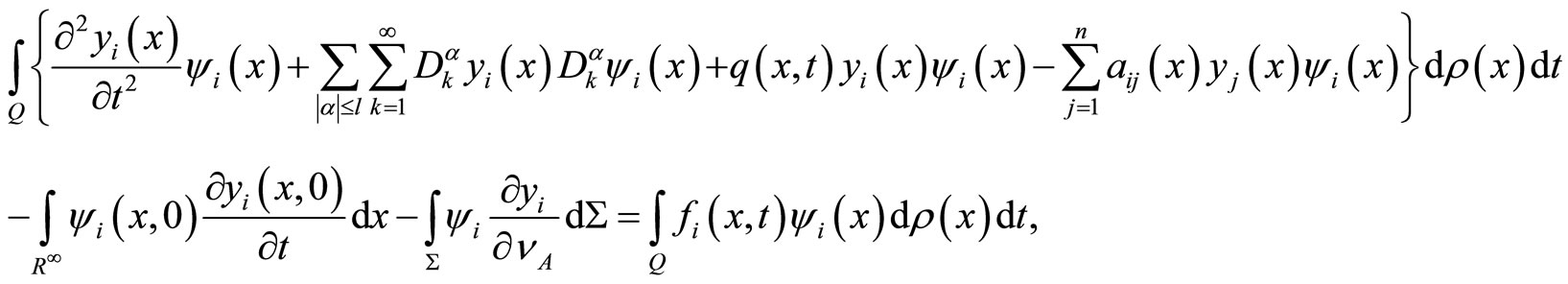
by entering the summation on the both sides, we have
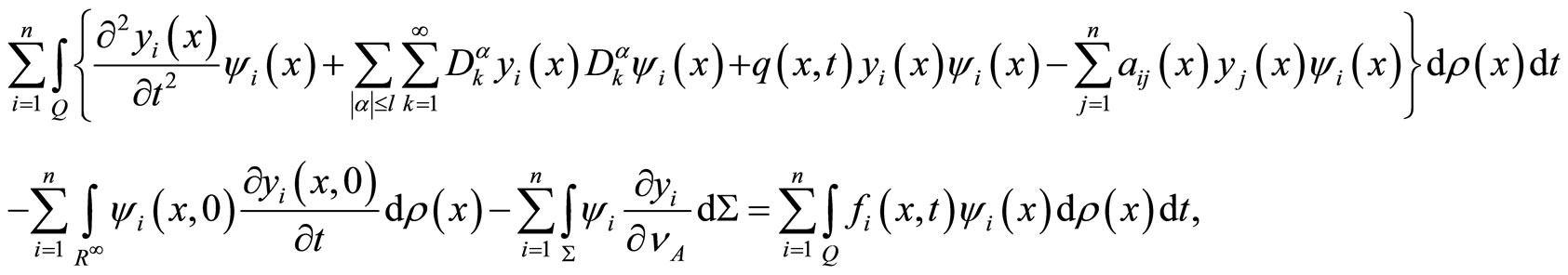
by comparing the summation with (6), (8) and (9) we obtain:
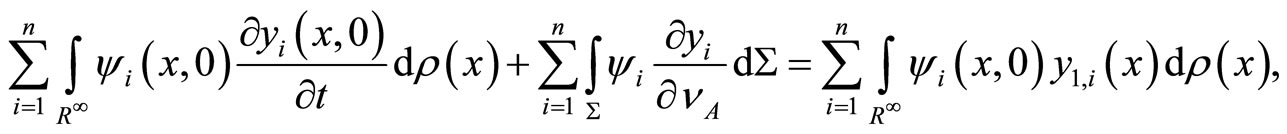
then we deduce that:
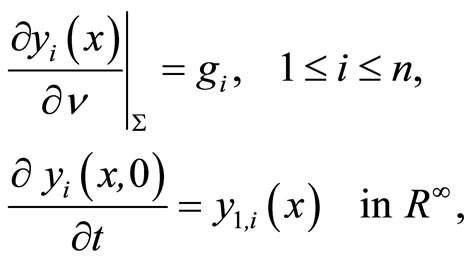
which completes the proof.
5.2. Formulation of Neumann Problem
The space 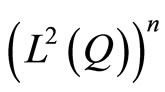 is the space of controls. The state
is the space of controls. The state
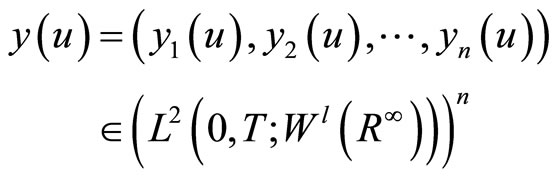
of system (16) is given by the solution of
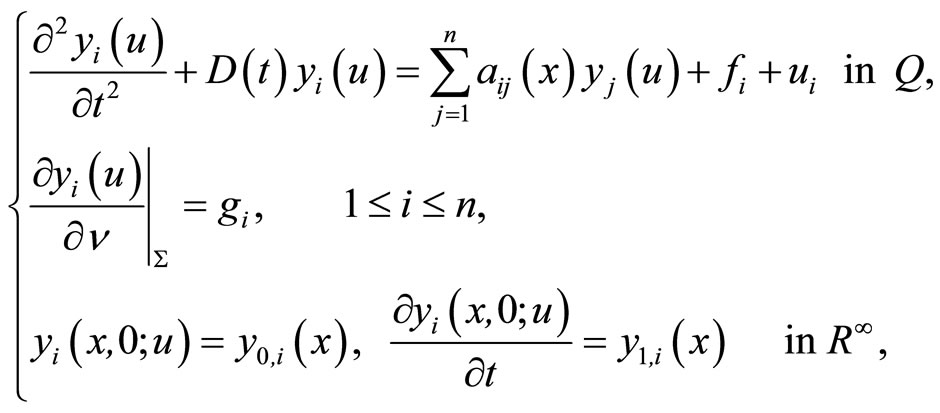 (20)
(20)
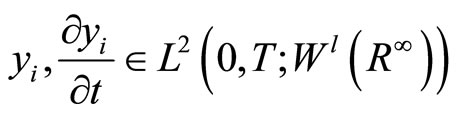 .
.
The observation equation is given by
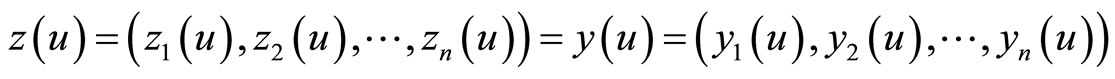 .
.
For a given , the cost function is given by
, the cost function is given by
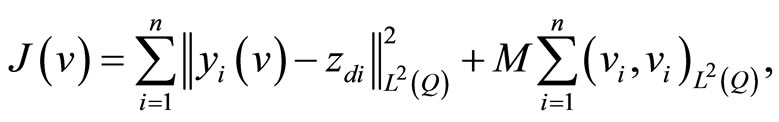 (21)
(21)
where M is a positive constant.
The control problem then is to find inf J(v) over Uad with the same control constraints in Section II.
Then as in Section II, there exists a unique optimal control uÎ Uad such that
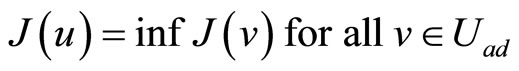 . (22)
. (22)
Under the given considerations, we may apply theorems of Lions [22] as in Section II to obtain the following theorem:
Theorem 4:
The necessary and sufficient conditions for optimality of the control problem (20), (21) and (22) are given by the following equations and inequalities:
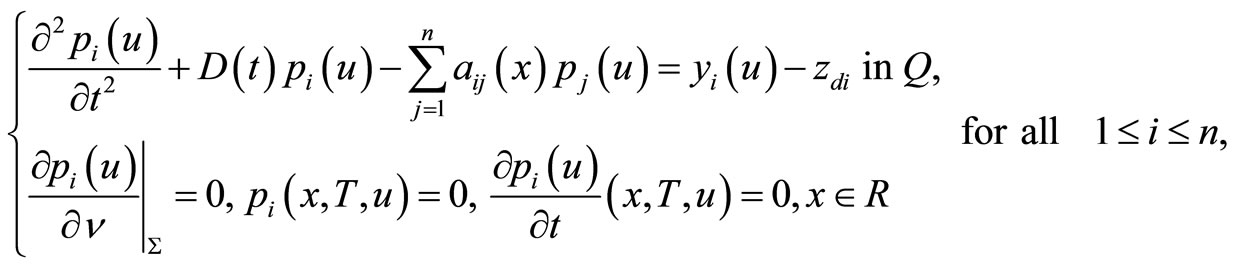 (23)
(23)
with
 ,
,
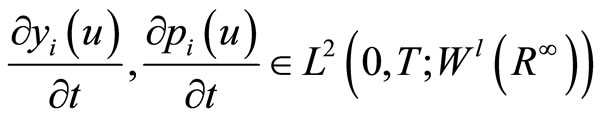 ,
,

together with (16).
The case of no constraints on the control:
In the case of no constraints on the control, i.e.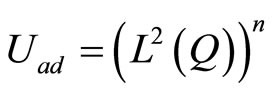 , the condition (13) reduces to
, the condition (13) reduces to
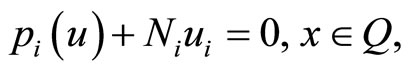
hence .
.
Example 1:
If we take n = 2 in Dirichlet problem (1) with the same conditions of coefficients (2) and (3), then the space of controls is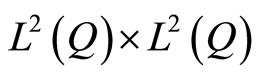 . For a control
. For a control
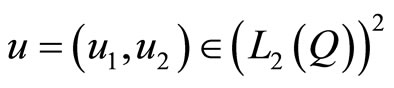 the state
the state
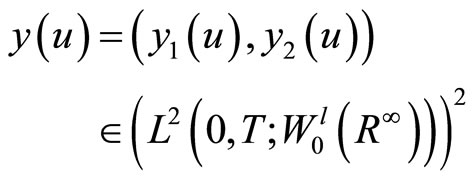
of the system is given by the solution of
 (24)
(24)
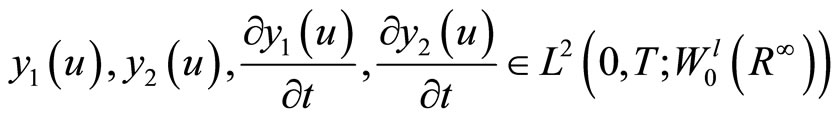 .
.
The necessary and sufficient conditions for the optimality are the following equations and inequalities:
 (25)
(25)
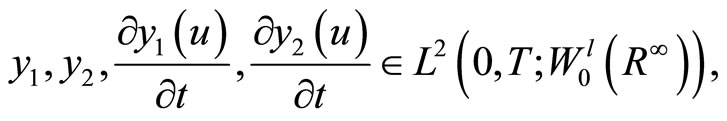
 ,
,
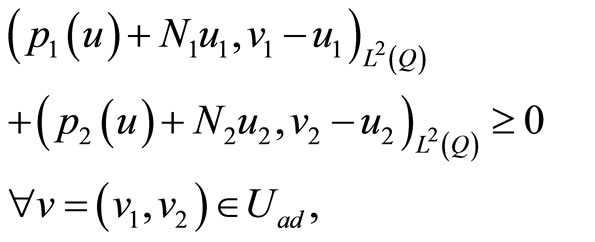 (26)
(26)
together with (24), where 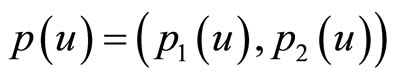 is the adjoint state.
is the adjoint state.
Example 2:
If we take
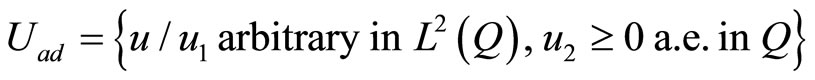 . (27)
. (27)
Thus there are no constraints on  then the inequality (26) is equivalent to
then the inequality (26) is equivalent to
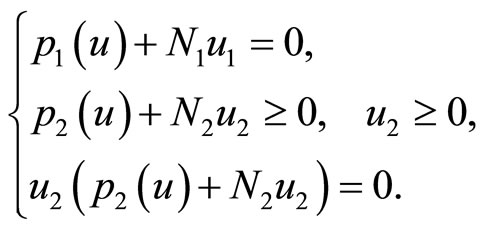 (28)
(28)
Thus the optimal control is given by the solution of the following set of equations and inequalities
 (29)
(29)
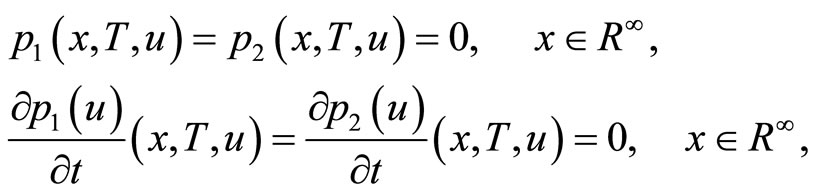
Further
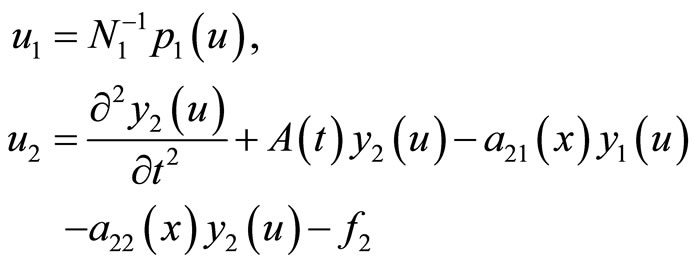 (30)
(30)
6. Conclusions
The main result of this paper finds the necessary and sufficient conditions of optimality of distributed control for 2l order (n ´ n) cooperative systems governed by Dirichlet and Neumann problems involving hyperbolic operators with an infinite number of variables and with variable coefficients that give the characterization of optimal control (Theorem 2, 4).
Also it is evident that by modifying:
• the boundary conditions (Dirichlet, Neumann, mixed)
• the nature of the control (distributed, boundary)
• the nature of the observation (distributed, boundary)
• the initial differential system
• the number of variables
• the type of equation (elliptic, parabolic and hyperbolic)
• the type of coefficients (constant, variable)
• the type of system (non-cooperative, cooperative)
• the order of equationmany of variations on the above problems are possible to study with the help of Lions formalism.
REFERENCES
- G. M. Bahaa, “Optimal Control Problems of Parabolic Equations with an Infnite Number of Variables and with Equality Constraints,” IMA Journal of Mathematical Control and Information, Vol. 25, No. 1, 2008, pp. 37-48. doi:10.1093/imamci/dnm002
- G. M. Bahaa and F. El-Shatery, “Optimal Control for n ´ n Coupled Parabolic Systems with Control-Constrained and Infinite Number of Variables,” International Journal of Mathematics & computation, Vol. 19, No. 2, 2013, pp. 106-118.
- G. M. Bahaa and F. El-Shatery, “Optimal Control for n ´ n Coupled Elliptic Systems with Control-Constrained and Infinite Number of Variables,” International Journal of Applied Mathematics & Statistics, Vol. 39, No. 9, 2013, pp. 93-104.
- H. A. El-Saify, “On Optimal Control for the Hyperbolic Operator with an Infinite Number of Variables,” Journal of Information and Optimization Sciences, Vol. 4, No. 3, 1983, pp. 249-253.
- H. A. El-Saify, H. M. Serag and G. M. Bahaa, “On Optimal Control for n ´ n Elliptic System Involving Operators with an Infinite Number of Variables,” AMSE, Vol. 37, No. 4, 2000, pp. 47-61.
- I. M. Gali and H. A. El-Saify, “Optimal Control of a System Governed by Hyperbolic Operator with an Infinite Number of Variables,” Journal of Mathematical Analysis and Applications, Vol. 85, No. 1, 1982, pp. 24-30. doi:10.1016/0022-247X(82)90023-3
- I. M. Gali and H. A. El-Saify, “Distributed Control of a System Governed by Dirichlet and Neumann Problems for a Self-Adjoint Elliptic Operator with an Infinite Number of Variables,” Journal of Optimization Theory and Applications, Vol. 39, No. 2, 1983, pp. 293-298. doi:10.1007/BF00934534
- W. Kotarski, “Optimal Control of a System Governed by a Parabolic Equation with an Infinite Number of Variables,” Journal of Optimization Theory and Applications, Vol. 60, No. 1, 1989, pp. 33-41. doi:10.1007/BF00938797
- A. H. Qamlo, “Boundary Control for Cooperative Systems Involving Parabolic Operators with an Infinite Number of Variables,” Advances in Differential Equations and Control Processes, Vol. 2, No. 2, 2008, pp. 135-151.
- A. H. Qamlo, “Distributed Control of Cooperative Systems Involving Hyperbolic Operators with an Infinite Number of Variables,” International Journal of Functional Analysis, Operator Theory and Applications, Vol. 1, No. 2, 2009, pp. 115-128.
- H. M. Serag, “Distributed Control for Cooperative Systems Involving Parabolic Operators with an Infinite Number of Variables,” IMA Journal of Mathematical Control and Information, Vol. 24, No. 2, 2007, pp. 149-161. doi:10.1093/imamci/dnl018
- W. Kotarski, “Optimal Control of a System Governed by a Parabolic Equation with an Infinite Number of Variables and Time Delay,” Journal of Optimization Theory and Applications, Vol. 63, No. 1, 1989, pp. 57-67. doi:10.1007/BF00940731
- W. Kotarski, H. A. El-Saify and G. M. Bahaa, “Optimal Control of Parabolic Equation with an Infnte Number of Variables for Non Standard Functional and Time Delay,” IMA Journal of Mathematical Control and Information, Vol. 19, No. 4, 2002, pp. 461-476. doi:10.1093/imamci/19.4.461
- G. M. Bahaa, “Time-Optimal Control Problem for Parabolic Equations with Control Constraints and Infinite Number of Variables,” IMA Journal of Mathematical Control and Information, Vol. 22, No. 3, 2005, pp. 364- 375. doi:10.1093/imamci/dni033
- H. A. El-Saify, H. M. Serag and M. A. Shehata, “Time Optimal Control Problem for Cooperative Hyperbolic Systems Involving the Laplace Operator,” Journal of Dynamical and Control Systems, Vol. 15, No. 3, 2009, pp. 405-423. doi:10.1007/s10883-009-9067-y
- W. Kotarski, H. A. El-Saify and M. A. Shehata, “Time Optimal Control of Parabolic Lag Systems with an Infinite Number of Variables,” Journal of the Egyptian Mathematical Society, Vol. 15, No. 1, 2007, pp. 21-34.
- A. H. Qamlo, “Distributed Control for Cooperative Hyperbolic Systems Involving Schrödinger Operator,” International Journal of Dynamics and Control, Vol. 1, No. 1, 2013, pp. 54-59. doi:10.1007/s40435-013-0007-z
- A. H. Qamlo, “Optimality Conditions for Parabolic Systems with Variable Coefficients Involving Schrödinger Operators,” Journal of King Saud University—Science, 2013, in press. doi:10.1016/j.jksus.2013.05.005
- H. M. Serag, “Optimal Control of Systems Involving Schrodinger operators,” Control and Intelligent Systems, Vol. 32, No. 3, 2004, pp. 154-157. doi:10.2316/Journal.201.2004.3.201-1319
- H. M. Serag and A. H. Qamlo, “On Elliptic Systems Involving Schrodinger Operators,” Mediterranean Journal of Measurement and Control, Vol. 1, No. 2, 2005, pp. 91-96.
- H. M. Serag and A. H. Qamlo, “Maximum Principle and Existence of Solutions for Non Necessarily Cooperative Systems Involving Schrodinger Operators,” Mathematica Slovaca, Vol. 58, No. 5, 2008, pp. 567-580. doi:10.2478/s12175-008-0094-z
- J. L. Lions, “Optimal Control of Systems Governed by Partial Differential Equations,” Springer Verlag, Berlin, 1971.
- Ju. M. Berezanskii, “Self-Adjiontness of Elliptic Operators with an Infnite Number of Variables,” Ukrainian Mathematical Journal, Vol. 27, 1975, pp. 729-742.
- Ju. M. Berezanskii and I. M. Gali, “Positive Definite Functions of an Infinite Number of Variables in a Layer,” Ukrainian Mathematical Journal, Vol. 24, No. 4, 1972, pp. 435-464.

