Advances in Pure Mathematics
Vol.3 No.7(2013), Article ID:38122,6 pages DOI:10.4236/apm.2013.37083
Order Relation on the Permutation Symbols in the Ehresmann Subvariety Class Associated to the Distinguished Monomials of Flag Manifolds
Department of Mathematics, University of Ibadan, Ibadan, Nigeria
Email: ph.adeyemo@mail.ui.edu.ng, ilorisa1@yahoo.com
Copyright © 2013 Praise Adeyemo, Samuel Ilori. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received June 2, 2013; revised July 8, 2013; accepted August 5, 2013
Keywords: Natural Asset; Financial Value; Neural Network
ABSTRACT
In this paper, we use the theory of lexicographical and graded lexicographical orders to compare two distinguished monomials through their codes of invariants  and study the effect of this comparison on their respective defining permutation symbols in the Ehresmann subvariety classes.
and study the effect of this comparison on their respective defining permutation symbols in the Ehresmann subvariety classes.
1. Introduction
A flag 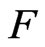 is a nested system
is a nested system
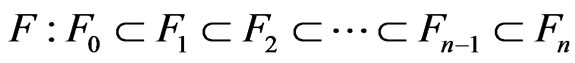 (1)
(1)
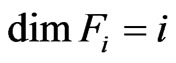 ,
, 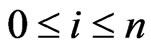 of subspaces of P(V), the projective space of an (n + 1)-dimensional vector space V over
of subspaces of P(V), the projective space of an (n + 1)-dimensional vector space V over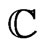 , the field of complex numbers. The set of all such flags is called flag manifold and will be denoted by
, the field of complex numbers. The set of all such flags is called flag manifold and will be denoted by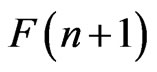 . The general linear group
. The general linear group  acts transitively on
acts transitively on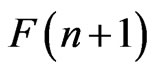 . Let E be a fixed reference flag in
. Let E be a fixed reference flag in . The isotropic group of
. The isotropic group of 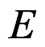 is a Borel subgroup
is a Borel subgroup 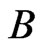 so that
so that
 (2)
(2)
Its dimension is . The flag manifold F(n + 1)
. The flag manifold F(n + 1)
is the disjoint union of 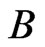 -orbits indexed by elements of symmetric group
-orbits indexed by elements of symmetric group 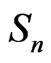
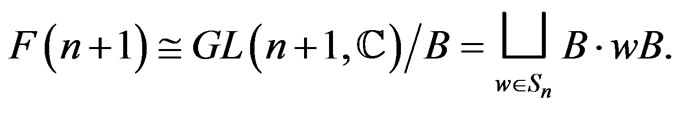 (3)
(3)
The major interest in this direction has been on the cohomology of these manifolds, where by cohomology, we mean in a general sense; singular and equivariant, K-theory and equivariant K-theory. For each of these theories, there are two descriptions of cohomology. One is in terms of Ehresmann classes, which are cohomology associated to the Ehresmann subvarieties of 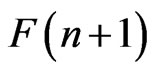 given in terms of permutation symbols. There is one Ehresmann class for each permutation symbol [1]. The Ehresmann classes form a basis for the cohomology over its ground ring and the other is in terms of generators and relations called the Borel-Hirzebruch basis elements [2].
given in terms of permutation symbols. There is one Ehresmann class for each permutation symbol [1]. The Ehresmann classes form a basis for the cohomology over its ground ring and the other is in terms of generators and relations called the Borel-Hirzebruch basis elements [2].
Definition 1. Let
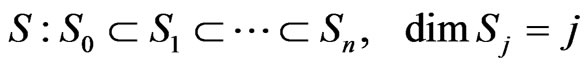
be a fixed flag. An Ehresmann symbol is a matrix
 (4)
(4)
where 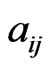 are the integers such that
are the integers such that
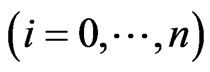
 .
.
Following Monk [3], the 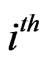 row of this symbol is to be interpreted as a Schubert condition
row of this symbol is to be interpreted as a Schubert condition  on the element
on the element 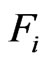 of
of . The matrix represents a subvariety of
. The matrix represents a subvariety of 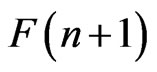 consisting of all the flags F satisfying the conditions:
consisting of all the flags F satisfying the conditions:
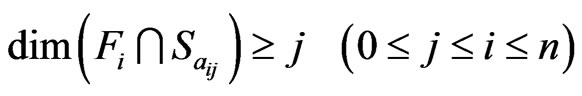 (5)
(5)
Definition 2. The variety of 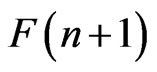 is said to be irreducible(and the corresponding symbol is called an irreducible symbol) if for every
is said to be irreducible(and the corresponding symbol is called an irreducible symbol) if for every 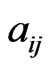
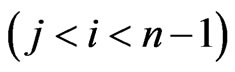 , there exists
, there exists  such that
such that 
The set of all such irreducible varieties is called the Ehresmann base.
Remark 1. Writing a matrix for each irreducible symbol is unwieldy and Monk [3] suggested representing the matrix by a permutation 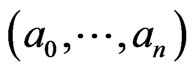 of
of  where
where  is the new element in the
is the new element in the  row and
row and 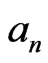 is the missing integer. Conversely every permutation of
is the missing integer. Conversely every permutation of 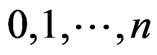 determines an irreducible symbol and hence the number of elements in the Ehresmann base is
determines an irreducible symbol and hence the number of elements in the Ehresmann base is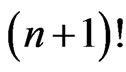 .
.
It has been proved that the dimension of the subvariety represented by the matrix when irreducible is
 (6)
(6)

2. Distinguished Monomials
It is well known in [4-6] that the flag manifold 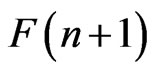 comes equipped with a flag of tautological vector bundles
comes equipped with a flag of tautological vector bundles  and associated sequence of line bundles
and associated sequence of line bundles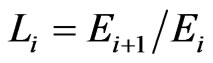 ,
, . The
. The 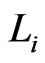 possess natural hermitian structures induced from the standard hermitian metric
possess natural hermitian structures induced from the standard hermitian metric 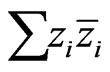 on
on  -dimensional vector space
-dimensional vector space  over
over . For
. For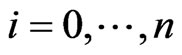 , we denote by
, we denote by , the
, the  -dimensional Chern form on
-dimensional Chern form on  of the hermitian line bundle
of the hermitian line bundle  [7-9]. In other words, they represent the Chern classes
[7-9]. In other words, they represent the Chern classes  in the cohomology of
in the cohomology of . The only nontrivial Chern class is the first Chern class, which is an element of the second cohomology group of the manifold [10]. The cohomology ring
. The only nontrivial Chern class is the first Chern class, which is an element of the second cohomology group of the manifold [10]. The cohomology ring  is therefore, generated by the Chern classes
is therefore, generated by the Chern classes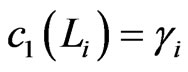 .
.
There is indeed a correspondence between the permutation symbols and the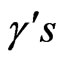 , viz,
, viz,

and it is interesting to note that any permutation symbol can be identified uniquely with certain product of these generators. These specialized products are called the distinguished monomials.
Definition 3. Let 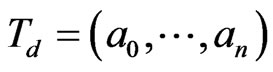 be any cycle of the Ehresmann subvariety class of dimension
be any cycle of the Ehresmann subvariety class of dimension  in the cohomology of the flag manifold
in the cohomology of the flag manifold , then the product
, then the product  is the distinguished monomial of
is the distinguished monomial of 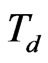
where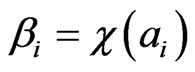 , that is,
, that is,

Example 1. The distinguished monomial of the cycle  in the Ehresmann cycle class of dimension 2 of the cohomology of F(4) is given by
in the Ehresmann cycle class of dimension 2 of the cohomology of F(4) is given by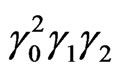 .
.
Definition 4. The degree  of the distinguished monomial
of the distinguished monomial  is given by
is given by , the index of the cycle
, the index of the cycle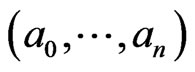 , that is,
, that is, 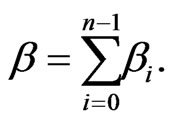
The collection of distinguished monomials is denoted by 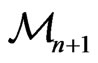
3. Main Results
We now compare any two distinguished monomials and study the effect of this comparison on their respective defining cycles via the code of invariants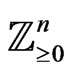 , the collection of
, the collection of 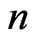 -tuple exponents of distinguished monomials. In order to this, we impose ordering on these monomials. In practice, we shall assume the following relation on the generators
-tuple exponents of distinguished monomials. In order to this, we impose ordering on these monomials. In practice, we shall assume the following relation on the generators 
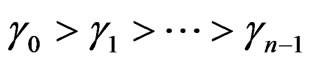
Several orderings can be defined on set of monomials but due to the characterization of , it seems lexicographic order and graded lexicographic order are most appropriate.
, it seems lexicographic order and graded lexicographic order are most appropriate.
Definition 5 (Lexicographic Order). Let
 and
and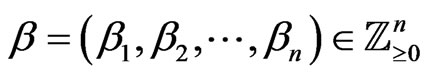 the collection of
the collection of  -tuple exponents of distinguished monomials.
-tuple exponents of distinguished monomials. 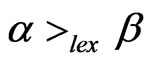 if in the vector difference
if in the vector difference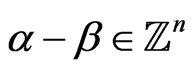 , the left-most nonzero entry is positive. We shall write
, the left-most nonzero entry is positive. We shall write

if 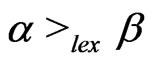

Definition 6 (Graded lexicographic Order). Let , the collection of
, the collection of  -tuple exponents of distinguished monomials. We say
-tuple exponents of distinguished monomials. We say
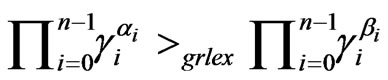
if
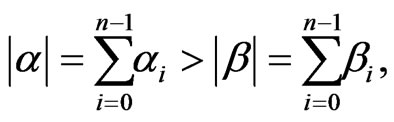
or  and
and .
.
The distinguished monomial ordering relation on  on the code of invariants
on the code of invariants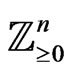 , the set of
, the set of  -tuple of collection of monomials is well-ordered. By the distinguished monomial ordering relation on
-tuple of collection of monomials is well-ordered. By the distinguished monomial ordering relation on  in this context, we mean graded lexicographic order on
in this context, we mean graded lexicographic order on 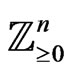 and denote it by
and denote it by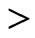 .
.
Definition 7. Let  and
and  be any two cycles in the Ehresmann cycle class
be any two cycles in the Ehresmann cycle class
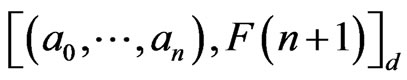
of dimension . We say
. We say

if
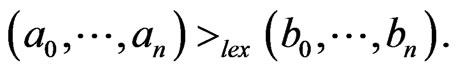
Remark 2. In general, the ordering extends over the the Ehresmann base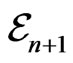 . In other words, the ordering still holds even if the cycles are not equivalent.
. In other words, the ordering still holds even if the cycles are not equivalent.
Lemma 1. If  and
and  are any two irreducible symbols of the Ehresmann subvarieties in the the flag manifold
are any two irreducible symbols of the Ehresmann subvarieties in the the flag manifold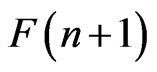 , then
, then  is equivalent to
is equivalent to 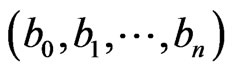 if and only if
if and only if
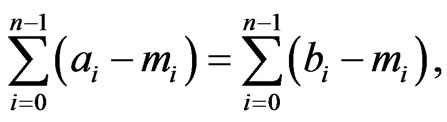
where
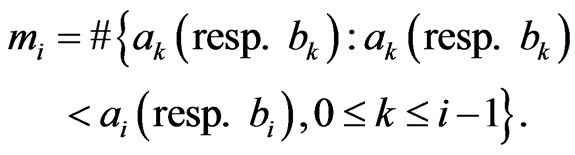
Remark 3. Equivalence of permutation symbols is an equivalence relation. Each of the partitions is called the Ehresmann cycle class and denoted by

where  is the dimension of the class and hence the flag manifold
is the dimension of the class and hence the flag manifold  is given by the disjoint union:
is given by the disjoint union:
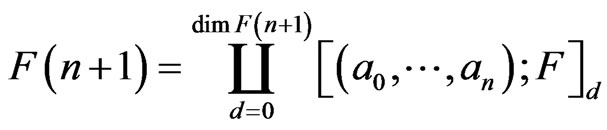 (7)
(7)
Theorem 1. Let 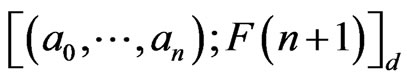 be an Ehresmann cycle class of the flag manifold
be an Ehresmann cycle class of the flag manifold . Let
. Let  be the subcollection of the distinguished monomials of degree
be the subcollection of the distinguished monomials of degree  of
of  in the cohomology ring of the manifold
in the cohomology ring of the manifold . Then the dimension of of the class
. Then the dimension of of the class
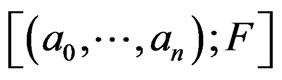 is expressed in terms of the degree of the monomials, that is
is expressed in terms of the degree of the monomials, that is

Proof. The dimension of any Ehresmann cycle class in the flag manifold 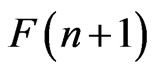 has been proved by Ehresmann[3] and given by
has been proved by Ehresmann[3] and given by
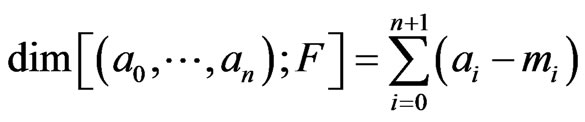 (8)
(8)
where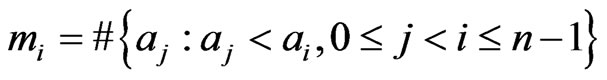 . Extending the summation to accommodate
. Extending the summation to accommodate  automatically puts
automatically puts  which makes equation 8 still stable. In this case,
which makes equation 8 still stable. In this case,  turns out to be index
turns out to be index 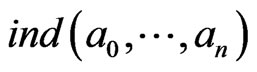
of any cycle  in the class
in the class 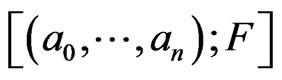
given by 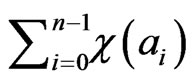 which coincides with the degree of the distinguished monomial of the cycle. The
which coincides with the degree of the distinguished monomial of the cycle. The 
is precisely the dimension of the flag manifold that is,
that is,  and hence
and hence
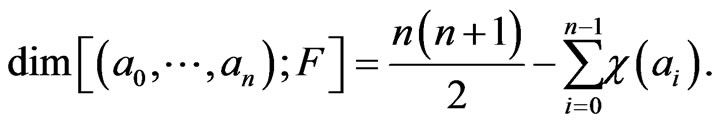
Theorem 2. Let
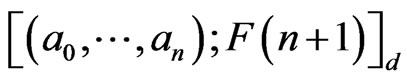
be the Ehresmann cycle class of dimension 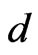 in the cohomology of
in the cohomology of , and let
, and let

be the disjoint union of such classes. Let

be the graded monoid of distinguished monomials of degrees 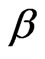 in the cohomology ring of the flag manifold
in the cohomology ring of the flag manifold . Then there is a natural bijection
. Then there is a natural bijection
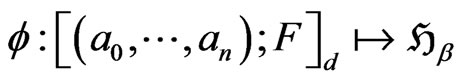
between 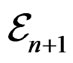 and
and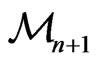 .
.
Proof
We define a map
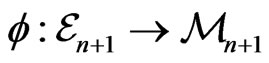
by
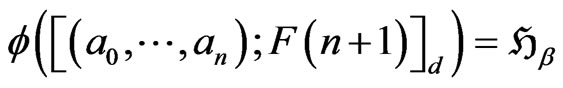 (9)
(9)
where  is a subcollection of
is a subcollection of , that is,
, that is,
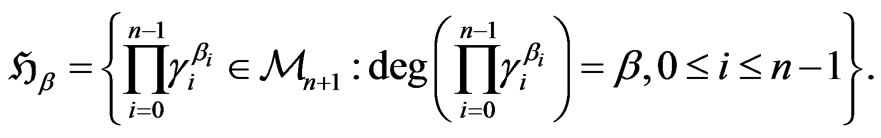
Let

and
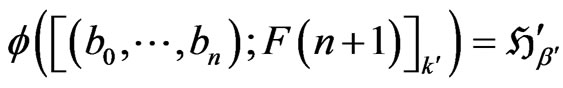 ,
,
 ,
,
 .
.
Suppose that
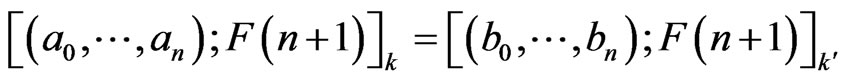
which implies that

where
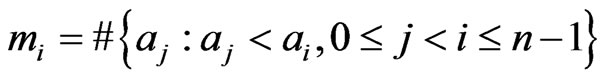

From the Theorem 1,

and hence
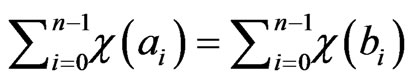
which implies that

Therefore,  is well defined.
is well defined.
Suppose that
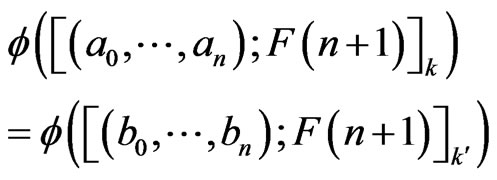
in other words 
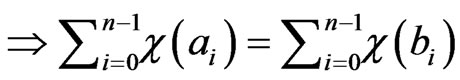


and therefore,

and hence  is injective.
is injective.
For any subcollection  in
in . By definition,
. By definition,
 implies that
implies that 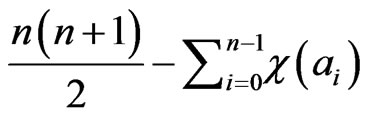 is the dimesion of the Ehresmann class
is the dimesion of the Ehresmann class
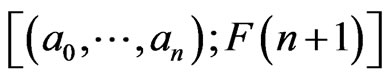 in
in 
such that
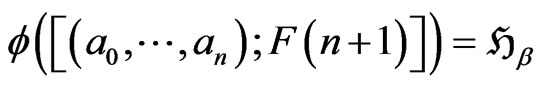 .
.
Theorem 3. If the distinguished monomials of two cycles 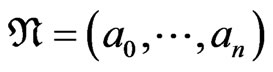 and
and 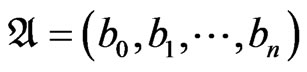 in the the Ehresmann base
in the the Ehresmann base  are equal then the two cycles coincide.
are equal then the two cycles coincide.
Proof
In other words, the theorem says no two distinct cycles share the same distinguished monomial. Suppose that  and
and  are not equivalent in the sense of Lemma 2, this leads to the fact that
are not equivalent in the sense of Lemma 2, this leads to the fact that

and hence different distinguished monomials. Now suppose they are equivalent, this implies that
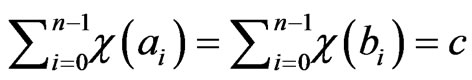 .
.
Consider the set  consisting of
consisting of
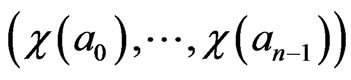 and
and .
.
 is a subcollection of
is a subcollection of 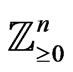 being the set of
being the set of  -tuple exponents of distinguished monomials. Since
-tuple exponents of distinguished monomials. Since  is well ordered,
is well ordered,  has a least element and therefore, the distinguished monomials defined by the two
has a least element and therefore, the distinguished monomials defined by the two  -tuple exponents differ.
-tuple exponents differ.
Corollary 1. If 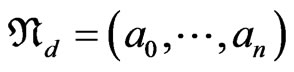 is a cycle in the Ehresmann cycle class
is a cycle in the Ehresmann cycle class

of dimension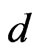 . Then
. Then  has at most one distinguished monomial.
has at most one distinguished monomial.
Proof
Suppose 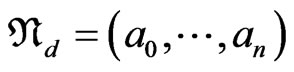 is identified with
is identified with
 and
and then the
then the
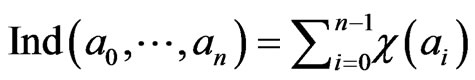
and
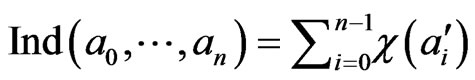 .
.
By the definition of 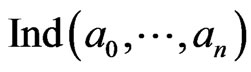 , the subset
, the subset 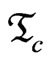 consisting of
consisting of
 and
and 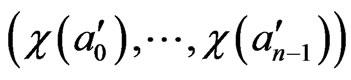
is singleton in  and hence
and hence 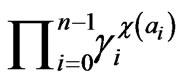 and
and 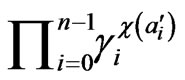 coincide.
coincide.
Using the definitions 5 and 6, we shall define ordering on the cycles of the Eheresmaan cycle class
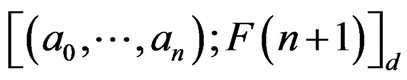
of dimension  and give some of its intrinsic properties in relation to the corresponding subcollection
and give some of its intrinsic properties in relation to the corresponding subcollection 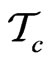 of distinguished monomials of degree
of distinguished monomials of degree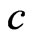 , where
, where 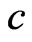 is given by
is given by
 (10)
(10)
Definition 8. Let 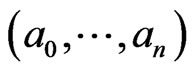 and
and  be any two cycles in the Ehresmann cycle class
be any two cycles in the Ehresmann cycle class
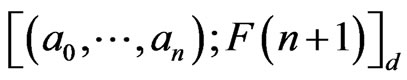
of dimension . We say
. We say

if

Remark 4. In general, the ordering extends over the Ehresmann base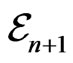 . In other words, the ordering still holds even if the cycles are not equivalent.
. In other words, the ordering still holds even if the cycles are not equivalent.
Definition 9. Let
 and
and 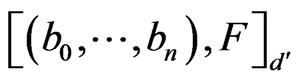
be Ehresmann cycle classes of dimension 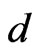 and
and  respectively, We say that
respectively, We say that
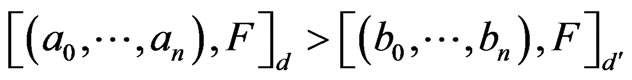
if for all cycles 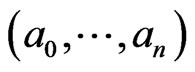 and
and 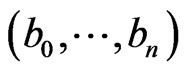 in
in
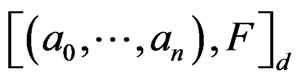 and
and 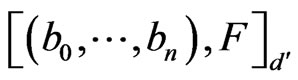
respectively, 
Given any two subcollections  and
and 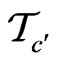 of distinguished monomials of degrees
of distinguished monomials of degrees 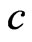 and
and  respectively
respectively
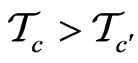 if for all distinguished monomials
if for all distinguished monomials 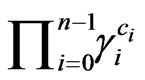
and 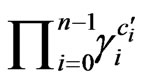 in
in 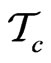 and
and  respectively,
respectively,
 .
.
Remark 5. The ordering on Ehresmann classes is characterized by dimensions while that of the subcollections of distinguished monomials is given by degrees.
Theorem 4. Let 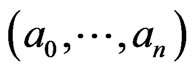 and
and  be any two cycles in the Ehresmann cycle class
be any two cycles in the Ehresmann cycle class
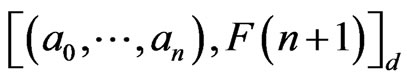
of dimension , with distinguished monomials
, with distinguished monomials 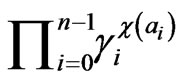 and
and 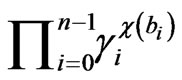 respectively then
respectively then

if and only if

Proof
Suppose that
 from 2.1,
from 2.1,  and
and 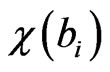 are given by
are given by

and

respectively,then there is ,
, 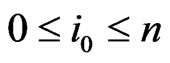 in the two
in the two 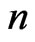 -tuple exponents
-tuple exponents


such that  and for all
and for all 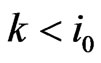
 coincides with
coincides with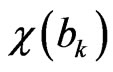 , if they exist. Therefore, in the the vector difference
, if they exist. Therefore, in the the vector difference
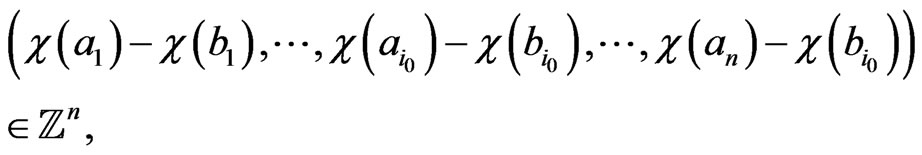
the leftmost nonzero entry is negative and and hence

and the results follows easily. On the other hand suppose

this implies that
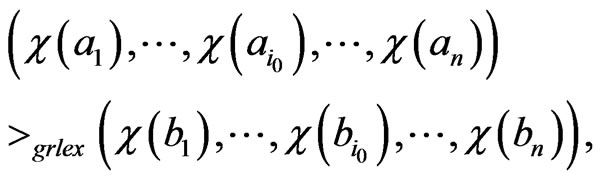
there is ,
,  such that for all
such that for all ,
, 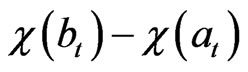 vanish, if
vanish, if  exist and
exist and
 (11)
(11)
Let the set 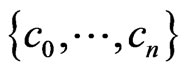 be the natural descending order of the cycles
be the natural descending order of the cycles
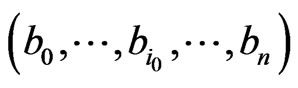 and
and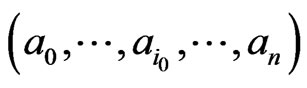 .
.
Then  is negative and
is negative and
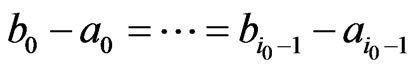 Since
Since 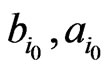 are the
are the

elements of the sets
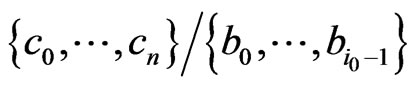 and
and 
respectively and therefore .
.
Corollary 2. Let
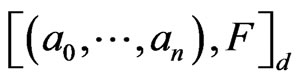 and
and 
be Ehresmann cycle classes of dimension 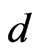 and
and  respectively, and let their corresponding subcollections of their distinguished monomials be
respectively, and let their corresponding subcollections of their distinguished monomials be 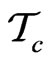 and
and  of distinguished monomials of degrees
of distinguished monomials of degrees  and
and  respectively,then
respectively,then

if and only if .
.
Corollary 3. Let
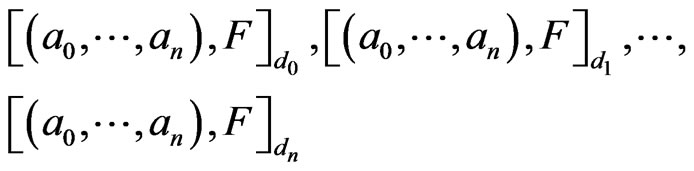
be Ehresmann cycles classes in the flag manifold  of dimensions
of dimensions 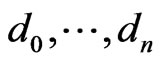 respectively such that
respectively such that , and Let
, and Let 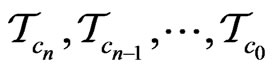 their corresponding subcollections of distinguished monomials of degrees
their corresponding subcollections of distinguished monomials of degrees 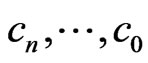 respectively,such that
respectively,such that  then the relation
then the relation
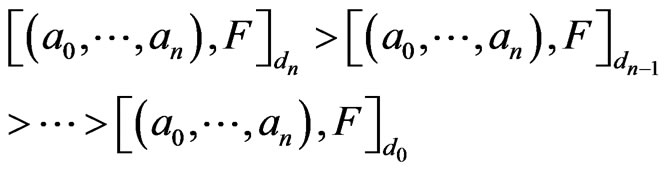
induces the relation 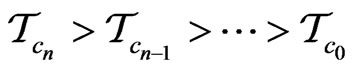 vice versa.
vice versa.
4. Acknowledgements
The first author would like to acknowledge the support provided by Education Trust Fund(Nigeria), University of Ibadan and University of New Mexico. Albuquerque, USA.
REFERENCES
- C. Ehresmann, “Sur la Topologie de Certains Espaces Homogene,” Annals of Mathematics, Vol. 35, No. 2, 1934, pp. 396-443. http://dx.doi.org/10.2307/1968440
- S. A. Ilori, “On the Geometry of Flag Manifolds and Flag Bundles. Presentata dal Corrisp. E. Martinelli,” Accademia Nazionale dei Lincei, Vol. 62, 1977, pp. 180-183.
- D. Monk, “The Geometry of Flag Manifolds,” Proceedings London Mathematical Society, Vol. 9, No. 2, 1959, pp. 252-286.
- A. Borel, “Sur La Cohomologie des Espace Fibres Principaux et des Espaces Homogenes de Groups de Lie Compacts,” Annals of Mathematics, Vol. 57, No. 1, 1953, pp. 115-207.
- A. Borel, “Topology of Lie Groups and Characteristic Classes,” Bulletin of the American Mathematical Society, Vol. 61, No. 5, 1953, pp. 397-432. http://dx.doi.org/10.1090/S0002-9904-1955-09936-1
- W. Fulton, “Flags, Schubert Polynomials, Degeneracy Loci and Determinantal Formulas,” Duke Mathematical Journal, Vol. 65, No. 3, 1992, pp. 381-420.
- A. Grothendieck, “Anneaux de Chow et Applications Chapter IV,” Seminaire Chevalley, 1958.
- F. Hirzebruch, “Topological Methods in Algebraic Geometry,” Springer, Berlin, Reprint, 1978.
- A. Kohnert, “Weintrauben, Polynome, Tableaux,” Bayreuther Mathematische Schriften, Vol. 38, 1991, pp. 1-97.
- F. Sottile, “Pieri’s Formula for Flag Manifolds and Schubert Polynomials,” Annales de L’institut Fourier (Grenoble), Vol. 46, No. 1, 1996, pp. 89-110.

