Advances in Pure Mathematics
Vol.3 No.3(2013), Article ID:31234,10 pages DOI:10.4236/apm.2013.33049
Derivation of Moment Equations for the Theoretical Description of Electrons in Nonthermal Plasmas
Leibniz Institute for Plasma Science and Technology, Greifswald, Germany
Email: markus.becker@inp-greifswald.de
Copyright © 2013 Markus M. Becker, Detlef Loffhagen. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received December 11, 2012; revised February 17, 2013; accepted March 19, 2013
Keywords: Moment Equations; Plasma Modelling; Electron Transport
ABSTRACT
The derivation of moment equations for the theoretical description of electrons is of interest for modelling of gas discharge plasmas and semiconductor devices. Usually, certain artificial closure assumptions are applied in order to derive a closed system of moment equations from the electron Boltzmann equation. Here, a novel four-moment model for the description of electrons in nonthermal plasmas is derived by an expansion of the electron velocity distribution function in Legendre polynomials. The proposed system of partial differential equations is consistently closed by definition of transport coefficients that are determined by solving the electron Boltzmann equation and are then used in the fluid calculations as function of the mean electron energy. It is shown that the four-moment model can be simplified to a new drift-diffusion approximation for electrons without loss of accuracy, if the characteristic frequency of the electric field alteration in the discharge is small in comparison with the momentum dissipation frequency of the electrons. Results obtained by the proposed fluid models are compared to those of a conventional drift-diffusion approximation as well as to kinetic results using the example of low pressure argon plasmas. It is shown that the results provided by the new approaches are in good agreement with kinetic results and strongly improve the accuracy of fluid descriptions of gas discharges.
1. Introduction
Nonthermal plasmas are widely used in many technical applications including plasma display panels, energy saving lamps, devices for microbial decontamination and ozonizers [1-4]. They are characterized by low gas temperatures 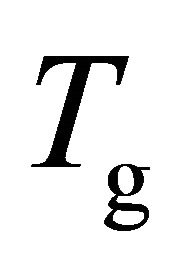 in the range from 300 to 1000 K and comparatively high mean electron energies
in the range from 300 to 1000 K and comparatively high mean electron energies 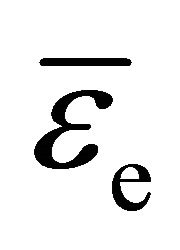 between 1 and 10 eV, where 1 eV corresponds to temperature of 11605 K. Computer simulations of electric gas discharges producing nonthermal plasmas are used since many years to get a deeper understanding of fundamental processes and to improve technical devices [5-10]. In order to describe all phenomena taking place in the discharge mechanism, in principle, a mathematical model comprising the kinetic Boltzmann equation [11]
between 1 and 10 eV, where 1 eV corresponds to temperature of 11605 K. Computer simulations of electric gas discharges producing nonthermal plasmas are used since many years to get a deeper understanding of fundamental processes and to improve technical devices [5-10]. In order to describe all phenomena taking place in the discharge mechanism, in principle, a mathematical model comprising the kinetic Boltzmann equation [11]
 (1)
(1)
for the distribution function 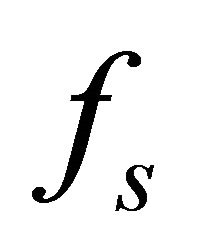 of each gas species “s” with charge
of each gas species “s” with charge 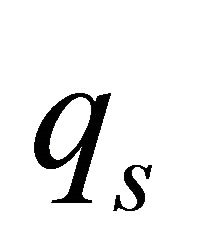 and mass
and mass 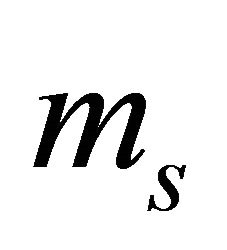 in seven-dimensional space of
in seven-dimensional space of , velocity
, velocity
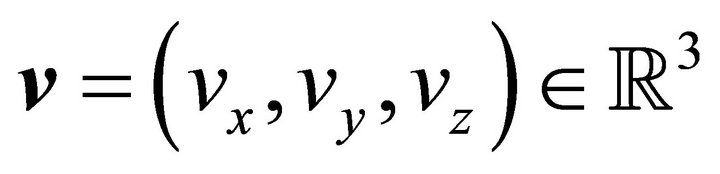 and time
and time 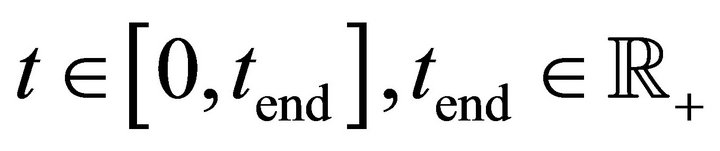 has to be solved in combination with Maxwell’s equations for the electric field
has to be solved in combination with Maxwell’s equations for the electric field  and the magnetic field
and the magnetic field . The right-hand side in (1) accounts symbolically for the change in the distribution function due to collision processes. However, such system is not solvable in reasonable computing time and several simplifying assumptions have to be taken into account. For the nonthermal plasmas under consideration, magnetic fields are negligible, and, instead of the hole system of Maxwell’s equations, the Poisson equation
. The right-hand side in (1) accounts symbolically for the change in the distribution function due to collision processes. However, such system is not solvable in reasonable computing time and several simplifying assumptions have to be taken into account. For the nonthermal plasmas under consideration, magnetic fields are negligible, and, instead of the hole system of Maxwell’s equations, the Poisson equation
 (2)
(2)
for the electric potential  is solved for determination of the electric field
is solved for determination of the electric field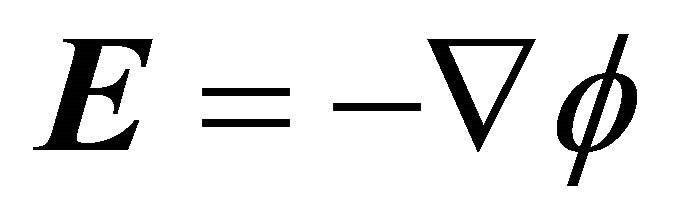 , where
, where 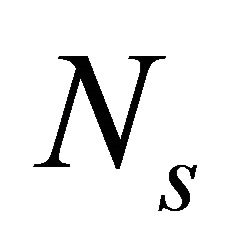 is the number of gas species with densities
is the number of gas species with densities 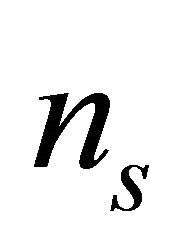 and
and 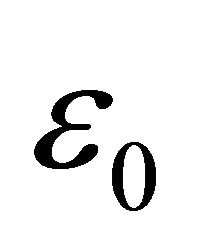 denotes the permittivity of free-space. Furthermore, heavy particles are frequently assumed to be in thermodynamic equilibrium and macroscopic fluid equations with constant temperature
denotes the permittivity of free-space. Furthermore, heavy particles are frequently assumed to be in thermodynamic equilibrium and macroscopic fluid equations with constant temperature 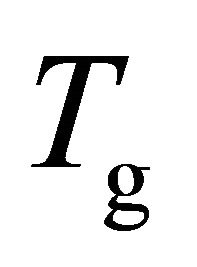 are taken into account for tracing the spatiotemporal behaviour of ions and neutral particles [12-15]. In contrast, the non-local kinetics of electrons plays an important role in the discharge mechanisms and the application range of fluid models which do not describe electrons adequately is very limited [16-18]. Therefore, hybrid models are frequently used in which fluid equations are solved for heavy particles and electrons are treated kinetically [19-21]. However, it has been pointed out recently that fluid models are able to capture electron kinetic effects, if the electron energy flux is adequately described [22,23].
are taken into account for tracing the spatiotemporal behaviour of ions and neutral particles [12-15]. In contrast, the non-local kinetics of electrons plays an important role in the discharge mechanisms and the application range of fluid models which do not describe electrons adequately is very limited [16-18]. Therefore, hybrid models are frequently used in which fluid equations are solved for heavy particles and electrons are treated kinetically [19-21]. However, it has been pointed out recently that fluid models are able to capture electron kinetic effects, if the electron energy flux is adequately described [22,23].
In the present paper, a high order fluid model comprising moment equations for particle density, particle flux, energy density and energy flux of the electron component is consistently derived from the electron Boltzmann equation. In addition a novel drift-diffusion approximation for electrons is proposed. Results are compared to those of a conventional drift-diffusion model frequently used [24,25] and to kinetically obtained results at the example of argon gas discharge plasmas.
2. Kinetic Description of Electrons
In spite of the increasing speed of computers, the solution of the electron Boltzmann equation in seven dimensions is computationally not feasible. A conventional approach for reducing computing time is to decrease dimensionality by decomposition of the electron velocity distribution function (evdf) 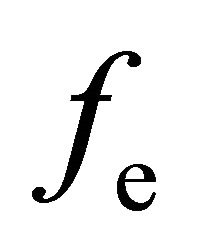 in terms of spherical harmonics in velocity space [26,27]. In the planar system considered in the present studies and depicted in Figure 1, where all gradients and the electric field are assumed to be normal to the electrodes, the general spherical harmonics expansion reduces to the Legendre polynomial expansion [27,28]
in terms of spherical harmonics in velocity space [26,27]. In the planar system considered in the present studies and depicted in Figure 1, where all gradients and the electric field are assumed to be normal to the electrodes, the general spherical harmonics expansion reduces to the Legendre polynomial expansion [27,28]
 (3)
(3)
In this case the velocity distribution function becomes symmetric around the electric field and depends on the space coordinate , the velocity magnitude
, the velocity magnitude , the direction cosine
, the direction cosine 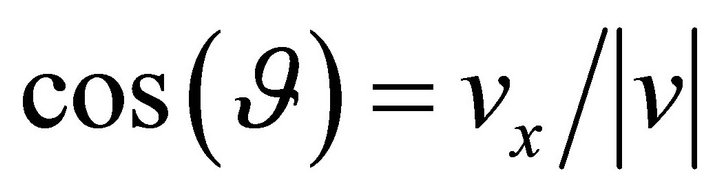 and time. The substitution of the expansion (3) into the electron Boltzmann equation
and time. The substitution of the expansion (3) into the electron Boltzmann equation
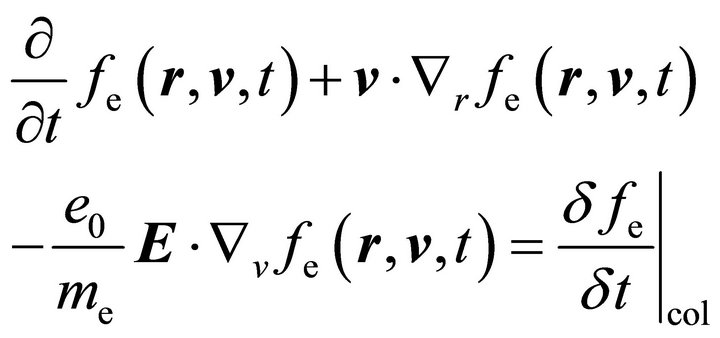 (4)
(4)

Figure 1. Planar discharge geometry.
with elementary charge  and the transformation of the expansion coefficients into the space of kinetic energy
and the transformation of the expansion coefficients into the space of kinetic energy 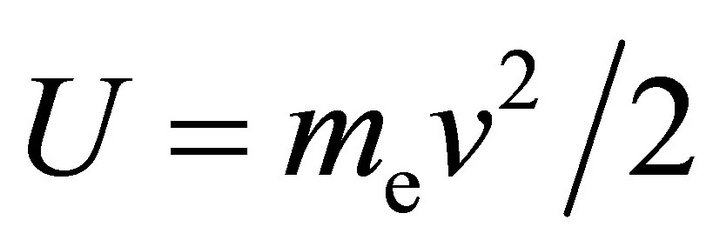 according to
according to
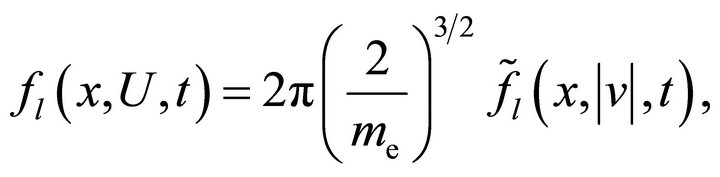 (5)
(5)
finally yields the infinite system of partial differential equations [16]
 (6a)
(6a)
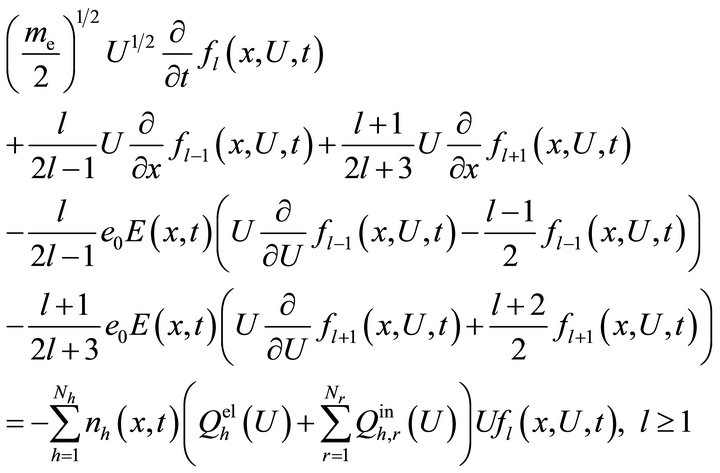
(6b)
for the expansion coefficients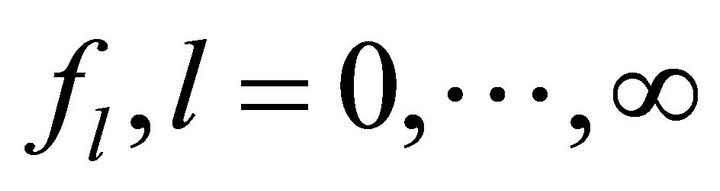 . Here,
. Here, 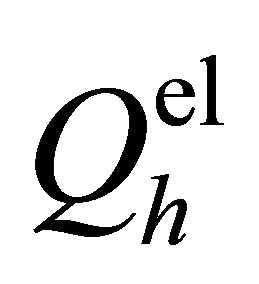 and
and  are the cross sections of elastic and inelastic collisions of electrons with heavy particles with density
are the cross sections of elastic and inelastic collisions of electrons with heavy particles with density 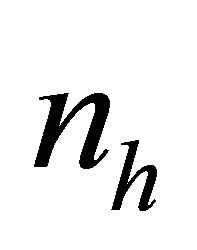 and mass
and mass 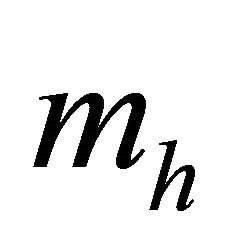 and
and 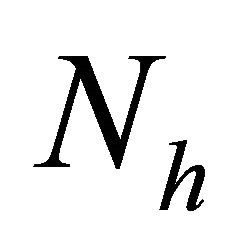 and
and 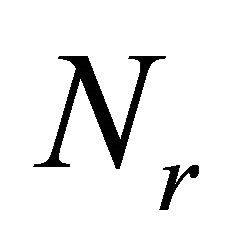 denote the number of heavy particle species and reactions, respectively. The kinetic energy that is lost in the corresponding inelastic electron collision is denoted by
denote the number of heavy particle species and reactions, respectively. The kinetic energy that is lost in the corresponding inelastic electron collision is denoted by  and the parameter
and the parameter 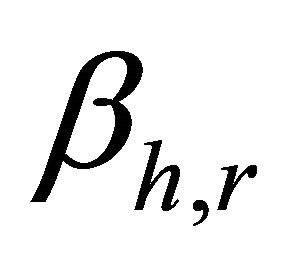 depends on the different kinds of inelastic electron collision processes. It is zero for dissociative attachment of electrons and one for excitation, dissociation and deexcitation processes. Using the assumption that the binding energy is equally shared between the two released electrons
depends on the different kinds of inelastic electron collision processes. It is zero for dissociative attachment of electrons and one for excitation, dissociation and deexcitation processes. Using the assumption that the binding energy is equally shared between the two released electrons 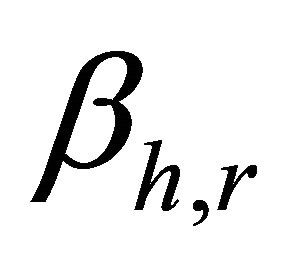 equals two for an ionization event [16].
equals two for an ionization event [16].
In order to solve system (1), it has to be truncated after a reasonable finite number of equations. Within the common framework of the two-term expansion [29-31], only the first two equations for  and
and 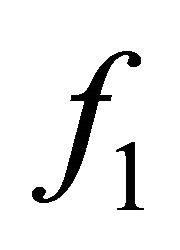 are taken into account and
are taken into account and 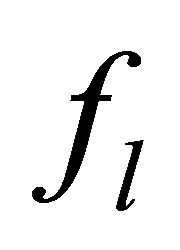 is set to zero for
is set to zero for . Usually, the rapidity of the temporal change of the anisotropic distribution f1 is by some orders of magnitude greater than that of the isotropic distribution f0 as long as the characteristic frequency for the field alteration is small compared to the power dissipation in elastic and inelastic collisions [30]. In this case, the time derivative term
. Usually, the rapidity of the temporal change of the anisotropic distribution f1 is by some orders of magnitude greater than that of the isotropic distribution f0 as long as the characteristic frequency for the field alteration is small compared to the power dissipation in elastic and inelastic collisions [30]. In this case, the time derivative term 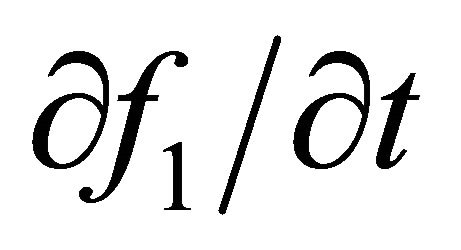 in (7) for
in (7) for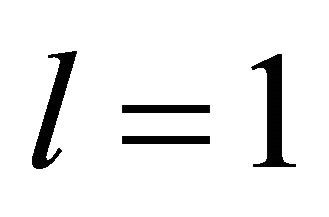 , which describes the establishment of
, which describes the establishment of 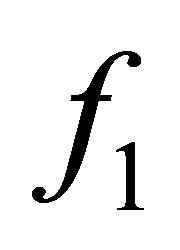 into the quasi-stationary state
into the quasi-stationary state
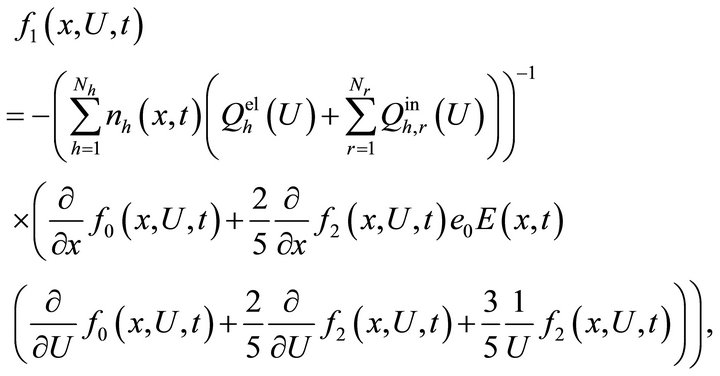
(7)
can be neglected. If in this case 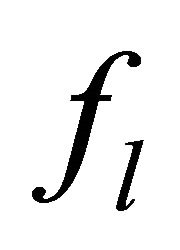 is set to zero for
is set to zero for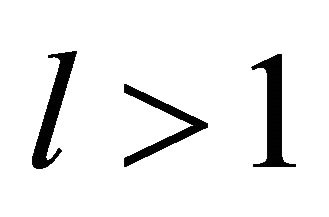 , the system (6) reduces to the single parabolic differential Equation (6a) using the expression (7) with
, the system (6) reduces to the single parabolic differential Equation (6a) using the expression (7) with  for the anisotropic contribution
for the anisotropic contribution  to the evdf [30].
to the evdf [30].
In the past, the system (6) has been solved in two-term approximation [29,30] using the expression (7) with 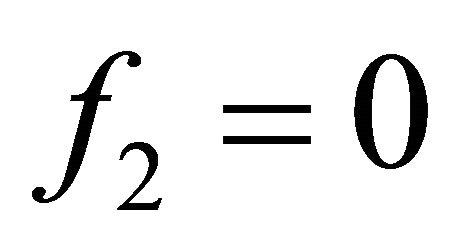 as well as in multiterm approximation considering higher order contributions to the evdf anisotropy [32-35] to study the behaviour of electrons in prescribed time-dependent as well as stationary electric fields. But the coupled solution (stationary or time-dependent) of the kinetic Equations (6) for electrons, fluid equations for heavy particles and Poisson’s equation for the electric field is still an ambitious task and has been achieved for a few discharge situations, only [21,36-38]. In the following a macroscopic system of moment equations is consistently derived from the system (6), which strongly simplifies the description of electron transport.
as well as in multiterm approximation considering higher order contributions to the evdf anisotropy [32-35] to study the behaviour of electrons in prescribed time-dependent as well as stationary electric fields. But the coupled solution (stationary or time-dependent) of the kinetic Equations (6) for electrons, fluid equations for heavy particles and Poisson’s equation for the electric field is still an ambitious task and has been achieved for a few discharge situations, only [21,36-38]. In the following a macroscopic system of moment equations is consistently derived from the system (6), which strongly simplifies the description of electron transport.
3. Macroscopic Transport Equations for Electrons
3.1. Four-Moment Model
The derivation of a system of moment equations for the description of electrons in nonthermal plasmas starts from the kinetic system (6). Multiplication of Equation
(6a) by factors 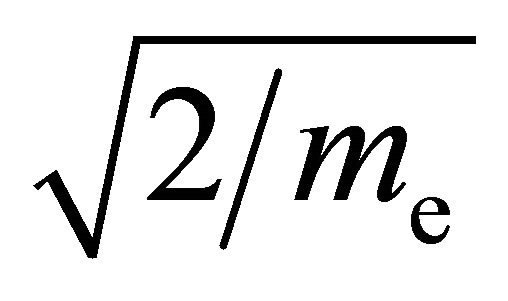 and
and , respectively, and subsequent integration over kinetic energy U directly provides the two moment equations
, respectively, and subsequent integration over kinetic energy U directly provides the two moment equations
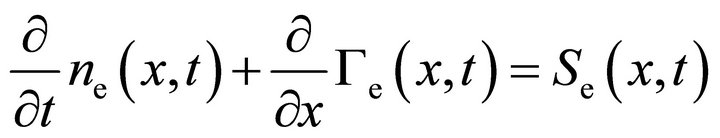 (8a)
(8a)
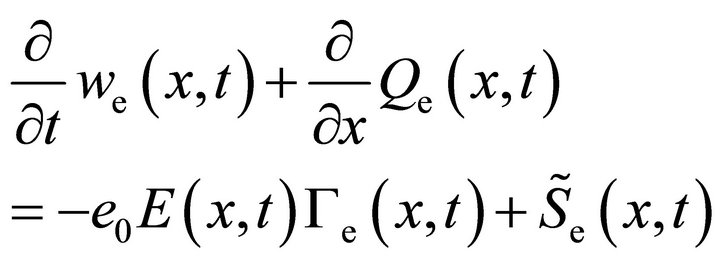 (8b)
(8b)
with macroscopic quantities
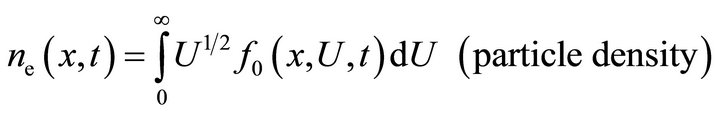 (9)
(9)
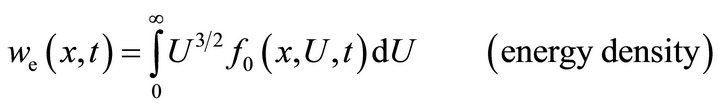 (10)
(10)
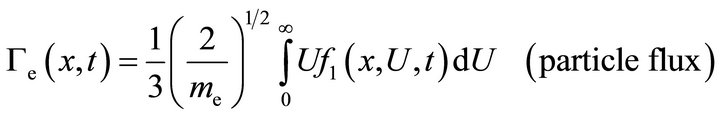 (11)
(11)
 (12)
(12)
The source terms 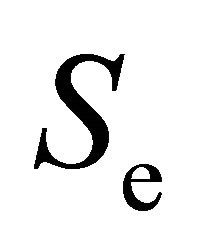 and
and 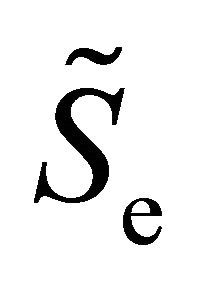 in Equations (8a) and (8b) describe the gain and loss of particles and energy due to collision processes. For a specific gas, they are given as the sum of rates of all relevant processes with rate coefficients depending on the mean electron energy
in Equations (8a) and (8b) describe the gain and loss of particles and energy due to collision processes. For a specific gas, they are given as the sum of rates of all relevant processes with rate coefficients depending on the mean electron energy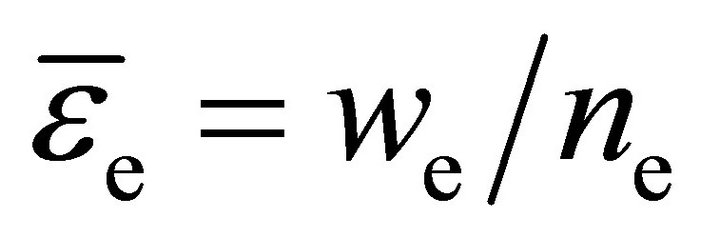 , see, e.g., [15,16] for more details.
, see, e.g., [15,16] for more details.
In order to consistently derive partial differential equations for the determination of the particle flux (11) and the energy flux (12), Equation (6b) for 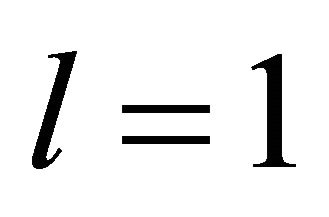 is multiplied by factors
is multiplied by factors 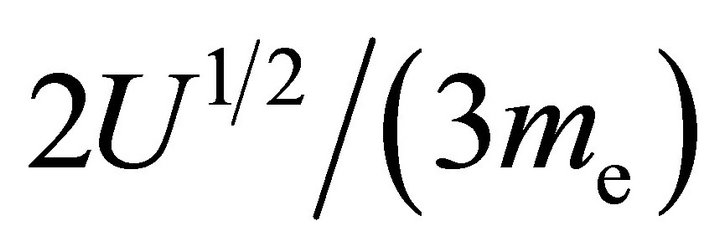 and
and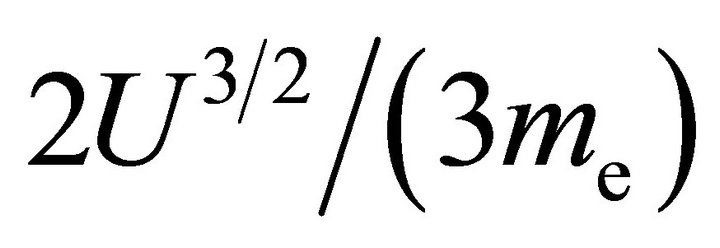 , respectively. As before, subsequent integration over kinetic energy
, respectively. As before, subsequent integration over kinetic energy 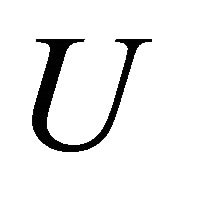 yields the two moment equations
yields the two moment equations

(13a)
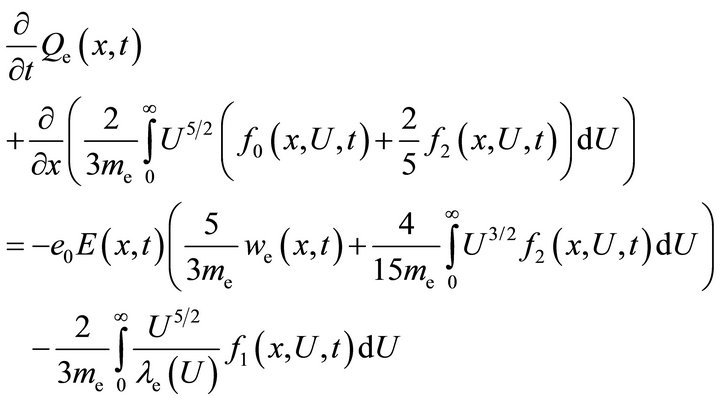
(13b)
with the mean free path of electrons
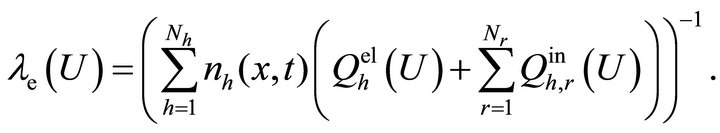 (14)
(14)
The definition of the set of transport coefficients
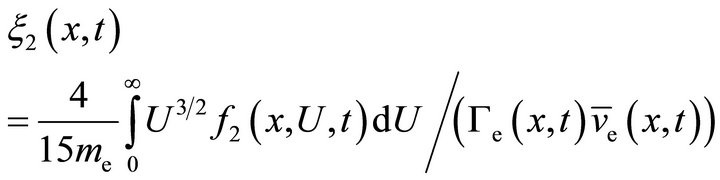 (15a)
(15a)
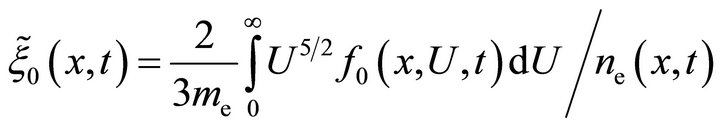 (15b)
(15b)
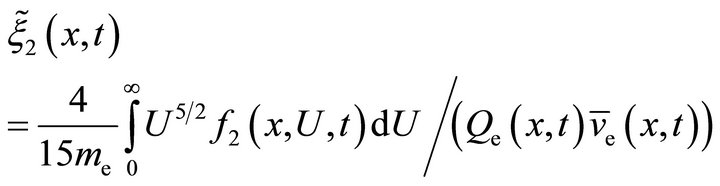 (15c)
(15c)
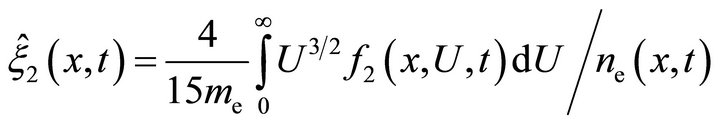 (15d)
(15d)
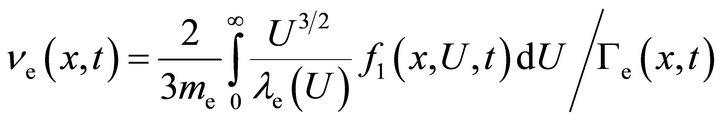 (15e)
(15e)
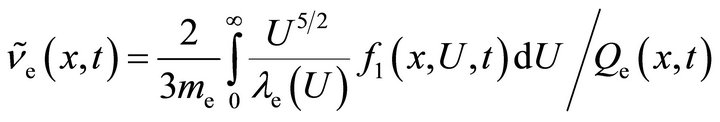 (15f)
(15f)
with the mean velocity of electrons 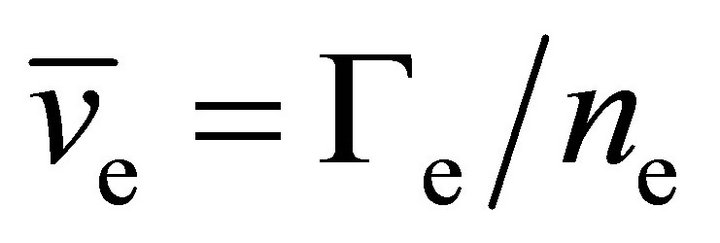 allows to write the four-moment model (4MM) for electrons in the form
allows to write the four-moment model (4MM) for electrons in the form
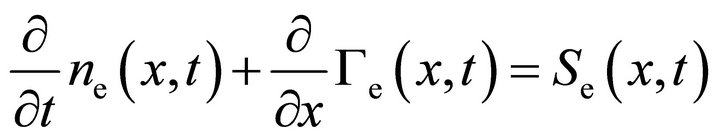 (16a)
(16a)
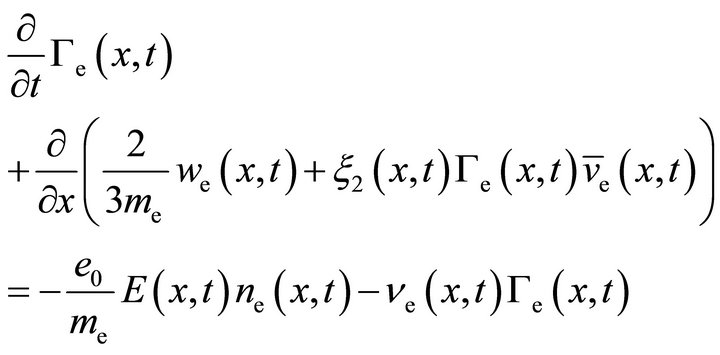 (16b)
(16b)
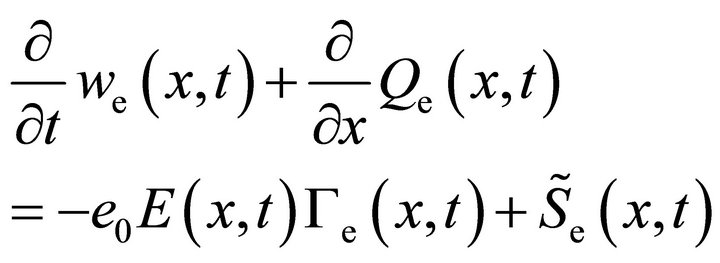 (16c)
(16c)
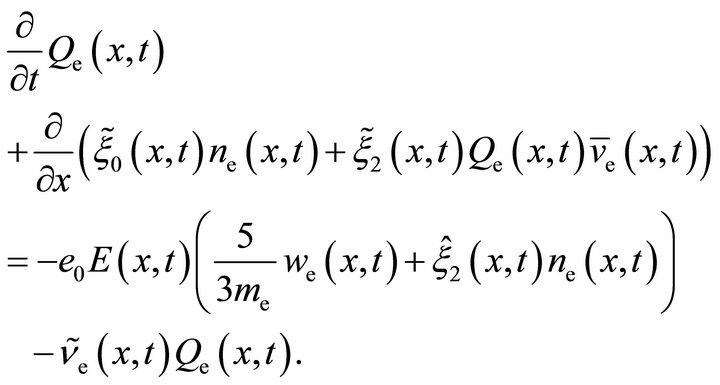 (16d)
(16d)
Electron transport coefficients used in fluid calculations are commonly obtained by solving the kinetic system (6) in multiterm approximation [16] or in twoterm approximation [39] for given values of the electric field, neglecting spatial and temporal derivatives. The resulting coefficients are then put into lookup tables as functions of the mean electron energy for the usage in fluid calculations. The same procedure, known as localmean-energy approximation [16,40], is used for the determination of the new transport coefficients (15).
3.2. Drift-Diffusion Approximation
As mentioned in Section 2, the rapidity of the temporal change of the anisotropic distribution 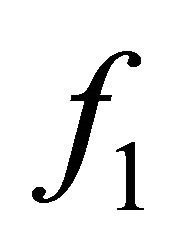 is by some orders of magnitude greater than that of the isotropic distribution
is by some orders of magnitude greater than that of the isotropic distribution 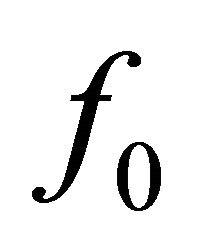 and the time derivative in Equation (6b) for
and the time derivative in Equation (6b) for 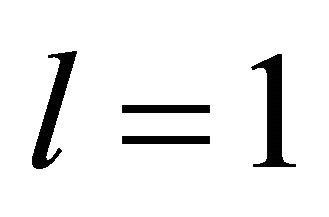 can be neglected in many discharge situations. With this assumption and definition of the coefficient
can be neglected in many discharge situations. With this assumption and definition of the coefficient
 (17)
(17)
the new drift-diffusion approximation (DDAn)
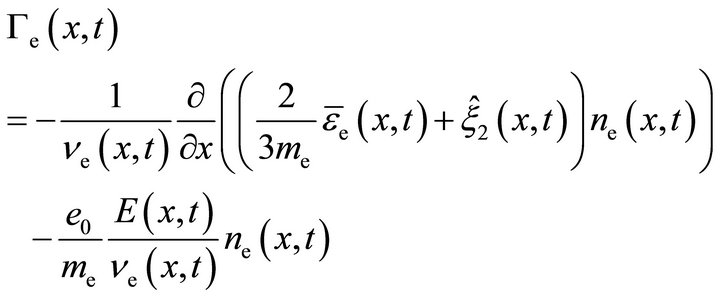 (18a)
(18a)
 (18b)
(18b)
is obtained for the particle flux  and energy flux
and energy flux 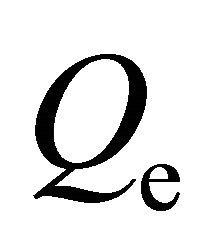 of the electrons. Substitution of (18a) and (18b) into Equations (16a) and (16c), respectively, reduces the fourmoment model to a system of two parabolic differential equations for the particle density
of the electrons. Substitution of (18a) and (18b) into Equations (16a) and (16c), respectively, reduces the fourmoment model to a system of two parabolic differential equations for the particle density 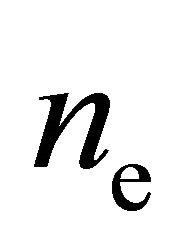 and the energy density
and the energy density 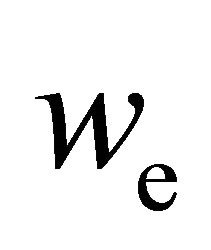 of electrons. The coefficient (17) is determined in the same way as the coefficients (15).
of electrons. The coefficient (17) is determined in the same way as the coefficients (15).
As an example, the transport coefficients (15) used in the four-moment model (16) and the drift-diffusion approximation (18) are shown in Figure 2 for argon gas, where the underlying cross sections are detailed in reference [15]. It becomes obvious that for mean electron energies 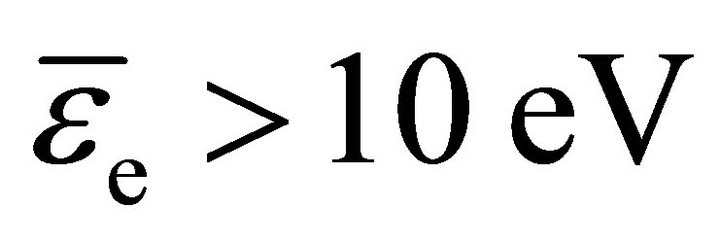 the distribution anisotropy
the distribution anisotropy 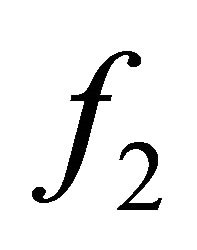 becomes important and should not be neglected by using the conventional two-term approximation.
becomes important and should not be neglected by using the conventional two-term approximation.
The derived drift-diffusion approximation (18) can be used for description of electron transport instead of the conventional drift-diffusion approximation DDAc
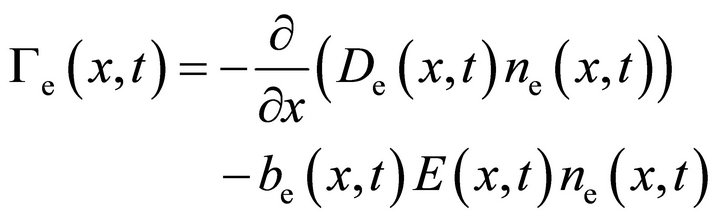 (19a)
(19a)
 (19b)
(19b)
which is deduced from Equation (7) with [16] and without [8,40,41] consideration of the higher order contribution 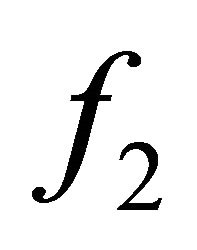 to the distribution anisotropy. The electron diffusion coefficients of particle
to the distribution anisotropy. The electron diffusion coefficients of particle 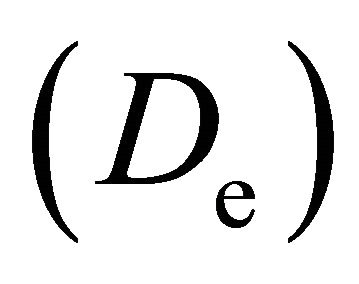 and energy
and energy 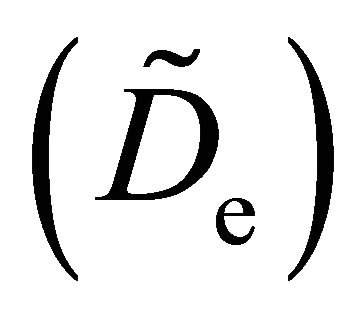 transport as well as the electron mobilities of particles
transport as well as the electron mobilities of particles 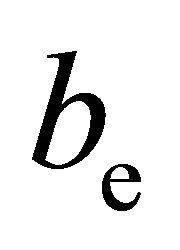 and energy
and energy  are determined in the same way as the coefficients of the four-moment model (15) and (17) as functions of the mean electron energy [16].
are determined in the same way as the coefficients of the four-moment model (15) and (17) as functions of the mean electron energy [16].
3.3. Conventional Three-Moment Model
The derivation of the four-moment model 4MM and the

Figure 2. Argon transport coefficients for electron particle flux in drift-diffusion approximation DDAn (a); energy flux in drift-diffusion approximation DDAn (b); particle and energy fluxes in four-moment model 4MM (c); and dissipation frequencies for particle and energy fluxes (d).
drift-diffusion model DDAn is consistent in the sense that beside the truncation of the expansion (3) no additional assumptions are needed in order to close the system of macroscopic moment equations. This is not the case if moment equations are derived directly from the electron Boltzmann Equation (4) and not from the kinetic system (6), see, e.g., [13,42,43]. The multiplication of Equation (4) by factors 1,  and
and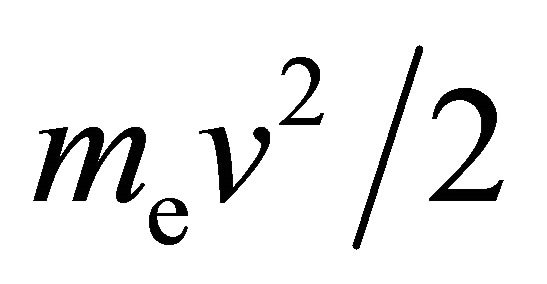 , respectively, and subsequent integration over velocity space yields the system of three moment equations [44]
, respectively, and subsequent integration over velocity space yields the system of three moment equations [44]
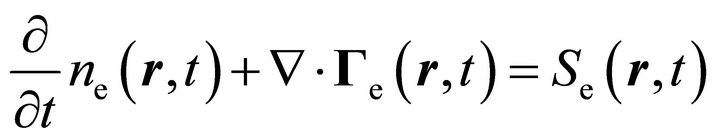 (20a)
(20a)
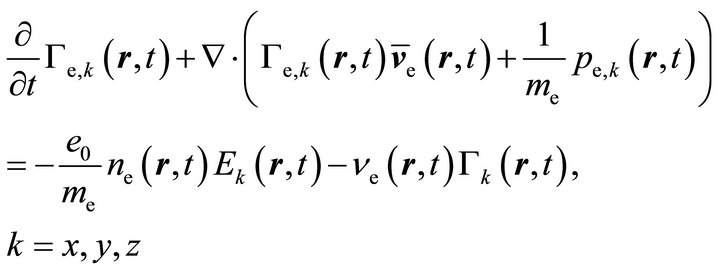 (20b)
(20b)
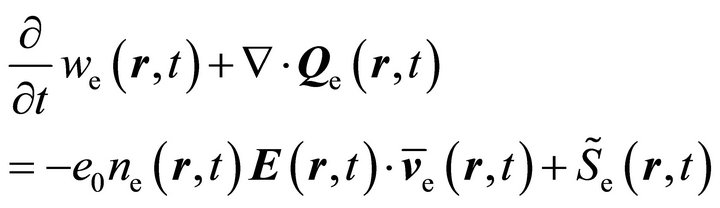 (20c)
(20c)
for the particle density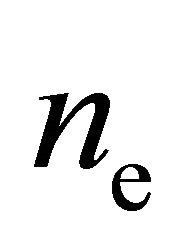 , the particle flux
, the particle flux 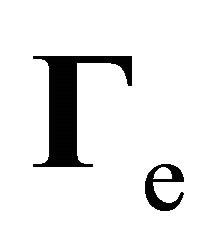 and the energy density
and the energy density 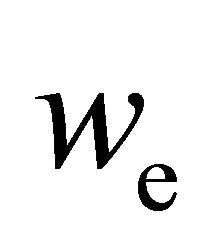 of electrons. In order to solve system (20) it has to be closed by certain expressions for the electron pressure tensor
of electrons. In order to solve system (20) it has to be closed by certain expressions for the electron pressure tensor
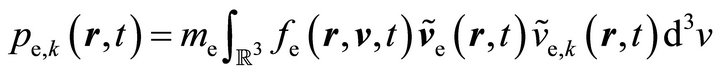 (21)
(21)
with 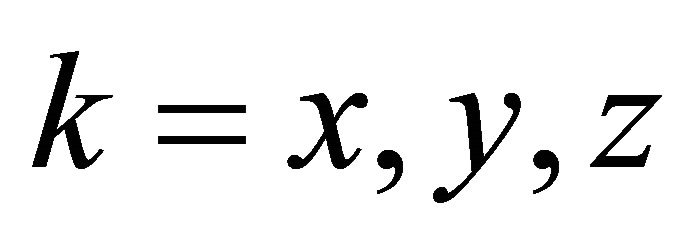 and the random electron velocity
and the random electron velocity 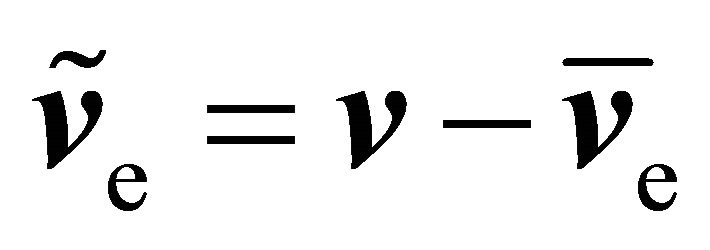 as well as for the electron energy flux
as well as for the electron energy flux
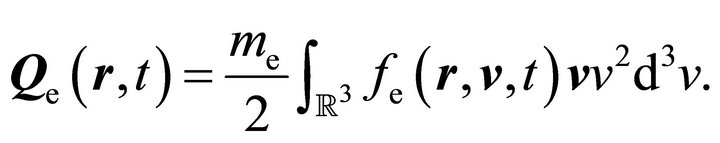 (22)
(22)
For light particles such as electrons, the pressure tensor  can be simplified to the scalar electron pressure [45,46]
can be simplified to the scalar electron pressure [45,46]
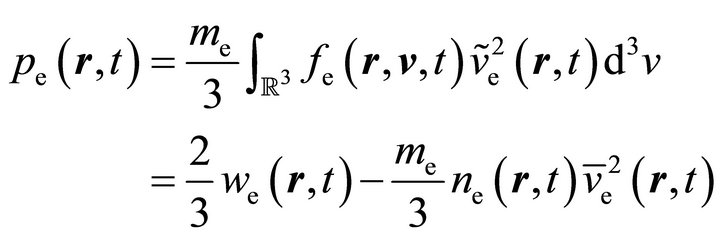 (23)
(23)
and is therefore determined in terms of the macroscopic quantities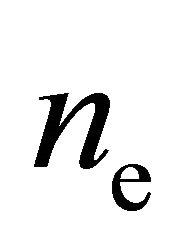 ,
, 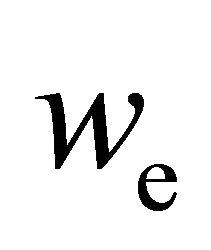 and
and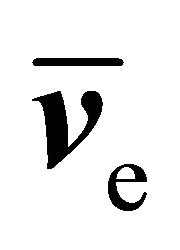 . The derivation of an adequate expression for the third order moment
. The derivation of an adequate expression for the third order moment 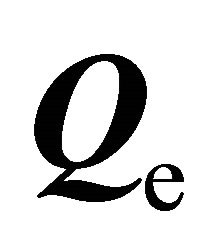 in terms of lower order moments is a much more difficult task. Most often, the electron energy flux is rewritten as [44]
in terms of lower order moments is a much more difficult task. Most often, the electron energy flux is rewritten as [44]
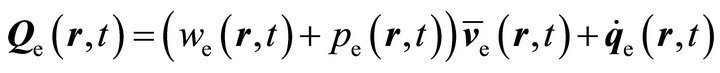 (24)
(24)
with the exact electron heat flux
 (25)
(25)
and then the heat flux is approximated by Fourier heat conduction according to [12,13]
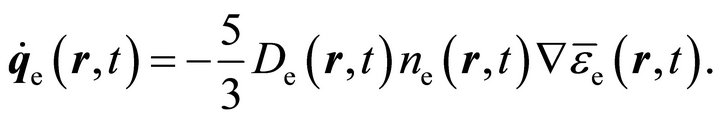 (26)
(26)
However, this approximation is known to be inaccurate in most discharge situations [22,43].
A more sophisticated heat flux ansatz has been derived by Robson et al. [22]. Unfortunately, their heat flux expression depends on parameters which are not known for real gases and is therefore not applicable without further benchmark calculations [23].
4. Comparison of Macroscopic and Kinetic Models
In order to show that the derived systems of partial differential equations 4MM and DDAn improve the accuracy of fluid models for the description of electrons, numerical calculations for two different discharge situations in argon were performed. First, the electron transport equations were solved for prescribed pulse-like electric field (benchmark model). Secondly, an abnormal glow discharge in low pressure argon was described selfconsistently in the sense that the electron transport equations were solved together with transport equations for heavy particles and Poisson’s equation for determination of the electric field. The finite-difference methods used to discretize the system of differential equations in space and time are detailed in reference [15].
4.1. Argon Benchmark Model
Probe measurements in plasmas cause an abrupt change of the local electric field. This situation is considered here, and the four-moment model 4MM (16) as well as the drift-diffusion model DDAn using the new flux representation (18) and the drift-diffusion model DDAc using the conventional flux representation (19) were solved for argon gas at a pressure of 133 Pa and a gas temperature of 300 K using the prescribed electric field profile shown in Figure 3(a). In order to rate the results of 4MM, DDAn and DDAc, the space-dependent electron Boltzmann equation was solved kinetically according to Sigeneger et al. [41] for the same electric field, taking into account elastic and inelastic electron collision processes. Figures 3(b) and 3(c) exhibit the results obtained for the mean velocity and the mean energy of the electrons by means of the different models.
Because the applied field is time-independent and therefore the temporal derivatives of all quantities are zero, results of 4MM and DDAn are almost the same. The spatial profile predicted by the models 4MM and DDAn for the mean velocity and the mean energy are in qualitative agreement with the kinetic results. In contrast,
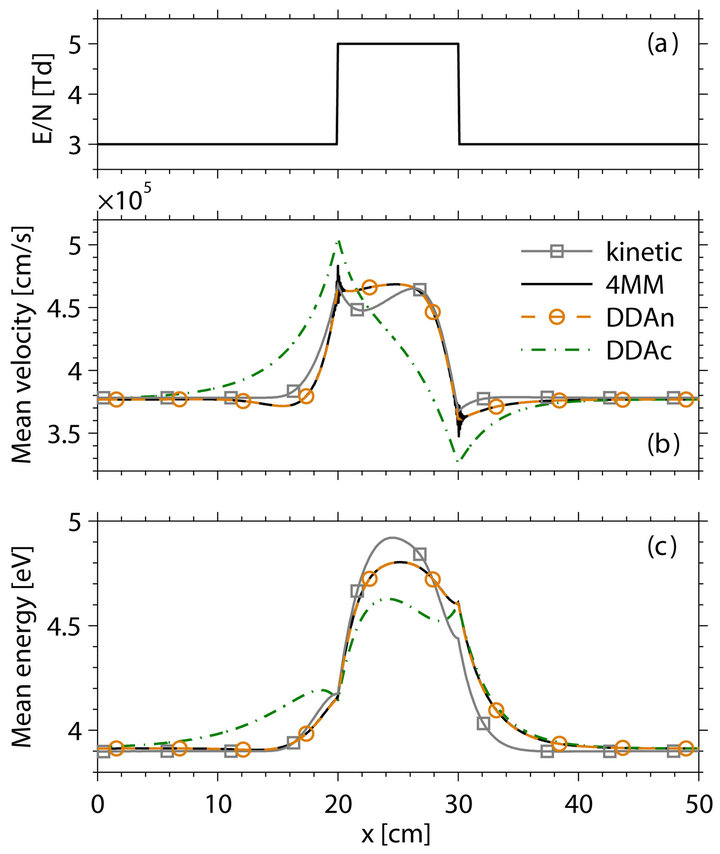
Figure 3. Prescribed electric field (a) and comparison of results for the mean velocity (b) and energy (c) of the electrons obtained by the four-moment model 4MM and drift-diffusion models DDAn and DDAc with kinetic results.
the results of DDAc strongly differ from those of the kinetic solution. The results show impressively that the accuracy of fluid models for the theoretical description of electrons is strongly increased by the proposed methods.
4.2. Abnormal Glow Discharge in Argon
To demonstrate the practical applicability of the derived moment equations, the ignition of an abnormal glow discharge in argon at a gas pressure of 133 Pa and a gas temperature of 300 K was theoretically described using the discharge geometry depicted in Figure 1. At the powered electrode at  (cathode) a voltage of –250 W was applied and the electrode at x = 1 cm (anode) was grounded. The general procedure for solving the coupled system of transport equations for the species and Poisson’s equation has been described in [15] and the data used for the electron-atom collisions are the same as those reported in this paper.
(cathode) a voltage of –250 W was applied and the electrode at x = 1 cm (anode) was grounded. The general procedure for solving the coupled system of transport equations for the species and Poisson’s equation has been described in [15] and the data used for the electron-atom collisions are the same as those reported in this paper.
The results obtained by the models 4MM, DDAn and DDAc for the mean electron velocity, the mean electron energy and the self-consistently determined electric field are shown in Figure 4 at three different instants of time. Obviously, all fluid models under consideration predict qualitatively the same dynamic behaviour. Shortly after switching on the discharge, at t = 1 μs, a quasi-stationary Townsend phase is reached which is characterized by an almost constant electric field and small spatial variations in the mean velocity and mean energy of electrons.
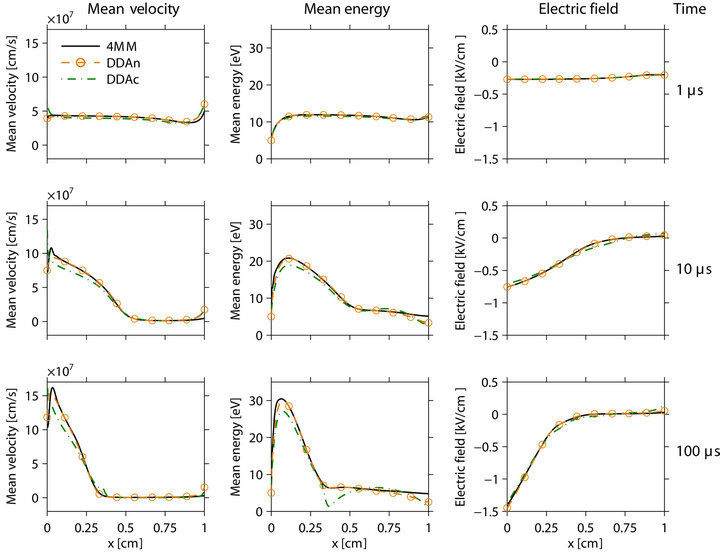
Figure 4. Comparison of results obtained by the fluid models 4MM, DDAn and DDAc for an abnormal glow discharge in argon at pressure of 133 Pa and applied voltage of –250 V.
Charge carriers are produced mainly in front of the grounded electrode by ionization of argon atoms in collisions with electrons and by secondary electron emission at the powered electrode due to ion bombardment. At  enough charge carriers are produced to distinctly perturb the homogeneous electric field. Due to the increase of the electric field in the cathode region strong charge carrier multiplication takes place and finally the discharge ignites. The discharge becomes stationary after approximately 100 μs. Electrons emitted at the cathode gain energy in the strong electric field and are then slowed down in electron collisions. The discharge is brightest in the negative glow region at approximately
enough charge carriers are produced to distinctly perturb the homogeneous electric field. Due to the increase of the electric field in the cathode region strong charge carrier multiplication takes place and finally the discharge ignites. The discharge becomes stationary after approximately 100 μs. Electrons emitted at the cathode gain energy in the strong electric field and are then slowed down in electron collisions. The discharge is brightest in the negative glow region at approximately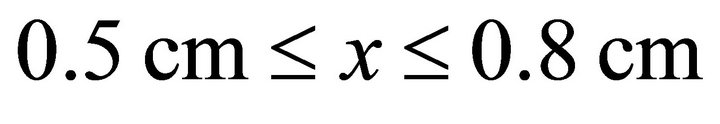 .
.
Because the characteristic frequency for the field alteration is small in the discharge situation considered here, the results of the four-moment model 4MM and the new drift-diffusion model DDAn are almost the same. Small differences occur in front of the boundaries due to the fact that different types of boundary conditions have to be applied for the system of first-order differential equations 4MM and the parabolic system DDAn. Again, the results of DDAc differ markedly. Particularly in the transition from the cathode region to the negative glow at 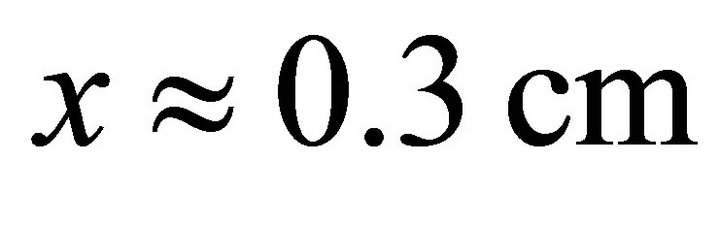 strong deviations in the results for the mean energy occur at steady state. The mean energy minimum is strongly overestimated by DDAc and it has been found that this issue causes the occurrence of a singular point in the temporal evolution of the discharge ignition if gas pressure, discharge chemistry or applied voltage are slightly changed.
strong deviations in the results for the mean energy occur at steady state. The mean energy minimum is strongly overestimated by DDAc and it has been found that this issue causes the occurrence of a singular point in the temporal evolution of the discharge ignition if gas pressure, discharge chemistry or applied voltage are slightly changed.
5. Conclusions
A new system of moment equations for the description of electrons in nonthermal plasmas was derived by an expansion of the electron velocity distribution function in Legendre polynomials and the definition of transport coefficients that are determined by means of the localmean-energy approximation. The new model 4MM is consistent in the sense that no additional assumptions are necessary to close the system of moment equations. It has been shown that the additional requirement of a small characteristic frequency for the field alteration allows to reduce the system of four first-order partial differential equations for particle density, particle flux, energy density and energy flux of electrons to a parabolic driftdiffusion model comprising two second-order partial differential equations for the particle density and energy density of electrons. If this requirement is fulfilled, the results provided by the new drift-diffusion model DDAn are in good agreement with those of the high order fluid model 4MM.
The comparison of results obtained by the models 4MM and DDAn with results of the conventional driftdiffusion model DDAc as well as kinetically obtained results has pointed out that the new approach strongly increases the accuracy of fluid models for the description of electron transport in nonthermal plasmas. Since similar partial differential equations for electrons arise in the theoretical description of semiconductors [47-49], it potentially improves the theoretical description of electrons in semiconductor devices, too.
6. Acknowledgments
This work was supported by the German Research Foundation within the Collaborative Research Centre Transregio 24.
REFERENCES
- B. Eliasson, M. Hirth and U. Kogelschatz, “Ozone Synthesis from Oxygen in Dielectric Barrier Discharges,” Journal of Physics D: Applied Physics, Vol. 20, No. 11, 1987, pp. 1421-1437. doi:10.1088/0022-3727/20/11/010
- U. Kogelschatz, “Dielectric-Barrier Discharges: Their History, Discharge Physics, and Industrial Applications,” Plasma Chemistry and Plasma Processing, Vol. 23, No. 1, 2003, pp. 1-46. doi:10.1023/A:1022470901385
- G. Lister, J. Lawler, W. Lapatovich and V. Godyak, “The Physics of Discharge Lamps,” Reviews of Modern Physics, Vol. 76, No. 2, 2004, pp. 541-598. doi:10.1103/RevModPhys.76.541
- J. Ehlbeck, U. Schnabel, M. Polak, J. Winter, T. von Woedtke, R. Brandenburg, T. von dem Hagen and K.-D. Weltmann, “Low Temperature Atmospheric Pressure Plasma Sources for Microbial Decontamination,” Journal of Physics D: Applied Physics, Vol. 44, No. 1, 2011, Article ID: 13002. doi:10.1088/0022-3727/44/1/013002
- M. J. Kushner, “Monte-Carlo Simulation of Electron Properties in rf Parallel Plate Capacitively Coupled Discharges,” Journal of Applied Physics, Vol. 54, No. 9, 1983, pp. 4958-4965. doi:10.1063/1.332763
- D. B. Graves, “Fluid Model Simulations of a 13.56-MHz rf Discharge: Time and Space Dependence of Rates of Electron Impact Excitation,” Journal of Applied Physics, Vol. 62, No. 1, 1987, pp. 88-94. doi:10.1063/1.339111
- J.-P. Boeuf, “A Two-Dimensional Model of dc Glow Discharges,” Journal of Applied Physics, Vol. 63, No. 5, 1988, pp. 1342-1349. doi:10.1063/1.339961
- G. J. M. Hagelaar, G. M. W. Kroesen, U. van Slooten and H. Schreuders, “Modeling of the Microdischarges in Plasma Addressed Liquid Crystal Displays,” Journal of Applied Physics, Vol. 88, No. 5, 2000, pp. 2252-2262. doi:10.1063/1.1287529
- R. Bussiahn, S. Gorchakov, H. Lange, D. Loffhagen and D. Uhrlandt, “Ac Operation of Low-Pressure He Xe Lamp Discharges,” Journal of Physics D: Applied Physics, Vol. 40, 2007, Article ID: 3882. doi:10.1088/0022-3727/40/13/S07
- M. Wendt, S. Peters, D. Loffhagen, A. Kloss and M. Kettlitz, “Breakdown Characteristics of High Pressure Xenon lamps,” Journal of Physics D: Applied Physics, Vol. 42, No. 18, 2009, Article ID: 185208. doi:10.1088/0022-3727/42/18/185208
- S. Chapman and T. G. Cowling, “The Mathematical Theory of Non-Uniform Gases: An Account of the Kinetic Theory of Viscosity, Thermal Conduction and Diffusion in Gases,” 3rd Edition, Cambridge University Press, Cambridge, 1998.
- M. Wilcoxson and V. J. Manousiouthakis, “Simulation of a Three-Moment Fluid Model of a Two-Dimensional Radio Frequency Discharge,” Chemical Engineering Science, Vol. 51, No. 7, 1996, pp. 1089-1106.
- H. C. Kim and V. I. Manousiouthakis, “Dually Driven Radio Frequency Plasma Simulation with a Three Moment Model,” Journal of Vacuum Science & Technology A, Vol. 16, No. 4, 1998, p. 2162. doi:10.1116/1.581324
- S. Elaissi, M. Yousfi, H. Helali, S. Kazziz, K. Charrada and M. Sassi, “Radio-Frequency Electronegative Gas Discharge Behaviour in a Parallel-Plate Reactor for Material Processing,” Plasma Devices and Operations, Vol. 14, No. 1, 2006, pp. 27-45. doi:10.1080/10519990500493874
- M. M. Becker, D. Loffhagen and W. Schmidt, “A Stabilized Finite Element Method for Modeling of Gas Discharges,” Computer Physics Communications, Vol. 180, No. 8, 2009, pp. 1230-1241. doi:10.1016/j.cpc.2009.02.001
- G. K. Grubert, M. M. Becker and D. Loffhagen, “Why the Local-Mean-Energy Approximation Should Be Used in Hydrodynamic Plasma Descriptions Instead of the Local-Field Approximation,” Physical Review E, Vol. 80, No. 3, 2009, Article ID: 036405. doi:10.1103/PhysRevE.80.036405
- A. Derzsi, P. Hartmann, I. Korolov, J. Karácsony, G. Bánó, and Z. Donkó, “On the accuracy and limitations of fluid models of the cathode region of dc glow discharges,” Journal of Physics D: Applied Physics, Vol. 42, No. 22, 2009, Article ID: 225204. doi:10.1088/0022-3727/42/22/225204
- I. Rafatov, E. A. Bogdanov and A. A. Kudryavtsev, “On the Accuracy and Reliability of Different Fluid Models of the Direct Current Glow Discharge,” Physics of Plasmas, Vol. 19, No. 3, 2012, Article ID: 033502.
- A. Bogaerts, R. Gijbels and W. J. Goedheer, “Hybrid Monte Carlo-Fluid Model of a Direct Current Glow Discharge,” Journal of Applied Physics, Vol. 78, No. 4, 1995, pp. 2233-2241. doi:10.1063/1.360139
- Z. Donkó, “Hybrid Model of a Rectangular Hollow Cathode Discharge,” Physical Review E, Vol. 57, No. 6, 1998, pp. 7126-7137. doi:10.1103/PhysRevE.57.7126
- D. Loffhagen and F. Sigeneger, “Advances in Boltzmann Equation Based Modelling of Discharge Plasmas,” Plasma Sources Science and Technology, Vol. 18, No. 3, 2009, Article ID: 034006. doi:10.1088/0963-0252/18/3/034006
- R. E. Robson, R. D. White and Z. L. Petrović, “Colloquium: Physically Based Fluid Modeling of Collisionally Dominated Low-Temperature Plasmas,” Reviews of Modern Physics, Vol. 77, No. 4, 2005, pp. 1303-1320. doi:10.1103/RevModPhys.77.1303
- P. Nicoletopoulos and R. E. Robson, “Periodic Electron Structures in Gases: A Fluid Model of the ‘Window’ Phenomenon,” Physical Review Letters, Vol. 100, No. 12, 2008, Article ID: 124502. doi:10.1103/PhysRevLett.100.124502
- L. L. Alves, “Fluid Modelling of the Positive Column of Direct-Current Glow Discharges,” Plasma Sources Science and Technology, Vol. 16, No. 3, 2007, p. 557. doi:10.1088/0963-0252/16/3/015
- M. Gnybida, D. Loffhagen and D. Uhrlandt, “Fluid Modeling and Analysis of the Constriction of the DC Positive Column in Argon,” IEEE Transactions on Plasma Science, Vol. 37, No. 7, 2009, pp. 1208-1218. doi:10.1109/TPS.2009.2021419
- R. E. Robson and K. F. Ness, “Velocity Distribution Function and Transport Coefficients of Electron Swarms in Gases: Spherical-Harmonics Decomposition of Boltzmann’s Equation,” Physical Review A, Vol. 33, No. 3, 1986, pp. 2068-2077. doi:10.1103/PhysRevA.33.2068
- R. E. Robson, R. Winkler and F. Sigeneger, “Multiterm Spherical Tensor Representation of Boltzmann’s Equation for a Nonhydrodynamic Weakly Ionized Plasma,” Physical Review E, Vol. 65, No. 5, 2002, Article ID: 056410. doi:10.1103/PhysRevE.65.056410
- R. Winkler, J. Wilhelm and V. Schüller, “Legendre Polynomial Expansion and General Spherical Harmonics Expansion in the Boltzmann Equation of the Lorentz Plasma,” Contributions to Plasma Physics, Vol. 10, No. 1, 1970, pp. 51-77. doi:10.1002/ctpp.19700100105
- S. Arndt, D. Uhrlandt and R. Winkler, “Space-Dependent Kinetics of Electrons in the Anode region of a Glow Discharge,” Journal of Physics D: Applied Physics, Vol. 34, No. 13, 2001, pp. 1982-1992. doi:10.1088/0022-3727/34/13/309
- D. Loffhagen and R. Winkler, “Spatiotemporal Relaxation of Electrons in Non-Isothermal Plasmas,” Journal of Physics D: Applied Physics, Vol. 34, No. 9, 2001, pp. 1355-1366. doi:10.1088/0022-3727/34/9/312
- V. I. Kolobov and R. R. Arslanbekov, “Simulation of Electron Kinetics in Gas Discharges,” IEEE Transactions on Plasma Science, Vol. 34, No. 3, 2006, pp. 895-909. doi:10.1109/TPS.2006.875850
- D. Loffhagen and R. Winkler, “Multi-Term Treatment of the Temporal Electron Relaxation in He, Xe and N2 Plasmas,” Plasma Sources Science and Technology, Vol. 5, No. 4, 1996, pp. 710-719. doi:10.1088/0963-0252/5/4/013
- D. Loffhagen, F. Sigeneger and R. Winkler, “Study of the Electron Kinetics in the Anode Region of a Glow Discharge by a Multiterm Approach and Monte Carlo Simulations,” Journal of Physics D: Applied Physics, Vol. 35, No. 14, 2002, pp. 1768-1776. doi:10.1088/0022-3727/35/14/319
- G. K. Grubert and D. Loffhagen, “Nonequilibrium Properties of Electrons in Oxygen Plasmas,” IEEE Transactions on Plasma Science, Vol. 35, No. 5, 2007, pp. 1215- 1222. doi:10.1109/TPS.2007.905115
- M. M. Becker, G. K. Grubert and D. Loffhagen, “Boundary Conditions for the Electron Kinetic Equation Using Expansion Techniques,” The European Physical Journal Applied Physics, Vol. 51, No. 1, 2010, p. 11001-11007. doi:10.1051/epjap/2010073
- G. M. Petrov and J. L. Giuliani, “Inhomogeneous Model of an Ar-Hg Direct Current Column Discharge,” Journal of Applied Physics, Vol. 94, No. 1, 2003, pp. 62-75. doi:10.1063/1.1576895
- D. Uhrlandt, M. Schmidt, J. F. Behnke and T. Bindemann, “Self-Consistent Description of the dc Column Plasma Including Wall Interaction,” Journal of Physics D: Applied Physics, Vol. 33, No. 19, 2000, pp. 2475-2482. doi:10.1088/0022-3727/33/19/318
- D. Loffhagen, S. Arndt, F. Sigeneger, D. Uhrlandt and R. Winkler, “Electron Kinetics and Self-Consistent Description of Inhomogeneous and Nonstationary Plasmas,” Contributions to Plasma Physics, Vol. 45, No. 5-6, 2005, pp. 309-318. doi:10.1002/ctpp.200510036
- G. J. M. Hagelaar and L. C. Pitchford, “Solving the Boltzmann Equation to Obtain Electron Transport Coefficients and Rate Coefficients for Fluid Models,” Plasma Sources Science and Technology, Vol. 14, No. 4, 2005, p. 722. doi:10.1088/0963-0252/14/4/011
- L. L. Alves, G. Gousset and S. Vallee, “Nonequilibrium Positive Column Revisited,” IEEE Transactions on Plasma Science, Vol. 31, No. 4, 2003, pp. 572-586. doi:10.1109/TPS.2003.815484
- F. Sigeneger and R. Winkler, “Nonlocal Transport and Dissipation Properties of Electrons in Inhomogeneous Plasmas,” IEEE Transactions on Plasma Science, Vol. 27, No. 5, 1999, pp. 1254-1261. doi:10.1109/27.799801
- J. H. Ingold, “Moment Method Applied to Gaseous Electronics,” Physical Review A, Vol. 40, No. 7, 1989, pp. 3855-3863. doi:10.1103/PhysRevA.40.3855
- M. Surendra and M. Dalvie, “Moment Analysis of rf Parallel-Plate-Discharge Simulations Using the Particle-inCell with Monte Carlo Collisions Technique,” Physical Review E, Vol. 48, No. 5, 1993, pp. 3914-3924. doi:10.1103/PhysRevE.48.3914
- V. E. Golant, A. P. Zilinskij, I. E. Sacharov and S. C. Brown, “Fundamentals of Plasma Physics,” Wiley, New York, 1980.
- R. E. Robson, “Physics of Reacting Particle Swarms in Gases,” Journal of Chemical Physics, Vol. 85, No. 8, 1986, pp. 4486-4501. doi:10.1063/1.451769
- R. E. Robson, P. Nicoletopoulos, B. Li and R. D. White, “Kinetic Theoretical and Fluid Modelling of Plasmas and Swarms: The Big Picture,” Plasma Sources Science and Technology, Vol. 17, No. 2, 2008, Article ID: 024020. doi:10.1088/0963-0252/17/2/024020
- K. Blotekjaer, “Transport Equations for Electrons in TwoValley Semiconductors,” IEEE Transactions on Electron Devices, Vol. 17, No. 1, 1970, pp. 38-47. doi:10.1109/T-ED.1970.16921
- S. F. Liotta and H. Struchtrup, “Moment Equations for Electrons in Semiconductors: Comparison of Spherical Harmonics and Full Moments,” Solid-State Electronics, Vol. 44, No. 1, 2000, pp. 95-103. doi:10.1016/S0038-1101(99)00215-4
- A. Bringer and G. Schön, “Extended Moment Equations for Electron Transport in Semiconducting Submicron Structures,” Journal of Applied Physics, Vol. 64, No. 5, 1988, pp. 2447-2455. doi:10.1063/1.341680

