Advances in Pure Mathematics
Vol.2 No.6(2012), Article ID:24368,6 pages DOI:10.4236/apm.2012.26058
Problems of Connectivity between the Sylow Graph, the Prime Graph and the Non-Commuting Graph of a Group
DIEETCAM, Università degli Studi di Palermo, Palermo, Italy
Email: francescog.russo@yahoo.com
Received August 13, 2012; revised September 14, 2012; accepted September 22, 2012
Keywords: Sylow Graph; Normalizers; Prime Graph; Non-Commuting Graph
ABSTRACT
The Sylow graph of a finite group originates from recent investigations on certain classes of groups, defined in terms of normalizers of Sylow subgroups. The connectivity of this graph has been proved only last year with the use of the classification of finite simple groups (CFSG). A series of interesting questions arise naturally. First of all, it is not clear whether it is possible to avoid CFSG or not. On the other hand, what happens for infinite groups? Since the status of knowledge of the non-commuting graph and of the prime graph is satisfactory, is it possible to find relations between these two graphs and the Sylow graph? In the present note we make the point of the situation and formulate the above questions in appropriate way.
1. Introduction
There is a large literature which is devoted to study the ways in which one can associate a graph with a group, for the purpose of investigating the algebraic structure using properties of the associated graph (see [1-4]). Many authors studied the so-called commuting graph 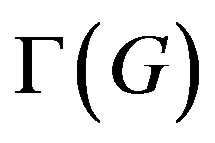 of a group G, whose vertices are the non-trivial elements of G and two vertices x, y are connected if xy = yx (see [5-8]). The connectivity of
of a group G, whose vertices are the non-trivial elements of G and two vertices x, y are connected if xy = yx (see [5-8]). The connectivity of 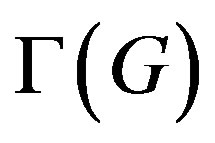 gives information of how far is G from being abelian, therefore the commuting graph of abelian groups is always connected. In particular,
gives information of how far is G from being abelian, therefore the commuting graph of abelian groups is always connected. In particular, 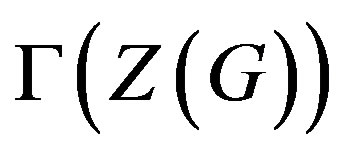 is a connected component of
is a connected component of 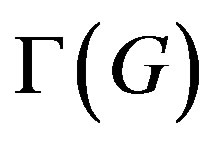 and this motivates us to focuse only on
and this motivates us to focuse only on 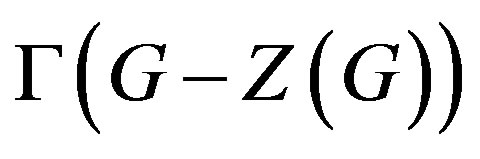 , which gives significant information on the connectivity of
, which gives significant information on the connectivity of .
.
By duality, the non-commuting graph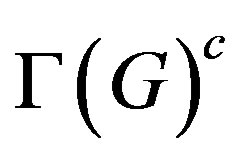 , associated to a group G, is the complement of
, associated to a group G, is the complement of , i.e., a graph with vertex set
, i.e., a graph with vertex set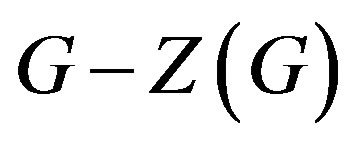 , where two distinct non-central elements x and y of G are joined by an edge if and only if xy ≠ yx. Obviously, we are always considering simple graphs through this paper, i.e., graphs with no loops or directed or repeated edges. The non-commuting graph of a non-abelian finite group has received much attention in the last years and [9-20] are some significant contributions. Moreover, there are recent results in [21], concerning graphs associated with conjugacy classes of groups and it is involved the probability of commuting pairs of [22-25].
, where two distinct non-central elements x and y of G are joined by an edge if and only if xy ≠ yx. Obviously, we are always considering simple graphs through this paper, i.e., graphs with no loops or directed or repeated edges. The non-commuting graph of a non-abelian finite group has received much attention in the last years and [9-20] are some significant contributions. Moreover, there are recent results in [21], concerning graphs associated with conjugacy classes of groups and it is involved the probability of commuting pairs of [22-25].
Herzog and others [8] consider a generalization of , namely, the graph
, namely, the graph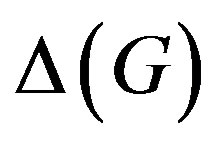 , associated with the conjugacy classes of a non-trivial group G. The vertices
, associated with the conjugacy classes of a non-trivial group G. The vertices 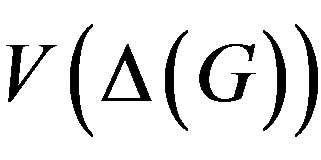 of
of 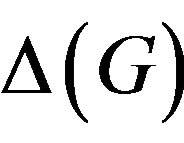 are the non-trivial conjugacy classes of G and we join two different vertices C, D, whenever there exist an x in C and a y in D such that xy = yx. Further generalizations can be found in [5-7,26,27], where notions of character theory are involved.
are the non-trivial conjugacy classes of G and we join two different vertices C, D, whenever there exist an x in C and a y in D such that xy = yx. Further generalizations can be found in [5-7,26,27], where notions of character theory are involved.
If G is finite, then  is obviously related to the prime graph
is obviously related to the prime graph 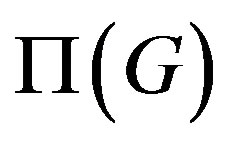 of G, whose vertices are the primes dividing the order of G and two vertices p and q of
of G, whose vertices are the primes dividing the order of G and two vertices p and q of 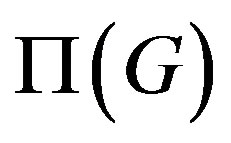 are joined by an edge if and only if G has an element of order pq.
are joined by an edge if and only if G has an element of order pq.
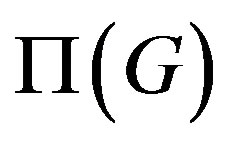 was introduced by Gruenberg and Kegel in an unpublished manuscript [28] of the 1975, not easily available, so that the main information about
was introduced by Gruenberg and Kegel in an unpublished manuscript [28] of the 1975, not easily available, so that the main information about 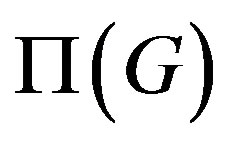 can be found directly in [29-37], which are fundamental contributions for the study of
can be found directly in [29-37], which are fundamental contributions for the study of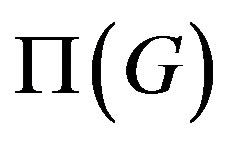 . Herzog and others [8] found an important relation between
. Herzog and others [8] found an important relation between 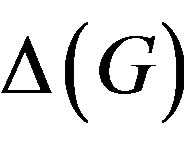 and
and :
:
Theorem 1.1 (See [8, Proposition 9]). 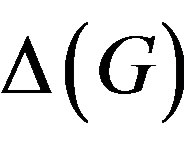 and
and  have the same number of connected components in a finite group G.
have the same number of connected components in a finite group G.
Since  has been largely studied in [19,38-47] and in further works of the same authors, Theorem 1.1 allows us to apply results on
has been largely studied in [19,38-47] and in further works of the same authors, Theorem 1.1 allows us to apply results on 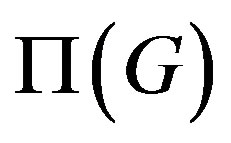 for investigating
for investigating 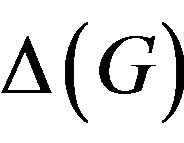 and viceversa.
and viceversa.
In the infinite case, some variations can be discussed once appropriate restrictions are done.
For instance, if G is an infinite group either residually solvable or residually finite, then 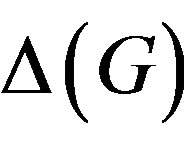 is complete if and only if G is abelian.
is complete if and only if G is abelian.
On the other hand, we know from [28-33] that, the prime graph 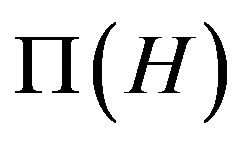 of a finite solvable group H has at most two connected components and, using CFSG, Williams [37] proved that
of a finite solvable group H has at most two connected components and, using CFSG, Williams [37] proved that 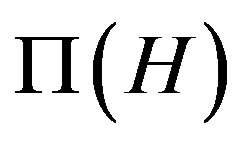 has at most 6 components, when H is arbitrary (not necessarily solvable). The proof of Williams analyses simple groups case-by-case and refers to the atlas [48]. Furthermore, Lucido [32] showed that the diameter of each connected component of
has at most 6 components, when H is arbitrary (not necessarily solvable). The proof of Williams analyses simple groups case-by-case and refers to the atlas [48]. Furthermore, Lucido [32] showed that the diameter of each connected component of 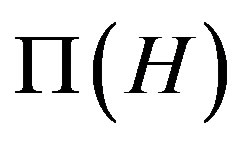 is at most 5 when H is arbitrary and, in the solvable case, this diameter becomes at most 3.
is at most 5 when H is arbitrary and, in the solvable case, this diameter becomes at most 3.
Moghaddamfar, Khosravi and other authors worked on the same line of investigation in [38,42-45,47] and they provide interesting characterizations of simple groups, only looking at their prime graph.
In the infinite case, a systematic treatment seems to be absent in literature. For instance, Herzog and others [8] deal with a meaningful theory of the prime graph and of the commuting graph for infinite locally finite groups, once we want to see whether the results of the finite case may be extended or not. They prove as follows.
Theorem 1.2. (See [8, Theorems 10, 12]) If G is a periodic solvable group, then 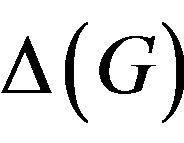 has at most two components, each of diameter at most 9. Moreover, if G is locally finite (not necessarily solvable), then
has at most two components, each of diameter at most 9. Moreover, if G is locally finite (not necessarily solvable), then 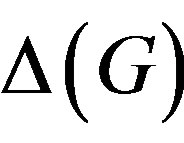 has at most 6 components, each of diameter at most 19.
has at most 6 components, each of diameter at most 19.
Roughly speaking, Theorem 1.2 and its converse would allow us to recognize an infinite group from its commuting graph. To the best of our knowledge, we haven’t found whether an infinite locally finite simple group can be recognized from information on its commuting graph or not. This is a missing point which we noted.
Problem 1.3. Recognition of an infinite locally finite simple group from its commuting graph and from its prime graph.
2. Some Open Questions of Iranmanesh
If G is a finite group, then we have seen that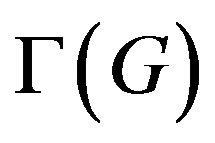 ,
, 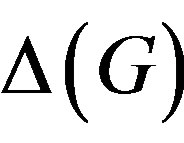 and
and  have relations. Some recent contributions of Iranmanesh and others [14,15,46] show that also
have relations. Some recent contributions of Iranmanesh and others [14,15,46] show that also 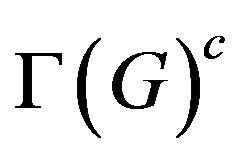 and
and 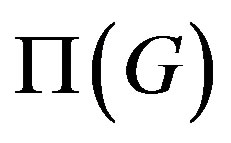 may be related.
may be related.
Theorem 2.1. (See [15, Lemmas 2.1, 2.2, Theorem 2.5, Corollary 2.7]) Let G and H be two non-abelian finite groups and 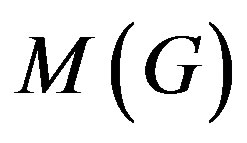 (resp.
(resp.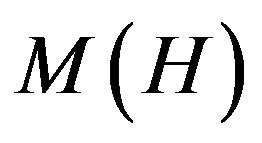 ) denote the set of orders of maximal abelian subgroups of G (resp. H).
) denote the set of orders of maximal abelian subgroups of G (resp. H).
1) If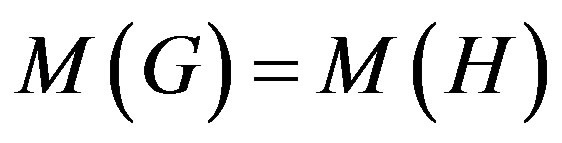 , then
, then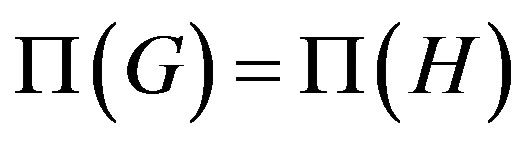 .
.
2) If G is simple and 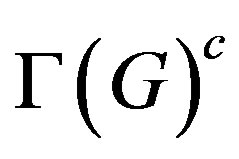 is isomorphic to
is isomorphic to , then
, then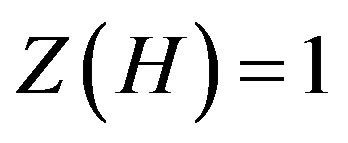 .
.
3) If 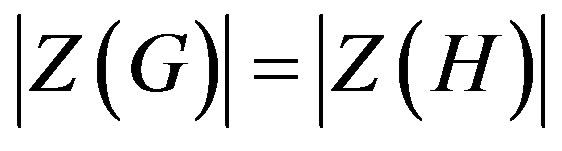 and
and 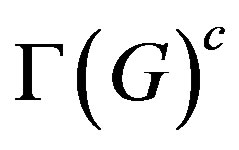 is isomorphic to
is isomorphic to
 , then
, then 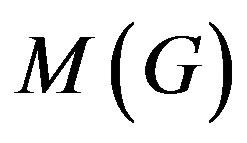 and
and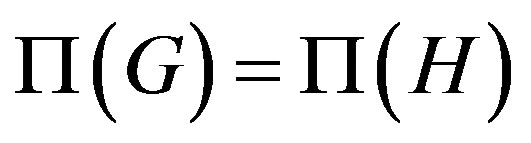 .
.
A consequence of Theorem 2.1 is [15, Corollary 2.8], where it is shown that for all even integers n bigger than 4, a finite group G is isomorphic to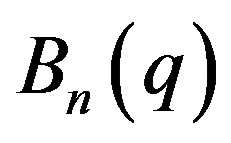 , provided
, provided 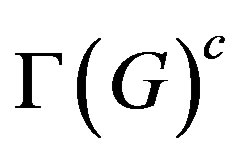 is isomorphic to
is isomorphic to 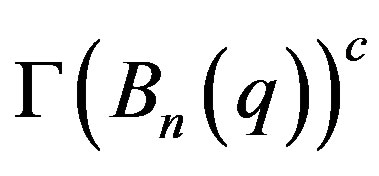 (here
(here 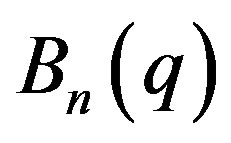 is a simple group of Lie type in the usual notation of [48]). This conclusion gives a positive answer to a famous conjecture of Abdollahi and others [9], which is interesting the researches of several authors in the last decades:
is a simple group of Lie type in the usual notation of [48]). This conclusion gives a positive answer to a famous conjecture of Abdollahi and others [9], which is interesting the researches of several authors in the last decades:
Conjecture 2.2. (See [49, Problem 16.1]) Let S be a non-abelian finite simple group and G a group such that 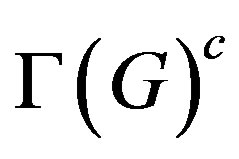 is isomorphic to
is isomorphic to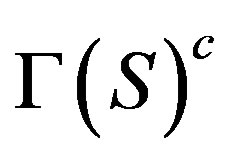 . Then S is isomorphic to G.
. Then S is isomorphic to G.
Iranmanesh and others [14,46] dealt with further generalizations of Theorem 2.1. There are in fact evidences which show that the following conjecture is true.
Conjecture 2.3. (See [46, Problem 1]) Let G and H be two non-abelian finite groups such that  is isomorphic to
is isomorphic to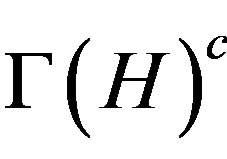 . If
. If  and
and 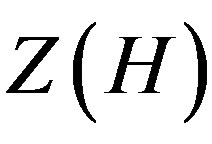 have the same prime divisors and
have the same prime divisors and , then
, then
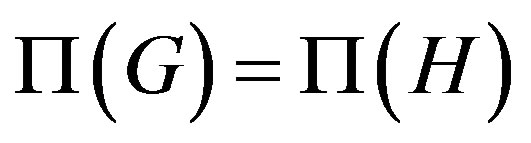 .
.
In virtue of all we have said up to now, we haven’t found information whether a variation of Theorem 2.1 holds or not in the infinite case. The references [50-53] show that there is a theory which we may use for this scope, even if the notion of Sylow subgroup should be examined carefully.
Problem 2.4. Given two infinite locally finite non-abelian groups, is it possible to get a variation of Theorem 2.1?
3. Sylow Graph and Properties of Normalizers of Sylow Subgroups
In the previous section, we have described only relations among the non-commuting graph, the commuting graph and the prime graph, both in finite and infinite case. A new graph, recently studied in [54-56] has motivated us to write the present note and there would be interesting perspectives of study in our opinion.
Let 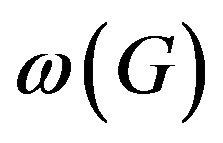 be the set of prime divisors of the orders of elements of
be the set of prime divisors of the orders of elements of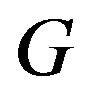 . Given a prime
. Given a prime 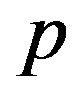 in
in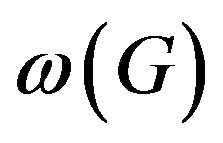 , the automiser
, the automiser 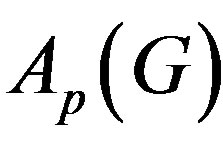 is the group
is the group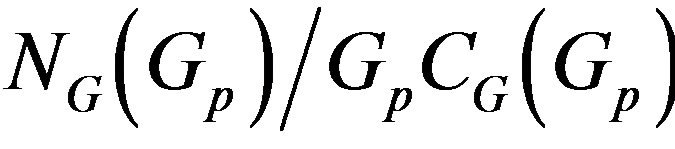 . The Sylow graph
. The Sylow graph 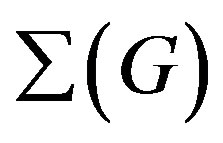 of G, with set of vertices
of G, with set of vertices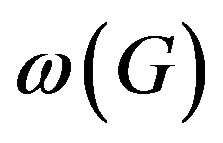 , is given by the following rules: Two vertices p, q in
, is given by the following rules: Two vertices p, q in  form an edge of
form an edge of 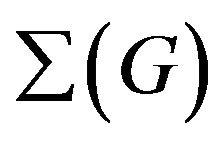 if either q is in
if either q is in 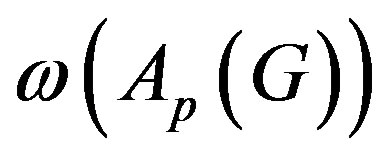 or p is in
or p is in .
.
If G is finite, then 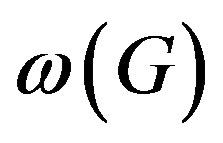 coincides with the set of all prime divisors of
coincides with the set of all prime divisors of  and
and 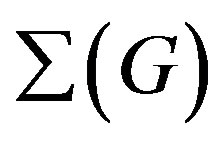 has been studied by Kazarin and others in [55], even if the origins go back to some works of De Vivo and others [54,57-60], where it appears for the first time a graph with the same properties of
has been studied by Kazarin and others in [55], even if the origins go back to some works of De Vivo and others [54,57-60], where it appears for the first time a graph with the same properties of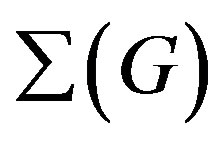 . The Sylow graph is useful for problems of formations of finite groups (see [61] for the notion of formation of finite groups) and properties of normalizers of Sylow subgroups. One of the main contributions about
. The Sylow graph is useful for problems of formations of finite groups (see [61] for the notion of formation of finite groups) and properties of normalizers of Sylow subgroups. One of the main contributions about  is the following.
is the following.
Theorem 3.1. (See [55, Main Theorem]) 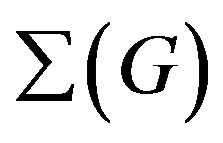 is connected and its diameter is at most 5 whenever G is a finite almost simple group.
is connected and its diameter is at most 5 whenever G is a finite almost simple group.
For solvable groups, the answer was known earlier as corollary of results in [54,57-60], where a different approach was adopted. [55, Main Theorem] influenced heavily [56], in which a gap occurred in the proof of the connectivity of 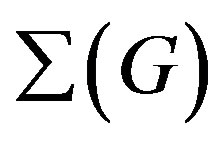 without CFSG. The following problem is in fact open.
without CFSG. The following problem is in fact open.
Problem 3.2. Can we prove Theorem 3.1 without CFSG?
Another question has combinatorial interest. Lucido [33] showed that 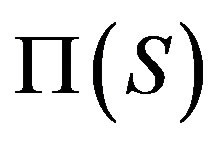 has diameter at most 5 for a non-abelian finite simple group S and Theorem 3.1 implies that
has diameter at most 5 for a non-abelian finite simple group S and Theorem 3.1 implies that  has also diameter at most 5. This means that the actions of
has also diameter at most 5. This means that the actions of 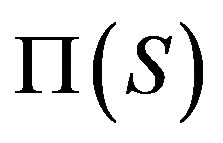 and
and 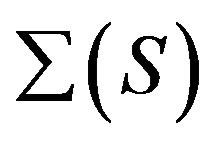 on
on 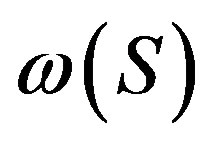 determine components in which the connectivity has the same bounds in terms of diameter.
determine components in which the connectivity has the same bounds in terms of diameter.
Problem 3.3. Is it possible to find relations between the connected components of 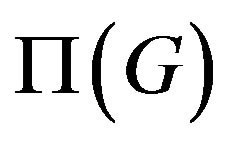 and those of
and those of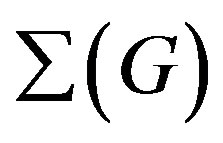 , when G is a finite group?
, when G is a finite group?
Once we move in the universe of all infinite groups, locally finite groups and periodic solvable groups seem to be natural contexts where we may generalize the notion of Sylow graph. Again [50-53] motivate this assertion. Of course, we cannot say that infinite locally finite groups satisfy Sylow Theorems, in order to carry out what we know from the finite case, but, results of Asar (see [51]) show that Sylow Theorems are true mutatis mutandis when we impose the minimal condition on suitable families of subgroups (for instance, the so-called locally finite groups with min-p in [51,52] have received much attention from the point of view of the Sylow theory).
Problem 3.4. It is missing a theory of Sylow graphs for infinite groups, which agrees with that of the finite case. Infinite locally finite groups seem to be good candidates for a first attempt.
Now we come back to the finite case (and we will deal only with finite groups until the end) and note that the knowledge of the Sylow graph and of the properties of the normalizers of the Sylow subgroups is relevant for various reasons.
If G is a (finite) group in which every Sylow subgroup is self-normalizing, then [62,63] show that G is a p-group for some prime p. [62,63] are classical results and belong to a long standing line of research which investigates the structural properties of a group, once restrictions on its normalizers are given (see [61, Chapter 5] or [64-71]).
As noted in [58], we may introduce the group class operator N, defined by the rule: G belongs to  if and only if the normalizer
if and only if the normalizer 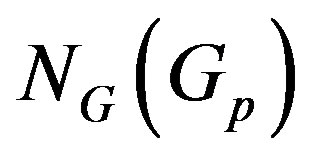 of
of 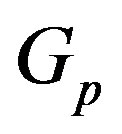 belongs to X for all p in
belongs to X for all p in . Here X is a class of groups and
. Here X is a class of groups and  a Sylow p-subgroup of G (N is called N-closed if
a Sylow p-subgroup of G (N is called N-closed if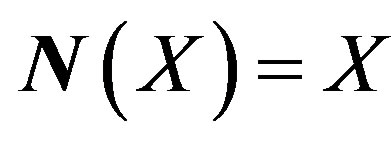 ).
).
N was largely studied in [54-60], but the study of properties of normalisers appear also [62-72]. For instance, [63, Corollary 2] shows that the class of all p-groups is N-closed and [68, Theorem 2] shows that the same is true for the class of all nilpotent groups.
A further improvement is [64, Theorem 2], where it is considered the class of all p-nilpotent groups. In the class of all solvable groups, relations among N and classes of groups which are closed with respect to forming subgroups (briefly said S-closed), were investigated in [56- 60]. These researches make strong use of some techniques of the theory of formations of groups, which has been largely exploited in the last years by BallesterBolinches, Shemetkov and Skiba (terminology and notations which we are using can be found in fact in [61,67]). For instance, a significant notion is that of lattice-formation, which is quite technical to explain here (see [56-60, 67]), but has a fundamental role in many topics of formations of finite groups. Indeed, an immediate consequence of Theorem 3.1 is:
Theorem 3.5. (See [55]) A lattice-formation is Nclosed.
Therefore 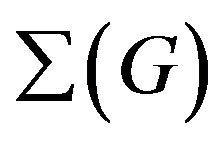 allows us to decide whether a class of groups is N-closed or not. Many other interesting applications can be found in [55, Section 3]. We note that there are some interesting examples also in [55,56], which help to visualize the topic.
allows us to decide whether a class of groups is N-closed or not. Many other interesting applications can be found in [55, Section 3]. We note that there are some interesting examples also in [55,56], which help to visualize the topic.
A final observation will have computational nature. The following condition is very easy to check empirically and, when it is true, the Sylow graph is connected.
Hypothesis. Assume that in a (finite) group G, if p is an odd prime in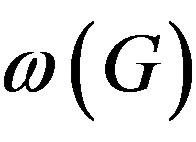 , then there exists another prime q in
, then there exists another prime q in 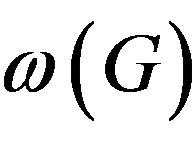 such that q < p and q divides
such that q < p and q divides
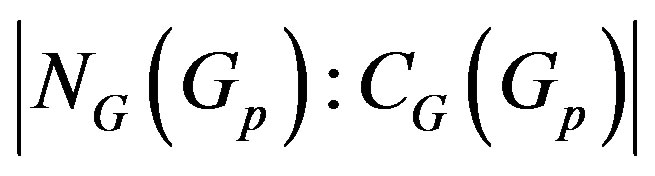 for each Sylow p-subgroup Gp of G.
for each Sylow p-subgroup Gp of G.
Based on the previous Hypothesis, it has been written an algorithm with GAP [73] in [56] (called ROSN1), which confirms numerically Theorem 3.1. Given two different primes p and q of 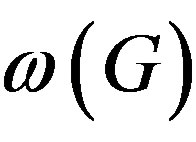 and a (finite) group G, ROSN1 answers YES, or NO, to the question: are p and q connected in
and a (finite) group G, ROSN1 answers YES, or NO, to the question: are p and q connected in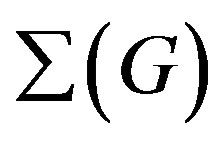 ?
?
This allows us to ask:
Problem 3.6. How can we improve numerical algorithms which confirm Theorem 3.1?
4. Acknowledgements
I thank the referees for comments and suggestions.
REFERENCES
- E. A. Bertram, “Some Applications of Graph Theory to Finite Groups,” Discrete Mathematics, Vol. 44, No. 1, 1983, pp. 31-43. doi:10.1016/0012-365X(83)90004-3
- B. Bollobas, “Graph Theory,” Springer, Berlin, 1979. doi:10.1007/978-1-4612-9967-7
- Y. Segev, “The Commuting Graph of Minimal Non-Solvable Groups,” Geometriae Dedicata, Vol. 88, No. 1-3, 2001, pp. 55-66.
- C. T. Marchionna, “Distance in a Group and Erdős-Type Graph,” Istituto Lombardo Accademia di Scienze e Lettere (Classe di Scienze Matematiche e Naturali), Vol. 125, 1992, pp. 3-23.
- E. A. Bertram, M. Herzog and A. Mann, “On a Graph Related to Conjugacy Classes of Groups,” Bulletin of the London Mathematical Society, Vol. 22, No. 6, 1990, pp. 569-575. doi:10.1112/blms/22.6.569
- M. Bianchi, D. Chillag, A. G. B. Mauri, M. Herzog, M. and C. Scoppola, “Applications of a Graph Related to Conjugacy Classes in Finite Groups,” Archiv der Mathematik, Vol. 58, 1992, pp. 126-132. doi:10.1007/BF01191876
- D. Chillag, M. Herzog and A. Mann, “On the Diameter of a Graph Related to Conjugacy Classes of Groups,” Bulletin of the London Mathematical Society, Vol. 25, No. 3, 1993, pp. 255-262. doi:10.1112/blms/25.3.255
- M. Herzog, P. Longobardi and M. Maj, “On a Commuting Graph on Conjugacy Classes of Groups,” Communications in Algebra, Vol. 37, No. 10, 2009, pp. 3369-3387.
- A. Abdollahi, S. Akbari and H. R. Maimani, “Non-Commuting Graph of a Group,” Journal of Algebra, Vol. 298, No. 2, 2006, pp. 468-492. doi:10.1016/j.jalgebra.2006.02.015
- S. Akbari and A. Mohammadian, “On the Zero-Divisor Graph of a Commutative Ring,” Journal of Algebra, Vol. 274, No. 2, 2004, pp. 847-855.
- S. Akbari, A. Mohammadian, H. Radjavi and P. Raja, “On the Diameters of Commuting Graphs,” Linear Algebra and Its Applications, Vol. 418, No. 1, 2006, pp. 161-176.
- S. Akbari, H. Bidkhori and A. Mohammadian, “Commuting Graphs of Matrix Algebras,” Communications in Algebra, Vol. 36, No. 11, 2008, pp. 4020-4031.
- M. Akbari, M. Kheirabadi and A. R. Moghaddamfar, “Recognition by Non-Commuting Graph of Finite Simple Groups L4(q),” Frontiers of Mathematics in China, Vol. 6, No. 1, 2011, pp. 1-16. doi:10.1007/s11464-010-0085-6
- N. Ahanjideh and A. Iranmanesh, “A Characterization of Bn(q) by the Set of Orders of Maximal Abelian Subgroups,” International Journal of Algebra and Computation, Vol. 19, No. 2, 2009, pp. 191-211. doi:10.1142/S0218196709005020
- N. Ahanjideh and A. Iranmanesh, “On the Relation between the Non-Commuting Graph and the Prime Graph,” International Journal of Group Theory, Vol. 1, No. 1, 2012, pp. 25-28.
- G. Y. Chen, “A Characterization of Alternating Groups by the Set of Orders of Their Maximal Abelian Subgroups,” Siberian Mathematical Journal, Vol. 47, No. 3, 2006, pp. 594-596. doi:10.1007/s11202-006-0070-1
- M. R. Darafsheh, “Groups with the Same Non-Commuting Graph,” Discrete Applied Mathematics, Vol. 157, No. 4, 2009, pp. 833-837. doi:10.1016/j.dam.2008.06.010
- M. R. Darafsheh and A. D. Monfared, “A Characterization of the Groups PSU(4,4) and PSL(4,4) by Non-Commuting Graph,” Utilitas Mathematica, Vol. 81, 2010, pp. 165-185.
- M. Kheirabadi and A. R. Moghaddamfar, “Recognizing Some Finite Simple Groups by Non-Commuting Graph,” Journal of Algebra and Its Applications, Vol. 11, No. 4, 2012, 14 pages. doi:10.1142/S0219498812500776
- M. C. Xu, “The Characterization of Finite Simple Groups, L3(32m-1) (m ≥ 2) by Their Element Orders,” Acta Mathematica Sinica, Vol. 21, No. 4, 2005, pp. 899-902. doi:10.1007/s10114-004-0448-6
- A. Erfanian and B. Tolue, “Relative Non-Commuting Graph of a Finite Group,” Journal of Algebra and Its Applications, in Press. doi:10.1142/S0219498812501575
- A. Erfanian and F. G. Russo, “Probability of Commuting n-Tuples in Some Classes of Compact Groups,” Bulletin of the Iranian Mathematical Society, Vol. 24, 2008, pp. 27-37.
- K. H. Hofmann and F. G. Russo, “The Probability That x and y Commute in a Compact Group,” Mathematical Proceedings of the Cambridge Philosophical Society, Vol. 153, 2012, pp. 557-571.
- P. Niroomand, R. Rezaei and F. G. Russo, “Commuting Prowers and Exterior Degree of Finite Groups,” Journal of the Korean Mathematical Society, Vol. 49, No. 4, 2012, pp. 855-865. doi:10.4134/JKMS.2012.49.4.855
- R. Rezaei and F. G. Russo, “n-th Relative Nilpotency Degree and Relative n-Isoclinism Classes,” Carpathian Journal of Mathematics, Vol. 27, No. 1, 2011, pp. 123- 130.
- S. Dolfi, E. Pacifici, L. Sanus and P. Spiga, “On the Vanishing Prime Graph of Finite Groups,” Journal of the London Mathematical Society, Vol. 82, No. 1, 2010, pp. 167-183.
- S. Dolfi, E. Pacifici, L. Sanus and P. Spiga, “On the Vanishing Prime Graph of Solvable Groups,” Journal of Group Theory, Vol. 13, No. 2, 2010, pp. 189-206. doi:10.1515/jgt.2009.046
- K. W. Gruenberg and O. Kegel, Manuscript, Unpublished, 1975.
- N. Iiyori and H. Yamaki, “Prime Graph Components of the Simple Groups of Lie Type over the Field of Even Characteristic,” Journal of Algebra, Vol. 155, No. 2, 1993, pp. 335-343. doi:10.1006/jabr.1993.1048
- A. Kondratev, “Prime Graph Components of Finite Simple Groups,” Mathematics of the USSR-Sbornik, Vol. 67, No. 1, 1990, pp. 235-247. doi:10.1070/SM1990v067n01ABEH001363
- A. Kondratev and V. D. Mazurov, “Recognition of Alternating Groups of Prime Degree from the Orders of Their Elements,” Siberian Mathematical Journal, Vol. 41, No. 2, 2000, pp. 294-302. doi:10.1007/BF02674599
- M. S. Lucido, “The Diameter of the Prime Graph of Finite Groups,” Journal of Group Theory, Vol. 2, No. 2, 1999, pp. 157-172. doi:10.1515/jgth.1999.011
- M. S. Lucido, “Prime Graph Components of Finite Almost Simple Groups,” Rendiconti del Seminario Matematico della Università di Padova, Vol. 102, 1999, pp. 1-22.
- M. S. Lucido and A. R. Moghaddamfar, “Groups in Which All the Connected Components of Their Prime Graphs are Complete,” Journal of Group Theory, Vol. 7, No. 3, 2004, pp. 373-384. doi:10.1515/jgth.2004.013
- A .V. Vasilev, “On a Relation between the Structure of a Finite Group and the Properties of Its Prime Graph,” Siberian Mathematical Journal, Vol. 46, No. 3, 2005, pp. 396-404. doi:10.1007/s11202-005-0042-x
- A. V. Vasilev and E. P. Vdovin, “An Adjacency Criterion in the Prime Graph of a Finite Simple Group,” Algebra Logic, Vol. 44, No. 6, 2005, pp. 381-406. doi:10.1007/s10469-005-0037-5
- J. S. Williams, “Prime Graph Components of Finite Groups,” Journal of Algebra, Vol. 69, No. 2, 1981, pp. 487-513. doi:10.1016/0021-8693(81)90218-0
- Z. Akhlaghi, B. Khosravi and M. Khatami, “Quasirecognition by Prime Graph of Simple Group Dn(3),” Publicationes Mathematicae Debrecen, Vol. 78, 2011, pp. 469- 484. doi:10.5486/PMD.2011.4851
- Z. Arad and W. Herfort, “Maximal Cyclic Subgroups and Prime Divisors in Finite Groups,” Archiv der Mathematik, Vol. 85, No. 1, 2005, pp. 31-36. doi:10.1007/s00013-005-1449-6
- M. R. Darafsheh, A. R. Moghaddamfar and A. R. Zokayi, “A Characterization of Finite Simple Groups by the Degrees of Vertices of Their Prime Graphs,” Algebra Colloquium, Vol. 12, 2005, pp. 431-442.
- H. He and W. Shi, “Recognition of Some Finite Simple Groups of Type Dn(q) by Spectrum,” International Journal of Algebra and Computation, Vol. 19, No. 1, 2009, pp. 681-698.
- A. Khosravi and B. Khosravi, “2-Recognizability of PSL(2,p2) by the Prime Graph,” Siberian Mathematical Journal, Vol. 49, No. 4, 2008, pp. 749-757. doi:10.1007/s11202-008-0072-2
- A. Khosravi and B. Khosravi, “Quasirecognition of the Simple Group 2G2(q) by the Prime Graph,” Siberian Mathematical Journal, Vol. 48, No. 3, 2007, pp. 570-577.
- B. Khosravi, B. Khosravi and B. Khosravi, “On the Prime Graph of PSL(2,p) Where p>3 Is a Prime Number,” Acta Mathematica Hungarica, Vol. 116, No. 4, 2007, pp. 295- 307. doi:10.1007/s10474-007-6021-x
- A. Khosravi and B. Khosravi, “A New Characterization of Almost Sporadic Groups,” Journal of Algebra and Its Applications, Vol. 1, No. 3, 2002, pp. 267-279. doi:10.1142/S021949880200015X
- A. Iranmanesh and A. Jafarzadeh, “On the Commuting Graph Associated with the Symmetric and Alternating Groups,” Journal of Algebra and Its Applications, Vol. 7, No. 4, 2008, pp. 129-146. doi:10.1142/S0219498808002710
- V. D. Mazurov and A. R. Moghaddamfar, “The Recognition of the Simple Group S8(2) by Its Spectrum,” Algebra Colloquium, Vol. 13, No. 4, 2006, pp. 643-646.
- J. Conway, R. Curtis, S. Norton, R. Parker and R. Wilson, “Atlas of Finite Groups,” Clarendon Press, Oxford, 1985.
- E. I. Khukhro and V. D. Mazurov, “Unsolved Problems in Group Theory: The Kourovka Notebook,” 17th Edition, Sobolev Institute of Mathematics, Novosibirsk, 2010.
- A. Arikan and U. Meierfrankenfeld, “Hypersolvable Groups,” Communications in Algebra, Vol. 34, No. 10, 2006, pp. 3643-3657. doi:10.1080/00927870600860742
- M. D. Dixon, “Sylow Theory, Formations and Fitting Classes in Locally Finite Groups,” World Scientific Publishing Corporation, River Edge, 1994.
- O. H. Kegel and B. A. F. Wehrfritz, “Locally Finite Groups,” North Holland, Amsterdam, 1973.
- F. G. Russo, “Generalized FC-Groups in Finitary Groups,” University of Naples Federico II, 2007. http://www.fedoa.unina.it/1305
- A. D’Aniello, C. De Vivo and G. Giordano, “Lattice Formations and Sylow Normalizers: A Conjecture,” Atti del Seminario Matematico e Fisico dell’Universita’ di Modena e Reggio Emilia, Vol. 55, 2007, pp. 107-112.
- L. Kazarin, A. Martinez-Pastor and M. D. Perez-Ramos, “On the Sylow Graph of a Group and Sylow Normalizers,” Israel Journal of Mathematics, Vol. 186, No. 1, 2011, pp. 251-271. doi:10.1007/s11856-011-0138-x
- F. G. Russo, “On the Connectivity of the Sylow Graph of a Finite Group,” Cornell University Library, 2010. http://arxiv.org/abs/1002.4853
- A. D’Aniello, C. De Vivo and G. Giordano, “Finite Groups with Primitive Sylow Normalizers,” Bollettino dell’Unione Matematica Italiana (Sezione B), Vol. 5, 2002, pp. 235-245.
- A. D’Aniello, C. De Vivo and G. Giordano, “Saturated Formations and Sylow Normalisers”, Bulletin of the Australian Mathematical Society, Vol. 69, No. 1, 2004, pp. 25-33.
- A. D’Aniello, C. De Vivo, G. Giordano and M. D. PerezRamos, “Saturated Formations Closed under Sylow Normalizers,” Communications in Algebra, Vol. 33, 2005, pp. 2801-2808. doi:10.1081/AGB-200065377
- [61] A. D’Aniello, C. De Vivo and G. Giordano, “On Certain Saturated Formations of Finite Groups,” Proceedings of Ischia Group Theory 2006, Singapore, 2008, pp. 12-31.
- [62] K. Doerk and T. Hawkes, Finite Soluble Groups, de Gruyter, Berlin, 1992.
- [63] G. Glauberman, “Prime-Power Factor Groups of Finite Groups,” Mathematische Zeitschrift, Vol. 107, No. 3, 1968, pp. 159-172. doi:10.1007/BF01110255
- [64] G. Glauberman, “Prime-Power Factor Groups of Finite Groups II,” Mathematische Zeitschrift, Vol. 117, No. 1-4, 1970, pp. 46-56. doi:10.1007/BF01109827
- [65] A. Ballester-Bolinches and L. A. Shemetkov, “On Normalizers of Sylow Subgroups in Finite Groups,” Siberian Mathematical Journal, Vol. 40, No. 1, 1999, pp. 3-5.
- [66] A. Ballester-Bolinches, A. Martinez-Pastor, M. C. PedrazaAguilera and M. D. Perez-Ramos, “On Nilpotent-Like Fitting Formations,” Cambridge University Press, Cambdridge, 2003, pp. 31-38.
- [67] A. Ballester-Bolinches, L. M. Ezquerro and A. N. Skiba, “Local Embeddings of Some Families of Subgroups of Finite Groups,” Acta Mathematica Sinica, Vol. 25, No. 6, 2009, pp. 869-882. doi:10.1007/s10114-009-8623-4
- [68] A. Ballester-Bolinches and L. M. Ezquerro, “Classes of Finite Groups,” Springer, Heidelberg, 2006.
- [69] B. Baumann and U. Meierfrankenfeld, “On Normalizers of Nilpotent Subgroups,” Journal of Algebra, Vol. 268, No. 2, 2003, pp. 373-403. doi:10.1016/S0021-8693(03)00094-2
- [70] M. Bianchi, A. G. B. Mauri and P. Hauck, “On Finite Groups with Nilpotent Sylow-Normalizers,” Archiv der Mathematik, Vol. 47, 1986, pp. 93-197.
- [71] R. Bryce, V. Fedri and L. Serena, “Bounds on the Fitting Length of Finite Solvable Groups with Supersoluble Sylow Normalisers,” Bulletin of the Australian Mathematical Society, Vol. 44, No. 1, 1991, pp. 19-31. doi:10.1017/S0004972700029427
- [72] B. Sirola, “Normalizers and Self-Normalizing Subgroups II,” Central European Journal of Mathematics, Vol. 9, No. 6, 2011, pp. 1317-1332. doi:10.2478/s11533-011-0091-2
- [73] B. Sirola, “On Centralizers and Normalizers for Groups,” Bulletin of the Australian Mathematical Society, 2012, in Press.
- [74] The GAP Group, “GAP: Groups, Algorithms and Programming,” Version 4.4, 2005. http://www.gap-system.org

