Advances in Pure Mathematics
Vol.2 No.5(2012), Article ID:22800,7 pages DOI:10.4236/apm.2012.25046
Second Order Periodic Boundary Value Problems Involving the Distributional Henstock-Kurzweil Integral*
Department of Mathematics, Hohai University, Nanjing, China
Email: xyzhouhhu@163.com, yegj@hhu.edu.cn
Received May 25, 2012; revised June 25, 2012; accepted July 4, 2012
Keywords: periodic boundary value problem; distributional Henstock-Kurzweil integral; distributional derivative; existence; upper and lower solutions; fixed point
ABSTRACT
We apply the distributional derivative to study the existence of solutions of the second order periodic boundary value problems involving the distributional Henstock-Kurzweil integral. The distributional Henstock-Kurzweil integral is a general intergral, which contains the Lebesgue and Henstock-Kurzweil integrals. And the distributional derivative includes ordinary derivatives and approximate derivatives. By using the method of upper and lower solutions and a fixed point theorem, we achieve some results which are the generalizations of some previous results in the literatures.
1. Introduction
This paper is devoted to the study of the existence of solutions of the second order periodic boundary value problem (PBVP for brevity)
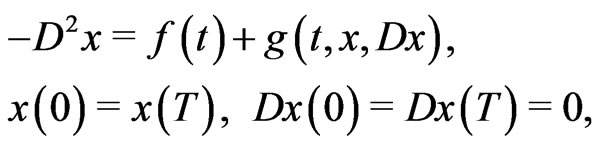 (1.1)
(1.1)
where 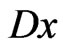 and
and 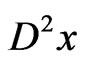 are the first and second order distributional derivatives of
are the first and second order distributional derivatives of  respectively,
respectively, 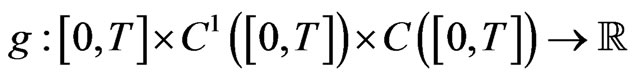 and
and 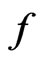 is a distribution (generalized function).
is a distribution (generalized function).
If the distributional derivative in the system (1.1) is replaced by the ordinary derivative and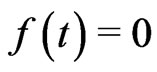 , then (1) converts into
, then (1) converts into
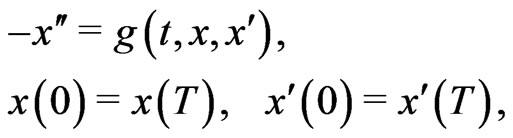 (1.2)
(1.2)
here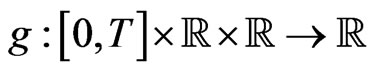 , and
, and 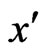 and
and 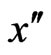 denote the first and second ordinary derivatives of
denote the first and second ordinary derivatives of . The existence of solutions of (1.2) have been extensively studied by many authors [1,2]. It is well-known, the notion of a distributional derivative is a general concept, including ordinary derivatives and approximate derivatives. As far as we know, few papers have applied distributional derivatives to study PBVP. In this paper, we have come up with a new way, instead of the ordinary derivative, using the distributional derivative to study the PBVP and obtain some results of the existence of solutions.
. The existence of solutions of (1.2) have been extensively studied by many authors [1,2]. It is well-known, the notion of a distributional derivative is a general concept, including ordinary derivatives and approximate derivatives. As far as we know, few papers have applied distributional derivatives to study PBVP. In this paper, we have come up with a new way, instead of the ordinary derivative, using the distributional derivative to study the PBVP and obtain some results of the existence of solutions.
This paper is organized as follows. In Section 2, we introduce fundamental concepts and basic results of the distributional Henstock-Kurzweil integral or briefly the 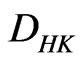 -integral. A distribution
-integral. A distribution  is
is 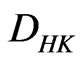 -integrable on
-integrable on 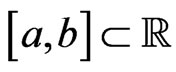 if there is a continuous function F on
if there is a continuous function F on  with
with 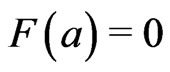 whose distributional derivative equals
whose distributional derivative equals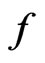 . From the definition of the
. From the definition of the 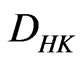 -integral, it includes the Riemann integral, Lebesgue integral, HK-integral and wide Denjoy integral (for details, see [3-5]). Furthermore, the space of
-integral, it includes the Riemann integral, Lebesgue integral, HK-integral and wide Denjoy integral (for details, see [3-5]). Furthermore, the space of  -integrable distributions is a Banach space and has many good properties, see [6-8].
-integrable distributions is a Banach space and has many good properties, see [6-8].
In Section 3, with the 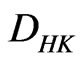 -integral and the distributional derivative, we generalize the PBVP (1.2) to (1.1). By using the method of upper and lower solutions and a fixed point theorem, we achieve some interesting results which are the generalizations of some corresponding results in the references.
-integral and the distributional derivative, we generalize the PBVP (1.2) to (1.1). By using the method of upper and lower solutions and a fixed point theorem, we achieve some interesting results which are the generalizations of some corresponding results in the references.
2. The Distributional Henstock-Kurzweil Integral
In this section, we present the definition and some basic properties of the distributional Henstock-Kurzweil integral.
Define the space
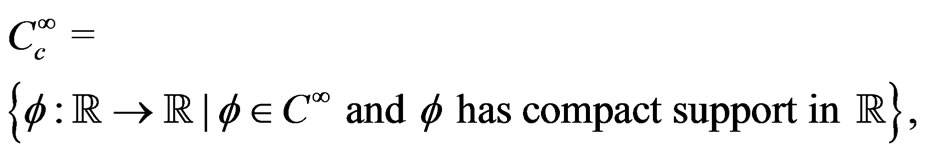
where the support of a function  is the closure of the set on which
is the closure of the set on which  does not vanish, denote by
does not vanish, denote by . A sequence
. A sequence 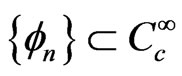 converges to
converges to 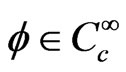 if there is a compact set
if there is a compact set  such that all
such that all  have support in
have support in 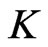 and for every
and for every 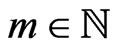 the sequence of derivatives
the sequence of derivatives 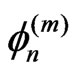 converges to
converges to  uniformly on
uniformly on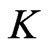 . Denote
. Denote 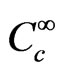 endowed with this convergence property by
endowed with this convergence property by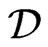 . Where
. Where 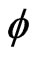 is called test function if
is called test function if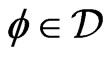 . The distributions are defined as continuous linear functionals on
. The distributions are defined as continuous linear functionals on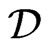 . The space of distributions is denoted by
. The space of distributions is denoted by , which is the dual space of
, which is the dual space of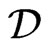 . That is, if
. That is, if  then
then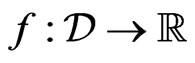 , and we write
, and we write , for
, for .
.
For all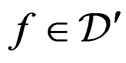 , we define the distributional derivative
, we define the distributional derivative 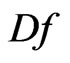 of
of  to be a distribution satisfying
to be a distribution satisfying  , where
, where 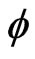 is a test function.
is a test function.
Let 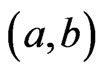 be an open interval in
be an open interval in , we define
, we define
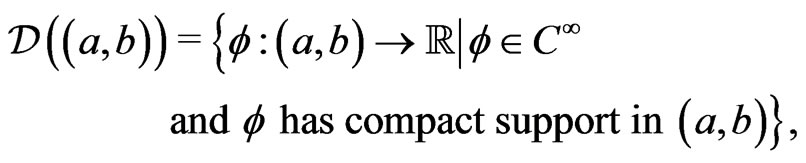
the dual space of 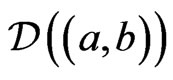 is denoted by
is denoted by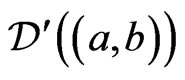 .
.
Remark 2.1. 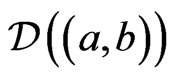 and
and  are
are 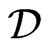 and
and  respectively if
respectively if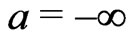 ,
, .
.
Let 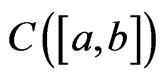 be the space of continuous functions on
be the space of continuous functions on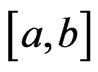 , and
, and
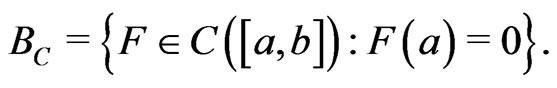
Note that  is a Banach space with the uniform norm
is a Banach space with the uniform norm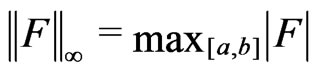 .
.
Now we are able to introduce the definition of the 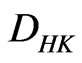 -integral.
-integral.
Definition 2.1. A distribution  is distributionally Henstock-Kurzweil integrable or briefly
is distributionally Henstock-Kurzweil integrable or briefly 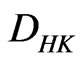 -integrable on
-integrable on 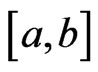 if
if 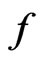 is the distributional derivative of a continuous function
is the distributional derivative of a continuous function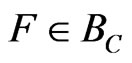 .
.
The 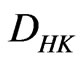 -integral of
-integral of 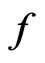 on
on 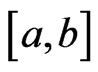 is denoted by
is denoted by
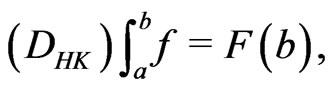 where
where 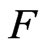 is called the primitive of
is called the primitive of
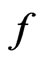 and “
and “ ” denotes the
” denotes the 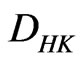 -integral. Analogously, we denote
-integral. Analogously, we denote  -integral and Lebesgue integral.
-integral and Lebesgue integral.
The space of 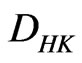 -integrable distributions is defined by
-integrable distributions is defined by
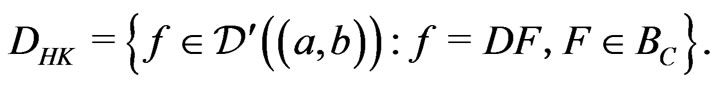
With this definition, if 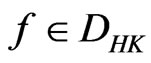 then we have for all
then we have for all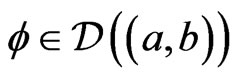 .
.
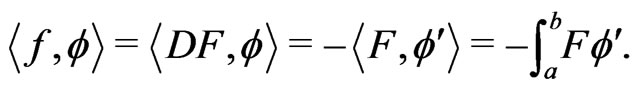 (2.1)
(2.1)
With the definition above, we know that the concept of the 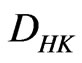 -integral leads to its good properties. We firstly mention the relation between the
-integral leads to its good properties. We firstly mention the relation between the 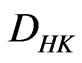 -integral and the
-integral and the 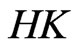 -integral.
-integral.
Recall that 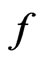 is Henstock-Kurzweil integrable on
is Henstock-Kurzweil integrable on 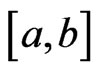 if and only if there exists a continuous function
if and only if there exists a continuous function 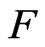 which is
which is 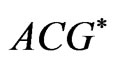 (generalized absolutely continuous, see [4]) on
(generalized absolutely continuous, see [4]) on 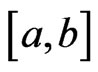 such that
such that  almost everywhere. P. Y. Lee pointed out that if
almost everywhere. P. Y. Lee pointed out that if 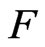 is a continuous function and pointwise differentiable nearly everywhere on
is a continuous function and pointwise differentiable nearly everywhere on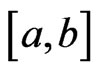 , then
, then  is
is . Furthermore, if
. Furthermore, if 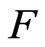 is a continuous function which is differentiable nowhere on
is a continuous function which is differentiable nowhere on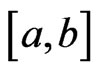 , then
, then 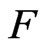 is not
is not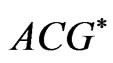 . Therefore, if
. Therefore, if  but differentiable nowhere on
but differentiable nowhere on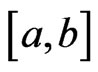 , then
, then  exists and is
exists and is 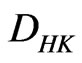 -integrable but not
-integrable but not 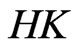 - integrable. Conversely, if
- integrable. Conversely, if 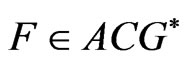 and it also belongs to
and it also belongs to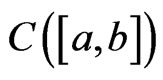 . Then
. Then 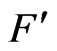 is not only
is not only  -integrable but also
-integrable but also 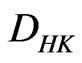 -integrable. Here
-integrable. Here 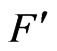 denotes the ordinary derivative of
denotes the ordinary derivative of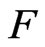 . Obviously, the
. Obviously, the 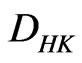 -integral includes the
-integral includes the 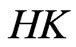 -integral.
-integral.
Now we shall give some corresponding results of the distributional Henstock-Kurzweil integral.
Lemma 2.1. ([3, Theorem 4], Fundamental Theorem of Calculus).
1) Let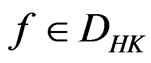 , define
, define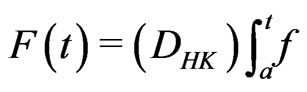 . Then
. Then 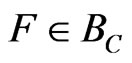 and
and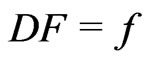 .
.
2) Let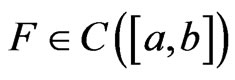 . Then
. Then 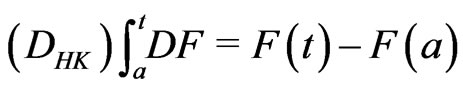 for all
for all 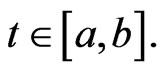
For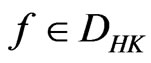 , we define the
, we define the  norm by
norm by
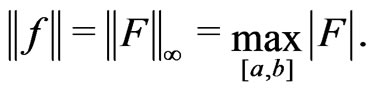
The following result has been proved.
Lemma 2.2. ([3, Thoerem 2]). With the  norm,
norm, 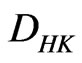 is a Banach space.
is a Banach space.
We now impose a partial ordering on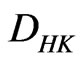 : for
: for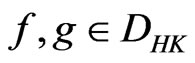 , we say that
, we say that 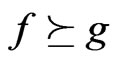 (or
(or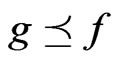 ) if and only if
) if and only if 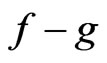 is a measure on
is a measure on 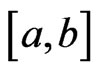 (see details in [9]). By this definition, if
(see details in [9]). By this definition, if 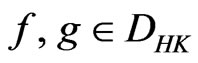 then
then
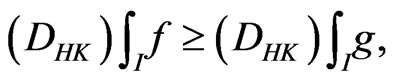 (2.2)
(2.2)
whenever ,
,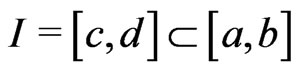 . We also have other usual relations between the
. We also have other usual relations between the 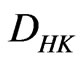 -integral and the ordering, for instance, the following result.
-integral and the ordering, for instance, the following result.
Lemma 2.3. ([9, Corollary 1]). If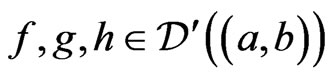 ,
, 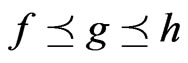 and if
and if  and
and 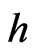 are
are 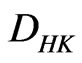 -integrable, then
-integrable, then 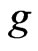 is also
is also  -integrable.
-integrable.
We say a sequence 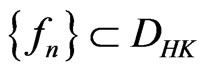 converges strongly to
converges strongly to 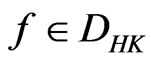 if
if 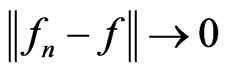 as
as . It is also shown that the following two convergence theorems hold.
. It is also shown that the following two convergence theorems hold.
Lemma 2.4. ([9, Corollary 4], Monotone convergence theorem for the 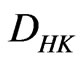 -integral). Let
-integral). Let 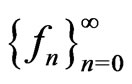 be a sequence in
be a sequence in 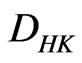 such that
such that 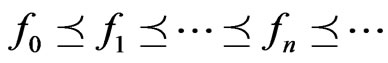 and that
and that 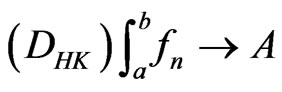 as
as . Then
. Then 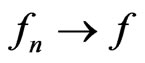 in
in
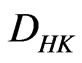 and
and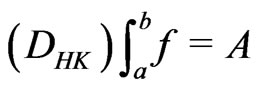 .
.
Lemma 2.5. ([7, Lemma 2.3], Dominated convergence theorem for the  -integral). Let
-integral). Let 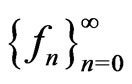 be a sequence in
be a sequence in  such that
such that 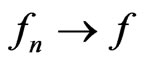 in
in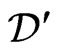 . Suppose there exist
. Suppose there exist  satisfying
satisfying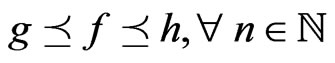 .
.
Then 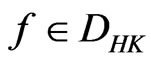 and
and .
.
We now give another result about the distributional derivative.
Lemma 2.6. Let  be the distributional derivative of
be the distributional derivative of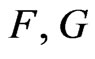 , where
, where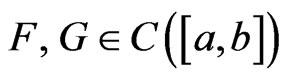 . Then
. Then
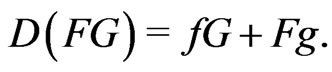 (23)
(23)
Proof. It follows from the definition of the distributional derivative and (3.1) that
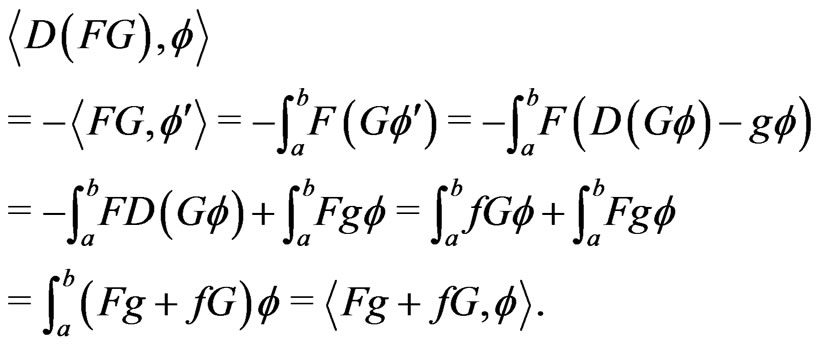
Consequently, the result holds.
If , its variation is
, its variation is
 where the supremum is taken over every sequence
where the supremum is taken over every sequence  of disjoint intervals in
of disjoint intervals in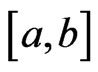 , then
, then 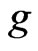 is called a function with bounded variation. The set of functions with bounded variation is denoted
is called a function with bounded variation. The set of functions with bounded variation is denoted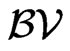 . It is known that the dual space of
. It is known that the dual space of 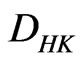 is
is 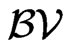 (see details in [3]), and the following statement holds.
(see details in [3]), and the following statement holds.
Lemma 2.7. ([3, Definition 6], Integration by parts). Let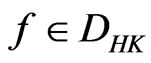 , and
, and . Define
. Define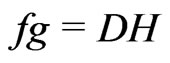 , where
, where  . Then
. Then 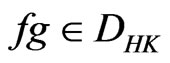 and
and

3. Periodic Boundary Value Problems
Consider the second order periodic boundary value problem (1.1)

where 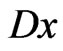 and
and 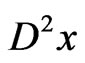 denote the first and second order distributional derivatives of
denote the first and second order distributional derivatives of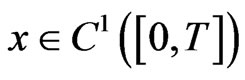 , respectively,
, respectively, 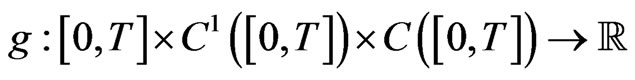 and
and 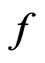 is a distribution (generalized function).
is a distribution (generalized function).
The distributional derivative subsumes the ordinary derivative. And if the first ordinary derivative of 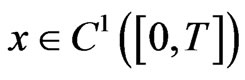 exists, the first ordinary derivative and first order distributional derivative of
exists, the first ordinary derivative and first order distributional derivative of  are equivalent. For
are equivalent. For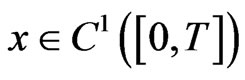 , then the distributional derivative
, then the distributional derivative 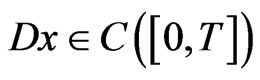 and
and , hence
, hence 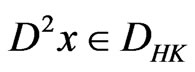 .
.
Recall that we say 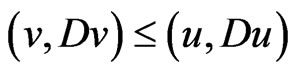 if and only if
if and only if  and
and 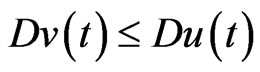 for all
for all .
.
We impose the following hypotheses on the functions 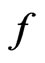 and
and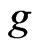 .
.
(D0) There exist 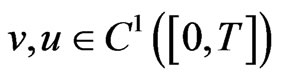 with
with 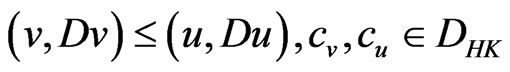 such that
such that
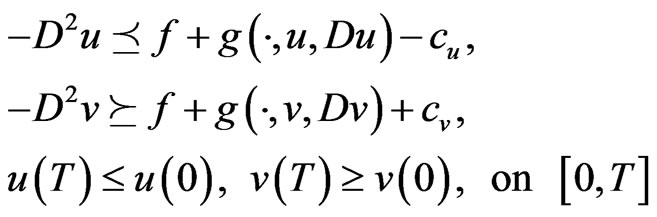
and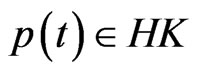 ,
, 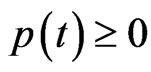 , with
, with 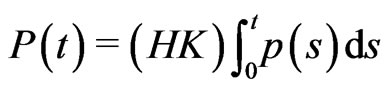 and
and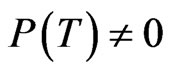 ,
, 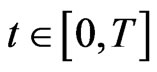 such that
such that
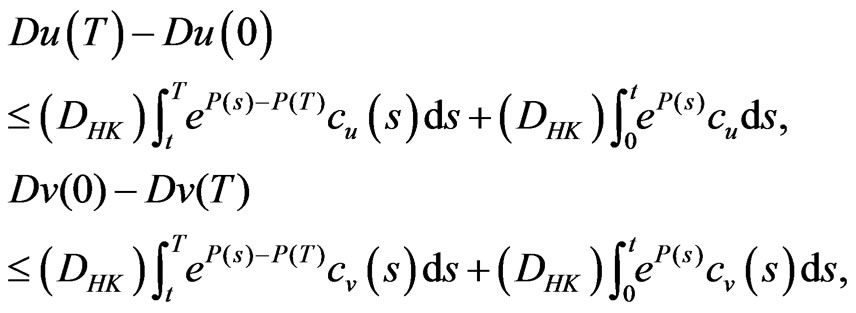
(D1) 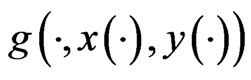 is Lesbesgue integrable on
is Lesbesgue integrable on 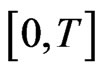 when
when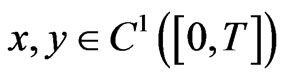 ,
, 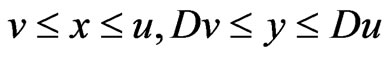 , and
, and 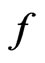 is
is 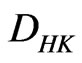 -integrable on
-integrable on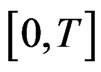 (D2)
(D2)  is nonincreasing with respect to
is nonincreasing with respect to 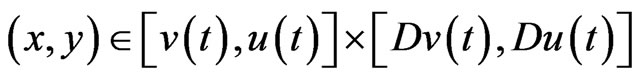 for all
for all
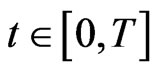 .
.
We say that  is a solution of PBVP (1) if
is a solution of PBVP (1) if 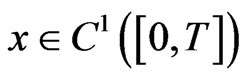 and satisfies (1). Before giving our main results in this paper, we first apply Lemma 2.1 to convert the PBVP (1) into an integral equation.
and satisfies (1). Before giving our main results in this paper, we first apply Lemma 2.1 to convert the PBVP (1) into an integral equation.
Lemma 3.1. Let  be a distribution and
be a distribution and
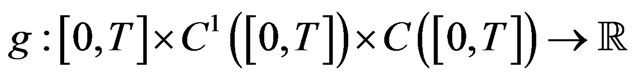 , a function
, a function
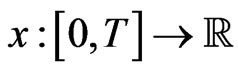 is a solution of the PBVP (1.1) on
is a solution of the PBVP (1.1) on 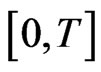 if and only if
if and only if 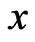 and
and 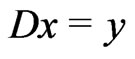 satisfy for any
satisfy for any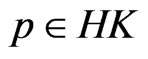 ,
, 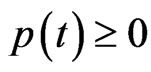 on
on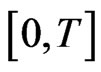 , with
, with 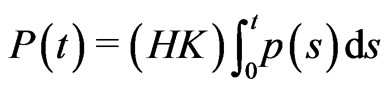 and
and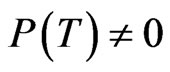 , the integral equation
, the integral equation
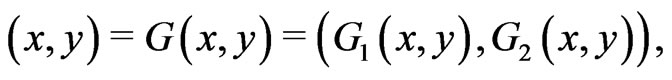 (3.1)
(3.1)
where
 (3.2)
(3.2)
and
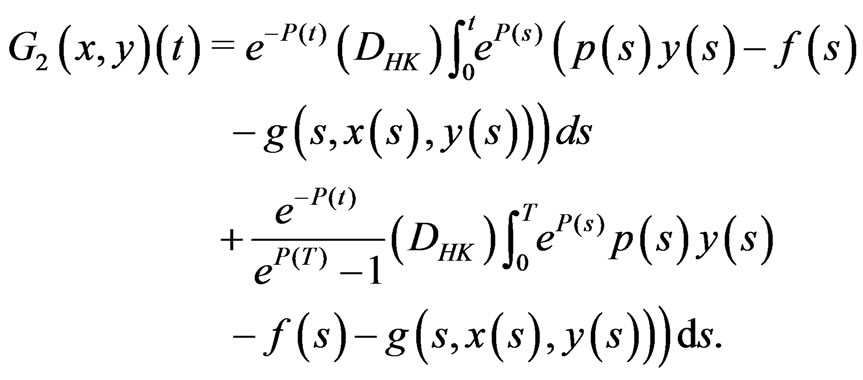 (3.3)
(3.3)
Proof. Let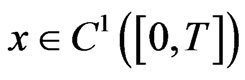 , then the function
, then the function  with
with 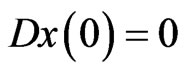 is continuous on
is continuous on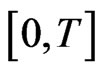 , so
, so 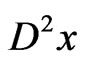 is
is 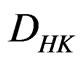 -integrable. Let
-integrable. Let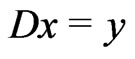 , then by (1.1) we have
, then by (1.1) we have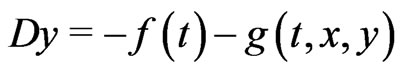 , or equivalently,
, or equivalently,
 (3.4)
(3.4)
Integrating (3.4) we have
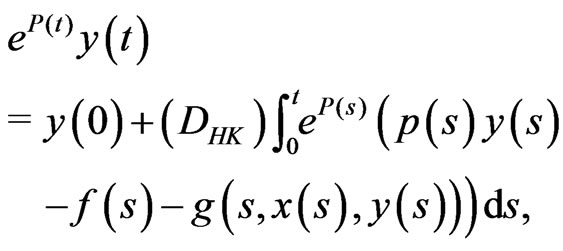
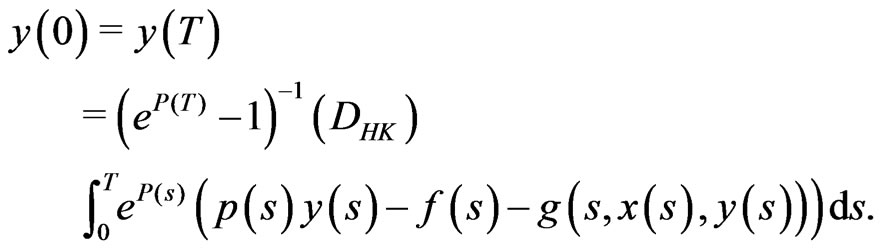
This implies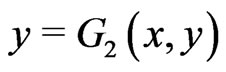 . We can prove that
. We can prove that 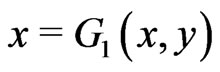 by the same way. Thus
by the same way. Thus  and
and 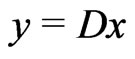 satisfy the operator equation (3.1).
satisfy the operator equation (3.1).
Conversely, assume that  satisfy (3.1). In view of (2) we then have for each
satisfy (3.1). In view of (2) we then have for each 
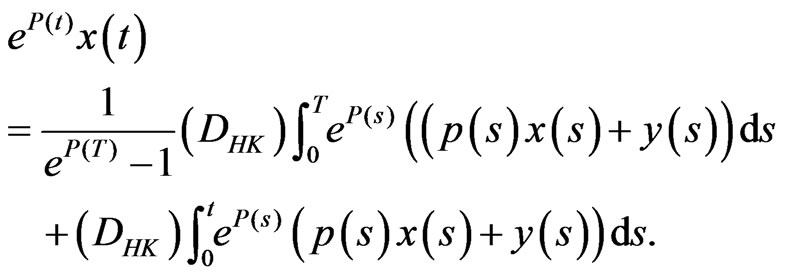 (3.5)
(3.5)
Noticing that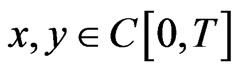 , then (3.5) implies by differentiation that
, then (3.5) implies by differentiation that
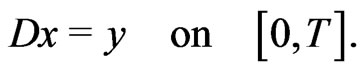 (3.6)
(3.6)
It follows from (3.1) and (3.3) that for each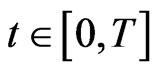 ,
,
 (3.7)
(3.7)
Applying Lemma 2.6 to (3.7), we obtain for all 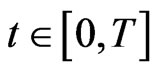
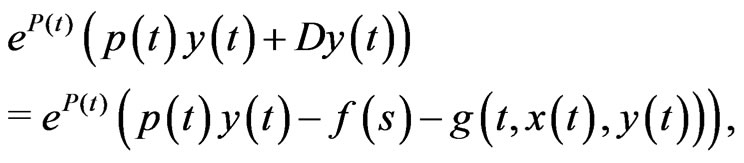
which together with (3.6) implies that
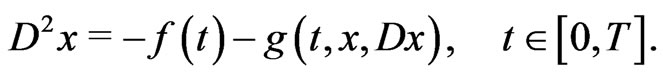
It follows from (5) that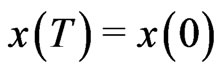 , and from (7) that
, and from (7) that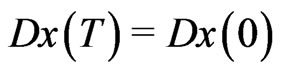 , so that
, so that 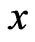 is a solution of the PBVP (1.1). □
is a solution of the PBVP (1.1). □
Let 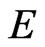 be an ordered Banach space,
be an ordered Banach space, 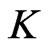 a nonempty subset of
a nonempty subset of . The mapping
. The mapping 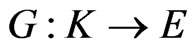 is increasing if and only if
is increasing if and only if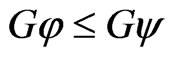 , whenever
, whenever 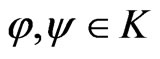 and
and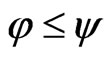 .
.
An important tool which will be used latter concerns a fixed point theorem for an increasing mapping and is stated next.
Lemma 3.2. ([10, Theorem 3.1.3]) Let 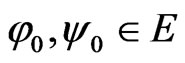 with
with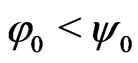 , and
, and 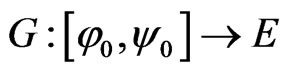 be an increasing mapping satisfying
be an increasing mapping satisfying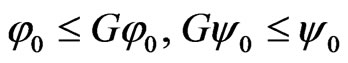 . If
. If 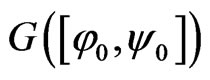 is relatively compact, then
is relatively compact, then 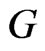 has a maximal fixed point
has a maximal fixed point 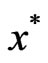 and a minimal fixed point
and a minimal fixed point 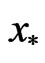 in
in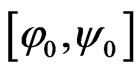 . Moreover,
. Moreover,
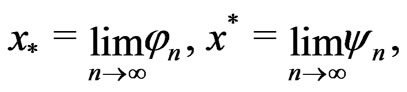 (3.8)
(3.8)
where  and
and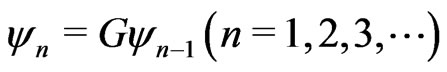 ,
,
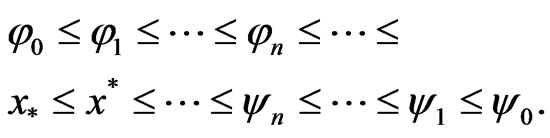 (3.9)
(3.9)
Lemma 3.3. Let conditions (d0)-(d2) be satisfied. Denoting
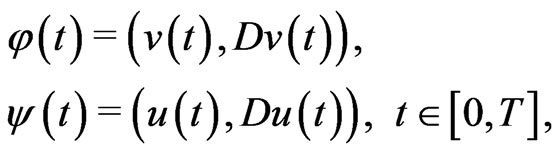 (3.10)
(3.10)
then 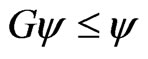 and
and 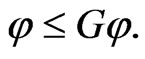
Proof. The hypotheses (d0) and (d2) imply that for all  in
in , satisfying
, satisfying
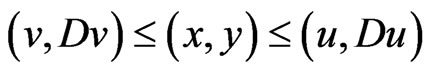 ,
,
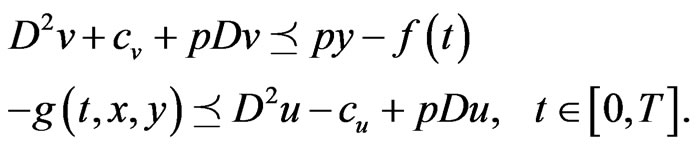 (3.11)
(3.11)
This and (d1) ensure that 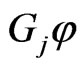 and
and 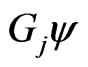 in (3.2) and (3.3) are defined for
in (3.2) and (3.3) are defined for . Condition (d0) implies that for each
. Condition (d0) implies that for each 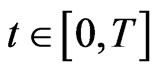
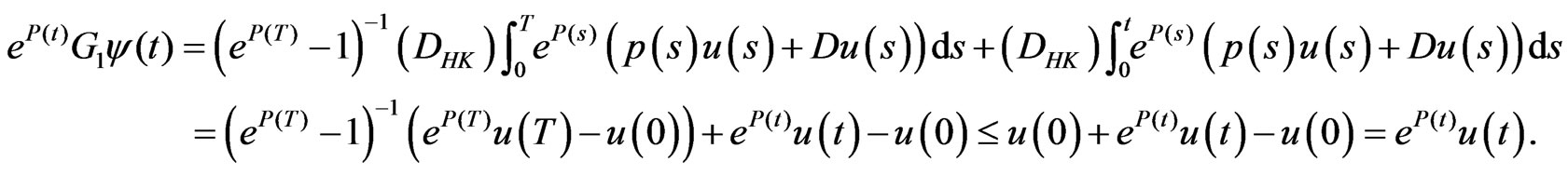
It follows from (3.7), (3.10) and (d0) that for each 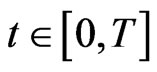
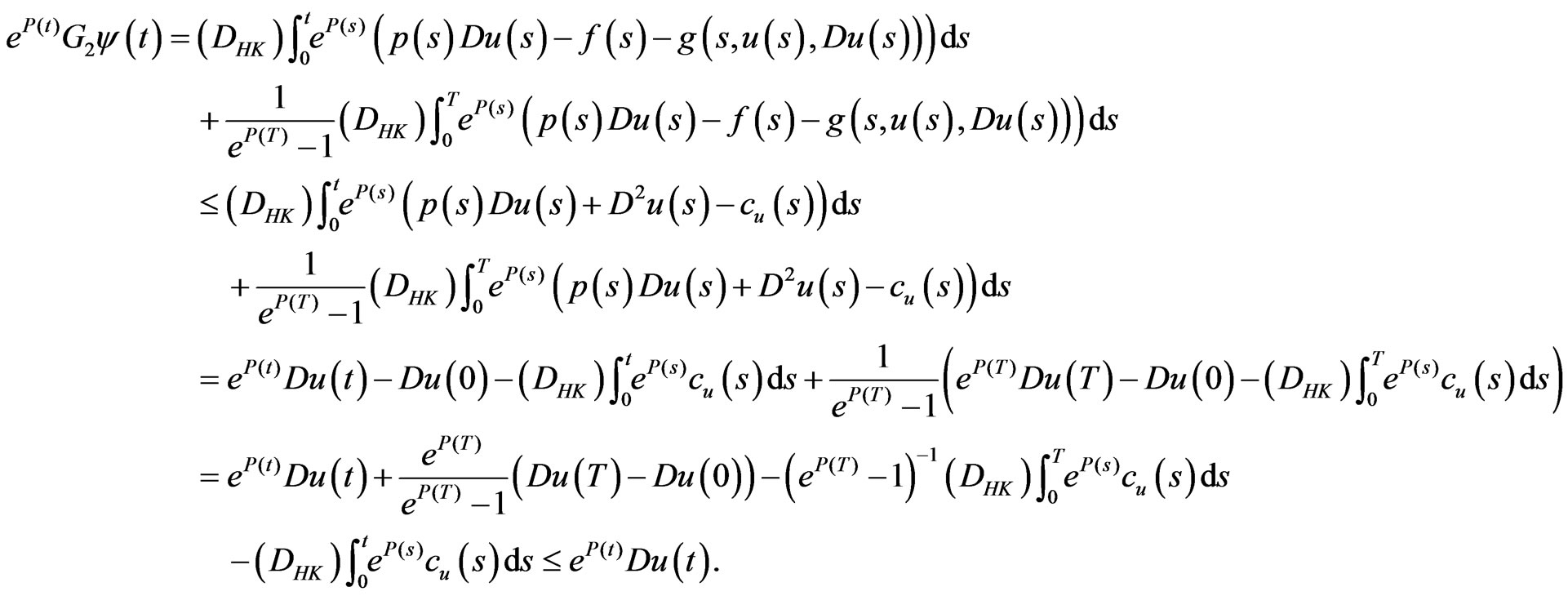
Thus, 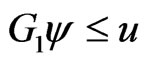 and
and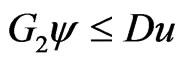 , whence
, whence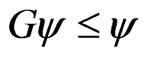 . The proof that
. The proof that 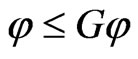 is similar.
is similar.
Lemma 3.4. Assume that conditions (D0)-(D2) hold. Denoting
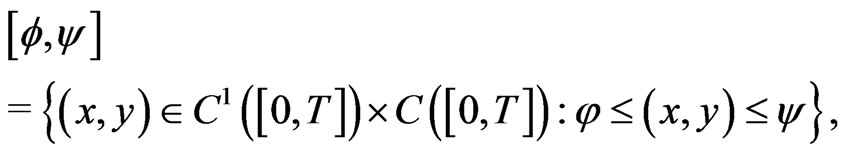
then the equations (1)-(3) define a nondecreasing mapping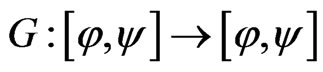 .
.
Proof. Let
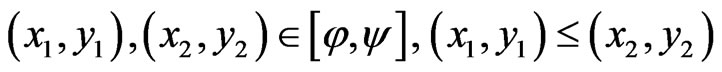 be given. The hypotheses (D0)-(D2) imply that for each
be given. The hypotheses (D0)-(D2) imply that for each 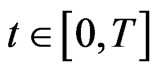
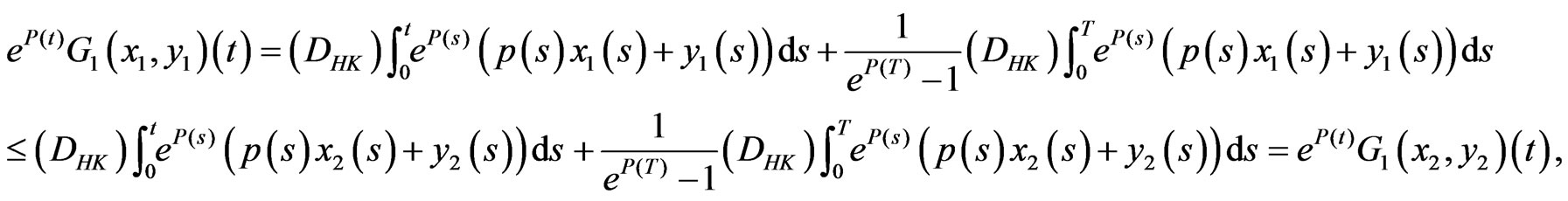
and

Thus  This and Lemma 3.3 imply the assertion.
This and Lemma 3.3 imply the assertion.
With the preparation above , we will prove our main result on the existence of the extremal solutions of the periodic boundary value problem (1.1).
Theorem 3.1. Assume that conditions (D0)-(D2) are satisfied. Then the PBVP (1.1) has such solutions  and
and  in
in 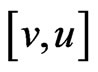 that
that  and
and 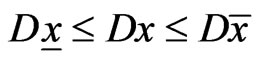 for each solution
for each solution  of (1.1) in
of (1.1) in  such that
such that 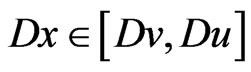 .
.
Proof. In view of Lemma 3.4 the equations (3.1)-(3.3) define a nondecreasing mapping . For any
. For any 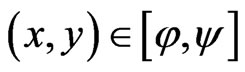 , we have
, we have
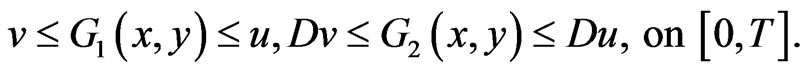
Since 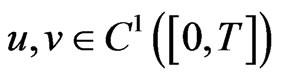 and
and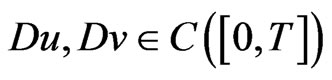 , there exists constant
, there exists constant  such that, for each
such that, for each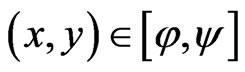 ,
,
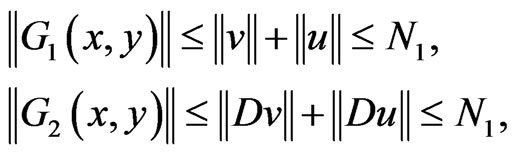 (3.12)
(3.12)
which implies 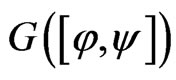 is uniformly bounded on
is uniformly bounded on 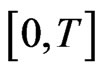 .
.
Let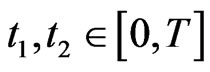 . Then by (3.2) and (3.3), for each
. Then by (3.2) and (3.3), for each 
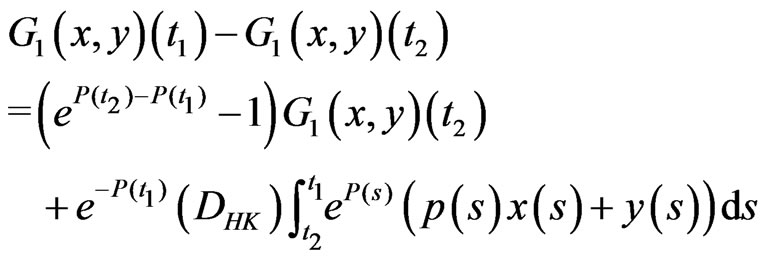 (3.13)
(3.13)
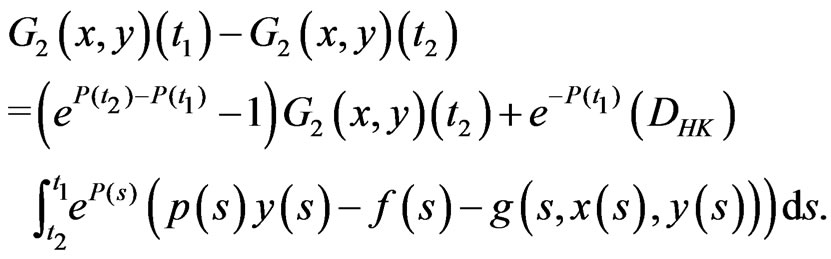 (3.14)
(3.14)
Since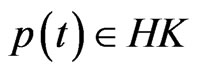 ,
, 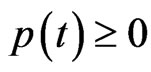 ,
,
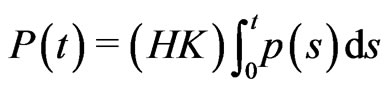 is continuous and so is uniformly continuous on
is continuous and so is uniformly continuous on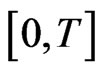 , i.e., for all
, i.e., for all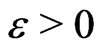 , there exists
, there exists  such that
such that
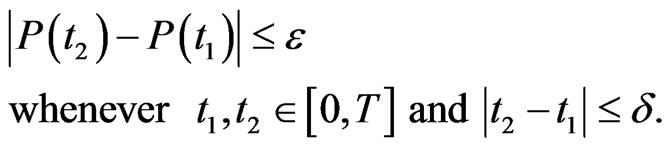
It is easy to see that  (so is
(so is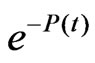 ) on
) on . Hence, there exists
. Hence, there exists  such that
such that
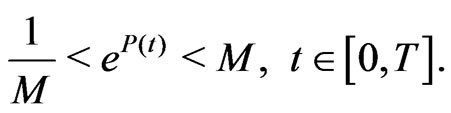
The result 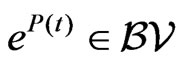 on
on 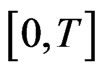 implies by Lemma 2.6 that
implies by Lemma 2.6 that 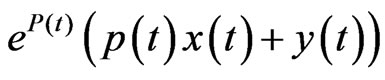 and
and
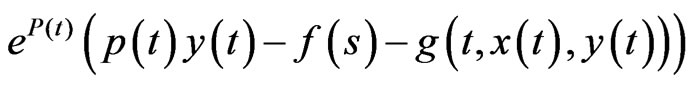 are
are
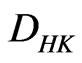 -integrable on
-integrable on , because
, because 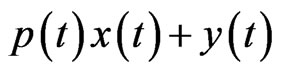 and
and 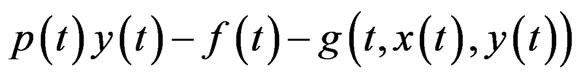 are
are 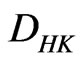 -integrable for all
-integrable for all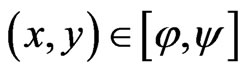 . This result and the monotonicity of
. This result and the monotonicity of  and
and
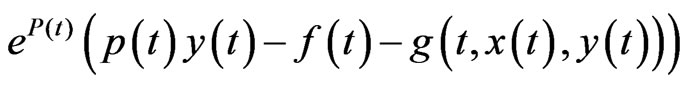 imply
imply
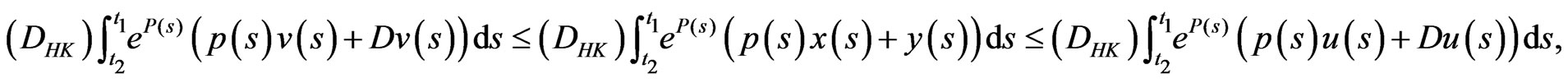
and

Then by (3.12)-(3.14), there exists  such that
such that
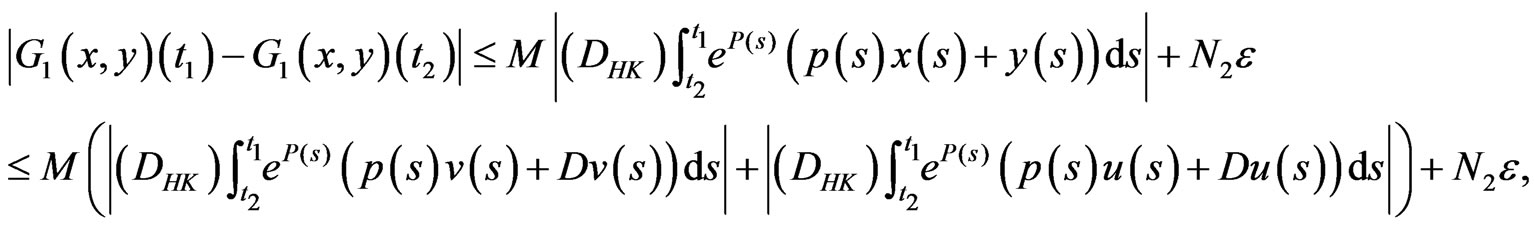 (3.15)
(3.15)
and
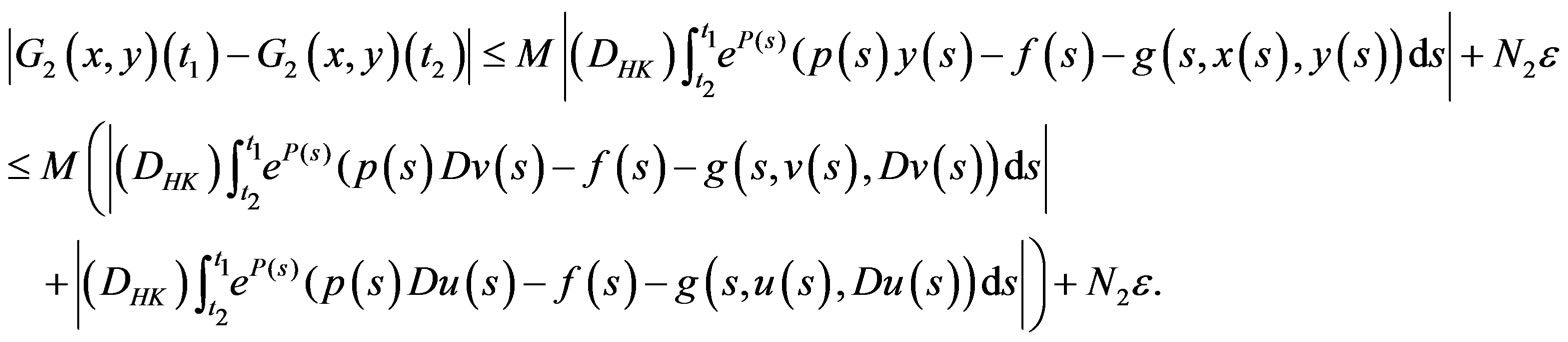 (3.16)
(3.16)
Since 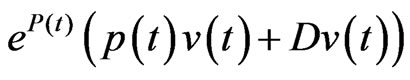 and
and  are
are 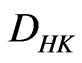 -integrable on
-integrable on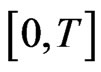 , the primitives of
, the primitives of  and
and 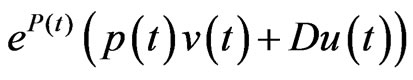 are continuous and so are uniformly continuous on
are continuous and so are uniformly continuous on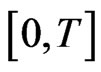 . Similarly, the primitives of
. Similarly, the primitives of  and
and 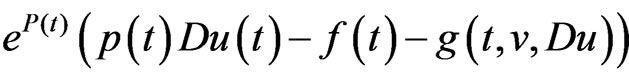 are uniformly continuous on
are uniformly continuous on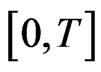 . Therefore, by inequalities (15) and (16),
. Therefore, by inequalities (15) and (16), 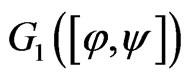 and
and 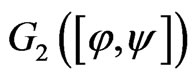 are equiuniformly continuous on
are equiuniformly continuous on 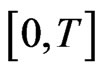 for all
for all . So
. So  is equiuniformly continuous on
is equiuniformly continuous on 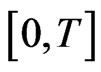 for all
for all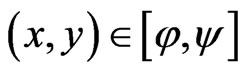 .
.
In view of the Ascoli-Arzelàtheorem, 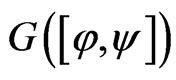 is relatively compact. This result implies that
is relatively compact. This result implies that 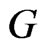 satisfies the hypotheses of Lemma 3.2, whence
satisfies the hypotheses of Lemma 3.2, whence 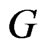 has the minimal fixed point
has the minimal fixed point 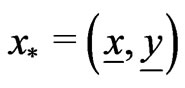 and the maximal fixed point
and the maximal fixed point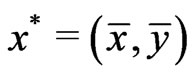 . It follows from Lemma 3.1 that
. It follows from Lemma 3.1 that 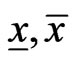 are solutions of PBVP (1), and that
are solutions of PBVP (1), and that 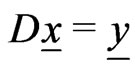 and
and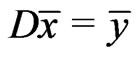 .
.
Let , and
, and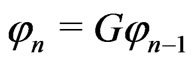 ,
, 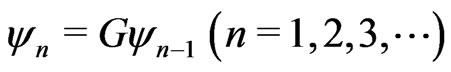 , then (3.8) and (3.9) hold. If
, then (3.8) and (3.9) hold. If  with
with 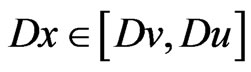 is a solution of (1), it follows from Lemma 3.1 that
is a solution of (1), it follows from Lemma 3.1 that 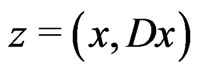 is a fixed point of
is a fixed point of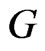 . It follows from the extremality of
. It follows from the extremality of 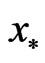 and
and 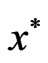 that
that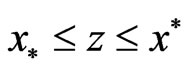 , i.e.,
, i.e., 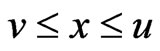 and
and 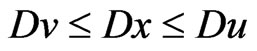 .
.
As a consequence of Theorem 3.1 we have Corollary 3.1. Given the functions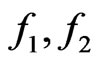 , assume that conditions (D0) and (D1) hold for the function
, assume that conditions (D0) and (D1) hold for the function
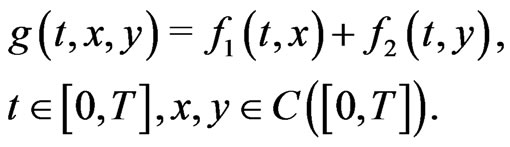
If 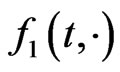 is nonincreasing in
is nonincreasing in 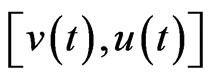 for all
for all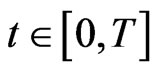 , and if
, and if 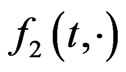 is nonincreasing in
is nonincreasing in  for all
for all , then the PBVP (1.1) has the extremal solutions in
, then the PBVP (1.1) has the extremal solutions in .
.
REFERENCES
- S. Leela, “Monotone Method for Second Order Periodic Boundry Value Problems,” Nonlinear Analysis, Vol. 7, No. 4, 1983, pp. 349-355. doi:10.1016/0362-546X(83)90088-3
- V. Lakshmikantham, V. Sree Hari Rao and A. S. Vatsala, “Monotone Method for a System of Second Order Periodic Boundary Value Problems,” Applied Mathematics Computation, Vol. 15, 1984, pp. 71-83. doi:10.1016/0096-3003(84)90054-7
- E. Talvila, “The Distributional Denjoy Integral,” Real Analysis, Exchang, Vol. 33, No. 1, 2008, pp. 51-82.
- P. Y. Lee, “Lanzhou Lecture on Henstock Integration,” World Scientific, Singapore City, 1989.
- Š. Schwabik and G. J. Ye, “Topics in Banach Space Integration,” World Scientific, Singapore City, 2005.
- Y. P. Lu, G. J. Ye and Y. Wang, “The Darboux Problem Involving the Distributional Henstock-Kurzweil Integral,” Proceedings of the Edinburgh Mathematical Society, Vol. 55, No. 1, 2012, pp. 197-205.
- Y. P. Lu, G. J. Ye and W. Liu, “Existence of Solutions of the Wave Equation Involving the Distributional Henstock-Kurzweil Integral,” Differential Integral Equation, Vol. 24, No. 11-12, 2011, pp. 1063-1071.
- Q. L. Liu and G. J. Ye, “Some Problems on the Convergence of the Distributional Denjoy Integral,” Acta Mathematics Sinica, Vol. 54, No. 4, 2011, pp. 659-664.
- D. D. Ang, K. Schmitt and L. K. Vy, “A Multidimensional Analogue of the Denjoy-Perron-Henstock-Kurzweil Integral,” Bulletin of the Belgian Mathematical Society, Vol. 4, No. 3, 1997, pp. 355-371.
- D. J. Guo, Y. J. Cho and J. Zhu, “Partial Ordering Methods in Nonlinear Problems,” Hauppauge, Nova Science Publishers, New York, 2004.
NOTES
*Supported by NNSF of China (10871059) and the Fundamental Research Funds for the Central Universities.

