ABSTRACT

We investigate correlations between neighbor degrees in the scale-free network. According to the empirical studies, it is known that the degree correlations exhibit nontrivial statistical behaviors. With an analytical approach, we show that the scale-freeness and one of statistical laws for degree correlations can be reproduced consistently in a unified framework. Our result would have its importance in understanding the mechanisms which generate the complex network.

1. Introduction

It is known that a diversity of complex networks includeing sociological, technological, and biological ones exhibit the scale-freeness [1-13]. These results pose us a problem about the origin of this feature and about mechanisms which produce such organized behavior in complex networks. Naturally it is considered that the complex networks are generated through processes in which nodes are correlated to each other. The experimental data which exhibits the organized and hierarchical structures enhances the importance of the node correlations in the complex networks [14-18]. Indeed the model based studies have shown that, in order to reproduce the network structure in the real world, additional ingredients other than the simple rule such as the preferential attachment are required in the simulation [11-18].

Recent empirical studies have revealed that there exist ordered structures of node correlations in real world complex networks. One example of these structures would be given by fractality which characterize geometrical structures of various complex systems, in which they show the self-similarity on all length scales [14,15]. On the other hand, more primitive relation between nodes would be represented by a joint probability for two neighbor nodes of degree and connected by an edge. In this paper, we investigate this basic statistics, the degree-degree correlation in the complex network. One characteristic feature of 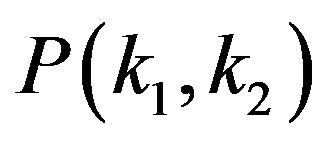can be quantified by for each fixed, the average of the neighbor degrees for a given value of. It has been reported that the 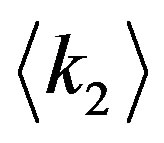profile is fitted with a power law

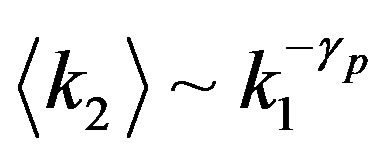(1)

with a constant 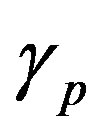for the interaction and regulatory networks of proteins [16]. The same tendency is also confirmed with the Internet, another typical example of the complex networks [17].

The ubiquity of scale-free networks in the real world is one of the fundamental issues in the complex network studies. It would suggest that there exist common mechanisms which underlie complex networks. Then one of our final goals is to obtain a theory which can describe various complex networks and their statistical behaviors in a unified framework. For this aim, we have introduced in the recent study an analytical approach in which conditions required for the scale-free degree distribution are considered [19]. Due to the ubiquity of the scale-freeness, it is expected that the analytical conditions are given by those which are independent to specific systems and common to a wide variety of networks. Indeed, it has been shown that the power law distribution can be obtained without introducing conditions except for general ones. In this paper we extend the framework given in this previous study and show that it gives the degree correlation which corresponds to the experimental measurement represented by Equation (1).

2. Framework for P(k₁, k₂)

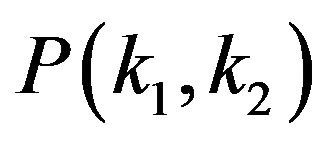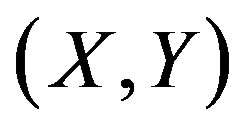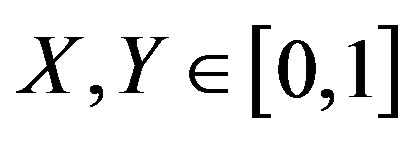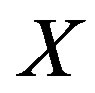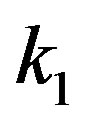By using a framework introduced in the recent study [19], we investigate the degree correlation. At first we normalize the pair of degrees and introduce variables which take their values respectively on the finite interval. For example, relations between and are given by

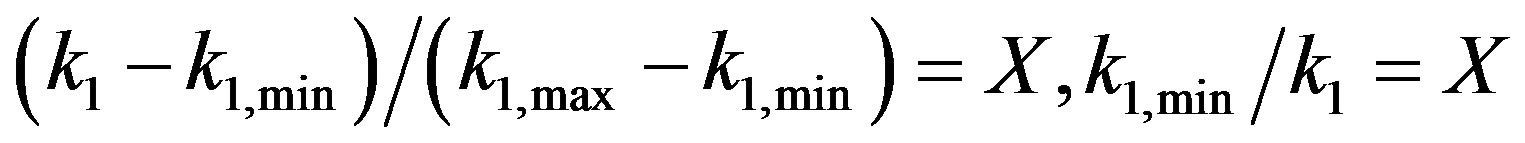(2)

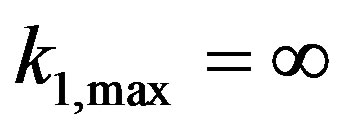where the former example is taken for cases such as and the latter for. These normalizations are summarized by the expression

(3)

with constants, , 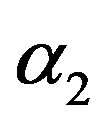and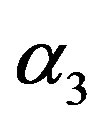. Under the transforms between 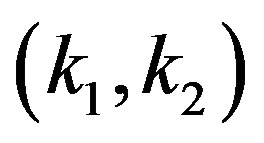and (X, Y) given by the expression (3), the probability 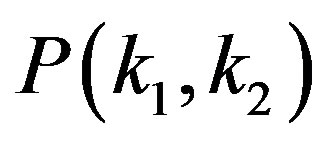is represented by.

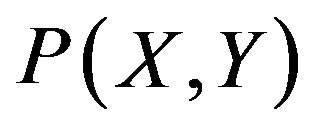In this approach we take an analytical expression of 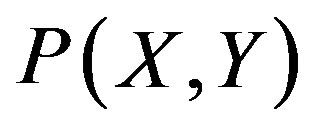in the expanded form and consider the condition required for this function. Then, for variables (X, Y) and the probability, we require conditions that and 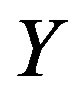are continuous and that 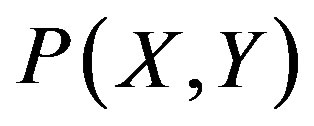is given by the smooth function with respect to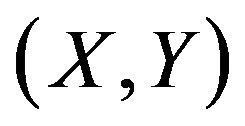. Also in order to investigate the scaling behavior of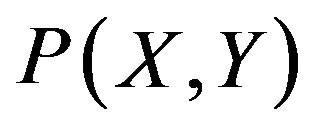, we take

(4)

where. Because 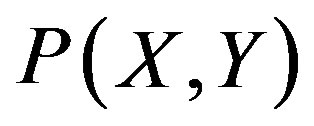is a positive function which takes its value in the finite interval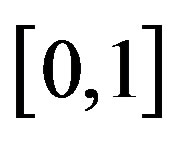, the analytical representation of as the function of is given in the form

(5)

with the scaling function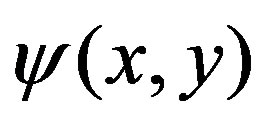

(6)

where 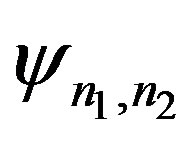are constant coefficients and 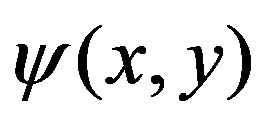is taken to satisfy the normalization

(7)

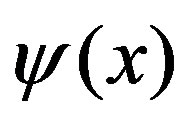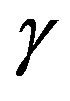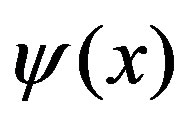For the single variable case, is transformed to with, the expansion of x. If is scale-free and given in the power law with a constant, is given by the first order expansion which satisfies

(8)

Although, according to the result given in the recent study [19], the converse fact has been shown that the condition (8) is derived without introducing special conditions except for the continuous conditions for 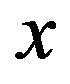and. The point of this result is that this condition (8) is obtained with using the identical relations which the continuous distribution function satisfies generally. Then this condition is required for arbitrary variables such as and.

3. The Representation of P(k₁, k₂)

Extending the analysis with the single variable given in the reference [19], we can show that representation is uniquely determined in our framework. At first we take a conditional probability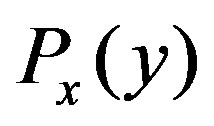, the function with respect to 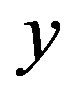for each fixed value of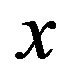, defined as

(9)

It apparently satisfies.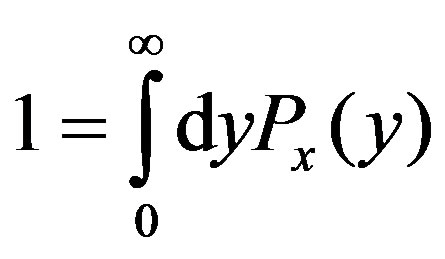

For convenience of calculation, we introduce the cumulative distribution of 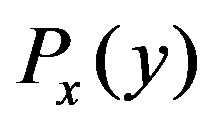by

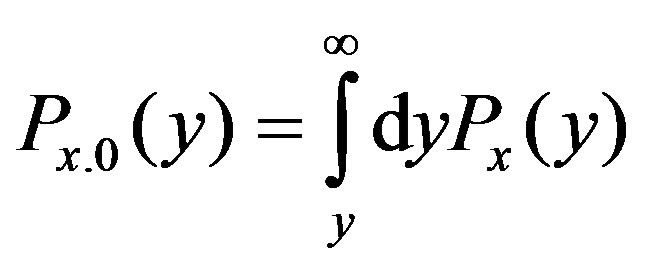(10)

Then we can represent it as

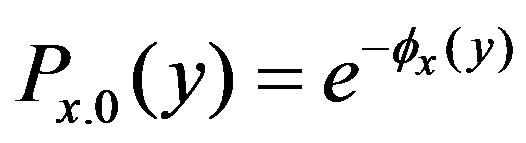(11)

with an expansion

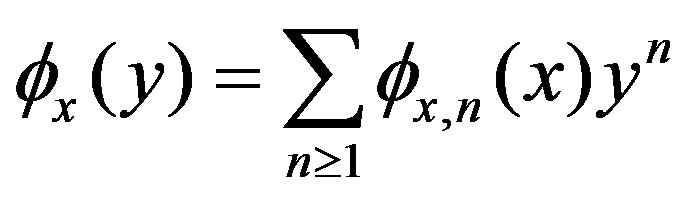(12)

where is given by the other expansion of. According to these definitions, is given by

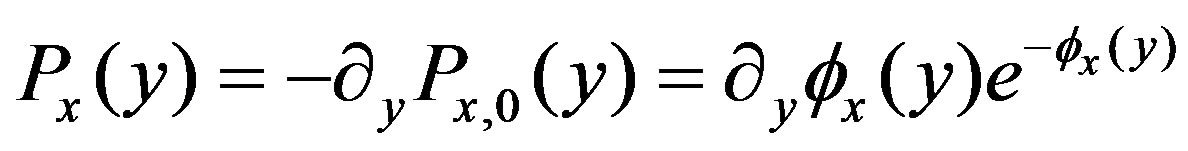(13)

Applying the condition (8), it is required that

(14)

and

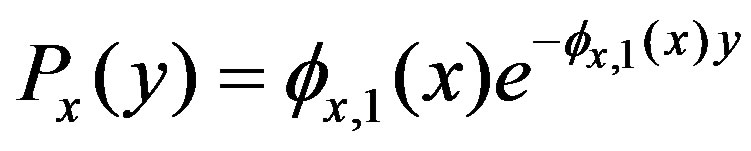(15)

For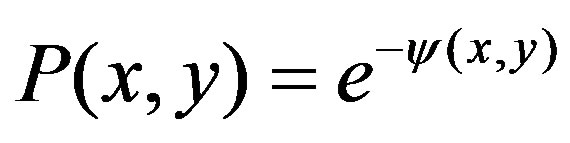, we can show that the same condition (11) requires that

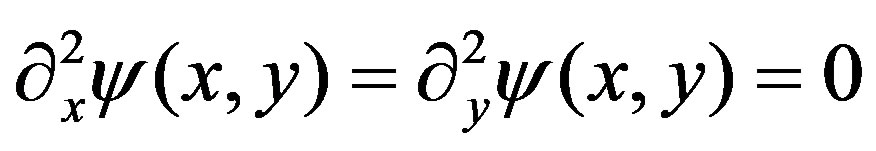(16)

If we take the conditional probability with respect to x, then from the condition (11) it is required to have the form

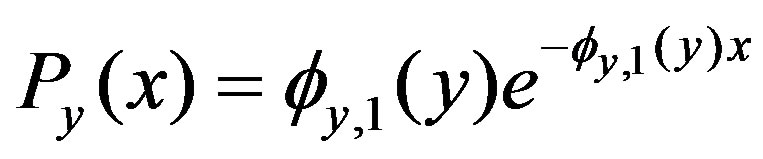(17)

Introducing and by

(18)

is represented by the equivalent two forms

(19)

and we obtain the identical relation

(20)

Because and 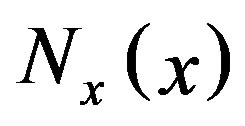are independent to x and y respectively, the condition (16) for 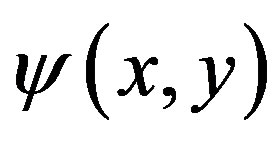is given by comparing each side of Equation (20). Thus we obtain the representation

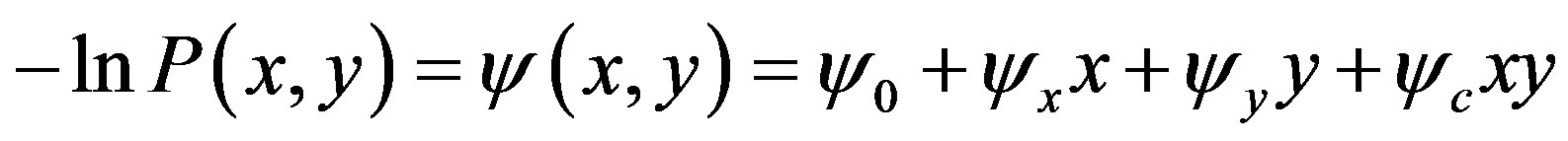(21)

with constants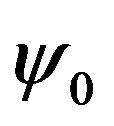, , 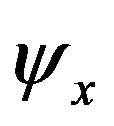and.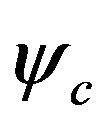

4. Degree Correlations in Real World Networks

In order to confirm our result in the previous section, we give a comparison to the experimental measurement of the real world networks. For the degree-degree correlations 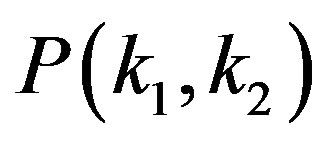given from Equation (21), we calculate 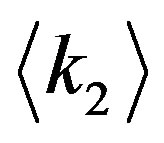for each fixed value of 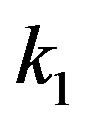and compare it to the experimental representation (1).

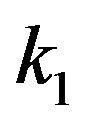At first, with using the expression (3) for the normalization of, the correspondence between and 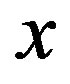is given by

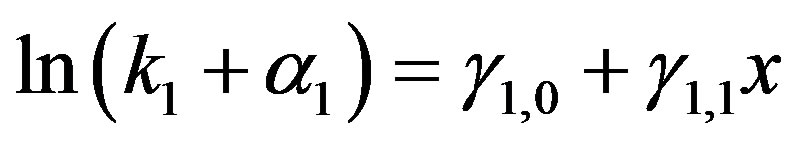(22)

with constants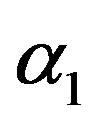, , 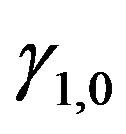and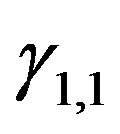. While, from the representation (21), the transform between 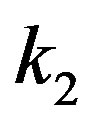and is generally given by

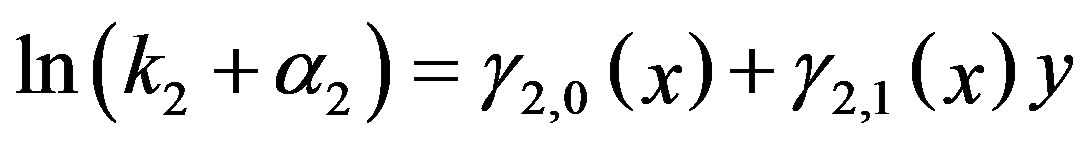(23)

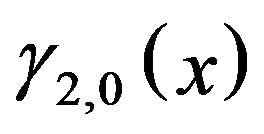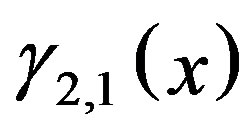where and are given by linear equations of and 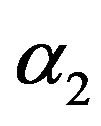is a constant.

Then is given by

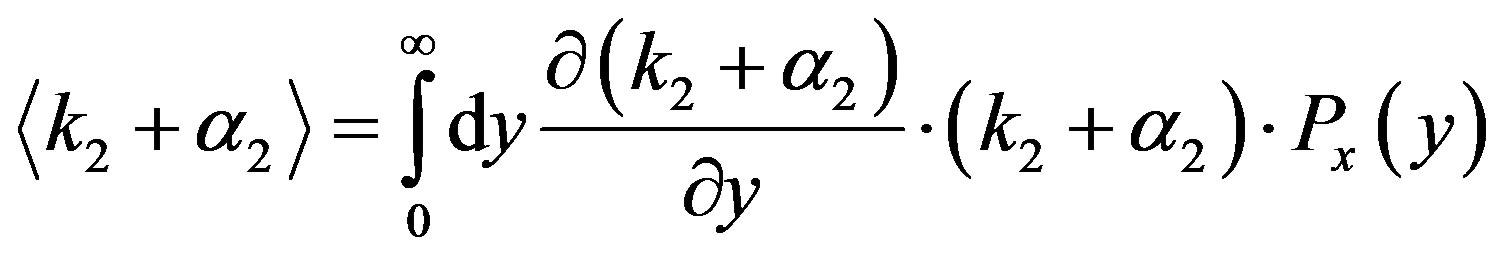(24)

Using the representation of 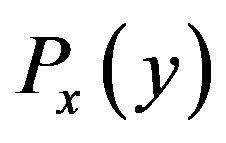given by Equation (9) and Equation (21), the average is given by

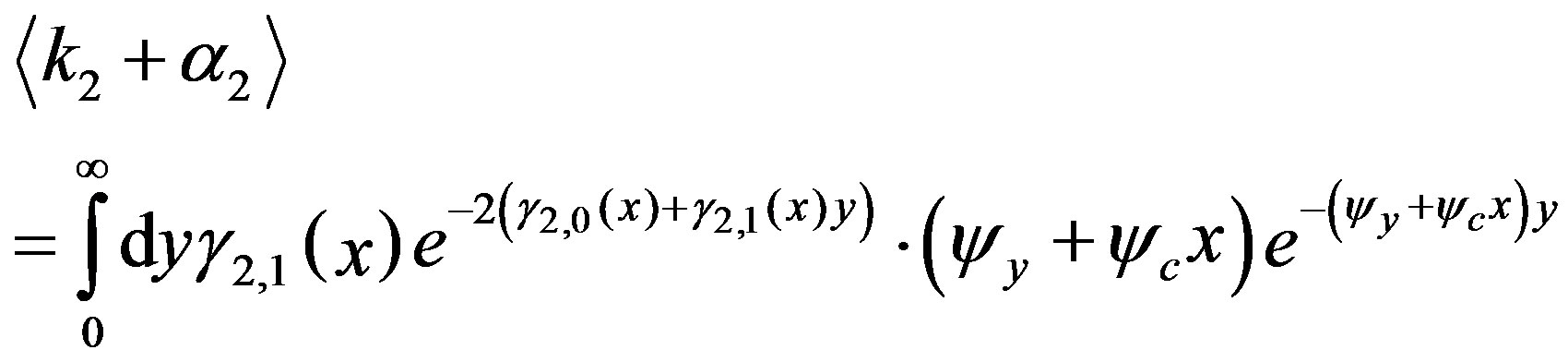(25)

with constants 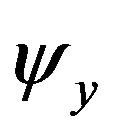and 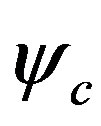and this is calculated as

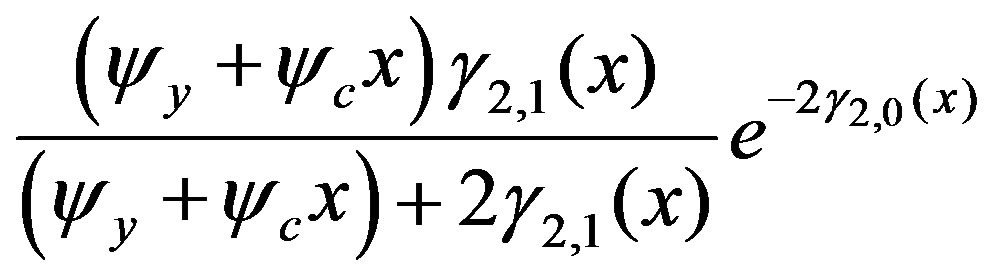
(26)

Because 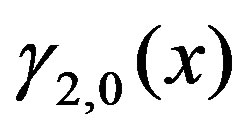and are represented by the linear equations of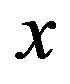, the first term in the above equation is estimated as

(27)

for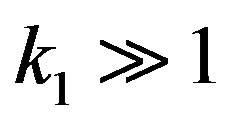. Furthermore, using the approximation , Equation (26) is approximated by a power law

(28)

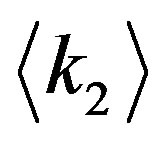with a constant for a large. Then behavior of tail for a large 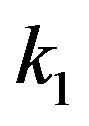agrees to the experimental representation (1).

5. Discussions

As we have mentioned in the introduction, our final goal is to give a description of the complex network in a unified framework. For this aim, it is required to obtain a theory which explains the organized structure of the complex network and allows to deal with different networks. In this final section, we discuss this issue.

In this paper we have shown that the extension of the framework introduced in the recent study [19] consistently produces the degree correlation in the form which corresponds to the experimental data. Applying the analytical condition (8) for the single variable distribution to the joint probability, we obtain a unique representation for, the distribution of the neighbor degrees. We should notice that some properties of the complex network, the scale-free distribution and the degree correlation represented by Equation (1), can be derived from the same condition (8). It would suggest that the rules which generate scale-free networks and their correlated structures can be described in a unified framework.

Also we should notice that our framework which gives the condition (8) does not depend on the specific system. Then we can apply our results straightforwardly to various complex networks such as the protein networks and the Internet. Then our result would provide a clue to understand the mechanism which underlies various types of complex networks.

Although, for our final goal, further investigations should be required. At first we should take into account some exceptional cases for which we can not apply our representation. An example is given by a random network, in which distributions take forms such as the Gaussian or the Poisson distributions. Then it would be required for us to describe explicitly the difference between our framework and these random systems. Also we should notice that the condition (8) is derived under the assumption that the variable is continuous. However some variables such as the degree take only the discrete number. We will deal with issues such as above in the future works.

REFERENCES