World Journal of Mechanics
Vol.2 No.1(2012), Article ID:17690,9 pages DOI:10.4236/wjm.2012.21006
Hard-to-Soft Transition in Radial Buckling of Multi-Concentric Nanocylinders
1Department of Urban and Environment Engineering, University of Incheon, Incheon, Korea
2Division of Engineering and Policy for Sustainable Environment, Faculty of Engineering, Hokkaido University, Sapporo, Japan
3Division of Engineering and Policy for Sustainable Environment, Graduate School of Engineering, Hokkaido University, Sapporo, Japan
4Division of Applied Physics, Faculty of Engineering, Hokkaido University, Sapporo, Japan
5Department of Environmental Sciences, University of Yamanashi, Kofu, Japan
Email: *tayu@eng.hokudai.ac.jp
Received November 29, 2011; revised January 5, 2012; accepted January 15, 2012
Keywords: Carbon Nanotube; Buckling; Radial Corrugation; High Pressure Phenomenon; Van der Waals Coupling; Multiple Core-Shell Structure; Thin Shell Theory
ABSTRACT
We investigate the cross-sectional buckling of multi-concentric tubular nanomaterials, which are called multiwalled carbon nanotubes (MWNTs), using an analysis based on thin-shell theory. MWNTs under hydrostatic pressure experience radial buckling. As a result of this, different buckling modes are obtained depending on the inter-tube separation d as well as the number of constituent tubes N and the innermost tube diameter. All of the buckling modes are classified into two deformation phases. In the first phase, which corresponds to an elliptic deformation, the radial stiffness increases rapidly with increasing N. In contrast, the second phase yields wavy, corrugated structures along the circumference for which the radial stiffness declines with increasing N. The hard-to-soft phase transition in radial buckling is a direct consequence of the core-shell structure of MWNTs. Special attention is devoted to how the variation in d affects the critical tube number Nc, which separates the two deformation phases observed in N -walled nanotubes, i.e., the elliptic phase for N < Nc and the corrugated phase for N > Nc. We demonstrate that a larger d tends to result in a smaller Nc, which is attributed to the primary role of the interatomic forces between concentric tubes in the hard-to-soft transition during the radial buckling of MWNTs.
1. Introduction
The term “buckling” refers to a deformation through which a pressurized material undergoes a sudden failure and exhibits a large displacement in a direction transverse to the load [1]. A typical example of buckling occurs when pressing opposite edges of a long, thin elastic beam toward one another. For small loads, the beam is compressed in the axial direction while keeping its linear shape and the strain energy is proportional to the square of the axial displacement. Beyond a certain critical load, however, it suddenly bends into an arc shape and the strain energy and displacements are no longer related by a quadratic expression. Besides axial compression, bending and torsion give rise to buckling of elastic objects, where the buckled patterns depend strongly on the geometric and material parameters.
An interesting class of elastic buckling can be observed in structural pipe-in-pipe cross sections under hydrostatic pressure [2,3]. Pipe-in-pipe (i.e., a pipe inserted inside another pipe) applications are commonly used in offshore oil and gas production systems in civil engineering. In subsea pipelines in deep water, for instance, buckling resistance to huge external hydrostatic pressure is a key structural design requirement. Pipe-inpipe systems may be an efficient design solution that meets this strict requirement, because their concentric structures enable the cross section to withstand high pressure without collapsing.
The above argument regarding macroscopic objects poses a question as to what buckling behavior may be observed in nanometer-scale (10–9 m) counterpart objects. In nanomaterial sciences, the buckling of carbon-based hollow cylinders with nanometric diameters (called carbon nanotubes) has drawn great attention [4]. Extensive studies on carbon nanotube mechanics have been thus far driven by their exceptional resilience against deformation; that is, the recovery of the original cylindrical shapes of the carbon nanotubes upon unloading, even when subjected to severe loading conditions. In addition to the excellent strain-relaxation reversibility, carbon nanotubes exhibit high fatigue resistance; therefore, they are a promising medium for the storage of mechanical energy with an extremely high energy density [5]. Nevertheless, due to their nanometric scales, the similarities and differences in the buckling patterns compared with those of their macroscopic counterparts are not trivial. This complexity has motivated tremendous efforts toward the analysis of the buckling of carbon nanotubes under diverse loading conditions: axial compression [6-10], radial compression [11-22], bending [23-28], torsion [29-32], and combinations of these [33].
In this article, we focus our attention on the radial buckling of carbon nanotubes observed under hydrostatic pressure on the order of several hundreds of megapascal. Thin-shell-theory based analysis on the cross-sectional deformation of nanotubes leads us to the conclusion that the buckled patterns strongly depend on the inter-tube separation , the number of constituent tubes
, the number of constituent tubes , and the innermost tube diameter
, and the innermost tube diameter . In particular, the expansion of
. In particular, the expansion of  from its equilibrium value (0.34 nm) causes a lowering of the critical tube number
from its equilibrium value (0.34 nm) causes a lowering of the critical tube number 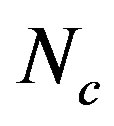 that characterizes the hard-to-soft transition in the nanotubes’ radial buckling. These results shed light on the possible control of the morphology of carbon nanotubes by experimentally tuning
that characterizes the hard-to-soft transition in the nanotubes’ radial buckling. These results shed light on the possible control of the morphology of carbon nanotubes by experimentally tuning .
.
2. What Are “Carbon Nanotubes”?
Carbon nanotubes are one of the most promising nanomaterials, and they consist of layers of graphene sheets that are each a single atom thick (two-dimensional hexagonal lattices of carbon atoms) rolled up into concentric cylinders [34]. By convention, they are categorized as single-walled nanotubes (SWNTs) or multi-walled nanotubes (MWNTs): the former is made by wrapping one single layer into one seamless cylinder, while the latter comprise two or more concentric graphitic tubes. The constituent tubes in MWNTs are coupled to one another via the van der Waals (vdW) interaction, wherein the separation between adjacent concentric tubes is approximately 0.34 nm in equilibrium conditions.
The excellent mechanical properties of carbon nanotubes are characterized by the remarkably high Young’s modulus, which is on the order of terapascal (i.e., several times stiffer than steel), and the tensile strength, which is as high as tens of gigapascal [33]. These properties are proof that carbon nanotubes are the stiffest and strongest materials on earth. In addition to the marked stiffness, carbon nanotubes exhibit astounding flexibility when subjected to external hydrostatic pressure. The radial deformation both of SWNTs and MWNTs is an important consequence of this flexibility; however, the theoretical understanding of the flexibility of MWNTs is still lacking due to their structural complexity.
Emphasis should be placed on the fact that on application of a mechanical deformation, carbon nanotubes show significant changes in their physical and chemical properties [34,35]. Precise knowledge of their deformation mechanism and available geometry is, therefore, crucial for understanding their structure-property relations and for developing next generation carbon-nanotube-based applications.
3. Formulation
3.1. Continuum Approximation
The aim of this section is to deduce the stable cross-sectional shape of a MWNT under a hydrostatic pressure . The continuum elastic approximation [36- 41] allows the mechanical energy
. The continuum elastic approximation [36- 41] allows the mechanical energy 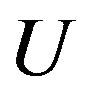 of a MWNT per axial length to be expressed as follows:
of a MWNT per axial length to be expressed as follows:
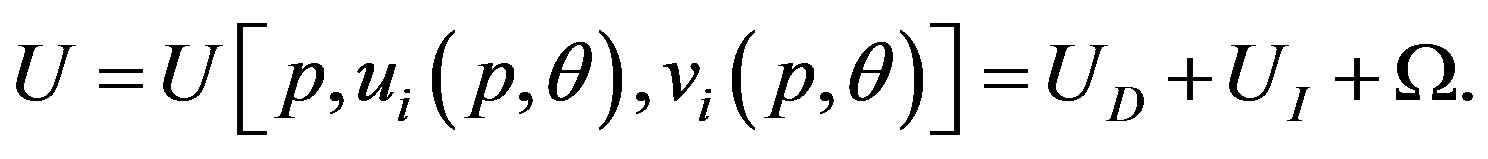 (1)
(1)
Here, 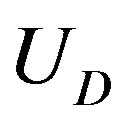 is the deformation energy of all concentric tubes,
is the deformation energy of all concentric tubes, 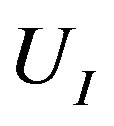 is the interaction energy of all adjacent pairs of tubes, and
is the interaction energy of all adjacent pairs of tubes, and  is the potential energy of the applied pressure. All these three energy terms are functions of
is the potential energy of the applied pressure. All these three energy terms are functions of 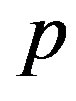 and the deformation amplitudes
and the deformation amplitudes  and
and  that describe the radial
that describe the radial  and circumferential
and circumferential  displacements, respectively, of the
displacements, respectively, of the 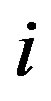 th tube. See Equation (7) below for the precise definitions of
th tube. See Equation (7) below for the precise definitions of  and
and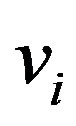 .
.
The optimal displacements 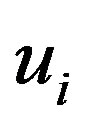 and
and  that minimize
that minimize  under a given
under a given 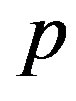 are obtained via the calculus of variations to
are obtained via the calculus of variations to  with respect to
with respect to  and
and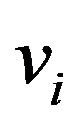 . To proceed, we derive the explicit forms of
. To proceed, we derive the explicit forms of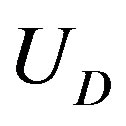 ,
,  , and
, and  as functions of
as functions of ,
, 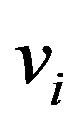 , and
, and 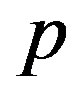 in the subsequent section.
in the subsequent section.
3.2. Strain-Displacement Relation
Evaluating the functional form of 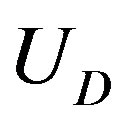 requires the relation between the displacements,
requires the relation between the displacements, 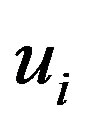 and
and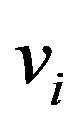 , and the circumferential strain,
, and the circumferential strain,  , of a hollow tube driven by cross-sectional deformation. Suppose there is a circumferential line element of length1
, of a hollow tube driven by cross-sectional deformation. Suppose there is a circumferential line element of length1 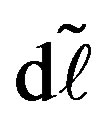 lying at an arbitrary point within the cross section of a tube with thickness
lying at an arbitrary point within the cross section of a tube with thickness . The hydrostatic pressure
. The hydrostatic pressure 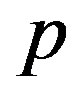 upon the tube causes an extensional strain
upon the tube causes an extensional strain 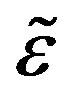 of the line element, which is defined as follows:
of the line element, which is defined as follows:
 (2)
(2)
Here, 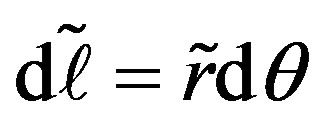 , and
, and 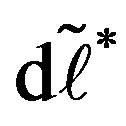 is the length of the line element after deformation (the asterisk symbolizes the quantity after deformation). The coordinates
is the length of the line element after deformation (the asterisk symbolizes the quantity after deformation). The coordinates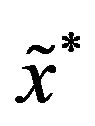 ,
,  of the element after deformation are given as follows:
of the element after deformation are given as follows:
 (3)
(3)
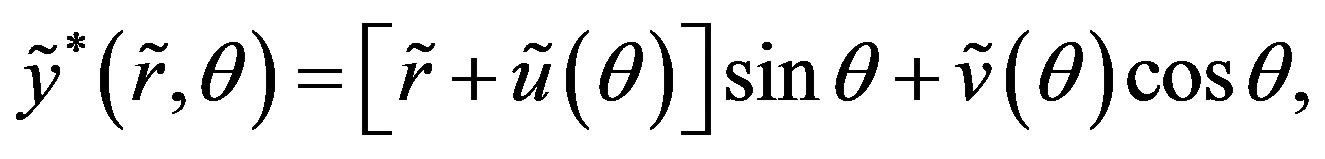 (4)
(4)
where 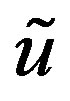 and
and  are the components of the displacement vector in the radial and circumferential directions, respectively. We can then write the following relationships:
are the components of the displacement vector in the radial and circumferential directions, respectively. We can then write the following relationships:
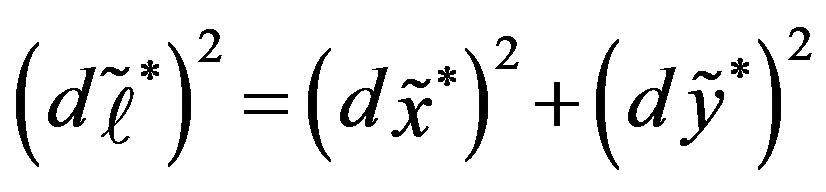 , (5)
, (5)
the following relationship can be obtained:
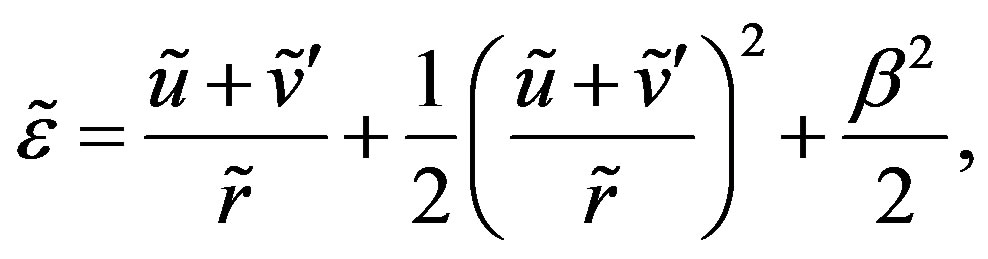 (6)
(6)
where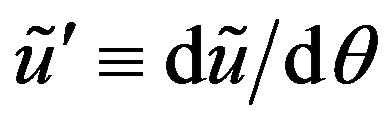 , etc. The term
, etc. The term 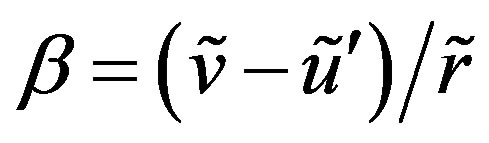 in Equation (6) accounts for the rotation of the line element due to the deformation [16]. The formula (6) is valid for an arbitrarily large rotation,
in Equation (6) accounts for the rotation of the line element due to the deformation [16]. The formula (6) is valid for an arbitrarily large rotation, .
.
Hereafter, we assume that  and
and 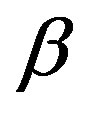 are both significantly smaller than unity, because an infinitesimal deflection of the initially circular cross section is assumed to determine the critical buckling pressure. The second term in the right side in Equation (6) can therefore be omitted if the possibility that
are both significantly smaller than unity, because an infinitesimal deflection of the initially circular cross section is assumed to determine the critical buckling pressure. The second term in the right side in Equation (6) can therefore be omitted if the possibility that 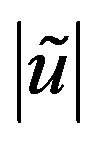 or
or  is larger than
is larger than 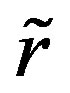 is excluded. We further assume that the normals to the undeformed centroidal circle
is excluded. We further assume that the normals to the undeformed centroidal circle  of the hollow tube’s cross section remain straight, normal, and unextended during the deformation [16]. The second assumption means that within each cross section, neither shear deformation nor thickness modulation arises in the circumferential direction; this leads to the following expressions:
of the hollow tube’s cross section remain straight, normal, and unextended during the deformation [16]. The second assumption means that within each cross section, neither shear deformation nor thickness modulation arises in the circumferential direction; this leads to the following expressions:
 (7)
(7)
where 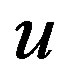 and
and  denote the displacements of a point that lies on
denote the displacements of a point that lies on , and
, and 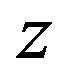 is a radial coordinate measured from
is a radial coordinate measured from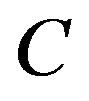 . By substituting Equation (7) into Equation (6), we can derive the following strain-displacement relationship:
. By substituting Equation (7) into Equation (6), we can derive the following strain-displacement relationship:
 (8)
(8)
where the following definitions hold true:
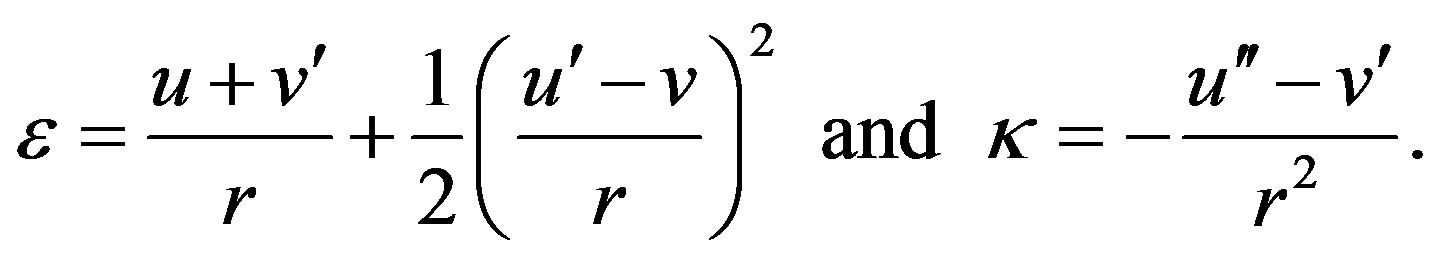 (9)
(9)
Here, 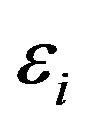 and
and  are the in-plane and bending strains, respectively, of the
are the in-plane and bending strains, respectively, of the 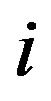 th tube;
th tube; 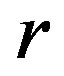 is the radius of the undeformed circle
is the radius of the undeformed circle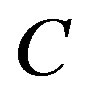 . Equations (8) and (9) state that the circumferential strain at an arbitrary point in the cross section is determined by the displacements
. Equations (8) and (9) state that the circumferential strain at an arbitrary point in the cross section is determined by the displacements  and
and 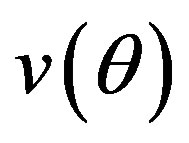 of a point that lies on the undeformed centroidal circle
of a point that lies on the undeformed centroidal circle .
.
3.3. Deformation Energy
We are now ready to derive the explicit form of the deformation energy . Suppose that the
. Suppose that the 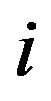 th constituent tube has a thickness
th constituent tube has a thickness . A surface element of the crosssection of the hollow tube can then be expressed by
. A surface element of the crosssection of the hollow tube can then be expressed by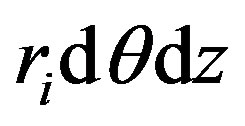 . The stiffness
. The stiffness  of the surface element for stretching along the circumferential direction is given as follows:
of the surface element for stretching along the circumferential direction is given as follows:
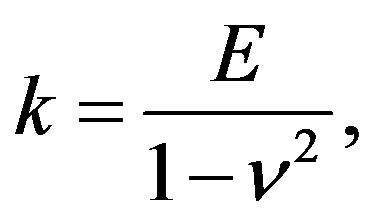 (10)
(10)
where  and
and 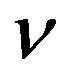 are the Young’s modulus and Poisson’s ratio, respectively, of the tube. Thus, the deformation energy
are the Young’s modulus and Poisson’s ratio, respectively, of the tube. Thus, the deformation energy  per axial length can be written as follows:
per axial length can be written as follows:
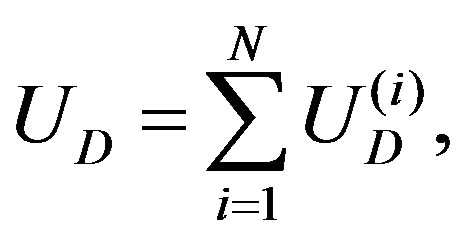 (11)
(11)
in which the component 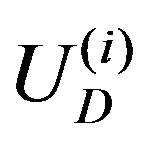 associated with the
associated with the  th tube is written as follows:
th tube is written as follows:
 (12)
(12)
From Equations (8) and (12) we obtain the following relationship:
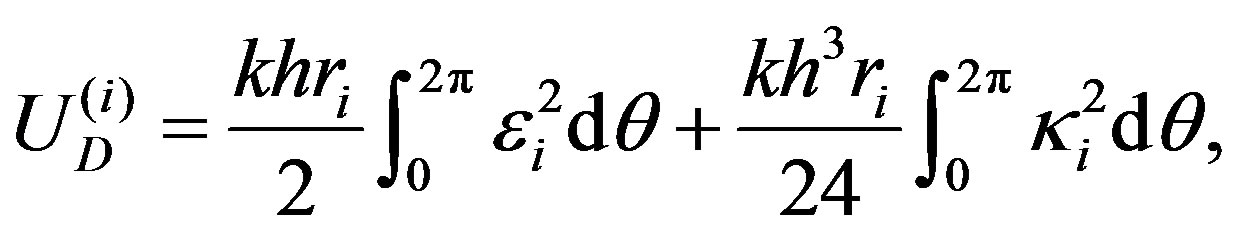 (13)
(13)
which can also be written as follows:
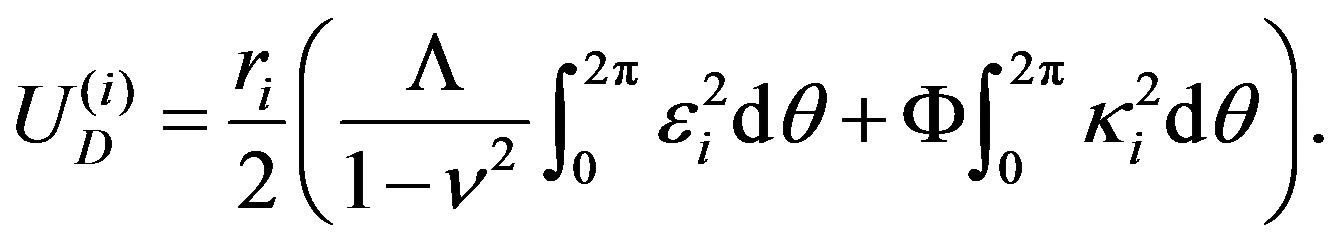 (14)
(14)
The constant  denotes the in-plane stiffness,
denotes the in-plane stiffness,  the flexural rigidity, and
the flexural rigidity, and 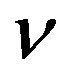 the Poisson ratio of each tube.
the Poisson ratio of each tube.
For quantitative discussions, the values of  and
and  must be carefully determined. In cases of macroscopic objects, they are defined as
must be carefully determined. In cases of macroscopic objects, they are defined as  and
and
 . However, for carbon nanotubesthe macroscopic relations for
. However, for carbon nanotubesthe macroscopic relations for  and
and  noted above fail because there is no unique way of defining the thickness of the graphene tube [42]2 Thus, the values of
noted above fail because there is no unique way of defining the thickness of the graphene tube [42]2 Thus, the values of  and
and  should be evaluated ab-initio from direct measurements or through computations involving the properties of carbon sheets, without reference to the macroscopic relations. In actual calculations, we substitute
should be evaluated ab-initio from direct measurements or through computations involving the properties of carbon sheets, without reference to the macroscopic relations. In actual calculations, we substitute  nN/nm,
nN/nm,  nN·nm, and
nN·nm, and  in a similar fashion as a previous study [43] based on the density functional theory.
in a similar fashion as a previous study [43] based on the density functional theory.
3.4. Inter-Tube Coupling Energy
The energy associated with the van der Waals (vdW) interaction between adjacent pairs of tubes, designated by  in Equation (1), can be written as a sum of components as follows:
in Equation (1), can be written as a sum of components as follows:
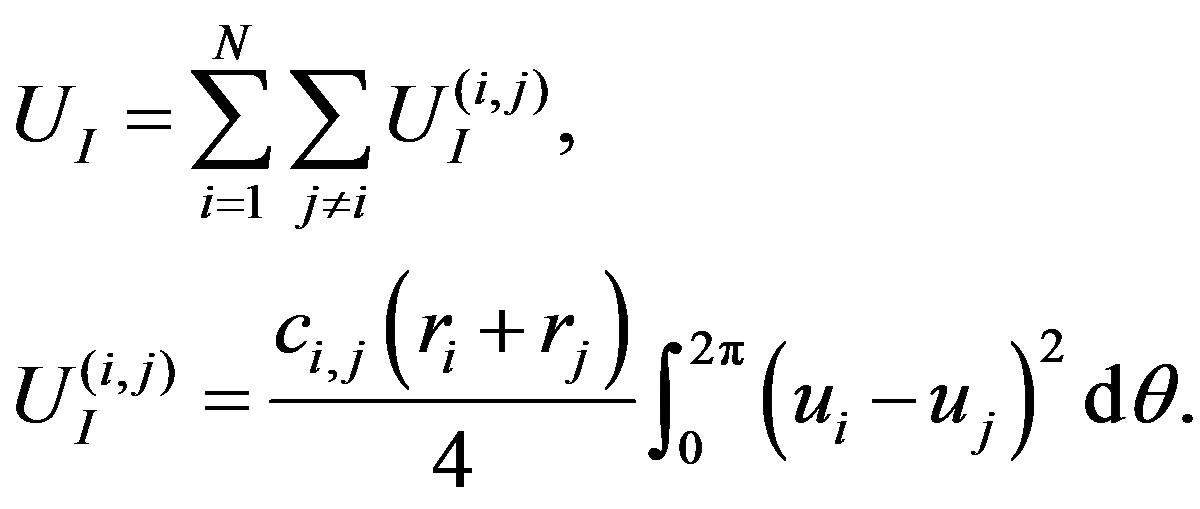 (15)
(15)
We derive the coefficients 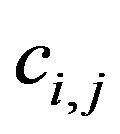 in Equation (15) through a first order Taylor approximation of the vdW pressure [39,44] associated with the vdW potential as follows:
in Equation (15) through a first order Taylor approximation of the vdW pressure [39,44] associated with the vdW potential as follows:
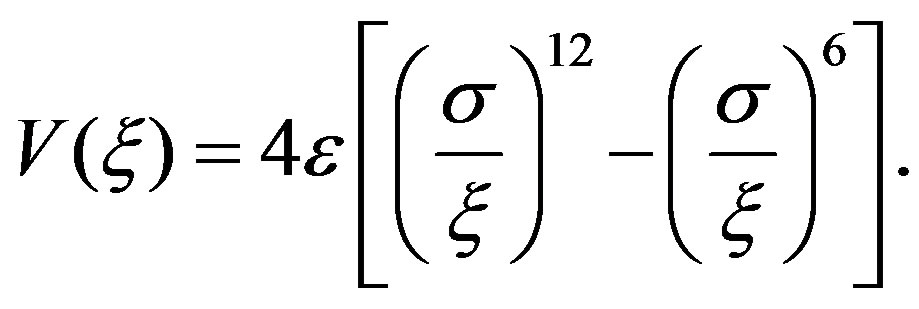 (16)
(16)
Here,  is the distance between a pair of carbon atoms,
is the distance between a pair of carbon atoms, 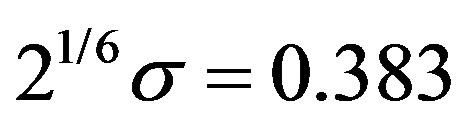 nm is the equilibrium distance between two interacting atoms, and
nm is the equilibrium distance between two interacting atoms, and  nN·nm is the well depth of the potential [45]. The resulting equilibrium spacing between neighboring tubes is 0.3415 nm. The derivative
nN·nm is the well depth of the potential [45]. The resulting equilibrium spacing between neighboring tubes is 0.3415 nm. The derivative 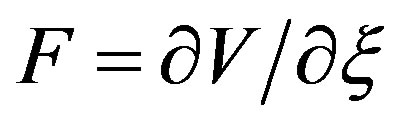 represents the force between two carbon atoms, and its surface integral provides the inter-wall pressure induced by the vdW coupling.
represents the force between two carbon atoms, and its surface integral provides the inter-wall pressure induced by the vdW coupling.
The vdW pressures on the inner and outer tubes of a concentric two-walled tube with radii  and
and 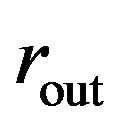 are given as follows [44] (with positive signs for compression):
are given as follows [44] (with positive signs for compression):
 (17)
(17)
where . The area density of carbon atoms is given by
. The area density of carbon atoms is given by 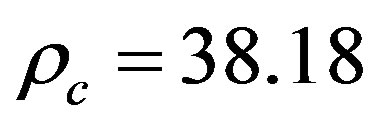 nm–2.
nm–2.
 (18)
(18)
In Equation (18), 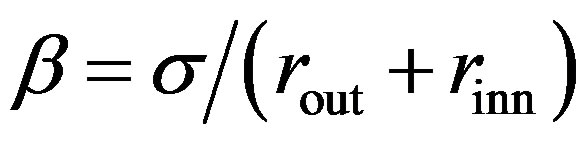 ,
,  ,
,
 , and
, and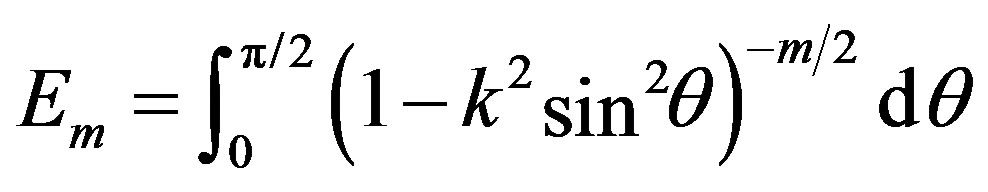 , and
, and
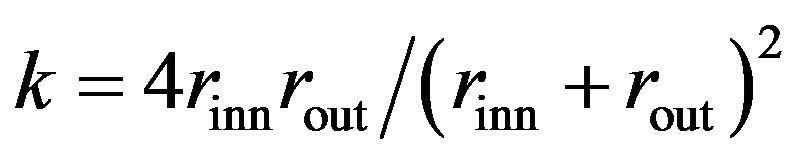 .
.
In the following, we obtain analytical expressions for 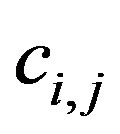 by linearizing the Equation (17) for the pressure [22]. Note that
by linearizing the Equation (17) for the pressure [22]. Note that 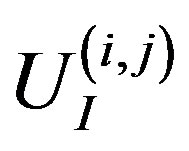 depends quadratically on the change in spacing between two adjacent tubes. Consider two consecutive tubes with radii
depends quadratically on the change in spacing between two adjacent tubes. Consider two consecutive tubes with radii  and
and , where the subscripts
, where the subscripts  and
and  correspond to
correspond to 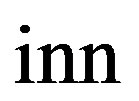 and
and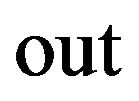 , respectively. The vdW energy stored due to a perturbation
, respectively. The vdW energy stored due to a perturbation  along the positive direction of pressure is given as follows:
along the positive direction of pressure is given as follows:
 (19)
(19)
where 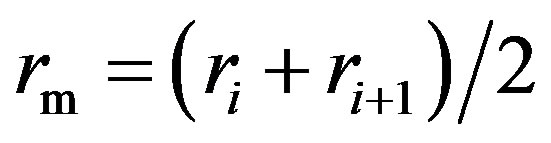 is the mean radius and
is the mean radius and 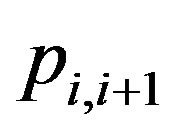 is the vdW pressure on the
is the vdW pressure on the  th tube. The corresponding linearized pressure is given by
th tube. The corresponding linearized pressure is given by . In Equation
. In Equation
(19), 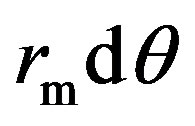 describes the length of the infinitesimal element on which the pressure is acting. Using the linearized pressure and comparing with Equation (15), the following expressions for the vdW coefficients can be found:
describes the length of the infinitesimal element on which the pressure is acting. Using the linearized pressure and comparing with Equation (15), the following expressions for the vdW coefficients can be found:
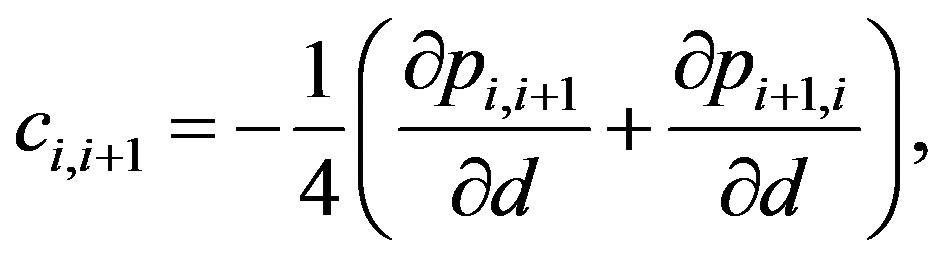 (20)
(20)
where the derivatives in Equation (20) are defined as follows:
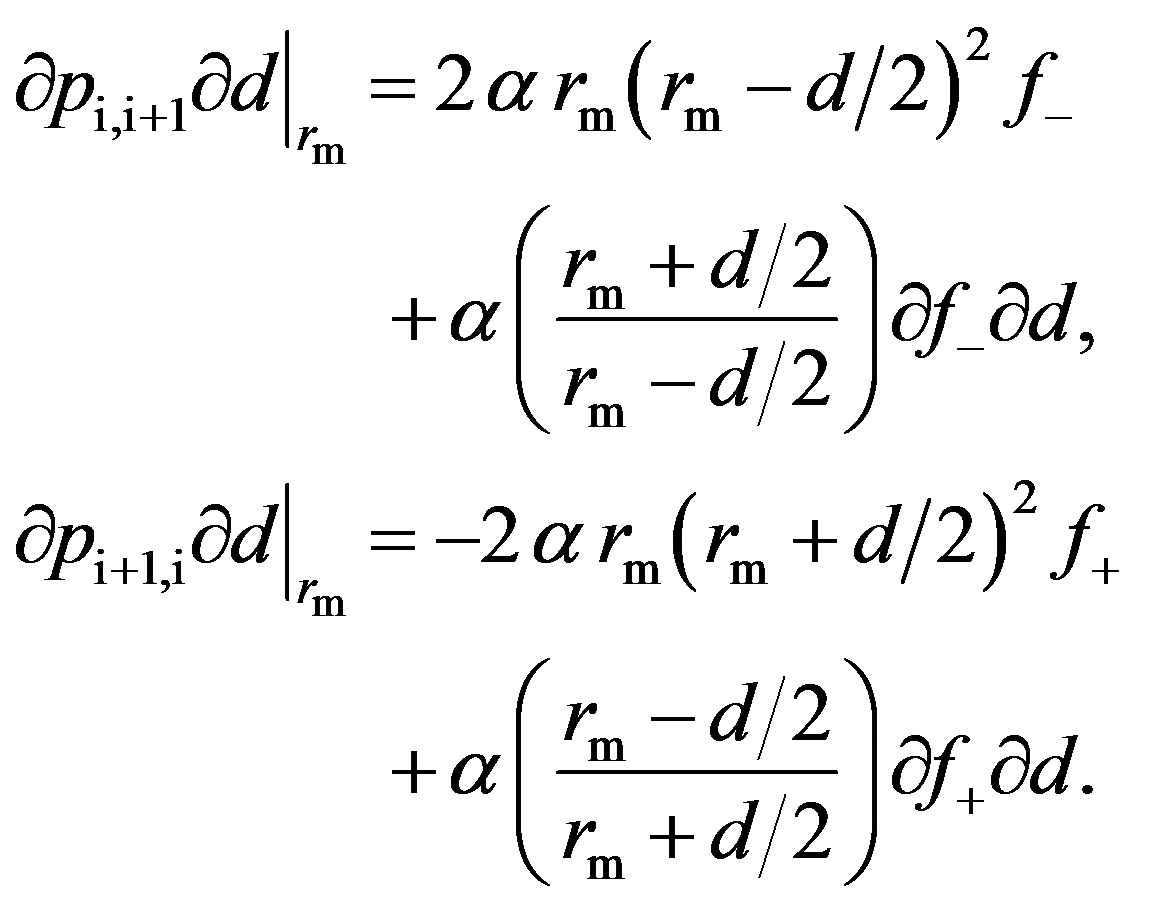 (21)
(21)
Note that  is symmetric. The set of Equations (15), (20), and (21) allows for the evaluation of
is symmetric. The set of Equations (15), (20), and (21) allows for the evaluation of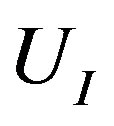 .
.
3.5. Pressure-Induced Energy
We finally derive an explicit form of , which is the negative of the work done by the external pressure
, which is the negative of the work done by the external pressure 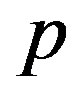 during cross-sectional deformation. Using this definition we can write the following expression:
during cross-sectional deformation. Using this definition we can write the following expression:
 (22)
(22)
where 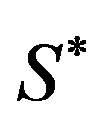 is the area surrounded by the
is the area surrounded by the  th tube after deformation (the sign of
th tube after deformation (the sign of  is assumed to be positive inward).
is assumed to be positive inward).  can then be obtained by evaluating the following expression:
can then be obtained by evaluating the following expression:
 (23)
(23)
By substituting Equations (3) and (4) into Equation (23), and by using the periodicity relation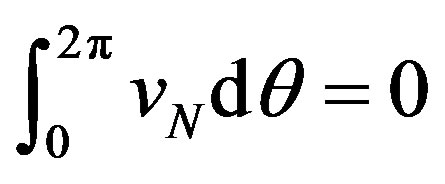 , the following expression can be obtained:
, the following expression can be obtained:
 (24)
(24)
3.6. Critical Pressure Evaluation
This section presents our method for determining the critical pressure 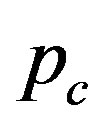 above which the circular cross section of MWNTs is elastically deformed into a noncircular one. To carry out this analysis, we decompose the radial displacement terms according to
above which the circular cross section of MWNTs is elastically deformed into a noncircular one. To carry out this analysis, we decompose the radial displacement terms according to  . Here,
. Here,  indicates a uniform radial contraction of the
indicates a uniform radial contraction of the  th tube at
th tube at , whose magnitude is proportional to
, whose magnitude is proportional to .
.  describes a deformed, non-circular cross section observed just above
describes a deformed, non-circular cross section observed just above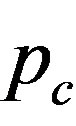 . Similarly, we can write
. Similarly, we can write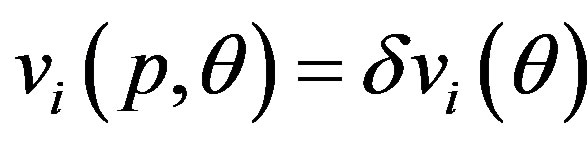 , because
, because  at
at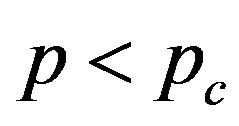 .
.
By applying the variational method to  with respect to
with respect to 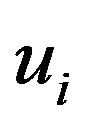 and
and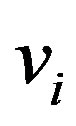 , we obtain the following system of 2N linear differential equations:
, we obtain the following system of 2N linear differential equations:
 (25)
(25)
 (26)
(26)
where  and
and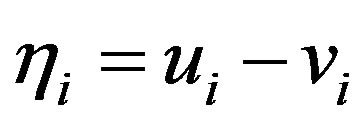 . In deriving Equations (25) and (26), the quadratic and cubic terms in
. In deriving Equations (25) and (26), the quadratic and cubic terms in 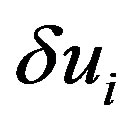 and
and 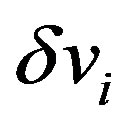 are omitted because we only consider elastic deformation with sufficiently small displacements. In addition, the terms consisting only of
are omitted because we only consider elastic deformation with sufficiently small displacements. In addition, the terms consisting only of 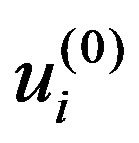 and
and  are also omitted; the sum of such terms should be equal to zero3 because
are also omitted; the sum of such terms should be equal to zero3 because  represents an equilibrium circular cross-section under
represents an equilibrium circular cross-section under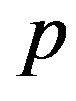 .
.
Because 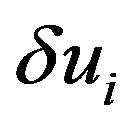 and
and 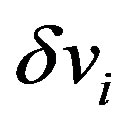 are periodic in
are periodic in , the general solutions of Equations (25) and (26) are given by the Fourier series expansions as follows:
, the general solutions of Equations (25) and (26) are given by the Fourier series expansions as follows:
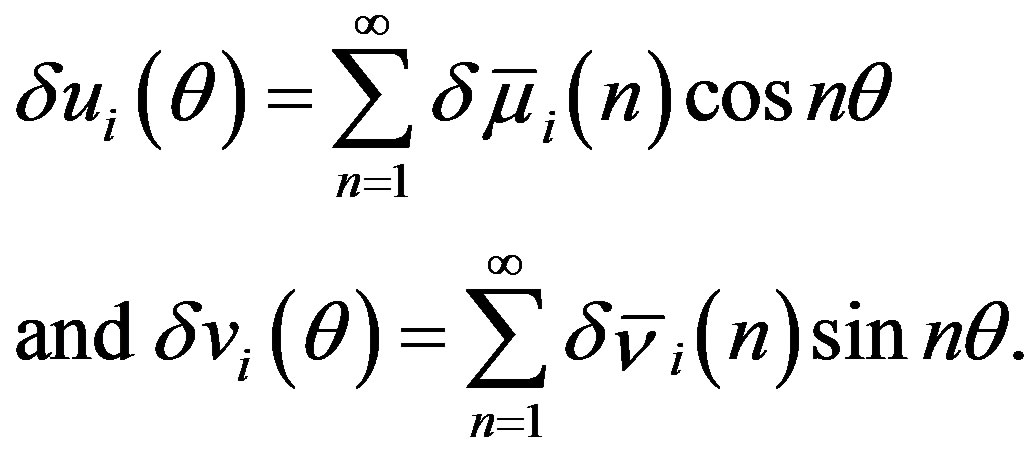
Substituting these into Equations (25) and (26) leads to the matrix equation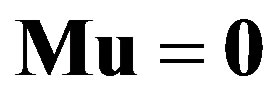 , in which the vector
, in which the vector 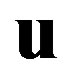 consists of
consists of  and
and 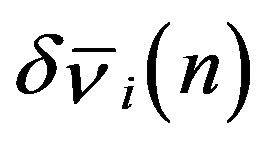 with all possible
with all possible 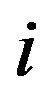 and
and , and the matrix
, and the matrix  involves one variable
involves one variable 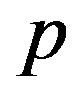 as well as parameters such as
as well as parameters such as  and
and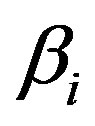 . The matrix
. The matrix  can be expressed as a block diagonal matrix of the form
can be expressed as a block diagonal matrix of the form 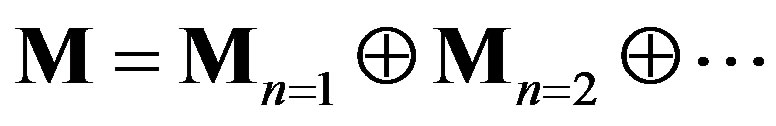 due to the orthogonality of
due to the orthogonality of  and
and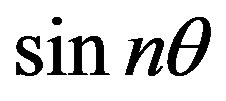 . Here,
. Here,  is a
is a  submatrix that satisfies
submatrix that satisfies , where
, where 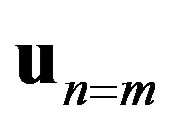 is a 2N-column vector composed of
is a 2N-column vector composed of 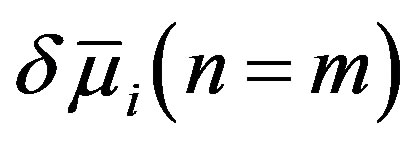 and
and 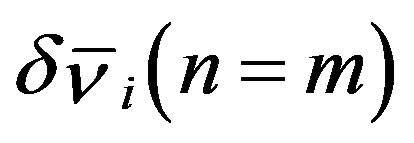 . As a result, the secular equation
. As a result, the secular equation  that provides nontrivial solutions of Equations (25) and (26) can be rewritten as follows:
that provides nontrivial solutions of Equations (25) and (26) can be rewritten as follows:
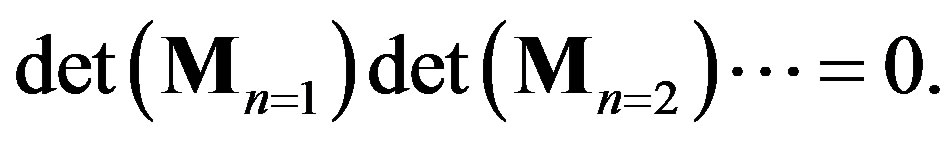 (27)
(27)
By solving Equation (27) with respect to , we obtain a sequence of discrete values of
, we obtain a sequence of discrete values of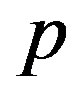 . Each of these values is the smallest solution of
. Each of these values is the smallest solution of 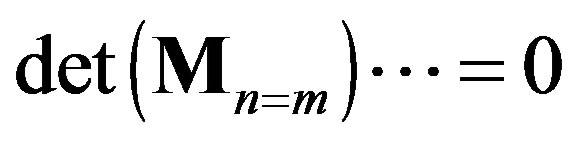
 . The minimum of these values serves as the critical pressure
. The minimum of these values serves as the critical pressure 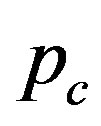 that is associated with a specific integer
that is associated with a specific integer . From the definition, the
. From the definition, the  associated with a specific m allows only
associated with a specific m allows only 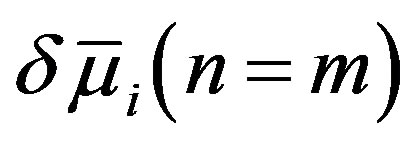 and
and 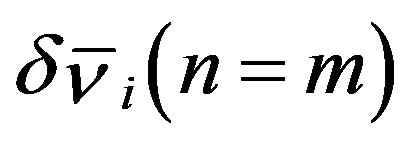 to be finite, however, it also requires
to be finite, however, it also requires 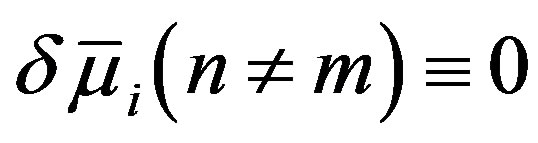 and
and . Immediately above
. Immediately above , therefore, the circular cross section of MWNTs becomes radially deformed as follows:
, therefore, the circular cross section of MWNTs becomes radially deformed as follows:
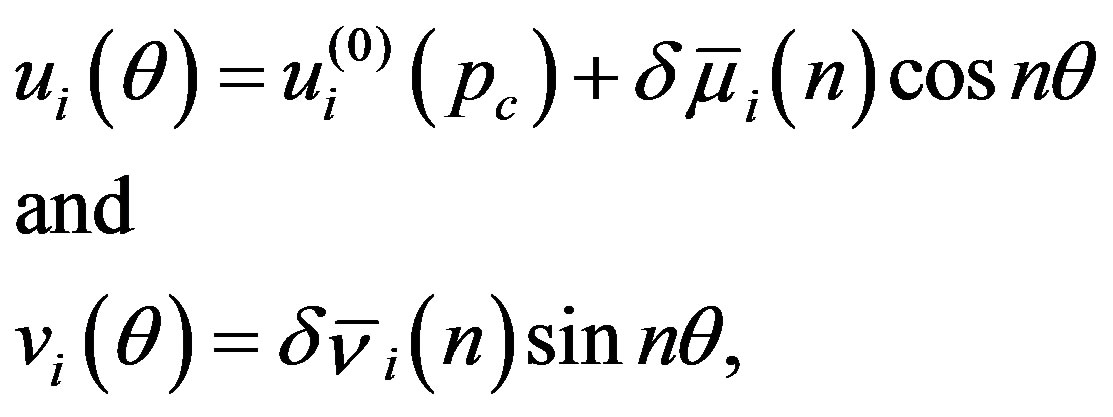 (28)
(28)
where the value of  is uniquely determined by the one-to-one relation between
is uniquely determined by the one-to-one relation between 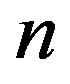 and
and .
.
4. Result and Discussion
4.1. Critical Pressure Curve
Figures 1(a) and (b) show  as a function of
as a function of 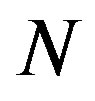 for various values of the initial tube-tube separation
for various values of the initial tube-tube separation 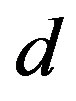 prior to the application of pressure. For all
prior to the application of pressure. For all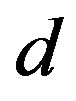 , we observe a rapid increase in
, we observe a rapid increase in  with
with , which is followed by a slow decay when
, which is followed by a slow decay when  nm (and also for smaller D).4 The increase in
nm (and also for smaller D).4 The increase in 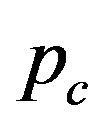 for small
for small 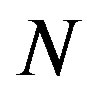 is interpreted as the “hardening” of the MWNTs, i.e., an enhancement of the radial stiffness of the entire MWNT by encapsulation. This hardening effect disappears with a further increase in
is interpreted as the “hardening” of the MWNTs, i.e., an enhancement of the radial stiffness of the entire MWNT by encapsulation. This hardening effect disappears with a further increase in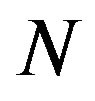 , which results in the decay of
, which results in the decay of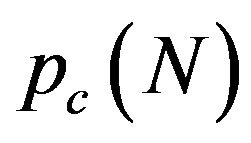 . A decay in
. A decay in  implies that a relatively low pressure suffices to produce a radial deformation, which indicates an effective “softening” of the MWNT. These two contrasting effects, i.e., hardening and softening, are both due to the encapsulation of MWNTs.
implies that a relatively low pressure suffices to produce a radial deformation, which indicates an effective “softening” of the MWNT. These two contrasting effects, i.e., hardening and softening, are both due to the encapsulation of MWNTs.
| 4Such a decay is also observed for D = 5.0 nm and larger D, in principle, if a sufficiently large N is considered [but omitted in Figure 1(b)]. |
We emphasize that in Figure 1(a), the softening region (i.e.,  -decay region) is enlarged by expanding the inter-tube distance
-decay region) is enlarged by expanding the inter-tube distance  prior to deformation. As will be confirmed later, this tendency agrees with the existing numerical simulations that were based on a coarsegrained model of MWNTs [21]. The variation of
prior to deformation. As will be confirmed later, this tendency agrees with the existing numerical simulations that were based on a coarsegrained model of MWNTs [21]. The variation of  is thought to be feasible in MWNT synthesis. During synthesis, the interlayer thermal contraction upon cooling and/or the intertube adhesion energy owing to the increased intertube commensuration may result in a deviation in
is thought to be feasible in MWNT synthesis. During synthesis, the interlayer thermal contraction upon cooling and/or the intertube adhesion energy owing to the increased intertube commensuration may result in a deviation in  from the equilibrium value [46,47].
from the equilibrium value [46,47].
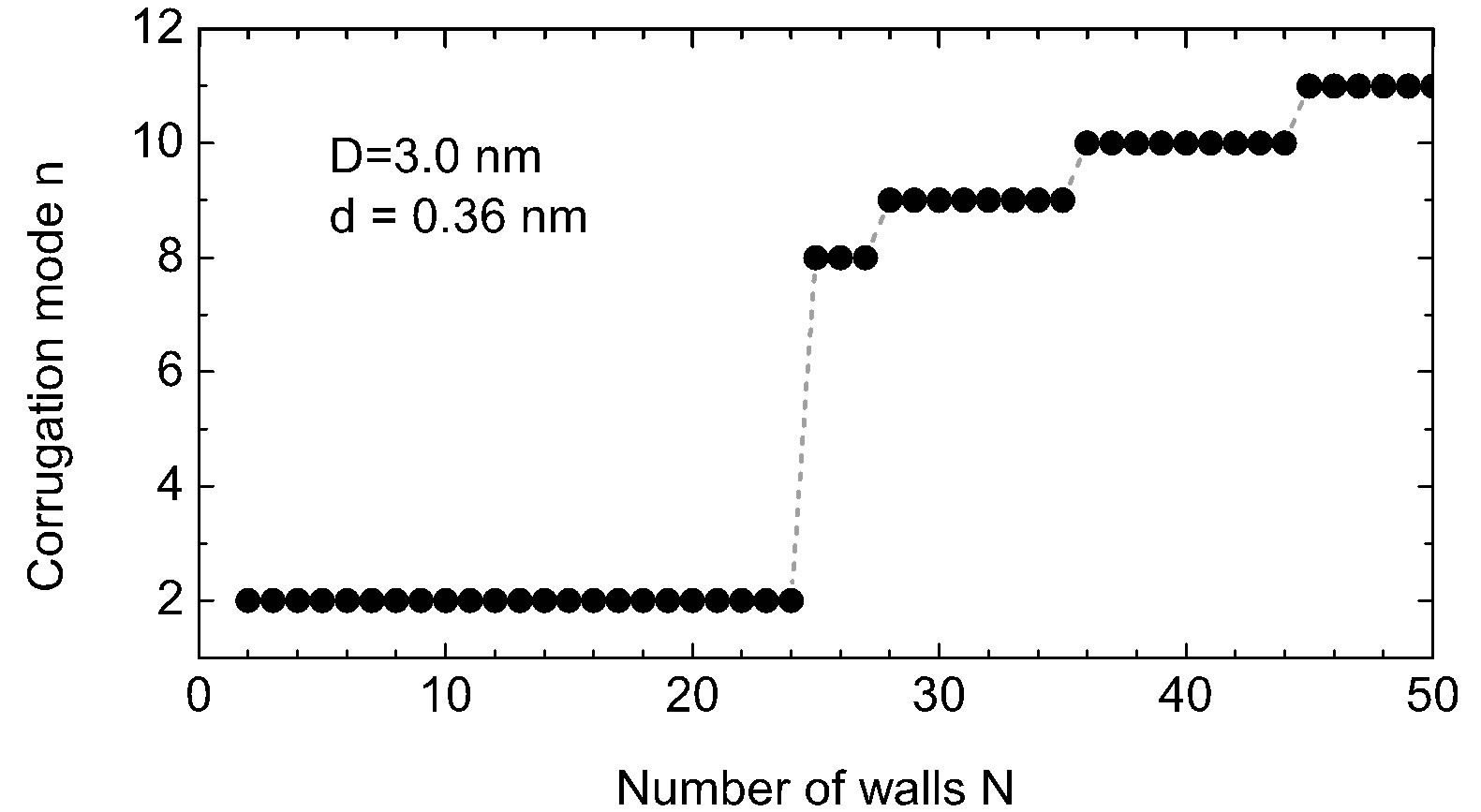
4.2. Sequential Change in Buckling Modes
Figure 2 provides (a) the index 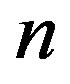 of deformation modes and (b)-(g) the cross-sectional views observed just
of deformation modes and (b)-(g) the cross-sectional views observed just
 (a)
(a)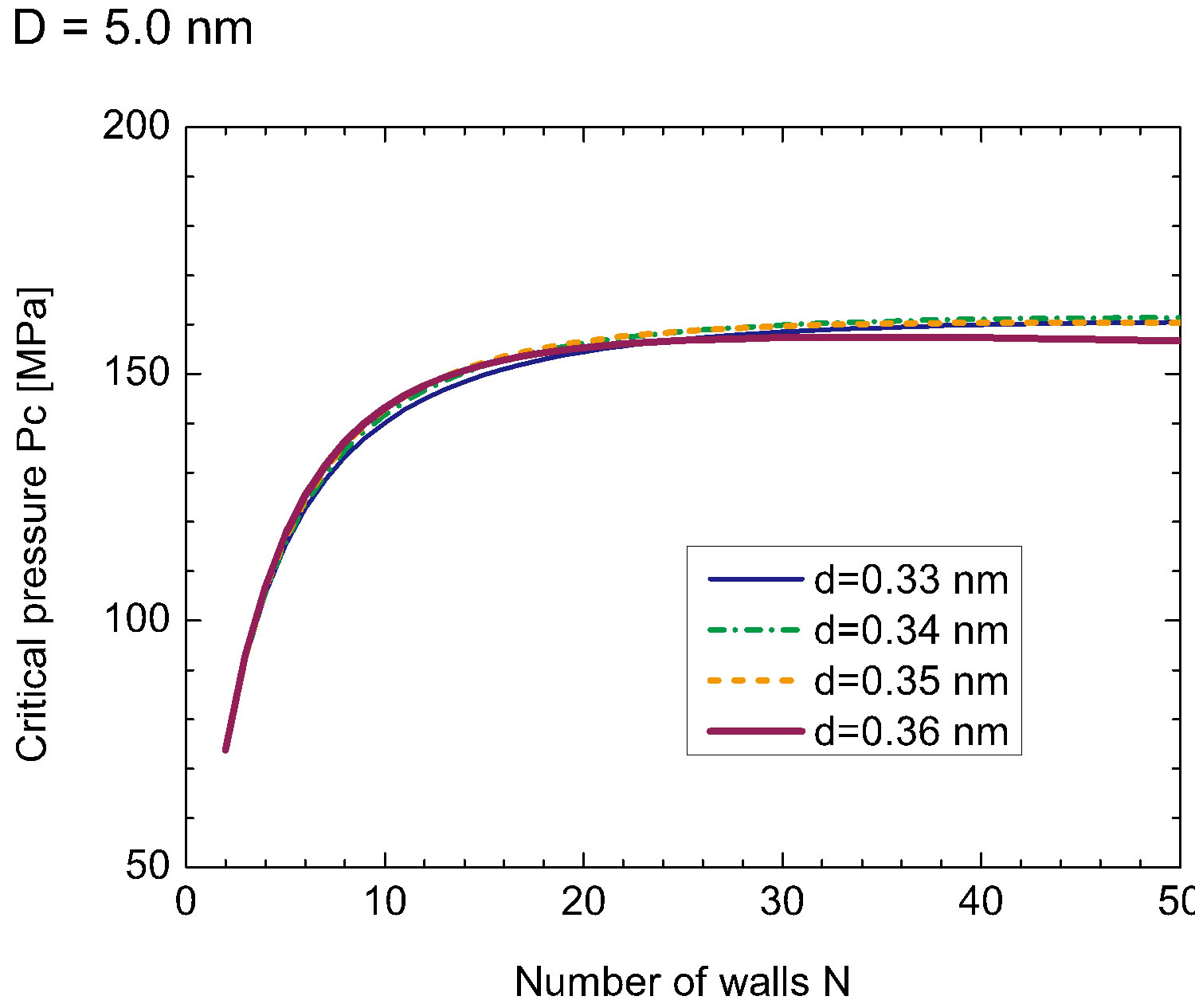 (b)
(b)
Figure 1. (Color online) Critical pressure curves showing Pc required to produce radial deformation of N-walled nanotubes with fixed D: (a) D = 3.0 nm, and (b) D = 5.0 nm.
above 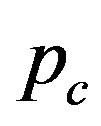 for fixed
for fixed 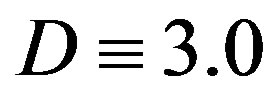 nm and
nm and 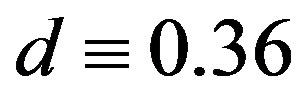 nm. The most striking observation is the successive transformation of the cross section with an increase in
nm. The most striking observation is the successive transformation of the cross section with an increase in . We see from Figure 2(a) that the deformation mode observed just above
. We see from Figure 2(a) that the deformation mode observed just above 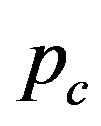 jumps abruptly from
jumps abruptly from 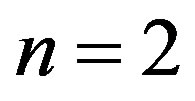 to n = 8 at
to n = 8 at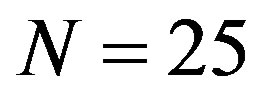 , which is followed by successive emergences of higher corrugation modes with larger
, which is followed by successive emergences of higher corrugation modes with larger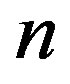 . These transitions in
. These transitions in 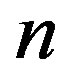 originate from the two competing effects inherent in MWNTs with N = 1, that is, the relative rigidity of the inner tubes and the mechanical instability of the outer tubes. A large discrepancy in the radial stiffness of the inner and outer tubes gives rise to an uneven distribution of the deformation amplitudes of concentric tubes that interact through the vdW forces, which consequently produces an abrupt change in the observed deformation mode at some
originate from the two competing effects inherent in MWNTs with N = 1, that is, the relative rigidity of the inner tubes and the mechanical instability of the outer tubes. A large discrepancy in the radial stiffness of the inner and outer tubes gives rise to an uneven distribution of the deformation amplitudes of concentric tubes that interact through the vdW forces, which consequently produces an abrupt change in the observed deformation mode at some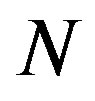 .
.
4.3. Hard-to-Soft Transition
Of further interest is that the critical number of tubes  separating the elliptic phase (
separating the elliptic phase (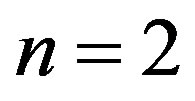 ) from the corrugation phase (
) from the corrugation phase (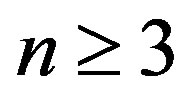 ) is identified as the
) is identified as the 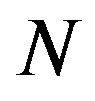 that
that
 (a)
(a)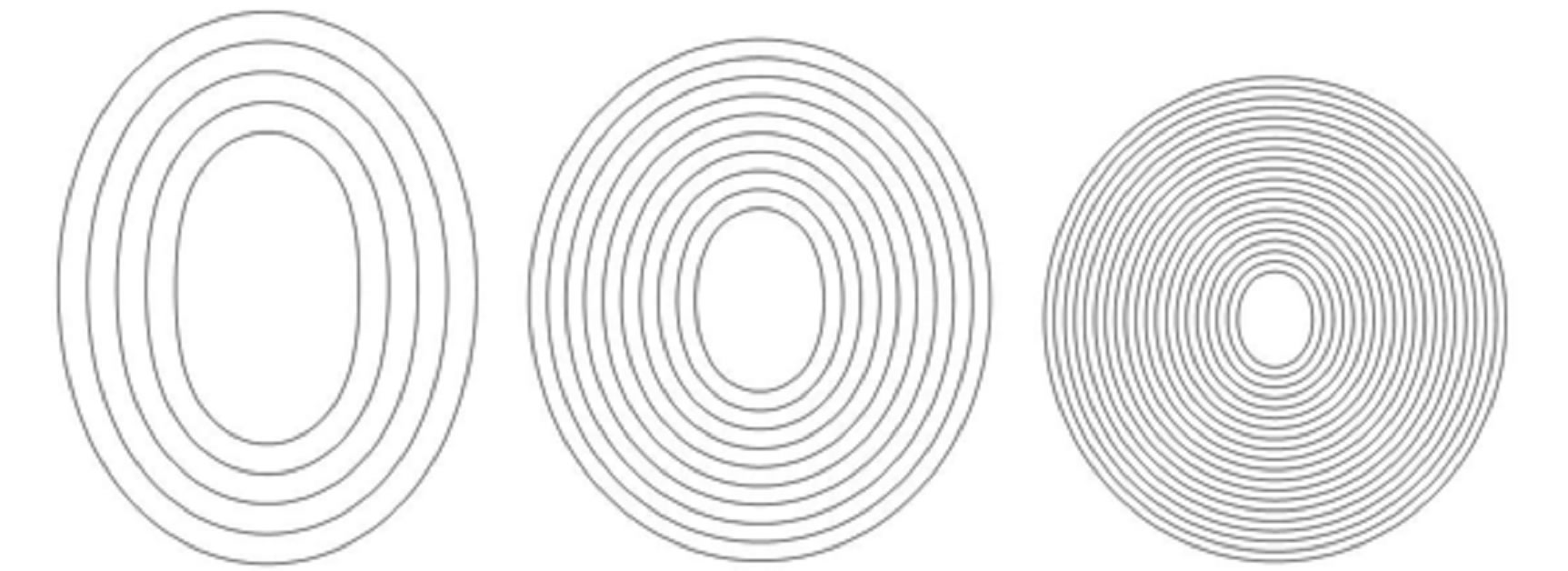 (b)
(b) (c)
(c)
Figure 2. [Upper panel] (a) Stepwise increase in the index n of radial buckling modes. The index n indicates the circumferential wave number of the deformed cross-section. [Bottom panel] Cross-sectional views of buckled MWNTs under high hydrostatic pressure: (b)-(d) Elliptic deformation mode (n = 2) for N = 5, 10, 20; (e) Radial corrugation mode with n = 8 for N = 25; (f) n = 9 for N = 35; (g) n = 11 for N = 50.
yields a cusp in the curve of  [see Figure 1(a)]. In contrast, no singularity is observed in the curve of
[see Figure 1(a)]. In contrast, no singularity is observed in the curve of 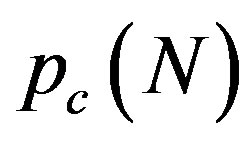 at any value of
at any value of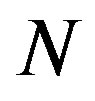 , which separates two neighboring corrugation phases. We emphasize that at these phase boundaries, one additional tube induces a drastic change in the cross-sectional shape of the MWNT under hydrostatic pressure.
, which separates two neighboring corrugation phases. We emphasize that at these phase boundaries, one additional tube induces a drastic change in the cross-sectional shape of the MWNT under hydrostatic pressure.
Figure 3 explains why the singular cusp in the 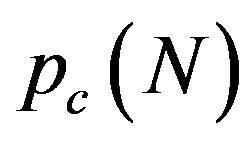 curve corresponds to the hard-to-soft transition point of
curve corresponds to the hard-to-soft transition point of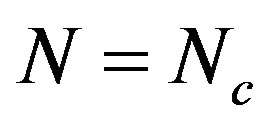 . This figure shows the N-dependence of the solutions
. This figure shows the N-dependence of the solutions 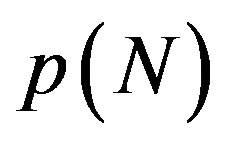 for the secular equation
for the secular equation . As mentioned earlier, the secular equation provides various values of
. As mentioned earlier, the secular equation provides various values of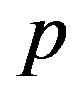 . Each of these values is associated with a specific mode index
. Each of these values is associated with a specific mode index . The minimum value of p gives the critical pressure
. The minimum value of p gives the critical pressure 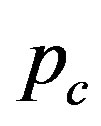 just above which cross-sectional deformation takes place. Figure 3 depicts the N-dependence of
just above which cross-sectional deformation takes place. Figure 3 depicts the N-dependence of 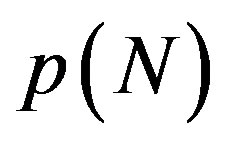 for several
for several  values, where the innermost tube radius is fixed to be
values, where the innermost tube radius is fixed to be 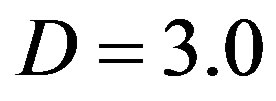 nm. For
nm. For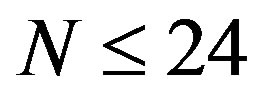 , the values of
, the values of 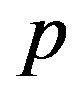 for
for  are less than those for
are less than those for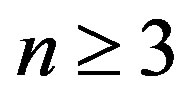 , which implies that the elliptic mode occurs for MWNTs with
, which implies that the elliptic mode occurs for MWNTs with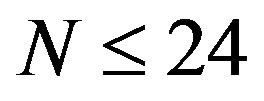 . However, at
. However, at  (and
(and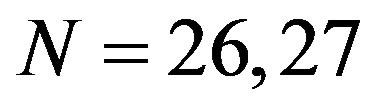 ), the minimum
), the minimum  corre-
corre-
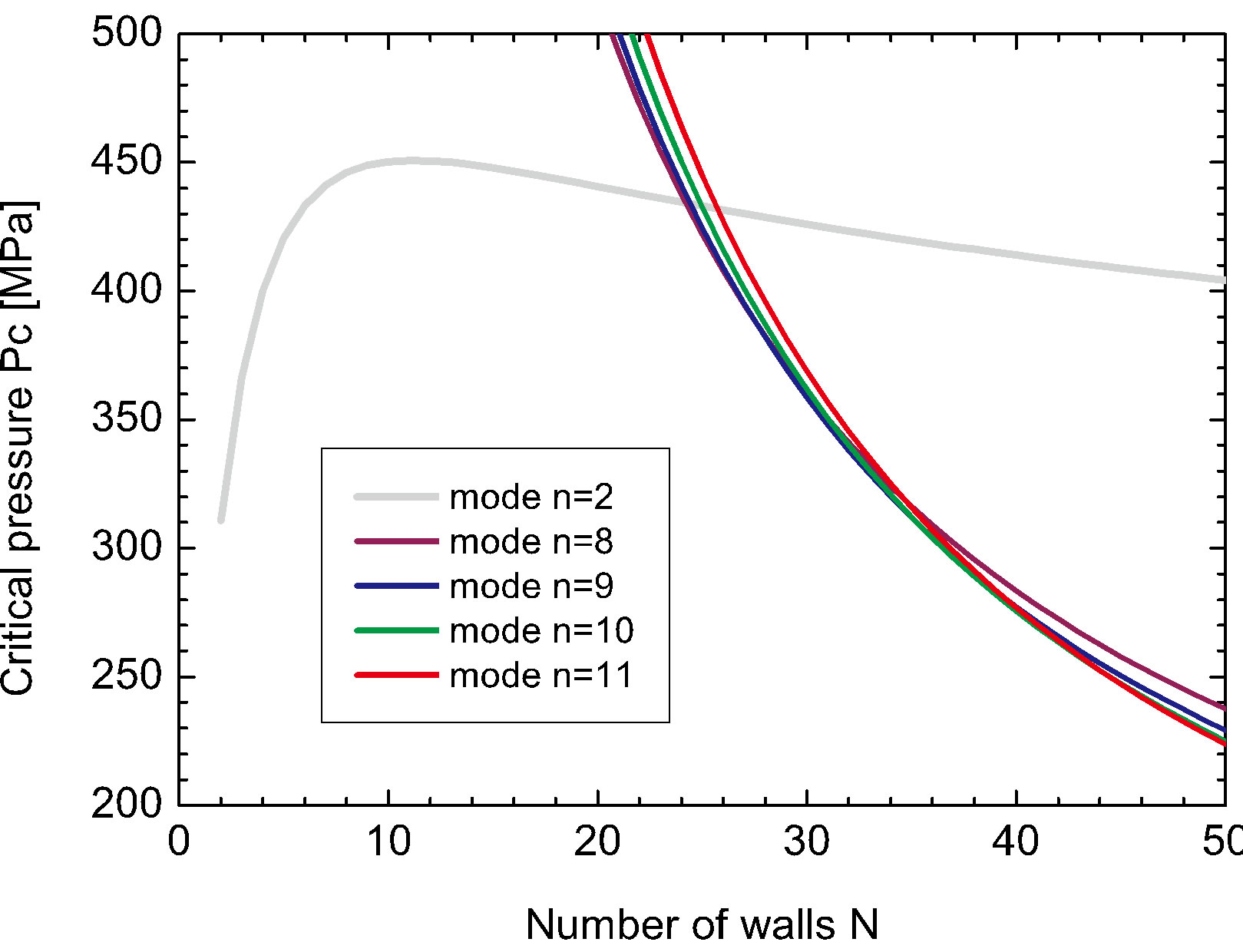
Figure 3. Branches of solutions p(N) for the secular equation det(M) = 0 (refer text). The innermost tube diameter is set to be D = 3.0 nm for all curves. For a fixed N, the minimum value of p among the branches takes a role of the critical pressure pc at that N.
sponds to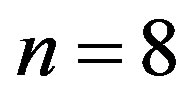 , which implies the occurrence of the corrugation mode of
, which implies the occurrence of the corrugation mode of . It should be noted that
. It should be noted that  for
for 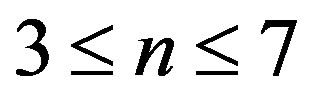 can never attain the minimum value at any
can never attain the minimum value at any . This is why the corrugation mode of
. This is why the corrugation mode of  with
with  cannot be observed for MWNTs with
cannot be observed for MWNTs with 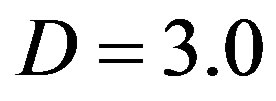 nm. It also follows from Figure 3 that the cusps in the curves
nm. It also follows from Figure 3 that the cusps in the curves  occur only at the phase boundary
occur only at the phase boundary  separating the elliptic phase
separating the elliptic phase  from a corrugation phase
from a corrugation phase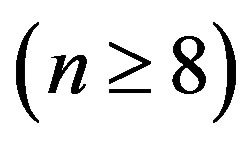 , while no singularity appears at the boundaries of
, while no singularity appears at the boundaries of 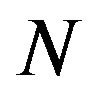 between neighboring corrugation phases.
between neighboring corrugation phases.
5. Summary
A thin-shell-theory based analysis has been employed to detect the mechanical hard-to-soft transition relevant to the radial buckling of MWNTs subject to hydrostatic pressure. Various buckled patterns are found to be available, and the parameters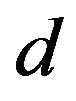 ,
, 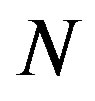 , and
, and  strongly influence which pattern is energetically favored. We have evaluated the phase boundary
strongly influence which pattern is energetically favored. We have evaluated the phase boundary 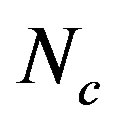 and the critical pressure
and the critical pressure  for several pairs of
for several pairs of 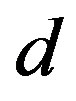 and
and , revealing that the artificial expansion of
, revealing that the artificial expansion of  results in a decrease in
results in a decrease in . Further studies will shed light on other mechanical properties of MWNTs and suggest applications based on their unique cross-sectional deformations.
. Further studies will shed light on other mechanical properties of MWNTs and suggest applications based on their unique cross-sectional deformations.
6. Acknowledgements
The fruitful discussion with S. Ghosh and M. Arroyo on the vdW-interaction formulas is greatly acknowledged. This work was supported by KAKENHI from MEXT, Japan. HS cordially thanks the Inamori Foundation and the Suhara Memorial Foundation for financial support.
REFERENCES
- D. O. Brush and B. O. Almroth, “Buckling of Bars, Plates, and Shells,” McGraw-Hill, New York, 1975.
- M. Sato and M. H. Patel, “Exact and Simplified Estimations for Elastic Buckling Pressures of Structural Pipein-Pipe Cross Sections under External Hydrostatic Pressure,” Journal of Marine Science and Technology, Vol. 12, No. 4, 2007, pp. 251-262. doi:10.1007/s00773-007-0244-y
- M. Sato, M. H. Patel and F. Trarieux, “Static Displacement and Elastic Buckling Characteristics of Structural Pipe-in-Pipe Cross-Sections,” Structural Engineering and Mechanics, Vol. 30, 2008, pp. 263-278.
- H. Shima, “Buckling of Carbon Nanotubes: A State of the Art Review,” Materials, Vol. 5, No. 1, 2012, pp. 47-84. doi:10.3390/ma5010047
- R. Zhang, Q. Wen, W. Qian, D. Sheng, Q. Zhang and F. Wei, “Superstrong Ultralong Carbon Nanotubes for Mechanical Energy Storage,” Advanced Materials, Vol. 23, No. 30, 2011, pp. 3387-3391. doi:10.1002/adma.201100344
- B. I. Yakobson, C. J. Brabec and J. Bernholc, “Nanomechanics of Carbon Tubes: Instabilities beyond Linear Response,” Physical Review Letters, Vol. 76, No. 14, 1996, pp. 2511-2514. doi:10.1103/PhysRevLett.76.2511
- C. Q. Ru, “Axially Compressed Buckling of a Doublewalled Carbon Nanotube Embedded in an Elastic Medium,” Journal of the Mechanics and Physics of Solids, Vol. 49, No. 6, 2001, pp. 1265-1279. doi:10.1016/S0022-5096(00)00079-X
- B. Ni, S. B. Sinnott, P. T. Mikulski and J. A. Harrison, “Compression of Carbon Nanotubes Filled with C60, CH4, or Ne: Predictions from Molecular Dynamics Simulations,” Physical Review Letters, Vol. 88, 2002, pp. 205505: 1-205505:4. doi:10.1103/PhysRevLett.88.205505
- M. J. Buehler, J. Kong and H. J. Gao, “Deformation Mechanism of Very Long Single-Wall Carbon Nanotubes Subject to Compressive Loading,” Journal of Engineering Materials and Technology, Vol. 126, No. 3, 2004, pp. 245-249. doi:10.1115/1.1751181
- A. Pantano, M. C. Boyce and D. M. Parks, “Mechanics of Axial Compression of Singleand Multi-Wall Carbon Nanotubes,” Journal of Engineering Materials and Technology, Vol. 126, No. 3, 2004, pp. 279-284. doi:10.1115/1.1752926
- J. Tang, J. C. Qin, T. Sasaki, M. Yudasaka, A. Matsushita and S. Iijima, “Compressibility and Polygonization of Single-Walled Carbon Nanotubes under Hydrostatic Pressure,” Physical Review Letters, Vol. 85, No. 9, 2000, pp. 1887-1889. doi:10.1103/PhysRevLett.85.1887
- A. Pantano, D. M. Parks and M. C. Boyce, “Mechanics of Deformation of Singleand Multi-Wall Carbon Nanotubes,” Journal of the Mechanics and Physics of Solids, Vol. 52, No. 4, 2004, pp. 789-821. doi:10.1016/j.jmps.2003.08.004
- J. A. Elliott, L. K. W. Sandler, A. H. Windle, R. J. Young and M. S. P. Shaffer, “Collapse of Single-Wall Carbon Nanotubes Is Diameter Dependent,” Physical Review Letters, Vol. 92, 2004, pp. 095501:1-095501:4. doi:10.1103/PhysRevLett.92.095501
- H. Shima and M. Sato, “Multiple Radial Corrugations in Multiwall Carbon Nanotubes under Pressure,” Nanotechnology, Vol. 19, 2008, pp. 495705:1-495705:8. doi:10.1088/0957-4484/19/49/495705
- J. Peng, J. Wu, K. C. Hwang, J. Song and Y. Huang, “Can a Single-Wall Carbon Nanotube Be Modeled as a Thin Shell?” Journal of the Mechanics and Physics of Solids, Vol. 56, No. 6, 2008, pp. 2213-2224. doi:10.1016/j.jmps.2008.01.004
- H. Shima and M. Sato, “Pressure-Induced Structural Transitions in Multi-Walled Carbon Nanotubes,” Physica Status Solidi (a), Vol. 206, 2009, pp. 2228-2233. doi:10.1002/pssa.200881706
- M. Sato and H. Shima, “Buckling Characteristics of Multiwalled Carbon Nanotubes under External Pressure,” Interaction and Multiscale Mechanics: An International Journal, Vol. 2, 2009, pp. 209-222.
- A. P. M. Barboza, H. Chacham and B. R. A. Neves, “Universal Response of Single-Wall Carbon Nanotubes to Radial Compression,” Physical Review Letters, Vol. 102, 2009, pp. 025501:1-025501:4. doi:10.1103/PhysRevLett.102.025501
- H. Shima, M. Sato, K. Iiboshi, S. Ghosh and M. Arroyo, “Diverse Corrugation Pattern in Radially Shrinking Carbon Nanotubes,” Physical Review B, Vol. 82, 2010, pp. 085401:1-085401:7. doi:10.1103/PhysRevB.82.085401
- M. Sato, H. Shima and K. Iiboshi, “Core-Tube Morphology of Multiwall Carbon Nanotubes,” International Journal of Modern Physics B, Vol. 24, No. 1-2, 2010, pp. 288- 294. doi:10.1142/S0217979210064228
- X. Huang, W. Liang and S. Zhang, “Radial Corrugations of Multi-Walled Carbon Nanotubes Driven by Inter-Wall Nonbonding Interactions,” Nanoscale Research Letters, Vol. 6, 2011, pp. 53-58. doi:10.1007/s11671-010-9801-0
- H. Shima, S. Ghosh, M. Arroyo, K. Iiboshi and M. Sato, “Thin-Shell Theory Based Analysis of Radially Pressurized Multiwall Carbon Nanotubes,” Computational Materials Science, Vol. 52, No. 1, 2012, pp. 90-94. doi:10.1016/j.commatsci.2011.04.005
- S. Iijima, C. Brabec, A. Maiti and J. Bernholc, “Structural Flexibility of Carbon Nanotubes,” Journal of Chemical Physics, Vol. 104, No. 5, 1996, pp. 2089-2092. doi:10.1063/1.470966
- M. R. Falvo, G. J. Clary, R. M. Taylor II, V. Chi, F. P. Brooks Jr., S. Washburn and R. Superfine, “Bending and Buckling of Carbon Nanotubes under Large Strain,” Nature, Vol. 389, 1997, pp. 582-584. doi:10.1038/39282
- P. Poncharal, Z. L. Wang, D. Ugarte and W. A. de Heer, “Electrostatic Deflections and Electromechanical Resonances of Carbon Nanotubes,” Science, Vol. 283, No. 5407, 1999, pp. 1513-1516. doi:10.1126/science.283.5407.1513
- Y. Shibutani and S. Ogata, “Mechanical Integrity of Carbon Nanotubes for Bending and Torsion,” Modelling and Simulation in Materials Science and Engineering, Vol. 12, No. 4, 2004, pp. 599-610. doi:10.1088/0965-0393/12/4/003
- A. Kutana and K. P. Giapis, “Transient Deformation Regime in Bending of Single-Walled Carbon Nanotubes,” Physical Review Letters, Vol. 97, 2006, pp. pp.245501: 1-245501:4. doi:10.1103/PhysRevLett.97.245501
- H. K. Yang and X. Wang, “Bending Stability of Multi-Wall Carbon Nanotubes Embedded in an Elastic Medium,” Modelling and Simulation in Materials Science and Engineering, Vol. 14, No. 1, 2006, pp. 99-116. doi:10.1088/0965-0393/14/1/008
- I. Arias and M. Arroyo, “Size-Dependent Nonlinear Elastic Scaling of Multiwalled Carbon Nanotubes,” Physical Review Letters, Vol. 100, 2008, pp. 085503:1-085503:4. doi:10.1103/PhysRevLett.100.085503
- Q. Wang, “Torsional Buckling of Double-Walled Carbon Nanotubes,” Carbon, Vol. 46, No. 8, 2008, pp. 1172- 1174. doi:10.1016/j.carbon.2008.03.025
- M. Arroyo and I. Arias, “Rippling and a Phase-Transforming Mesoscopic Model for Multiwalled Carbon Nanotubes,” Journal of the Mechanics and Physics of Solids, Vol. 56, No. 4, 2008, pp. 1224-1244. doi:10.1016/j.jmps.2007.10.001
- B. W. Jeong and S. B. Sinnott, “Unique Buckling Responses of Multi-Walled Carbon Nanotubes Incorporated as Torsion Springs,” Carbon, Vol. 48, No. 6, 2010, pp. 1697-1701. doi:10.1016/j.carbon.2009.12.048
- H. Shima and M. Sato, “Elastic and Plastic Deformation of Carbon Nanotoubes,” Pan Stanford Publishing, Singapore, 2012.
- R. Saito, M. S. Dresselhaus and G. Dresselhaus, “Physical Properties of Carbon Nanotubes,” World Scientific Publishing Company, 1998.
- A. Loiseau, P. Launois. P. Petit, S. Roche and J. -P. Salvetat, “Understanding Carbon Nanotubes: From Basics to Application,” Springer-Verlag, Berlin, 2006.
- C. Q. Ru, “Column Buckling of Multiwalled Carbon Nanotubes with Interlayer Radial Displacements,” Physical Review B, Vol. 62, 2000, pp. 16962-16967. doi:10.1103/PhysRevB.62.16962
- C. Y. Wang, C. Q. Ru and A. Mioduchowski, “Axially Compressed Buckling of Pressured Multiwall Carbon Nanotubes,” International Journal of Solids and Structures, Vol. 40, No. 15, 2003, pp. 3893-3911. doi:10.1016/S0020-7683(03)00213-0
- H. S. Shen, “Postbuckling Prediction of Double-Walled Carbon Nanotubes under Hydrostatic Pressure,” International Journal of Solids and Structures, Vol. 41, No. 9-10, 2004, pp. 2643-2657. doi:10.1016/j.ijsolstr.2003.11.028
- X. Q. He, S. Kitipornchai and K. M. Liew, “Buckling Analysis of Multi-Walled Carbon Nanotubes: A Continuum Model Accounting for van der Waals Interaction,” Journal of the Mechanics and Physics of Solids, Vol. 53, No. 2, 2005, pp. 303-326. doi:10.1016/j.jmps.2004.08.003
- N. Silvestre, “Length Dependence of Critical Measures in Single-Walled Carbon Nanotubes,” International Journal of Solids and Structures, Vol. 45, No. 18-19, 2008, pp. 4902-4920. doi:10.1016/j.ijsolstr.2008.04.029
- N. Silvestre, C. M. Wang, Y. Y. Zhang and Y. Xiang, “Sanders Shell Model for Buckling of Single-Walled Carbon Nanotubes with Small Aspect Ratio,” Composite Structures, Vol. 93, No. 7, 2011, pp. 1683-1691. doi:10.1016/j.compstruct.2011.01.004
- S. S. Gupta, F. G. Bosco and R. C. Batra, “Wall Thickness and Elastic Moduli of Single-Walled Carbon Nanotubes from Frequencies of Axial, Torsional and Inextensional Modes of Vibration,” Computational Materials Science, Vol. 47, 2010, pp. 1049-1059. doi:10.1016/j.commatsci.2009.12.007
- K. N. Kudin, G. E. Scuseria and B. I. Yakobson, “C2F, BN, and C Nanoshell Elasticity from ab initio Computations,” Physical Review B, Vol. 64, 2001, pp. 235406: 1-235406:10. doi:10.1103/PhysRevB.64.235406
- W. B. Lu, B. Liu, J. Wu, J. Xiao, K. C. Hwang, S. Y. Fu and Y. Huang, “Continuum Modeling of van der Waals Interactions between Carbon Nanotube Walls,” Applied Physics Letters, Vol. 94, 2009, pp. 101917:1-101917:3. doi:10.1063/1.3099023
- L. A. Girifalco, M. Hodak and R. S. Lee, “Carbon Nanotubes, Buckyballs, Ropes, and a Universal Graphitic Potential,” Physical Review B, Vol. 62, No. 19, 2000, pp. 13104-13110. doi:10.1103/PhysRevB.62.13104
- K. Koziol, M. Shaffer and A. Windle, “Three-Dimensional Internal Order in Multiwalled Carbon Nanotubes Grown by Chemical Vapor Deposition,” Advanced Materials, Vol. 17, 2005, pp. 760-763. doi:10.1002/adma.200401791
- C. Ducati, K. Koziol, S. Friedrichs, T. J. V. Yates, M. S. Shaffer, P. A. Midgley and A. H. Windle, “Crystallographic Order in Multi-Walled Carbon Nanotubes Synthesized in the Presence of Nitrogen,” Small, Vol. 2, No. 6, 2006, pp. 774-784. doi:10.1002/smll.200500513
NOTES
*Corresponding author.
1Throughout this subsection, the tilde  attached to variables indicates to take a quantity at arbitrary point within the cross section of the
attached to variables indicates to take a quantity at arbitrary point within the cross section of the  -thickness tube. On the other hand, variables with no tilde indicates the quantity just on the centroidal arc of the
-thickness tube. On the other hand, variables with no tilde indicates the quantity just on the centroidal arc of the 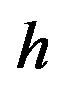 -thickness tube. See the difference between
-thickness tube. See the difference between  and
and  given in Equation (8) for a clear example.
given in Equation (8) for a clear example.
2The tube is made out of a monoatomic graphitic layer, and consequently, the notion of a tube thickness becomes elusive.
3The fact that the sum equals zero determines the functional form of .
.

