World Journal of Condensed Matter Physics
Vol.06 No.01(2016), Article ID:63710,6 pages
10.4236/wjcmp.2016.61006
Quantum Theory of Mesoscopic Fractional Electric Fields in a Cavity of Viscous Medium
Saleem Iqbal1, Salma Jabeen2, Farhana Sarwar1,3, Syed Mohsin Raza2
1Department of Mathematics, University of Balochistan, Quetta, Pakistan
2Department of Physics, University of Balochistan, Quetta, Pakistan
3Department of Mathematics, F. G. Girls Degree College, Quetta Cantt, Pakistan

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 14 January 2016; accepted 21 February 2016; published 24 February 2016
ABSTRACT
With conjecture of fractional charge quantization (quantum dipole/multiple moments), Fourier transform stretching, twisting and twigging of an electron quanta and waver strings of electron quanta, the mathematical expressions for mesoscopic fractional electron fields in a cavity of viscous medium and the associated quantum dielectric susceptibility are developed. Agreement of this approach is experimentally evidenced on barite and Fanja site molecular sieves. These findings are in conformity with experimental results of 2012 Physics Nobel prize winning scientists, Serge Haroche and David J. Wineland especially for cavity quantum electro-dynamics electron and its associated mesoscopic electric fields. The mover electron quanta strings lead to warping of space and time following the behaviour of quantum electron dynamics.
Keywords:
Mesoscopic Fractional Electric Fields, Quantum Dielectric Susceptibility, Giant Magneto Resistance (GMR), Fourier Transform (FT), Woven Strings of Electron Quanta, Warping of Space and Time Following QED (Quantum Electrodynamics)

1. Introduction
Jonscher [1] [2] studied the diverse dielectric properties extensively by using Fourier transform. The quantum behaviour of dielectricity was deciphered by exploiting the conjecture of fractional change quantization (quantum mechanical dipole moment) [3] - [5] . With this conjecture [3] - [5] , a theory of “quantum dielectricity” is floated [6] . The same theory is further extended by using the Fourier transform. The concepts of electron quanta stretching, twisting and twigging giant magneto resistance (GMR) due to fractional change distribution on twigs and the mesoscopic fractional electric fields due to woven electron strings and their corresponding twigs (sub quanta) in a cavity are evolved [7] - [9] . In this manuscript, the mesoscopic electric fields due to fractional quantization and the quantum mechanical dielectric susceptibility (imaginary part of susceptibility) are theoretically calculated and evidenced with experimental results on barite. The theory is found in agreement with experimental
results. The orientation polarizability, i.e.,  (where k is the Boltzmann’s constant, T is the temperature in Kelvin and
(where k is the Boltzmann’s constant, T is the temperature in Kelvin and 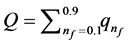 is the total charge, where
is the total charge, where 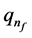 is the fragmented of fractional charges)
is the fragmented of fractional charges)
and the deformation polarizibility, i.e., 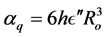 (where
(where 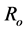 is the radial function for a space quantization) are calculated following the quantum theory of dielectricity in Faunja site-typed molecular sieves [10] . The behaviour of quantum capacitance is experimentally evidenced [10] . Dielectric anomalies [11] [12] can be resolved by considering quantum observations [6] [7] [10] .
is the radial function for a space quantization) are calculated following the quantum theory of dielectricity in Faunja site-typed molecular sieves [10] . The behaviour of quantum capacitance is experimentally evidenced [10] . Dielectric anomalies [11] [12] can be resolved by considering quantum observations [6] [7] [10] .
2. Theory of Mesoscopic Fractional Electric Fields in a Cavity of Viscous Medium
When a dielectric material at a fixed voltage is subjected to varying frequencies, polarization occurs with different magnitude of energies [1] [2] . The Debye classical model of relaxation deals with the rate equation for the polarization 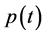 of single dipole floating in a viscous medium, i.e.,
of single dipole floating in a viscous medium, i.e.,
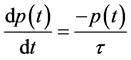 (1)
(1)
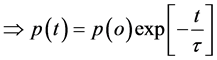 (2)
(2)
where 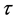 is relaxation time. But the polarization is directly proportional to electric field.
is relaxation time. But the polarization is directly proportional to electric field.
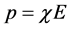 (3)
(3)
where 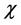 is the dielectric susceptibility and E the applied electric field. It is conjectured that electric field is fractionally quantized (quantum dipole moment) in a cavity of a viscus medium [3] - [6] .
is the dielectric susceptibility and E the applied electric field. It is conjectured that electric field is fractionally quantized (quantum dipole moment) in a cavity of a viscus medium [3] - [6] .
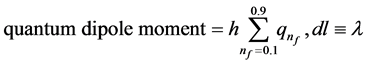 (4)
(4)
where in Equation (4), h is a plank’s constant (quantum action),  the polarized displacement,
the polarized displacement, 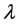 the wave length of photon causing fractional change quantization in a single electron or many electron systems and, º, the congruent operator. With momentum impact, the electron quanta is first stretched, twisted and then twigged. The momentum impact causes the oscillatory energy (quantum action) of the electron quanta to loose energy, as a consequence of which, wavelength of the quanta increases thereby maintaining
the wave length of photon causing fractional change quantization in a single electron or many electron systems and, º, the congruent operator. With momentum impact, the electron quanta is first stretched, twisted and then twigged. The momentum impact causes the oscillatory energy (quantum action) of the electron quanta to loose energy, as a consequence of which, wavelength of the quanta increases thereby maintaining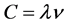 . The hypothetical wall of the electron quanta behaves like an adiabatic wall. The increase in wave length and decrease in energy or in frequency causes stretching of electron quanta (remember
. The hypothetical wall of the electron quanta behaves like an adiabatic wall. The increase in wave length and decrease in energy or in frequency causes stretching of electron quanta (remember 
Due to fractional charge quantization or sub quanta or twigs of an electron string, electric field is also fractionally quantized. Thus Equation (3) changed into

putting Equation (5) in Equation (2), we have

Equation (6) can be transformed into frequency domain by taking its Fourier transform [1] and the final results are


The imaginary part of dielectric susceptibility 

For our case, the above equation is written as follows

where 

The time dependent eigenfunction would lead to fractional quantization of electric fields within molecules or atoms. Using
One would have

where 
The fractional quantum electric fields have already been obtained [6] , i.e.,

where 



where 

where 


where r equivalent to displacement due to polarization

The relaxation time in classical wave mechanics is defined by 
mechanical system. With quantum action, energies oscillate between two arbitrary fixed points at the atomic or molecular level. Atoms or molecules when polarized and fractionally quantized behave like micro wave cavity resonators (mesoscopic fluid resonators) with their sub-quanta or twigs on an electron quanta string or many electron woven quanta string. So, a new definition of relaxation time for quantum behaviour is introduced, i.e.,

Equation (17) shows relaxation time for quantum action of atoms, molecules or ions in the viscous medium and is inversely proportional to applied frequencies. Using Equation (17) in Equation (16), i.e.,

The term 

Equation (19) is obtained by using Fourier transformed with new definition of relaxation time in a mesoscopic cavity resonator with woven electron string and their corresponding twigs (sub-quanta) for fractional charge quantization.
The Equation (18) can be re written in this form
the negative sign for eigenfunction 


where 


Taking cube of both sides

Equation (21) is the expression for mesoscopic electric fields due to fractional charge quantization of atoms, molecules or ions only due to woven electron quanta string. This observation is consistent [9] . Considering the term 
The negative sign shows quantum wells with woven electron strings of varying lengths in a cavity for mesoscopic electric fields and follows periodicity of 





Rewriting Equation (21) for molecular field

Now rewriting Equation (21) for

The term 



Taking the cube root of Equation (26) we have

Equation (27) shows that the giant magnate resistance (GMR) [8] appears as constant for imaginary part of dielectric susceptibility i.e.,

Hence, the imaginary dielectric susceptibility in a viscous medium is directly proportional to the cube root of real permittivity and square cube root of imaginary permittivity
where




3. Conclusion
The mathematical result for electrical susceptibility is obtained in terms of giant magneto resistance (GMR), real permittivity and the imaginary permittivity and the imaginary permittivity, i.e., 
GMR is given in Equation (28), the polarization at zero frequency
and 

Cite this paper
SaleemIqbal,SalmaJabeen,FarhanaSarwar,Syed MohsinRaza, (2016) Quantum Theory of Mesoscopic Fractional Electric Fields in a Cavity of Viscous Medium. World Journal of Condensed Matter Physics,06,39-44. doi: 10.4236/wjcmp.2016.61006
References
- 1. Jonscher, A.K. (1975) Physical Basis of Dielectric Loss. Nature, 253, 717-719.
http://dx.doi.org/10.1038/253717a0 - 2. Jonscher, A.K. (1983) Dielectric Relaxation in Solids. Chelsea Dielectrics Press Limited, London.
- 3. Gormani, M., Rehman, F., et al. (2006) Quantum Behaviour of Dielectric in Dolomite of Balochistan, Pakistan. Journal of the Chemical Society of Pakistan, 28, 414-416.
- 4. Yousaf, S., Raza, S.M. and Ahmed, M.A. (2008) Newly Developed Recursive Relationship for Fractional Quantum States and Associated Energy Eigen Values. Science International Lahore, Pakistan, 20, 255-260.
- 5. Yousaf, S., Raza, S.M., et al. (2008) Absorption of Radiant Energy in Water: A New Conjecture and Theory of Charge Quantization in Chromotized Water Samples. Science International Lahore, Pakistan, 20, 189-195.
- 6. Rehman, F., Raza, S.M. and Ahmed, M.A. (2009) Quantum Theory of Dielectricity and Its Application to Dolomite. Science International Lahore, Pakistan, 21, 29-32.
- 7. Saleem, I., Sarwar, F., Raza, S.M. and Rehman, A. (2015) How Fractional Charge on an Electron in the Momentum Space Is Quantized? ASRJETS, 14, 265-272.
- 8. Peter, A. and Grubber, P. (2007) Giant Magnetoresistance. APS News Letter.
- 9. Haroche, S. and Daniel, K. (1989) Cavity Quantum Electodynamics. Physics Today, 42, 24-30.
http://dx.doi.org/10.1063/1.881201 - 10. Jabeen, S., Raza, S.M., et al. (2012) Quantum Mechanical Analysis on Faujasite-Type Moleculer Sieves by Using Fermi Dirac Statistics and Quantum Theory of Dielectricity. Journal of the Chemical Society of Pakistan, 24, 251-255.
- 11. Tu, C., Siny, I.G. and Schmidt, V.H. (1994) Sequence of Dielectric Anomalies and High-Temperature Relaxation Behavior in Na1/2Bi1/2TiO3. Physical Review B, Condensed Matter, 49, 11550-11559.
http://dx.doi.org/10.1103/PhysRevB.49.11550 - 12. Christen, H.M., Mannhart, J., et al. (1994) Dielectric Properties of Spuutered Sr1/2TiO3 Films. Physical Review B, 49, 120905-12104.
http://dx.doi.org/10.1103/PhysRevB.49.12095









