World Journal of Condensed Matter Physics
Vol.05 No.04(2015), Article ID:61512,18 pages
10.4236/wjcmp.2015.54031
Decoupling the Electrical and Entropic Contributions to Energy Transfer from Infrared Radiation to a Power Generator
Aidan L. Gordon, Yosyp Schwab, Brian N. Lang, Graham P. Gearhart, Tara R. Jobin, Justin M. Kaczmar, Zachary J. Marinelli, Harkirat S. Mann, Brian C. Utter*, Giovanna Scarel*
Department of Physics and Astronomy, James Madison University, Harrisonburg, USA

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 19 October 2015; accepted 24 November 2015; published 27 November 2015

ABSTRACT
The interaction between infrared radiation and a power generator device in time is studied as a route to harvest infrared, and possibly other electromagnetic radiations. Broadening the spectrum of the usable electromagnetic spectrum would greatly contribute to the renewable and sustainable energy sources available to humankind. In particular, low frequency and low power radiation is important for applications on ships, satellites, cars, personal backpacks, and, more generally, where non-dangerous energy is needed at all hours of the day, independent of weather conditions. In this work, we identify an electric and an entropic contribution to the energy transfer from low power infrared radiation to the power generator device, representing electrical and thermal contributions to the power generation. The electric contribution prevails, and is important because it offers multiple ways to increase the voltage produced. For example, placing black-colored gaffer tape on the illuminated face doubles the voltage produced, while the temperature difference, thus the entropic contribution, is not sensitive to the presence of the tape. We recognize the electric contribution through the fast changes it imparts to the voltage output of the power generator device, which mirror the instabilities in time of the infrared radiation. The device thus acts as sensor of the infrared radiation’s behavior in time. On the other hand, we distinguish the entropic contribution through the slow changes it causes to the voltage output of the power generator device, which reflect the relative delay with which the two faces of the device respond to thermal perturbations.
Keywords:
Infrared, Power Generators, Energy Harvesting, Electric Contribution

1. Introduction
A power generator (PG) device can be used to harvest electromagnetic (EM) and, in particular, infrared (IR) radiation.
The interaction between the radiation and the device is a complex phenomenon of energy transfer (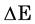 ). The rate of
energy transferred from the EM radiation per area a of the device is the Poynting vector
). The rate of
energy transferred from the EM radiation per area a of the device is the Poynting vector
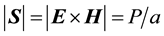 , where
, where
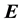 and
and
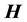 are the
electric and magnetic fields, respectively, and P is power. Therefore, because of
are the
electric and magnetic fields, respectively, and P is power. Therefore, because of
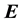 and
and
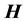 , the interaction between
radiation and device involves the charges on the device surface. Electromagnetic radiation with large frequency
, the interaction between
radiation and device involves the charges on the device surface. Electromagnetic radiation with large frequency
 interacts through, e.g., Compton scattering [1], X-ray photoelectron effect [2], photoelectric effect [3],
photovoltaic effect [4], and plasmon generation [5]. Electromagnetic radiation with low frequency
interacts through, e.g., Compton scattering [1], X-ray photoelectron effect [2], photoelectric effect [3],
photovoltaic effect [4], and plasmon generation [5]. Electromagnetic radiation with low frequency
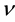 , e.g. in
the IR and microwave regions, resonates with molecular rotation and oscillation frequencies [6] or generates
polaritons [7]-[10]. When the photon frequency
, e.g. in
the IR and microwave regions, resonates with molecular rotation and oscillation frequencies [6] or generates
polaritons [7]-[10]. When the photon frequency
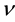 or
or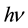 energy , where h is Planck’s constant, do not match with the
frequency or the energy of a specific phenomenon involving charges, the energy of the EM radiation contributes to
temperature T changes. In photosynthesis this phenomenon is known as internal conversion [11].
energy , where h is Planck’s constant, do not match with the
frequency or the energy of a specific phenomenon involving charges, the energy of the EM radiation contributes to
temperature T changes. In photosynthesis this phenomenon is known as internal conversion [11].
We name the energy transferred from the EM radiation to a PG device through the action of the electric
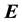 and
and
 magnetic fields as the electric contribution:
magnetic fields as the electric contribution:
 , (1)
, (1)
where q is the charge and V voltage. We name the energy transferred through changes in temperature T
at entropy
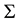 as the entropic contribution:
as the entropic contribution:
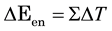 . (2)
. (2)
The energy transferred from IR and microwave radiation is usually associated with the entropic contribution in Equation (2). For example, sun light gives the sensation of temperature increase, and therefore of warmth, on human skin. The microwave radiation in microwave ovens is used to increase the temperature, i.e., cook food and heat-up beverages. Similarly, through laser radiation it is possible to increase temperature, even with nanoscale control [12].
The effects of the electric contribution
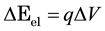 are less apparent in the energy transfer from low frequency and
low power EM radiation. In the current literature, the existence of the electric contribution is
acknowledged [13]-[16], but the interplay between the electric and the entropic contributions is not
investigated. Specifically, there is a lack of knowledge of 1) the possibility of decoupling the electric
from the entropic contributions, 2) the factors that promote the electric over the entropic contribution,
or vice-versa, 3) the existence of a threshold where one contribution prevails over the other, and 4) the
benefits of the electric over the entropic contributions, or vice-versa.
are less apparent in the energy transfer from low frequency and
low power EM radiation. In the current literature, the existence of the electric contribution is
acknowledged [13]-[16], but the interplay between the electric and the entropic contributions is not
investigated. Specifically, there is a lack of knowledge of 1) the possibility of decoupling the electric
from the entropic contributions, 2) the factors that promote the electric over the entropic contribution,
or vice-versa, 3) the existence of a threshold where one contribution prevails over the other, and 4) the
benefits of the electric over the entropic contributions, or vice-versa.
In this work we aim at decoupling
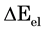 and
and
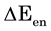 in a PG device illuminated by low power IR radiation. The device
is expected to respond to the entropic contribution by exploiting the Seebeck effect [17]-[20], i.e.
producing a voltage difference
in a PG device illuminated by low power IR radiation. The device
is expected to respond to the entropic contribution by exploiting the Seebeck effect [17]-[20], i.e.
producing a voltage difference
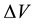 directly proportional to the temperature difference
directly proportional to the temperature difference
 applied to the
two faces of the PG device, so that
applied to the
two faces of the PG device, so that
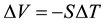 . Here, S is the Seebeck coefficient. On the other hand, we expect
the PG device to also respond to the electric contribution through its capacitor-type of structure
consisting of a sequence of conducting and insulating layers, as illustrated in Figure 1. For
the device used in this work, the sequence is, starting from the face illuminated by the IR radiation,
a copper (Cu) plate, a layer of pillars made of adoped Bi2Te3-based alloy, another Cu plate, and,
finally, an alumina (AlO) plate. On the Cu plates there are electrons whose surface density
. Here, S is the Seebeck coefficient. On the other hand, we expect
the PG device to also respond to the electric contribution through its capacitor-type of structure
consisting of a sequence of conducting and insulating layers, as illustrated in Figure 1. For
the device used in this work, the sequence is, starting from the face illuminated by the IR radiation,
a copper (Cu) plate, a layer of pillars made of adoped Bi2Te3-based alloy, another Cu plate, and,
finally, an alumina (AlO) plate. On the Cu plates there are electrons whose surface density
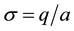 is sensitive to the
is sensitive to the
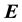 and
and
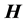 fields of the IR radiation, thus enabling changes in the electric
contribution
fields of the IR radiation, thus enabling changes in the electric
contribution
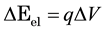 .
.
In our experiment, the voltage difference
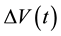 , generated by the PG device through the electric
and the entropic contributions, and the temperature difference
, generated by the PG device through the electric
and the entropic contributions, and the temperature difference
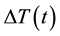 , related to the entropic contribution,
are observed as a function of time t. The measurements capture the first minutes after starting the
illumination, and in the 30 hours thereafter. We hypothesize that changes in
, related to the entropic contribution,
are observed as a function of time t. The measurements capture the first minutes after starting the
illumination, and in the 30 hours thereafter. We hypothesize that changes in
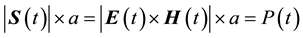 slowly vary the amplitude
of the surface electron density
slowly vary the amplitude
of the surface electron density
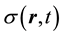 . To prove this hypothesis, we study the power
. To prove this hypothesis, we study the power
 of the IR radiation
using a power-meter sensor and compare its behavior with that of
of the IR radiation
using a power-meter sensor and compare its behavior with that of
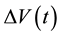 and
and
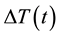 .
.
Summarizing, we consider the total energy transfer in time from the IR radiation to a PG device as the sum of the electric and the entropic contributions such that:
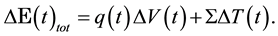 (3)
(3)

Figure 1.Schematics of the away (a) and toward (b) architectures of the PG device. In the away architecture (a) the face of the PG device exposed to the IR radiation is free from contact with the sample holder. In the toward architecture (b), the il-luminated face is in contact with the sample holder. The PG device is a stack of conducting (Cu plates), non-conducting (AlO plate), and semiconducting (set of pillars made of a doped Bi2Te3-based alloy) layers.
Consequently, we assume the voltage difference
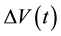 produced by the PG device in time to be the
addition of two summands:
produced by the PG device in time to be the
addition of two summands:
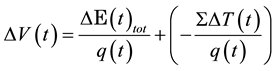 . (4)
. (4)
The first summand relates to the electric and the second to the entropic contribution.
The term
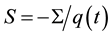 can be associated with the Seebeck coefficient.
can be associated with the Seebeck coefficient.
We will show that with the low power irradiation employed in our measurements, the electric contribution can be
decoupled from the entropic contribution, and largely dominates. Decoupling the two contributions is important for
IR energy harvesting, because the electric contribution offers a variety of ways to increase the voltage produced
by the PG device, e.g. by placing black-colored gaffer tape on the illuminated face of the device, as we will
show in Appendix-1. The entropic contribution, instead, is limited by the temperature difference
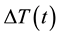 established
between the two faces of the PG device.
established
between the two faces of the PG device.
2. Experimental Set-Up
For this experiment, continuous broadband IR radiation in the middle IR (MIR) region (i.e. frequency between
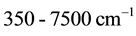 ,
or wavelength between
,
or wavelength between
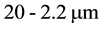 ) was produced by a globar (Q301) source. The power
) was produced by a globar (Q301) source. The power
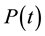 of the IR radiation was monitored
versus time using a power-meter sensor Coherent Power Max RS PS19, sensitive to the
of the IR radiation was monitored
versus time using a power-meter sensor Coherent Power Max RS PS19, sensitive to the
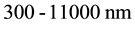 wavelength range, and to
the 100 μW to 1 W power range.
wavelength range, and to
the 100 μW to 1 W power range.
The voltage difference
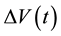 , generated by the electric and the entropic contributions to
, generated by the electric and the entropic contributions to
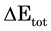 according to Equation (4),
was produced using a PG device 07111-9L31-04B by Custom Thermoelectric Inc. The device consists of a sequence of
layers: 1) a Cu plate on the face exposed to the IR radiation, 2) a layer of pillars made of a doped Bi2Te3-based
alloy, 3) another Cu plate, and 4) an AlO plate. The Cu plate not illuminated by the IR radiation is non-continuous,
as highlighted through the white hole in the left side of Figure 1(a) and Figure 1(b). In the away architecture,
illustrated in Figure 1(a), we established the continuity by placing the sample holders, made of anodized aluminum,
in contact with the non-continuous Cu plate. Thus, the Cu plate together with the sample holder behaves as the
electrode of a capacitor. The illuminated Cu plate, instead, was free of contact with the sample holder. In the
toward architecture, pictured in Figure 1(b), we left non-continuous the Cu plate opposite to the IR radiation,
while the illuminated Cu plate was kept in contact with the sample holder.
according to Equation (4),
was produced using a PG device 07111-9L31-04B by Custom Thermoelectric Inc. The device consists of a sequence of
layers: 1) a Cu plate on the face exposed to the IR radiation, 2) a layer of pillars made of a doped Bi2Te3-based
alloy, 3) another Cu plate, and 4) an AlO plate. The Cu plate not illuminated by the IR radiation is non-continuous,
as highlighted through the white hole in the left side of Figure 1(a) and Figure 1(b). In the away architecture,
illustrated in Figure 1(a), we established the continuity by placing the sample holders, made of anodized aluminum,
in contact with the non-continuous Cu plate. Thus, the Cu plate together with the sample holder behaves as the
electrode of a capacitor. The illuminated Cu plate, instead, was free of contact with the sample holder. In the
toward architecture, pictured in Figure 1(b), we left non-continuous the Cu plate opposite to the IR radiation,
while the illuminated Cu plate was kept in contact with the sample holder.
The temperatures
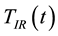 and
and
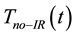 of the illuminated and non-illuminated faces, respectively, of the PG
device were measured using OMEGA type E Ni-Cr/Cu-Ni thermocouple probes. The temperature
difference
of the illuminated and non-illuminated faces, respectively, of the PG
device were measured using OMEGA type E Ni-Cr/Cu-Ni thermocouple probes. The temperature
difference
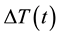 was obtained as
was obtained as
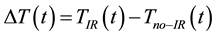 . The trends of
. The trends of
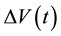 ,
,
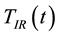 and
and
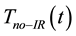 were measured using Keithley 2000
multi-meters. The data were collected using LabView 2012 and a National Instruments PXI-1042q
communications chassis.
were measured using Keithley 2000
multi-meters. The data were collected using LabView 2012 and a National Instruments PXI-1042q
communications chassis.
During the measurements, the PG device and the power-meter sensor were positioned vertically and at an angle
of incidence
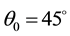 with respect to the IR radiation. The instrumentation was placed in a closed sample compartment
purged with N2 to prevent disturbances for the whole duration of the measurements versus time
of
with respect to the IR radiation. The instrumentation was placed in a closed sample compartment
purged with N2 to prevent disturbances for the whole duration of the measurements versus time
of
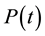 ,
,
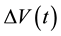 ,
,
 and
and
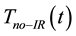 [21]. The experimental parameters are summarized in Table 1.
[21]. The experimental parameters are summarized in Table 1.
3. Results and Discussion
a) Behavior in time of
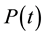
In the 100 seconds immediately after starting the illumination of the power-meter sensor,
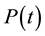 , displayed in Figure 2(a), rises exponentially as follows:
, displayed in Figure 2(a), rises exponentially as follows:
Table 1.Summary of the experimental parameters in the main text and in the appendices.

Figure 2. (a) Exponential rise, as in Equation (5), of the power
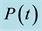 versus time of the IR radiation emitted by the globar source in the 100 seconds immediately after starting the illumination of the power-meter sensor; (b) Graph of
versus time of the IR radiation emitted by the globar source in the 100 seconds immediately after starting the illumination of the power-meter sensor; (b) Graph of
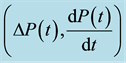 in the same time interval of (a) reporting the slope and amplitude
in the same time interval of (a) reporting the slope and amplitude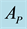 ; (c) The power
; (c) The power
 in the 50 hours after starting the illumination of the power-meter sensor; (d) Same as (c), with the vertical scale expanded to highlight the sinusoidal instability region fitted with Equation (6). The zero of the time-scale coincides with the start of the illumination with the IR radiation. The parameters
in the 50 hours after starting the illumination of the power-meter sensor; (d) Same as (c), with the vertical scale expanded to highlight the sinusoidal instability region fitted with Equation (6). The zero of the time-scale coincides with the start of the illumination with the IR radiation. The parameters
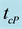 and
and
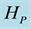 are labeled; (e) Graph of
are labeled; (e) Graph of
 in the 50 hours after starting the illumination of the power-meter sensor.
in the 50 hours after starting the illumination of the power-meter sensor.
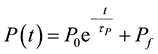 , (5)
, (5)
where
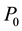 is the offset,
is the offset,


reported in Table 2. The slope of the

of


the




along the horizontal scale of the

ing the illumination of the power-meter sensor, the power


where
















inferred from

with frequency



We observed that the power


Table 2. (Top rows) Fitting parameters



























To sketch
the electric field


turn,









tion through Jones matrices [23] -[25] . Thus,
ence system, phases, and positions in the 2D plane can be obtained by selecting magnitude and sign of



With this choice of

ing to


sities,




In the subsequent 30 hours, from Equation (6) we expect

that

tion 3(a). With the choice of


Here,








tion from equilibrium, respectively, we obtain


While












the Cu plate as
C, we expect









Summarizing, we expect





Figure 3. Panels (a), (b), and (c) correspond to the away architecture and refer to the 400 seconds immediately following the start the illumination of the PG device with IR radiation. (a) Voltage difference






Table 3. Fitting parameters










Figure 4. Panels (a) and (b) correspond to the away architecture and refer to the 400 seconds immediately following the start of the illumination of the PG device with IR radiation. (a) Temperature difference









In this expression,









Figure 5. Panels (a), (b), (c), and (d) correspond to data collected from the toward architecture in the whole time span of about 30 hours following the start of the illumination of the PG device with IR radiation. (a) Voltage difference












and unstable fixed points [20] alternate in a complex fashion without periodicity.
Since the time-dependence is enclosed in a hyperbolic secant function, we name the instability in






Here we highlight the correlations existing between the power



We found that Equation (11), used to fit the hyperbolic instability in


Figure 6. Panels (a), (b), and (c) correspond to data collected from the away architecture in the whole time span of about 30 hours following the start of the illumination of the PG device with IR radiation. (a) Voltage difference








Table 4. Parameters of





illumination of the PG device with IR radiation, can be a solution of the equation:



4. Summary and Significance

Figure 7. “Acceleration” of the inverse voltage



Acknowledgements
This work was supported by the U.S. Office of Naval Research (awards # N000141410378 N000141512158), JMU 4-VA Consortium (2013), Thomas F. Jeffress and Kate Miller Jeffress Memorial Trust (grant # J-1053), the Madison Trust―Fostering Innovation and Strategic Philanthropy-Innovation Grant 2015, the JMU Program of Grants for Faculty Assistance 2014, the JMU Center for Materials Science, and the JMU Department of Physics and Astronomy. The authors thank Dr. A. V. Zenkevich (Moscow Institute of Physics and Technology), Prof. G. Casati (University of Insubria, Italy), and Prof. D. J. Lawrence (JMU) for fruitful discussions.
Cite this paper
Aidan L.Gordon,YosypSchwab,Brian N.Lang,Graham P.Gearhart,Tara R.Jobin,Justin M.Kaczmar,Zachary J.Marinelli,Harkirat S.Mann,Brian C.Utter,GiovannaScarel, (2015) Decoupling the Electrical and Entropic Contributions to Energy Transfer from Infrared Radiation to a Power Generator. World Journal of Condensed Matter Physics,05,301-318. doi: 10.4236/wjcmp.2015.54031
References
- 1. Christillin, P. (1986) Nuclear Compton Scattering. Journal of Physics G: Nuclear and Particle Physics, 12, 837-851.
http://dx.doi.org/10.1088/0305-4616/12/9/008 - 2. Siegbahn, K.M. (1981) Electron Spectroscopy for Atoms, Molecules and Condensed Matter. Nobel Lecture, 8 December.
- 3. Einstein, A. (1905) Concerning an Heuristic Point of View toward the Emission and Transformation of Light. Annalen der Physik, 17, 132-148.
http://dx.doi.org/10.1002/andp.19053220607 - 4. Becquerel, E. (1839) Mémoire sur les effets électriques produits sous l’influence des rayons solaires. Comptes Rendus, 9, 561-567.
- 5. Burdick, G.A. (1963) Energy Band Structure of Copper. Physical Review, 129, 138-150.
http://dx.doi.org/10.1103/PhysRev.129.138 - 6. Newnham, R.E., Jang, S.J., Xu, M. and Jones, F. (1991) Fundamental Interaction Mechanisms between Microwaves and Matter. Ceramic Transactions, 21, 51-67.
- 7. Kliewer, K.L. and Fuchs, R. (1966) Optical Modes of Vibration in an Ionic Crystal Slab including Retardation. I. Nonradiative Region. Physical Review, 144, 495-503.
http://dx.doi.org/10.1103/PhysRev.144.495 - 8. Kliewer, K.L. and Fuchs, R. (1966) Optical Modes of Vibration in an Ionic Crystal Slab including Retardation. II. Radiative Region. Physical Review, 150, 573-588.
http://dx.doi.org/10.1103/PhysRev.150.573 - 9. Fuchs, R., Kliewer, K.L. and Pardee, W.J. (1966) Optical Properties of an Ionic Crystal Slab. Physical Review, 150, 589-596.
http://dx.doi.org/10.1103/PhysRev.150.589 - 10. Berreman, D.W. (1963) Infrared Absorption at Longitudinal Optic Frequency in Cubic Crystal Films. Physical Review, 130, 2193-2198.
http://dx.doi.org/10.1103/PhysRev.130.2193 - 11. Gest, H. (2002) History of the Word Photo Synthesis and Evolution of Its Definition. Photosynthesis Research, 73, 7-10.
http://dx.doi.org/10.1023/A:1020419417954 - 12. Kuesco, G., Mauer, P.C., Yao, N.Y., Kubo, M., Noh, H.J., Lo, P.K., Park, H. and Lukin, M.D. (2013) Nanometre-Scale Thermometry in a Living Cell. Nature, 500, 54-59.
http://dx.doi.org/10.1038/nature12373 - 13. Jameson, A.D., Tomaino, J.L., Lee, J.-S., Khitrova, G., Gibbs, H.M., Böttge, C.N., Klettke, A.C., Kira, M. and Koch, S.W. (2014) Direct Measurement of Light-Matter Energy Exchange inside a Microcavity. Optica, 1, 276-280.
http://dx.doi.org/10.1364/OPTICA.1.000276 - 14. Kumar, A., Low, T., Fung, K.H., Avouris, P. and Fang, N.X. (2015) Tunable Light-Matter Interaction and the Role of Hyperbolicity in Graphene-hBN System. Nano Letters, 15, 3172-3180.
http://dx.doi.org/10.1021/acs.nanolett.5b01191 - 15. Richter, C.-P., Rajguru, S., Stafford, R. and Stock, S.R. (2013) Radiant Energy during Infrared Neural Stimulation at the Target Structure. Proceedings of SPIE, 8565, Article ID: 85655P.
http://dx.doi.org/10.1117/12.2013849 - 16. Eisen, D., Janssen, D., Chen, X., Choa, F.-S., Kotsov, D. and Fan, J. (2013) Closing a Venus Flytrap with Electrical and Mid-IR Photon Stimulations. Proceedings of SPIE, 8565, Article ID: 85655I.
http://dx.doi.org/10.1117/12.2005351 - 17. Tritt, T.M., Böttner, H. and Chen, L. (2008) Thermoelectrics: Direct Solar Thermal Energy Conversion. MRS Bulletin, 33, 366-368.
http://dx.doi.org/10.1557/mrs2008.73 - 18. Tritt, T.M. (2011) Thermoelectric Phenomena, Materials, and Applications. Annual Review of Materials Research, 41, 433-438.
http://dx.doi.org/10.1146/annurev-matsci-062910-100453 - 19. Bell, L.E. (2008) Cooling, Heating, Generating Power, and Recovering Waste Heat with Thermoelectric Systems. Science, 321, 1457-1461.
http://dx.doi.org/10.1126/science.1158899 - 20. Vining, C.B. (2009) An Inconvenient Truth about Thermoelectrics. Nature Materials, 8, 83-85.
http://dx.doi.org/10.1038/nmat2361 - 21. Schwab, Y., Mann, H.S., Lang, B.N., Lancaster, J.L., Parise, R.J., Vincent-Johnson, A.J. and Scarel, G. (2013) Infrared Power Generation in an Insulated Compartment. Complexity, 19, 44-55.
http://dx.doi.org/10.1002/cplx.21484 - 22. Strogatz, S.H. (1994) Nonlinear Dynamics and Chaos. Westview Press, Cambridge, MA.
- 23. Jones, R.C. (1941) A New Calculus for the Treatment of Optical Systems. I. Description and Discussion of the Calculus. Journal of the Optical Society of America, 31, 488-493.
http://dx.doi.org/10.1364/JOSA.31.000488 - 24. Jones, R.C. (1941) A New Calculus for the Treatment of Optical Systems. III. The Sohncke Theory of Optical Activity. Journal of the Optical Society of America, 31, 500-503.
http://dx.doi.org/10.1364/JOSA.31.000500 - 25. Jones, R.C. (1942) A New Calculus for the Treatment of Optical Systems. IV. Journal of the Optical Society of America, 32, 486-493.
http://dx.doi.org/10.1364/JOSA.32.000486 - 26. Korteweg, D.J. and de Vries, G. (1895) On the Change of Form of Long Waves Advancing in a Rectangular Canal and a New Type of Long Stationary Waves. Philosophical Magazine Series, 39, 422-443.
http://dx.doi.org/10.1080/14786449508620739 - 27. Smaoui, N. and Zribi, M. (2009) A Finite Dimensional Control of the Dynamics of the Generalized Korteweg-de Vries Burgers Equation. Applied Mathematics & Information Sciences, 3, 207-221.
- 28. Jiang, Y., Tian, B., Liu, W.-J., Sun, K. and Qu, Q.-X. (2010) Soliton Solutions for a Variable-Coefficient Korteweg-de Vries Equation in Fluids and Plasmas. Physica Scripta, 82, Article ID: 055008.
http://dx.doi.org/10.1088/0031-8949/82/05/055008 - 29. Vlieg-Hulstman, M. and Halford, W.D. (1995) Exact Solutions to KdV Equations with Variable Coefficients and/or Nonuniformities. Computers & Mathematics with Applications, 29, 39-47.
http://dx.doi.org/10.1016/0898-1221(94)00205-Y - 30. Mann, H.S., Schwab, Y., Lang, B.N., Lancaster, J.L., Parise, R.J. and Scarel, G. (2014) Effective Thermoelectric Power Generation in an Insulated Compartment. World Journal of Condensed Matter Physics, 4, 153-165.
http://dx.doi.org/10.4236/wjcmp.2014.43020
Appendix-1
To highlight the effects of the entropic contribution and decouple it from the electric contribution, we collected the voltage difference




In the 400 seconds immediately following the start the activation of the PG device by either conductive heat transfer or IR radiation, we measured the rate of increase of















Figure A1. (a) Rate of increase of the voltage difference (







value of the ratio R is larger when the PG device is activated by IR radiation through the electric contribution.
In the 400 seconds immediately following the start the activation of the PG device by either conductive heat transfer or IR radiation, we also measured the jump in voltage





In the time span of about 50 hours following the start of the activation of the PG device with conductive heat transfer from a 100 W resistor, the voltage difference















The results in Figures A1-A3, together with those of Figures 3-5, further support that the electric and the entropic contribution to energy transfer from low power IR radiation to the PG device are decoupled.
Appendix-2
Figure 6 shows the hyperbolic instability revealed in the voltage difference






Figure A2. Jump in voltage




Figure A3. Panels (a), (b), (c), and (d) correspond to data collected from the away architecture in the whole time span of about 50 hours following the start of the activation of the PG device with conductive heat transfer from a 100 W resistor. (a) Voltage difference




Figure A4. (a) Averages of the critical time (







the layer of tape facing the IR radiation, the surface density




















We summarize the findings in Figure A4 as follows: the hyperbolic instability in

phenomenon, which is linked with the sinusoidal instability in the power

NOTES

*Corresponding authors.


