World Journal of Condensed Matter Physics
Vol.05 No.03(2015), Article ID:58600,18 pages
10.4236/wjcmp.2015.53018
Modeling of a Cubic Antiferromagnetic Cuprate Super-Cage
Hans Hermann Otto
Materialwissenschaftliche Kristallographie, TU Clausthal, Clausthal-Zellerfeld, Germany
Email: hhermann.otto@web.de
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 18 May 2015; accepted 2 August 2015; published 5 August 2015
ABSTRACT
Convex polyhedral cuprate clusters are being formed through lateral frustration when the a and c lattice parameters of the tetragonal ACuO2 infinite layer structure will become identical by substitution of a large cation (A = Ba2+). However, the corner-shared CuO2 plaquettes of the infinite network suffer a topotactic rearrangement forming edge-connected units, for instance Cu18O24 cages (polyhedron notation [4641238]) with <90˚ ferromagnetic super-exchange interaction as found in cubic BaCuO2. Cage formation via a hypothetical tetragonal BaCuO2 compound (space group P4/ nmm) will be discussed. The possibility to construct a cuprate super-cage with m3m symmetry (polyhedron notation [4641242438]) is being reported. This super-cage still consists of edge-con- nected CuO2 plaquettes when fully decorated with copper ions, but with different curvatures, arranged in circles of 9.39 Å of diameter with 139.2˚ Cu-O-Cu antiferromagnetic super-exchange interaction. On the one hand, the realization of such a quite stable cuprate super-cage as a candidate for high-Tc superconductivity depends on whether a template of suitable size such as the 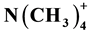 cation or C(CH3)4 enables its formation, and on the other hand the cage can further be stabilized by highly charged cations located along the [111] direction. Synthesis options will be proposed based on suggested cage formation pathways. An X-ray powder pattern was calculated for a less dense cluster structure of Im3m space group with a lattice parameter of a = 14.938 Å and two formula units of Cu46O51 to facilitate future identification. Characteristic X-ray scattering features as identification tool were obtained when the electron distribution of the hollow polyhedron was approximated with electron density in a spherical shell.
cation or C(CH3)4 enables its formation, and on the other hand the cage can further be stabilized by highly charged cations located along the [111] direction. Synthesis options will be proposed based on suggested cage formation pathways. An X-ray powder pattern was calculated for a less dense cluster structure of Im3m space group with a lattice parameter of a = 14.938 Å and two formula units of Cu46O51 to facilitate future identification. Characteristic X-ray scattering features as identification tool were obtained when the electron distribution of the hollow polyhedron was approximated with electron density in a spherical shell.
Keywords:
Super-Cage, Convex Polyhedra, Cuprate, BaCuO2, T-CuO, Superconductivity, Bond Strength, Frustration, X-Ray Pattern

1. Introduction
Almost thirty years of intense research on high-Tc superconductors have elapsed this year. Since the discovery of high-Tc superconductivity by Bednorz and Müller in 1986 [1] , rich results have been obtained in distinct fields of science and technology, physics, solid state chemistry, material science and crystallography. Many comprehensive papers [2] - [4] report on the great variety of new crystal structures of superconducting compounds, often showing an optimum hole doping as intrinsic quality. Owing to the ability of the d9 transition metal ion to form, apart from 3D networks, chains, ladders, and small and medium clusters, copper compounds are among the most interesting phases. Low-dimensional quantum spin systems are of considerable theoretical and experimental interest together with new applications to which they may lead. The Cu2+ ion owes its network forming property to a high electronegativity, similar to Si4+, but in contrast to the tetrahedral networks of Si4+, Cu2+ mainly forms oxo-compounds with chains and networks of connected “octahedra”. In the crystal structure of CuSiO3 [5] [6] , isostructural to CuGeO3, such “octahedral” edge-connected chains are combined with ideally stretched corner-connected silicate tetrahedral ones.
Cupric oxide cages of both corner-connected and edge-shared CuO octahedra, formed around 6-membered silicate rings and H2O, are found in the crystal structure of the gemstone dioptase, Cu6Si6O18∙6H2O. Crystal water can escape on heating trough openings in the cages. Whereas magnetic properties have been extensively investigated, the synthesis of pure dioptase is not successful yet but may benefit from ideas of cluster formation expressed in this work.
It came as a great surprise when Sigrist et al. [7] succeeded in synthesizing Ca0.86Sr0.14CuO2, a very simple compound of tetragonal symmetry (space group P4/mmm) with lattice parameters of a = 3.8611(2) Å and c = 3.1995(2) Å and Z = 1, which they named parent structure of the layered high-temperature superconductors. Other authors call it infinite-layer or all-layer compound owing to the feature that the structure may be described as oxygen-deficient perovskite that has lost a complete oxygen layer thus making the large Ca2+ or Sr3+ cations [8] -coordinated instead of [12] -coordinated and leaving infinite CuO2 layers with square-coordinated Cu2+ instead of octahedral layers. Figure 1 depicts the CuO2 net of the parent structure, one of the building blocks of most high-Tc superconducting compounds. It should be noted that the CuO4 squares in the infinite CuO2 layers are corner-connected.
Recently, Siemons [8] discovered that cupric oxide could be epitaxially grown as thin film on a (100) SrTiO3 substrate in a tetragonally elongated rocksalt structure with lattice parameters of a = 3.905 Å and c = 5.32 Å, as a result of the Jahn-Teller effect [9] . The existence of such an edge-connected T-CuO net is exciting as it will serve to support my ideas of cagey cluster formation and synthesis routes. Without substrate support, the planar CuO net suffers folding in two directions resulting in the monoclinic tenorite structure. The folding of the T-CuO net may be accompanied by a latent Cu1+-Cu3+ disproportionation, which can help to better understand
Figure 1. Corner-connected cuprate plaquettes, representing the building units of high-Tc superconductors.
the high-Tc multiferroic properties and frustration induced spiral spin-ordering of this compound.
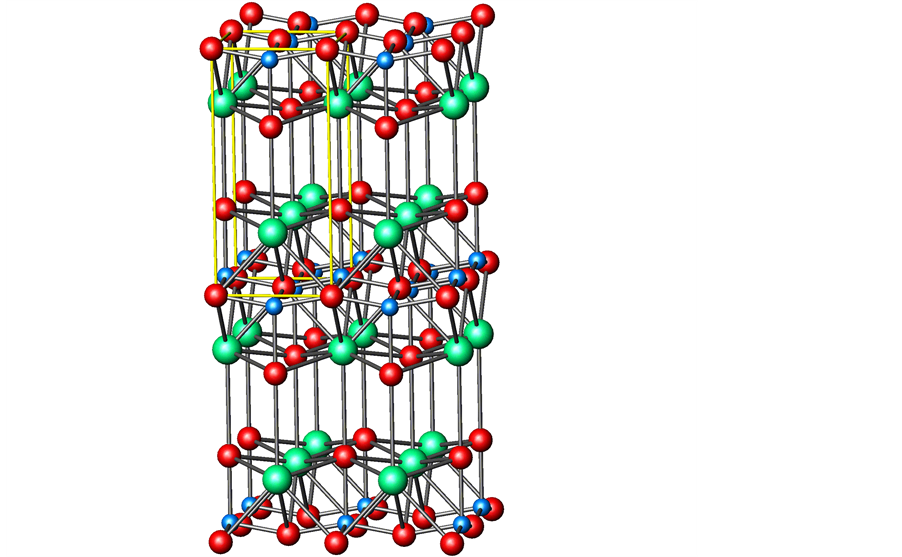
Turning back to the parent structure, the already known crystal structures of similar compounds of the larger group II elements Sr and Ba are very complex and less dense compared to the parent structure. The cubic compound BaCuO2 showing distinct copper-oxygen clusters has really a large lattice parameter of a = 18.2855(3) Å and contains Z = 90 formula units in its unit cell. In contrast to the infinite layer structure, the CuO4 quadrilaterals of the clusters are edge-connected. The 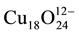 polyhedral cluster is depicted in Figure 2.
polyhedral cluster is depicted in Figure 2.
The question arises, why BaCuO2 does not exist in the simple prototypic structure of the parent compound, explicitly disregarding air-sensitive and highly strained BaCuO2 epitaxial layers. Since the <90˚ super-exchange interaction of edge-connected clusters is unfavourable for the development of superconducting properties, the idea emerges to construct a super-cage cluster of cuprate units with larger radius of curvature and then >90˚ Cu-O-Cu antiferromagnetic super-exchange interaction favouring high-Tc superconductivity.
Promising new opportunities such as crystal structure prediction from first principles (Woodley and Catlow [10] ) or application of advanced tiling theory for the systematic generation of 4-connected crystalline networks (Forster et al. [11] ) have stimulated condensed matter sciences. In addition, the recent discovery of a new class of convex Goldberg polyhedra (Schein and Gayed [12] ) should encourage scientists to synthesize such cages. For example, the successful synthesis of earlier predicted, yet not perfectly smooth B40 boronspherene shows what possible is [13] . The cuprate super-cage may as well a worthwhile object of synthesis effort in the near future.
A summary assessment of synthesis routes and crystal chemistry of infinite-layer compounds in contrast to the cubic cluster compound BaCuO2 suggests an explanation of cluster formation, finally leading to the proposal of a cuprate super-cage structure.
2. Planar Cuprate Networks versus Polyhedral Clusters
The formation and crystal chemistry of two ACuO2 structure types are summarized in the appendix: the simple “infinite-layer” Ca0.86Sr0.14CuO2 structure type and the very complex BaCuO2 type. Ca0.86Sr0.14CuO2 is tetragonal, space group P4/mmm, with lattice parameters of a = 3.8611(2) Å, c = 3.1995(2) Å. In contrast, the BaCuO2 structure is cubic, space group Im3m, but shows a very large lattice parameter of a = 18.2855(3) Å, obviously indicative of a conflicting formation scenario. A series of compounds are known with infinite-layer structure type with steadily increasing c lattice parameters, obtained by the substitution of Ca2+ by the larger Sr2+ and Ba2+ ions (see Table 1).
For the case of an unstrained fictive infinite-layer BaCuO2 end member the c lattice parameter would reach or exceed the separation of the initially larger a parameter. At that point the two-dimensional CuO2 nets of the
Figure 2. (a) 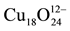 cluster of the cubic BaCuO2 structure consisting of closed strips of edge- sharing CuO4 squares. (b) Unfolded hemi-polyhedron of that cluster showing edge-connected CuO units.
cluster of the cubic BaCuO2 structure consisting of closed strips of edge- sharing CuO4 squares. (b) Unfolded hemi-polyhedron of that cluster showing edge-connected CuO units.
Table 1. Infinite-layer compounds of ACuO2 composition, A = Ca, Sr, Ba.
*)lattice parameters obtained by bond strength―bond length calculations.
infinite-layer structure turn into different sorts of cuprate clusters, characteristic for the actual BaCuO2 structure. This rolling-up of the CuO2 nets forming clusters is explained by lattice spacing frustration. This occurs when the separation between the CuO2 layers of the infinite-layer structure exceeds the translation period a within the layer. In this case infinite CuO2 nets have the chance to be formed in all three directions but are not allowed to exist in all.
The end member BaCuO2, as already mentioned, hardly exists in the parent structure as less strained compound. Its fictive lattice parameters shown in Table 1 were obtained by bond strength―bond length calculation. For Ba2+ surrounded by 8 oxygen atoms in a regular fashion, one obtains the Ba-O distance of d = 2.800 Å, using the empirical formula of Brown and Shannon [14] that was rewritten into the specialized equation , where s represents the bond valence (valence divided by the coordination number). The parameters used are d0 = 2.297 Å and N = 7 [15] . The length of the c axis is then
, where s represents the bond valence (valence divided by the coordination number). The parameters used are d0 = 2.297 Å and N = 7 [15] . The length of the c axis is then  Å, equal to the a parameter. It would be also possible to obtain an extrapolation of the a and c lattice parameters, respectively when these parameters of the compound series are plotted against the mean ionic radii of the group II elements (see Figure 3). The lattice parameters a increase only slightly from about 3.85 Å to 3.96 Å owing to the strength of the covalent bonds of the planar CuO2 nets thus obviating much strain. More crystal-chemical details are summarized below as supplementary information.
Å, equal to the a parameter. It would be also possible to obtain an extrapolation of the a and c lattice parameters, respectively when these parameters of the compound series are plotted against the mean ionic radii of the group II elements (see Figure 3). The lattice parameters a increase only slightly from about 3.85 Å to 3.96 Å owing to the strength of the covalent bonds of the planar CuO2 nets thus obviating much strain. More crystal-chemical details are summarized below as supplementary information.
The results provide a possible explanation of the astonishing structural differences between the infinite-layer and the cubic BaCuO2 structures. The degeneracy of the lattice parameters is all equal for of BaCuO2 in the fictive all-layer structure, or at least the c lattice parameter exceeding the a lattice parameter. This has the consequence that this structure is non-existent, because it is impossible that CuO2 layers can be formed in all three dimensions, only fragments of such layers could grow. However, potential layer fragments will be unstable against folding and will close into clusters, a mechanism well consistent with cubic symmetry. The formation of different clusters can reduce the strain in the structure and finally leads to the observed large unit cell of the actual structure. The degeneracy of lattice spacing is evidently the reason for the formation of the complex BaCuO2 structure required to overcome the lateral frustration.
Let us draw attention again to the very simple BaCuO2 stoichiometry. Does the structure retain some memory of its formation history? Could it be that the first small nuclei formed, occur as infinite-layer blocks with simple
Figure 3. Plot of lattice parameters versus mean ionic radii for infinite layer compounds (square symbols) as listed in Table 1. The circles indicate extrapolated values for pure, non-existent CaCuO2 according to a linear regression. The arrow-marked diamond symbol depicts the fictive parameter (a and c equal) for BaCuO2 in the infinite layer structure, which is non-existent in this structure type under ambient conditions. The vertical dashed line indicates the assumed phase borderline between the infinite-layer and the cubic BaCuO2 prototypes.
stoichiometry, maybe as three-dimensional chessboard-like ordered assemblies, and then pass on this simple stoichiometry before the structural transformation to cubic BaCuO2 happens? If so, we have to explain the origin of different connections of the CuO2 squares, first being corner-connected and then edge-connected.
Fluctuations in the concentration or growth conditions (thermodynamic variables) are responsible for structural distortions, which have been observed by electron-microscopy in the parent structure. For instance, occasionally small clusters in the form of CuO5 pyramids exist in compounds of high Ba content near the end member composition, but the general layer structure still persists [16] . Thus the members with high Ba content already indicate a certain readiness for structural phase transition.
If the c lattice parameter approaches the a-axis length, oxygen can penetrate into the otherwise oxygen-free Ba layer with simultaneous oxygen depletion of the CuO2 layer. The stoichiometry tells us that in the limiting case one T-CuO layer with twice as many Cu could sandwich two BaO layers. Locally, nano-scaled phase separation may occur into rocksalt-type BaO and T-CuO, but a complete separation is excluded because of the high reactivity of BaO. The lattice parameter of BaO of a = 5.534 Å matches almost perfectly that of T-CuO with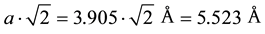 , strongly suggesting the possibility for a topotactic intergrowth at nano-scale dimension. Then we are faced with edge-connected T-CuO fragments containing peripherally edge-dangling bonds, which may easily curl up into polyhedral cages. Another possibility is the existence of a hypothetical BaCuO2 phase with tetragonal symmetry that would show nearly perfect lattice dimensions for a topotactic reaction, too. Figure 4 illustrates this model structure of space group P4/nmm with lattice parameters of a = 3.87 Å and c = 8.20 Å. A puckered edge-connected CuO layer of alternatively up and down directed CuO pyramids is sandwiched between layers of BaO with 9-fold oxygen environment, representing the average of the rocksalt and the perovskite coordinations ([6] + [12])/2 = [9]), similar to the La3+ coordination in La2CuO4. Table 2 and Table 3 show the atomic coordinates and bond lengths and bond angles, respectively. X-ray powder data are given in Table 4.
, strongly suggesting the possibility for a topotactic intergrowth at nano-scale dimension. Then we are faced with edge-connected T-CuO fragments containing peripherally edge-dangling bonds, which may easily curl up into polyhedral cages. Another possibility is the existence of a hypothetical BaCuO2 phase with tetragonal symmetry that would show nearly perfect lattice dimensions for a topotactic reaction, too. Figure 4 illustrates this model structure of space group P4/nmm with lattice parameters of a = 3.87 Å and c = 8.20 Å. A puckered edge-connected CuO layer of alternatively up and down directed CuO pyramids is sandwiched between layers of BaO with 9-fold oxygen environment, representing the average of the rocksalt and the perovskite coordinations ([6] + [12])/2 = [9]), similar to the La3+ coordination in La2CuO4. Table 2 and Table 3 show the atomic coordinates and bond lengths and bond angles, respectively. X-ray powder data are given in Table 4.
Notably, a long time ago this simulated structure was considered responsible for unstable superconductivity at very high Tc = 220 K [17] . Its formation as ultrathin film, possibly peroxide-expanded because of oxygenation during the experiment, was conjectured as intermediate reaction layer between the chosen (110)-SrTiO3 substrate and the YBa2Cu3O7-X superconducting film. More recently, it was assumed that filamentory superconductivity at 220 K is caused by a small content of oxygen depleted cupric oxide CuO1-x within the multi-phase sample [18] -[20] . Crystallographic data of the different BaCuO2 phases are compared in Table 5.
Remarkably, BaO transforms under a pressure of 18 GPa into the PbO type sheet structure with a P4/nmm space group identical to that of the BaCuO2 model structure, with lattice parameters of a = 4.397(7) Å and c = 3.196(5) Å [21] . In this structure Ba is located off-centre between 8-coordinating oxygen atoms.
Figure 4. Hypothetical crystal structure of tetragonal BaCuO2 with a = 3.87 Å, c = 8.20 Å, space group P4/nmm (No. 129/1). Unit cell yellow outlined, Cu blue, Ba green, O red.
Table 2. Atomic coordinates of hypothetical BaCuO2, tetragonal space group P4/nmm (No. 129/1) with lattice parameters of a = 3.87 Å, c = 8.20 Å, Z = 2.
Table 3. Bond lengths (Å) and bond valence sums, respectively of hypothetical BaCuO2.
Table 4. Calculated X-ray powder pattern for hypothetical BaCuO2 (Cu-Kα1 radiation, λ = 1.5406 Å).
Table 5. Comparison of crystallographic data for distinct BaCuO2 phases.
The investigation of frustration is a current research field of physics and mostly applied to spin systems and magnetism. In geometrically frustrated structures magnets are unable to attain order by virtue of their local geometric arrangement. A prominent example is the frustration-induced spiral ordering of spins of the high-Tc multiferroic monoclinic CuO (Kimura et al. [22] [23] ). However, pure mechanical systems can also be frustrated. Examples are the multitude of ice structures and the way, in which the hydrogen atoms of the polar H2O molecule can order with two hydrogen atoms nearby and two further away from the oxygen atom. A further example of a frustrated system is the isotropic negative thermal expansion (contraction) of ZrW2O8 over a wide temperature range including room temperature owing to transverse thermal motion of a non-bonded oxygen atom on the apex of the ZrO8 octahedron. Here, the mechanical under-constraint is reminiscent of magnetic spin systems (Ramirez et al. [24] ). In our case of the fictive infinite-layer structure of BaCuO2 we are dealing simply with a sort of lateral frustration. This may simply be considered as the inability of structural building units to attain order in the simplest arrangements possible. Any which way nature reacts to this situation, the cubic BaCuO2 structure is unprecedented in its complexity.
Although p-type current carriers are found for the cubic BaCuO2+δ prototype with δ = 0.07, superconductivity was never observed. This is attributed not so much to a non-optimum hole doping as to the <90˚ Cu-O-Cu super-exchange interaction and the stiffness of the edge-sharing cuprate strips, which form the clusters and show a distance of less than 2.7 Å among Cu atoms, compared with more than 3.8 Å of the corner-sharing cuprate layer of superconducting compounds.
3. Proposal for a Cuprate Super-Cage
The topology and stoichiometry of cuprate cages can be described with the symbol 

Applying Euler’s topologic invariant for convex polyhedra [25] ,

the number of corner c yields

which equals the oxygen number of the cage, whereas the number of decorated faces 
number of copper atoms. In the cubic BaCuO2 structure, the octahedral faces of the [4641238] polyhedron are not occupied by Cu. Therefore, the cage formula is found to be Cu6+12O24.
One may ask, which properties a cluster compound of corner-sharing cuprate stripes might show. A cluster, extending its cage diameter by 
If all faces of the polyhedron are occupied by copper, a formula of 
Figure 5. [4641242438] super-cage polyhedron with 9.39 Å diameter down [001], showing for reasons of clarity, apart from red oxygen atoms, only the decoration of the 46 and the 412 faces with copper in light blue colour. This reduced decoration would lead to corner-sharing cuprate plaquettes.
bond length of 1.894 Å may be a bit small for this Jahn-Teller cation, but favours an occupation with highly charged other ions such as Ge4+. Even though one would somewhat enlarge the lattice parameter in order to match the ideal environment for copper in the 2+ oxidation state, there is no need to change much the distance, if this cation is 3+ charged.
In the [100] direction an additional oxygen atom at the 1/2, 0, 0 site can bond the cages through elongated CuO5 pyramids. Then the unit-cell content amounts to 2 formula units of
Atomic coordinate and bond length respectively bond angle of the hypothetic structure are given in Table 6 respectively Table 7. In addition, an X-ray powder pattern was calculated for rapid identification in case of synthesis success, characterized by two very strong peaks with d-values of 7.47Å respectively 6.10 Å (see Table 8). The cluster calculation method is to refine a trial structure step by step using bond length and bond angles as geometrical constraints together with oxygen-oxygen distances, finally adapting the required bond valence sums. To calculate the Cu-O bond valance sum by the empirical Brown relation s = Σ(d/d0)−N [14] [15] the new coefficients d0 = 1.713(9) Å and N = 5.76(0.16) were used. The calculations were carried out using the software modules of Reference [26] .
Figure 6. Fully decorated cuprate super-cage with 46 and 412 faces centered with light blue copper atoms, 424 with blue ones respectively 48 ones capped with green colored atoms. The cage deviates somewhat from a sphere towards a cube.
Table 6. Proposed atomic coordinates for a cluster structure of space group Im3m (No. 229) with the lattice parameter of a = 14.938 Å. Cage radii for the different ions are given as rc(Å) = 
Table 7. Calculated bond length (Å), Cu-O-Cu bond angles (˚) and bond valence sums s of the super-cage structure.
*)If this site could be actually filled with Cu2+ ions, then the lattice parameter can be adapted in order to enlarge the Cu(4)-O bond length to a more realistic value near 2.07 Å.
Table 8. Calculated X-ray powder pattern of the super-cage structure (Cu-Kα1 radiation, λ = 1.5406 Å).
Since the suggested templates lack a centre of symmetry, one could adapt this fact to the cage structure, too, and hence would create an acentric space group such as I432 with more degrees of freedom to account for energetically favoured bond lengths and angles, respectively. However, this option has not been calculated in detail.
The cluster would shows different paths of >90˚ antiferromagnetic Cu-O-Cu super-exchange interaction (see Table 7), a prerequisite for superconductivity. For instance, the Cu(1)-O-Cu(2) bond angle amounts to Φ = 139.2˚, resulting in an assumed principal super-exchange interaction of Jz(Φ) = 0.091(Φ - 90)1.651 meV ≈ 56.6 meV (see Figure 7 and [27] , respectively).
Figure 7. Principal super-exchange interaction Jz(Φ) versus Cu-O-Cu bond angle Φ (afm = antiferromagnetic, fm = ferromagnetic). The red arrow marks the cuprate super-cage position. This relation was first published by Rocquefelte et al. [27] . Data for minerals outlined in blue like dioptase have been added and included in the Jz(Φ) fit by the present author.
The cluster compound is expected to carry a super-current through its lattice, when optimum doped. Besides superconductivity one should think about other properties like light-harvesting features for solar cell application, relying on ball antennas instead of linearly extended ones. In this case also other non-cage atoms such as iodine replacing oxygen or Sn4+ replacing Ge4+ should be also considered to enhance the solar efficiency.
A synthesis route is proposed as follows. First, ultrathin T-CuO films may be deposited onto a substrate such as (001)-oriented SrTiO3 by pulsed laser deposition (PLD) using a CuO target (Siemons et al. [28] ; Samal et al. [29] ). Then, this film is peeled off from the surface by assistance of a surfactant, simultaneously offering a template, around which T-CuO film fragments can roll up. The free accessible space of the super-cage to be filled with the template is about 6.63 Å (smallest cage diameter of 9.39 Å minus diameter of 2.76 Å for an oxygen atom). Two quaternary organic templates of about the same Van der Waals dimension of 6.3 Å are favoured to accomplish well such space filling: the cation 
Besides SrTiO3, as the most favourable substrate, one should consider also BaO in the rocksalt type, but considering the limitations formulated in the previous chapters.
4. Characteristic of X-Ray Scattering from Hollow Polyhedral Structures
The X-ray powder pattern of the cubic cuprate super-cage structure (Table 7) was calculated with the aid of the FullProf program (Carvajal [30] ). It shows a pronounced intensity modulation of the peaks, which can be understood as resulting from a uniform electron density distribution ρ on the shell of a hollow sphere of radius rs, approximating the empty polyhedral cage. Because the copper atoms, occupying the face centers of the polyhedron, have smaller distances to the cage center compared to the oxygen atoms at the corners, an electron density weighted radius R will be introduced (see Table 5).
Calculating the structure factor F(k) as the Fourier transform of the radial charge density ρ(r), the property of the Dirac delta function δ is used, where the integral of δ times some other function f(r) is equal to the value of f(r) at the position of δ:

Following in part the calculation concept of Alloul and Lyle [31] applied to C60 buckyballs, one obtains the scale factor A from the total number Ne of electrons of the polyhedron, confined to a shell of radius R as

Using polar coordinates r, φ, θ, for spherically symmetric functions, one obtains d3r = r2drdφsinθdθ. Then the Fourier transform yields


Substituting cosθ = ζ gives

Hence,

Finally, the intensity results as

Replacing |k| = k = 2π/d with the interplanar spacing
I(k) shows zeros for R/d = n/2 with integer n and maxima near


In addition, the intensity I(k) of an actual powder pattern has to be corrected for LpG factors and overall atomic displacement exp(−2T), respectively. This was applied in Figure 8 to display the modulated intensity of the super-cage structure.
Subtracting this modulation from the actual pattern would indicate reflections with a pronounced contribution of non-cage atoms. It should be stressed that some complication results when the sphere is inflated towards a cube as shown above in Figure 6. The Fourier transform for such rounded cube will be calculated and published later.
The outlined concept is particularly favorable for the analysis of unknown cage structures. One can simply calculated the center of gravity kg of a batch of foremost intense reflections, corrected by LpG and exp(-2T), and therefrom determine the cage radius R using Equation (11). This information may be important to rapidly solve the complete crystal structure.
Although the chosen example of the super-cage model is not ideal insofar as it deviates somewhat from the spherical shape with diminishing characteristic diffraction features at high k values, the recovery of the (predetermined) super-cage radius R using Equation (11) gives still a remarkable result (see Table 9).
Figure 8. Spherical shell diffraction pattern (red) enveloping the super-cage X-ray powder pattern (blue). Coinciding reflections were slightly offset side by side.
Table 9. Redetermination of the cage radius R from reflection batches around the maxima of I(k), yielding a mean value of R = 5.00 Å.
5. Conclusions
Possible formation pathways of cupric oxide clusters of cubic BaCuO2 are analysed in this article. The author has entertained the idea to construct more voluminous CuO clusters, the larger radii of curvature of which allows greater than 90˚ Cu-O-Cu bonding angles and possible antiferromagnetic super-exchange interaction as a prerequisite for high-Tc superconductivity. An Cu(1)-O-Cu(2) exchange pathway within such 
An X-ray powder pattern was also calculated for a super-cage structure of space group Im3m and a lattice parameter of 14.938 Å. This identification possibility was supplemented by hollow sphere scattering calculations, approximating the electron distribution on the polyhedron through a radial shell electron density assumption. Characteristics of such X-ray scattering may serve to identify unknown hollow clusters. In addition, model calculations have suggested a new tetragonal BaCuO2 phase of space group P4/nmm with up and down puckered pyramidal T-CuO nets, a possibly step towards edge-connected cluster formation.
Research into novel copper oxide clusters may also stimulate associated scientific fields similar to carbon clusters with their full basket of remarkable properties, all the more so since the T-CuO net shows similar low- energy excitations as the CuO2 net of the known high-Tc superconductors (Moser et al. [32] ). Materials scientists are encouraged to attempt their synthesis.
Acknowledgements
The author wishes to thank Prof. Dr. R. B. Heimann for critical reading of the manuscript.
Cite this paper
Hans HermannOtto, (2015) Modeling of a Cubic Antiferromagnetic Cuprate Super-Cage. World Journal of Condensed Matter Physics,05,160-178. doi: 10.4236/wjcmp.2015.53018
References
- 1. Bednorz, J.G. and Müller, K.A. (1986) Possible High Tc Superconductivity in the Ba-La-Cu-O System. Zeitschrift für Physik, B64,189-193. http://dx.doi.org/10.1007/BF01303701
- 2. Müller-Buschbaum, H. (1989) Zur Kristallchemie der oxidischen Hochtemperatur-Supraleiter und deren kristallchemischen Verwandten. Zeitschrift für anorganische und allgemeine Chemie, 101, 1503-1524.
http://dx.doi.org/10.1002/ange.19891011105 - 3. Yvon, K. and François, M. (1989) Crystal Structures of High-Tc Oxides. The Years 1987 and 1988. Zeitschrift für Physik, B76, 413-444. http://dx.doi.org/10.1007/BF01307892
- 4. Baltrusch, R. (1997) Zur Kristallchemie von Systemen oxidischer Hochtemperatursupraleiter. Dissertation, TU Clausthal, Clausthal-Zellerfeld.
- 5. Otto, H.H., Brandt, H.-J. and Meibohm, M. (1996) über die Existenz des Kupferpolysilicats Cu{uB11∞1}Cu{uB11∞1} [1SiO3]. Beihefte zu European Journal of Mineralogy, 8, 206.
- 6. Otto, H.H. and Meibohm, M. (1999) Crystal Structure of Copper Polysilicate, Cu [SiO3]. Zeitschrift für Kristallographie, 214, 558-565. http://dx.doi.org/10.1524/zkri.1999.214.9.558
- 7. Sigrist, T., Zahurak, S.M., Murphy, D.W. and Roth, R.S. (1988) The Parent Structure of the Layered High-Temperature Superconductors. Nature 334, 231-232. http://dx.doi.org/10.1038/334231a0
- 8. Siemons, W. (2008) Nanoscale Properties of Complex Oxide Films. Ph.D. Thesis, University of Twente, Enschede.
- 9. Jahn, H.A. and Teller, E. (1937) Stability of Polyatomic Molecules in Degenerate Electronic States. I. Orbital Degeneracy. Proceedings of the Royal Society, A161, 220-235.
http://dx.doi.org/10.1098/rspa.1937.0142 - 10. Woodley, S.M. and Catlow, R. (2008) Crystal Structure Predictions from First Principles. Nature Materials, 7, 907-946. http://dx.doi.org/10.1038/nmat2321
- 11. Forster, M.D., Simperler, A., Bell, R.G., Friedrich, O.D., Paz, F.A. and Klinowski, J. (2004) Chemically Feasible Hypothetical Crystalline Networks. Nature Materials, 3, 234-238.
http://dx.doi.org/10.1038/nmat1090 - 12. Schein, S. and Gayed, J.M. (2014) Fourth Class of Convex Equilateral Polyhedron with Polyhedral Symmetry Related to Fullerenes and Viruses. Proceedings of the National Academy of Sciences of the United States of America, 111, 2920-2925. http://dx.doi.org/10.1073/pnas.1310939111
- 13. Zhai, H.-J., Zhao, Y.-F., Li, W.-L., Chen, Q., Bai, H., Hu, H.-S., Piazza, Z.A., Tian, W.-J., Lu, H.-G., Wu, Y.-B., Mu, Y.-W., Wie, G.-F., Liu, Z.-P., Li, J., Li, S.-D. and Wang, L.-S. (2014) Observation of an All-Boron Fullerene. Nature Chemistry, 6, 727-731. http://dx.doi.org/10.1038/nchem.1999
- 14. Brown, I.D. and Shannon, R.D. (1973) Empirical Bond-Strength—Bond-Length Curves for Oxides. Acta Crystallographica Section A, 29, 266-282. http://dx.doi.org/10.1107/S0567739473000689
- 15. Brown, I.D. (1981) The Bond-Valence Method: An Empirical Approach to Chemical Structure and Bonding. Structure and Bonding in Crystals. Volume II, Academic Press, New York.
- 16. Zhu, S., Norton, D.P., Chamberlain, J.E., Shahedipour, F. and White, H.W. (1996) Evidence of Apical Oxygen in Artificially Superconducting SrCuO2-BaCuO2 Thin Films: A Raman Characterization. Physical Review B, 54, 97-100. http://dx.doi.org/10.1103/PhysRevB.54.97
- 17. Schönberger, R., Otto, H.H., Brunner, B. and Renk, K.F. (1991) Evidence for Filamentary Superconductivity up to 220 K in Oriented Multiphase Y-Ba-Cu-O Thin Films. Physica C: Superconductivity, 173, 159-162. http://dx.doi.org/10.1016/0921-4534(91)90363-4
- 18. Azzoni, C.B., Paravicini, G.B.A., Samoggia, G., Ferloni, P. and Parmigiani, F. (1990) Electrical Instability in CuO1-x: Possible Correlations with the CuO-Based High Temperature Superconductors. Zeitschriftfür Naturforschung, A45, 790-794.
- 19. Osipov, V.V., Kochev, I.V. and Naumov, S.V. (20010) Giant Electric Conductivity at the CuO-Cu Interface: HTSL-Like Temperature Variations. Journal of Experimental and Theoretical Physics, 93, 1082-1090.
- 20. Mitkin, A.V. (2012) Striped Organization of Hole Excitations and Oxygen Interstitials in Cuprates as a Route to Room-Temperature Superconductivity. Journal of Superconductivity and Novel Magneti, 25, 1277-1281.
- 21. Liu, L. and Bassett, W.A. (1972) Effect of Pressure on the Crystal Structure and Lattice Parameters of BaO. Journal of Geophysical Research, 77, 4934-4937. http://dx.doi.org/10.1029/JB077i026p04934
- 22. Kimura, T, Goto, T., Shintani, H., Ishizaka, K., Arima, T. and Tokura, Y. (2003) Magnetic Control of Ferroelectric Polarization. Nature, 426, 55-58. http://dx.doi.org/10.1038/nature02018
- 23. Kimura, T., Sekio, Y., Nakamura, H., Siegrist, T. and Ramirez, A.P. (2008) Cupric Oxide as an Induced-Multiferroic with High-Tc. Nature Materials, 7, 291-294. http://dx.doi.org/10.1038/nmat2125
- 24. Ramirez, A.P., Broholm, C.I., Cava, R.J. and Kowach, G.R. (2000) Geometrical Frustration, Spin Ice and Negative Thermal Expansion—The Physics of Under-Constraint. Physica B, 280, 290-295.
http://dx.doi.org/10.1016/S0921-4526(99)01695-6 - 25. Euler, L. (1752) Elementa doctrine solidorum. Novi commentarii academiae scientiarum imperialis petropolitanae, 4, 109-160.
- 26. Otto, H.H. (1980) Manual for Turbo-Basic Crystal Structure Programs: Strufit, Guinkorr, Binwin, Bondval. Regensburg University, Regensburg.
- 27. Rocquefelte, X., Schwarz, K. and Blaha, P. (2012) Theoretical Investigation of the Magnetic Exchange Interaction in Copper(II) Oxides under Chemical and Physical Pressures. Scientific Reports, 2, Article No. 759. http://dx.doi.org/10.1038/srep00759
- 28. Siemons, W., Koster, G., Blank, D.H.A., Hammond, R.H., Geballe, T.H. and Beasley, M.R. (2009) Tetragonal CuO: End Member of the 3d Transition Metal Monoxides. Physical Review B, 79, Article ID: 195122. http://dx.doi.org/10.1103/PhysRevB.79.195122
- 29. Samal, D., Tan, H., Takamura, Y., Siemons, W., Verbeeck, J., Van Tendeloo, G., Arenholz, E., Jenkins, C.A., Rijnders, G. and Koster, G. (2014) Direct Structural and Spectroscopic Investigation of Ultrathin Films of Tetragonal CuO: Six-Fold Coordinated Copper. Europhysics Letters, 105, Article ID: 17003.
http://dx.doi.org/10.1209/0295-5075/105/17003 - 30. Carvajal, J.R. (2004) Introduction to the Program FULLPROF. Laboratoire Leon Brillon (CEA-CNRS), Saclay France.
- 31. Alloull, H. and Lyle, S. (2010) Introduction to the Physics of Electrons in Solids. E-Book, Springer Verlag, Berlin.
- 32. Moser, S. Moreschini, L. Yang, H.-Y., Innocenti, D., Fuchs, F., Hansen, N.H., Chang, Y.J., Kim, K.S., Walter, A.L., Bostwick, A., Rotenberg, E., Mila, F. and Grioni, M. (2014) Angle-Resolved Photoemission Spectroscopy of Tetragonal CuO: Evidence for Intralayer Coupling between Cupratelike Sublattices. Physical Review Letters, 113, Article ID: 187001. http://dx.doi.org/10.1103/PhysRevLett.113.187001
- 33. Takano, M., Takeda, Y., Okada, H., Miyamoto, M. and Kusaka, T. (1989) A CuO2 (A: Alkaline Earth) Crystallizing in a Layered Structure. Physica C, 159, 375-378.
http://dx.doi.org/10.1016/S0921-4534(89)80007-3 - 34. Sakurai, T., Sugii, N., Takizawa, H., Ichikawa, M., Yaegashi, Y., Adachi, S., Shimada, M. and Yamauchi, H. (1992) Ba0.5Sr0.5CuO2: A New Perovskite Related Structure Which Forms at High Pressure. Physica C, 193, 471-475. http://dx.doi.org/10.1016/0921-4534(92)90973-G
- 35. Karpinsky, J., Schwer, H., Mangelshots, I., Conder, K., Morawski, A., Lade, T. and Paszewin, A. (1994) Single crystals of Hg1-xPbxBa2Can-1CunO2n+1-δ and Infinite-Layer CaCuO2. Synthesis at Gas Pressure of 10 kbar, Properties and Structure. Physica C, 234, 10-18.
http://dx.doi.org/10.1016/0921-4534(94)90047-7 - 36. Takano, M., Azuma, M., Bando, Y. and Takeda, Y. (1991) Superconductivity in the Ba-Sr-Cu-O System. Physica C, 176, 441-444.
- 37. Teske, C.L. and Müller-Buschbaum, H. (1970) über Erdalkalimetallcuprate. V. Zur Kenntnis von Ca2CuO3 und SrCuO2. Zeitschrift für anorganische und allgemeine Chemie, 379, 234.
- 38. Smith, M.G., Manthiram, A., Zhou, J., Goodenough, J.B. and Markert, J.T. (1991) Electron-Doped Superconductivity at 40 K in the Infinite-Layer Compound Sr1-yNdyCuO2. Nature, 351, 549-551.
http://dx.doi.org/10.1038/351549a0 - 39. Er, G., Miyamoto, Y., Kanamaru, F. and Kikkawa, S. (1991) Superconductivity in the Infinite-Layer Compound Sr1-xLaxCuO2. Physica C, 181, 206-208. http://dx.doi.org/10.1016/0921-4534(91)90356-4
- 40. Hiroi, Z., Azuma, M., Takano, M. and Bando, Y. (1991) A New Family of Copper Oxide Superconductors Srn+2CunO2n+1+δ Stabilized at High Pressure. Physica C, 188-189, 523-524.
http://dx.doi.org/10.1016/0921-4534(91)92064-I - 41. Azuma, M., Hiroi, Z., Takano, M., Bando, Y. and Takeda, Y. (1992) Superconductivity at 110 K in the Infinite-Layer Compound (Sr1-xCax)1-yCuO2. Nature, 356, 775-776.
http://dx.doi.org/10.1038/356775a0 - 42. Hiroi, Z., Azuma, M., Takano, M. and Takeda, Y. (1993) Structure and Superconductivity in the Infinite-Layer Compound (Ca1-ySry)1-xCuO2-z. Physica C, 208, 286-296.
http://dx.doi.org/10.1016/0921-4534(93)90200-A - 43. Adachi, S., Yamauchi, H., Tanaka, S. and Mori, N. (1993) High-Pressure Synthesis of Superconducting Sr-Ca-Cu-O Samples. Physica C, 208, 226-230. http://dx.doi.org/10.1016/0921-4534(93)90192-S
- 44. Adachi, S., Yamauchi, H., Tanaka, S. and Mori, N. (1993) New Superconducting Cuprates in the Sr-Ca-Cu-O System. Physica C, 212, 164-168. http://dx.doi.org/10.1016/0921-4534(93)90498-F
- 45. Sugii, N., Ichikawa, M., Hayachi, K., Kubo, K., Yamamoto, K. and Yamauchi, H. (1993) Microstructure of the Infinite-Layer Structural Sr1-xCuO2-d Thin Films. Physica C, 213, 345-352.
http://dx.doi.org/10.1016/0921-4534(93)90451-U - 46. Li, X., Kanai, M., Kawai, T. and Kawai, S. (1993) Epixial Growth and Properties of Ca1-xSrxCuO2 Thin Films (x = 0.18 to 1.0) Prepared by Co-Deposition and Atomic Layer Stacking. Japanese Journal of Applied Physics, 31, L217-L220. http://dx.doi.org/10.1143/JJAP.31.L217
- 47. Terashima, Y., Sato, R., Takeno, S., Nakamura, S. and Miura, T. (1993) Preparation of Epitaxial SrCuOx Thin Films with an Infinite-Layer Structure. Japanese Journal of Applied Physics, 32, L48-L50.
http://dx.doi.org/10.1143/JJAP.32.L48 - 48. Maeda, T., Yoshimoto, M., Shimozono, K. and Koinuma, H. (1995) Two-Dimensional Laser Molecular Beam Epitaxy and Carrier Modulation of Infinite-Layer BaCuO2 Films. Superconductivity, 247, 142-146.
http://dx.doi.org/10.1016/0921-4534(95)00067-4 - 49. Wang, J., Rak, Z., Zhang, F., Ewing, R.C. and Becker, U. (2011) Electronic Structure and Energetics of Tetragonal SrCuO2 and Its High-Pressure Superstructure Phase. Jounal of Physics: Condensed Matter, 23, Article ID: 465503.
- 50. Kipka, R. and Müller-Buschbaum, H. (1977) über Oxocuprate. XX Ein Erdalkalimetallcuprat (II) mit geschlossenen Baueinheiten. Zeitschrift für Naturforschung, 32, 121.
- 51. Weller, M.T. and Lines, D.R. (1989) Structure and Oxidation State Relationship in Ternary Copper Oxides. Journal of Solid State Chemistry, 82, 21-29. http://dx.doi.org/10.1016/0022-4596(89)90217-X
- 52. Insausti, M., Lezama, L., Cortés, R., Gil de Muro, I., Rojo, T. and Arriortua, M.I. (1995) Evolution with Time of the Magnetic and Spectroscopic Properties of the BaCuO2+δ Phase. Study of Ba1-xSrxCuO2+δ Solid Solution. Solid State Communications, 93, 823-929.
http://dx.doi.org/10.1016/0038-1098(94)00876-0 - 53. Wang, Z.-R., Wang, X.-L., Fernandez-Baca, J.A., Johnston, G.C. and Vaknin, D. (1994) Antiferromagnetic Ordering and Paramagnetic Behaviour of Ferromagnetic Cu6 and Cu18 Clusters in BaCuO2+x. Science, 264, 202-204. http://dx.doi.org/10.1126/science.264.5157.402
A1. Supplementary Information Used in Table 1 and Figure 3, Respectively
Of all available information about the a lattice parameters for superconducting cuprates and related phases build-up of square-planar CuO2 layers and containing high Ba content, the upper limit appears to be 3.96 Å. The dependence of lattice parameters on the averaged alkaline earth ion radius of the parent structure compounds was first illustrated by Takano et al. [33] and then by Sakurai et al. [34] . In Figure 3 this data, including the data subsequently reported for CaCuO2, Ba0.5Sr0.5CuO2 and BaCuO2 compounds, are drawn differently to support my intention. However, some details need a further consideration. In Figure 3 straight lines represent results of a linear regression using only the first five consecutive lattice parameter values. Extrapolation to the pure Ca compound revealed the parameters a = 3.85 Å and c = 3.17 Å in agreement with the experimental results of Karpinsky et al. [35] . Takano et al. [36] reported extrapolated values of 3.849 Å and 3.160 Å, respectively. Of the pure Sr compound to the few available compounds with substituted Ba for Sr the a lattice parameters deviate from the linear curve to yield an upper value of about 3.93 Å. However, a quadratic regression curve extends well to the 3.96 Å value of the fictive BaCuO2. In a more complicated manner behaves the c lattice parameter on substitution of Ba. The compounds with high Ba content show c lattice parameters and densities, deviating more strongly to lower or higher values as expected from the assumed trend. Takano et al. (1989) [33] did not explicitly report the lattice parameters for Ba0.33Sr0.67CuO2 that I extracted from their picture given and from the related X-ray powder pattern. However, the peaks on this pattern are very broad. In addition, some peaks exist at low diffraction angles of the pattern that I attribute to the presence of cubic BaCuO2. Hence, the given Ba0.33Sr0.67CuO2 composition may be altered to one with slightly lower Ba content. However, the Ba-rich compound Ba0.5Sr0.5CuO2 may be a special case as its structure exhibits an ordering of the Sr and Ba ions in layers parallel to (001) with a different layer thickness of 3.64 Å and 4.29 Å, respectively. At first sight the large separation of the Ba layer appears to contradict my hypothesis further explained below. Given the a lattice parameter constraint as a result of tensile stress of the CuO2 net, the distinct bond strength of the two ions are leading to the different layer thickness observed, and consequently the structure expands in the c direction. The cationic ordering may be energetically favourable. One could argue that Sr layers, located between two Ba layers, can act as a sort of substrate for the Ba layer to grow upon and thus stabilize this layer. Whatever the argument is, the result is a compound near the stability limit of the infinite layer prototype with a remarkably low density of about Dx = 5.64 g∙cm−3, showing for the first time that the lattice parameter c’ = c/2 (because of the cell doubling) exceeds the a parameter by only a small margin. Owing to this complication the third-order regression curve in Figure 3 may be taken only as guide to the eye to indicate the tendency of the c lattice parameter development up to the fictive BaCuO2 composition. It should be stressed that for the actual member of the Ba0.5Sr0.5CuO2 solid solution the structural change from tetragonal to orthorhombic with lattice parameters of a = 3.92 Å and b = 3.94 Å already indicates that the otherwise squared CuO2 net may suffer a lateral distortion in compositions with high Ba content.
A2. History of Synthesis Routes and Crystal Chemistry of Infinite Layer Cuprates and Cubic BaCuO2
First, additional details will be summarized that have been reported on the crystal-chemistry and materials synthesis effort of both compounds. This may lead to better understanding of the crystallographic conclusion drawn from this information. In the course of superconductor research different compounds, isostructural or similar to the parent structure, have been obtained. Some of these compounds show superconducting properties, if hole-doping by off-stoichiometry or electron-doping by substitution of elements with higher valence is done. Table 1 summarizes these infinite-layer compounds with their lattice parameters. The CaCuO2 end member does not exist under ambient conditions as a stable compound of this structure type, but can be prepared under high gas pressure together with a defined oxygen partial pressure. The resulting compound shows a small off-stoichiometry of about Ca0.98CuO2 (Karpinsky et al. [35] ). The lattice parameters were determined to be a = 3.8556(6) Å and c = 3.1805(4) Å. The infinite layer compound is found as building unit in many high Tc superconductors, the lattice parameters of which may also be derived from an extrapolation of the parameters for these compounds. In addition, the other end member BaCuO2, as already mentioned, is non-existent as unstrained parent structure type, but can be formed as a highly strained epitaxially grown compound. The fictive parameters for the non-strained compound are obtained by bond strength ? bond length calculation.
The application of high pressure to transform the less dense compounds of the orthorhombic SrCuO2 structure type (Teske and Müller-Buschbaum [37] to the denser type of the infinite-layer structure was first reported by Takano et al. [33] . The phases Sr1/3Ca2/3CuO2 and SrCuO2 have been obtained. Whereas non superconducting in its ambient pressure prototypic composition, the newly discovered infinite-layer phase became an electron- doped superconductor by substitution of some alkaline earth ions by Nd3+. Understanding the importance of the in-plane bond length of CuO2 nets for the appearance of superconducting properties, Smith et al. [38] obtained the compound Sr0.84Nd0.16CuO2 at 1273 K and 25 MPa with a transition temperature of 40 K, remarkably high for an n-type material. Meanwhile Tc could be enhanced to ≤43 K (Er et al. [39] ). Hiroi et al. [40] pressed their cuprate samples isostatically up to 6 GPa at 1273 K and succeeded in the synthesis of the first p-type superconductor Sr1-xCuO2 (Tc = 100 K) of the infinite-layer type. Later, Azuma et al. [41] prepared under similar conditions compounds ranging from Ca2/3Sr1/3CuO2 through SrCuO2 to Ba1/3Sr2/3CuO2. Azuma et al. [41] and Hiroi et al. [42] reported on an alkaline earth-deficient sample (Ca1-ySry)1-xCuO2-z with a transition temperature of 110 K characterized by defect layers of alkaline earth vacancies almost randomly inserted into the parent structure.
With an already high Ba content the non-superconducting compound Ba0.5Sr0.5CuO2 has been observed by Sakurai et al. [34] formed at 1473 K under a high pressure of 6 GPa for 2 h. This phase is orthorhombic with lattice parameters a = 3.92 Å, b = 3.94 Å and c = 2·3.965 Å, space group Pmmm. The doubling of the c parameter is attributed to the ordering of the alkaline earth ions Ba and Sr in separate sheets parallel to (001), but the wide FWHM of the reflections may be due to non-uniform ordering. Furthermore, a superstructure in the a-b plane was found. The reported lattice parameters were discussed in chapter A1 in more details.
Further investigations performed by Adachi et al. [43] [44] reported the formation of some stoichiometric infinite-layer compositions under high pressure and their decomposition with increasing, but nevertheless small uptake of oxygen beyond two in the formula unit.
Another synthesis route was successfully carried out to prepare infinite-layer phases by depositing epitaxial thin films on (001)-oriented SrTiO3 single crystal substrates at about 843 K (Sugii et al. [45] ; Li et al. [46] ; Terashima et al. [47] ).
Finally, Maeda et al. [48] reported the two-dimensional laser beam epitaxy of infinite-layer BaCuO2 with a strain-expanded lattice parameter of c = 4.08 Å, whereas the a parameter was found difficult to determine due to the air-sensitivity of the surface. A mean value around 3.90 Å may be derived from the unit-cell volume.
On a properly chosen substrate the crystal lattice of the thin film is put under considerable compressive strain imitating high pressure conditions, but the compression in the plane of the film causes an expansion perpendicular to it. Therefore, since the lattice parameters of thin films may be altered in comparison with those of the bulk material the reported values have to be treated with some caution.
Recently, first principle calculations were applied to unravel the electronic structure of SrCuO2 with both the simple parent structure and the high-pressure superstructure, existing in the space group 
The complex crystal structure of cubic BaCuO2, the second prototype considered, was solved by Kipka & Müller-Buschbaum [50] . Distinct copper-oxygen clusters were found in the unit cell with space group Im3m. The largest cluster is a 26-hedron with 24 vertices and 48 edges, occupied by one of the soft Ba2+ with a surrounding of 24 oxygen atoms, and composed of 18 quadrilaterals and 8 triangles. It represents a combination of a cube, a rhombic dodecahedron and an octahedron. Thus the polyhedron notation is written as [4641238] or simply as [41838]. The quadrilaterals are centred by Cu2+. This large sphere cluster of Cu18O24 composition is located at 0, 0, 0 and 1/2, 1/2, 1/2. In addition, 8-ring clusters of composition Cu6O12 are suggested to be at the position 1/4, 1/4, 1/4 of the unit cell, apart from further 6 lone CuO4 units to complete the unit cell content to Z = 90. It then remains to explain why in the description of the crystal structure such large number of general sets and special ones of equivalent positions add up to the simple BaCuO2 stoichiometry, even though one site for Cu and oxygen show only partial occupation. Weller and Lines [51] have demonstrated that by thermal treatment at 1073 K in air or pure oxygen atmosphere the oxygen site in question may be slightly filled up from 0.25 to 0.379 atoms, leading to the formula BaCuO2.07, whereas stoichiometric material can be prepared under vacuum at 673 K.
From an unreasonably high displacement factor for the Ba atom on the origin the authors concluded that an unoccupied site exists, giving at least the formulas Ba0.98CuO2 and Ba0.98CuO2.07, respectively. Indeed, on the one hand the very long bonds of 3.926 Å between the 24 oxygen atoms and Ba in the central position would contribute just 28.2% of the required bond strength of +2. On the other hand, the conclusion drawn from the displacement factor does not indicate evidence for an empty position. It is rather assumed that this Ba atom occupies an off-centre position and shows a rapid agitation between the distinct symmetry-allowed sites. The cluster cage is too large even for the soft Ba2+ ion.
Soon thereafter, Insausti et al. [52] reported the preparation of the Ba1-xSrxCuO2+δ solid solution by thermal decomposition of metallo-organic complexes and investigated its magnetic and spectroscopic properties. The presence of Sr modifies the magnetic properties and reduces the ferromagnetic interaction. The substitution of Sr for Ba could be demonstrated up to x = 0.4, but the lattice parameter reduces only slightly from 18.272(1) Å (x = 0) to 18.181(1) Å (x = 0.4). This behaviour may be attributed to the stiffness of the large cuprate clusters and their connection through lone cuprate units along the main crystal axes without any bonding contribution of the alkaline earth ions in these directions.
Turning again to physical properties, Wang et al. [53] revealed the magnetic structure of BaCuO2+x by magnetization and neutron diffraction measurements. The individual clusters order ferromagnetically. Among the ring clusters an AF order was observed below 15 K, whereas among the spherical clusters paramagnetic order remains down to 2 K.
In summary, with respect to the alkaline earth content the parent structure exists up to the limiting concentration range of Ba0.5Sr0.5CuO2 under high pressure condition, and further up to pure BaCuO2, but only in highly strained thin films, whereas the BaCuO2 prototypic structure exists down to Ba0.6Sr0.4CuO2 under ambient pressure condition.
In this appended chapter a large part of published work about the parent structure and BaCuO2 has put together in order to develop the new idea of the possible formation of large antiferromagnetic cuprate cages respective cupric oxide ones.