World Journal of Condensed Matter Physics
Vol.05 No.01(2015), Article ID:54314,4 pages
10.4236/wjcmp.2015.51006
The Temperature Dependence of the Thermodynamic Density of States and Urbach Rule
G. Gulyamov1,2, N. Yu. Sharibaev1,2, U. I. Erkaboev1,2
1Namangan Engineering Pedagogical Institute, Namangan, Uzbekistan
2Namangan Engineering Technological Institute, Namangan, Uzbekistan
Email: gulyamov1949@mail.ru
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 7 February 2015; accepted 25 February 2015; published 28 February 2015
ABSTRACT
It is invited statistical explanation of the frequency and temperature dependence of the absorption coefficients of semiconductors on the long-wave edge of the fundamental absorption. With the help of mathematical modeling, it shows that the thermal broadening of the energy states of the conduction band and the discrete states in the band gap can cause long-wave decline according to the Urbach rule.
Keywords:
The Density of States, The Absorption Coefficient, The Fundamental Absorption, The Urbach Rule

1. Introduction
In [1] , with the help of mathematical modeling, it has shown that the experimentally determined continuum thermodynamic density of surface states at low temperatures, will turn to the discrete spectrum of the surface states. It is shown changing the width of the band gap with increasing temperature as explained by thermal broadening of the energy states of the conduction band and valence band of the semiconductor [2] . The temperature dependence of the density of states in quantizing magnetic fields was considered as a result of thermal broadening of the Landau levels [3] - [5] .
Changing in the thermodynamic density of states with temperature leads to the temperature dependence of the absorption coefficient. The light absorption coefficient is particularly sensitive to external influences at frequencies near the fundamental absorption edge. The light absorption coefficient on the long edge of the fundamental absorption is often described by the Urbach rule [6] [7] .
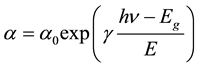 (1)
(1)
where  is the coefficient of light absorption at
is the coefficient of light absorption at ;
; 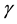 is a relatively slowly varying function of frequency
is a relatively slowly varying function of frequency ;
; 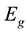 is the band gap;
is the band gap; 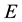 is the value of the dimension of energy which is constant at low temperatures and at high proportional
is the value of the dimension of energy which is constant at low temperatures and at high proportional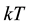 .
.
One of the main assumptions used in the analysis of experimental data is that the combined density of states determines the light absorption coefficient of the band gap of the semiconductor [6] ,
 (2)
(2)
where 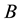 is relatively slowly varying function of frequency and temperature.
is relatively slowly varying function of frequency and temperature.
Temperature dependence must also occur in the absorption coefficient of light in the band gap of the semiconductor. Every model is used to explain the exponential absorption edge in semiconductors should explain and its temperature dependence.
The aim of this work is to study the influence of the temperature dependence of the thermodynamic density of states by a factor of light absorption (Urbach rule) on the long edge of the fundamental absorption.
2. The Temperature Dependence of the Thermodynamic Density of States
Here we will use the results of this work and the final expression of the thermodynamic density of states at GN- functions [1] .
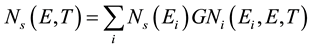 (3)
(3)
The degree of empting discrete levels is determined by the statistics of Shockley-Read-Hall. When the time of ionization state with energy  is exponentially dependent on
is exponentially dependent on 
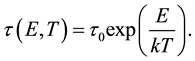 (4)
(4)
GN-function takes the following form:
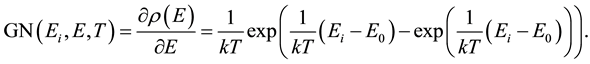 (5)
(5)
GN―a derivative of the ionization probability of the energy states in the energy and characterizes the thermal broadening of the energy state with energy .
.


For direct transitions chosen in the following form

Here
Analyze the temperature dependence by means of numerical experiments. Figure 1 shows plots of the thermodynamic density of states at different temperatures. As can be seen from the figure, at low temperatures, the conduction band edge and discrete levels are separated by an energy gap (Figure 1, curves 1 and 2). In this case, the thermal broadening is rather weak, and does not affect the spectrum of the conduction band and the discrete levels. With increasing temperature, the thermodynamic density of states of the conduction band due to thermal broadening begins to penetrate into the depth of the band gap. Energy between the individual discrete levels in the band gap and continuous levels of the conduction band are replenished with new levels came from the conduction band and of the discrete levels

Figure 1. The temperature dependence of the thermodynamic density of states is calculated from the Formula (3) of different temperatures 1―T = 77 K; 2―T = 173 K; 3―T = 273 K; 4―T = 400 K; 5―T = 500 K; 6―T = 600 K.
With increasing temperature, the thermodynamic density of states of the conduction band are beginning to blur, and the intervals between the edge of the conduction band and the discrete levels begin to fill the new states of these levels. Just show how at a temperature T = 77 K. The solid density of states of the conduction band and the state of the discrete levels in the forbidden band merge (3 - 4). The total number of levels after the thermal smearing of states of the conduction band and the discrete levels remain constant. With further increase in temperature the fraction of states that have come from the conduction band, a much stronger increase in comparison with the share of the states due to the expansion of the discrete levels. In this case, the discrete levels and smeared across the band gap, and mixed with the states, will come from the conduction band. With increasing temperature, the contribution of the discrete states and the thermodynamic density of states are becomes noticeable and the thermodynamic density of states below the bottom of the conduction band is completely determined by the distribution of the density of states in the conduction band.
As a result, the total thermodynamic density of states is determined mainly levels received from the conduction band (line 5, 6). At a temperature T = 300 K, the relative share of localized states, and in the empty, is less than 1%. It follows that the density of states in the band gap below the bottom of the conduction band is completely determined by the states will come from the conduction band. This will be due to the broadening of the huge number of levels allowed zone.
Next, we consider the exponential dependence of (1) and the dependence of the thermodynamic density of states (2) in the band gap below the bottom of the conduction bands. Figure 2 shows plots of the function (1). As can be seen from the comparison charts at temperatures above 

3. Comparison with Experiment
The results obtained are compared with experimental data [7] . Figure 3 shows graphs of the absorption coefficient for amorphous and liquid selenium [7] measured at three different temperatures and the theoretical density of states obtained by the Formula (3). A comparison of the graphs considered energy range the experimental results (1) diamonds satisfactorily described by the theoretical of the curve calculated by the Formula (3). The comparison of these curves show, that the temperature dependence of the thermodynamic density of states can satisfactorily explain the frequency and temperature dependence of the long-wavelength fundamental absorption edge.
Figure 2. Temperature dependence of the thermodynamic density of states calculated from the Formula (3) the solid line. (1) Urbach rule at different temperatures (◊). 1―T = 100 K; 2―T = 200 K; 3―T =300 K; 4―T = 400 K; 5―T = 500 K; 6―T = 600 K; Since the temperature T = 100 thermodynamic density of states and Urbach rule practically merge.
Figure 3. Frequency dependence of the absorption coefficient at different temperatures. The solid-line calculated by the Formula (3), (◊)―diamonds experimental results from [7] .
4. Conclusion
Based on these studies, we can conclude that the thermodynamic state density at elevated temperatures penetrates into the band gap of the semiconductor. This gives an additional contribution to the tail states at the bottom of the conduction band, which falls into the band gap. Temperature dependence of the thermodynamic density of states with a common position may explain the long-wavelength edge of the fundamental absorption in semiconductors. The temperature dependence of the Urbach rule may be due to the thermal broadening of the energy states of the conduction band and the valence band of semiconductors. Approach and the mechanism proposed in this paper can simultaneously coexist with other mechanisms proposed in the literature as Urbach rule and encourage the most complete explanation of the experimental results.
References
- Gulyamov, G. and Sharibaev, N.Yu. (2011) Determination of the Density of Surface States at the Semiconductor- Insulator Interface in a Metal-Insulator-Semiconductor Structure. Semiconductor, 45, 174-178. http://dx.doi.org/10.1134/S1063782611020084
- Gulyamov, G. and Sharibaev, N.Yu. (2011) Effect of Temperature on the Band Gap of the Semiconductor. Physical Surface Engineering, 9, 4-7.
- Gulyamov, G., Erkaboev, U.I. and Sharibaev, N.Yu. (2014) FTP.-St. Petersburg, 48, 1323-1328.
- Gulyamov, G., Sharibaev, N.Yu. and Erkaboev, U.I. (2013) The Temperature Dependence of the Density of States in Semiconductors. World Journal of Condensed Matter Physics, 3, 216-220. http://dx.doi.org/10.4236/wjcmp.2013.34036
- Gulyamov, G., Erkaboev, U.I. and Sharibaev, N.Yu. (2014) Simulation of the Temperature Dependence of the Density of States in a Strong Magnetic Field. Journal of Modern Physics, 5, 680-686. http://dx.doi.org/10.4236/jmp.2014.58079
- Bonch Bruyevich, V.L. and Kalashnikov, S.G. (1977) Physics of Semiconductors. Nuka, 672.
- Mott, N. and Devis, E. (1979) Electronic Processes in Non-Crystalline Materials. Clarendon Press, Oxford.




