World Journal of Condensed Matter Physics
Vol.3 No.1(2013), Article ID:28304,10 pages DOI:10.4236/wjcmp.2013.31006
Theoretical Study of Specific Heat and Density of States of MgB2 Superconductor in Two Band Models
![]()
1Department of Physics, Sangam University, Bhilwara, India; 2Shastri Nagar, New Housing Board, Bhilwara, India.
Email: anuj.nuwal2011@gmail.com, *slkakani28@gmail.com
Received October 15th, 2012; revised November 18th, 2012; accepted November 29th, 2012
Keywords: Green’s Function; p and d Holes; Specific Heat; Density of States
ABSTRACT
MgB2 with Tc ≈ 40 K, is a record-breaking compound among the s-p metals and alloys. It appears that this material is a rare example of the two band electronic structures, which are weakly connected with each other. Experimental results clearly reveal that boron sub-lattice conduction band is mainly responsible for superconductivity in this simple compound. Experiments such as tunneling spectroscopy, specific heat measurements, and high resolution spectroscopy show that there are two superconducting gaps. Considering a canonical two band BCS Hamiltonian containing a Fermi Surface of π- and σ-bands and following Green’s function technique and equation of motion method, we have shown that MgB2 possess two superconducting gaps. It is also pointed out that the system admits a precursor phase of Cooper pair droplets that undergoes a phase locking transition at a critical temperature below the mean field solution. Study of specific heat and density of states is also presented. The agreement between theory and experimental results for specific heat is quite convincing. The paper is organized in five sections: Introduction, Model Hamiltonian, Physical properties, Numerical calculations, Discussion and conclusions.
1. Introduction
The surprising discovery of superconductivity in the novel system MgB2 with Tc = 39 K by Nagamatsu et al. [1] has stimulated new excitement in condensed matter physics. This discovery certainly revived the interest in the field of superconductivity especially in non-oxides, and initiated a search for superconductivity in related boron compounds [2]. Its high critical temperature gives hope for obtaining even higher Tc for similar compounds.
The crystal structure of MgB2 is very simple. It is composed of layers of boron and magnesium, alternating along the c-axis. Each boron layer has a hexagonal lattice similar to that of graphite. The magnesium atoms are arranged between the boron layers in the centers of the hexagons. This has allowed to perform consistent calculations of its electronic structure. Band structure calculations of MgB2 show that there are at least two types of nearly separated bands with two superconducting gaps in the excitation spectrum at the Fermi surface. The first one is a heavy hole band, built up of boron σ orbitals. The second one is the broader band with a smaller effective mass, built up mainly of π boron orbitals [3-7].
It is now well established that MgB2 is an anisotropic two-gap superconductor [4]. The gap ratio 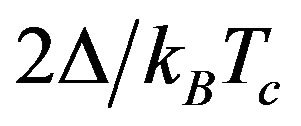 for the larger gap
for the larger gap 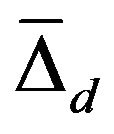 is 7.6. For the smaller gap
is 7.6. For the smaller gap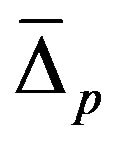 , this ratio is around 2.78, so that
, this ratio is around 2.78, so that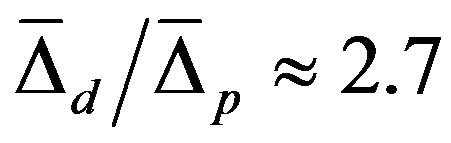 . Seemingly, both the energy gaps have s-wave symmetries, the larger gap is highly anisotropic, while the smaller one is either isotropic or slightly anisotropic. The induced character of
. Seemingly, both the energy gaps have s-wave symmetries, the larger gap is highly anisotropic, while the smaller one is either isotropic or slightly anisotropic. The induced character of  manifests itself in its temperature dependence. The larger energy gap
manifests itself in its temperature dependence. The larger energy gap 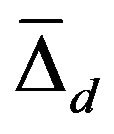 occurs in σ-orbital band, while
occurs in σ-orbital band, while 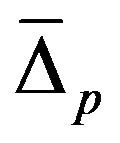 in the π-orbital band. For a simplified description, single effective σ- and π-bands can be introduced.
in the π-orbital band. For a simplified description, single effective σ- and π-bands can be introduced.
The Fermi surface consists of four sheets: two three dimensional sheets form the π bonding and antibonding bands , and two nearly cylindrical sheets form the two-dimensional σ-band
, and two nearly cylindrical sheets form the two-dimensional σ-band 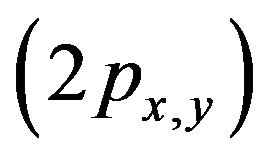 [4,8]. There is a large difference in the electron-phonon coupling on different Fermi surface sheets and this leads to multiband description of superconductivity. The average electronphonon coupling strength is found to have small values [9-11]. Ummarino et al. [12] proposed that MgB2 is a weak coupling two band phononic system where the Coulomb pseudopotential and the interchannel paring mechanism are key terms to interpret the superconducting state. Garland [13] has remarked that Coulomb potential in the d-orbitals of the transition metal reduce the isotope exponent, whereas sp-metals generally shows a nearly full isotope effect. Clearly, like sp metal, for MgB2 the Coulomb effect cannot be considered to explain the reduction of isotope exponent.
[4,8]. There is a large difference in the electron-phonon coupling on different Fermi surface sheets and this leads to multiband description of superconductivity. The average electronphonon coupling strength is found to have small values [9-11]. Ummarino et al. [12] proposed that MgB2 is a weak coupling two band phononic system where the Coulomb pseudopotential and the interchannel paring mechanism are key terms to interpret the superconducting state. Garland [13] has remarked that Coulomb potential in the d-orbitals of the transition metal reduce the isotope exponent, whereas sp-metals generally shows a nearly full isotope effect. Clearly, like sp metal, for MgB2 the Coulomb effect cannot be considered to explain the reduction of isotope exponent.
It is quite natural to describe a two-gap superconductor by means of a two-band model with interband coupling [14,15]. For MgB2, an approach of such kind is also directly proposed by the nature of the electron spectrum mentioned. There is a number of two band type approaches for superconductivity in MgB2 [16]. We may note that two band models have been exploited in various realizations for high-Tc cuprate superconductivity [16,17].
Liu et al. [4] pointed the role of the electron-phonon interaction between effective σ- and π-bands in the two gap system MgB2. In the present study, we use σ-π interband coupling with a strong σ-interband contribution of electron-phonon and Coulobmic nature. Following Liu et al. [4], the interband interaction is considered to be repulsive (an advantage of two band models) corresponding to electron-electron interaction.
Using two band models, we study the basic MgB2 superconductivity characteristics, specific heat and density of states and compare the theoretical results qualitatively with the available experimental data.
2. The Model Hamiltonian
The model Hamiltonian has the form [18]
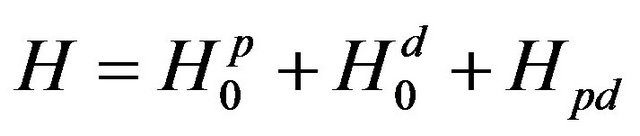 (1)
(1)
where
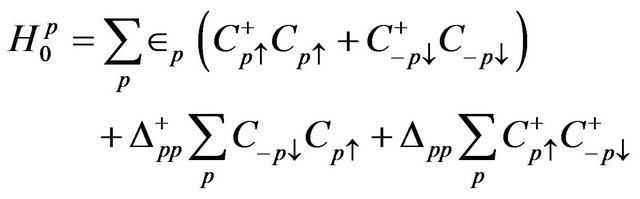 (2)
(2)
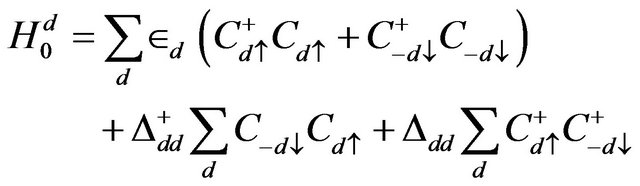 (3)
(3)
and
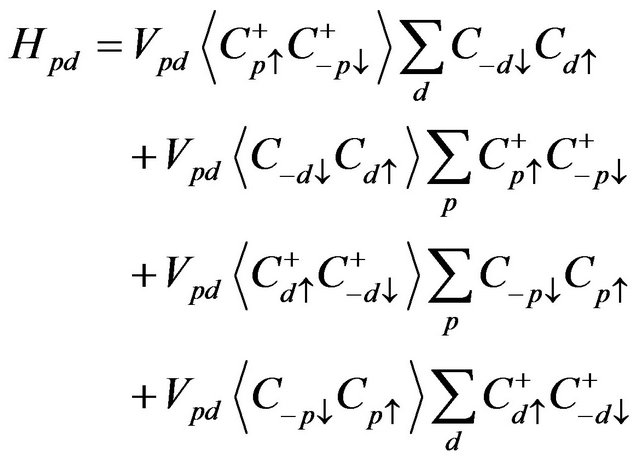 (4)
(4)
Here p and d are momentum labels in the π- and σ- bands respectively with energies 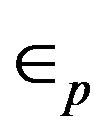 and
and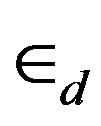 , μ is the common chemical potential. Each band has its proper pairing interaction
, μ is the common chemical potential. Each band has its proper pairing interaction 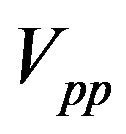 and
and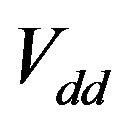 , while the pair interchange between the two bands is assured by
, while the pair interchange between the two bands is assured by 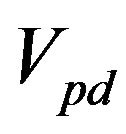 term.
term.
We have assumed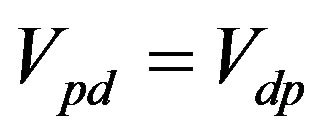 , and we define the following quantities
, and we define the following quantities
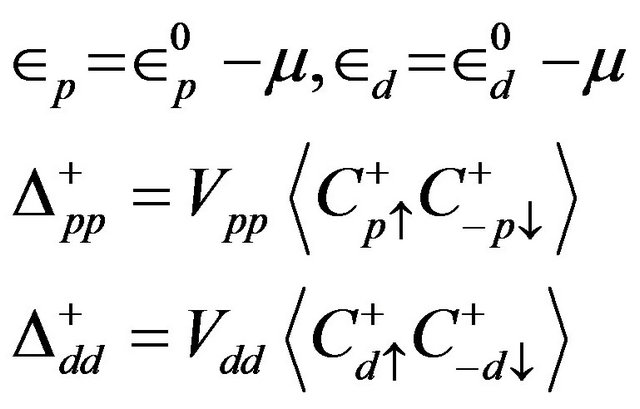
Further we define
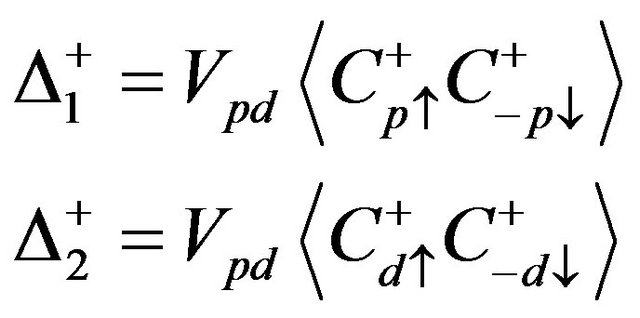 (5)
(5)
Now 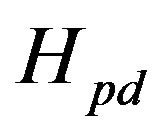 in Equation (1) read as
in Equation (1) read as
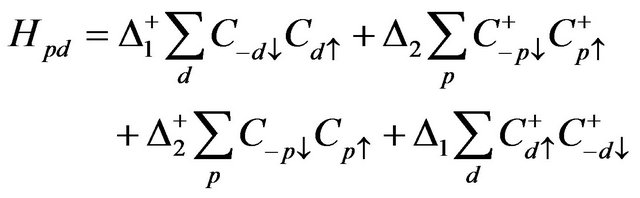
Final Hamiltonian can be written as
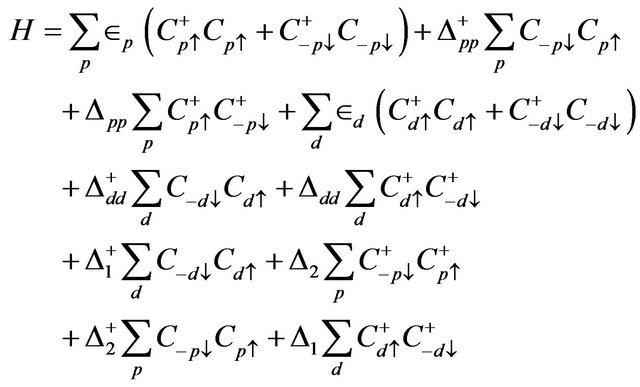 (6)
(6)
We study the Hamiltonian (6) with the Green’s function technique and equation of motion method.
2.1. Green’s Functions
In order to study the physical properties, we define the following normal and anomalous Green’s functions [18- 28]:
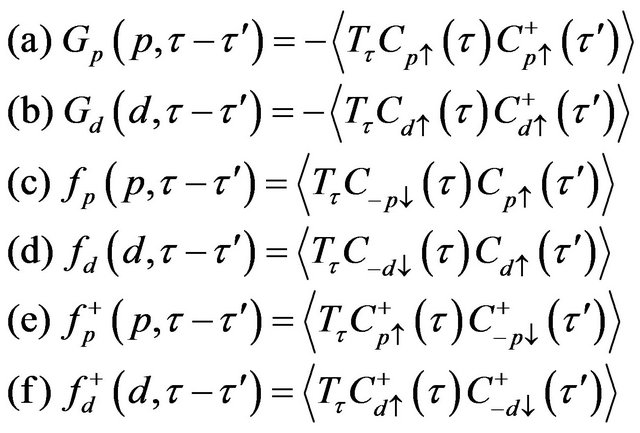 (7)
(7)
Following equation of motion method, we obtain Green’s functions as follows. In obtaining Green’s functions, we have assumed
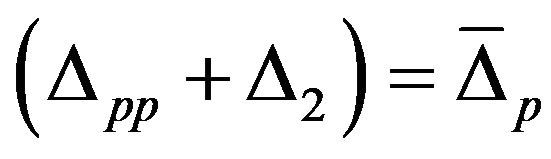 and
and 
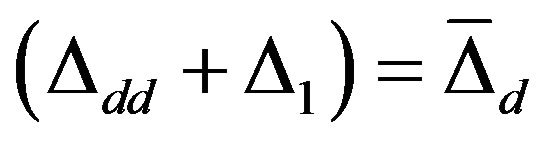 and
and 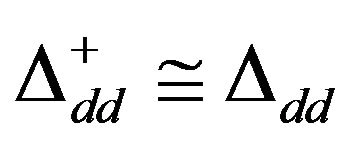
Then
 (8)
(8)
1) Green’s functions for π-band
 (9)
(9)
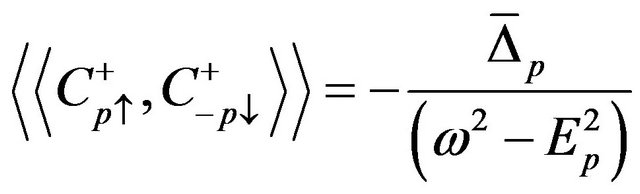 (10)
(10)
2) Green’s functions for σ-band
 (11)
(11)
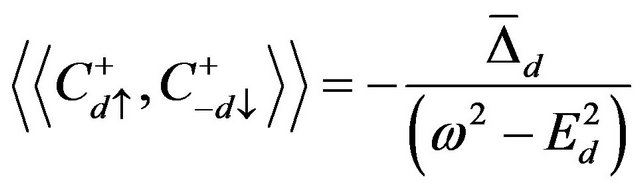 (12)
(12)
2.2. The Correlation Functions
Using the following relation [23-27],
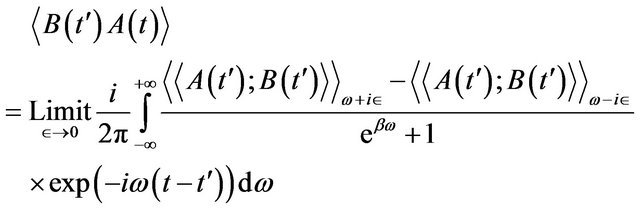 (13)
(13)
and employing the following identity,
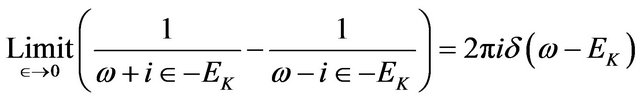
we obtain the correlation functions for the Green’s functions given by Equations (9) and (10) as:
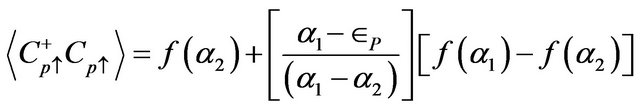 (14)
(14)
 (15)
(15)
where
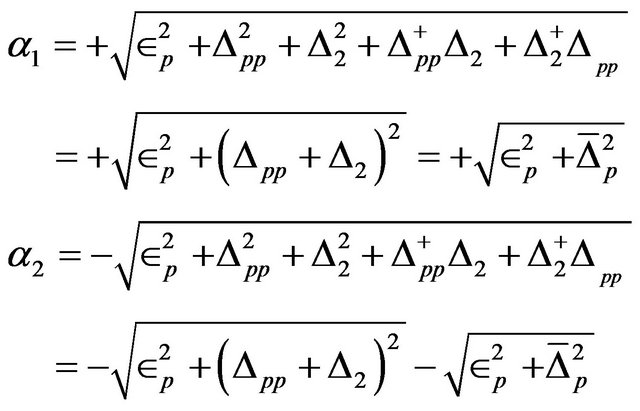 (16)
(16)
and 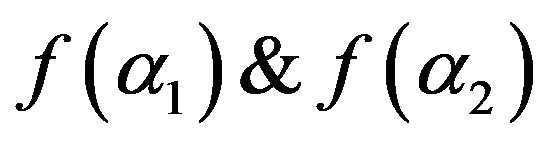 are Fermi functions.
are Fermi functions.
Similarly correlation functions for Green’s functions (11) and (12) for σ holes are obtained.
One can define the two superconducting order parameters related to the correlation functions corresponding to Green’s functions  and
and  for π- and σ-bands respectively. In a similar manner electronic specific heat can also be defined related to both π- and σ-bands.
for π- and σ-bands respectively. In a similar manner electronic specific heat can also be defined related to both π- and σ-bands.
3. Physical Properties
3.1. Superconducting Order Parameters
Gap parameter  is the superconducting order parameter, which can be determined self consistently from the gap equations
is the superconducting order parameter, which can be determined self consistently from the gap equations
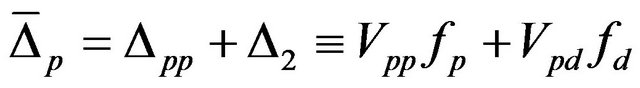 (17)
(17)
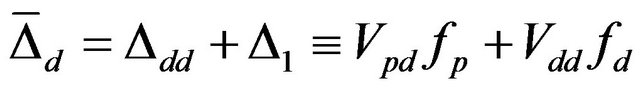 (18)
(18)
In a matrix form, the order parameter for the superconducting state is given by [19]
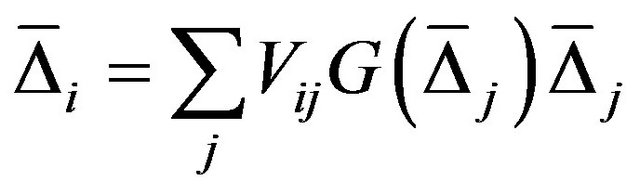 (19)
(19)
where 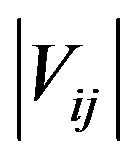 is the pairing interaction constant and function G’s are defined as
is the pairing interaction constant and function G’s are defined as
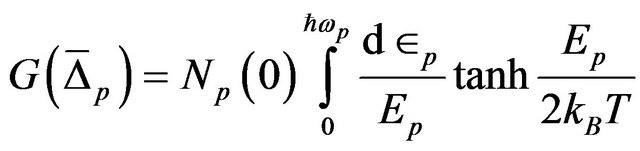 (20)
(20)
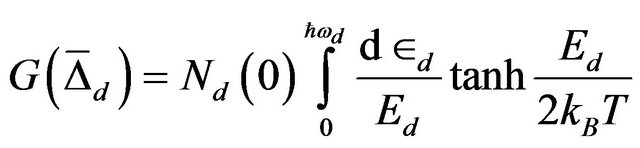 (21)
(21)
Here 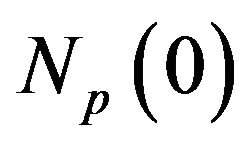 and
and 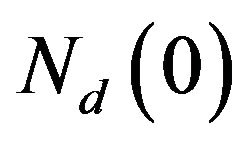 are density of states for π- and σ-bands respectively at the Fermi level.
are density of states for π- and σ-bands respectively at the Fermi level.
There are two superconducting gaps corresponding to π- and σ-bands in this interband model. One can write the equations for superconducting gaps corresponding to π- and σ-bands as follows
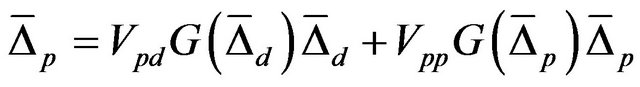 (22)
(22)
 (23)
(23)
where 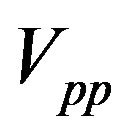 and
and 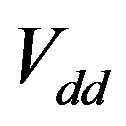 is pairing interaction for π- and σ- bands respectively, while the pair interchange between the two bands is assured by the
is pairing interaction for π- and σ- bands respectively, while the pair interchange between the two bands is assured by the 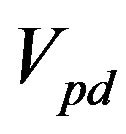 term. The quantity
term. The quantity 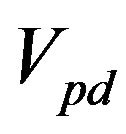 has been supposed to be operative and constant in the energy interval for higher band and lower band, keeping in mind the integration ranges, the gap parameter satisfy the system if the interband interactions are missing, i.e.
has been supposed to be operative and constant in the energy interval for higher band and lower band, keeping in mind the integration ranges, the gap parameter satisfy the system if the interband interactions are missing, i.e.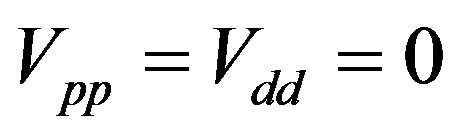 , the transition is solely induced by the interband interaction [16] and given by
, the transition is solely induced by the interband interaction [16] and given by
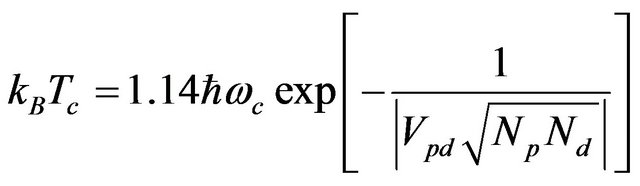 (24)
(24)
Using Equations (24), we can write the simultaneous equation as
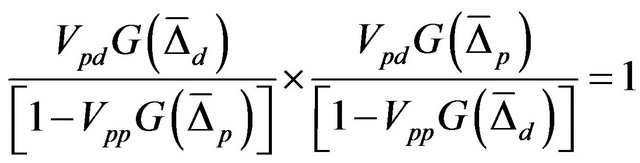 (25)
(25)
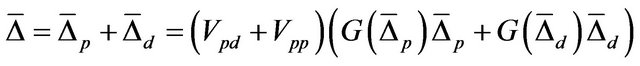 (26)
(26)
3.2. Electronic Specific Heat (Ces)
The electronic specific heat per atom of a superconductor is determined from the following relation [3,23-28]1) For π-band
 (27)
(27)
where 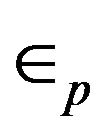 is the energy of π-band and μ is the common chemical potential.
is the energy of π-band and μ is the common chemical potential.
Substituting 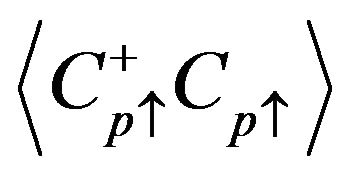 from (10) and changing the summation over p into an integration by using the relation
from (10) and changing the summation over p into an integration by using the relation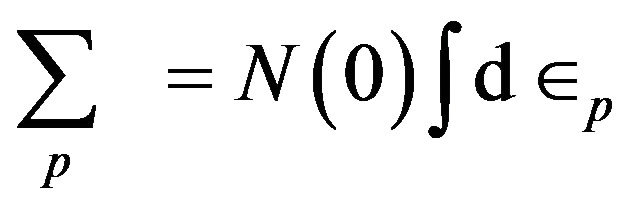 , we obtain
, we obtain
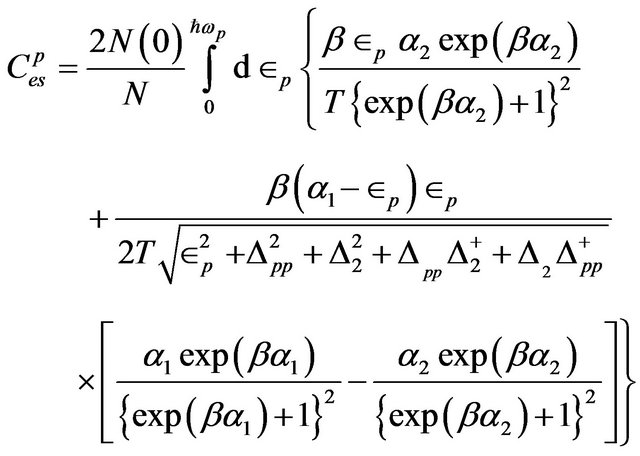 (28)
(28)
where  and
and 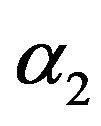 are given by Equation (16).
are given by Equation (16).
2) For σ-band Similarly one can write the expression for electronic specific heat 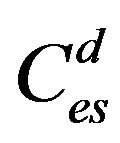 for σ-band, as
for σ-band, as
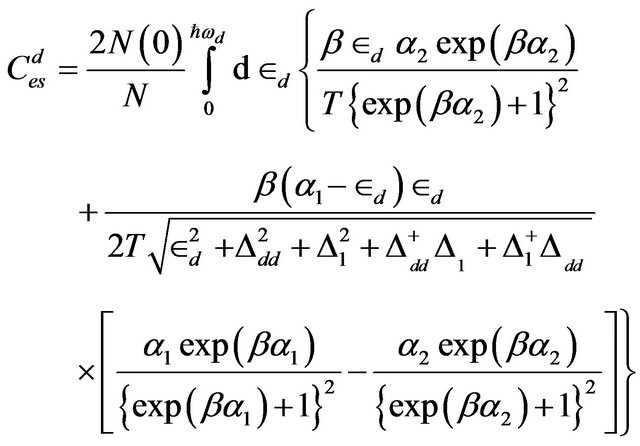 (29)
(29)
where 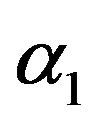 and
and 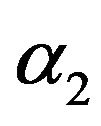 are
are

Electronics specific heat for π-band and σ-band are given by Equations (28) and (29) respectively.
3.3. Density of States N (ω)
The density of states is an important function. This helps in the interpretation of several experimental data e.g. many processes that could occur in crystal but are forbidden because they do not conserve energy. Some of them nevertheless take place, if it is possible to correct the energy imbalance by phonon-assisted processes, which will be proportional to 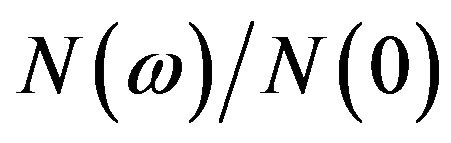 [25]. For
[25]. For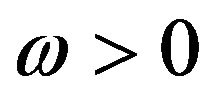 , the density of states per atom
, the density of states per atom  is defined as [26,27].
is defined as [26,27].
 (30)
(30)
where, 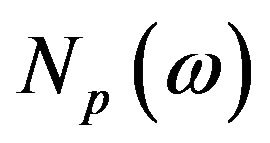 is the density of state function for π- band. For σ-band we have
is the density of state function for π- band. For σ-band we have
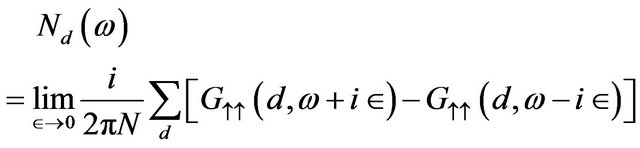 (31)
(31)
where 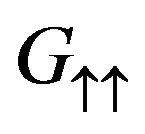 is one particle Green function for π- and σ-bands, defined by Equations (9) and (11) respectively. We have the Green’s function Equation (9),
is one particle Green function for π- and σ-bands, defined by Equations (9) and (11) respectively. We have the Green’s function Equation (9),
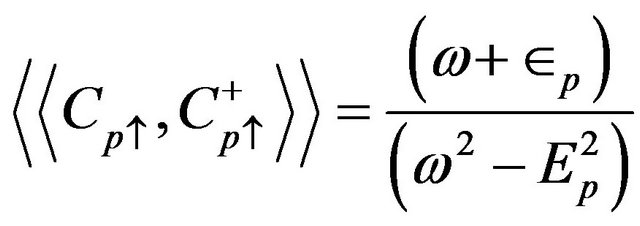 (32)
(32)
where . Now solving Equation (32) and using partial fraction method, we obtain
. Now solving Equation (32) and using partial fraction method, we obtain
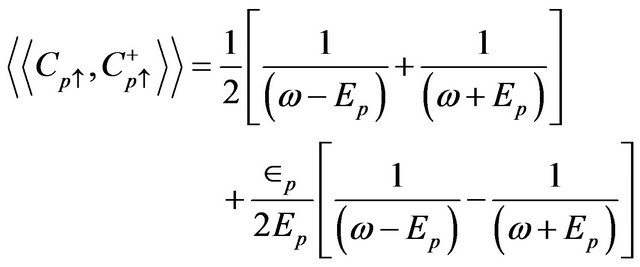 (33)
(33)
Now substituting the Green function from Equation (33) in Equation (30) and using the delta function property,

we obtain
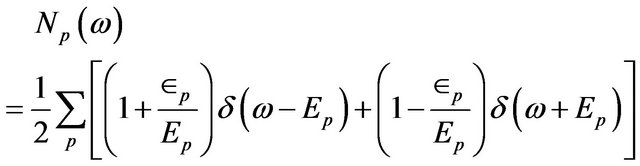 (34)
(34)
Changing the summation into integration and after simplification, one obtains
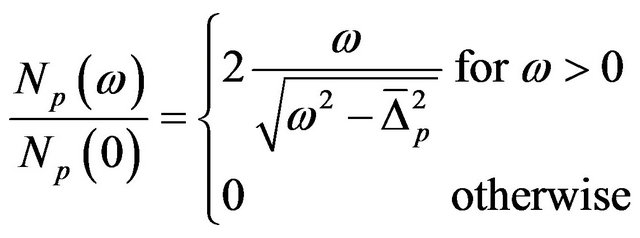 (35)
(35)
Similarly, for σ-band
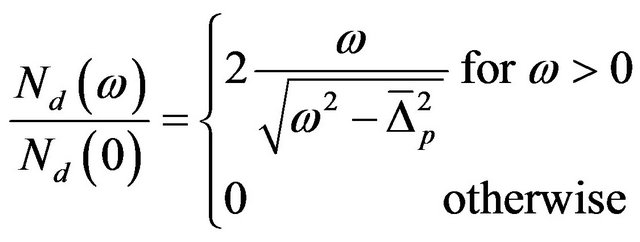 (36)
(36)
4. Numerical Calculations
Values of various parameters appearing in equations obtained in the previous section are given in Table 1. Using these values, we study the various parameters for the system MgB2.
4.1. Superconducting Order Parameter 
For the study of superconducting order parameter for MgB2 system within two band models, one finds the following situations1) The SC order parameter for π- and σ-bands. Using Equation (25), one can write
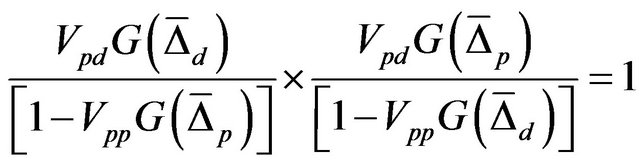
and 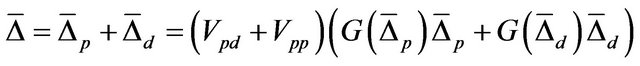
Changing the variables as ,
, 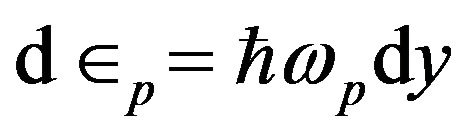 , and taking
, and taking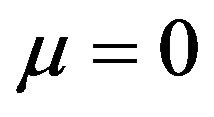 , we obtain Solving Equation (37) numerically, one can study the variation of superconductivity order parameters
, we obtain Solving Equation (37) numerically, one can study the variation of superconductivity order parameters  and
and 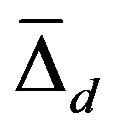 with temperature corresponding π- and σ-bands. The behavior of superconducting order parameters corresponding to π- and σ-bands with temperature is shown in Figure 1.
with temperature corresponding π- and σ-bands. The behavior of superconducting order parameters corresponding to π- and σ-bands with temperature is shown in Figure 1.
2) SC order parameter in the presence of both π- and σ-bands.
The superconducting order parameter for combined π- and σ-bands can be studied by taking a simple sum of both the parameters. Taking the sum of order parameters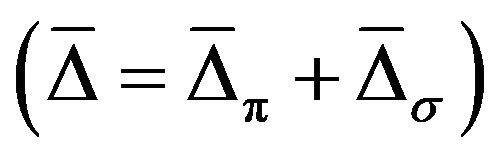 , one can obtain the values by solving numerically. A comparison of
, one can obtain the values by solving numerically. A comparison of  with BCS type curve is shown in Figure 2.
with BCS type curve is shown in Figure 2.
4.2. Electronic Specific Heat (Ces)
1) For π-band Using Equation (28) and putting a1, a2 and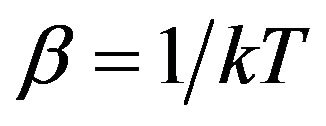 , after simplification, we obtain
, after simplification, we obtain
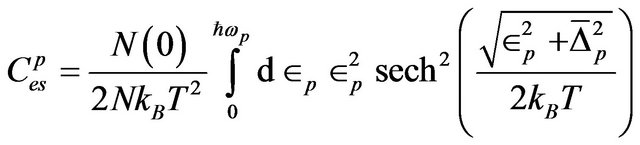 (38)
(38)
Changing the variables as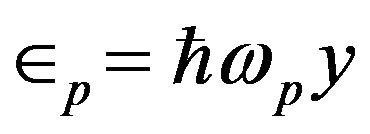 ,
, 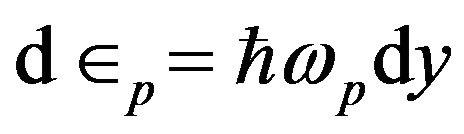 , and using parameters from Table 1 with taking
, and using parameters from Table 1 with taking , we obtain
, we obtain
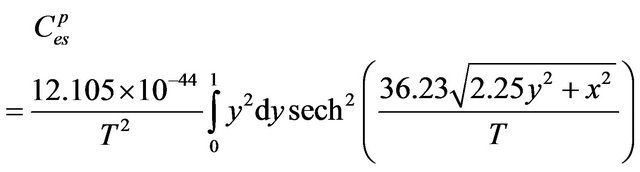 (39)
(39)
2) For σ-band Similarly, we can write expression for specific heat for σ-band using Equation (29)
 (37)
(37)
Table 1. Values of various parameters for MgB2 system.

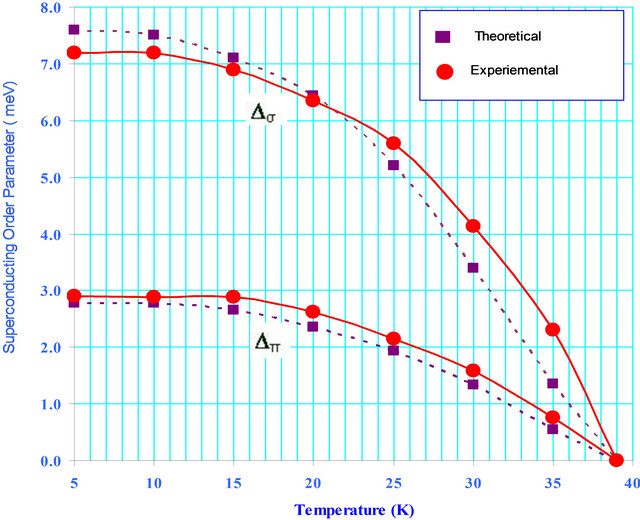
Figure 1. Variation of superconducting order parameter corresponding to π- and σ-bands with temperature [29].

Figure 2. Variation of superconducting order parameter Δ = (Δπ + Δσ) corresponding to π- and σ-bands with temperature.
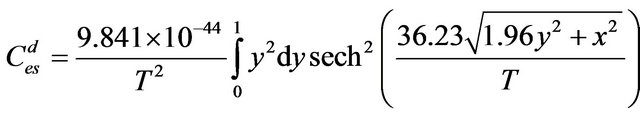 (40)
(40)
The variation electronic specific heat (Ces) with temperature (T) for π- and σ-band is shown in Figure 3. There is a good agreement with experiment data.
4.3. Density of States
Density of states function for the π-band is given by Equation (35). Now using the following values of y, x1 for 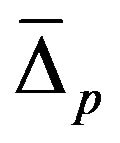 and x2 for
and x2 for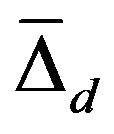 , and taking
, and taking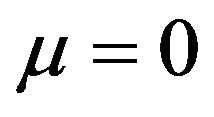 , one obtains,
, one obtains,
 (41)
(41)
Similarly, using Equation (36), density of states for σ- band is obtained as
 (42)
(42)
The above two expressions of density of states function for π- and σ-bands are similar, hence we have evaluated the values with different values of x1 and x2 for π- and σ-bands. The behavior of density of states function for both π- and σ-bands is shown in Figure 4.
5. Discussion and Conclusions
- In the foregoing sections, we have presented the study of superconductivity in MgB2 by canonical two band BCS Hamiltonian containing Fermi surfaces of π- and σ-bands. Following the Green’s function technique and equation of motion method, we have obtained the expressions for superconducting order parameters
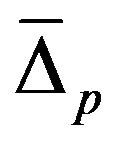 and
and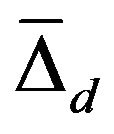 , electronic specific heat, and density of states. Making use of values of various parameters given in Table 1 for the system MgB2, we have made study of various physical properties and wherever possible, compared our results with the available experimental data. We observe that
, electronic specific heat, and density of states. Making use of values of various parameters given in Table 1 for the system MgB2, we have made study of various physical properties and wherever possible, compared our results with the available experimental data. We observe that - 1) The transition temperature for our system MgB2 is found 39 K .
- 2) The temperature dependent two superconducting gaps
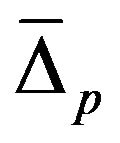 and
and 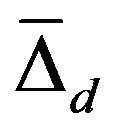 corresponding to π- and σ-bands for MgB2 is found. The two gaps structure is perfectly in agreement with experimental observations .
corresponding to π- and σ-bands for MgB2 is found. The two gaps structure is perfectly in agreement with experimental observations . -
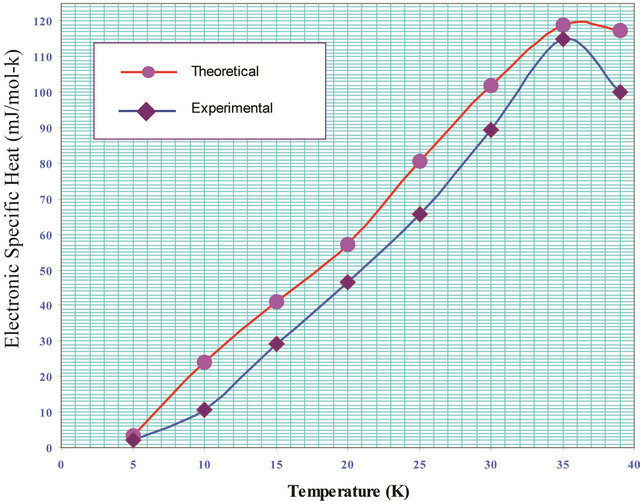
- Figure 3. Variation of electronic specific heat with temperature for both π- and σ-bands.
-
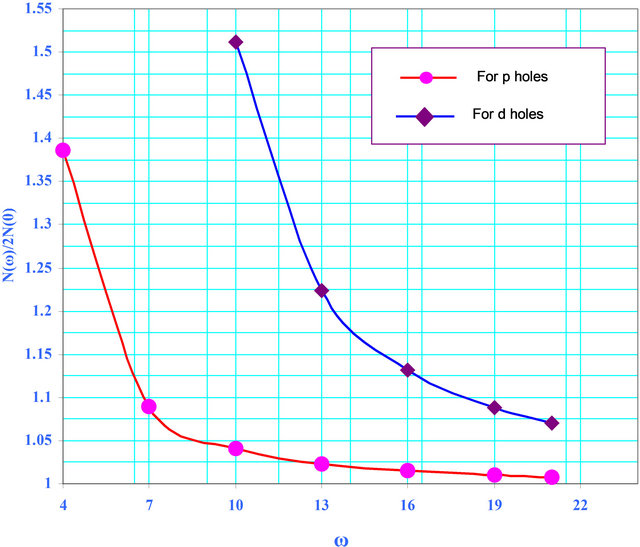
- Figure 4. Variation of density of states function with ω for both π- (p holes) and σ- (d holes) bands.
- 3) The specific heat behaviour obtained from our model, i.e. Ces versus T is in satisfactory agreement with experimental results . However, the theoretical values obtained are slightly higher than the experimental ones. This can be attributed to mean field approximations. In our model, the main interaction is
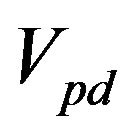 and
and 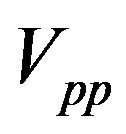 &
& 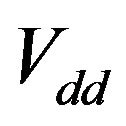 are taken zero (being negligibly small). For better agreement
are taken zero (being negligibly small). For better agreement 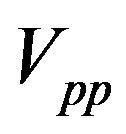 and
and 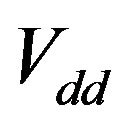 have to be considered. Although these interactions are very small in comparison to
have to be considered. Although these interactions are very small in comparison to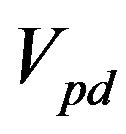 , but still they have some contribution to the specific heat of the system.
, but still they have some contribution to the specific heat of the system. - 4) The density of states behaviour is similar to BCS weak coupling superconductors (Figure 4) corresponding to π- and σ-bands. There is marked difference between two curves. This reveals that MgB2 superconductors differ from conventional metallic superconductors. However, the behavior of MgB2 superconductors in this respect resembles to that of high Tc cuprates. This is a major difference between the two classes of superconductors and may be partly responsible for the difference in their properties. We may note that the density of states for the system MgB2 is quite high .
- Our model shows reasonable agreement with available experimental data. This mechanism emerges as a strong contender for an acceptable model for MgB2, non cuprate high-Tc superconductor. The efforts to understand the pairing mechanism in this and other similar systems need to continue, for such efforts go hand-in-hand with enhancing future prospects for new HTSC materials and novel applications [32-35].
- REFERENCES
- J. Nagamatsu, N. Nakagawa, T. Muranaka, Y. Zenitani and J. Akimitsu, “Superconductivity at 39 K in Magnesium Diboride,” Nature, Vol. 410, No. 6824, 2001, pp. 63-64. doi:10.1038/35065039
- C. Buzea and T. Yamashita, “Review of the Superconducting Properties of MgB2,” Superconductor Science and Technology, Vol. 14, No. 11. 2001, p. R115.
- S. L. Kakani and S. Kakani, “Superconductivity,” Anshan, Ltd., Kent, 2009.
- A. Y. Liu, I. I. Mazin and J. Kortus, “Beyond Eliashberg Superconductivity in MgB2: Anharmonicity, Two-Phonon Scattering, and Multiple Gaps,” Physical Review Letters, Vol. 87, No. 8, 2001, pp. 087005-087009. doi:10.1103/PhysRevLett.87.087005
- J. M. An and W. E. Pickett, “Superconductivity of MgB2: Covalent Bonds Driven Metallic,” Physical Review Letters, Vol. 86, No. 19, 2001, pp. 4366-4369. doi:10.1103/PhysRevLett.86.4366
- K. D. Belaschenko, M. von Schilfgaarde and A. V. Antropov, “Coexistence of Covalent and Metallic Bonding in the Boron Intercalation Superconductor MgB2,” Physical Review B, Vol. 64, No. 9, 2001, pp. 092503-092507. doi:10.1103/PhysRevB.64.092503
- D. A. Papaconstantopoulos and M. J. Mehl, “Precise Tight- Binding Description of the Band Structure of MgB2,” Physical Review B, Vol. 64, No. 17, 2001, pp. 2510-2514
- I. I. Mazin and V. P. Antropo, “Electronic Structure, Electron-Phonon Coupling, and Multiband Effects in MgB2,” Physica C: Superconductivity, Vol. 385, No. 1-2, 2003, pp. 49-65. doi:10.1016/S0921-4534(02)02299-2
- F. Bouqut, Y. Wang, R. A. Fisher, D. G. Hinks, J. D. Jorgensen, A. Junod and N. E. Phillips, “Phenomenological Two-Gap Model for the Specific Heat of MgB2,” Europhysics Letters, Vol. 56, No. 6, 2001, p. 856. doi:10.1209/epl/i2001-00598-7
- F. Bouquet, R. A. Fisher, N. E. Phillips, D. G. Hinks and D. Jorgensen, “Specific Heat of Mg11B2: Evidence for a Second Energy Gap,” Physical Review Letters, Vol. 87, No. 4, 2001, pp. 047001-047005. doi:10.1103/PhysRevLett.87.047001
- Y. Wang, T. Plackowski and A. Junod, “Specific Heat in the Superconducting and Normal State (2-300 K, 0-16 T), and Magnetic Susceptibility of the 38 K Superconductor MgB2: Evidence for a Multicomponent Gap,” Physica C: Superconductivity, Vol. 355, No. 3-4, 2001, pp. 179-193. doi:10.1016/S0921-4534(01)00617-7
- G. A. Ummarino, R. S. Gonnelli, S. Massidda and A. Bianconi, “Electron-Phonon Coupling and Two-Band Superconductivity of Aland C-Doped MgB2,” 2010.
- S. L. Bud’ko, G. Lapertot, C. Petrovic, C. E. Cunningham, N. Anderson and P. C. Canfield, “Boron Isotope Effect in Superconducting MgB2,” Physical Review Letters, Vol. 86, No. 9, 2001, pp. 1877-1880. doi:10.1103/PhysRevLett.86.1877
- H. Shul, B. T. Matthias and L. R. Walker, “Bardeen-Cooper-Schrieffer Theory of Superconductivity in the Case of Overlapping Bands,” Physical Review Letters, Vol. 3, No. 12, 1959, pp. 552-554. doi:10.1103/PhysRevLett.3.552
- V. A. Moskalenko, M. E. Palistrant and V. M. Vakalyuk, “High-Temperature Superconductivity and the Characteristics of the Electronic Energy Spectrum,” Soviet Physics Uspekhi, Vol. 34, No. 8, 1991, p. 717. doi:10.1070/PU1991v034n08ABEH002466
- N. Kristoffel, P. Konsin and T. Ord, “Two-Band Model for High-Temperature Superconductivity,” Rivista Del Nuovo Cimento, Vol. 17, No. 9, 1994, pp. 1-41. doi:10.1007/BF02724515
- N. Kristoffel and P. Rubin, “Pseudogap and Superconductivity Gaps in a Two Band Model with Doping Determined Components,” Solid State Communications, Vol. 122, No. 5, 2002, pp. 265-268.
- B. K. Chakraverty, “Superconductivity in Two Band Model,” Physical Review B, Vol. 48, No. 6, 1993, pp. 4047-4053. doi:10.1103/PhysRevB.48.4047
- R. Lal, Ajay, R. L. Hota and S. K. Joshi, “Model for c-Axis Resistivity of Cuprate Superconductors,” Physical Review B, Vol. 57, No. 10, 1998, pp. 6126-6136. doi:10.1103/PhysRevB.57.6126
- A. Pratap, Ajay and A. S. Tripathi, “Effect of Interlayer Interactions in High-Tc Cuprate Supercoductors,” Journal of Superconductivity, Vol. 9, No. 6, 1996, pp. 595-597. doi:10.1007/BF00728239
- S. Khandka and P. Singh, “Effect of Interlayer Interaction on Tc with Number of Layers in High Tc Cuprate Superconductors,” Physica Status Solidi B, Vol. 244, No. 2, 2007, pp. 699-708. doi:10.1002/pssb.200542285
- S. Das and N. C. Das, “Erratum: Theory of Hole Superconductivity,” Physical Review B, Vol. 46, No. 10, 1992, pp. 6451-6457. doi:10.1103/PhysRevB.46.6451
- S. L. Kakani and U. N. Upadhyaya, “Cooperative Phenomena in Ternary Superconductors,” Journal of Low Temperature Physics, Vol. 53, No. 1-2, 1983, pp. 221-253. doi:10.1007/BF00685781
- S. L. Kakani and U. N. Upadhyaya, “Superconducting and Magnetic Order Parameters in the Coexistence Region of Ternary Superconductors,” Physica Status Solidi B, Vol. 125, No. 2, 1984, pp. 861-867. doi:10.1002/pssb.2221250249
- S. L. Kakani and U. N. Upadhyaya, “Frequency Dependent Susceptibility of Rare Earth Ternary Superconductors,” Physica Status Solidi B, Vol. 136, No. 1, 1986, pp. 115-121. doi:10.1002/pssb.2221360113
- S. L. Kakani and U. N. Upadhyaya, “Coexistence of Superconductivity and Ferromagnetism in Rare Earth Ternary Systems,” Physica Status Solidi A, Vol. 99, No. 1, 1987, pp. 15-36. doi:10.1002/pssa.2210990104
- S. L. Kakani and U. N. Upadhyaya, “Magnetic Superconductors: A Review,” Journal of Low Temperature Physics, Vol. 70, No. 1-2, 1988, pp. 5-82. doi:10.1007/BF00683246
- A. L. Fetter and J. D. Walecka, “Quantum Theory of Many Particle Physics,” McGraw-Hill, New York, 1971.
- C. Buzea and T. Yamashita, “Review of the Superconducting Properties of MgB2,” Superconductor Science and Technology, Vol. 14, No. 11, 2001, p. R115. doi:10.1088/0953-2048/14/11/201
- C. Walti, E. Felder, C. Degen, G. Wigger, R. Monnier, B. Delley and H. R. Ott, “Strong Electron-Phonon Coupling in Superconducting MgB2: A Specific Heat Study,” Physical Review B, Vol. 64, No. 17, 2001, pp. 172515- 172519. doi:10.1103/PhysRevB.64.172515
- N. E. Phillips and R. A. Fisher, “Superconducting-State Energy Gap Parameters from Specific Heat Measurements,” Journal of Thermal Analysis and Calorimetry, Vol. 81, No. 3, 2005, pp. 631-635. doi:10.1007/s10973-005-0835-y
- S. L. Kakani, “Superconductivity: Current Topics: Chapters 2 and 3,” Bookman Associate, Jaipur, 1999.
- S. Kakani and S. L. Kakani, “Theoretical Study of Specific Heat, Density of States and Free Energy of Itinerant Ferromagnetic Superconductor URhGe,” Journal of Superconductivity and Novel Magnetism, Vol. 22, No. 7, 2009, pp. 677-685. doi:10.1007/s10948-009-0465-x
- A. Kashyap, S. C. Tiwari, A. Surana, R. K. Paliwal and S. L. Kakani, “Theoretical Study of Specific Heat, Density of States, Free Energy,and Critical Field of High Temperature Cuprate Superconductors Based on Intra and Interlayer Interactions,” Journal of Superconductivity and Novel Magnetism, Vol. 21, No. 2, 2008, pp. 129-143. doi:10.1007/s10948-008-0308-1
- A. Nuwal, R. K. Paliwal, S. L. Kakani and M. L. Kalara, “Theoretical study of Photoinduced Superconductors in a Two Band Model,” Physica C: Superconductivity, Vol. 471, No. 9-10, 2011, pp. 318-331. doi:10.1016/j.physc.2011.03.004
- G. Alecu, “Reports in Physics,” Romanian Reports in Physics, Vol. 56, No. 3, 2004, pp. 404-412.
NOTES
*Corresponding author.

