World Journal of Condensed Matter Physics
Vol.2 No.1(2012), Article ID:17645,6 pages DOI:10.4236/wjcmp.2012.21006
Ground State Properties of Monolayer Doped Graphene
![]()
1Physics Department, Faculty of Science, The Maharaja Sayajirao University of Baroda, Vadodara, India; 2Applied Physics Department, Zakir Hussain College of Engineering and Technology, Aligarh Muslim University, Aligarh, India.
Email: *kavita.physics@hotmail.com
Received November 29th, 2011; revised January 29th, 2012; accepted February 6th, 2012
Keywords: Screening Charge Density; Self Energy; Compressibility; Screened Potential
ABSTRACT
We performed theoretical investigations on self-energy, screening charge density, screened potential and pair distribution function for a doped single layer graphene. Random phase approximation density-density response function and graphene’s massless Dirac-fermions concept have been used in our calculations. Local field effects have been included using Hubbard approximation to go beyond random phase approximation. Ultraviolet wave vector cutoff has been used to exclude the effect of vacuum states. Our computed self energy of graphene though displays a behavour similar to that of 2DEG, its magnitude differs drastically from that of 2DEG. Freidel oscillations are seen in computed screened potential and density of screening charge of graphene, which can be seen as a signature of Fermi liquid state in doped graphene. In agreement with experimental results, our computed pair distribution function, as a function of carrier density, suggests that exchange and correlation terms make negligible contribution to compressibility of graphene. Incorporation of LFC reduces the magnitude of self energy, screening charge density and screened potential.
1. Introduction
Graphene has developed into one of the currently most active research in nano-scale physics and can be considered as the building block of many carbon allotropes with vast potential for applications in future technology. Monolayer Graphene (MLG) system has properties of chiral Dirac gas which leads to some important consequences for transport behavior. Graphene’s unique properties arise from the collective behavior of electrons. The interaction between electrons and the honeycomb lattice causes electrons to behave as if they have absolutely no mass. The spectrum of Fermions near intersection points is conical and they obey charge conjugation symmetry. Because of the linear energy dispersion, conduction electrons in graphene are governed by Dirac equation which describes relativistic Fermions.
Knowledge of ground state properties of a system is essential in understanding its basic physics and to make use of it for device making. Single-particle spectral function, associated mean free paths, quasiparticle properties, such as inelastic quasiparticle lifetimes quasiparticle decay, renormalization factor, and renormalization velocity can be studied by knowing electron self-energy [1,2]. Selfenergy can also be used to obtain ARPES spectra which have been reported by a host of authors for graphene [3- 5]. When a positive charge is placed in an electron gas, the electrons gather around the charge tries to compensate for the electrostatic potential it has induced. The phenomenon is known as screening and it is one of the simplest and most important manifestations of electronelectron interaction [6]. Because of reduced dimensionality and especially because of the semi-metallic nature of graphene’s π-electron bands, the problem of screening of charged impurities remains open. In this context, various authors have reported calculations on screening, few of which include scattering treatment of Coulomb impurities embedded within the graphene plane [7,8]. Calculations on charged impurity screening in graphene with the use of vacuum polarization has received a huge attention because of its importance for transport properties and a general understanding of the theory of graphene. Static screening determines transport properties through screened Coulomb carrier scattering by charged impurities [9,10]. The property of screening is also of interest for sensor applications of graphene in detecting atoms or molecules, which may be either absorbed on the upper surface of graphene or intercalated in the gap between the graphene substrate. It has been shown that within the RPA approach, screening of external charges by intrinsic graphene at zero temperature is characterized merely by a renormalization of graphene’s background dielectric constant due to interband electron transitions [9-13]. The most common feature observed in screened potential is Friedel oscillations, which arise because of derivative discontinuity.
In an interacting electron system of uniform density, the inverse electronic compressibility is a fundamental physical quantity that is intimately related to the strength of inter-electron interactions. The compressibility of electron gas provides valuable information about the nature of the interacting ground state, particularly in the strongcoupling regime where (in addition to the exchange energy) Coulomb interaction energy also plays a dominant role. It also provides information about the chemical potential, stability of the system and so on. Change of local electrostatic potential and thereby change in local chemical potential of MLG was measured with the use of scanning single-electron transistor microscopy when the carrier density was modulated [14]. Observed results on local inverse compressibility were found to be quantitatively described by kinetic energy alone with the electron velocity renormalized by 10% - 15%. It has been speculated that the exchange and correlation energy contributions to compressibility either cancel each other out or are negligibly small. It has been argued that in MLG linear energy dispersion and chirality conspire to allow complete cancellation of exchange and correlation contributions just as was observed in the experiment [15]. This motivated us to compute pair distribution function as a function of carrier density, n to study the n-dependence of compressibility of graphene.
Many-body effects in MLG with zero gap and doping at zero temperature have been the subject of great interests [10,11]. Aim of this paper is to study the ground state properties of doped MLG with the use of modified RPA density-density response function and a wave vector cutoff method, at zero temperature. We have numerically calculated self energy, density of screening charge, screened potential, pair distribution function of doped graphene, using static polarization function with and without local field corrections (LFC). To best of our knowledge these properties have not yet been reported using wave vector cut-off method, which is essential to exclude the contributions from vacuum states. This is in continuation with our earlier work on static and dynamic structure factor of undoped and doped graphene and pair correlation function [16]. The RPA polarization function for low energy excitation involves graphene’s π-electron energy bands that have linear energy dispersion. We have calculated Screening charge density for different values of coupling constant and carrier density. Friedel oscillations are observed in the case of screening charge density and screened potential, which can be used to gain insight into microscopic range of disorder. The computed self energy is found to be greater than that for 2D electron gas. We computed pair distribution function as a function of carrier density n to study the n-dependence of compressibility of graphene. The RPA is a many body theoretical method by which quantitative predictions beyond the HartreeFock model can be made. And, though it is very successful in describing many properties nevertheless it has its shortcoming, one of which is that it misses to accommodate the local field effects due to electronic exchange and correlation. The electron-electron correlation and exchange effect beyond the RPA is taken into account by incorporating a term containing the local field corrections in the effective potential. The paper is organized as follows: Formalism is presented in Section 2, numerical results are discussed in Section 3 and the work is concluded in Section 4.
2. Essential Formalism
For a 2D system, self-energy, 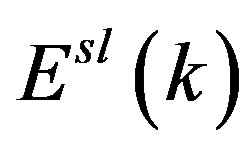 , density of screening charge,
, density of screening charge, 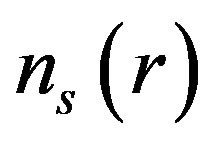 and Screened potential,
and Screened potential, 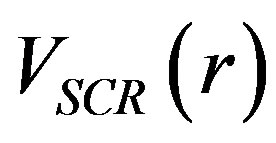 can be given, respectively, by the following Equation [17];
can be given, respectively, by the following Equation [17];
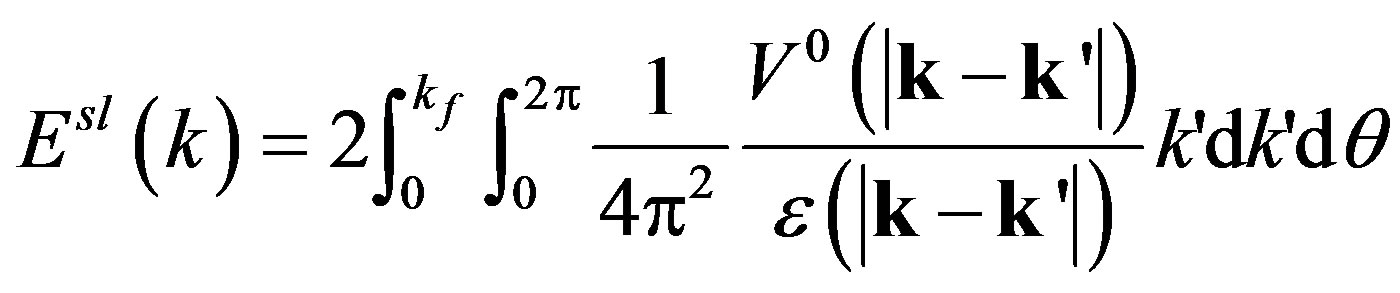 (1)
(1)
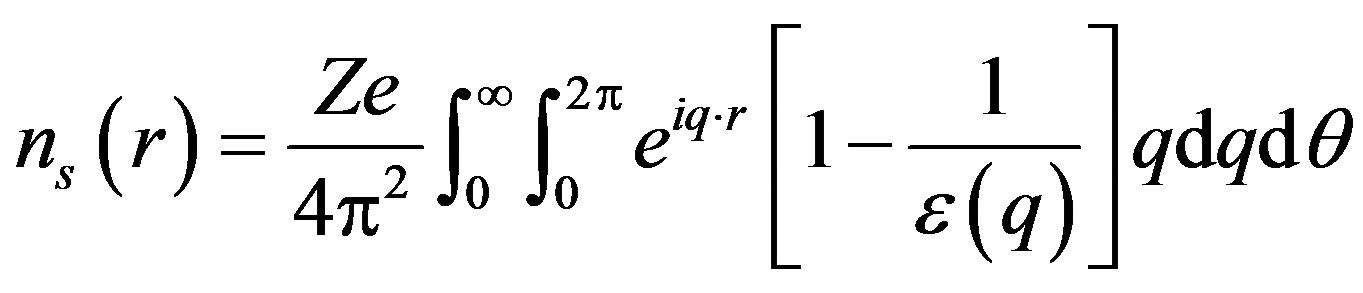 (2)
(2)
 (3)
(3)
The static dielectric function  is defined as;
is defined as;
 (4)
(4)
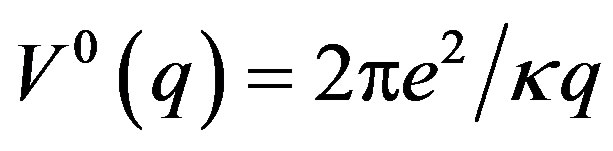 is the Fourier transform of 2D bare Coulomb interaction potential, κ is the background dielectric constant and kf is Fermi momentum. q is replaced by
is the Fourier transform of 2D bare Coulomb interaction potential, κ is the background dielectric constant and kf is Fermi momentum. q is replaced by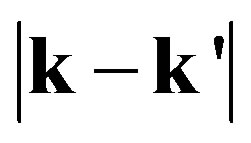 , in obtaining Equation (1).
, in obtaining Equation (1).  is the static polarization function, which for graphene is given by [10]:
is the static polarization function, which for graphene is given by [10]:

where, 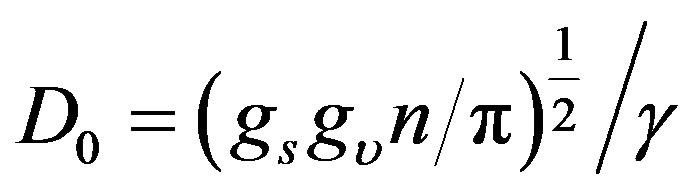 is the density of states at Fermi energy,
is the density of states at Fermi energy,  and
and 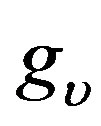 are the spin and valley degeneracy, and
are the spin and valley degeneracy, and 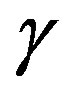 is the band parameter. The charge carriers in graphene behave like massless chiral Dirac Fermions. The low energy quasiparticle dynamics of the noninteracting electrons on the hexagonal graphene sheet close to the Fermi energy is described by the spin-independent mass less Dirac-Weyl Hamiltonian,
is the band parameter. The charge carriers in graphene behave like massless chiral Dirac Fermions. The low energy quasiparticle dynamics of the noninteracting electrons on the hexagonal graphene sheet close to the Fermi energy is described by the spin-independent mass less Dirac-Weyl Hamiltonian,  , where
, where
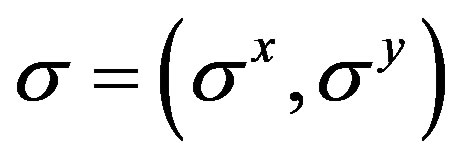 denote the two Pauli matrices that act on the graphene’s pseudo spin degrees of freedom and k is 2D wave-vector measured from the two-degenerate K and
denote the two Pauli matrices that act on the graphene’s pseudo spin degrees of freedom and k is 2D wave-vector measured from the two-degenerate K and  points. This Hamiltonian leads to the linear energy dispersion relation
points. This Hamiltonian leads to the linear energy dispersion relation  where
where 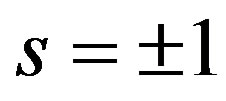 indicate the conduction (+1) and valence band (–1),
indicate the conduction (+1) and valence band (–1), 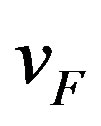 is the Fermi velocity, which is density independent and about 300 times smaller than velocity of light in vacuum. Integration over entire q-range (0 to
is the Fermi velocity, which is density independent and about 300 times smaller than velocity of light in vacuum. Integration over entire q-range (0 to ) in Equations (2) and (3) gives unphysical results because the polarizability response function of graphene includes the vacuum fluctuations of the infinite sea of negative particles. The nonzero vacuum weight is a relativistic signature of graphene and it is a conesquence of particle-antiparticle pair creation or the Dirac sea. To overcome this we introduce an ultraviolet wave vector cut off
) in Equations (2) and (3) gives unphysical results because the polarizability response function of graphene includes the vacuum fluctuations of the infinite sea of negative particles. The nonzero vacuum weight is a relativistic signature of graphene and it is a conesquence of particle-antiparticle pair creation or the Dirac sea. To overcome this we introduce an ultraviolet wave vector cut off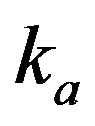 , which becomes necessary to make quantitative predictions for the peculiar case of graphene [18]. The upper limit of q-integration is therefore taken
, which becomes necessary to make quantitative predictions for the peculiar case of graphene [18]. The upper limit of q-integration is therefore taken 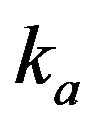 in place of
in place of  in Equations (2) and (3).
in Equations (2) and (3). 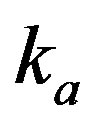 is determined in a way so as to keep the number of states in Brillouin zone fixed, that is,
is determined in a way so as to keep the number of states in Brillouin zone fixed, that is,  , in which
, in which 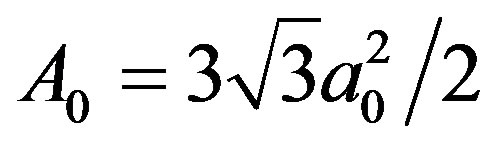 is the area of the unit cell in the honeycomb lattice and
is the area of the unit cell in the honeycomb lattice and 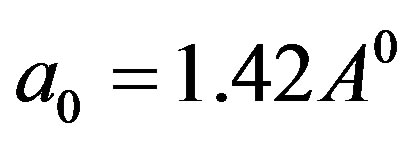 is the carbon-carbon distance [16].
is the carbon-carbon distance [16].
We have computed pair distribution function as a function of n to study the n-dependence of compressibility of graphene. The compressibility can be defined by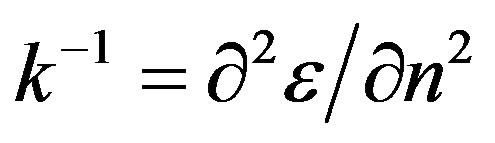 , where energy per particle functional,
, where energy per particle functional,  can be expressed in terms of kinetic energy per particle, t0, Coulomb potential, Vcoul, pair correlation function, g(r) as follows [19];
can be expressed in terms of kinetic energy per particle, t0, Coulomb potential, Vcoul, pair correlation function, g(r) as follows [19];
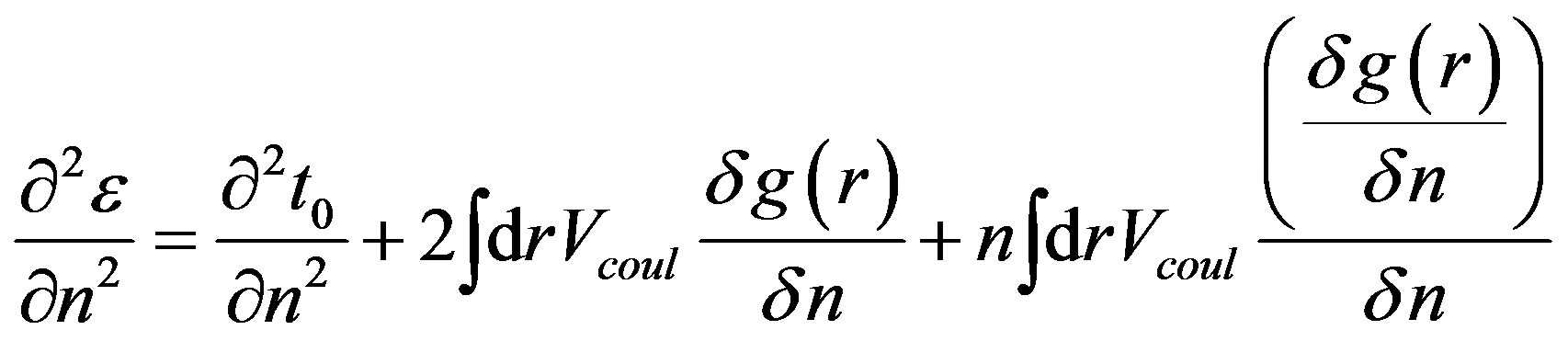 (7)
(7)
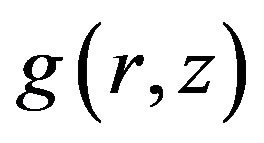 for graphene can be given by:
for graphene can be given by:
 (8)
(8)
where n = z × 1014 cm–2.
 is static structure factor, which has been defined elsewhere for graphene [16]. To go beyond RPA in calculating
is static structure factor, which has been defined elsewhere for graphene [16]. To go beyond RPA in calculating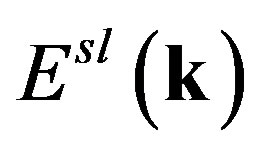 ,
, 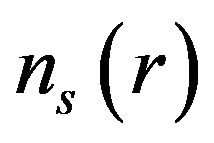 and
and , bare coulomb interaction is replaced by effective electron-electron interaction,
, bare coulomb interaction is replaced by effective electron-electron interaction, 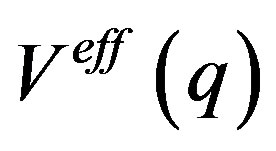 that includes local field effects can be given by [17];
that includes local field effects can be given by [17];
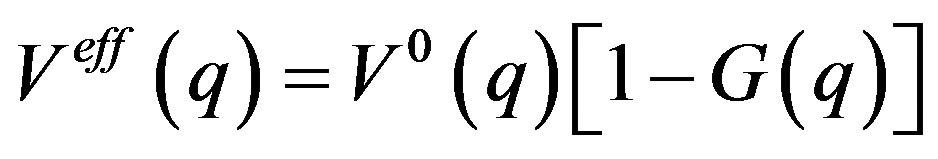 (9)
(9)
where 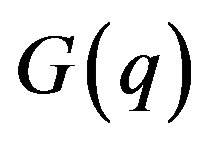 is the static local field correction (LFC) term, which in simplest manner can be defined within Hubbard approximation (HA) to give
is the static local field correction (LFC) term, which in simplest manner can be defined within Hubbard approximation (HA) to give
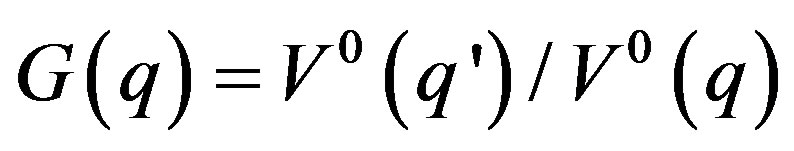 , with
, with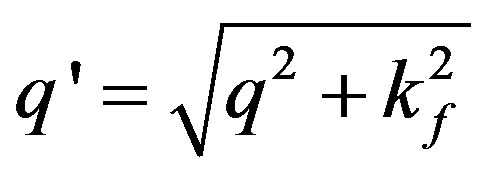 .
.
3. Results and Discussions
We computed Equations (1), (2), (3) and (8) numerically for MLG in terms of dimensional less quantities 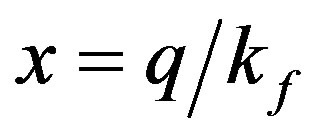 and
and 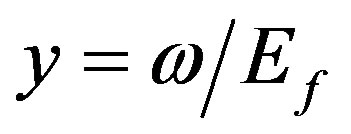 and the dimensionless coupling constant
and the dimensionless coupling constant
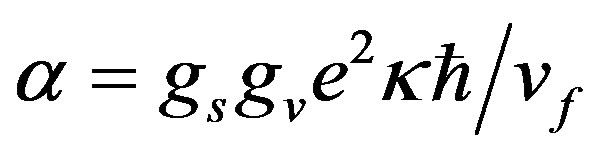 , where κ varies between 1 and 2 for SiC and SiO2 substrate. The coupling constant is a ratio of coulomb energy to kinetic energy and it is independent of the electronic density. It depends only on material properties and environmental conditions and it is the measure of the strength of the Columbic attraction.
, where κ varies between 1 and 2 for SiC and SiO2 substrate. The coupling constant is a ratio of coulomb energy to kinetic energy and it is independent of the electronic density. It depends only on material properties and environmental conditions and it is the measure of the strength of the Columbic attraction. 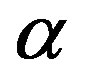 is also used to characterize the ratio of coulomb interaction and band energy scales in graphene.
is also used to characterize the ratio of coulomb interaction and band energy scales in graphene.
The self-energy is the central quantity for determining the many Fermi liquid parameters. Our computed  from Equation (1) is plotted as a function of x in Figure 1(a) without LFC and in Figure 1(b) with the inclusion
from Equation (1) is plotted as a function of x in Figure 1(a) without LFC and in Figure 1(b) with the inclusion
 (a)
(a)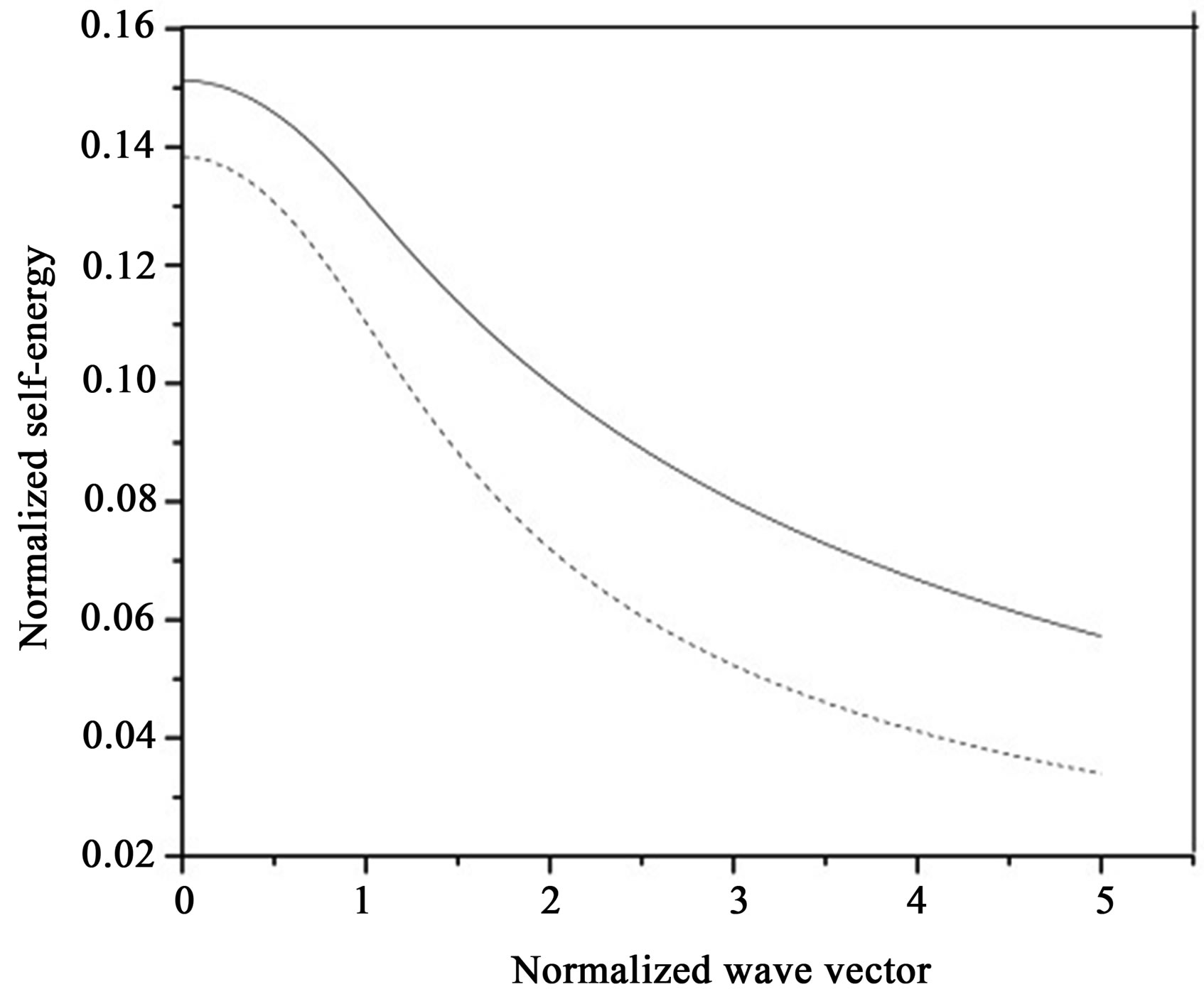 (b)
(b)
Figure 1. (a) Normalized screened self energy, Esl/e2kf is plotted against normalized wave vector k/kf Solid Curve displays Self energy of graphene while dashed curve is for 2DEG, without LFC; (b) Normalized screened self energy, Esl/e2kf as a function of k/kf without LFC (solid line curve) with LFC (dashed line curve).
of LFC. We also computed self-energy of 2DEG to compare it with that of doped MLG. As is seen from Figure 1(a), behavior of computed  of MLG with x is very similar to that of 2DEG. However, magnitude of
of MLG with x is very similar to that of 2DEG. However, magnitude of  of doped MLG is greater than of that of 2DEG. The differnce in magnitude of
of doped MLG is greater than of that of 2DEG. The differnce in magnitude of 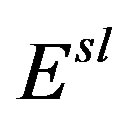 of MLG and of 2DEG is because of different values of intrinsic parameters of two systems, which enter into self-energy through static dielectric function that can be described by
of MLG and of 2DEG is because of different values of intrinsic parameters of two systems, which enter into self-energy through static dielectric function that can be described by
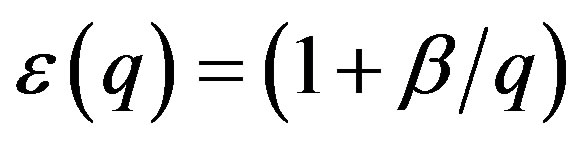 for both MLG and 2DEG. Where
for both MLG and 2DEG. Where 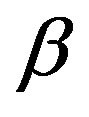 is equal to
is equal to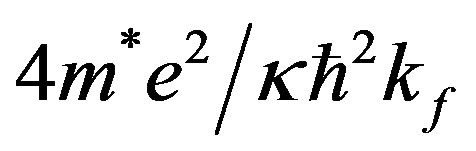 which depends on n in case of 2DEG, while for graphene it is independent of n. For computing
which depends on n in case of 2DEG, while for graphene it is independent of n. For computing 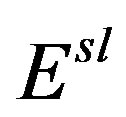 of 2DEG, we have used m* = 0.067 me and κ = 13. Further to see the effect of LFC on self-energy, we computed
of 2DEG, we have used m* = 0.067 me and κ = 13. Further to see the effect of LFC on self-energy, we computed 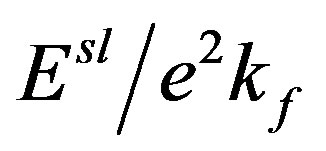 including LFC within HA for doped MLG. As is seen from Figure 1(b); 1) magnitude of self-energy reduces marginally; and 2) downward slope of
including LFC within HA for doped MLG. As is seen from Figure 1(b); 1) magnitude of self-energy reduces marginally; and 2) downward slope of 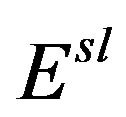 verses x enhances, especially for x > 1, on inclusion of LFC. This suggests that local fields does not play very important role in determination of self-energy in a doped MLG.
verses x enhances, especially for x > 1, on inclusion of LFC. This suggests that local fields does not play very important role in determination of self-energy in a doped MLG.
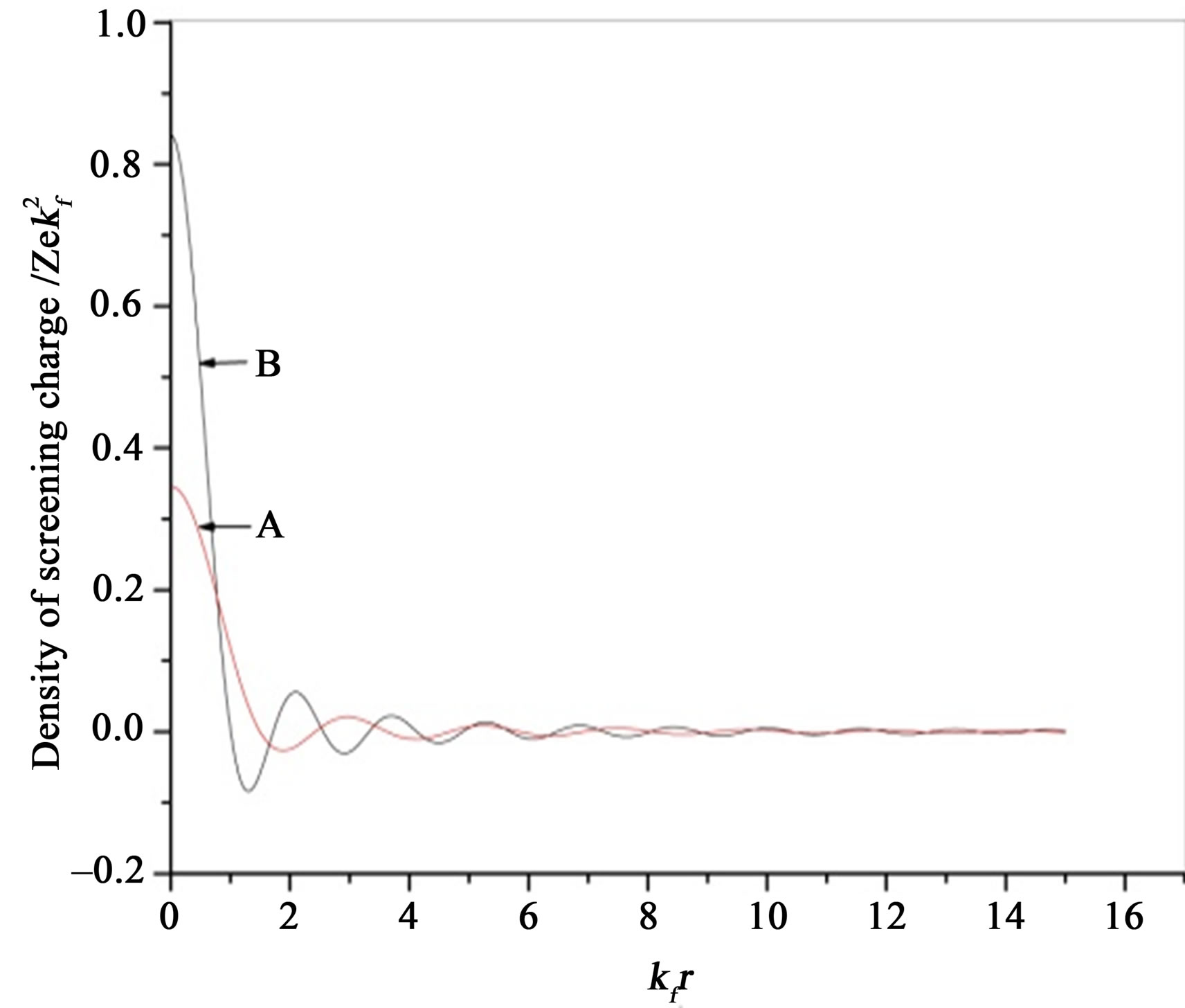
Our computed  is plotted as a function of
is plotted as a function of 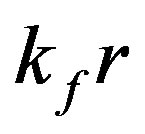 in Figure 2(a) for two values of
in Figure 2(a) for two values of 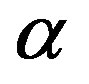 (=2 & 4) at fix value of n and in Figure 2(b) for two values of n (n = 4.77 × 1014 cm–2 & 8.04 × 1014 cm–2) for
(=2 & 4) at fix value of n and in Figure 2(b) for two values of n (n = 4.77 × 1014 cm–2 & 8.04 × 1014 cm–2) for 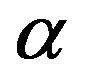 = 4. Computed
= 4. Computed 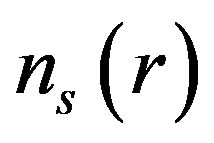 is finite for r tending to zero and it exhibits oscillations, which eventually decays for larger values of r. These oscillations are known as Friedel oscillations and are the result of the non-analyticity which occurs because of the discontinuity in second derivative, the first being continuous [11,20]. As is displayed in Figure 2(a), on increasing the value of
is finite for r tending to zero and it exhibits oscillations, which eventually decays for larger values of r. These oscillations are known as Friedel oscillations and are the result of the non-analyticity which occurs because of the discontinuity in second derivative, the first being continuous [11,20]. As is displayed in Figure 2(a), on increasing the value of 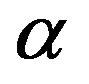 for fixed value of n; 1)
for fixed value of n; 1)  substantially enhances for lower values of r (close to
substantially enhances for lower values of r (close to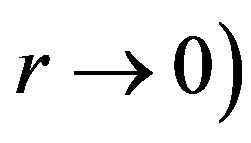 ; and 2) Friedel oscillations becomes more pronounced. The behaviour of our computed
; and 2) Friedel oscillations becomes more pronounced. The behaviour of our computed 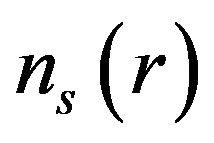 is very similar to that observed in a Fermi liquid where many body effects influence the amplitude of oscillations which are characterized by power law decay and depend on the strength of the interactions [11]. Figure 2(b), shows that on increasing carrier density at fixed value of
is very similar to that observed in a Fermi liquid where many body effects influence the amplitude of oscillations which are characterized by power law decay and depend on the strength of the interactions [11]. Figure 2(b), shows that on increasing carrier density at fixed value of , magnitude of
, magnitude of  reduces specially for
reduces specially for 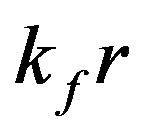 close to zero and the amplitude of Friedel oscillations decreases. Inclusion of LFC reduces the magnitude of
close to zero and the amplitude of Friedel oscillations decreases. Inclusion of LFC reduces the magnitude of 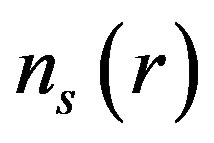 at all rvalues and makes it better behaved for
at all rvalues and makes it better behaved for , as is seen from Figure 2(c). Our computed screened potential with the use of Equation (3) is plotted in Figure 3. Friedel Oscillations are clearly observed in the potential images which are in good agreement with the experimental work conducted on 2D electron gas, using low temperature Scanning tunneling microscope [21]. Inclusion of LFC reduces the magnitude of
, as is seen from Figure 2(c). Our computed screened potential with the use of Equation (3) is plotted in Figure 3. Friedel Oscillations are clearly observed in the potential images which are in good agreement with the experimental work conducted on 2D electron gas, using low temperature Scanning tunneling microscope [21]. Inclusion of LFC reduces the magnitude of 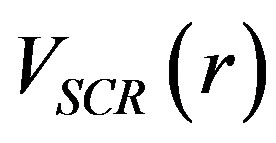 too and makes it better behaved as is displayed in Figure 3. Under the RPA approximation, which assumes that the induced charge
too and makes it better behaved as is displayed in Figure 3. Under the RPA approximation, which assumes that the induced charge
 (a)
(a)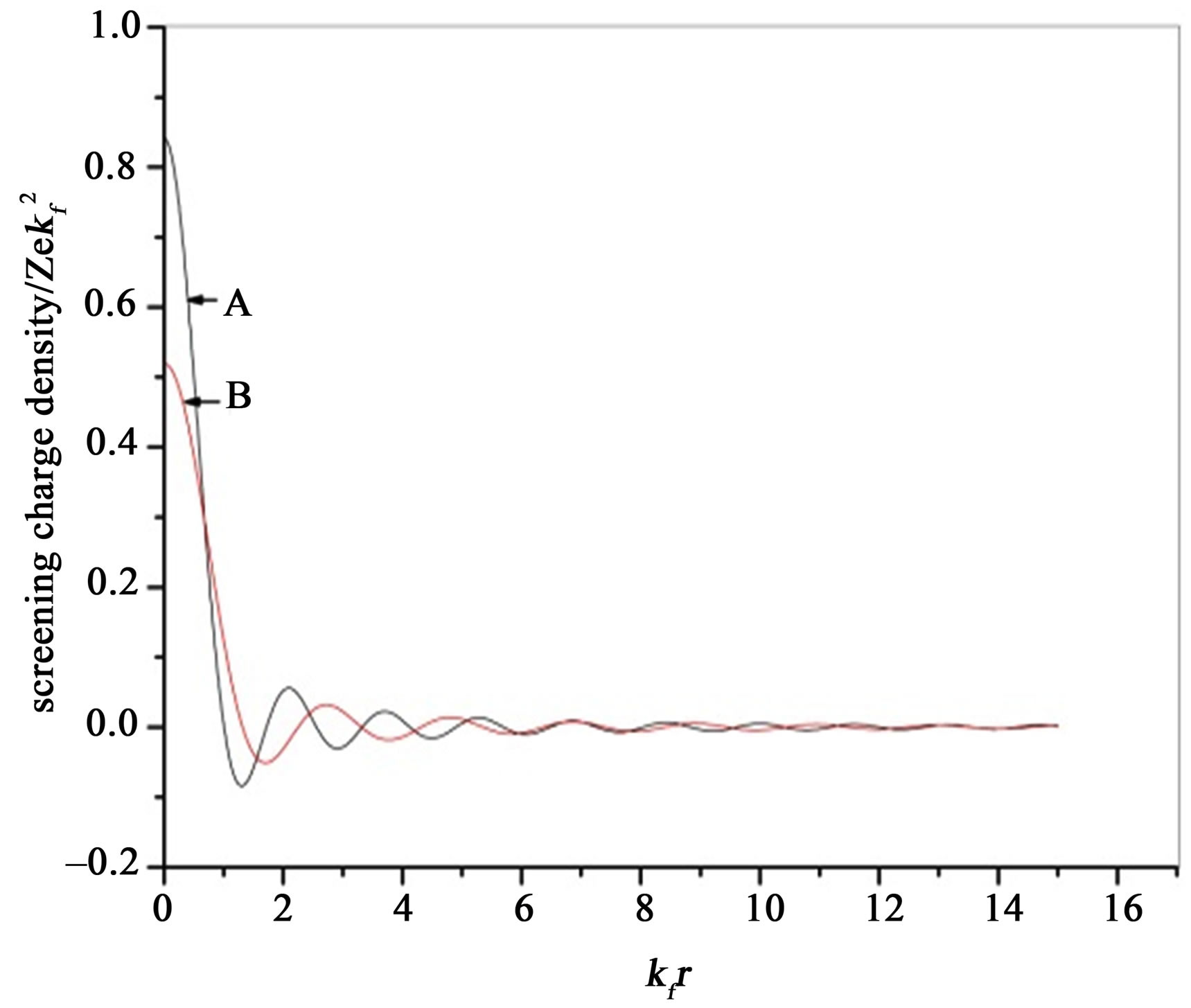 (b)
(b)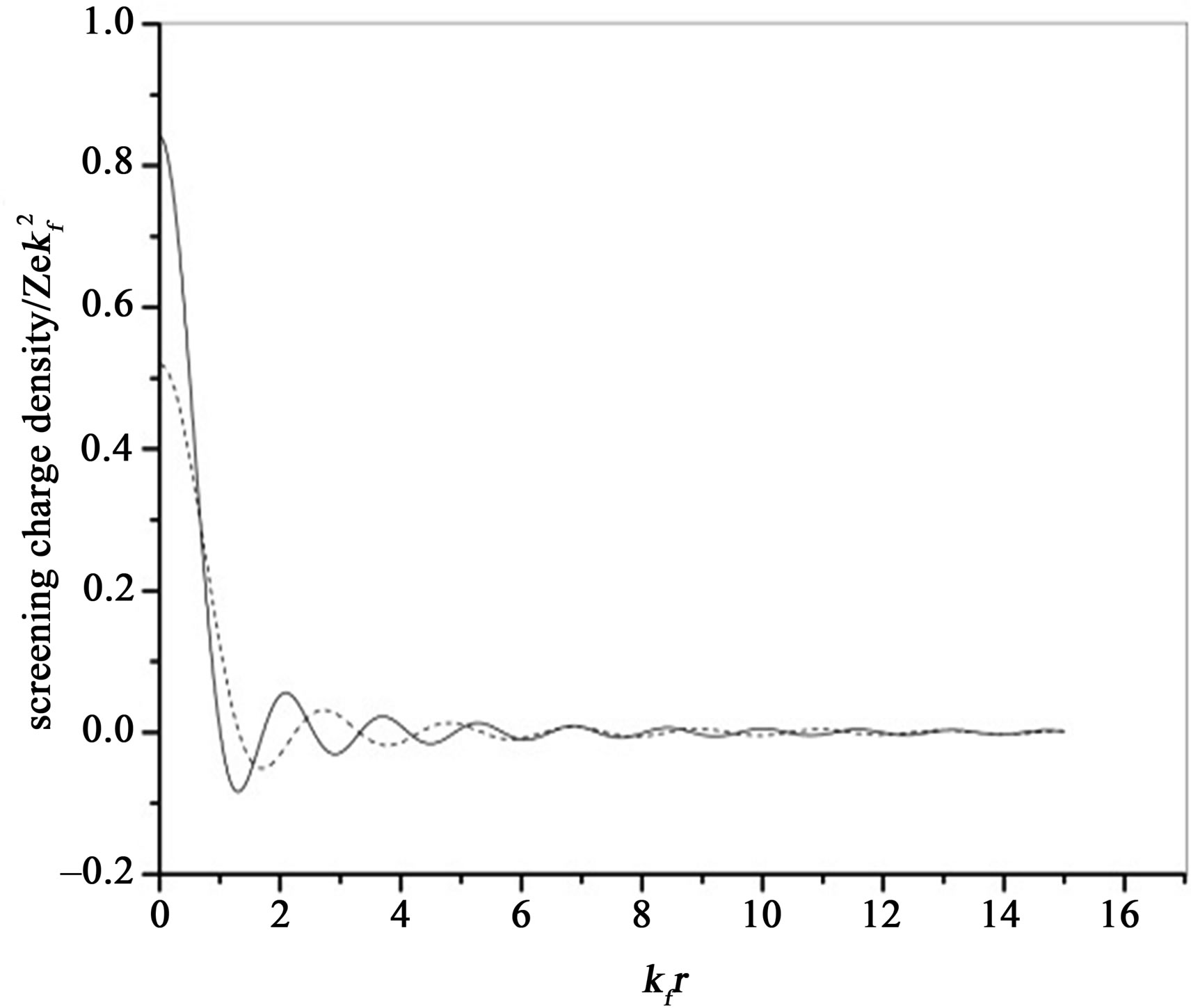 (c)
(c)
Figure 2. (a) Density of screening charge plotted against kfr for n = 4.77 × 1014 cm–2 at 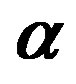 = 2 (Curve-A) and for
= 2 (Curve-A) and for 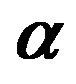 = 4 (curve-B); (b) Density of screening charge plotted agains kfr for
= 4 (curve-B); (b) Density of screening charge plotted agains kfr for  = 4 at n = 8.04 × 1014 cm–2 (curve-B) and n = 4.77 × 1014 cm–2 (curve-A); (c) Screening charge density with LFC (dashed line) and without LFC (solid line) for
= 4 at n = 8.04 × 1014 cm–2 (curve-B) and n = 4.77 × 1014 cm–2 (curve-A); (c) Screening charge density with LFC (dashed line) and without LFC (solid line) for 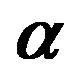 = 4 at n = 8.04 × 1014 cm–2.
= 4 at n = 8.04 × 1014 cm–2.
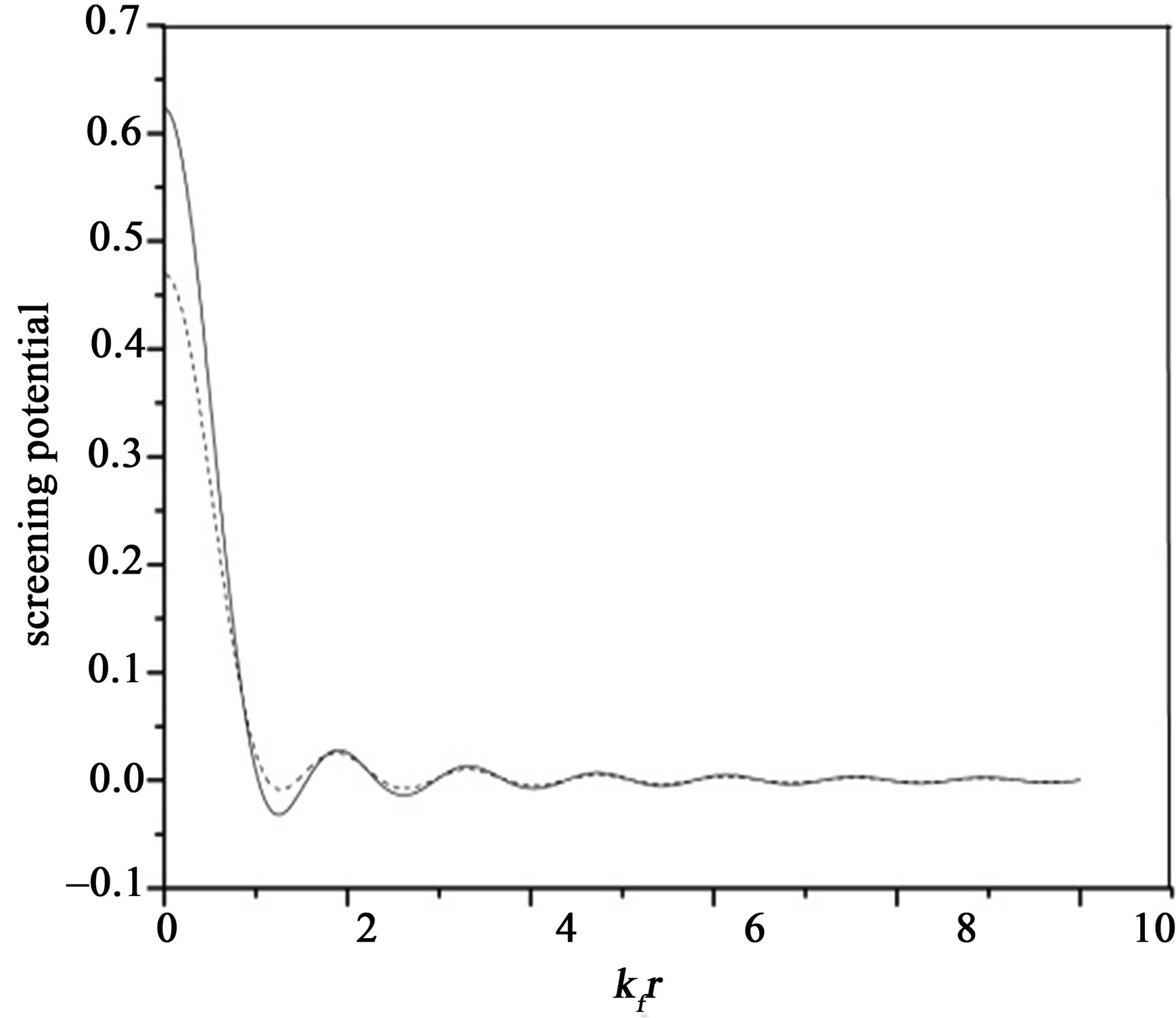
Figure 3. Screened potential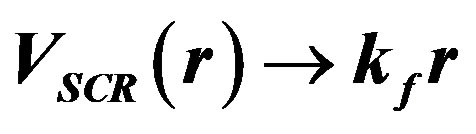 ; with LFC (dashed line), without LFC (solid line).
; with LFC (dashed line), without LFC (solid line).
density is proportional to the total potential, the screened potential oscillates spatially. The observation of Friedel oscillations in screened potential and screening charge density can be seen as a signature of Fermi liquid state in graphene [22]. The Friedel oscillations can be used to gain insight into the microscopic nature of disorder. We compared our computed  and
and  of doped MLG with that of 2DEG. It is found that the overall behavior of
of doped MLG with that of 2DEG. It is found that the overall behavior of  and
and  of doped MLG is not very different from that of 2DEG, though the nature of charge carriers in two systems is very different [17]. It therefore can be inferred that the linear energy dispersion and chirality of MLG does not significantly influence gross many particle properties.
of doped MLG is not very different from that of 2DEG, though the nature of charge carriers in two systems is very different [17]. It therefore can be inferred that the linear energy dispersion and chirality of MLG does not significantly influence gross many particle properties.
The pair distribution function gives the probability that another electron is a distance r away from the first [23]. We computed  as a function of carrier density at different
as a function of carrier density at different 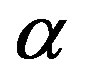 -values. To study the pair distribution function as a function of carrier density we took n = z × 1014 cm–2 at a fixed r = 1 × 10–7 cm Further for computation we take dimensional less quantity
-values. To study the pair distribution function as a function of carrier density we took n = z × 1014 cm–2 at a fixed r = 1 × 10–7 cm Further for computation we take dimensional less quantity , where q0 = 1 × 107 cm–1 Our computed results are displayed in Figure 4 for different values of
, where q0 = 1 × 107 cm–1 Our computed results are displayed in Figure 4 for different values of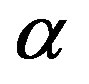 . For all values of
. For all values of , computed g (r, z) as a function of carrier density saturates at higher values of z, as is exhibited in the Figure 4, clearly suggests that the variation of g (r, z) with n is roughly zero over the experimentally observed range of n in doped MLG. Looking at Figure 4 and Equation (7), we can conclude that exchange and correlation terms make negligible contribution to compressibility in MLG, as has been observed in experimental results on compressibility of MLG [14].
, computed g (r, z) as a function of carrier density saturates at higher values of z, as is exhibited in the Figure 4, clearly suggests that the variation of g (r, z) with n is roughly zero over the experimentally observed range of n in doped MLG. Looking at Figure 4 and Equation (7), we can conclude that exchange and correlation terms make negligible contribution to compressibility in MLG, as has been observed in experimental results on compressibility of MLG [14].
4. Conclusion
In summary, we studied the self energy, density of screen-

Figure 4. Pair distribution function  for
for  = 1 (soild line),
= 1 (soild line),  = 2 (dotted line) and
= 2 (dotted line) and  = 3 (dashed line).
= 3 (dashed line).
ing charge and screened potential within and beyond RPA. Local field corrections were incorporated in the Hubbard approximation to go beyond RPA. Ultraviolet cutoff for wave vector integral has been used to exclude the effect of vacuum states in MLG. Self energy, density of screening charge and screened potential of MLG are found to behave similar to that of 2DEG since the dielectric function is almost similar upto q < 2kf . Freidel oscillations have been observed in screened potential and density of screening charge. With increase in the value of  for a fixed value of carrier density, Friedel oscillations enhance, whereas on keeping
for a fixed value of carrier density, Friedel oscillations enhance, whereas on keeping  fixed and increasing carrier density reduces the amplitude of the oscillations. The observation of Friedel oscillations in screened potential and screening charge density can be seen as a signature of Fermi liquid state in graphene. Pair distribution function is calculated as a function of carrier density suggests that exchange and correlation terms make negligible contribution to compressibility of graphene. Incorporation of LFC reduces the magnitude of self energy, screening charge density and screened potential.
fixed and increasing carrier density reduces the amplitude of the oscillations. The observation of Friedel oscillations in screened potential and screening charge density can be seen as a signature of Fermi liquid state in graphene. Pair distribution function is calculated as a function of carrier density suggests that exchange and correlation terms make negligible contribution to compressibility of graphene. Incorporation of LFC reduces the magnitude of self energy, screening charge density and screened potential.
5. Acknowledgements
Kavita N. Mishra acknowledges the Research fellowship in Science for Meritorious Students (RFSMS) from the University Grants Commission, New Delhi. A. C. Sharma thanks the Board of Research in Nuclear Sciences, Department of Atomic Energy, Mumbai, for financial support through research project No. 2008/37/14/BRNS/1486. S. S. Z. Ashraf is grateful to DST New Delhi for the monetary help via the project No. SR/FTP/PS-39/2008.
REFERENCES
- E. H. Hwang, B. Y.-K. Hu and S. Das Sarma, “ManyBody Exchange-Correlation Effects in Graphene,” Physica E, Vol. 40, No. 5, 2008, pp. 1653-1655. doi:10.1016/j.physe.2007.10.043
- S. Das Sarma, E. H. Hwang and W.-K. Tse, “Many-Body Interaction Effects in Doped and Undoped Graphene: Fermi Liquid Versus Non-Fermi Liquid,” Physical Review B, Vol. 75, No. 12, 2007, pp. 121406-121409. doi:10.1103/PhysRevB.75.121406
- M. Calandra and F. Mauri, “Electron-Phonon Coupling and Electron Self-Energy in Electron-Doped Graphene: Calculation of Angular-Resolved Photoemission Spectra, ” Physical Review B, Vol. 76, No. 20, 2007, pp. 205411-205419. doi:10.1103/PhysRevB.76.205411
- C. H. Park, F. Giustino, M. L. Cohen and S. G. Louie, “Velocity Renormalization and Carrier Lifetime in Graphene from the Electron-Phonon Interaction,” Physical Review Letters, Vol. 99, No. 8, 2007, pp. 086804-086807. doi:10.1103/PhysRevLett.99.086804
- W. K. Tse and S. Das Sarma, “Phonon-Induced ManyBody Renormalization of the Electronic Properties of Graphene,” Physical Review Letters, Vol. 99, No. 23, 2007, pp. 236802-236805. doi:10.1103/PhysRevLett.99.236802.
- N. W. Ashcroft and N. D. Mermin, “Solid State Physics,” Saunders College, Philadelphia, 1976.
- I. S. Terekov, A. I. Milstein, V. N. Kotov and O. P. Sushkov, “Screening of Coulomb Impurities in Graphene,” Physical Review Letters, Vol. 100, No. 7, 2008, pp. 076803-076806. doi:10.1103/PhysRevLett.100.076803;
- A. V. Shytov, M. I. Katsnelson and L. S. Levitov, “Vacuum Polarization and Screening of Supercritical Impurities in Graphene,” Physical Review Letters, Vol. 99, No. 23, 2007, pp. 236801-236804. doi:10.1103/PhysRevLett.99.236801
- T. Ando, “Screening Effect and Impurity Scattering in Monolayer Graphene,” Journal of the Physical Society of Japan, Vol. 75, No. 7, 2006, pp. 074716-074722. doi:10.1143/JPSJ.75.074716
- E. Hwang and S. D. Sarma, “Dielectric Function, Screening, and Plasmons in Two-Dimensional Graphene,” Physical Review B, Vol. 75, No. 6, 2007, pp. 205418-205423. doi:10.1103/PhysRevB.75.205418
- B. Wunsch, T. Stauber, F. Sols and F. Guinea, “Dynamical Polarization of Graphene at Finite Doping,” New Journal of Physics, Vol. 8, No. 12, 2006, p. 318. doi:10.1088/1367-2630/8/12/318
- P. K. Pyatkovskiy, “Dynamical Polarization, Screening, and Plasmons in Gapped Graphene,” Journal of Physics: Condensed Matter, Vol. 21, No. 2, 2009, p. 025506. doi:10.1088/0953-8984/21/2/025506
- A. H. C. Neto, F. Guinea, N. M. Peres, K. S. Novoselov and A. K. Geim, “The Electronic Properties of Graphene,” Reviews of Modern Physics, Vol. 81, No. 1, 2009, pp. 109-162. doi:10.1103/RevModPhys.81.109
- J. Martin, N. Akerman, G. Ulbricht, T. Lohmann, J. H. Smet, K. von Klitzing and A. Yacoby, “Observation of Electron-Hole Puddles in Graphene Using a Scanning Single-Electron Transistor,” Nature Physics, Vol. 4, No. 2, 2008, pp. 144-148. doi:10.1038/nphys781
- D. S. L. Abergel, P. Pietilainen and T. Chakraborty, “Electronic Compressibility of Graphene: The Case of Vanishing Electron Correlations and the Role of Chirality,” Physical Review B, Vol. 80, No. 8, 2009, pp. 081408- 081411. doi:10.1103/PhysRevB.80.081408
- S. S. Z. Ashraf, K. N Mishra and A. C. Sharma, “Static Structure Factor and Pair Correlation Function of Graphene,” Journal of Physics: Condensed Matter, Vol. 22, No. 35, 2010, p. 355303. doi:10.1088/0953-8984/22/35/355303
- S. S. Z. Ashraf and A. C. Sharma, “Many Particle Aspects of a Semiconductor Quantum Wire within an Improved Random Phase Approximation,” Journal of Physics: Condensed Matter, Vol. 17, No. 19, 2005, p. 3043. doi:10.1088/0953-8984/17/19/018
- Y. Barlas, T. Pereg-Barnea, M. Polini, R. Asgari and A. H. M. Donald, “Chirality and Correlations in Graphene,” Physical Review Letters, Vol. 98, No. 23, 2007, pp. 236601-236604. doi:10.1103/PhysRevLett.98.236601
- D. S. L. Abergel, V. Apalkov, J. Berashevich, K. Ziegler and T. Chakraborty, “Properties of Graphene: A Theoretical Perspective,” Advances in Physics, Vol. 59, No. 4, 2010, pp. 261-482. doi:10.1080/00018732.2010.487978
- V. V. Cheianov and V. I. Fal’ko, “Friedel Oscillations, Impurity Scattering, and Temperature Dependence of Resistivity in Graphene,” Physical Review Letters, Vol. 97, No. 22, 2006, pp. 226801-226804. doi:10.1103/PhysRevLett.97.226801
- M. Ono, et al., “Observation of the Screened Potential and the Friedel Oscillation by Low-Temperature Scanning Tunneling Microscopy/Spectroscopy,” Applied Surface Science, Vol. 256, No. 2, 2009, pp. 469-474. doi:10.1016/j.apsusc.2009.07.023
- G. E. Simion and G. F. Giuliani, “Friedel Oscillations in a Fermi Liquid,” Physical Review B, Vol. 72, No. 4, 2005, pp. 045127-045134. doi:10.1103/PhysRevB.72.045127
- G. D. Mahan, “Many Particle Physics,” 2nd Edition, Plenum, New York, 1990.
NOTES
*Corresponding author.

