World Journal of Condensed Matter Physics
Vol.1 No.3(2011), Article ID:6932,4 pages DOI:10.4236/wjcmp.2011.13015
Concentration Dependence of Thermodynamic Properties of NaPb Liquid Alloy
![]()
1University Department of Physics, T.M. Bhag. University, Bihar, India; 2Metals and Ceramics Division, Research Institute, University of Dayton, Dayton, USA; 3Department of Physics, M.M.A.M. Campus, Tribhuvan University, Biratnagar, Nepal.
Email: *indusekharjha@yahoo.com
Received May 28th, 2011; revised June 15th, 2011; accepted July 1st, 2011.
Keywords: Liquid Alloys, Free Energy of Mixing, Entropy of Mixing, Mole Fraction
ABSTRACT
We have determined integral excess free energy of mixing, heat of mixing and entropy of mixing of NaPb alloys in molten state at 700 K. The observed asymmetry in the properties of mixing of NaPb alloy in molten state is successfully explained on the basis of regular associated solution model. The theoretical analysis reveals that the pairwise interaction energies between the species depend considerably on temperature.
1. Introduction
Most of the binary alloys are grown from their corresponding liquid phase. In order to improve the quality of growth and to understand the energetic of the formation of alloys, it is important to have as good an understanding as possible of the properties of the liquid alloys. The thermodynamic properties of liquid Na-Pb alloy in molten state exhibits anomalous behaviour as a function of concentration [1]. In present paper, we have used regular associated solution model to understand the thermodynamic properties of Na-Pb alloys in the liquid state at 700 K. Regular associated solution model has been proved to study the thermodynamic and structural properties of weakly, moderately and highly interacting liquid alloys [2-6] by assuming the formation of complex. Such assumptions have been used in different models [7-13]. We have assumed Na and Pb atoms are energetically favoured to form NaPb complex in the molten state.
Theoretical formalism is given in Section 2; Section 3 deals with the numerical result and discussion. Conclusions are provided in Section 4.
2. Theory
Let one mole of binary solution of NaPb alloy comprising of x1 mole of A (=Na) atoms and x2 moles of B (=Pb) atoms. The presence of AB (=NaPb) type complex in the solution results in a depletion of concentration of free atoms of the components of A and B. The liquid solution is thus composed of three species namely free atoms A and B and the complex AB. As a result of associations, the thermodynamic behaviour of the components A and B is governed by the true mole fractions xA and xB rather than the gross mole fraction x1 and x2. Thus it is convenient to operate with two frames of references, one referring to gross mole fractions x1 and x2 and other referring to actual mole fractions of each species (xA, xB and xAB). Further, it is assumed that there are n1 moles of species A, n2 moles of species B and n3 moles of species AB per mole of the binary solution. From the conservation of mass, the two frames of reference can be interrelated as follows:
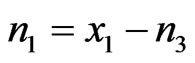 ,
, 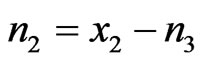
and 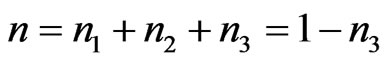 (1)
(1)
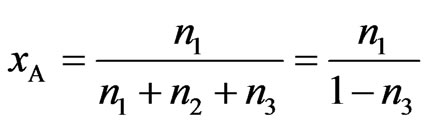 ,
, 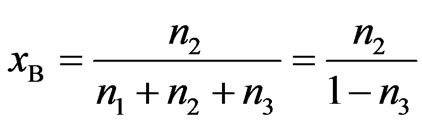
and
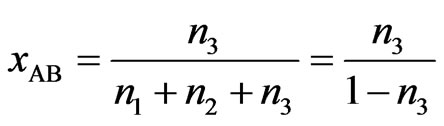 (2)
(2)
Here,
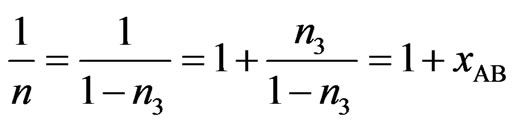 (3)
(3)
Now using Equation (3) in Equation (2), we have,
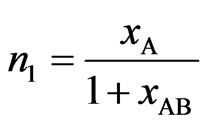 ,
, 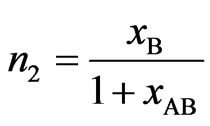
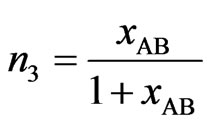 (4)
(4)
For the sake of convenience one or more of these frames of reference may be used.
Now xA, xB and xAB can be inter-related with each other as follows

Using 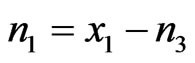 and
and , we get
, we get

After performing some algebraic operations and rearranging the terms, we obtain
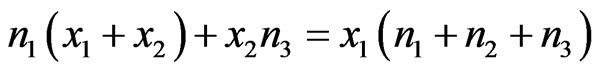
and
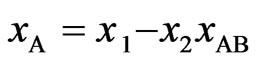 (5a)
(5a)
Similarly we can obtain
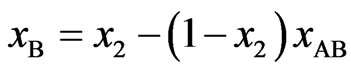 (5b)
(5b)
In regular associated solution, the gross chemical potentials of components 1 and 2 are equal to the chemical potentials of the monomeric species A and B [2-7]. The activity coefficients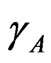 ,
, 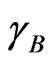 and
and 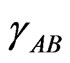 of monomers and complex can be expressed in terms of pairwise interaction energies through [3-5]
of monomers and complex can be expressed in terms of pairwise interaction energies through [3-5]
 (6a)
(6a)
 (6b)
(6b)
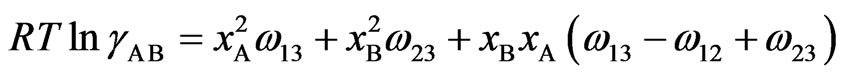 (6c)
(6c)
where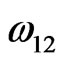 ,
, 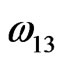 and
and 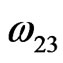 are interaction energies for the species A, B; A, AB and B, AB respectively, T the temperature and R stands for the universal gas constant. The equilibrium constant in a regular associated can be obtained [3,4] as
are interaction energies for the species A, B; A, AB and B, AB respectively, T the temperature and R stands for the universal gas constant. The equilibrium constant in a regular associated can be obtained [3,4] as
 (7)
(7)
Now using the equations listed above the free energy G is given by
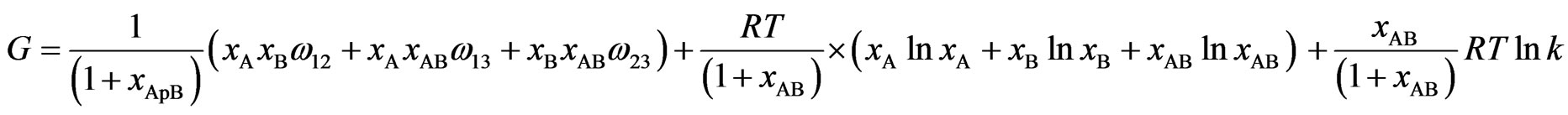 (8)
(8)
Once the expressions for G are obtained, other thermodynamic and microscopic functions follow readily. Enthalpy of mixing (H), entropy of mixing (SM) are related to G through standard thermodynamic relations
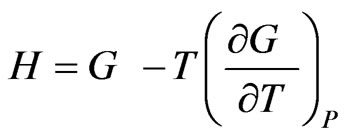 (9)
(9)
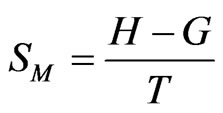 (10)
(10)
In a regular associated solution 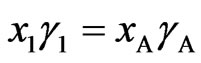 and
and , where
, where 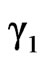 and
and 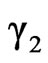 are respective gross activity coefficients of components 1 and 2. Thus
are respective gross activity coefficients of components 1 and 2. Thus
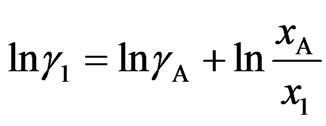 (11a)
(11a)
and 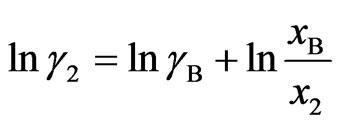 (11b)
(11b)
The pairwise interaction energies, the equilibrium constants and the activity coefficients at infinite dilution can be written as [5]
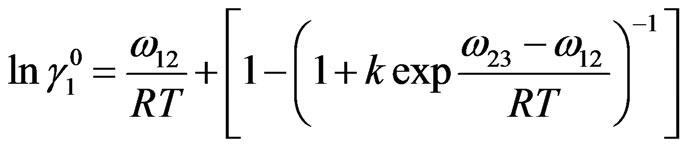 (12a)
(12a)
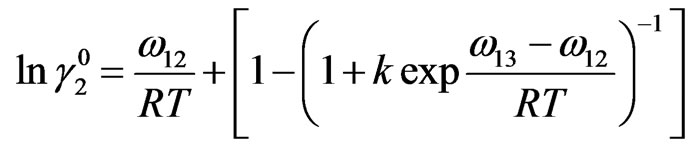 (12b)
(12b)
where and
and  are the respective activity coefficients of component A and that of B at zero concentrations.
are the respective activity coefficients of component A and that of B at zero concentrations.
Solving Equations (6a) and (6b) we obtain
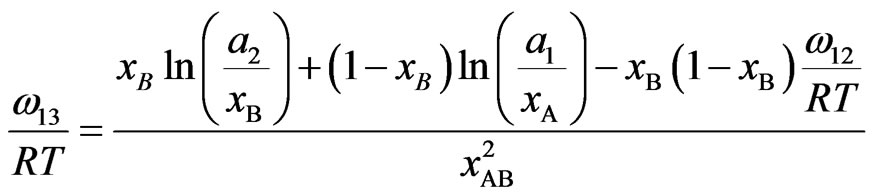 (13a)
(13a)
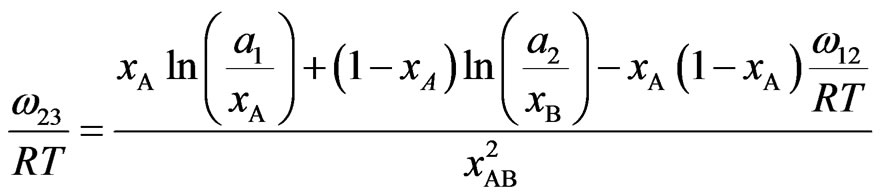 (13b)
(13b)
where a1 and a2 are activities of the components Na and Pb Using Equations (7), (12) and (13) we can derive
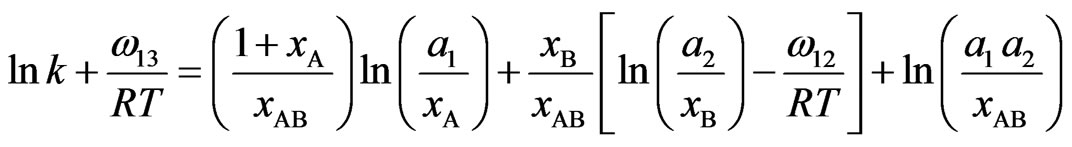 (14a)
(14a)
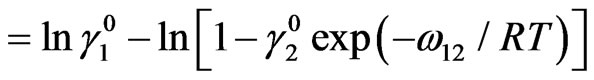 (14b)
(14b)
At equiatomic composition, where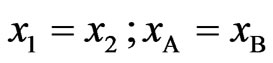 , we have
, we have
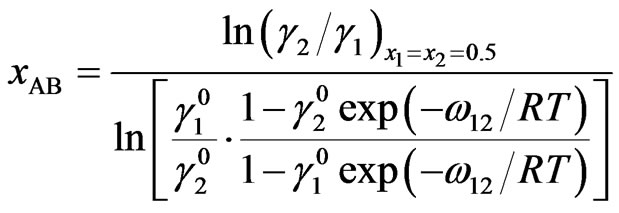 (15)
(15)
3. Results and Discussion
We have calculated the concentration of complex, equilibrium constant and pairwise interaction energies following the method employed by Lele and Ramchancrarao [2] and D. Adhikari et al [3,5,6] using Equations (11)-(15) by iterative procedure. The equilibrium constant and interaction energies for the alloy Na-Pb in liquid state at 700 K are found to be K = 0.0118, 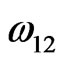 = –27.747 kJ·mol–1,
= –27.747 kJ·mol–1,  = –21.930 kJ·mol–1 and
= –21.930 kJ·mol–1 and 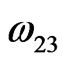 = –7.562 kJ·mol–1.The calculated and observed value of integral excess free energy of mixing (
= –7.562 kJ·mol–1.The calculated and observed value of integral excess free energy of mixing (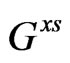 ) is in good agreement (Figure 1). The calculated integral excess free energy of mixing is minimum (–12.22 kJ·mol–1) at xNa = 0.6 which almost matches with the observed value [1]. The observed asymmetry in integral excess free energy of mixing is well explained by our theoretical model.
) is in good agreement (Figure 1). The calculated integral excess free energy of mixing is minimum (–12.22 kJ·mol–1) at xNa = 0.6 which almost matches with the observed value [1]. The observed asymmetry in integral excess free energy of mixing is well explained by our theoretical model.
We have observed that if the interaction energies are supposed to be independent of temperature, i.e.
 , then H and
, then H and 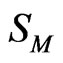 so obtained are in very poor agreement with experimental data. This simply suggests importance of the dependence of interaction energies on temperature. On using Equation (10) and observed values of H [11] we have chosen the following values for the given parameters as the best fit values for the heat of formation of NaPb complex
so obtained are in very poor agreement with experimental data. This simply suggests importance of the dependence of interaction energies on temperature. On using Equation (10) and observed values of H [11] we have chosen the following values for the given parameters as the best fit values for the heat of formation of NaPb complex
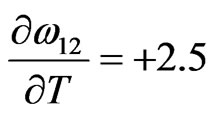 Jmol–1·K–1,
Jmol–1·K–1, 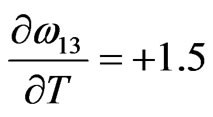 Jmol–1·K–1,
Jmol–1·K–1,
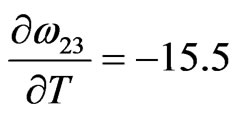 Jmol–1·K–1
Jmol–1·K–1
and 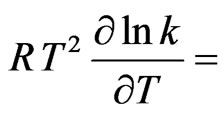 43530
43530 1200 J·mol–1.The dependence of energy parameters on temperature can be observed from the study of H and SM. It is found that the pairwise interaction energies to be considerably dependent on temperature. It is found from the analysis that the heat of mixing is negative at all concentration. Our theoretical calculation shows that the minimum value of the heat of mixing is –18.02 kJ·mol–1 at
1200 J·mol–1.The dependence of energy parameters on temperature can be observed from the study of H and SM. It is found that the pairwise interaction energies to be considerably dependent on temperature. It is found from the analysis that the heat of mixing is negative at all concentration. Our theoretical calculation shows that the minimum value of the heat of mixing is –18.02 kJ·mol–1 at  = 0.6. The observed minimum value is also at
= 0.6. The observed minimum value is also at  = 0.6 [1]. The calculated values are in reasonable agreement with the observed values (Figure 2). The concentration dependence of asymmetry in H is well explained.
= 0.6 [1]. The calculated values are in reasonable agreement with the observed values (Figure 2). The concentration dependence of asymmetry in H is well explained.
We have calculated entropy of mixing of NaPb alloy in liquid state using Equation (10). The calculated values always match in sign with observed values. The calculated values and experimental values are in reasonable agreement at all concentration range (Figure 3).
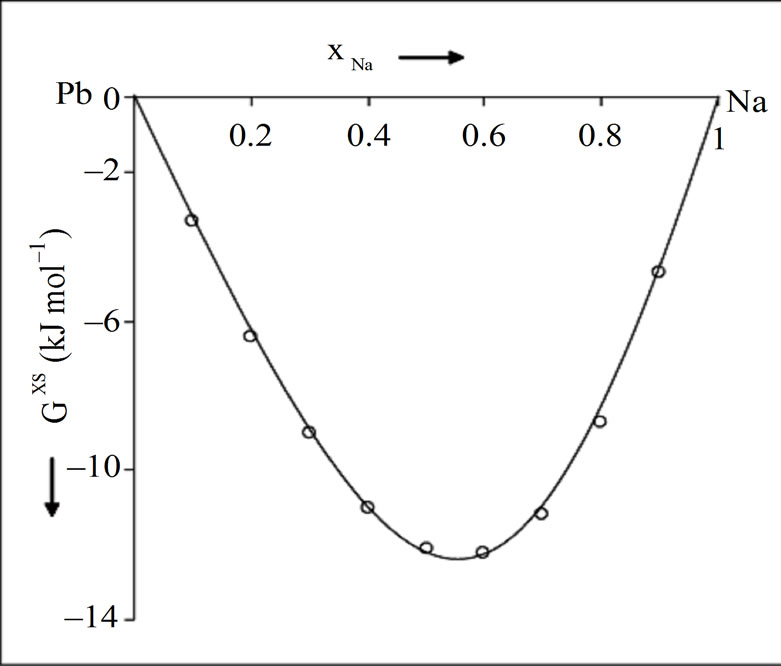
Figure 1. Integral excess free energy of mixing (Gxs) versus xNa (concentration of Na) in the liquid NaPb solution (700 K); (––––) theory, (ooo) experiment [1].
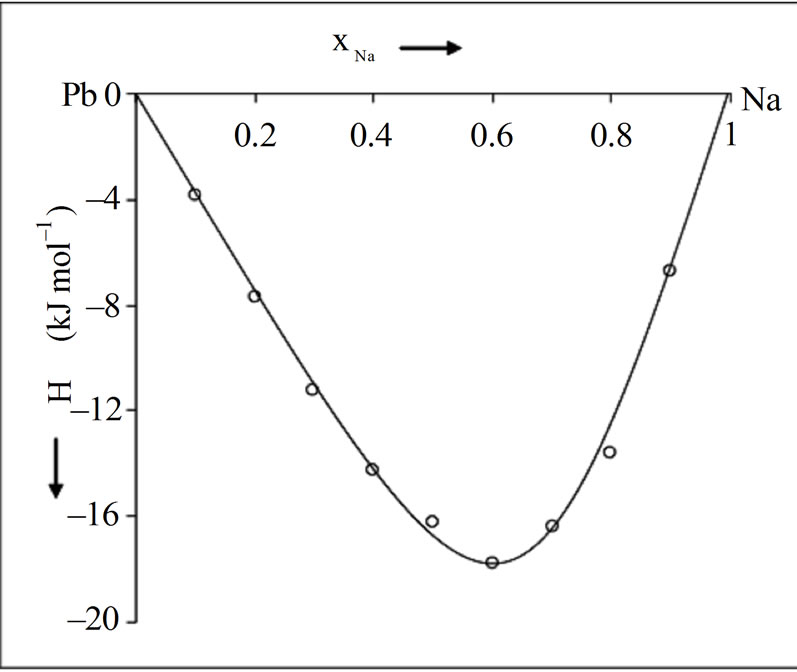
Figure 2. Heat of mixing (H) versus xNa of liquid NaPb solution (700 K); (––––) theory, (ooo) experiment [1]

Figure 3. Entropy of mixing (SM) versus xNa of liquid NaPb (700 K ) (––––) theory, (ooo) experiment [1]
4. Conclusions
The asymmetry in thermodynamic properties like, integral excess free energy of mixing, heat of mixing and entropy of mixing of NaPb liquid alloys at 700 K is well explained by the present theoretical model. Present theoretical analysis shows that there exist complexes NaPb in NaPb alloy in molten state and the pairwise interaction energies are temperature dependent.
REFERENCES
- R. Hultgren, P. D. Desai, D. T. Hawkins, M. Gleiser and K. K. Kelley, “Selected Values of the Thermodynamic Properties of Binary Alloys,” ASM, Metal Park, 1973.
- S. Lele, P. Ramchandrarao, “Estimation of Complex Concentration in a Regular Associated Solution” Metallurgical and Materials Transactions B, Vol. 12, No. 4, 1981, pp. 659-666. doi:10.1007/BF02654134
- D. Adhikari, I. S. Jha and B. P. Singh, “Thermodynamic and Microscopic Structure of Liquid Cu-Sn Alloys” Physica B: Condensed Matter, Vol. 405, No. 7, 2010, pp.1861-1865. doi:10.1016/j.physb.2010.01.064
- A. S. Jordan, “A Theory of Regular Associated Solution Applied to the Liquidus Curves of the Zn-Te and Cd-Te Systems,” Metallurgical and Materials Transactions B, Vol. 1, No. 1, 1970, pp. 239-249.
- D. Adhikari,, B. P. Singh, I. S. Jha and B. K. Singh, “Thermodynamic Properties and Microscopic Structure of Liquid Cd-Na Alloys by Estimating Complex Concentration in a Regular Associated Solution” Journal of Molecular Liquids, Vol. 156, No. 2-3, 2010, pp. 115-119. doi:10.1016/j.molliq.2010.05.020
- D. Adhikari, I. S. Jha and B. P. Singh, “Structural Asymmetry in Liquid Fe-Si Alloys” Philosophical Magazine, Vol. 90, No. 20, 2010, pp. 2687-2694. doi:10.1080/14786431003745302
- B. P. Singh, D. Adhikari and I. S. Jha, “Concentration Dependence of the Structure and Thermodynamic Properties of Silver-Antimony Alloys” Journal of Non-Crystalline Solids, Vol. 356, No. 3-4, 2010, pp. 1730-1734. doi:10.1016/j.jnoncrysol.2010.06.004
- A. B. Bhatia and D. E. Thornton, “Structural Aspects of the Electrical Resistivity of Binary Alloys” Physical Review B, Vol. 8, No. 2, 1970, pp. 3004-3012.
- M. Gluyas, R. Hunter and B. W. James, “The Elastic Constants of Thallium Chloride in the Range 150 to 300 K,” Journal of Physics C: Solid State Physics, Vol. 8, No. 3, 1975, pp. 271-282.
- K. Hoshino and W. H. Young, “Entropy of Mixing of Compound Forming Liquid Binary Alloys” Journal of Physics F: Metal Physics, Vol. 10, No. 7, 1980, pp. 1365- 1376. doi:10.1088/0305-4608/10/7/006
- S. P. McAlister and E. D. Crozier, “The ConcentrationConcentration Correlation Function in the Long-Wavelength Limit for Binary Liquid Alloys,” Journal of Physics C: Solid State Physics, Vol. 7, No. 19, 1974, pp. 3509-3519. doi: 10.1088/0022-3719/7/19/011
- I. S. Jha, R. N. Singh, P. L. Shrivastava and N. R. Mitra, “Stability of HgNa and HgK Liquid Alloys” Philosophical Magazine Part B, Vol. 61, No. 1, 1990, pp. 15-24. doi:10.1080/13642819008208649
- R. N. Singh and F. Sommer, “Segregation and Immiscibility in Liquid Binary Alloys,” Reports on Progress in Physics, Vol. 60, No. 1, 1997, pp. 57-150. doi:10.1088/0034-4885/60/1/003
- A. B. Bhatia and N. H. March, “Size Effects, Peaks in Concentration Fluctuations and Liquidus Curves of Na-Cs,” Journal of Physics F: Metal Physics, Vol. 5, No. 6, 1975, pp. 1100-1106. doi:10.1088/0305-4608/5/6/011

