Atmospheric and Climate Sciences
Vol.3 No.2(2013), Article ID:30783,6 pages DOI:10.4236/acs.2013.32023
The Formation of Lee Reversal Flow and Moisture Distribution Effect on the Characteristics of Precipitation
Department of Marine Meteorology, Ocean University of China, Qingdao, China
Email: *liziliang@ouc.edu.cn
Copyright © 2013 Jinqing Liu, Ziliang Li. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received February 28, 2013; revised March 30, 2013; accepted April 6, 2013
Keywords: Lee Precipitation; Lee Reversal Flow; Moisture Distribution; Upslope Rain; Seesaw Phenomenon
ABSTRACT
Moist flow over a bell-shaped mountain is investigated using the advanced regional prediction system (ARPS). Three closely related issues are addressed: the upslope precipitation mechanism, periodic evolution of precipitation associated with mountain waves, and lee precipitation induced by reversal flow. The results show that precipitation is strongly the moist distribution and terrain scale dependent. Beginning with the case of uniformly stratified flow over mountain, upslope precipitation and lee wave precipitation pattern are obtained. Most importantly, lee precipitation induced by reversal flow can be caused by layered flow over mountain, wherein lee reversal flow exerts a significant influence on the orographic precipitation.
1. Introduction
Orographic precipitation is a central part of the interaction between the land surface and the atmosphere, which influences water resources, flooding and landslides [1,2]. Both modeling and observational studies have shown that there have been many advances in understanding of orographic flows [3,4]. Previous studies on moist flow dynamics are mainly based on the numerical simulations with cloud physics [5,6] as well as the moist static stability strategy [7,8] and the highly idealized treatment of moist processes by using the simple heating functions [9]. After decades of effort, a number of orographic precipitation mechanisms have been proposed [10-12]. The classic example is that precipitation is greatly enhanced on the windward side and suppressed in the lee of the mountain, resulting in the well-known rain shadow, which is probably caused by lee side descent, dry air entrainment, or increased static stability. The full gamut of orographic influences involves that precipitation can be enhanced in the lee, over the crest, or well upwind of a mountain [13, 14]. However, the mechanisms of orographic precipitation are still poorly understood, and the forecasting of precipitation in mountainous areas is still an elusive goal.
The motivation of the present paper is to carry out the numerical study to understand the precipitation distribution associated with the moist flow spatial distribution. The numerical model used here is the advanced regional prediction system (ARPS), described in Section 2. Section 3 describes the effect of moisture distribution on precipitation generated by uniform flow over mountain. Layered moist flow over mountain is discussed in Section 4. Finally, Section 5 presents the discussion and conclusion.
2. Model Design
The experiments are conducted in there using the Version 5.0 IHOP5 of the advanced regional prediction system (ARPS), which are well suited to study complex terrain precipitation for its non-hydrostatic dynamics and generalized terrain-following coordinates. The governing equations of the ARPS include conservation equations for momentum, heat, mass, water substance (water vapor, liquid, and ice), sub-grid-scale (SGS) turbulent kinetic energy (TKE), and the equation of state of moist air.
In ARPS, the microphysics package is based on a program developed by Tao [15]. It includes the Kessler [16] warm rain microphysics and a three-category ice-phase parameterization following Lin [17]. There are six water categories in Lin’s cloud scheme, which include water vapor, cloud water, rainwater, cloud ice, snow, and hail. In this work, the 1.5 order TKE (turbulent model) and Kessler cloud physics are used. Other physical processes, such as the radiation model, cumulus parameterization and the soil model are not included for the sake of simplicity. The topography is a 2D ideal bell-shaped mountain specified by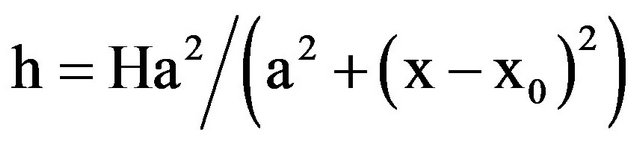 , where H is the maximum mountain height (H = 0.5 km, or H = 2 km) and a is the mountain half-width (a = 10 km), and the mountain is located at x0 = 60 km in horizontal direction. While the gap between our idealized study and the real world is obvious, the concepts developed in this paper may help to improve our understanding of terrain precipitation.
, where H is the maximum mountain height (H = 0.5 km, or H = 2 km) and a is the mountain half-width (a = 10 km), and the mountain is located at x0 = 60 km in horizontal direction. While the gap between our idealized study and the real world is obvious, the concepts developed in this paper may help to improve our understanding of terrain precipitation.
The model domain size is 160 km by 20 km, the horizontal resolution is 1 km with 263 grid points, and there are 83 layers with vertical grid spacing 0.25 km, where the vertical grid spacing varies smoothly from 0.05 km at the ground stretching to 0.25 km near the top of the domain via cubic function, and Rayleigh damping is applied over the top half depth to absorb gravity waves. The radiation boundary condition is applied to east-west lateral boundaries, while periodic boundaries are applied to north-south lateral boundaries.
Experiment one is initialized using the basic state velocity U = 20 ms–1, static stability N = 0.01 s–1 for the case study of uniform flow over mountain, which helps to generate a hydrostatic field of mountain waves. A preference experiment involves N = 0.02 s–1 below 2.5 km height and N = 0.01 s–1 above 2.5 km height in the case study of two-layered flow over mountain. As shown by Scorer [18], if the lower layer is slower or more stable than the upper layers, waves propagating upward through the lower layer may become evanescent aloft. This will result in the downward reflection of the wave and a trapped lee wave may exist. The trapped lee waves are of two types, diverging and transverse, which help to generate lee wave precipitation.
In addition, numerical simulations are integrated to 3.33 h time and the moisture is involved in two cases. One is the moisture in the middle layer, in which surface air temperature T0 = 270 K and relative humidity RH = 95% between the heights of 2.5 km and 5 km. The other is the moist everywhere with surface air temperature T0 = 270 K and relative humidity RH = 95% in whole domain.
3. Uniformly Stratified Flow over Mountain
The interaction of moist flow and topography finally determines the characteristics of precipitation. One of the most striking of ways in which topography influences the weather is in its strong local control of rainfall distributions.
The precipitation distribution generated by uniformly moist flow over mountain shows the upslope precipitation, both for 0.5 km mountain and 2 km mountain. The pattern of rain water mixing ratio show that (Figure 1), the rainfall is strongly controlled by mountain with the rainfall maxima on the upwind side, which is usually termed as the typical upslope precipitation mechanism.
Considering an inhomogeneous humidity distribution, the moisture distribution at initial time is defined so that the atmosphere is divided into three different levels, where the moist region between vertical level of 2.5 km and 5 km, and the other is dry region. The results show that the precipitation distribution exist seesaw phenomenon and have the remarkably characters of periodic waves, which consist of alternate terrain rain bands and rain shadow
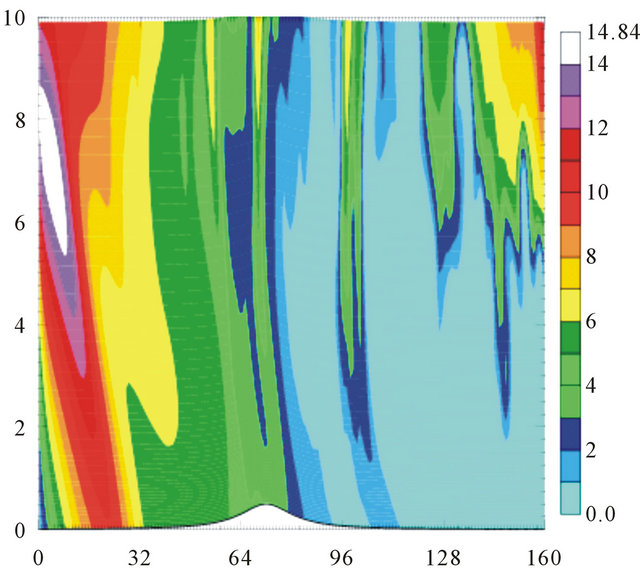

Figure 1. Distributions of water rain mixing ratio generated by uniform flow over 0.5 km mountain (upper) and 2 km mountain (bottom) after 3.33-hour integration with moisture everywhere.
bands, both for a 0.5 km mountain and for a 2 km mountain.
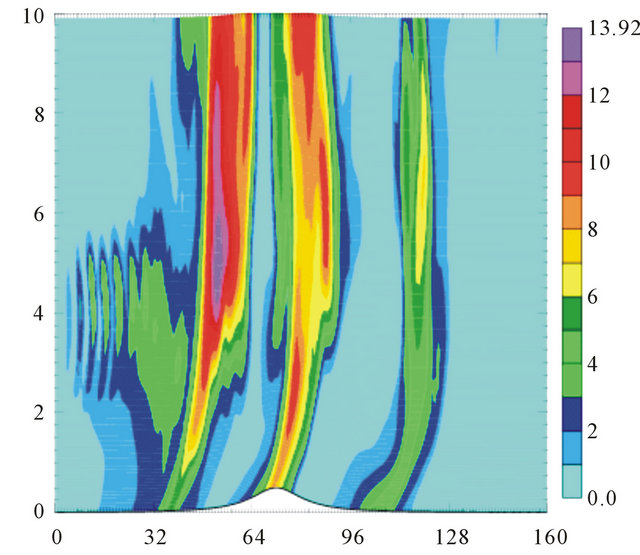
On one hand, from the vertical distributions of water rain mixing ratio generated by flow over a 0.5 km mountain (Figure 2(a)), we can see that, the terrain rain mainly occurs in upslope side and down-slope side of mountain, and no-rain occurs over the mountain. On the other hand, from experiment of flow over a 2 km mountain (Figure 2(b)), we can see that, the most obvious features are also periodic rainfall distribution. Besides the upslope rain, lee precipitation form in the lee of the mountain barriers and has the remarkably characteristics of lee waves, which consist of alternate lee precipitation bands and lee rain shadow bands. In addition, time evolution show that the precipitation maybe occurs mainly over the mountain barriers accompanied by alternate rain-shadow and precipitation along the mountain.
Due to the latent heat generated by moisture in the middle layer changes the atmospheric stability and spatial distribution of Scorer parameters, which help to satisfy the resonant conditions associated with mountain lee waves generated by layered flow over mountain. So the precipitation distributions have dual characteristics of vertical propagating gravity waves and lee waves, which play a significantly role in the forming of orographic precipitation generated by moist flow over mountain.
 (a)
(a) (b)
(b)
Figure 2. (a) Distributions of water rain mixing ratio generated by uniform flow over a 0.5 km mountain, after 3.33 hour (upper) and 20 hour (bottom) integration with middle moisture layer; (b) Distributions of water rain mixing ratio generated by uniform flow over a 2 km high mountain, after 3.33 hour (upper) and 20 hour (bottom) integration with middle moisture layer.
4. Layered Stratified Flow over Mountain
Considering the case of two-layered moist flow over mountain with H = 0.5 km, precipitations are highly dependent on the spatial distribution of moisture. When moisture is introduced into the middle layer, precipitations form in the downstream region of mountain, as well as the mountain top. When moisture is introduced into domain everywhere, however, precipitations dominate over mountain, as well as an upstream region of mountain.
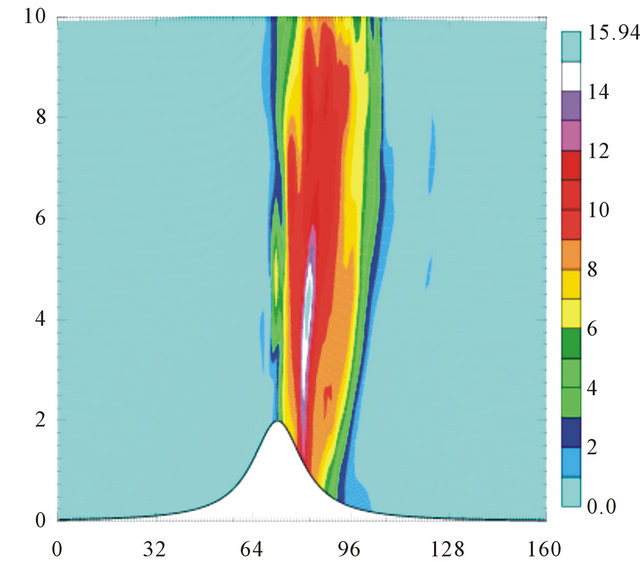
When mountain height increased by H = 2 km, precipitation pattern combined with horizontal velocity field shows that the influences of moisture are apparent on the forming of reversal flow in the lee of mountains, where lee precipitation is induced by lee reversal flow. When introducing moisture into the middle layer (Figure 3(a)), precipitation induced by lee reversal flow only occurs on the lee side of mountain, with maximum rainfall development appearing down slope of the mountain peak. When moisture is introduced into model domain everywhere (Figure 3(b)), precipitation also occurs on the upstream away from the mountain peak, as well as lee precipitation.
The appearance of lee reversal flow over mountain is an important characteristic for lee precipitation occurring, in which horizontal velocity is negative within the lee of
 (a)
(a) (b)
(b)
Figure 3. (a) Distributions of horizontal velocity (upper) and water rain mixing ratio (bottom) generated by layered flow over a 2 km high mountain, after 3.33-hour integration with middle moisture layer; (b) Same as (a), except for moisture everywhere in the atmosphere at initial time.
mountain, so lee precipitation is probably caused by reversal flow over mountain. It is well-known that precipitation of lee reversal flow are one of the major synoptic situations of precipitation, this numerical results can be used to explain lee reversal flow inducing precipitation mechanism.
5. Conclusion and Discussion
The moist air current crossing over mountains and the forming of lee waves and lee reversal flow weather situation in the lee side of the mountain are investigated using the advanced regional prediction system (ARPS). The results show that the effects of moisture are apparent on the forming of mountain wave weather in the lee of mountain. The elevation of mountain and moist distribution are the most important factors in the influence of terrains on weather and climate, and mountain plays a positive role in the forming of lee reversal flow weather and mountain wave weather. We suggest that precipitation mechanism should include lee precipitation mechanism induced by lee reversal flow, except upslope precipitation. For the uniformly stratified moist airflow over higher mountain, the wind shear critical layer forms far beyond the mountain and the reversal flow generate precipitation in the leeside of the mountain. When introducing the moisture into the middle layer, lee waves generated by moist flow over mountain and orographic precipitation show lee wave characters.
The interactions of moisture, wind and topography finally determine the characteristics of precipitation. It is well-known that reversal flow precipitation is the major synoptic situation of large scale precipitation in China regions, where the southwest flow in the upper layer over topography generate the wind shear critical layer with northeast reversal flow in the lower layer. However, the mechanisms of lee reversal flow precipitation are still poorly understood, these numerical experiment help us to understand the role of topography in the forming of wind shear critical layer and reversal flow precipitation, especially the periodic characteristics and seesaw phenomenon of lee wave rainstorm.
6. Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 41176005).
REFERENCES
- E. J. Becker, “Understanding the Characteristics of Daily Precipitation over the United States Using the North American Regional Reanalysis,” Journal of Climate, Vol. 22, No. 23, 2010, pp. 6268-6286. doi:10.1175/2009JCLI2838.1
- C. A. Davis, “Environmental Controls on the Simulated Diurnal Cycle of Warm-Season Precipitation in the Continental United States,” Journal of Atmospheric Science, Vol. 67, No. 4, 2000, pp. 1066-1090.
- P. K. Smolarkiewicz and R. Rotunno, “Low Froude Number Flow Past Three-Dimensional Obstacles. Part I: Baroclinically Generated Lee Vortices,” Journal of Atmospheric Science, Vol. 46, No. 8, 1989, pp. 1154-1164. doi:10.1175/1520-0469(1989)046<1154:LFNFPT>2.0.CO;2
- R. B. Smith and I. Barstad, “The Linear Theory of Orographic Precipitation,” Journal of Atmospheric Science, Vol. 61, No. 14, 2004, pp. 1377-1391. doi:10.1175/1520-0469(2004)061<1377:ALTOOP>2.0.CO;2
- Q. F. Jiang, “Moist Dynamics and Orographic Precipitation,” Tellus, Vol. 55A, 2003, pp. 301-316.
- B. A. Colle, “Sensitivity of Orographic Precipitation to Changing Ambient Conditions and Terrain Geometries: An Idealized Modeling Perspective,” Journal of Atmospheric Science, Vol. 61, No. 5, 2004, pp. 588-606. doi:10.1175/1520-0469(2004)061<0588:SOOPTC>2.0.CO;2
- A. B. Fraser, R. C. Easter and P. V. Hobbs, “A Theoretical Study of the Flow of Air and Fallout of Solid Precipitation over Mountains Terrain. Part 1: Airflow Model,” Journal of Atmospheric Science, Vol. 30, No. 5, 1973, pp. 801-812. doi:10.1175/1520-0469(1973)030<0801:ATSOTF>2.0.CO;2
- A. Barcilon, J. C. Jusem and P. G. Drazin, “On the TwoDimensional Hydrostatic Flow of a Stream of Moist Air over a Mountain Ridge,” Geophysical & Astrophysical Fluid Dynamics, Vol. 13, No. 1, 1979, pp. 125-140. doi:10.1080/03091927908243765
- R. B. Smith and Y. L. Lin, “The Addition of Heat to a Stratified Air Stream with Application to the Dynamics of Orographic Rain,” Quarterly Journal of the Royal Meteorological Society, Vol. 108, No. 456, 1982, pp. 353-379. doi:10.1002/qj.49710845605
- D. R. Durran, “Mountain Waves and Down-Slope Flows. Atmospheric Processes over Complex Terrain Metero Monographs,” American Meteorological Society, No. 23, 1990, pp. 59-81.
- R. B. Smith, “The Influence of Mountains on the Atmosphere,” Advances in Geophysics, Vol. 29, 1979, pp. 87- 230.
- R. B. Smith, “Stratified Flow over Topography, Environment Stratified Flows,” Academic Press, Waltham, 2002.
- H. R. Gerard, “Orographic Precipitation,” Annual Review of Earth and Planetary Sciences, Vol. 33, 2005, pp. 645- 671. doi:10.1146/annurev.earth.33.092203.122541
- R. B. Smith, “Orographic Precipitation in the Tropics: The Dominica Experiment,” American Meteorological Society, Vol. 93, No. 10, 2012, pp. 1567-1579. doi:10.1175/BAMS-D-11-00194.1
- W. K. Tao and J. Simpson, “Goddard Cumulus Ensemble Model. Part I: Model description,” Terrestrial Atmospheric and Oceanic Sciences, Vol. 4, 1993, pp. 35-72.
- E. Kessler, “On the Distribution and Continuity of Water Substance in Atmospheric Circulations,” Meteorological Monographs, No. 32, 1969, p. 84.
- Y. L. Lin, R. D. Farley and H. D. Orville, “Bulk Parameterization of the Snow Field in a Cloud Model,” Journal of Climate and Applied Meteorology, Vol. 22, 1983, pp. 1065-1092. doi:10.1175/1520-0450(1983)022<1065:BPOTSF>2.0.CO;2
- R. S. Scorer, “Theory of Waves in the Lee of Mountains,” Quarterly Journal of the Royal Meteorological Society, Vol. 82, No. 351, 1949, pp. 75-81. doi:10.1002/qj.49708235107
NOTES
*Corresponding author.

