Received 15 December 2015; accepted 25 March 2016; published 29 March 2016

ABSTRACT

In accreting neutron star (NS) low-mass X-ray binaries (LMXBs), the turbulent flow in accretion disk may show magnetic structures. Its emission will vary in time due to inhomogeneous motions through and with the accretion flow. These emissions contribute to considerable X-ray variability on a wide range of timescales in all wavelengths, and down to milliseconds. In this article, we give a brief review for quasi-periodic oscillations (QPOs), one of a periodic X-ray variability, in NS/ LMXBs. Firstly, we give a brief introduction to NS/LMXBs and the fruitful QPO components. As an example, the energy dependence of normal branch oscillations in Scorpius X-1 is discussed. We mostly focus on the properties and mechanism of kilohertz QPOs―the fastest variability components that have the same order as the dynamical timescales of the innermost regions of accretion flow. Finally, we discuss the success and questions for theoretical interpretations and present the possible entry for investigation of nature of QPOs.

Keywords:

Accretion, Accretion Disks, Neutron Star, QPOs, X-Ray Binaries

1. Neutron Stars in Low-Mass X-Ray Binaries

X-ray binary system consists of a compact object, usually a neutron star (NS) or a black hole, and an optical companion star. According to the ratio of X-ray luminosity to optical wavelength and the mass of companion star, X-ray binaries fall into three categories [1] - [3] , i.e., high-mass X-ray binaries, intermediate-mass X-ray binaries and low-mass X-ray binaries (LMXBs).

In NS/LMXBs, the companions of NSs are low-mass (⊙) stars, such as late-type main-sequence stars, white dwarfs, or subgiant stars with F-G type spectra [4] [5] . Neutron stars accrete material via Roche lobe overflow through the inner Lagranigian point, emitting soft X-ray, with typical luminosity of 10³⁶ - 10³⁸ ergs/s. Their galactic distribution is concentrated towards the galactic center, which characterizes a relatively old stellar population, with ages in the range of (0.5 - 1.5) × 10¹⁰ yrs. They possess relatively weak surface magnetic fields of 10⁸ - 10⁹ G and short spin periods of a few milliseconds [6] .

Z sources and atoll sources are two classes of NSs in LMXBs [7] [8] , which are characterized by Z-like and atoll-like shapes on X-ray color-color diagrams (CCDs) or hardness-intensity diagrams (HIDs), respectively. Z sources accrete matter at an appreciable fraction of the Eddington critical rate, 0.5 - 1 L_Edd. The Z-like track consists of three branches (see panel (c) in Figure 1), which are referred to as horizontal branch (HB), normal branch (NB) and flaring branch (FB) from top left to bottom right, differing somewhat between sources [7] [9] and showing slow drifts [10] [11] . Atoll sources cover a much wider range in luminosity, from 0.001 L_Edd all the way up to the range of Z sources. At high luminosity, atoll sources describe a curved banana branch in CCD/ HIDs (Figure 1(a) and Figure 1(b)), along which sources move back and forth on timescales of hours to a day or so [7] [12] . The banana branch is further subdivided into the upper banana (UB), the lower banana (LB) and the lower left banana (LLB). The spectra become harder in CCD/HIDs at lower luminosity, and the CCD motion is often much slower here, from days to weeks, which causes isolated patches to form. These patterns are called island state (IS, see Figure 1(a)), and a hardest, lowest luminosity extreme island state (EIS [13] and references therein).

2. Description of Quasi-Periodic Oscillations

Quasi-periodic oscillations (QPOs) in time series stands out in the power density spectrum (PDS) as a peak with finite width (e.g. Figure 2), whose profile usually can be described by a Lorentzian function

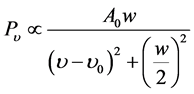(1)

where is the peak frequency (or centroid frequency); w denotes the full width at half maximum (FWHM); and A₀ represents the amplitude of the signal. A QPO signal is characterized by three characteristic quantities,

i.e. centroid frequency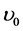, quality factor, and the fractional root-mean-squared (rms)

amplitude. The centroid frequency 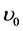tells us the position of the signal. While FWHM w that is related to the

coherence time is often reported in terms of quality factor Q, which is a measure of coherence. Con-

ventionally, signals with Q > 2 are called QPOs and those with Q < 2 are peaked noises. The rms, as a function of the source flux, represents a measure of strength, which is proportional to the square root of the integrated

power of its contribution to the PDS, 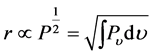and is often expressed in percent.

Neutron stars in LMXBs show considerable QPO components, and their frequencies display some correlations.

Low-frequency QPOs―Low-frequency QPOs are observed in the range of 5 - 60 Hz, with Q ≥ 2, and amplitudes of 1% - 10% [14] , see Figure 2. They come in different types, which were named horizontal branch oscillations (HBOs), normal branch oscillations (NBOs), and flaring branch oscillations (FBOs), and correlate with the spectral states in CCDs of NS/LMXBs. The frequencies of HBOs come in a characteristic range of about 15 - 55 Hz and display a strong positive correlation with X-ray intensity [15] , for which the magnetospheric beat-frequency model was proposed [16] . In a range of about 5 - 7 Hz, a signal with approximately constant frequency is often observed in the middle of NB, with a similar coherence and strength as HBO. Such NBOs have no obvious strong trend of correlation with the X-ray intensity. FBOs, as an intensity-dependent peak, have been reported in frequency range of about 10 - 20 Hz, which merge smoothly with NBOs. The frequency becomes strongly correlated to X-ray intensity as soon as the source rounds the corner from NB into FB. The peak gets broader as the source moves up FB and finally dissolves into a very broad excess noise component. QPOs belonging to different branches could sometimes occur simultaneously in the same source.

Hectohertz QPOs―The hectohertz (hHz) QPO [17] is a peaked noise, sometimes coherent enough to be called a QPO, with frequency in the range of 100 - 200 Hz (see panel (b) in Figure 3 for example) that is seen in most states of atoll sources and the millisecond pulsar SAX J1808.4-3658 when the break frequency ≥ 1 Hz. They may also occur in Z sources. It stands out from all other NS components by its approximately constant frequency. The hHz QPO usually has rather low quality factor but occasionally peaks up to Q > 2 and has a rms amplitude between 2% and 20%, which becomes weaker and more coherent as the break frequency rises.

Kilohertz QPOs―The fastest variability components in X-ray binaries are the kilohertz (kHz) QPOs, which were firstly detected by the Rossi X-ray Timing Explorer (RXTE) [19] in Scorpius X-1 [20] and 4U 1728-34 [21] , respectively, see [6] [22] for a historical account. Sometimes only one peak can be detected, but in some sources the kHz QPOs occur in pairs (see panel (a) of Figure 3 and Figure 4 for examples). The twin peaks move up and down in frequencies together in the range from 200 Hz to 1300 Hz, in correlation with source states [6] . The peak with higher frequency in PDS is called the upper kHz QPO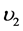, and the signal with

lower frequency is assigned to be the lower kHz QPO. Towards the edges of their observed frequency range peaks also occur alone. In all Z sources and in 4U 1728-34 the kHz QPOs are seen down to the lowest inferred accretion rate 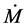levels (HB and upper NB) these sources reach. The QPOs always become undetectable at the highest 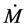levels. In most atoll sources, QPOs are seen in the part of LLB closest to the islands, i.e. near the lower left corner of UB, and they are often not detected in IS that may be related to low sensitivity at the low count rates there [23] .

Frequency correlations of QPOs in NS/LMXBs―The frequencies between twin kHz QPOs and other components display some correlations [13] , which are consistent in Z and atoll sources. The frequencies of HBOs turn out to correlate well with those of kHz QPOs [18] [26] - [30] , and the same is true for NBO in Scorpius X-1 [20] . A systematical study for 0.1 - 1200 Hz QPOs and broad noise components [31] of non-pulsing NS indicates that the frequencies between lower kHz QPOs and low frequency QPOs follow a tight correlation (e.g. see Figure 5), which can be described by an empirical model that is based on a superposition of multiple Lorentzians [32] . It was proposed that the origin of these correlations is a physical dependence of the frequencies on one another [33] , and a combination of the sonic-point and magnetospheric beat-frequency models can explain these correlations [34] .

3. Normal Branch Oscillation in Scorpius X-1

The brightest persistent NS/LMXB Scorpius X-1 traces a “Z” track in CCD, whose typical Fourier PDS are composed of noise components (broad structure) and QPOs in most of these branches. There are three distinct types of QPOs, i.e. the NBO at about 6 Hz, the HBO at about 45 Hz with a harmonic at about 90 Hz, and the twin kHz QPOs of 800 - 1000 Hz [18] [20] , see Figure 6.

About 6 Hz NBO in Scorpius X-1, which occurs on the mid- and lower NB, show some correlations with variability of about 45 Hz HBO and the twin kHz QPOs [20] [37] , and therefore imply some kind of coupling between the three types of QPOs [20] [38] .

The NBO frequency remains approximately constant at about 6 Hz, in general. However, the timing properties along the Z track show that the NBO frequency extends to at most about 21 Hz and its position moves

smoothly into the lower part of the FB [38] [39] . This smooth transition indicates that NBO and FBO are physically related to each other [38] [40] [41] . Properties of both twin kHz QPO and 45 Hz HBO depend on the NBO flux. The upper kHz QPO frequency is anti-correlated with the NBO flux, and the lower kHz QPO becomes stronger when the NBO flux is low [42] . Significant HBOs are detected during the NBO phase of high flux, while the HBO disappears at the low flux of NBO phase [37] . The coupling between the properties of kHz QPO and HBOs and the phase of the NBO makes the NBO a unique phenomenon.

The characteristic quantities of NBO display energy dependence on the oscillation photons [43] . The centroid frequency of NBO changes with energy of photons from a negative correlation to a positive one, and the turning points are located at 6 - 8 keV (see left panel of Figure 7). The rms amplitude increases significantly with the photon energy below 13 keV (see middle panel of Figure 7), which means that the strength of the NBO signal increases with the photon energy. However, the increase of rms amplitude with photon energy seems to stop

when the photon energy is higher than around 13 keV, the quality factors have no obvious relation with the photon energy (see the right panel of Figure 7).

The non-monotonic energy dependence of centroid frequency implies that the emission zone of NBO experiences a radial variation during the accretion process. The dependence of rms amplitude on photon energy may indicate that the NBO signals reach the strongest strength at 13 - 20 keV. Higher energy photons are often emitted from the inner region of an accretion disk. Consequently, the most likely region responsible for such physics can be referred to the transition zone between the inner boundary of accretion disk and the magnetosphere, in which the transition of the properties for accretion flow occurs [44] - [46] . NBO occurs at high accretion rates, i.e. near the Eddington rate. The high-mass flux deposits increasingly more matter in the transition zone, leading to expansion and radial scale change of this region. However, the pile of more deposits with greater viscosity can contribute to the radiation enhancement, as well as to the emission of photons with higher energies. As a result, the radial scale change of the transition zone is responsible for the observed non-monotonic energy dependence of the centroid frequency. In addition, because of the limited region of the transition zone, more deposits enhance the viscosity and thus suppress the further monotonically increasing strength of NBO, which explain the energy dependence of rms amplitude at high energy. We therefore suggest that NBO is a type of oscillation in the transition zone. This kind of oscillation may originate in transition layer due to the viscosity of clumps [47] . On the other hand, this oscillation may also carry the information of frequency oscillation modes in the accretion disk and manifest itself as modulation of the accretion rate during the course when disk matter penetrates the transition layer [48] - [50] .

4. Kilohertz QPOs

The kHz QPOs was discovered in February 1996, just two months after RXTE was launched, which have the timescales of the same order as the dynamical timescales in the inner region of accretion disk. Therefore, it may open a window that allows us to see down to the very bottoms of the potential wells of NSs in LMXBs, to investigate the motion of clumps of matter orbiting in strong field and of hot spots corotating on NS surfaces, and thereby to map out curved space-time near accreting compact objects, and directly to measure the compactness of NSs and study the dense matter.

4.1. Observations

The frequencies of kHz QPOs increase with source states in all cases. Statistically, a tight correlation between upper and lower QPOs was found, which was fitted, in general, by a power-law function [51] or a linear relation [52] . The frequencies increase with luminosity on timescales of a few hours in a given source, while the frequency separation between two peaks decreases as the luminosity increases, such as in Scorpius X-1 [53] . However, it was found a positive correlation between the frequency separation and luminosity in Circulus X-1 [54] . On longer timescales, and across sources, this frequency-luminosity correlation is lost, with the result that similar QPO frequencies are observed over two orders of magnitude in X-ray luminosity.

The amplitudes of kHz QPOs increase strongly with photon energy. In similar X-ray photometric bands the QPOs tend to be weaker in more luminous sources, with 2 - 60 keV amplitudes ranging from about 20% (rms) in atoll sources to typically 2% - 5% (rms) in Z sources. At high energy, amplitudes are much higher. Both in a given source and across sources, QPO amplitude is affected much less by the X-ray luminosity shifts between tracks that were caused by an extra source of X-rays unrelated to the QPOs.

The twin kHz QPOs display high coherence. Each peak has a corresponding quality factor, i.e. for upper signal and for lower one. In a quality factor versus frequency diagram, the upper and lower QPOs follow two different tracks [55] - [57] . For atoll sources, the quality factor of the lower kHz QPO increases with frequency up to a maximum (~200), and then drops abruptly (for details see [58] and reference therein). While for Z sources, the quality factors are low (about 2 - 10) and increase with the frequencies. At the same time, the upper quality factor for both Z and atoll sources increase steadily from ~5 to ~15 with frequency all the way to the detected highest frequencies. On the whole, the quality factors of lower kHz QPOs for atoll sources are about 10 times higher than that for Z sources in same frequency range, which implies a

Q₁-luminosity relation of between Z and atoll sources [59] . For three atoll sources (4U 1608-52, 4U

1636-53 and 4U 1728-34) with detected spin frequencies and sidebands, it was found that the source with higher maximum presented higher spin frequency, but with lower frequency difference between $\nu_1$ and the sideband frequency [58] .

The rms amplitudes of both the upper and lower kHz QPOs decrease steadily towards higher frequencies. The rough similarity was also extended to other sources, i.e., 4U 1608-52, 4U 1735-44, 4U 0614+09, 4U 1820-30, and 4U 1728-34 [60] - [63] . The rms amplitudes of twin peaks become equal when the frequencies of the twin QPOs pass through a certain ratio (), which is roughly the same for each of the sources. It is also predicted that in a more general context, the behavior of the amplitude difference suggests a possible energy interchange between the upper and lower QPO modes [63] .

Both the quality factors and rms amplitudes have relations with luminosity [61] . The maximum rms amplitudes of twin signals, respectively, decrease more or less exponentially with increasing luminosity, while the maximum coherence of the lower kHz QPO first increases and then decreases exponentially with luminosity, at a faster rate than both lower and upper rms amplitudes. The maximum coherence of the upper kHz QPO is more or less independent of luminosity. The maximum rms and quality factor show the opposite behaviour with hardness of the source, consistent with the fact that there is a general anti-correlation between luminosity and spectral hardness in these sources.

4.2. Theoretical Explanation

Around a NS, the orbital motion occur at a frequency of

(2)

where is the NS mass in units of. The kHz QPOs in NS/LMXBs are detected in the frequency

range of 200 - 1300 Hz [13] , which are, thus, the same order as the dynamical timescales of the innermost regions of the accretion disk around the stellar-mass compact objects [13] [64] . It was immediately realized that the observed high frequencies of kHz QPOs could arise in orbital motion of accreting matter very closely around the NS. The interpretations of kHz QPOs can generally be ascribed to two concerns [65] : 1) the interaction between magnetosphere and accretion flow at the innermost boundary of accretion disk; 2) relativistic effects, such as frame-dragging effects and different oscillation modes of plasma.

4.2.1. Interaction between the Innermost Accretion Flow and Magnetic Field of Neutron Star

Magnetospheric beat-frequency mechanism―The firstly detected kHz QPOs [21] [66] display constant separation between two peaks, leading to the idea of magnetospheric beat-frequency mechanism (MBFM), which explains the emission for 20 - 40 Hz HBO in GX 5-1 and for 5 - 50 Hz HBO in Cyg X-2 [67] . It was claimed that the magnetosphere is surrounded by a thick disk corona containing cooler and denser plasma, as a result of the release of gravitational potential energy due to the friction and viscosity in accretion disk. Disk surface is heated by acoustic flux, magnetic flaring and radiation from the NS, forming a radiation dominant region in the inner part of disk. Because of the thermal instability, plasma in the inner disk is expected to be spatially inhomogeneous, which causes the formation of clumps. The formed high-density clumps moves, at Keplerian velocity, on the innermost boundary of the accretion disk, forming the observed upper frequency . In the meantime, plasma drifts radially inward as they lose angular momentum and is stripped from the clumps. If the radiation from the disk is non-axisymmetric, the interaction of a given clump with the magnetosphere is greater at some azimuths than at the others. As a result, the rate at which plasma is stripped from the clump at the corresponding azimuths is greater than others. The pattern, for a given clump at the special directions, and the steepness of varying stripping rate affect the harmonic content of the X-ray intensity waveform produced by accretion of matter from the clump. Hence the X-rays waveform approximately repeats with magnetospheric beat frequency, which is ascribed to be the lower frequency of kHz QPOs. The MBFM was further modified and developed, to interpret the 15 - 60 Hz HBO in Z source [68] .

Sonic-point beat-frequency model―Considering the relation between falling velocity of accreting material and sound speed [69] proposed the sound-point model, which ascribes the frequency of upper kHz QPO as the Keplerian motion of accretion flow at a radius near the sonic point at the inner edge of accretion disk, whereas the lower frequency is the difference between the Keplerian frequency at a radius near the sonic point and the fundamental or first overtone of the NS spin frequency. The difference between twin frequencies is therefore close to (but not necessarily equal) the spin frequency of NS. The amplitudes of QPOs at the sonic-point Keplerian frequency and at the beat frequency depend on the strength of magnetic field and accretion rate, and hence one or both of these QPOs may sometimes be undetectable. The sound-point model is consistent with the magnetic field strengths, accretion rates, and scattering optical depths inferred from previous modeling of the X-ray spectra and rapid X-ray variability of Z and atoll sources. It explains naturally the frequencies of kHz QPOs, the similarity of these frequencies in sources with different accretion rates and magnetic fields, the high coherence and large amplitudes, and the steep increase of amplitude with photon energy. However, it was found that the frequency separation between twin signals does not exactly equal the spin frequency. Accordingly, this model was modified, by considering that although the stellar spin interacts with the orbital motion of accreting gas at the sonic radius with a frequency equaling the sonic-point beat frequency. The X-ray oscillations are produced by interaction between accretion flow and NS surface, and their frequencies are therefore affected by the flow from the sonic radius to the NS surface [70] . With more and more data released for kHz QPOs, the beat-fre- quency mechanism cannot match the observations.

Disk mode model―In disk models, one of twin peaks is ascribed to the Keplerian orbital frequency at some radius in the disk. The centrifugal-barrier (CB) model claimed that, during accretion process, some part of accreting matter with large angular momentum forms a Keplerian disk, while another part (participating in a sub-Keplerian rotation) undergoes practically a free-fall accretion until the CB becomes sufficient to halt the flow [71] . Thus, there are two distinct zones in the vicinity of NS, i.e. a disk and a barrier. The disk structure begins deflecting from a Keplerian one at a certain point to adjust itself to the boundary conditions at NS surface, resulting in a transition from Keplerian to sub-Keplerian flow [44] [46] [72] [73] through the setting up of a CB, where a centrifugal force slightly exceeds the gravitational force, within the adjustment radius. Consequently, some kinks and shocks form in the supersonic regime of accretion flow, which also are responsible for some super-Keplerian rotations. Therefore, matter may experience the relaxation oscillations in vertical and radial directions, which are expected to be in a resonance with local angular velocity in the disk. The variation in an emitting area caused by the oscillations around a transition point produces QPOs in X-ray flux. The upper frequency is ascribed to a resonant frequency when a resonance between different oscillation modes occurs, while the lower frequency is the Keplerian orbital frequency. In addition, it was claimed that the main QPO frequency, which is very close to the Keplerian frequency, is split into separate frequencies (hybrid and low branch) under the influence of gravitational forces in the rotational frame of reference. The observed lower and upper QPO frequencies are an intrinsic signature of Rossby gravity waves, i.e. large-scale fluid motion in the rotational frame of reference [74] .

Magnetohydrodynamics Alfven wave oscillation model―The magnetohydrodynamics (MHD) Alfv\’en wave oscillations occur at a preferred radius, where a MHD tube loop forms to conduct the accreted matter to the polar cap of NS. Nevertheless, this preferred radius is a transitional radius, where the spherical falling flow with low mass density is transferred to polar channel accretion with high mass density. The critical transition gives rise to MHD turbulence so that much more energy is released than at other positions. Accordingly, the MHD Alfven wave oscillation model [75] associates the twin kHz QPO frequencies with the Alfven wave oscillation frequencies (AWOFs) at a preferred radius, where the AWOF with the spherical accretion mass density coincides with the Keplerian orbital frequency, which is the upper frequency, and that with the polar accretion mass density corresponds to the lower frequency.

4.2.2. Relativistic Effects

In the vicinity of NS, frame dragging and compactness will lead to some relativistic effects, which have influence on behavior of accretion flow and lead to some variability. Based on this consideration, a class of models was proposed as alternative mechanisms for kHz QPOs, as well as high-frequency QPOs in black hole.

Relativity precession model―When a test particle moves around a rotating NS, the orbital plane of the particle will not coalign with the equatorial plane of NS, because of the relativistic frame-dragging effects, which leads to both Lense-Thirring precession [76] and relativistic periastron precession. The relativistic precession model [33] [77] identifies with an orbital frequency. In weak-field limit, the nodal precession frequency

is given by, which depends strongly on the equation of state of NSs [33] . In addition,

the rotation of NS leads to a stellar oblateness, and thus to a quadrupole term in the gravitational potential, which produces a classical precession of orbits tilted away from the NS equatorial plane, with precession fre-

quency. Therefore, the precession frequency contains a Lense-Thirring part and a classical part, i.e.. At the innermost boundary of accretion disk, the recession frequency is given by the frequencies of vertical oscillation and radial oscillation of the test particle, i.e. [78] , which is explained as the lower frequency.

In this model the NS spin frequencies do not cluster in the range of 240 - 360 Hz, and frequency separation is not expected to be equal as in beat-frequency interpretations. A clear prediction is that should decrease not only when increases (as observed) but also when it sufficiently decreases [77] [78] . In addition, a structure-dependent quantity I/M is present in the nodal precession frequency. As a result, by measuring a kHz QPO peak at frequency corresponding to stable Keplerian motion, we can set limits on NS mass M and radius R [69] . Considering Schwarzschild geometry, on one hand, the radius R of NS must be smaller than the ra-

dius of Keplerian orbit, i.e., which is a mass-dependent upper limit on R. On the other hand, the innermost circular orbit 6GM/c²) must locate inside, i.e., which gives an upper limit on M. According to these constraints, NSs, with masses of 1.8 - 2.0 M_⊙, with relatively stiff equations of state, and with spin frequencies in the range of 300 - 900 Hz, follow from this model.

Relativistic resonance model―The relativistic resonant model was firstly proposed to explain the discovered 450 Hz frequency of black hole candidate GRO J1655-40, with a 3:2 ratio to the previously known 300 Hz QPO in the same source [79] , which makes use of the fact that the orbital and epicyclic frequencies of accreting plasma have simple integer ratios at particular radii. The resonant oscillations in accretion disk were indicated when twin kHz QPOs have been detected in an accreting millisecond X-ray pulsar with 2.5 ms spin period [80] . Actually, non-linear acoustic coupling of different oscillation modes allows a parametric resonance between epicyclic motions [81] . Different modes in the disk are coupled through terms involving derivatives of enthalpy, for example, p-mode, resulting from the pressure gradient, and g-mode, i.e. the internal gravitational oscillation because of gravitational gradient and pressure gradient. Oscillations are resonantly excited by horizontal resonance in one-armed deformed disks [82] and by a vertical resonance in two-armed deformed disk [83] . Oscillations of pressure in one mode lead to harmonic variations of the eigenfrequency in another mode. In the limit of small pressure corrections, particular ratios of the epicyclic frequencies correspond to the condition for parametric resonance, leading to exponential growth for one of the modes [84] , and thus the particular ratio of high- frequency QPOs. If we take the properties of geometrically thin relativistic disks into account [82] , the trapped non-axisymmetric g-mode oscillations, which are excited by a corotation resonance, would be the cause of observed kHz QPOs [85] - [87] .

4.3. Formation of the upper Quality Factor

According to MHD Alfven wave oscillation model of kHz QPOs [75] , the upper kHz QPO frequency has been ascribed to Keplerian orbital frequency at the magnetosphere-disk boundary with radius r, while the lower frequency is MHD Alfven wave propagation frequency,

(3)

(4)

Here, the NS mass M is in units of solar mass, and 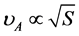is the AWOF where the area S represents the spherical area or the polar cap area, respectively. X = R/r is the ratio of the star radius R to disk radius r, , and m is the mass M in the units of solar masses. We ascribe the

profile of upper kHz QPO frequency to radial drift of preferred radius in the transition layer, as shown in the upper panel of Figure 8). Thus the range of the upper frequency () should be an indication of radial extent

in the transition layer. The FWHM w corresponds to the scale of transition layer, i.e., and the upper Q-factor is given by

(5)

We consider a transition layer (see the upper panel of Figure 8) between the innermost Keplerian orbit and the magnetosphere [88] - [90] , in which the transition of the radial velocity of accretion flow from Keplerian to corotation with the NS may occur [44] [45] . However, in this region some kinks and shocks form due to the inhomogeneous density which is responsible for super-Keplerian rotation [44] . After self-adjustment in this layer, the coupling between sub-Keplerian flow and super-Keplerian rotation leads to a Keplerian zone. When the accreted matter falls into the innermost Keplerian orbit and transition zone, the plasma strikes the magnetospheric boundary and bends the field lines, leading to a change of magnetospheric shape and the Alfven wave oscillation. In the meantime, the plasma is threaded by field lines and falls onto polar caps. However, on magnetospheric boundary, the accreted matter has a range of different velocities and different densities from the former arrivals, which produce some instabilities [91] [92] and inhomogeneities [93] . Consequently, the unstable disk-magne- tosphere boundary results in the penetration of disk matte into magnetosphere. In addition, the disk matter threaded by field lines onto polar caps may move to the equatorial region and swell the magnetosphere. On the basis of this idea and the geometry of the accretion-disk boundary layer [94] , the radial extent direction can be written as [88] - [90]

(6)

where the quantity represents the scale of the magnetosphere-disk boundary to stellar surface, and a constant ratio coefficient. Therefore, we can obtain

(7)

For the detected twin kHz QPOs, the mass density parameter η is found to be about 0.7, e.g. Scorpius X-1 [75] , except for the two unusual X-ray millisecond pulsar cases SAX J1804.5-3654 and XTE J1807-294, for which η = 0.45 and 0.4, respectively [95] . In most cases (except Circulus X-1), the position parameter X = R/r lies in the range from 0.7 to 0.92, or the kHz QPO emission position radius is from r = 1.1 R to r = 1.4 R [95] . On average, the upper Q-factor is

(8)

By fitting to the observations, we find that the radial extent of the preferred radius is about half of the thickness of the magnetosphere-disk boundary to the stellar surface [96] .

5. Rotation Effects and QPO Formation

NSs are rotating objects, and the rotation of NS has influence on the behavior of accretion flow in its vicinity. On the one hand, the rotational gravitational mass, in analogy with electromagnetism described by Maxwell’s equations, gives rise to Gravitoelectro-magnetism (GEM) [97] - [99] . The GEM of rotating NS contributes to a

gravitational Larmor frequency (is the angular velocity of NS) of the orbiting

plasma, leading to orbital split in vertical direction of disk. On the other hand, the rotation of NS will break the spherical symmetry and produce axisymmetric spacetime. As a result, the plasma obtain a local angular velocity

that makes the orbits of particles deform the original circular orbits. In general, the

motion of accretion flow follows helical trajectories, i.e. open circular orbits at each radius, and spiral in towards the NS. If and only if the gravitational Larmor frequency and angular velocity of accreted plasma satisfy [100]

(9)

where n and l are integers with n, l ≥ 1, the vertical split along disk and deformation in the direction of rotation of NS can be harmonious [101] . Consequently, the orbital motion of accreted matter is holonomy invariant, and the physical orbits for accreted particles will be closed. The radii of closure circular orbits are given by

(10)

Moving on these closure circular orbits, the accreted material is in a stable state, with first derivative of angular momentum larger than or equal zero, which correspond to a minimum of an effective potential. With a slight perturbation, the test particle will oscillate around the minimum, manifesting as drift of the orbital frequency. If the perturbation is strong enough to transfer sufficient angular momentum outwardly and drive the particles to leave the stable state, the plasma will continue to follow the original helical track and spirals in. In a turbulent and viscous accretion disk, the dissipative processes, i.e., viscosity, collisions of elements, shocks, and so on, are responsible for the perturbation.

From astrophysical accretion point of view, the sudden change of physical environment may give rise to particular phenomenon. In the quasi-quantized structure of inner accretion disk, the motion of accretion flows changes from helical infall to closure circular orbital motion at some preferred radii, which accordingly contribute to special emission. On a closure orbit at radius r, the plasma moves at Keplerian velocity, radiating X-ray

photons with an observed flux modulated at the Keplerian frequency. However, a slight perturbation due to dissipative processes in the turbulent disk will lead to an oscillation around r. As a result, the original Keplerian frequency at r goes with some drift, instead of the exact Keplerian frequency.

Such phenomenon can manifest as some width of frequency in the Fourier PDS, which is referred to as signals of QPOs [2] [13] .

6. Final Remarks

We review the properties and theoretical explanations of QPOs in NS/LMXBs. The fastest X-ray variability, with timescales on the same order as the dynamical timescale of region under strong field and general relativity in accreting low-magnetic-field NSs, comes closer towards the strong-field physics. Consequently, these components, especially the kHz variability, can be the diagnostics of accretion flow in strong magnetic field and general relativity of rotating NSs.

Theoretical framework for the fastest variability has been emerging, which falls into two concerns: 1) the interaction between magnetosphere and accretion flow at the innermost boundary of accretion disk and 2) relativistic effects near the NS. Most interpretations identified the mechanism of upper kHz QPO as the orbital frequency at a preferred radius in the innermost region of disk. With more and more released data, the beat-fre- quency mechanism has been excluded due to a predicted constant frequency separation that conflicts with observations. The disk mode that involves different oscillation modes should have, in nature, similar origin to the relativistic models. The relativistic precession model [33] [77] seems fascinating, but remains questionable. The modulation of X-ray flux at the predicted frequencies, the reasons for variation of with luminosity, and the correlation with burst oscillations are still open questions. The relativistic resonance model [102] based on a purely mathematical scheme, offers exact description of the intrinsic oscillatory properties of QPOs, without developments of detailed physical interpretations. Considering the relatively weak gravity of NSs but strong magnetic field and fast rotation, we investigate the rotational effects of NSs in the framework of general relativity, which produce some closure circular orbits in the inner region of accretion disk [100] . We expect that the radial oscillation of plasma, with different fixed frequencies on closure orbits, e.g. epicyclical frequencies, may result in resonance or certain frequency correlations.

The photons from different regions of accretion disk carry different energies and present distinct physical properties. Therefore, the QPOs detected in different energy band may have varying characteristics, which can be an entry to investigate the nature of QPOs. It was found that about 6 Hz NBO in Scorpius X-1 displayed some photon energy dependence [43] . However, to study the energy dependence of twin kHz QPOs, we require high quality data with both good time resolution and enough spectral information in future observations.

Acknowledgements

This work is supported by the Fundamental Research Funds for the Central Universities (Grant No. 161gpy49) at Sun Yat-sen University.

Cite this paper

Jing Wang, (2016) A Brief Review for Quasi-Periodic Oscillations in Neutron-Star Low-Mass X-Ray Binaries. International Journal of Astronomy and Astrophysics,06,82-98. doi: 10.4236/ijaa.2016.61006

References